This post is an analysis of a June 2013 paper by Mehmet Koca, Nazife Koca, and Ramazan Koc. That paper contains various well-known Coxeter plane projections of hyper-dimensional polytopes as well as a new direct point distribution of the quasicrystallographic weight lattice for E6 (their Figure 3), as well as the quasicrystal lattices of B6 and F4.

Wha‍t is interesting about this projection is that it precisely matches the point distribution (to within a small number of vertices) from a rectified E8 projection using a set of basis vectors I discovered in December of 2009, published in Wikipedia (WP) in February of 2010 here.

Rectification of E8 is a process of replacing the 240 vertices of E8 with points that represent the midpoint of each of the 6720 edges. In this projection, there are overlaps which are indicated by different colors in the color-coded WP image linked above.

The image below is an overlay of the above images highlighting the 12*(9+3+26+7)=540 points that are not overlapping:

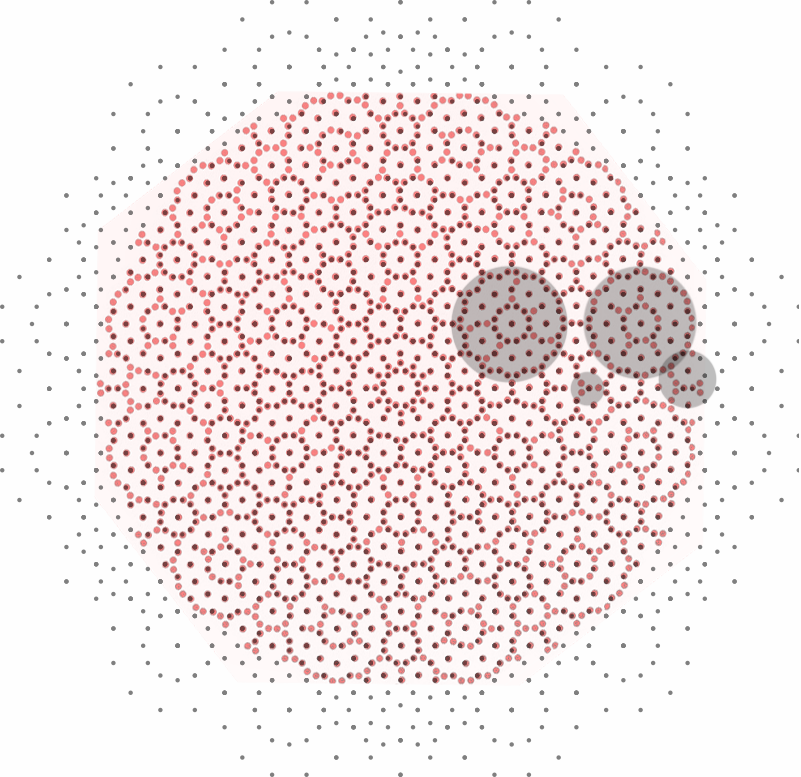
It is interesting to note that with a 30° rotation of my projection, the missing overlaps are reduced to 12*(15+2)=204.

Given the paper’s explanation for the methods using E6 (720) with 6480 edges as a projection through a 4D 3-sphere window defined by q1 and q6, it may be insightful to study my projection basis for E8’s triality relationships with the Koca/Koc paper’s defined 4D 3-sphere.

For more information on why my projection basis is called the E8 Triality projection, see this post.