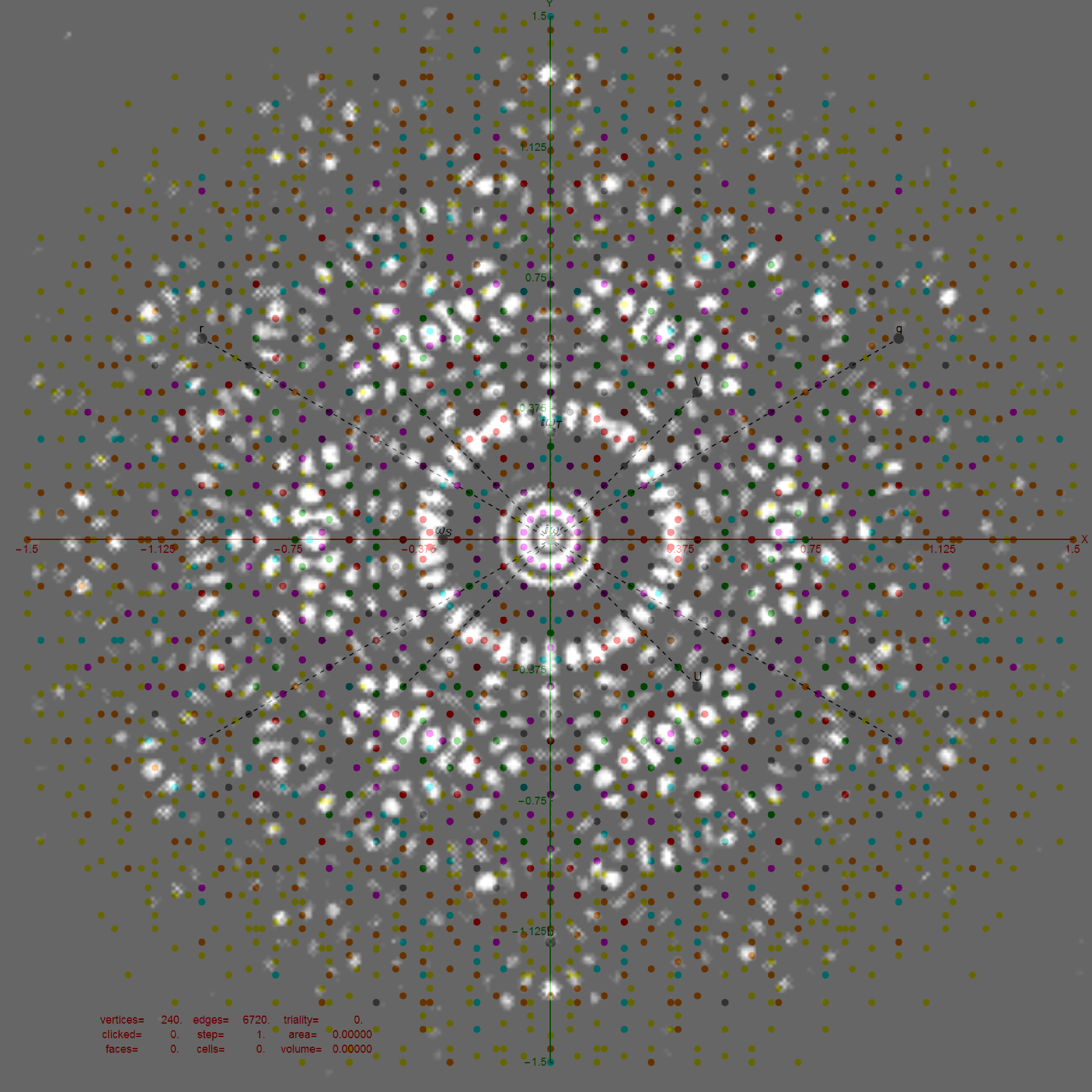
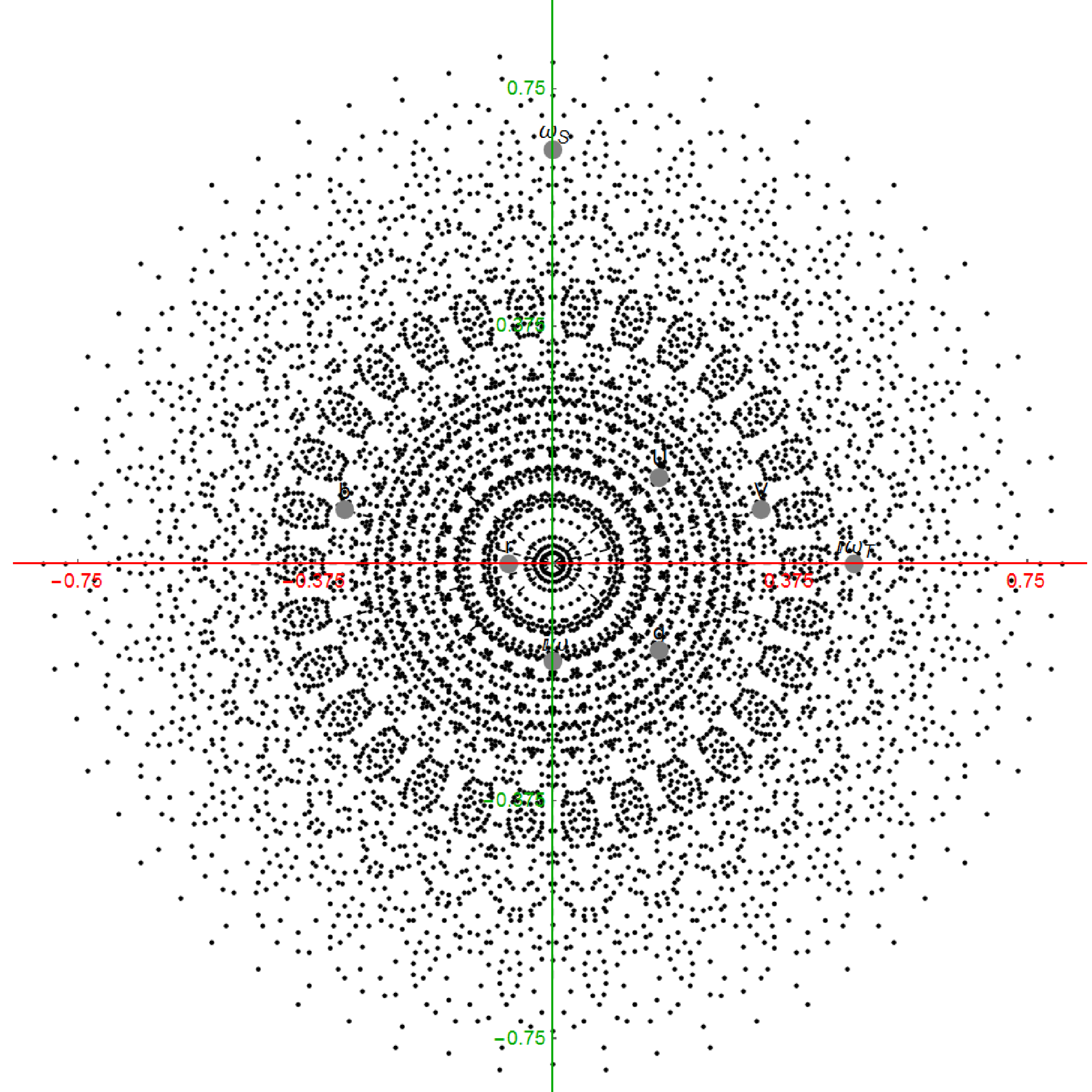
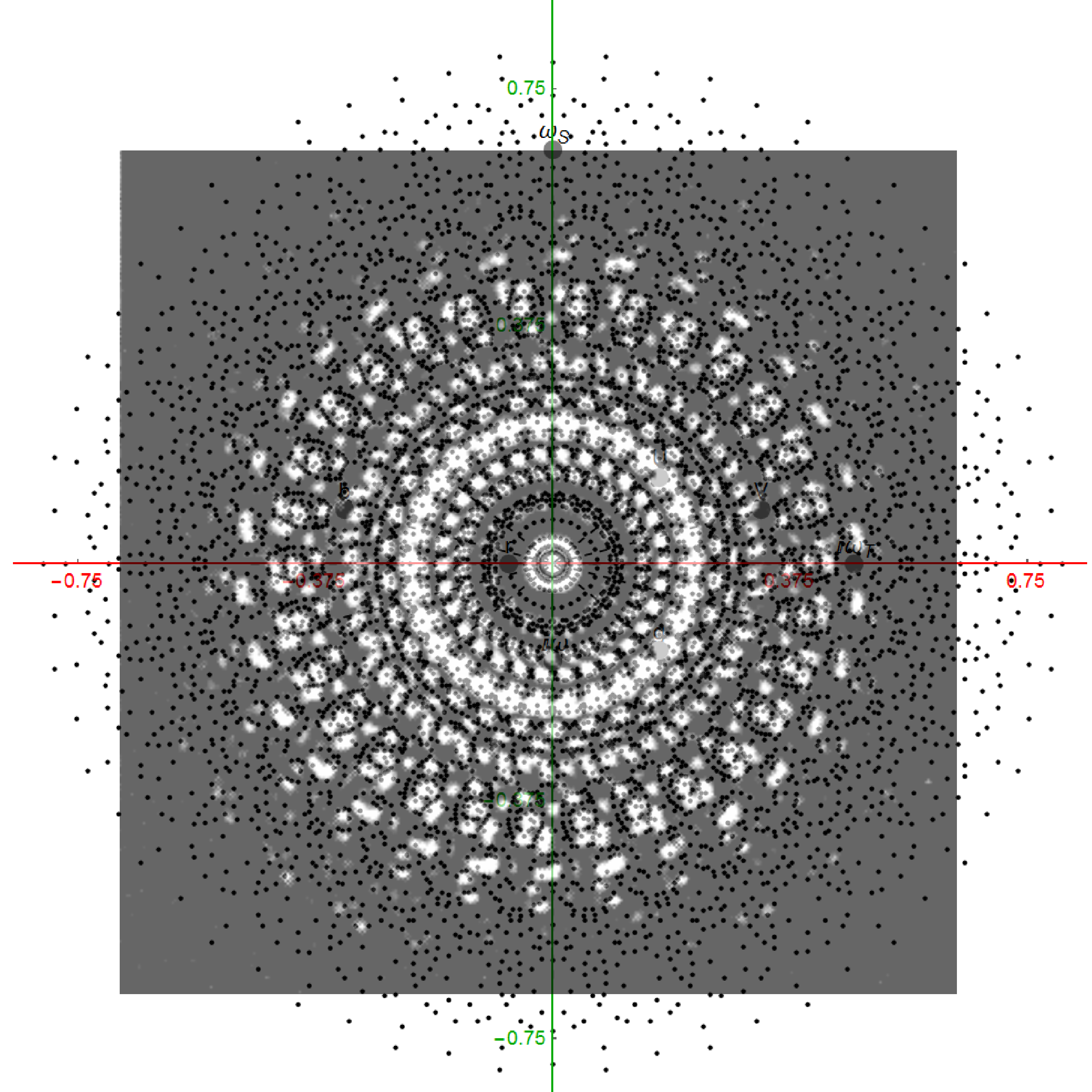
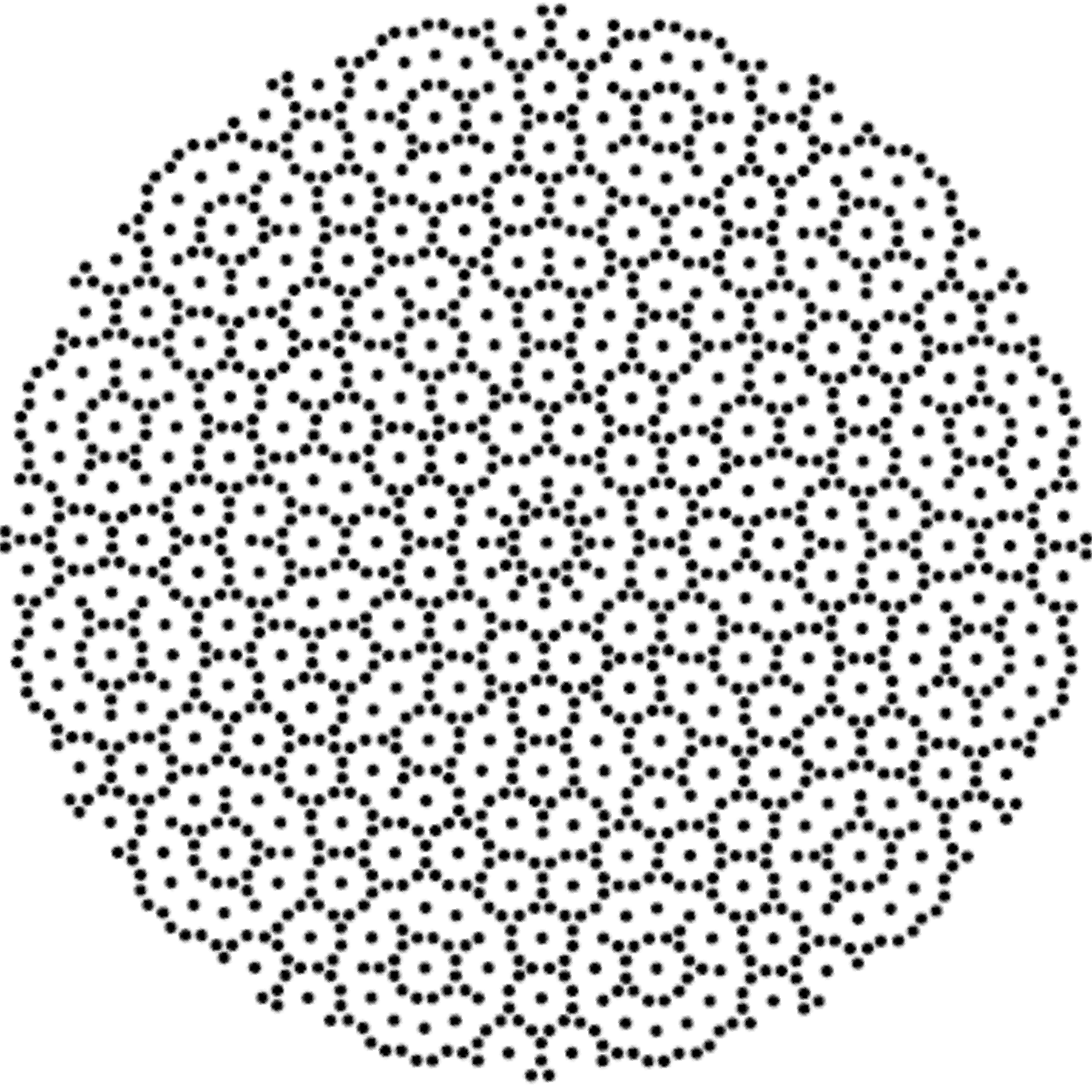
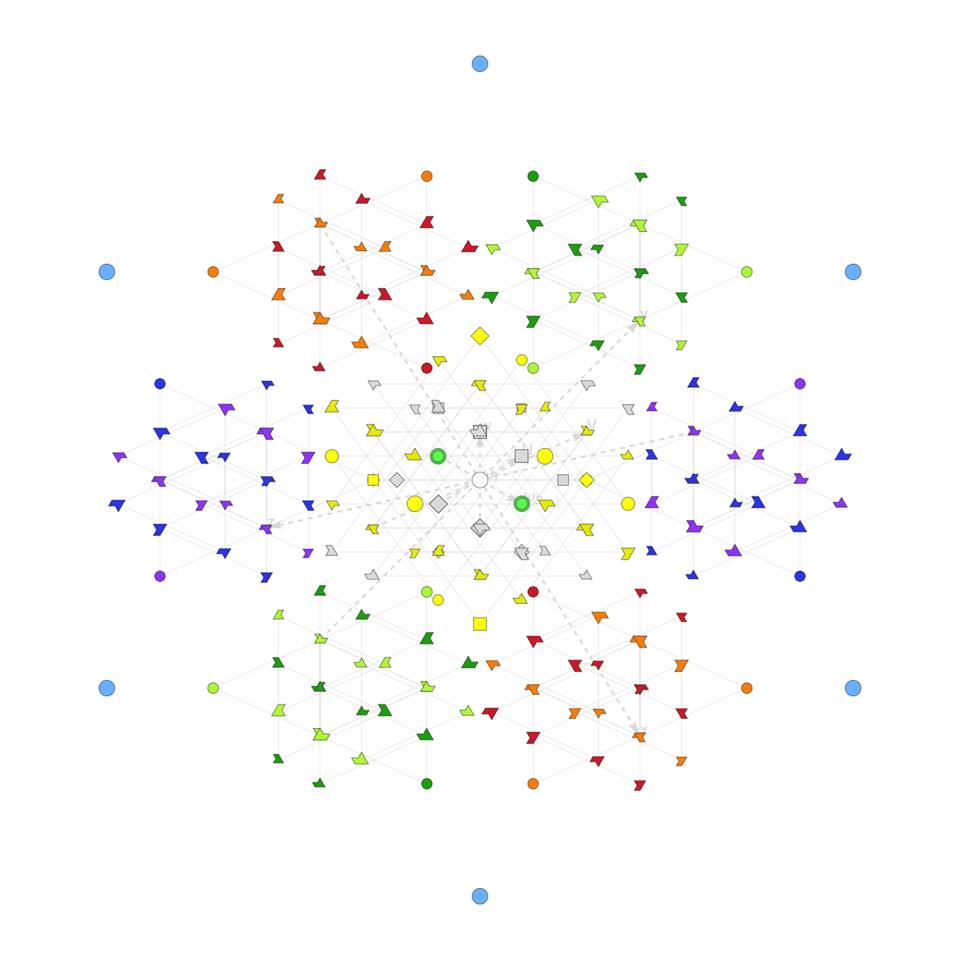
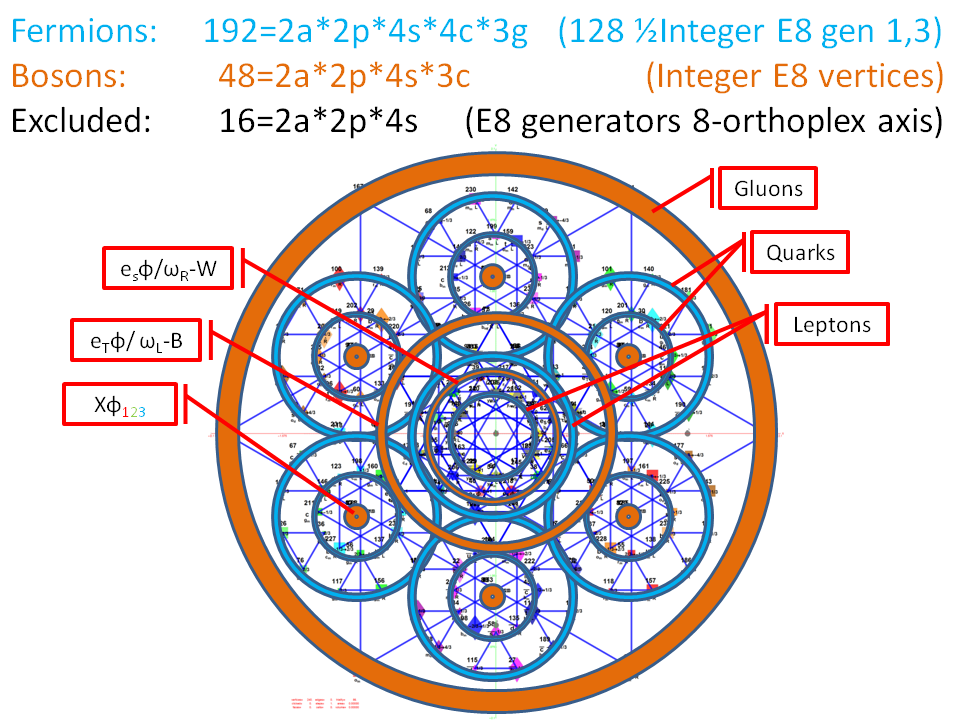
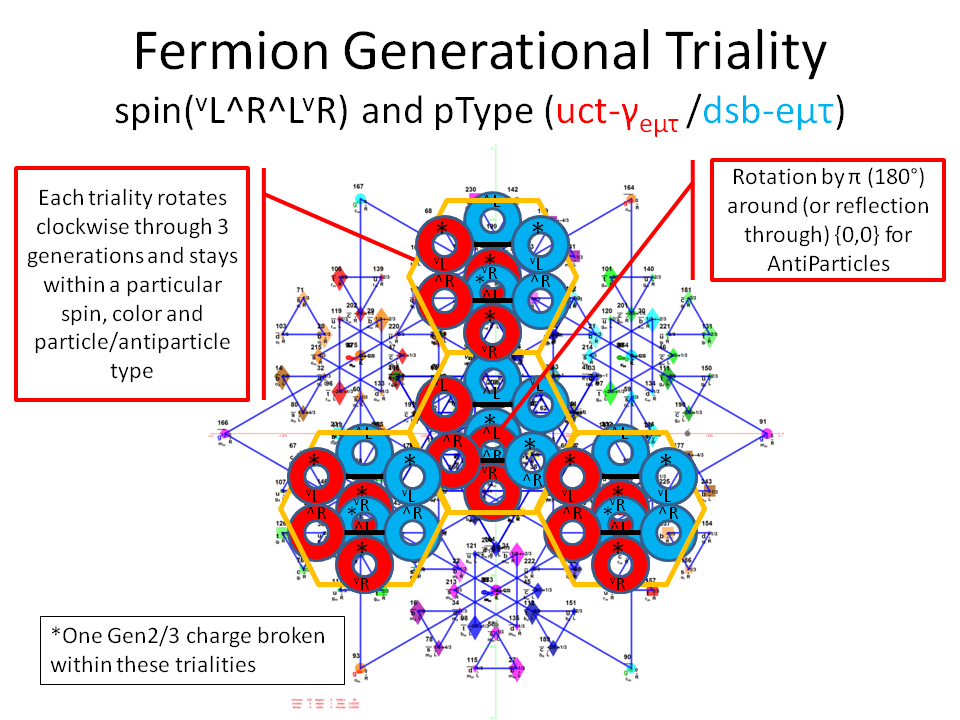
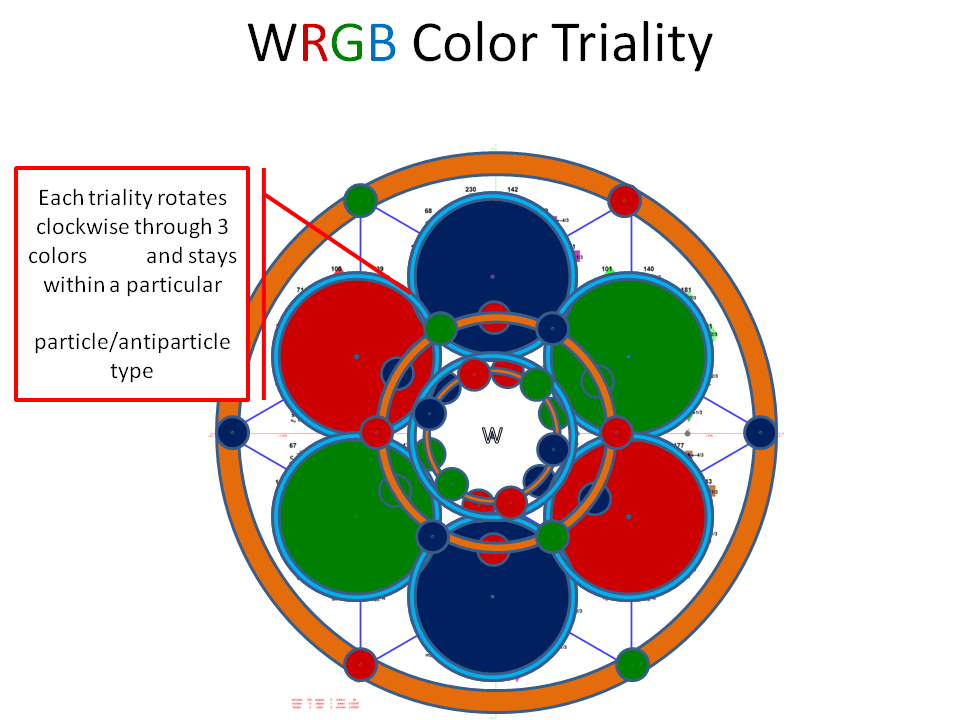
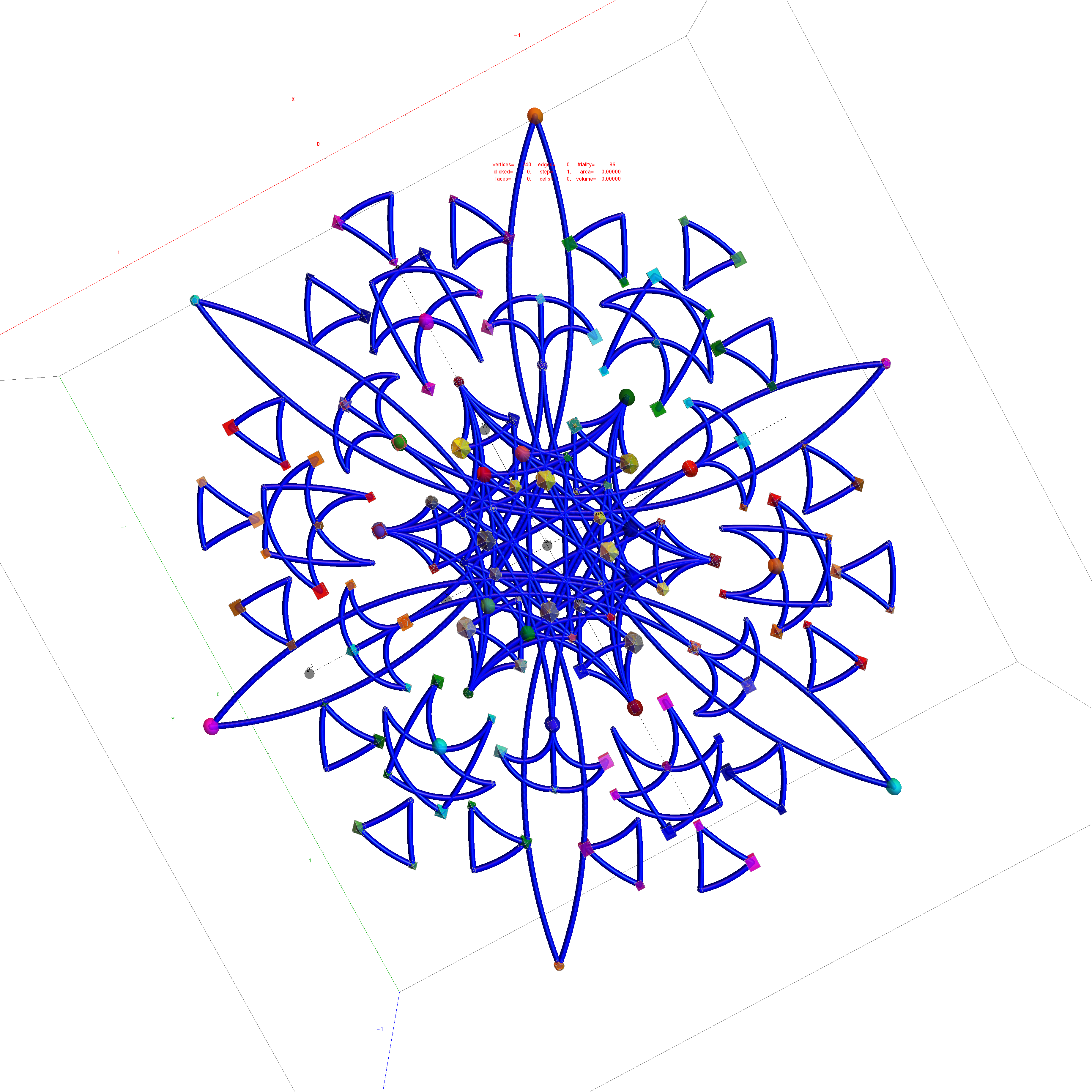
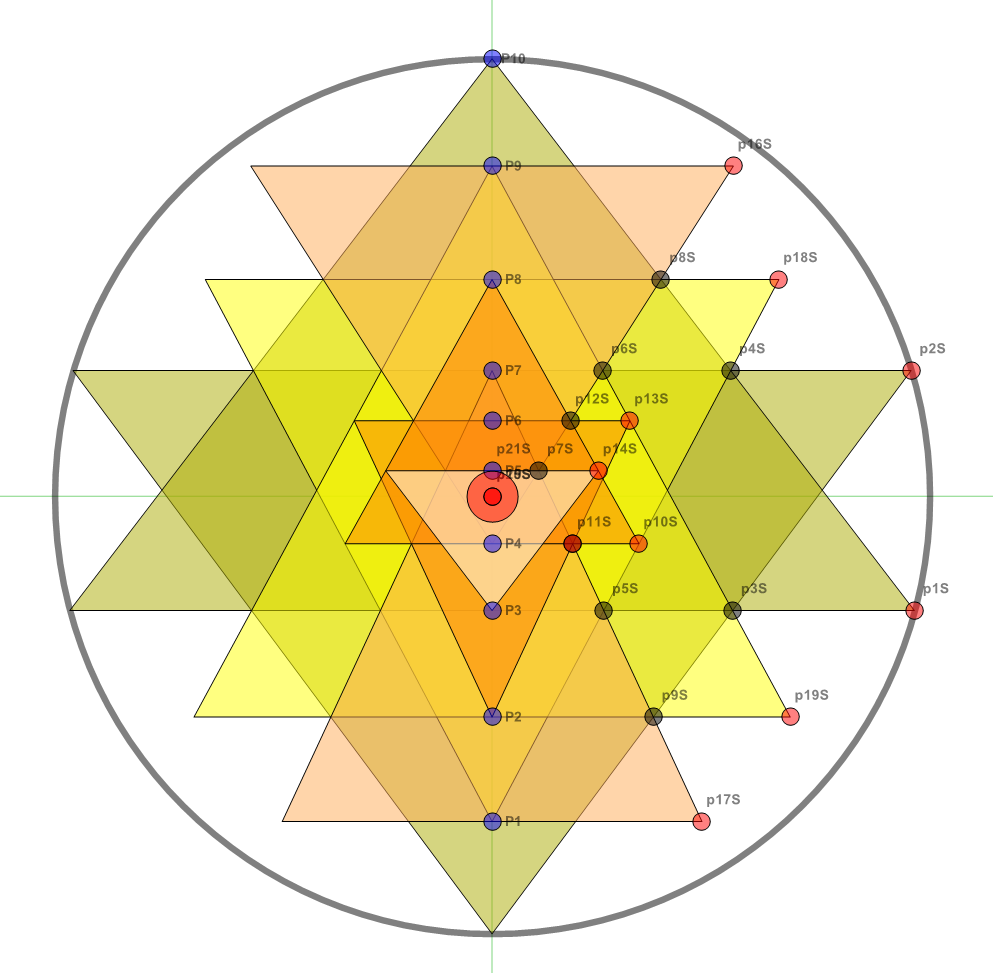
I have been intrigued with Richter’s arXiv 0704.3091 “Triacontagonal Coordinates for the E8 root system” paper.
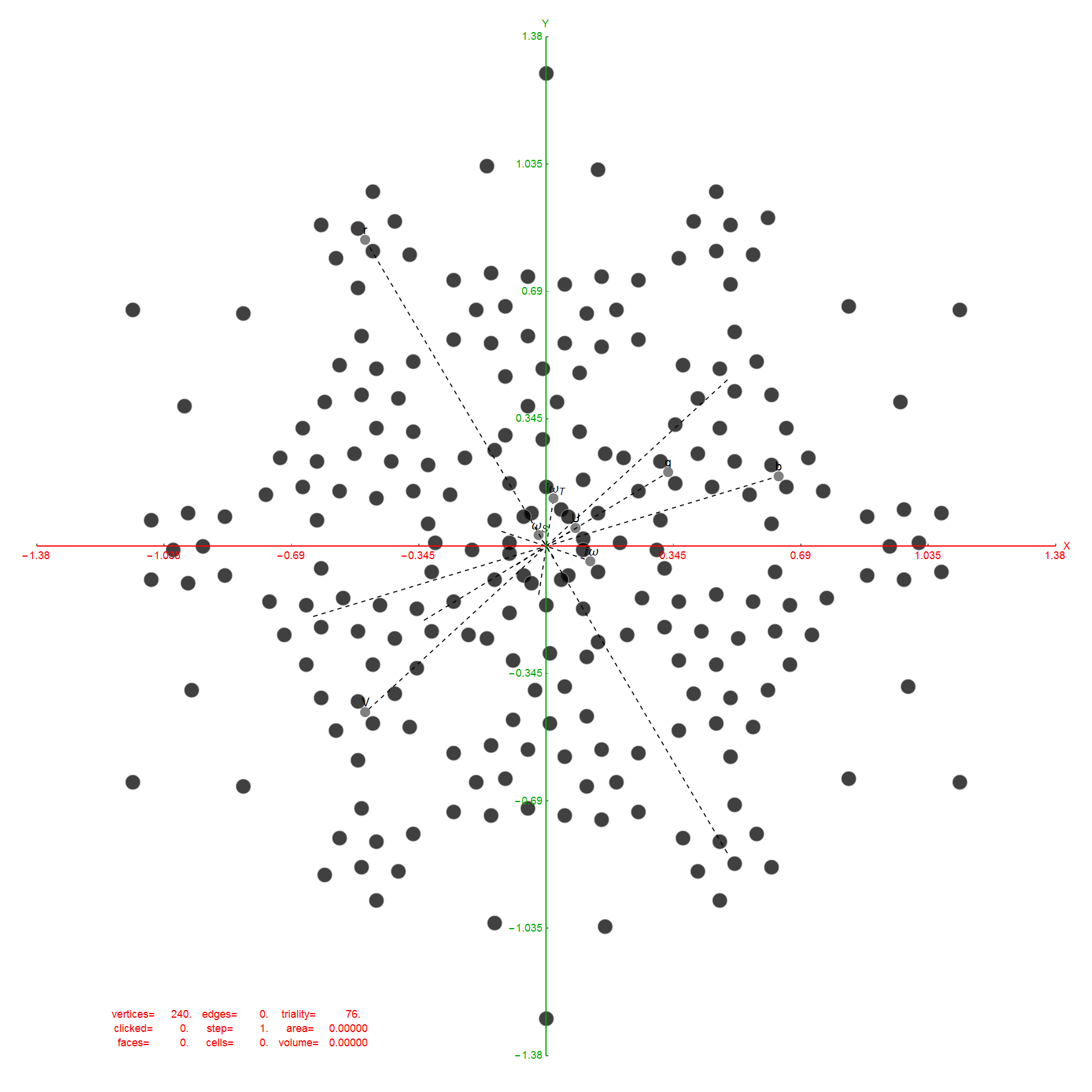
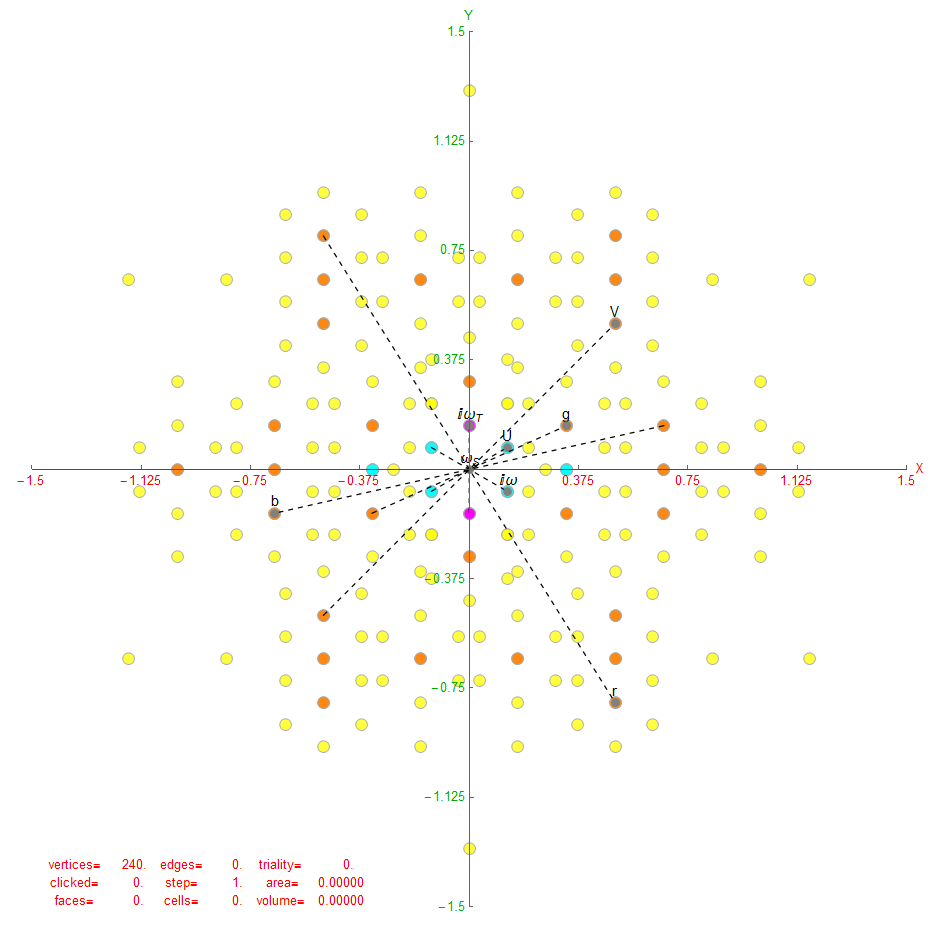
Comparing nearest edges between Split Real Even (SRE) E8 and Richter’s Complex 4D Golden Ratio Petrie Projection Model:
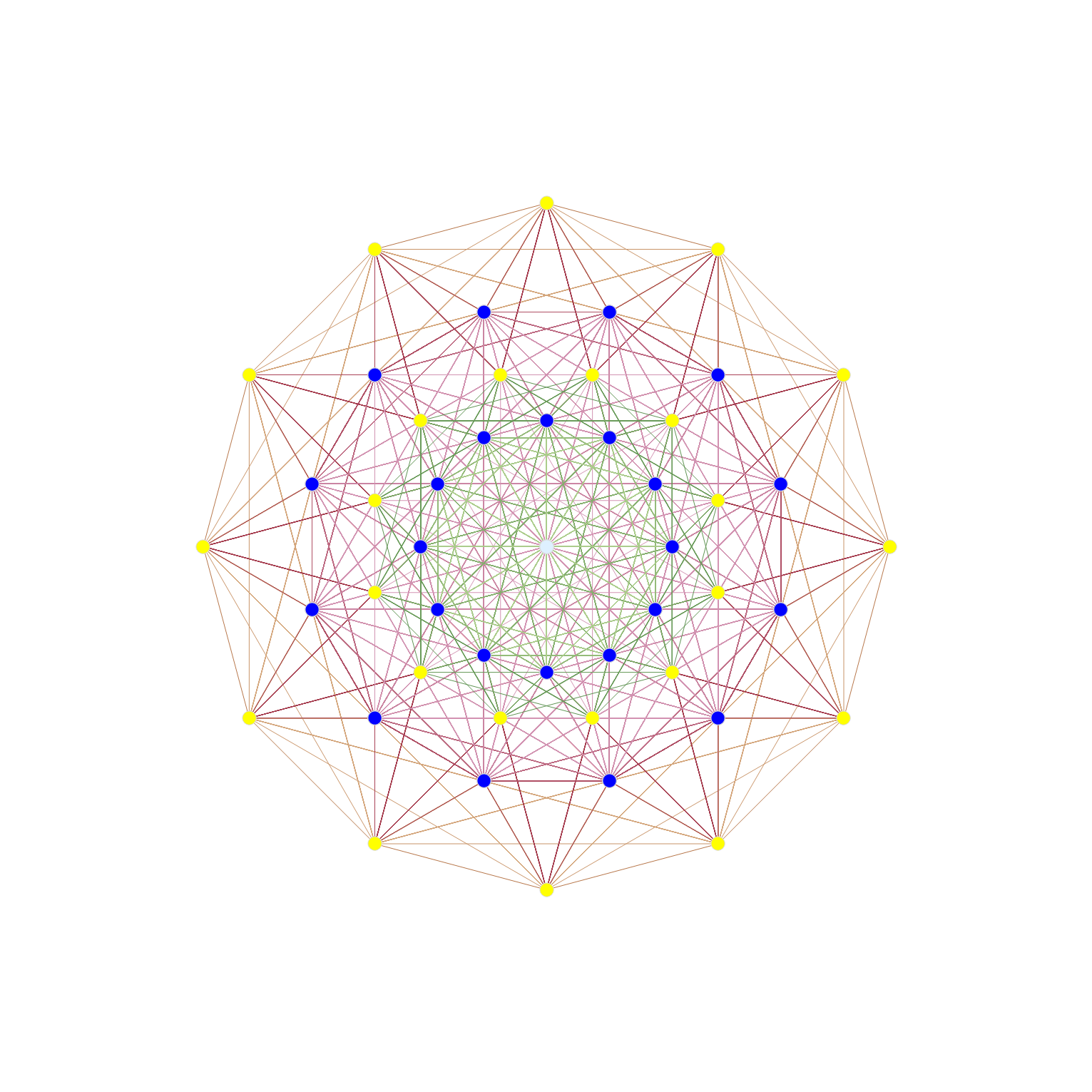
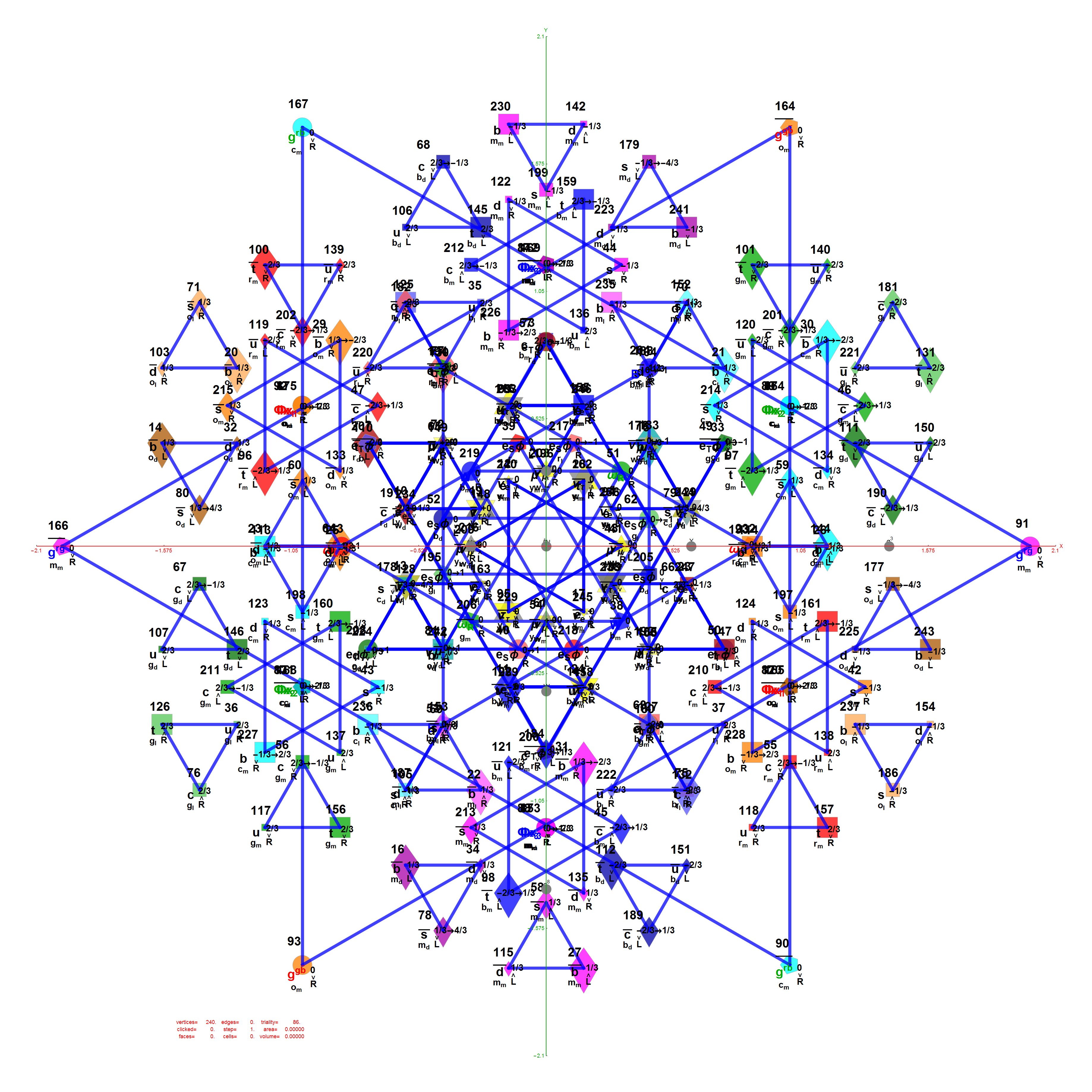
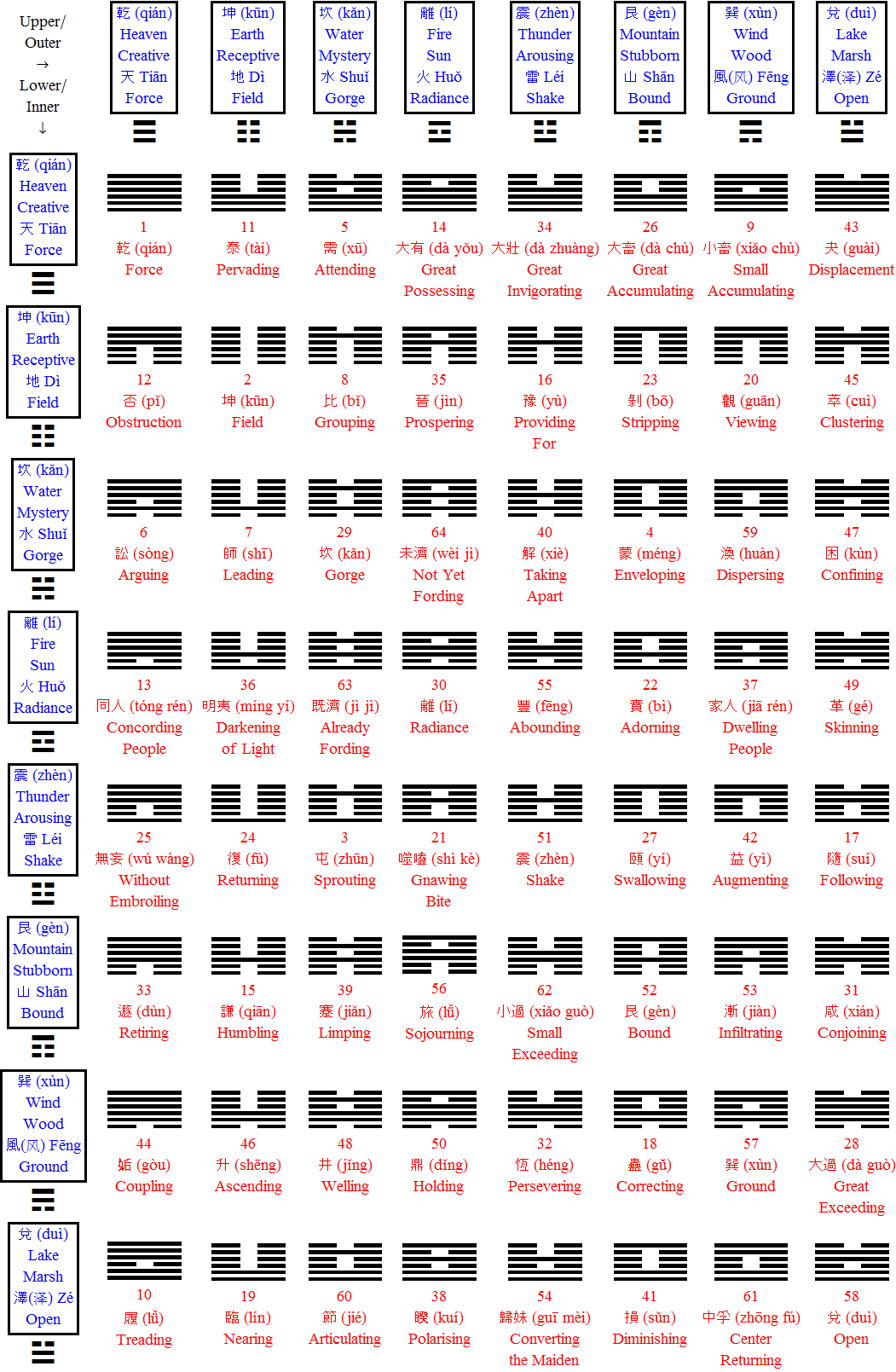
Please note, the vertex numbers are reordered from Richter’s paper in order to be consistent with ArXiv quant-ph 1502.04350 “Parity Proofs of Kochen-Specker theorem based on the Lie Algebra E8” by Aravind and Waegell. This paper uses the beautiful symmetries of E8 as a basis for proof sets related to the Bell inequalities of quantum mechanics. Below is a graphic showing that vertex number ordering:

Richter’s model with 74 nearest edges per vertex (Complex 4D Norm’d length Sqrt[2], with 8880 total):

Richter’s model with only 26 nearest edges per vertex (Complex 4D Norm’d length 1, 3120 total):
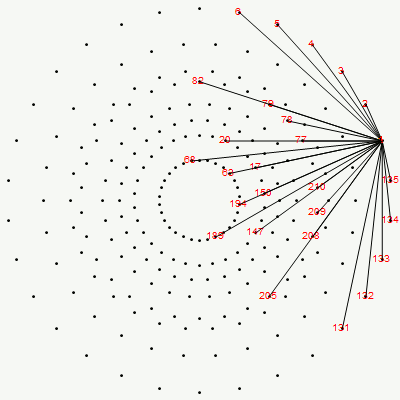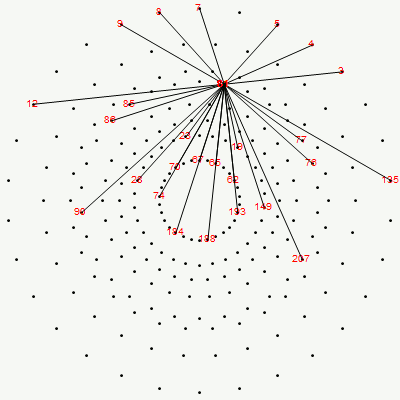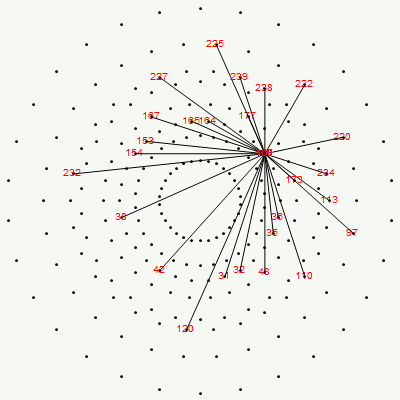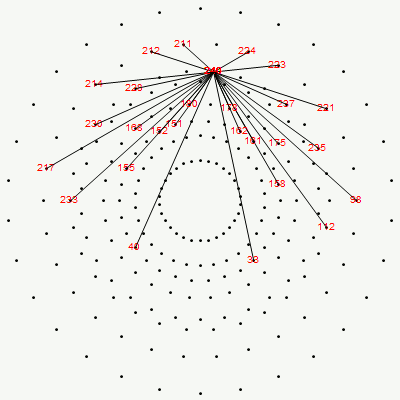
The above unity length edge pattern has is more consistent with the SRE E8 below.
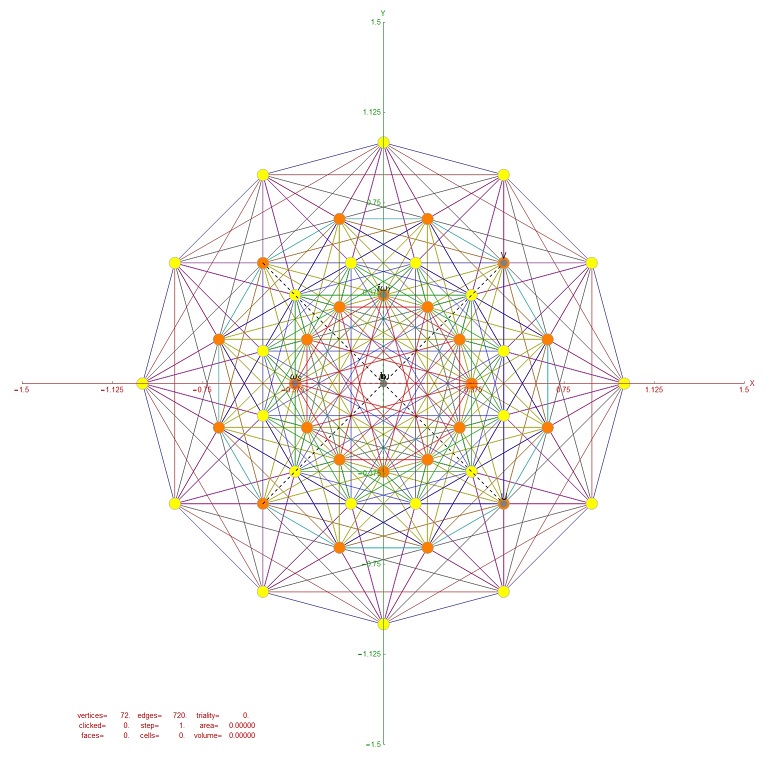
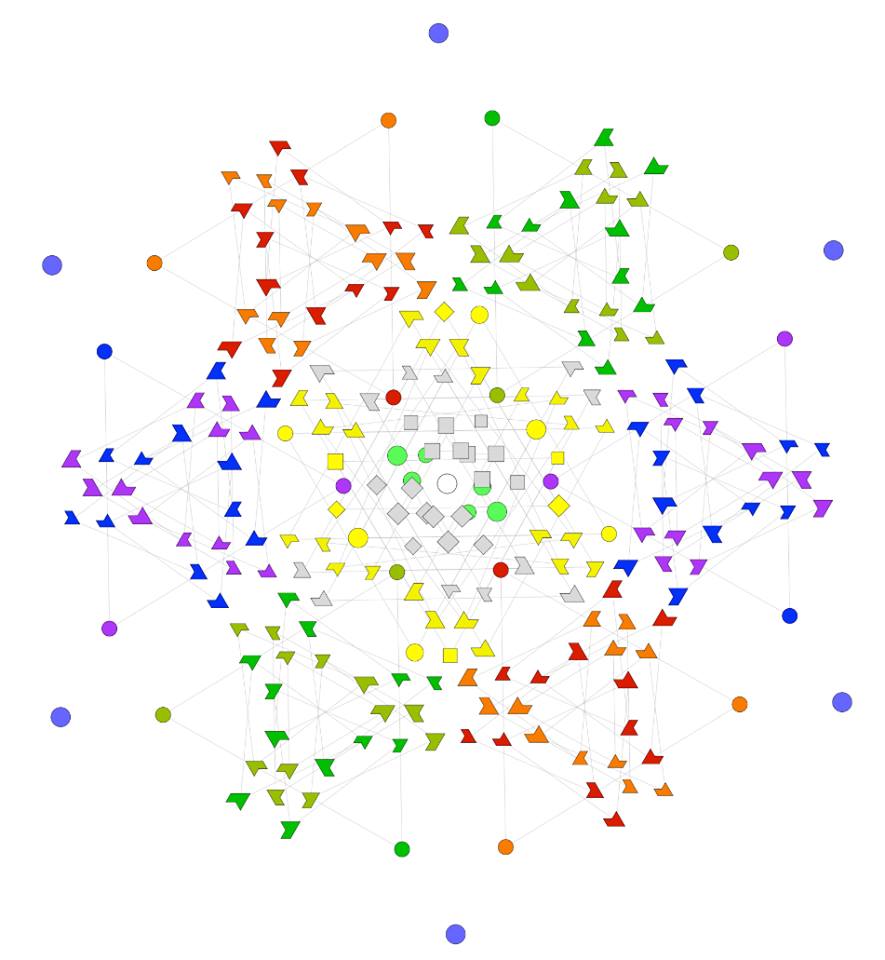
The SRE E8 Petrie Projection (with 56 Norm’d edge length Sqrt[2] for each vertex, 6720 total). This is equivalent to folding E8 to H4 with an 8×8 rotation matrix which creates a 4D-left H4+H4*Phi and a 4D-right H4+H4*Phi.
Please note, the vertex number is that of the E8 vertices rotated (or “folded”) to H4 in 2D Petrie projection. The vertex numbers are in canonical binary order from E8’s 1:1 correspondence with the 9th row of the Pascal Triangle (eliminating the 16 generator/anti-generator vertices of E8 found in the 2nd and 8th column of the Pascal Triangle). The graphic below shows the vertex number ordering:

Here we take the 4D-left half and project to two concentric rings of H4 and H4 Phi (Golden Ratio) with 56 nearest edges per vertex (Norm’d length of unity or Phi for each vertex):

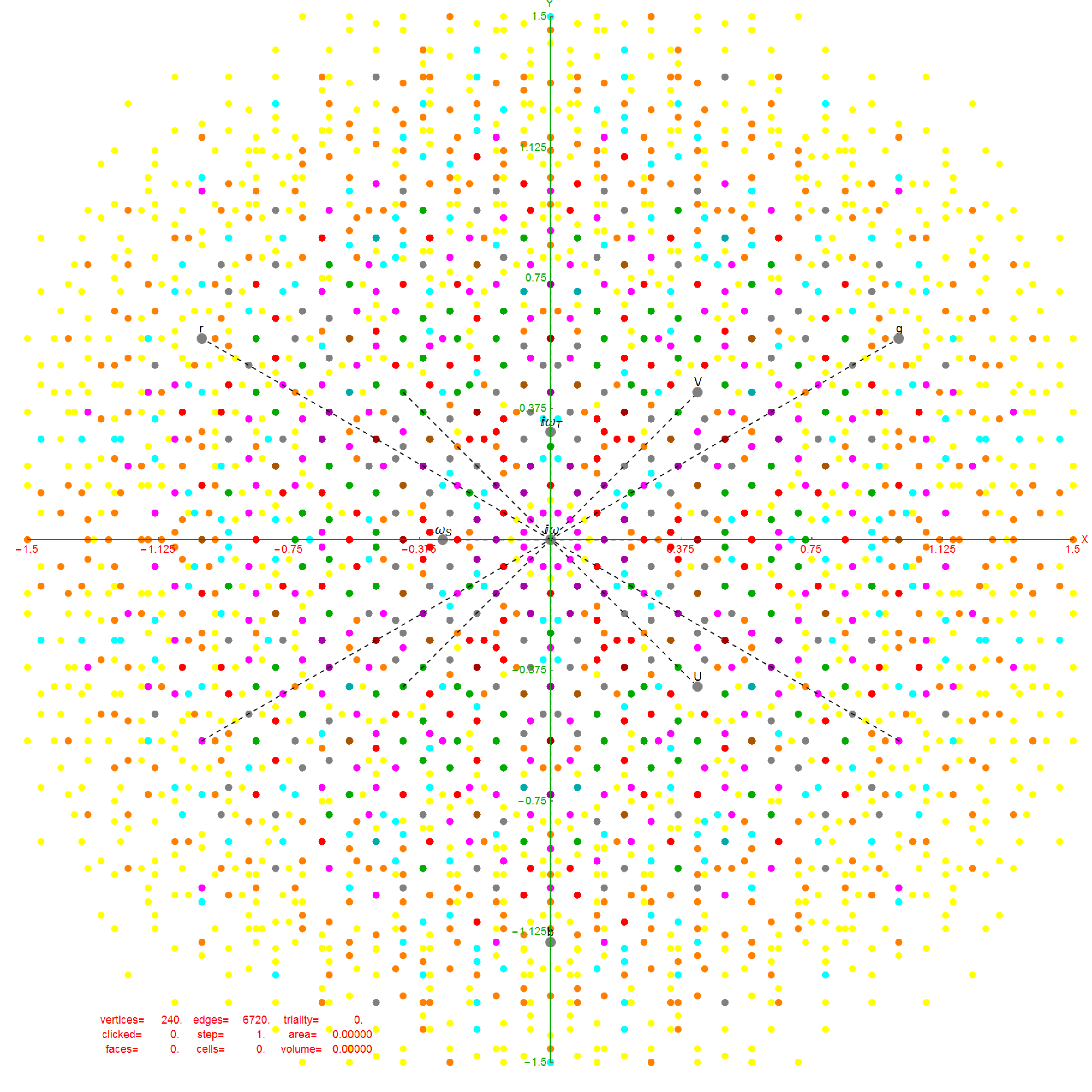
The animation frames are sorted by the ArcTan[y/x] of the vertex position in each ring (sorted H4*Phi outer to inner, then H4 outer to inner).
BTW – if you find this information useful, or provide any portion of it to others, PLEASE make sure you cite this post. If you feel a blog post citation would not be an acceptable form for academic research papers, I would be glad to clean it up and put it into LaTex format in order to provide it to arXiv (with your academic sponsorship) or Vixra. Just send me a note at: jgmoxness@theoryofeverthing.org.