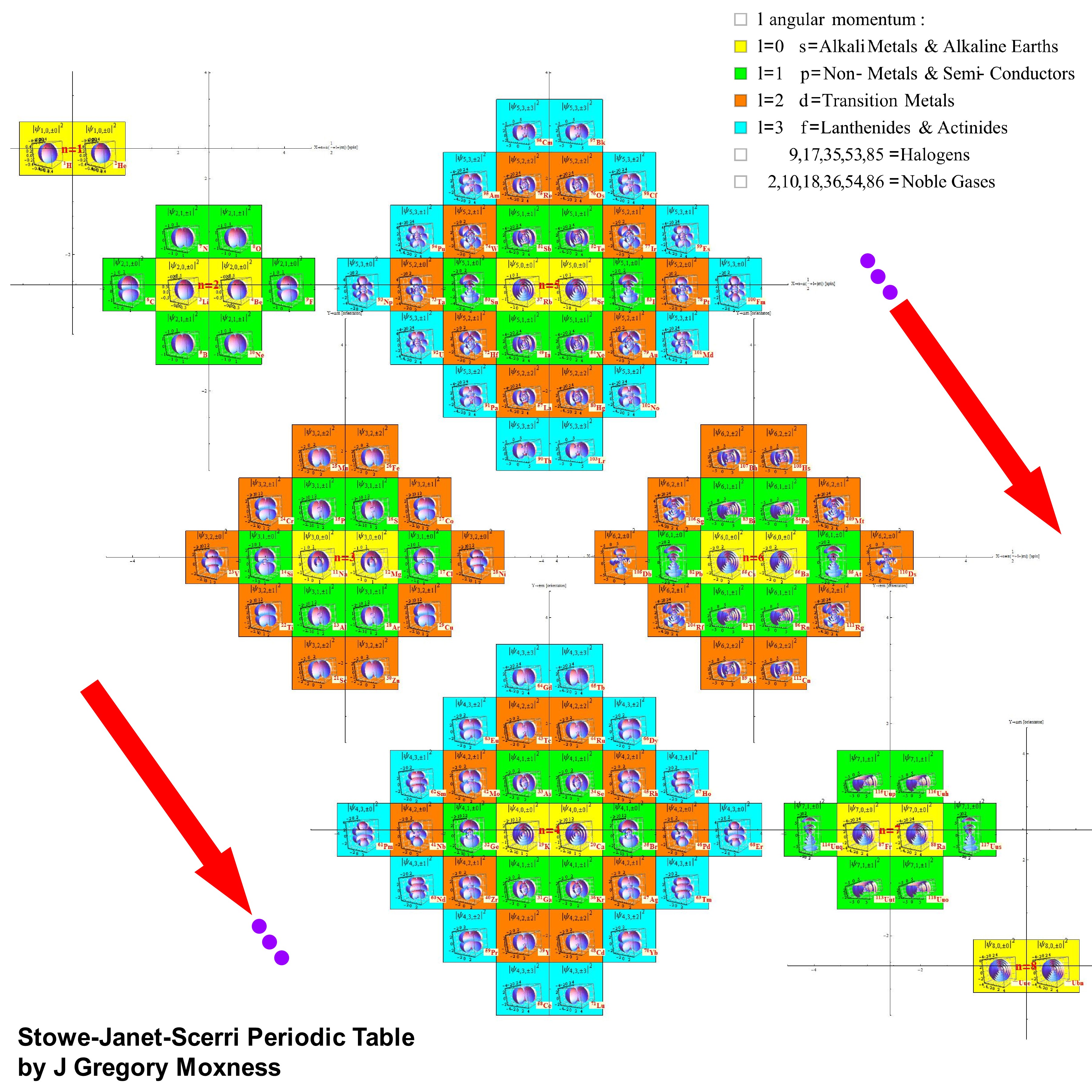
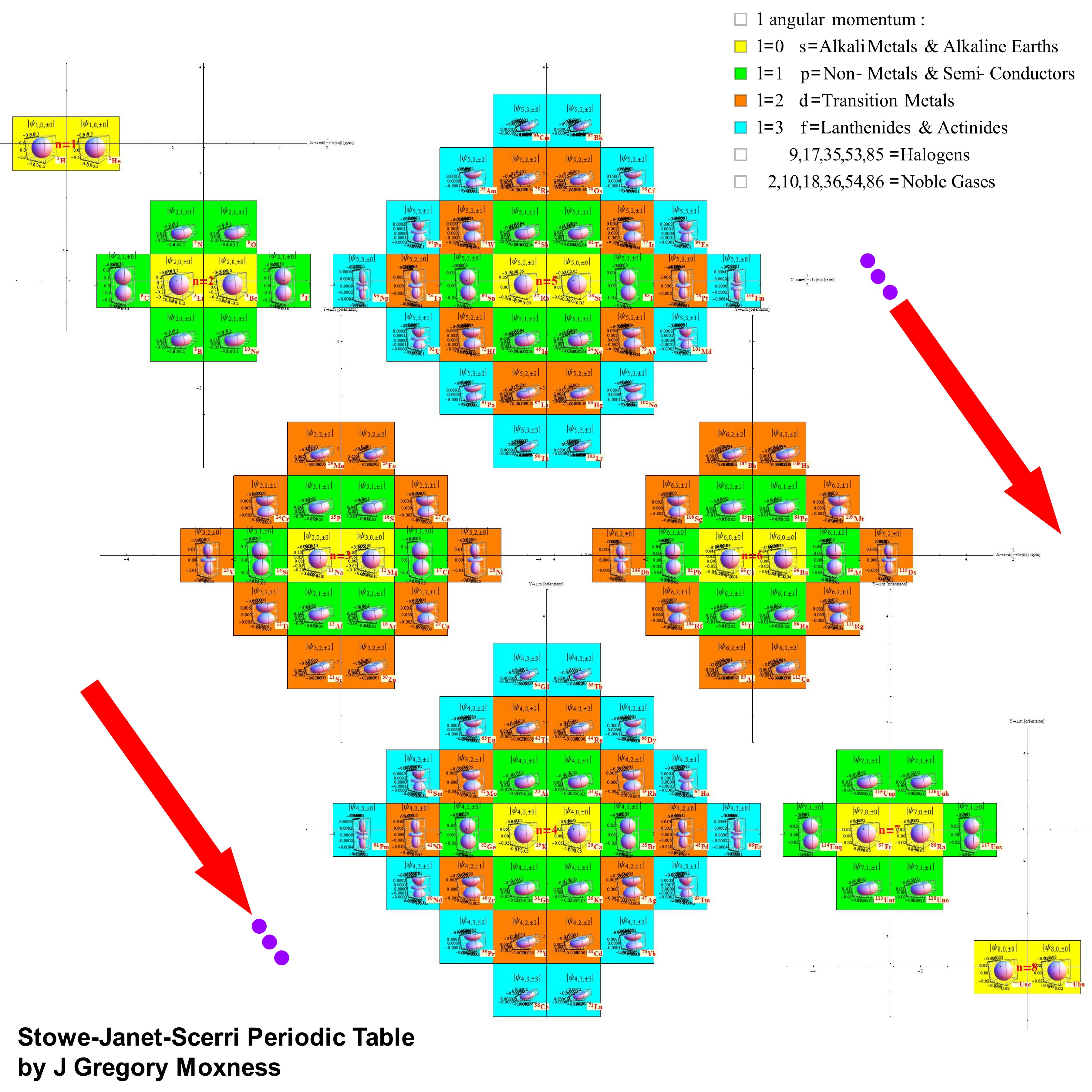
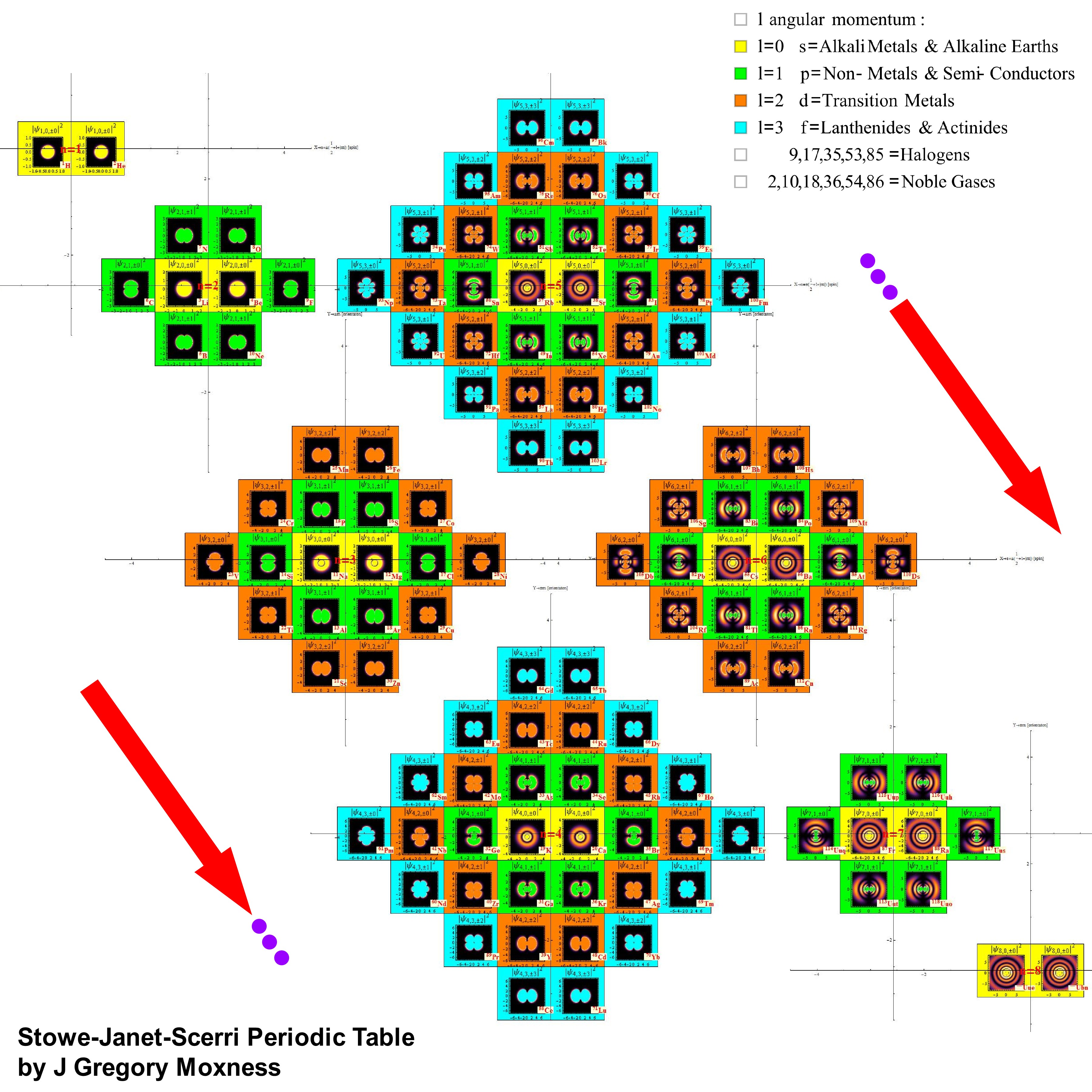
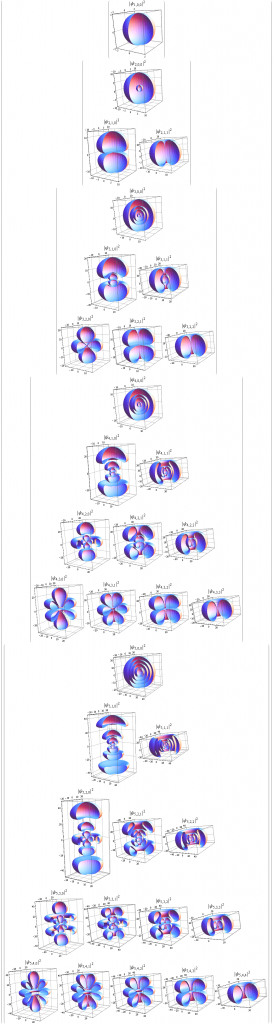
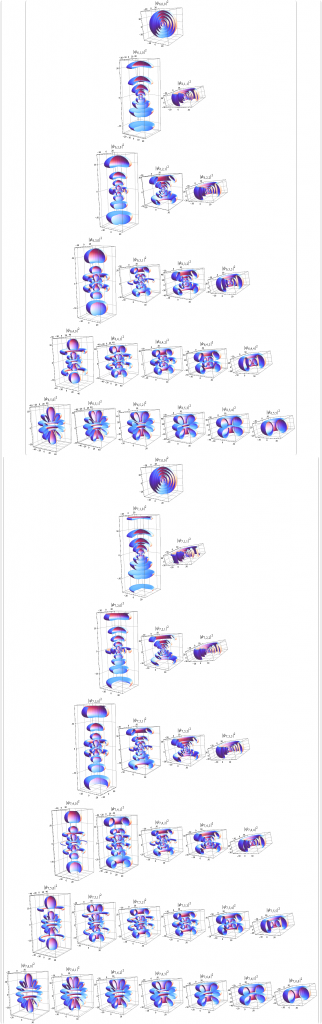
This has color coded 3D cut-away views of the spherical Schroedinger electron probability densities (making it 4D with 3D objects). The color is based on the l (angular momentum) quantum number. The X-Y-Z position is based n,m,s(pin) quantum numbers.
Tag Archives: Chemistry
Connecting the Octonion Fano Plane to the Atomic Elements
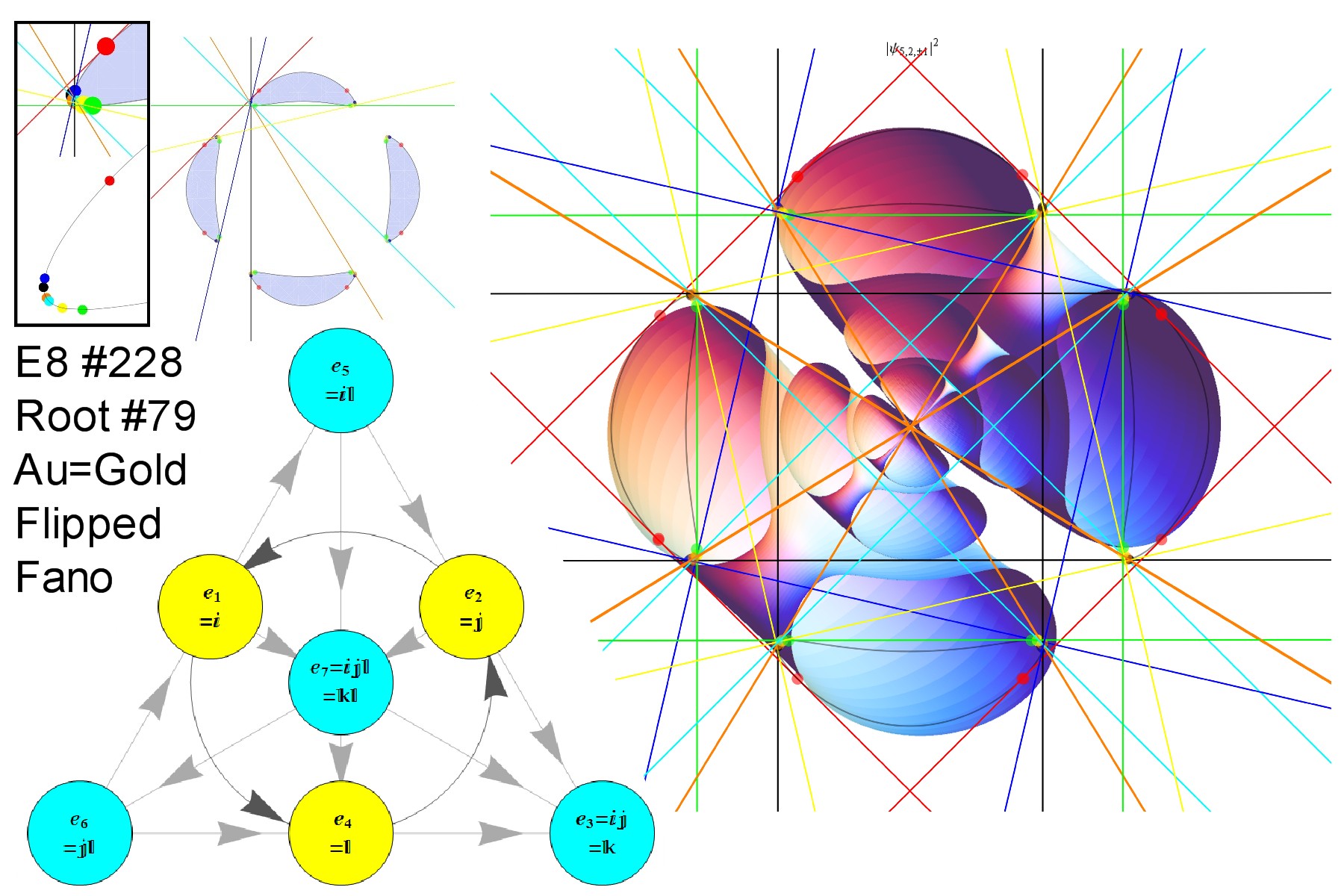
There are 28 octonion Fano plane triangles that correspond directly to the 28 Trott quartic curve bitangents. These bitangents are directly related to the Legendre functions used in the Shroedinger spherical harmonic electron orbital probability densities. Shown below is a graphic of these overlaid onto the n=5, l=2, m=1 element, which is assigned to gold (Au). When using an algorithm based on the E8 positive algebra root assignments, the “flipped” Fano plane has E8 algebra root number 79 (the atomic number of Au) and split real even group number of 228 (in Clifford/Pascal triangle order). For more information, please see the complete list of integrated Fano indices here with full explanation of the layout here.
Detail explanation of E8 Integration with Octonions, Particles, and the Periodic Table
Please see Integrated E8, Binary, Octonion for a tutorial that explains the detail of the content of Fano.pdf. It outlines the relationships in the integration of E8 with Octonions, Binary, Particles, NKS, and the Periodic Table of Elements. Other formats are also available (.ppt or .pps and .pdf).
Improved complete index of E8, Binary, Octonions, Particles, NKS CA & Periodic Table
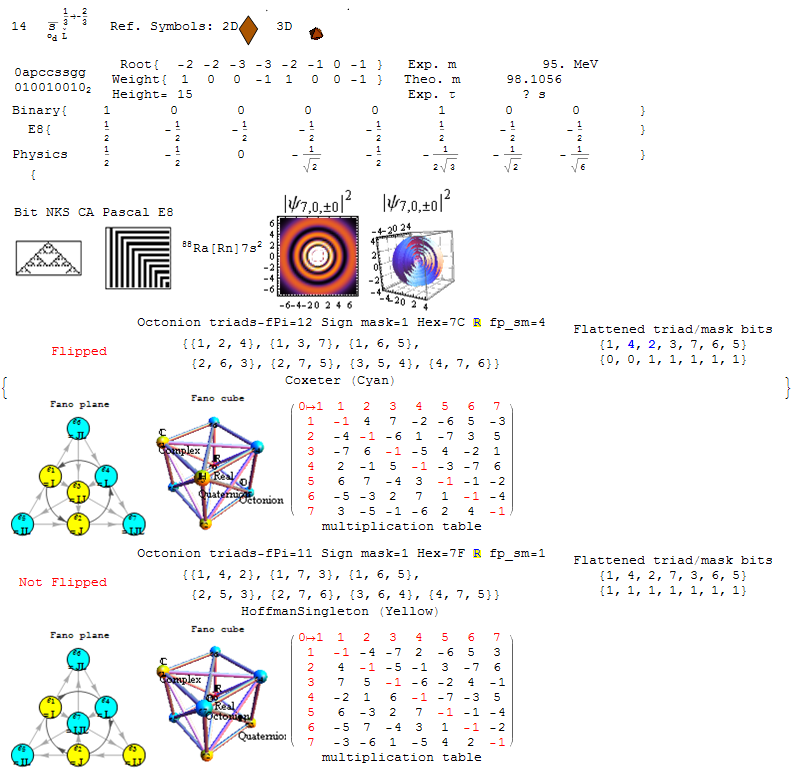
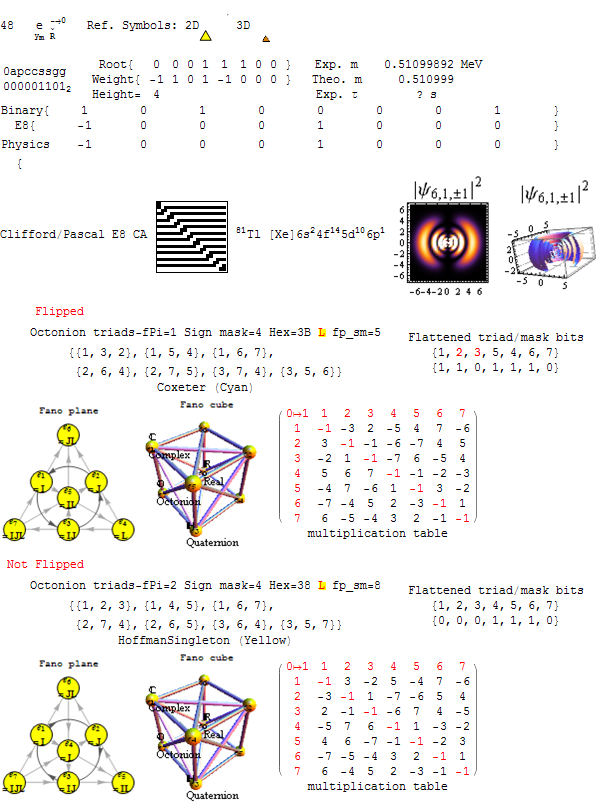
The main change was an improved association of the 120 periodic table elements to the 120 root vectors weighted by their simple root grading. See the full 241 page reference here.
Integration of the Atomic Elements to E8 and Octonions
While it still needs some work – I’ve integrated the atomic elements to the Octonions, E8 and theoretical Lisi eSM model particle assignments (along with Wolfram’s NKS Cellular Automata linked to the Clifford Algebra/Pascal Triangle binary assignments). I have combined all these visualizations with the 2D/3D electron orbitals (based on the symmetry of the {n,l,m,s} quantum numbers (from the Stowe-Janet-Scerri Periodic Table. I totally understand this is not easy to dig into w/o some effort, but … it looks cool 😉
It is shown in an updated version of Fano.pdf. This is a very large and complex 30Mb file – with 241 pages. It shows the Lisi particle assignments, the E8 roots, split real even (SRE) E8 vertex and the Lisi “physics rotation”. It also shows two Fano plane and cubic derived from the symmetries of the E8 particle assignments (and all the relevant construction of it). See the interactive demo or the Mathematica Notebook for a more “navigational look” at the integration.
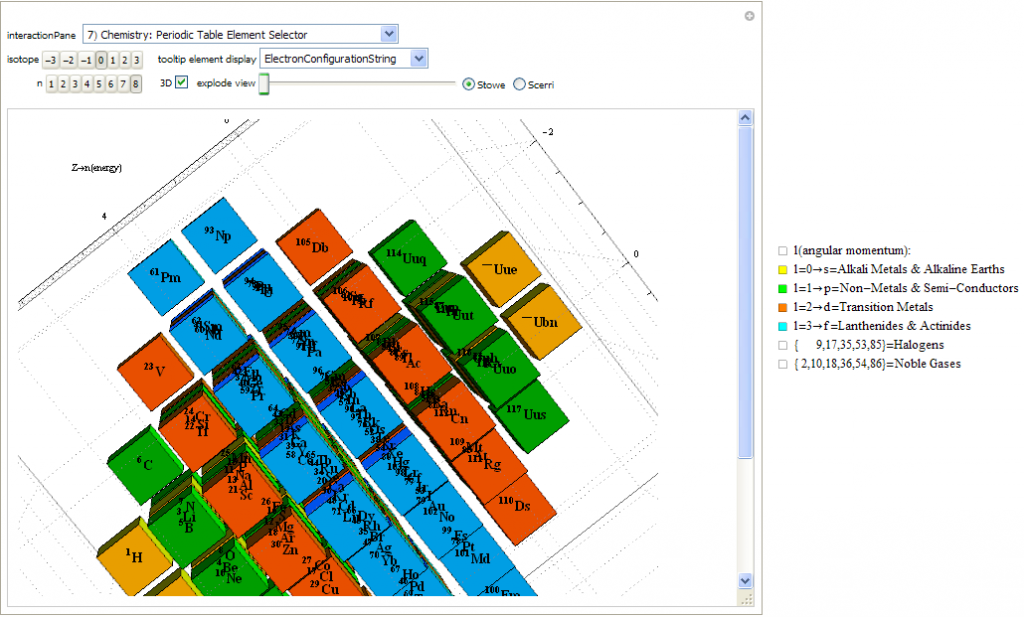
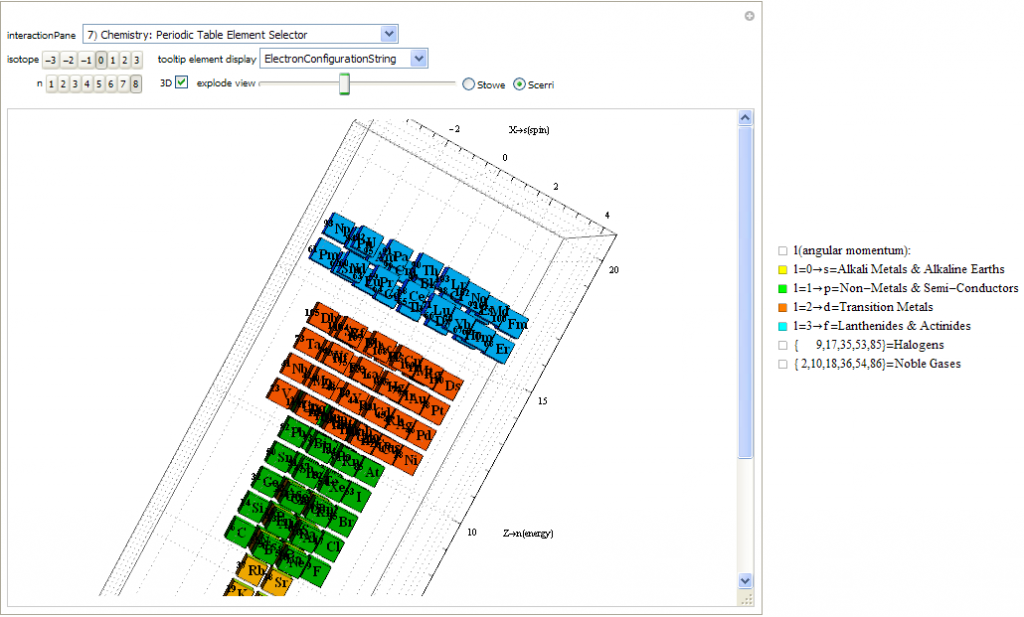
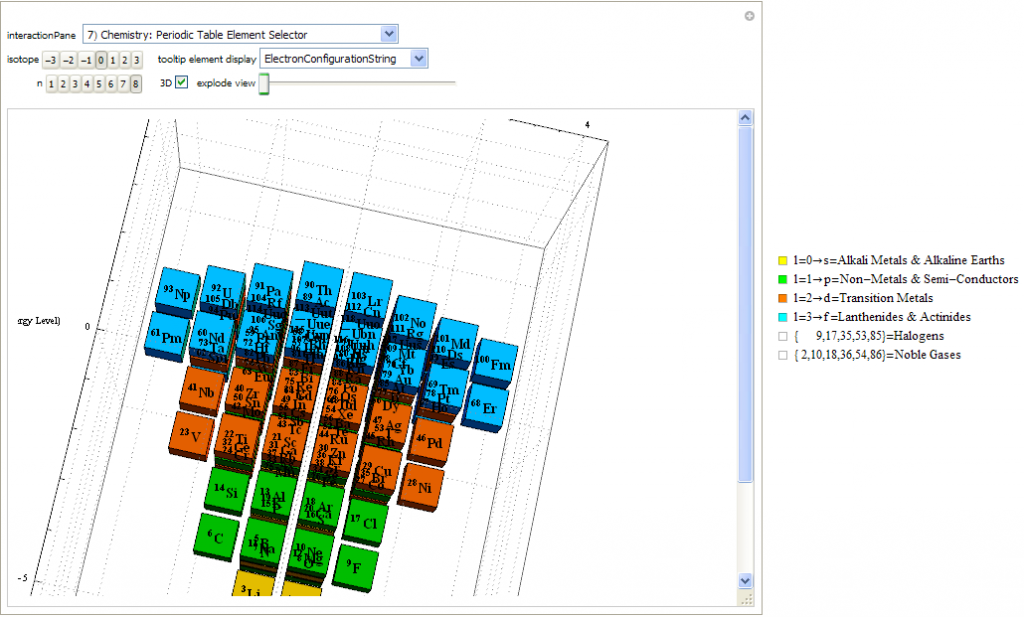
Created a new 4D Stowe-Janet-Scerri Periodic Table
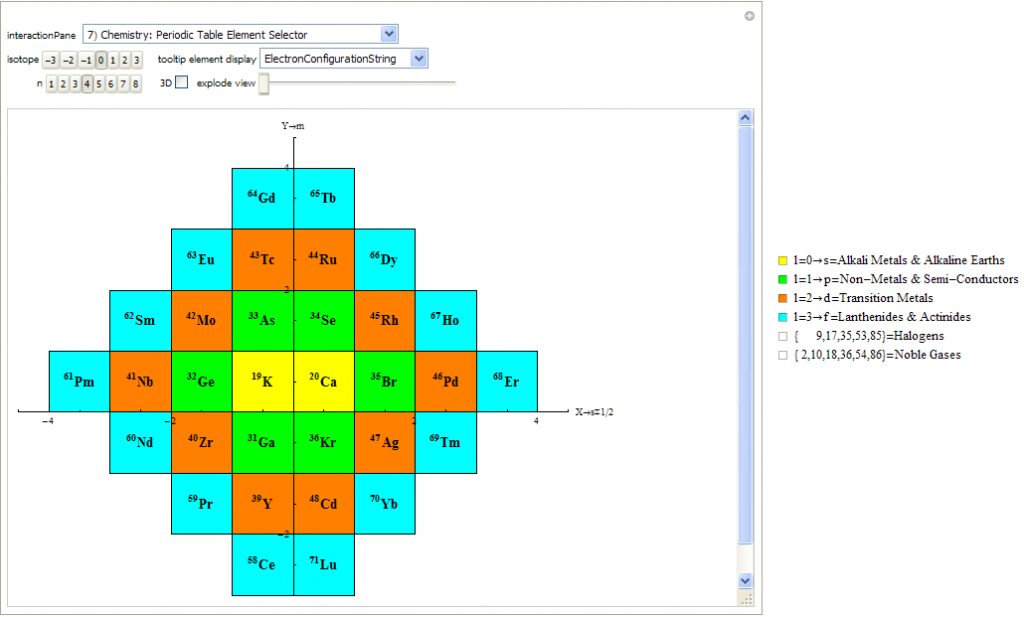
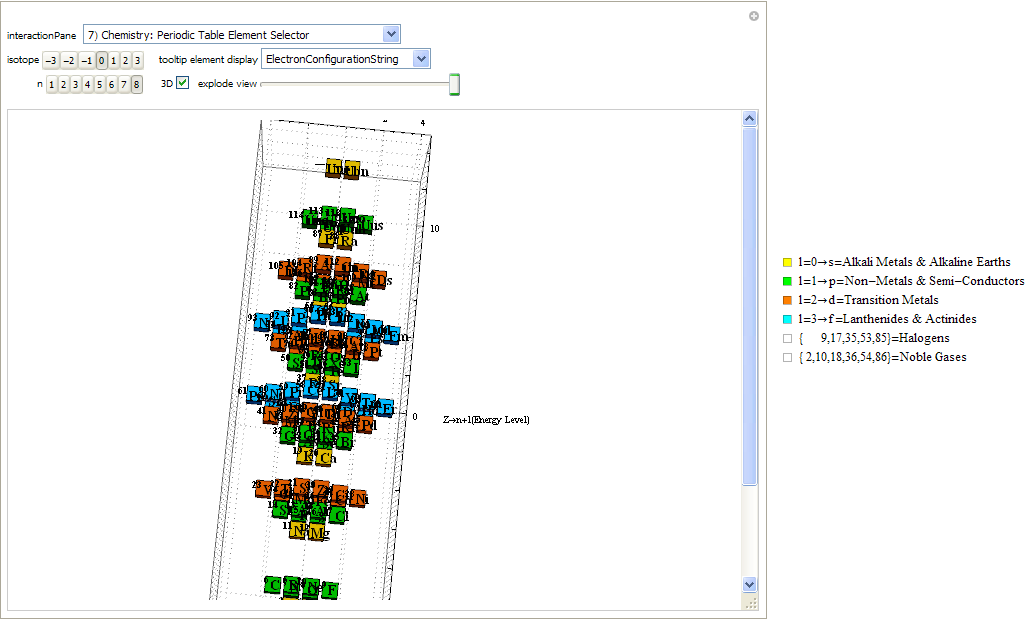
I’ve replaced the standard periodic table in the 7th “Chemistry Pane” of my E8 visualizer with a 2D/3D/4D Stowe-Janet-Scerri version of the Periodic Table.
Interestingly, it has 120 elements, which is the number of vertices in the 600 Cell or the positive half of the 240 E8 roots. It is integrated into VisibLie_E8 so clicking on an element adds that particular atomic number’s E8 group vertex number to the 3rd E8 visualizer pane.
The code is a revision and extension of Enrique Zeleny’s Wolfram Demonstration