Click here for a PDF of my latest paper. This has been accepted by the arXiv as 2311.11918 (math.GR & hep-th) with an ancillary Mathematica Notebook here. These links have (and will continue to have) minor descriptive improvements/corrections that may not yet be incorporated into arXiv, so the interested reader should check back here for those. The prior related paper on THE ISOMORPHISM OF H4 AND E8 is referenced in the blog post here.

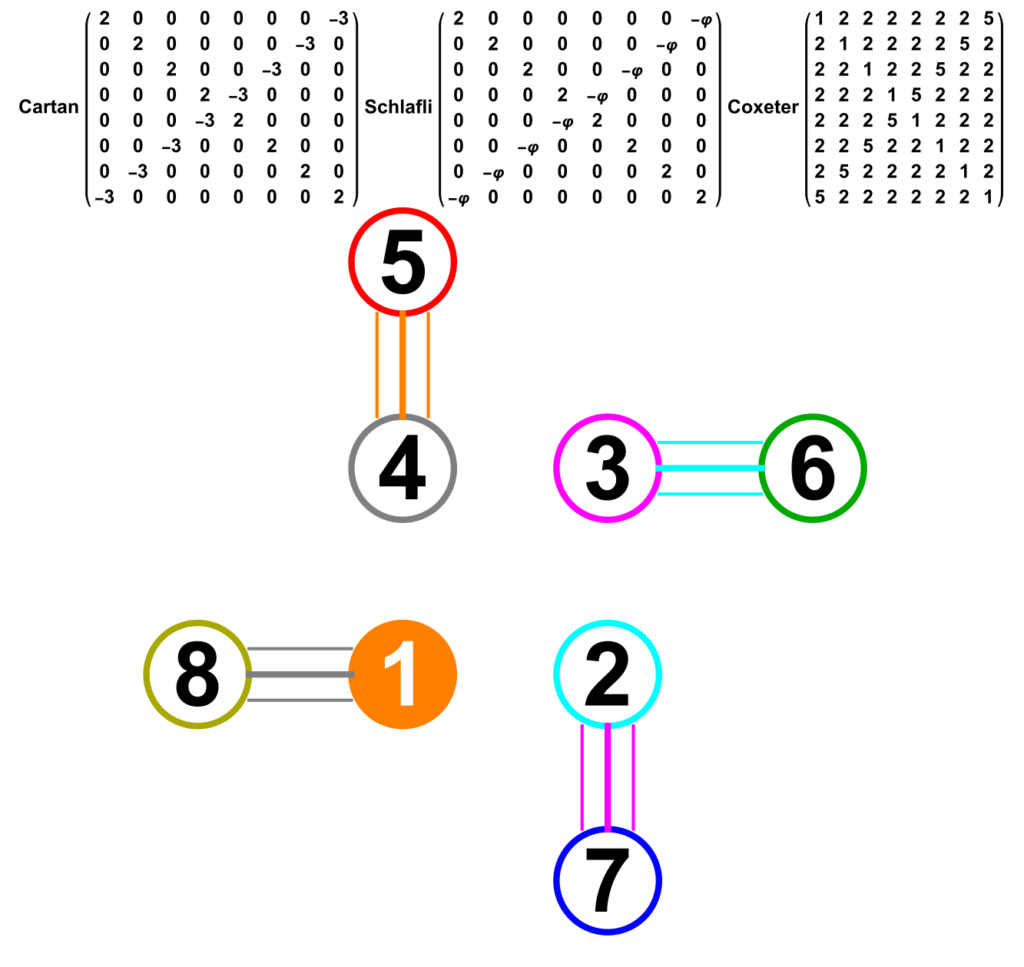
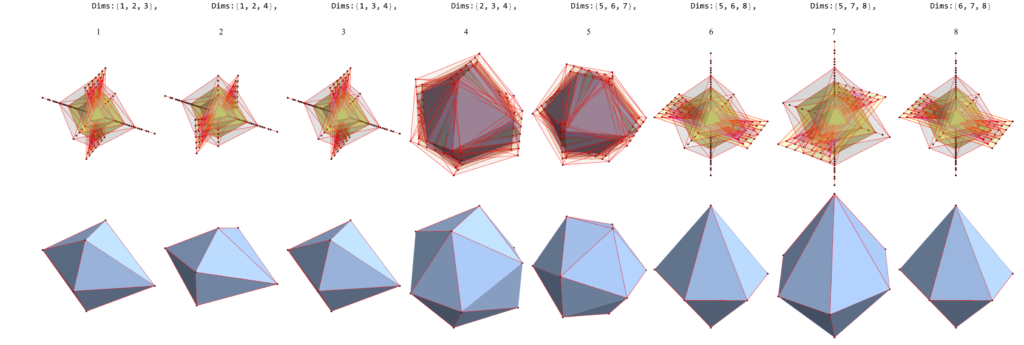
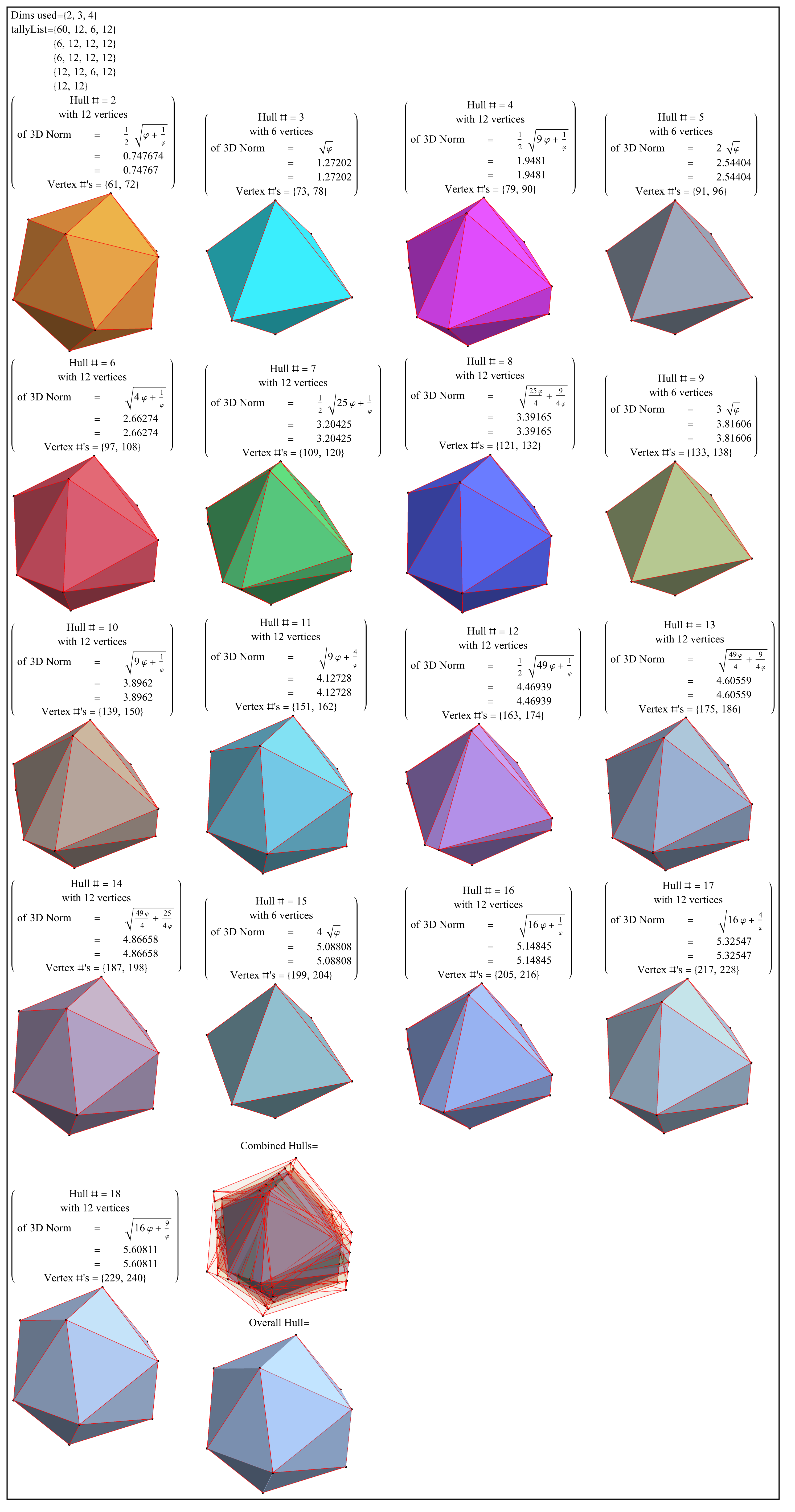
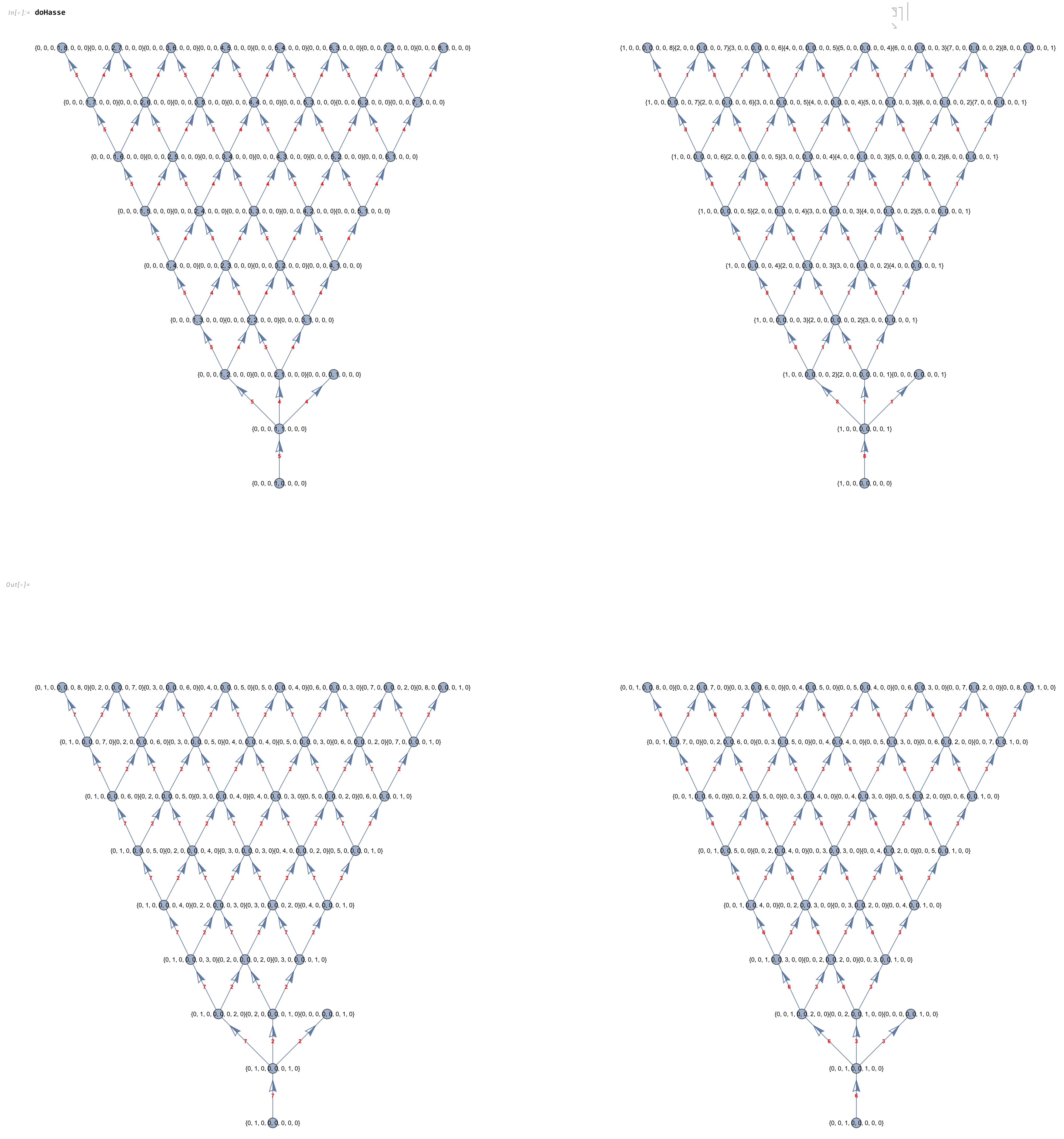
Abstract: This paper presents several notable properties of the matrix U shown to be related to the isomorphism between H4 and E8. The most significant of these properties is that U.U is to rank 8 matrices what the golden ratio is to numbers. That is to say, the difference between it and its inverse is the identity element, albeit with a twist. Specifically, U.U-(U.U)^-1 is the reverse identity matrix or standard involutory permutation matrix of rank 8. It has the same palindromic characteristic polynomial coefficients as the normalized 3-qubit Hadamard matrix with 8-bit binary basis states, which is known to be isomorphic to E8 through its (8,4) Hamming code.