Tag Archives: Amplituhedron
More amplituhedron capability (projected hull surface area and volume)
Getting more capability built into ToE_Demonstration.nb where it can now calculate the scattering amplitude by calculating the volume of the projected hull of selected edges in the n-Simplex Amplituhedron (based on a theory by Nima Arkani-Hamed, with some Mathematica code from J. Bourjaily for the positroid diagram). Of course, there is still much work to get this wrapped up…
A few more pics of Positive Grassmannian Amplituhedrons…
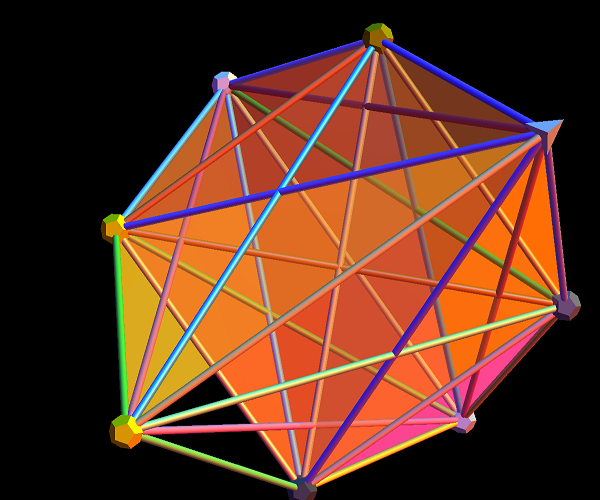
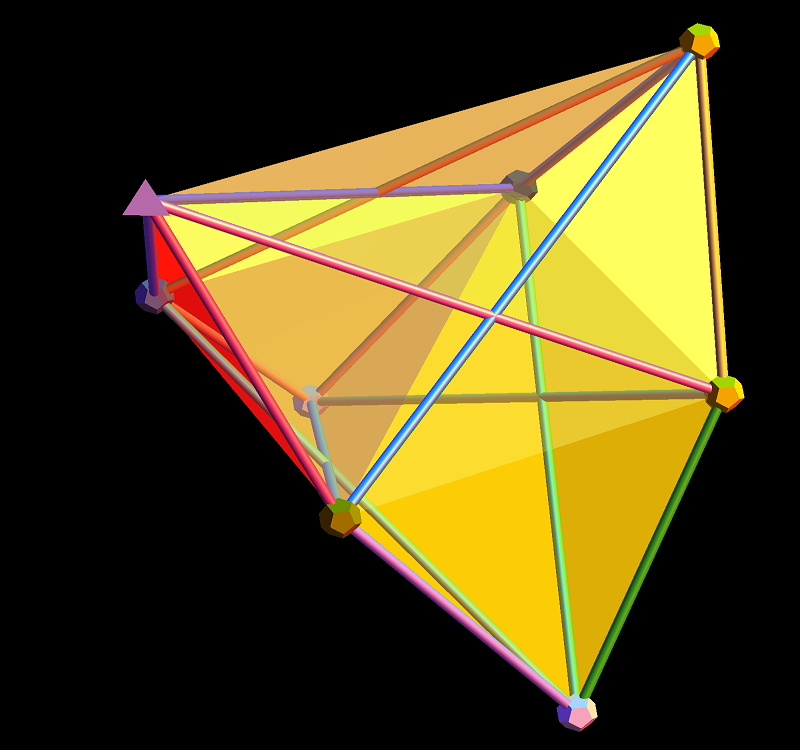
This last diagram is obtained using the following amplituhedron0.m as input to the ToE_Demonstration.nb (when using fully licensed Mathematica) as shown below:
* This is an auto generated list from ToE_Demonstration.nb *)
new := {
artPrint=True;
scale=0.1;
cylR=0.018;
range=2.;
pt={-0.3, 0.0, 0.6};
favorite=1;
showAxes=False;
showEdges=True;
showPolySurfaces=True;
eColorPos=False;
dimTrim=5;
ds=6;
pListName=”First8″;
dsName=”nSimplex”;
p3D=” 3D”;
edgeVals={{Sqrt[11/2], 8}, {Sqrt[9/2 – Sqrt[2]], 4}, {Sqrt[9/2 + Sqrt[2]], 4}};
};new;
Amplituhedron Visualizations!
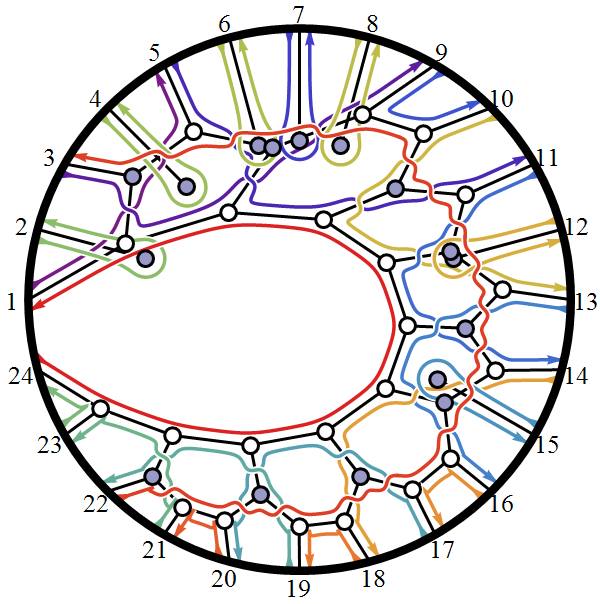
Playing around trying to visualize the latest in the theoretical high energy particle physics (HEP/TH) determining how particle masses might be predicted from geometric principles (based on a theory by Nima Arkani-Hamed, with some Mathematica code from J. Bourjaily for the positroid diagram).
Positive Grassmannian Amplituhedrons
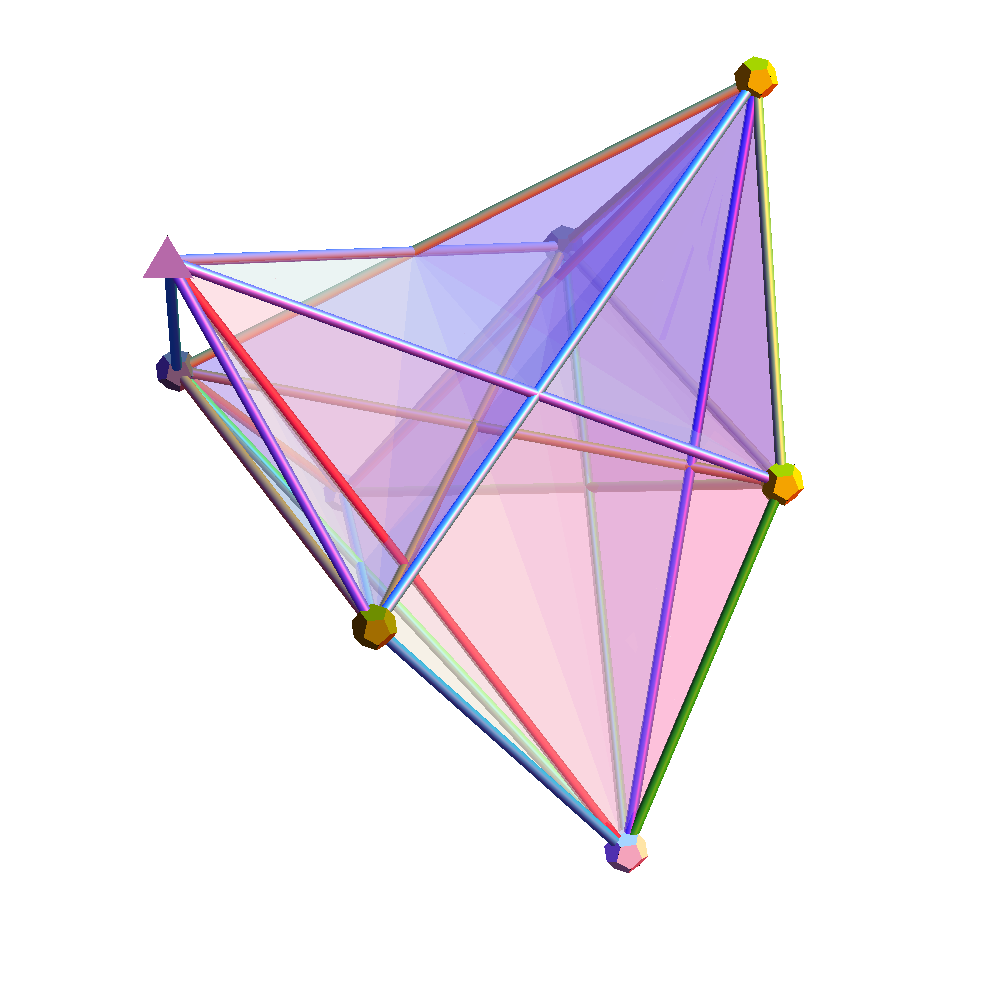
Compare this Mathematica(l) basis to the artistic representation by Andy Gilmore