Category Archives: Physics
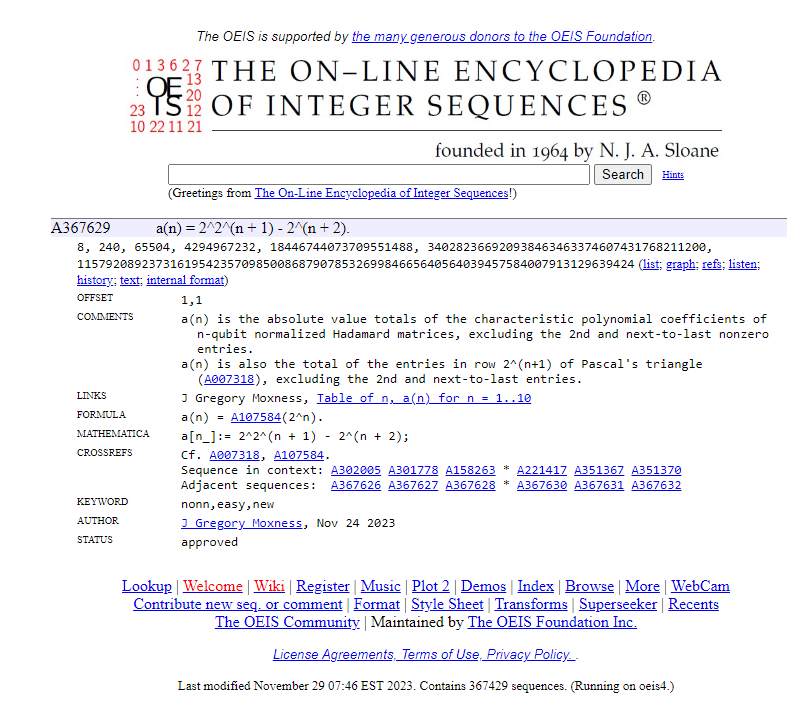
My E8, Hadamard, and Pascal Triangle related OEIS Integer Sequence A367629
In my research that has produced two arXiv papers on the topic of the isomorphisms of E8, I found a sequence derived from the sum of coefficients in Hadamard matrices that relates to certain rows of the Pascal triangle and E8. Please see that OEIS database entry here.
One of my arXiv papers is featured as a Wolfram Community Editor’s Pick
Please take a look here to view a paper I wrote about in a recent blog post here. The paper registered in arXiv is here and titled: The_Isomorphism_of_H4_and_E8.
As I like to provide more than just type-set text and graphics, I include in the arXiv the Mathematica notebooks with code snippets and actual output w/interactive 3D graphics. This gets attached in the ancillary files and is also linked as “Papers with Code” using my GitHub account here.
That caught the eye of the Wolfram editors who graciously offered to help with this post. My hats off to them. Enjoy the paper, with a follow-on paper: The_Isomorphism_of_3-Qubit_Hadamards_and_E8 here, including the notebook 😉
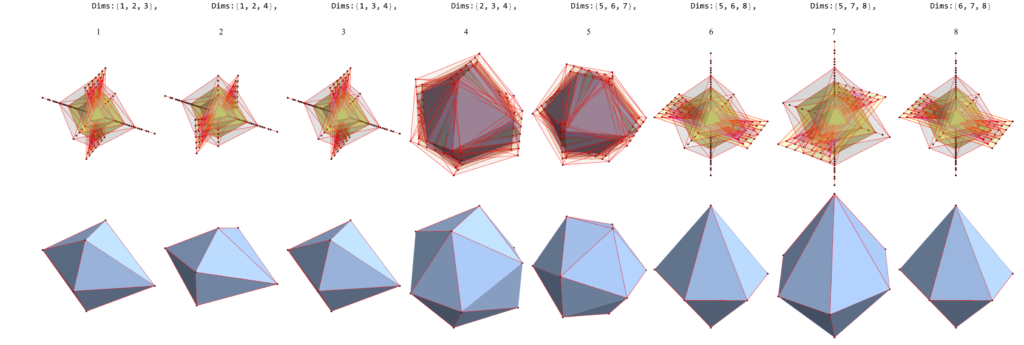
The Isomorphism of 3-Qubit Hadamards and E8
Click here for a PDF of my latest paper. This has been accepted by the arXiv as 2311.11918 (math.GR & hep-th) with an ancillary Mathematica Notebook here. These links have (and will continue to have) minor descriptive improvements/corrections that may not yet be incorporated into arXiv, so the interested reader should check back here for those. The prior related paper on THE ISOMORPHISM OF H4 AND E8 is referenced in the blog post here.
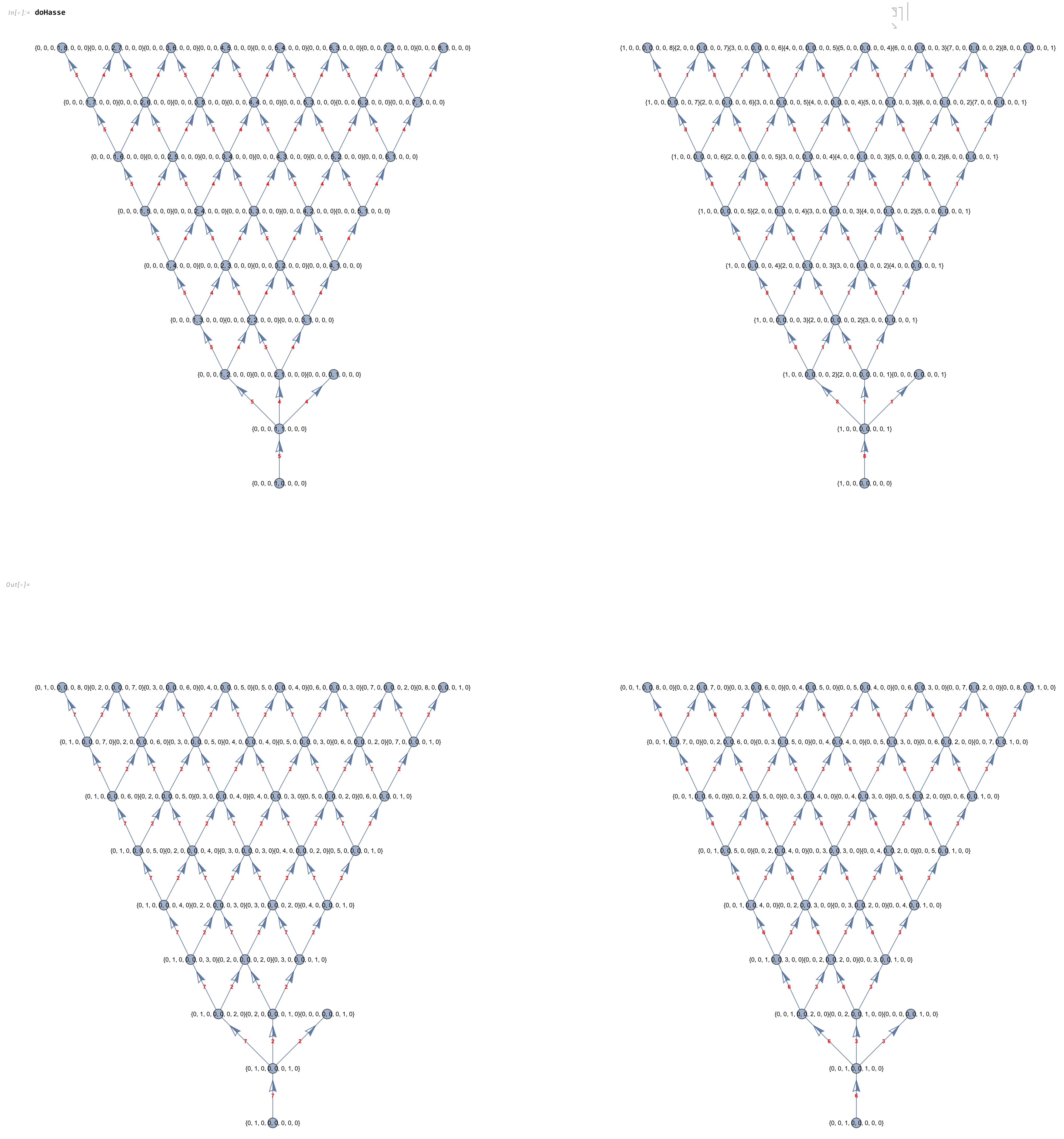
Abstract: This paper presents several notable properties of the matrix U shown to be related to the isomorphism between H4 and E8. The most significant of these properties is that U.U is to rank 8 matrices what the golden ratio is to numbers. That is to say, the difference between it and its inverse is the identity element, albeit with a twist. Specifically, U.U-(U.U)-1 is the reverse identity matrix or standard involutory permutation matrix of rank 8. It has the same palindromic characteristic polynomial coefficients as the normalized 3-qubit Hadamard matrix with 8-bit binary basis states, which is known to be isomorphic to E8 through its (8,4) Hamming code.



My patent for Rapid 3D prototyping and fabricating of slow-wave structures, including electromagnetic meta-material structures, for millimeter-wavelength and terahertz-frequency high-power vacuum electronic devices
A few years ago and 5 1/2 years after I retired, the patent I worked on with Andrey and Maysa finally made it through the US Patent Office!

The Isomorphism of H4 and E8
Click here for a PDF of my recent paper. This has been accepted by the arXiv as 2311.01486 (math.GR & hep-th) with an ancillary Mathematica Notebook here. These links have (and will continue to have) minor descriptive improvements/corrections that may not yet be incorporated into arXiv, so the interested reader should check back here for those. Another related follow-on paper on THE ISOMORPHISM OF 3-QUBIT HADAMARDS AND E8 is referenced in the blog post here.
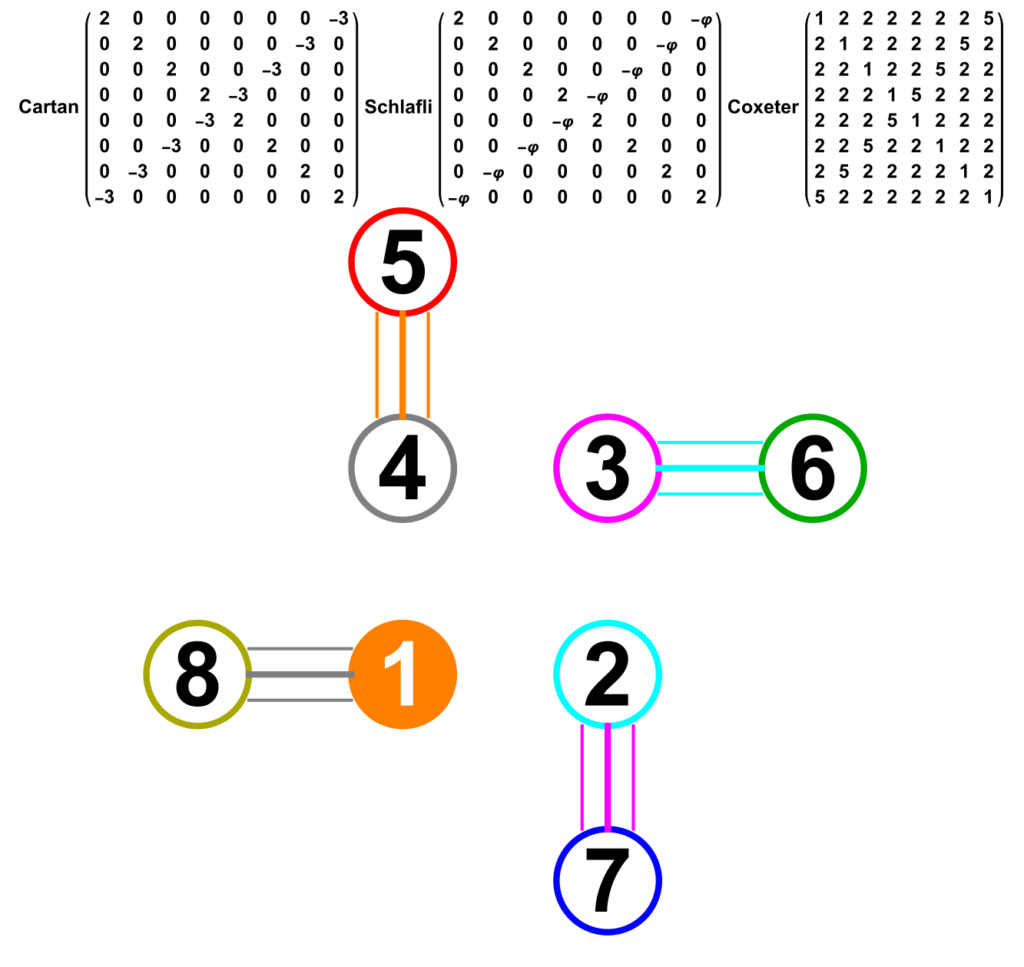
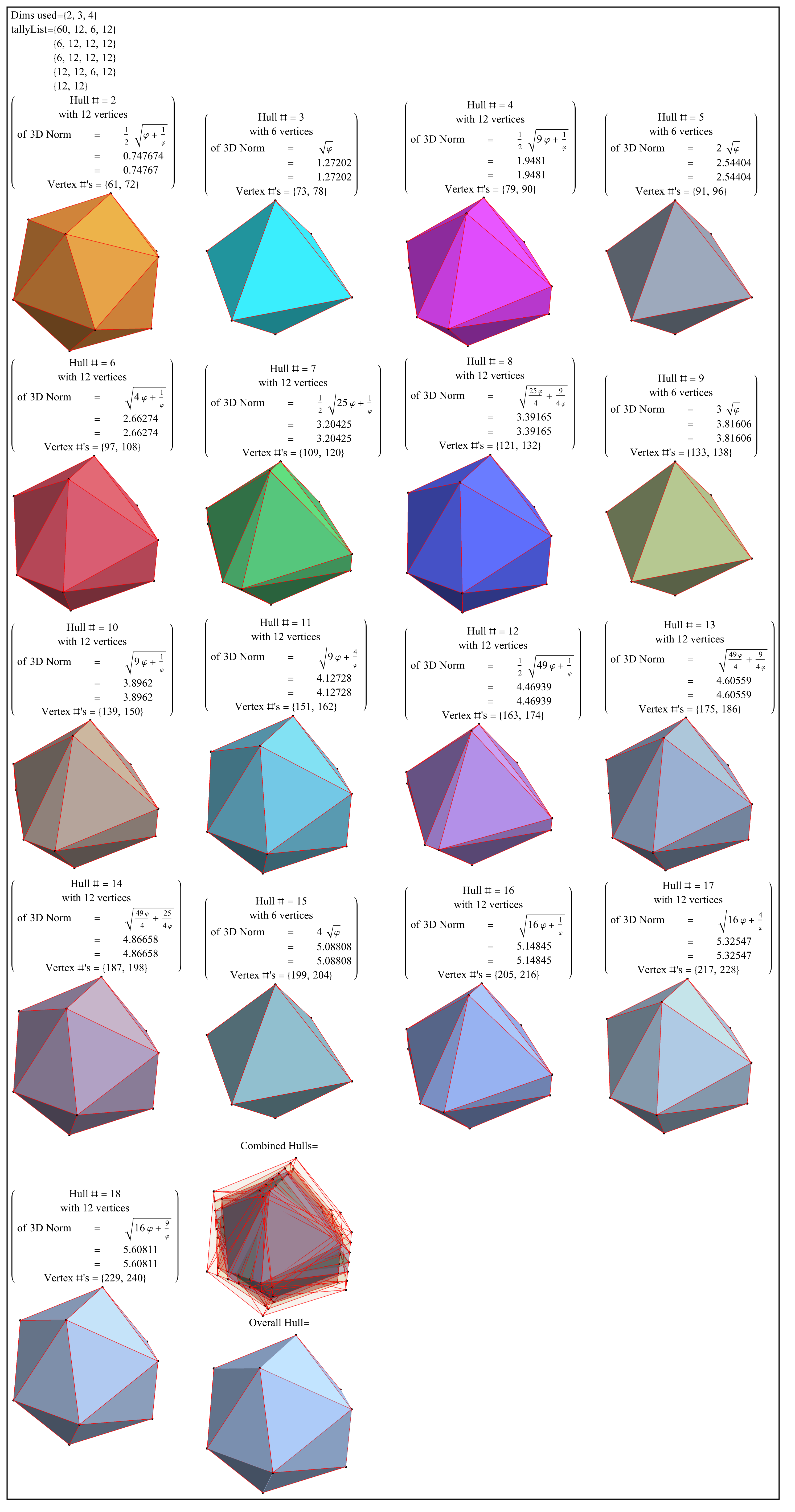
The abstract: This paper gives an explicit isomorphic mapping from the 240 real R^8 roots of the E8 Gossett 4_{21} 8-polytope to two golden ratio scaled copies of the 120 root H4 600-cell quaternion 4-polytope using a traceless 8×8 rotation matrix U with palindromic characteristic polynomial coefficients and a unitary form e^{iU}. It also shows the inverse map from a single H4 600-cell to E8 using a 4D<->8D chiral L<->R mapping function, phi scaling, and U^{-1}. This approach shows that there are actually four copies of each 600-cell living within E8 in the form of chiral H4L+phi H4L+H4R+phi H4R roots. In addition, it demonstrates a quaternion Weyl orbit construction of H4-based 4-polytopes that provides an explicit mapping between E8 and four copies of the tri-rectified Coxeter-Dynkin diagram of H4, namely the 120-cell of order 600. Taking advantage of this property promises to open the door to as yet unexplored E8-based Grand Unified Theories or GUTs.
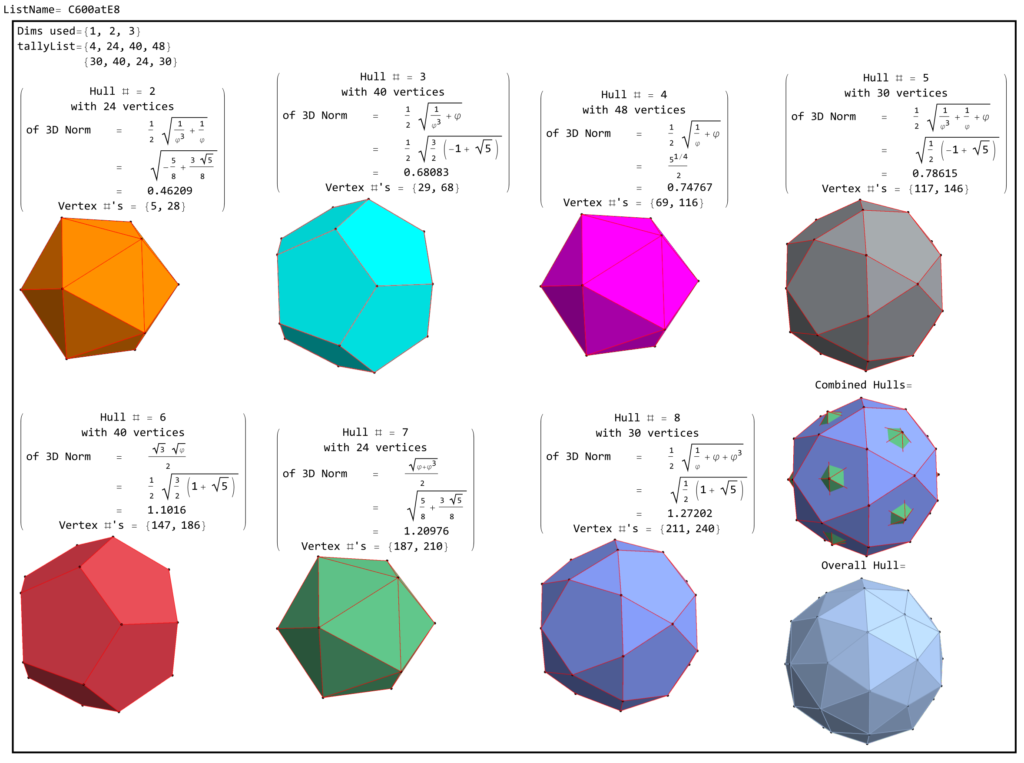
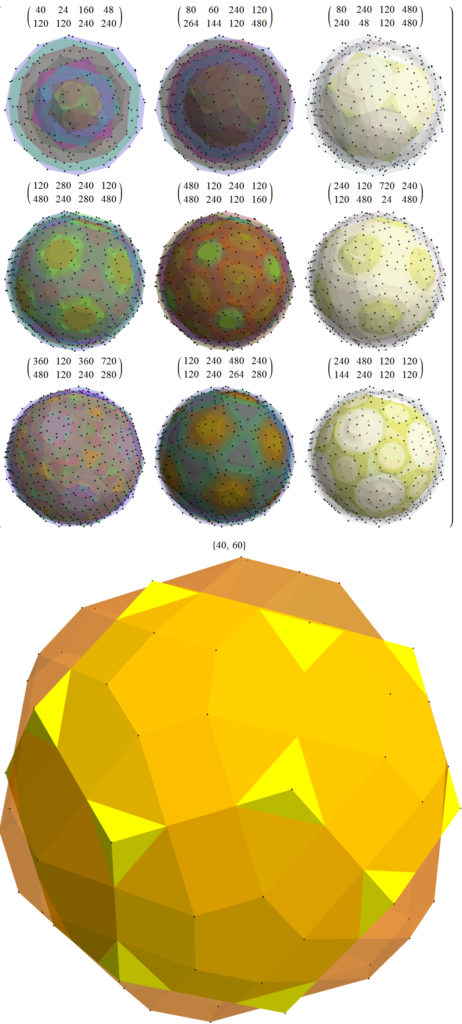



These include the specified 3D quaternion Weyl orbit hulls for each subgroup identified

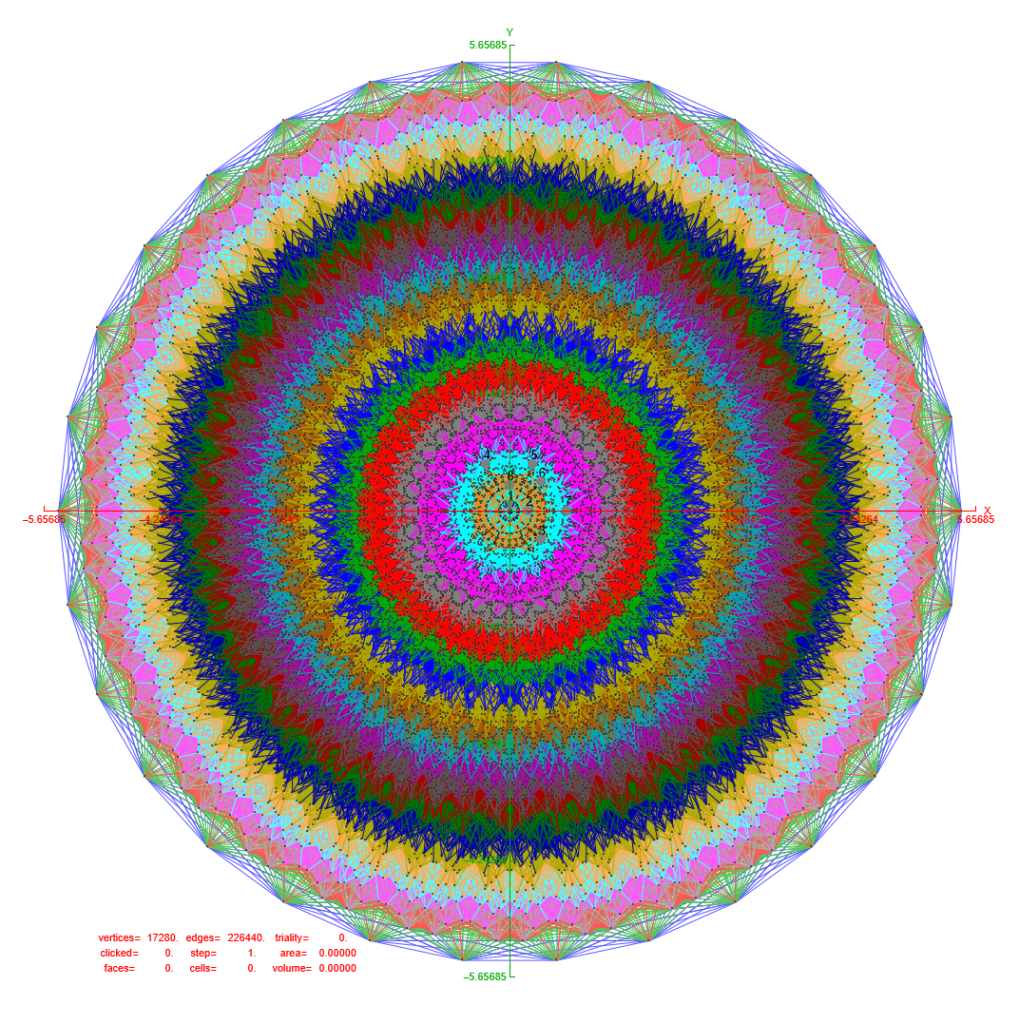
Collections of 3D Surfaces, 3D Chaotic Attractors, 2D/3D Fractals, and 3D Cellular Automaton
Below are SVG images of output from Pane 1 (Chaos) and Pane 17 (AI) of the VisibLie_E8 visualization tool:
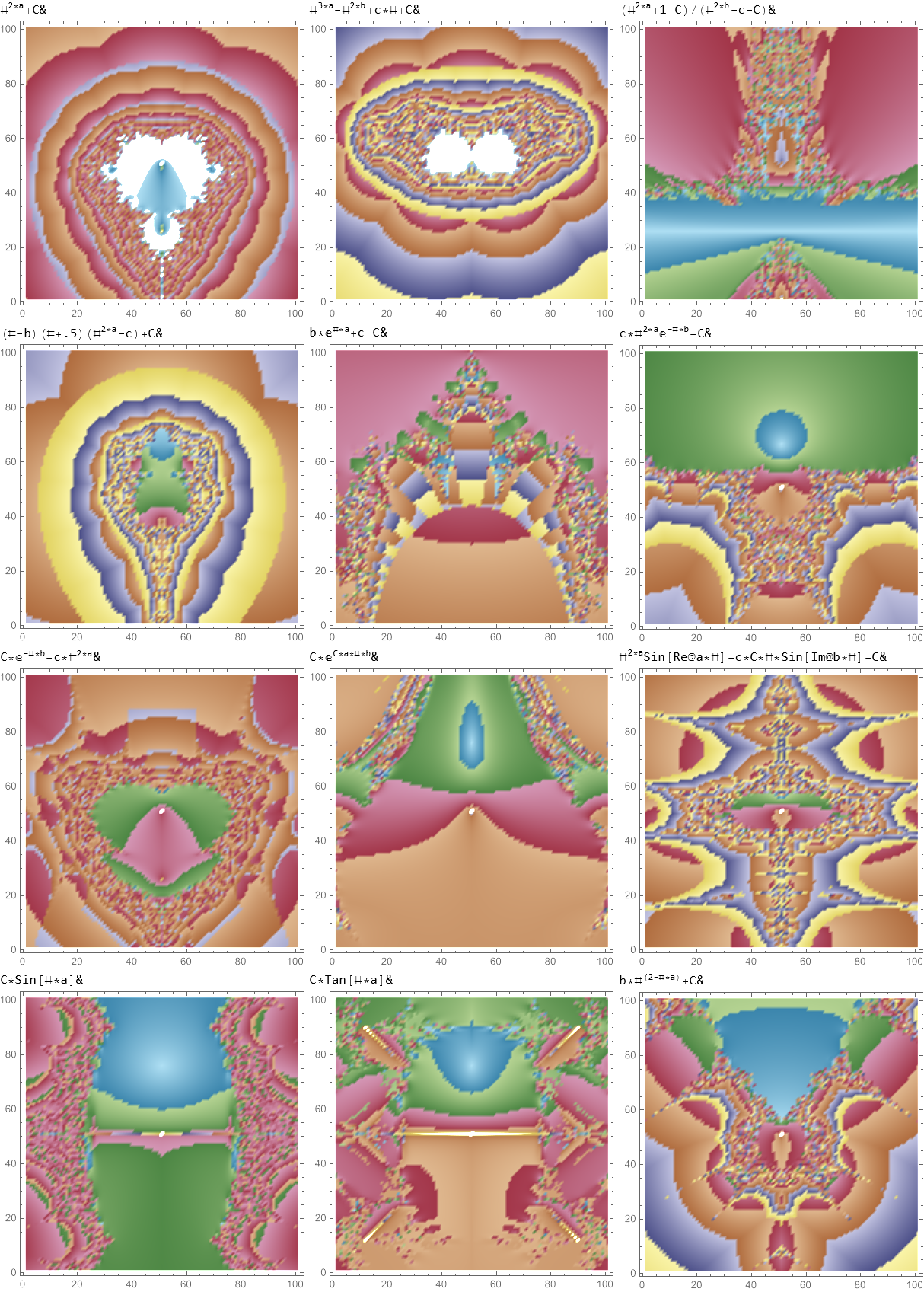

Greg Moxness, Tucson AZ
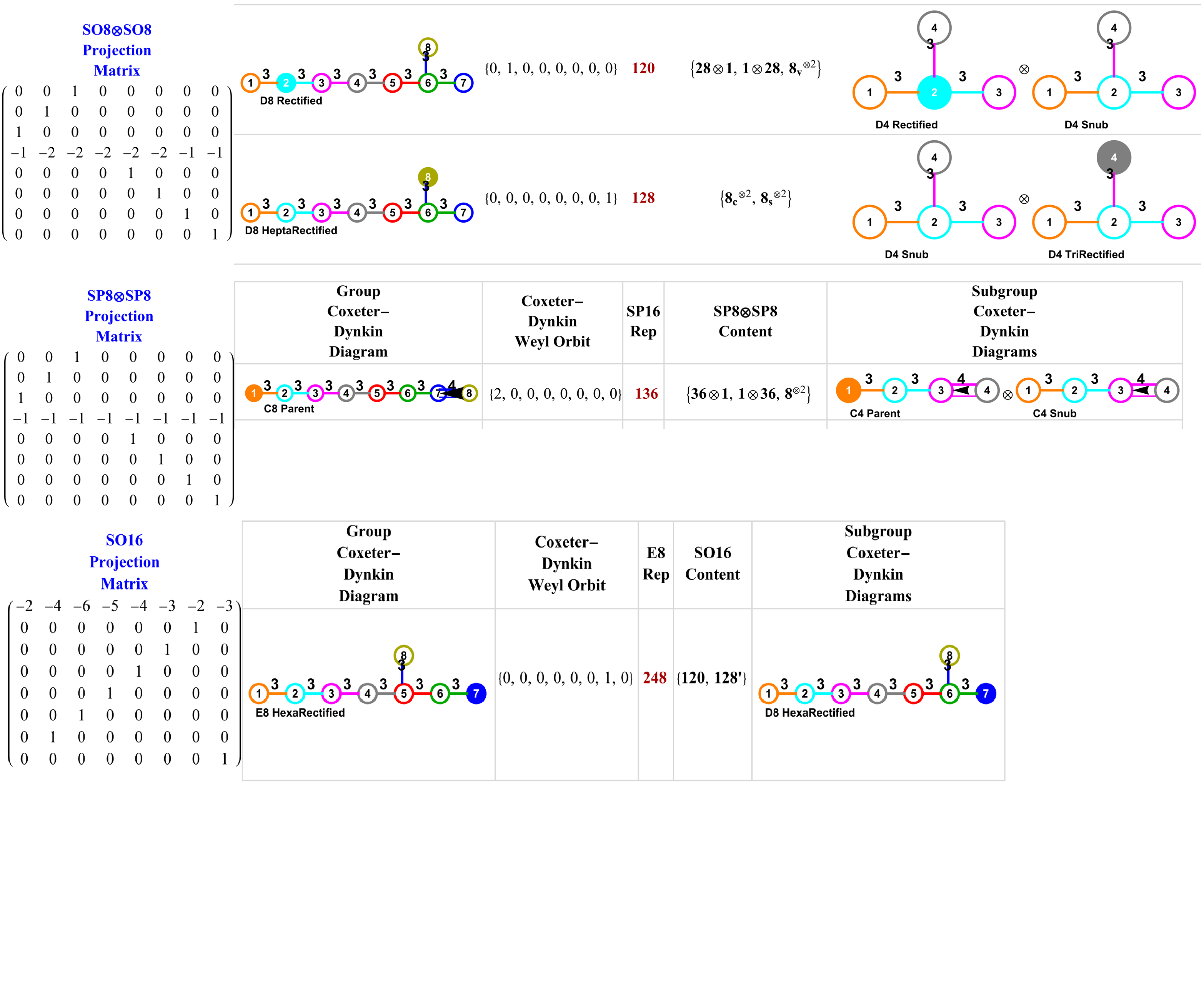
Added visualization of the embeddings of the maximal subgroups with associated projection matrices of Lie Algebras in the Dynkin Diagram pane (#4) of VisibLie_E8
This is constructed from VisibLie_E8 and uses the Mathematica package Mathgroup. A comprehensive PowerPoint/PDF that gives an overview of the underlying theory and VisibLie_E8 tool capability is in this post.
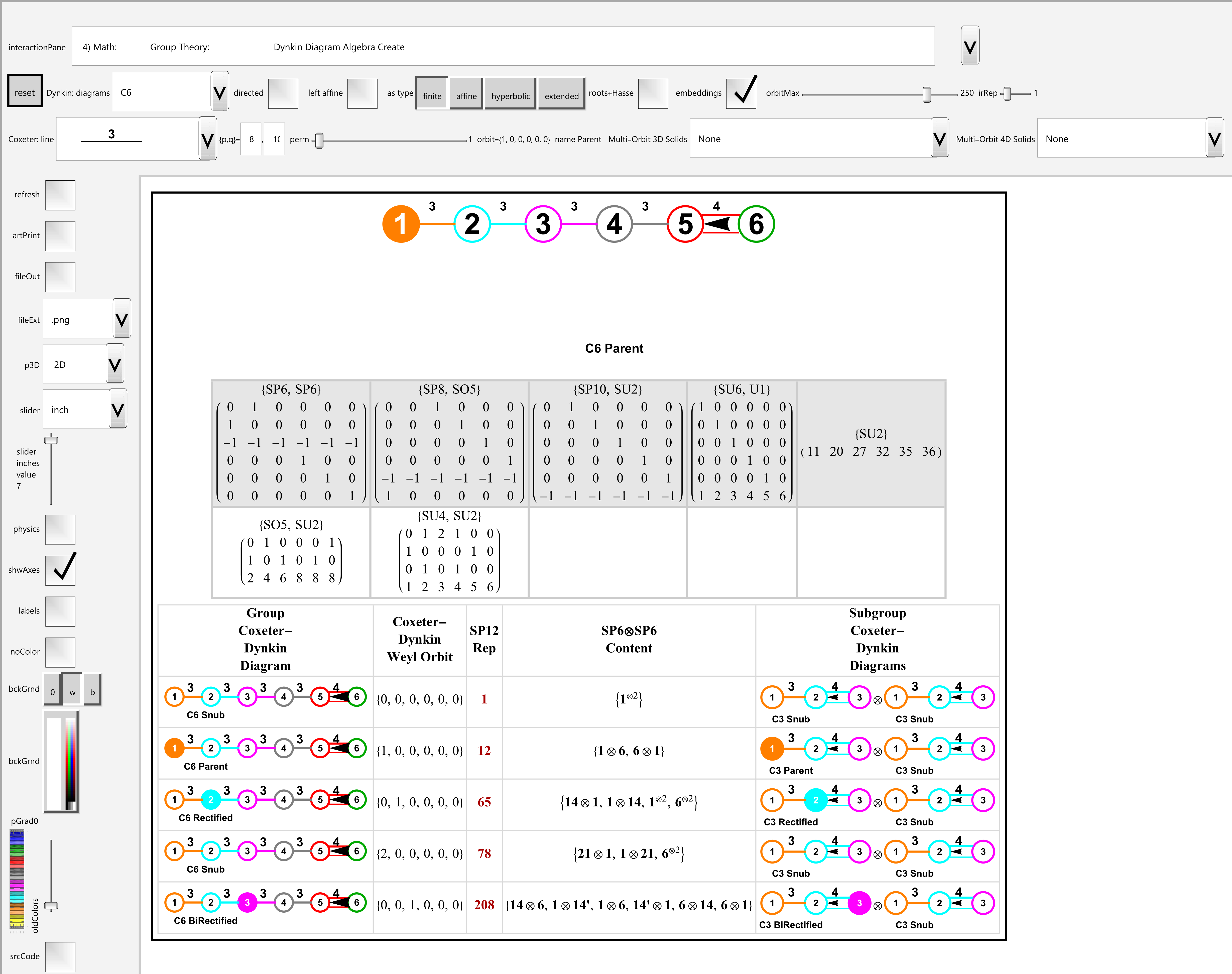
Greg Moxness, Tucson AZ
Disdyakis Triacontahedron Coordinates
I discovered an error in the WP article on the Disdyakis Triacontahedron. It seemed the scaling factor for determining the coordinates of the Icosidodecahedron hull was added and changed without any citation references. Since the factor seemed off, I analyzed it using the Koca, Mehmet’s paper and Weisstein, Eric W. “Disdyakis Triacontahedron.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/DisdyakisTriacontahedron.html
Please see this Mathematica Notebook for the results here or the PDF here.

Below is the SVG image of the notebook.
Greg Moxness, Tucson AZ