I read an interesting article about a pattern discovered by Warren D. Smith (discussed at length here):
“The sum of the first three terms in the Eisenstein E_4(q) Series Integers of the Theta series of the E8 lattice is a perfect fourth power: 1 + 240 + 2160 = 2401 = 7^4”
So I decided to visualize the 2401=1+240+2160 vertex patterns of E8 using my Mathematica codebased toolset based on some previous work I put on my Wikipedia talk page.
The image below represents various projections showing 6720 edges of the 240 E8 vertices, plus a black vertex at the origin, and the 2160 Witting Polytope E8 2 _ 41 vertices using the same projection basis (listed at the top of each image along with the color coded vertex overlaps). Click these links for a higher resolution PNG or the SVG version.
Some of the particular projections of the Witting Polytope may need 8D rotations applied to the basis vectors to find better symmetries with the Gosset, but this is a start using my standard set of projections.
The 240 vertices of the Gosset Polytope are generated using various permutations:
(* E8 4_21 vertices *)
e8421 = Union@Join[
Eperms8@{1, 1, 1, 1, 1, 1, 1, 1}/2,
perms8@{1, 1, 0, 0, 0, 0, 0, 0}];
The 2160 vertices of the Witting Polytope are generated using various permutations:
(* E8 2_41 vertices *)
e8241=Union@Join[
perms8[{1,0,0,0,0,0,0,0}4],
perms8[{1,1,1,1,0,0,0,0}2],
Eperms8[({2,0,0,0,0,0,0,0}+1)]]/4;
Another view shows just the 2160 Witting Polytope vertices. Click these links for a higher resolution PNG or the SVG version.
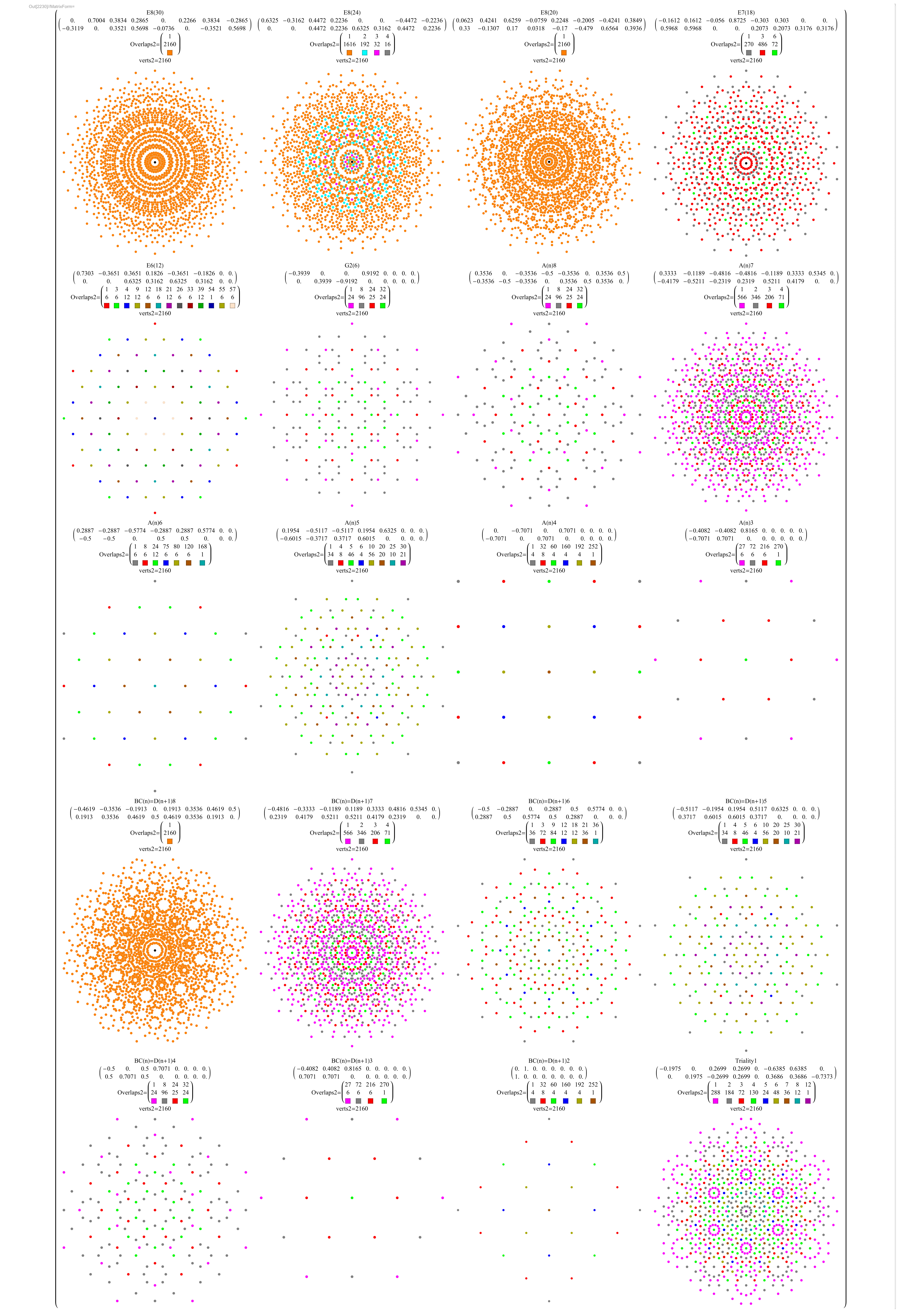
Another great source of visualizations on E8 and this Witting Polytope is here.
Now visualizing in 3D the structure in 3D using rows 2-4 of the E8->H4 folding matrix, we get:



