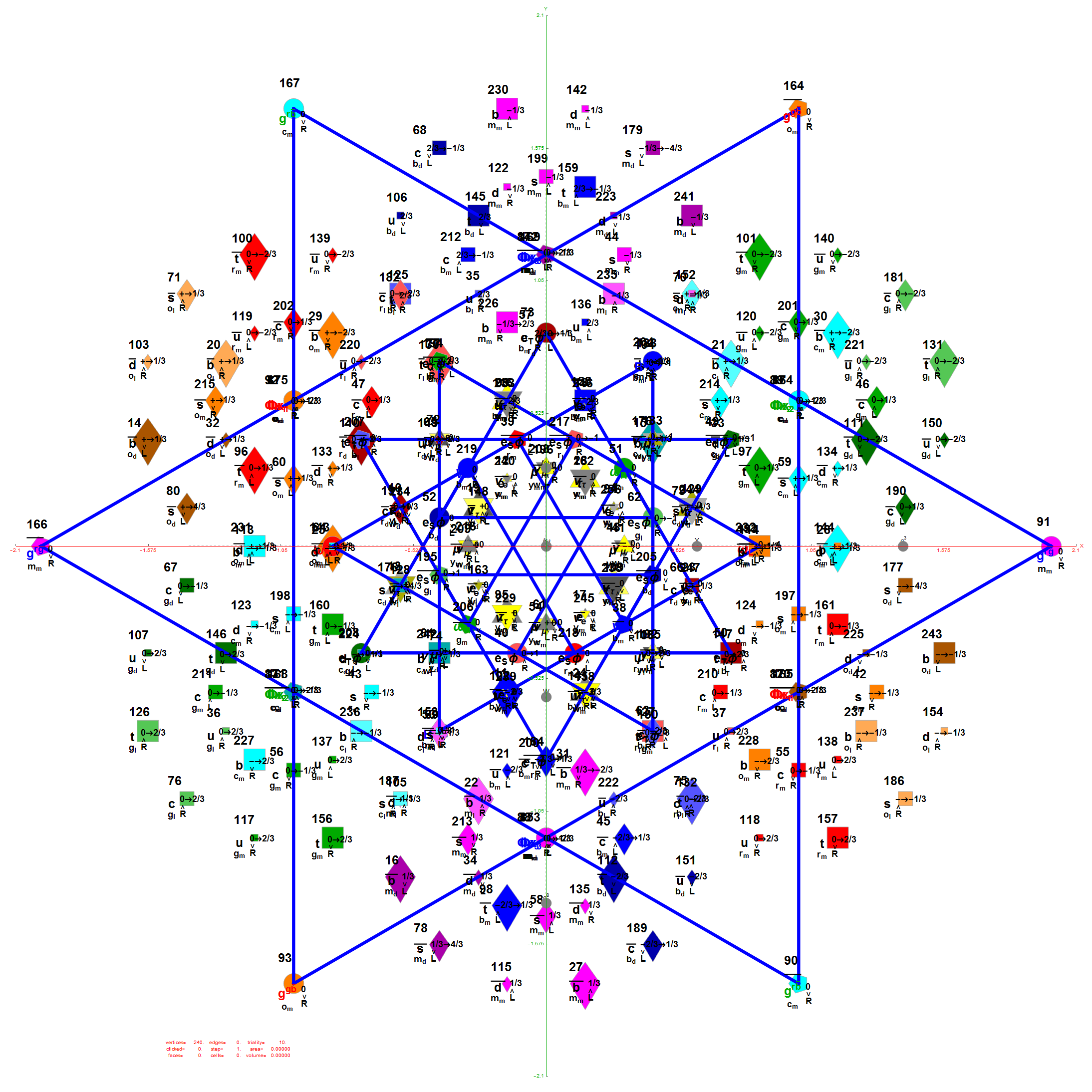
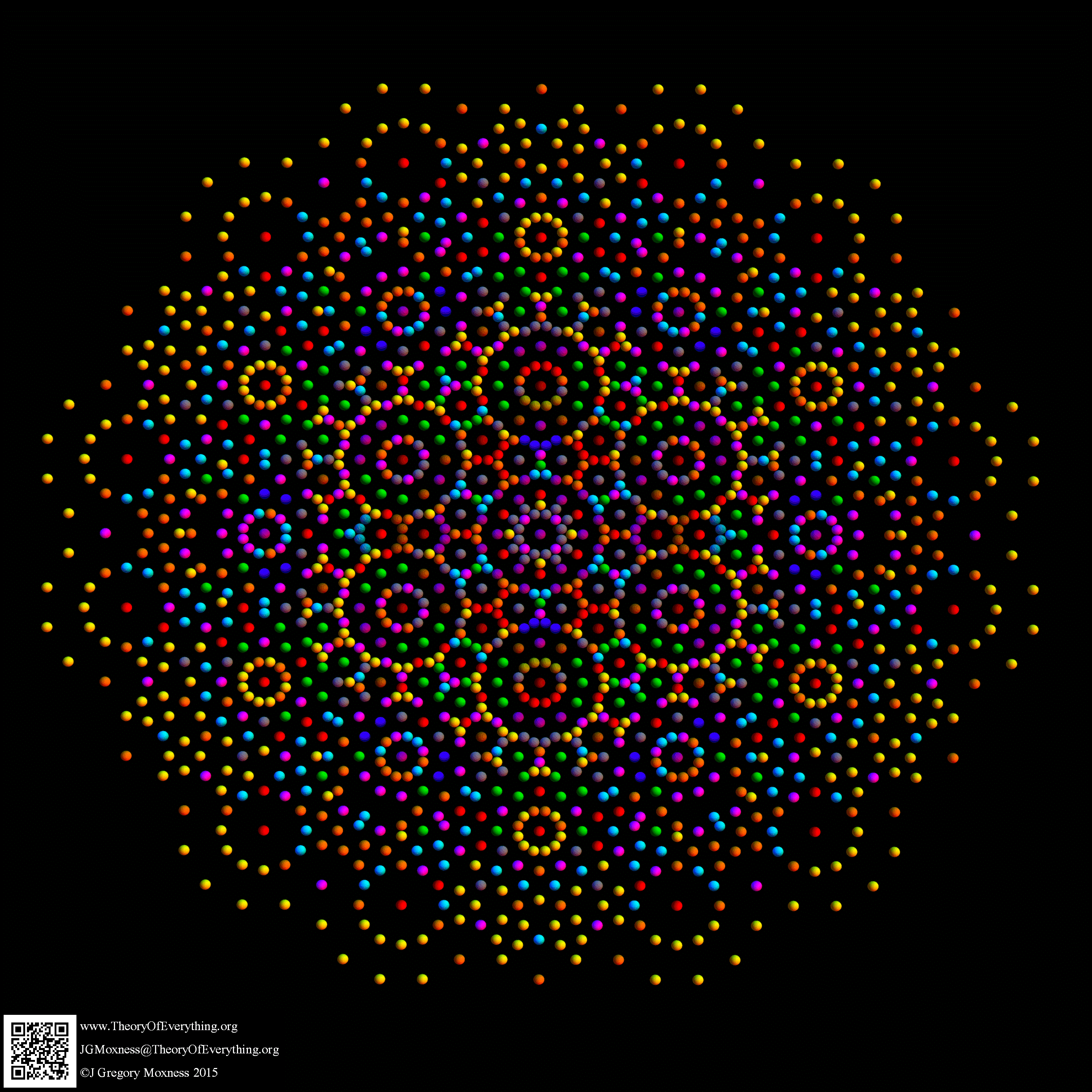
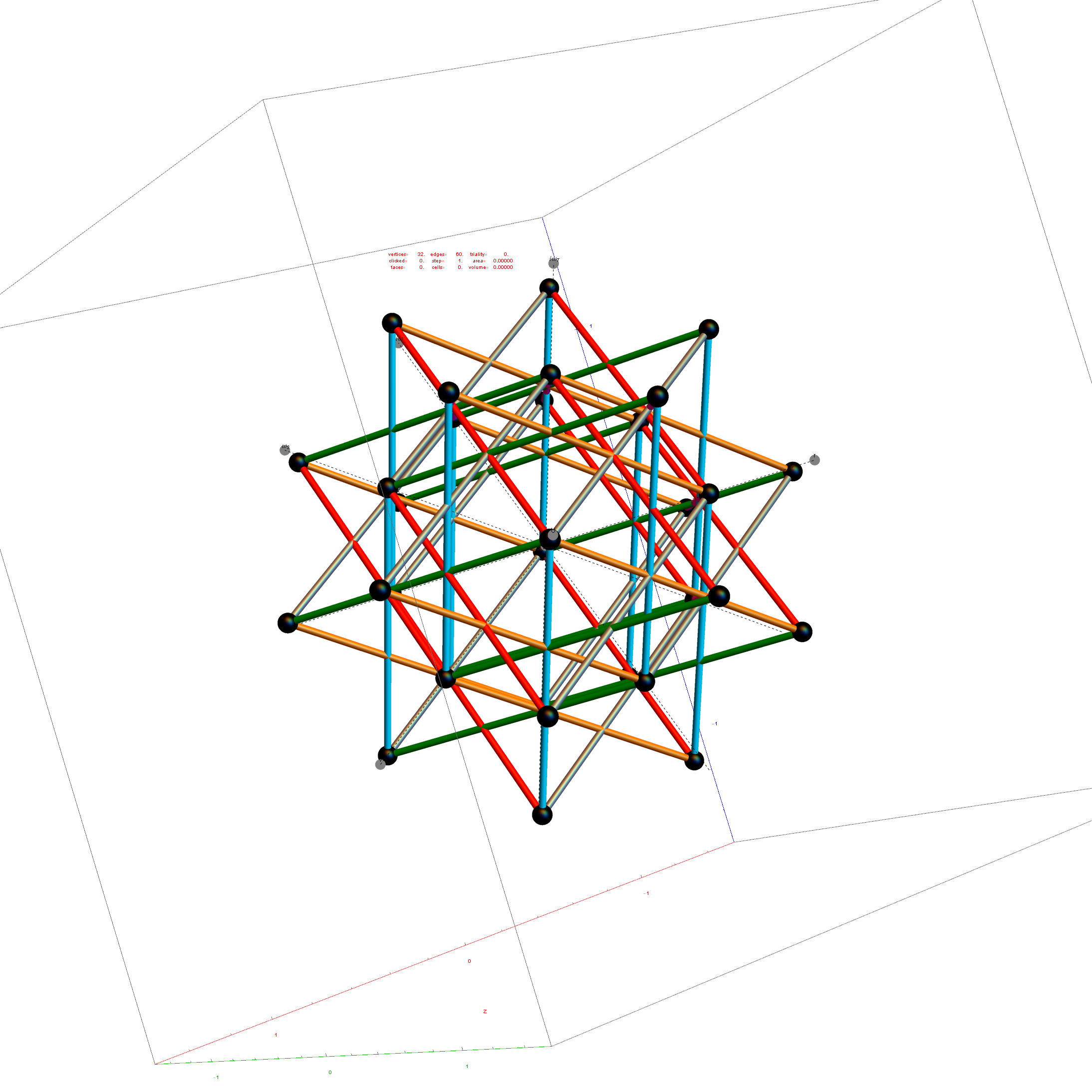
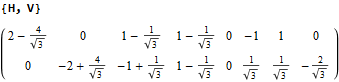I was asked to clarify a particular projection of the Rhombic Triacontahedron from the 6-Cube subgroup of E8, which had I created for WikiPedia (WP) back in 2011 based on an E8 to H4+H4Φ rotation matrix I discovered in 2010.
The edge coloring on the projection above is defined by which of the 6 dimensional axis the edge aligns with.
BTW – if you find this information useful, or provide any portion of it to others, PLEASE make sure you cite this post. If you feel a blog post citation would not be an acceptable form for academic research papers, I would be glad to clean it up and put it into LaTex format in order to provide it to arXiv (with your academic sponsorship) or Vixra. Just send me a note at: jgmoxness@theoryofeverthing.org.
The following projection (basis) vectors take the 6-Cube as a subset of E8 and projects it into 3D using the following basis vectors:

Notice the last two dimensions in each vector are 0, which effectively takes the 128 8D 1/2 integer vertices of the E8 BC8 DemiCube into the 6D 6-Cube.
For the following data analysis, it is useful to reference the full list of E8 and H4+H4Φ data at the end of my blog post here.
The clarification desired was due to a conjecture that since E8 folds to H4+H4Φ (600 cells) and D6 folds to H3+H3Φ, that the 6-Cube should fold to an outer and inner rhombic triacontahedron scaled by Φ.
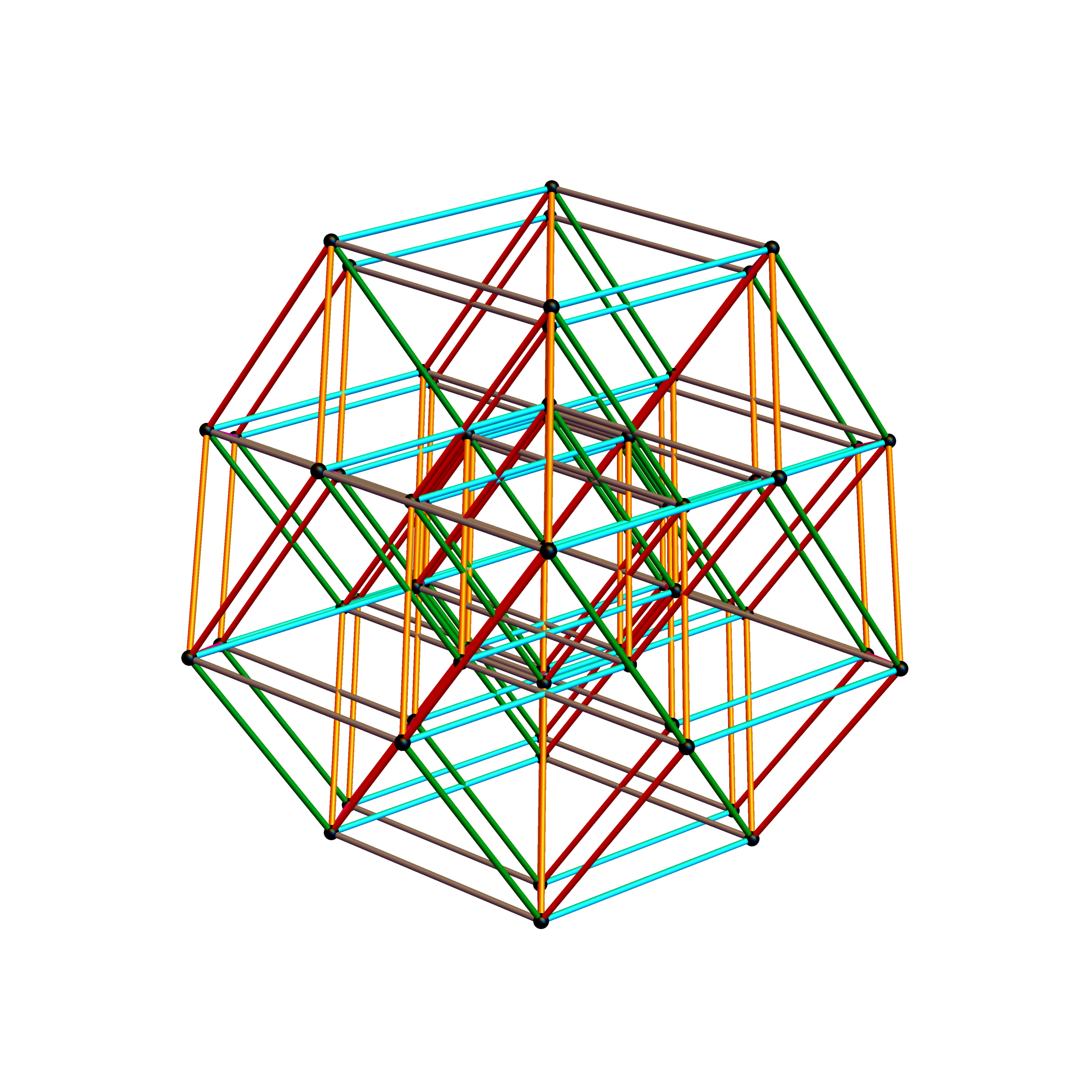
Below is a visualization of D6 folding into 2 concentric H3 icosadodecahedrons at a ratio of Φ using the same projection as described above. The edging displays the 480 Norm’d 6D Sqrt[2] length edges, clearly showing the outer and inner H3 polytopes.

Shown with exterior faces on edges (not a pure convex hull algorithm)…
The data below shows two sets of 30 vertices (outer on the left and inner on the right). They are sorted by the 3D Norm’d length of the vertex ray from {0,0,0}, followed by the vertex number in the E8 to H4+H4Φ list at the end of the post referenced above, along with the 6D E8 vertex that is a member of the D6 set, and the {x,y,z} projected vertex position

The last line of the data set shows that the first set of outer 30 projected vertex locations on the left is numerically equal to the second inner set after multiplication by Φ.

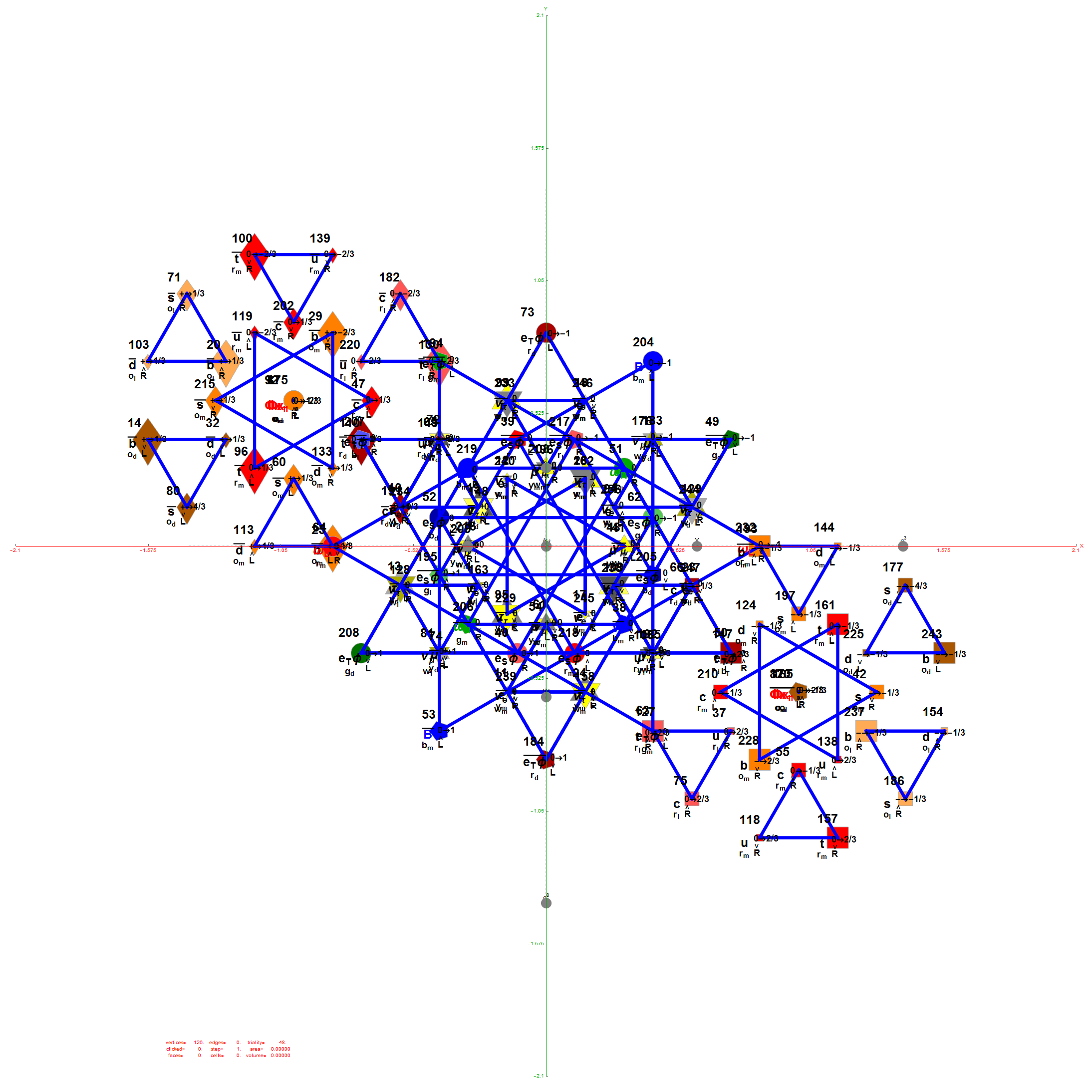
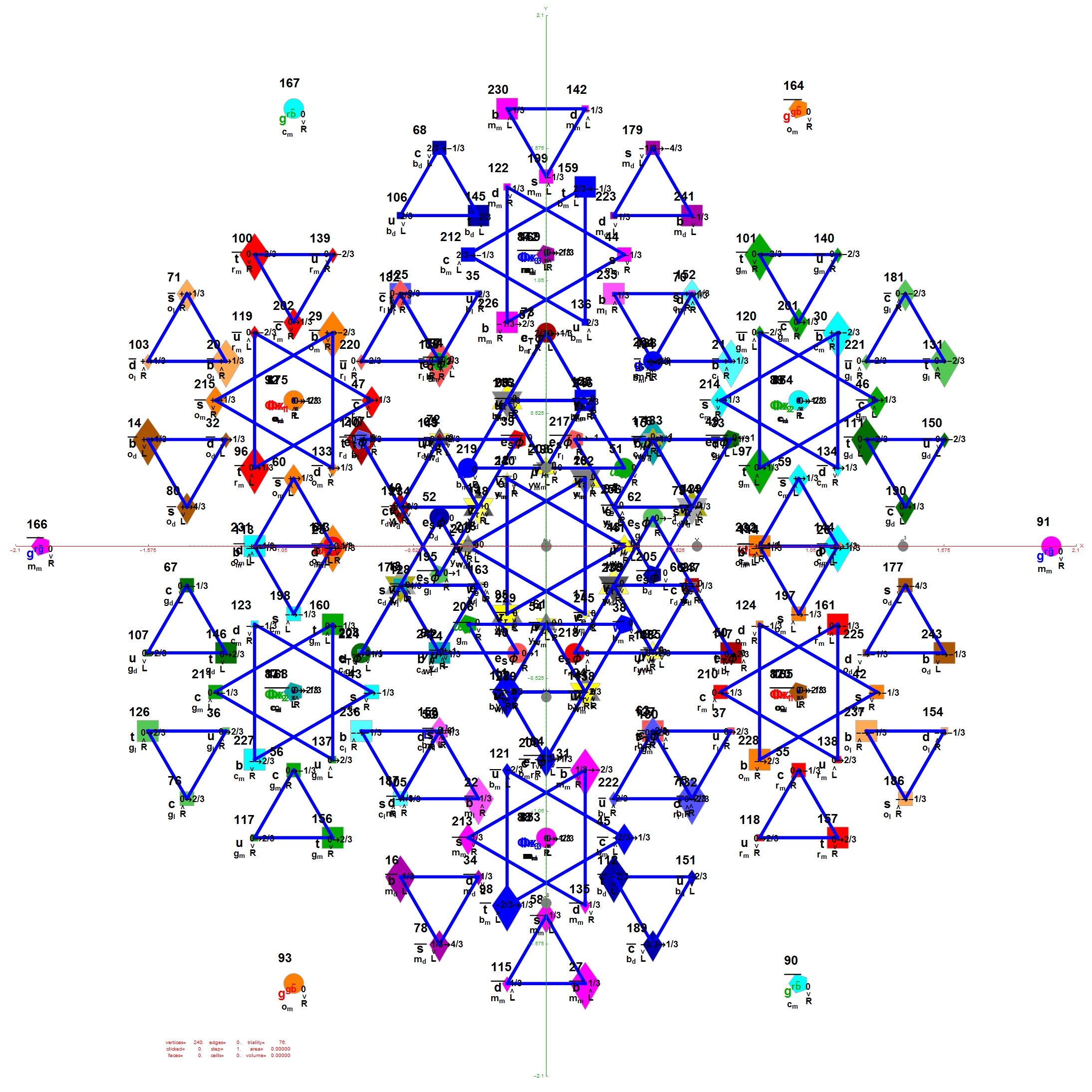
I did the same for the Rhombic Triacontahedron projected out of the 6-Cube.
I separated the outer and inner vertices used to make the WP projection at the top of the post. There are 64 vertices and 192 6D unit length edges forming pentagonal symmetry along specific axis (as well as hexagonal symmetries on other axis). It is clear that scaling the inner 32 vertex locations by Φ is not going to give the outer 32 vertex positions. Yet there is a similarity- they both have 12 vertices of one 3D Norm’d length and 20 of another.
Outer 32 vertices and 60 unit length Norm’d 6D edges.
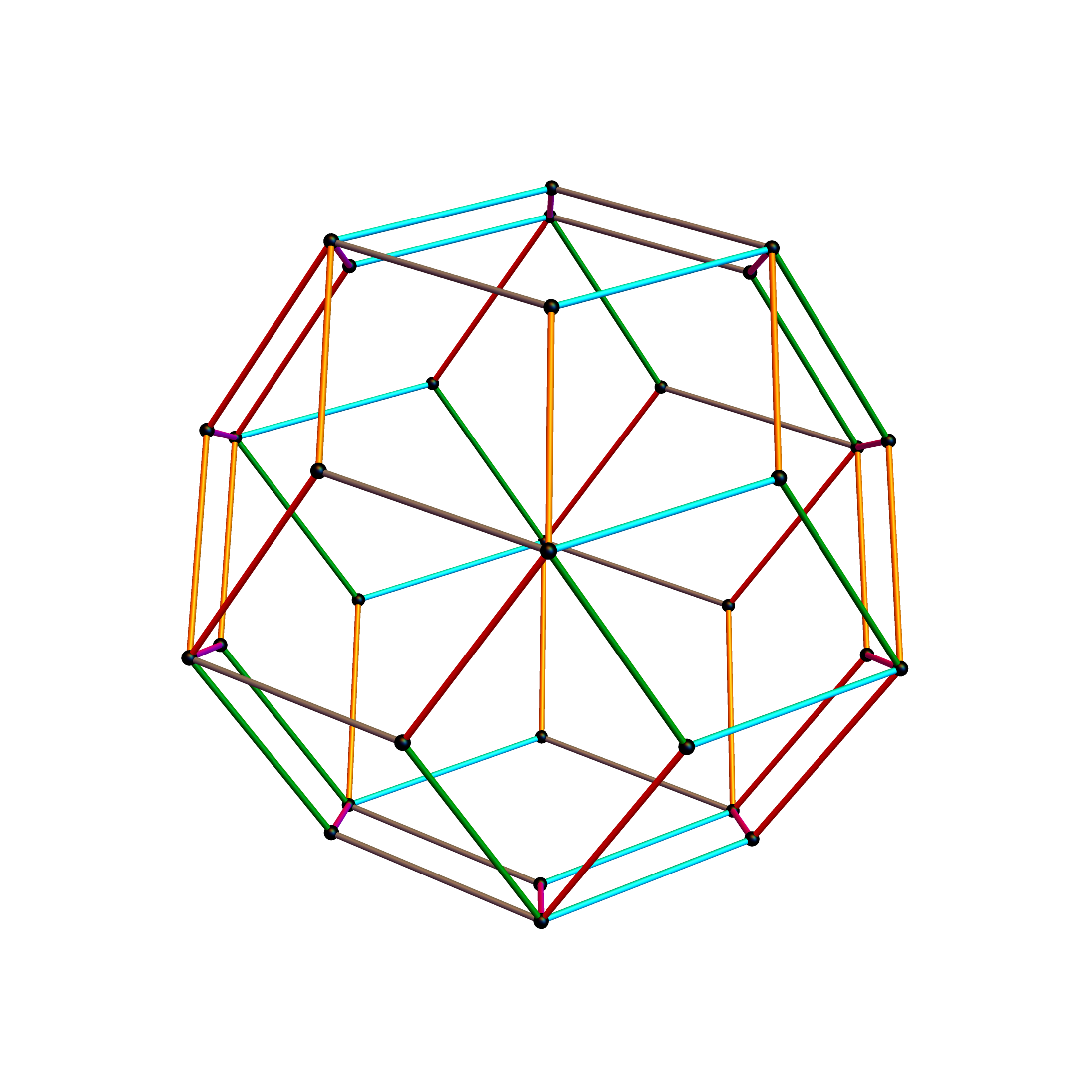
The edge coloring on the projection above is defined by which of the 6 dimensional axis the edge aligns with.
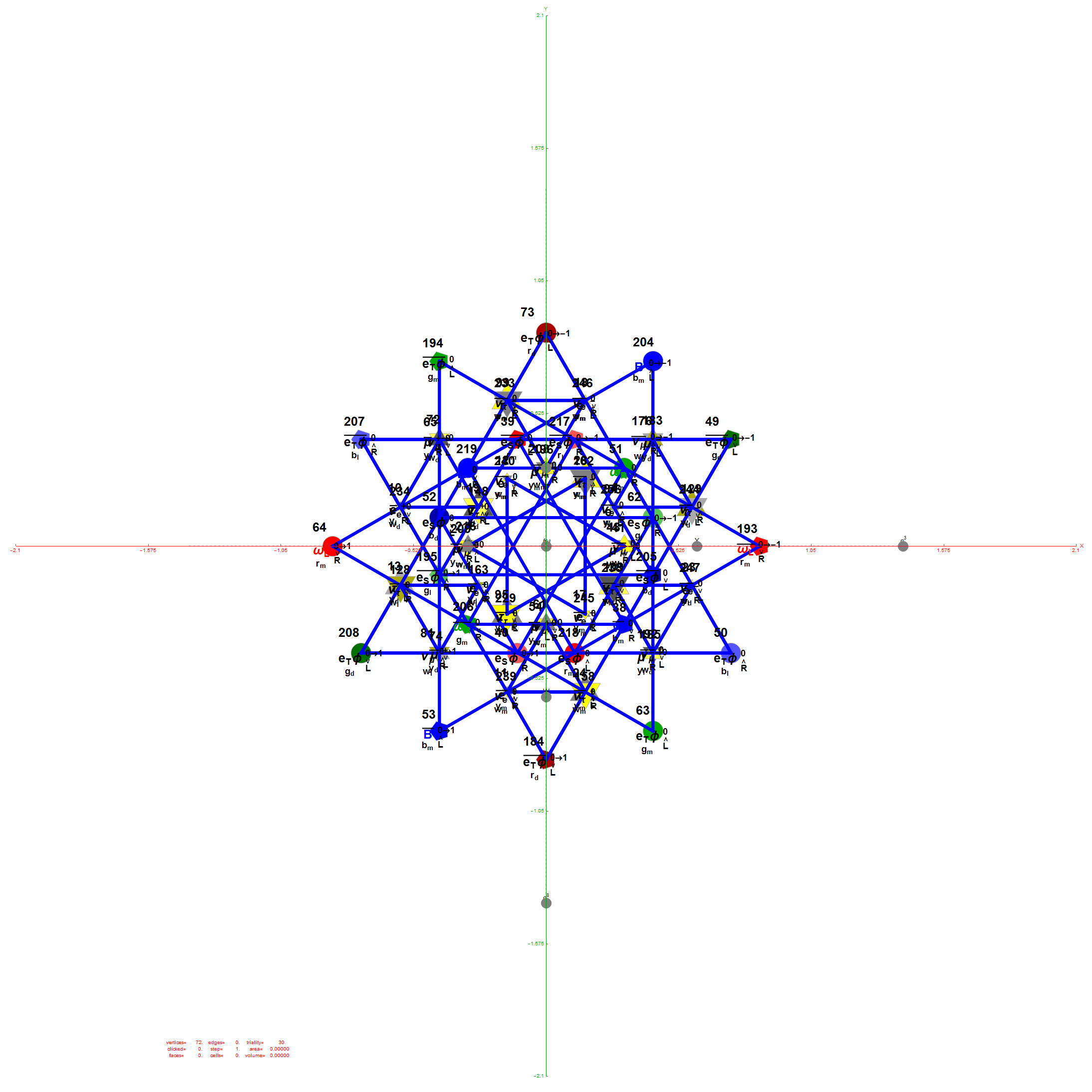
Inner 32 vertices and 60 unit length Norm’d 6D edges.
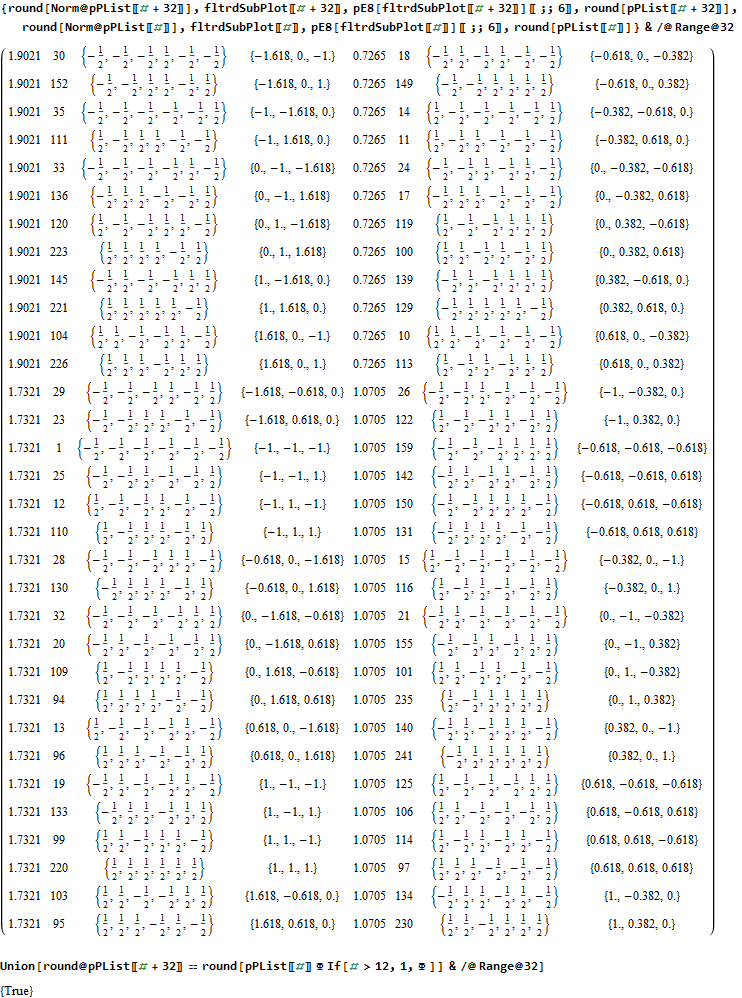
The last line of the data set above shows that the outer data (left) is the same as the inner data set multiplied by a factor of Φ when the first 12 (shorter 3D Norm’d) inner vertices (right) are multiplied by an additional factor of Φ.
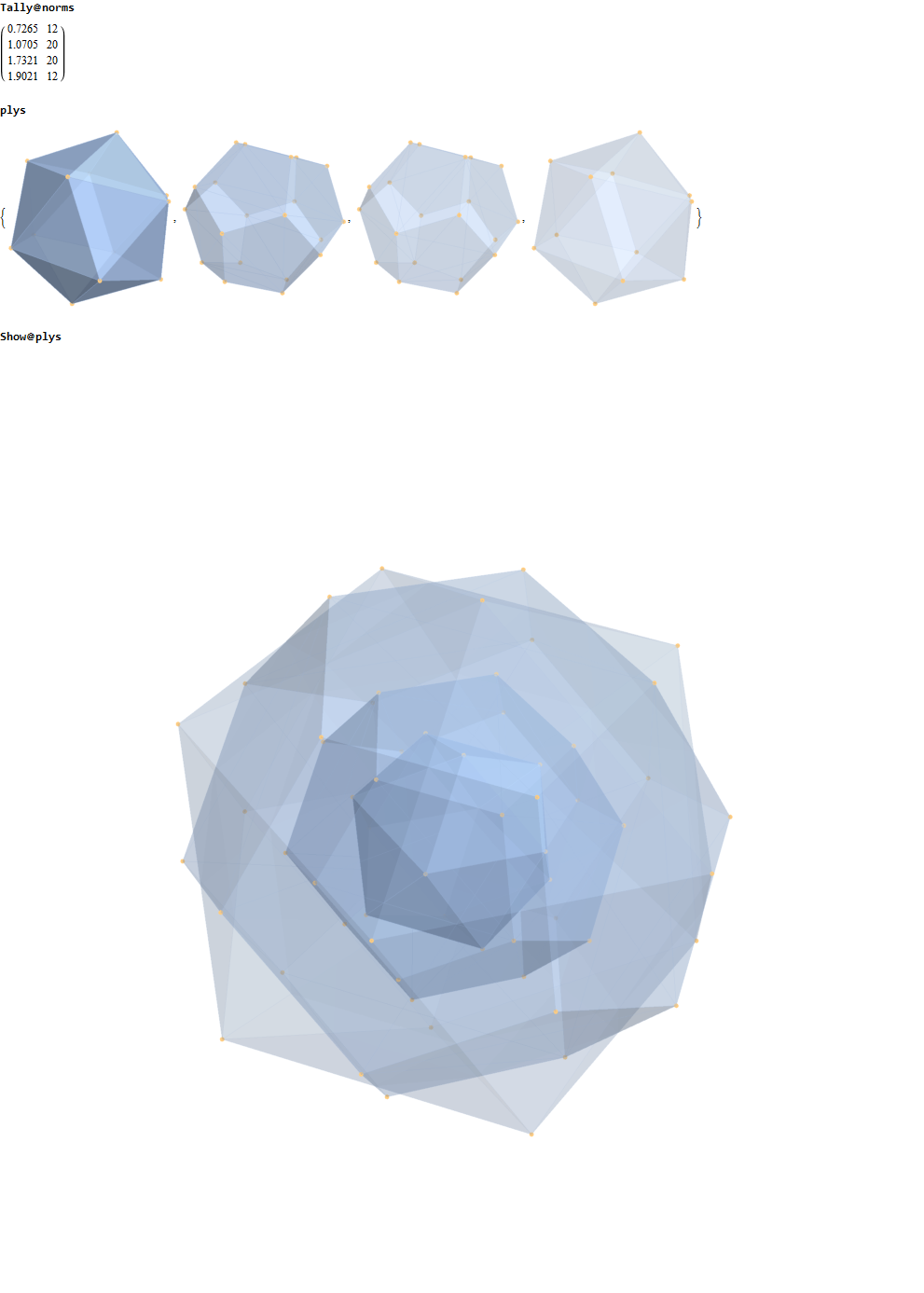
This explains the lack of isomorphism, but why is it not like the D6 to H3+H3Φ and E8 to H4+H4Φ in the symmetry of Φ scaling?
The best explanation I can give involves the pattern of left vs. right 3 digits in the 6-Cube E8 vertices. This is due to the left right symmetry of the basis vectors applied to binary pattern of half integer vertices in the 6-Cube.
All vertices have a consistent pattern that differentiates the 20 longer Norm’d vertices from the 12 shorter ones. Specifically, the shorter 12 that have the inner ones needing the added factor of Φ always show that:
- the right inner vertices all have an even number in 6 +/- elements but not always evenly split across the left and right
- the left outer vertices all have an odd number of in 6 +/- elements always unevenly split across the left and right
Whereas, the longer 20 that match the Φ scaling reverse the pattern where:
- the right inner vertices all have an odd number in 6 of +/- elements always unevenly split across the left and right
- the left outer vertices all have an even number in 6 of +/- elements but not always evenly split across the left and right
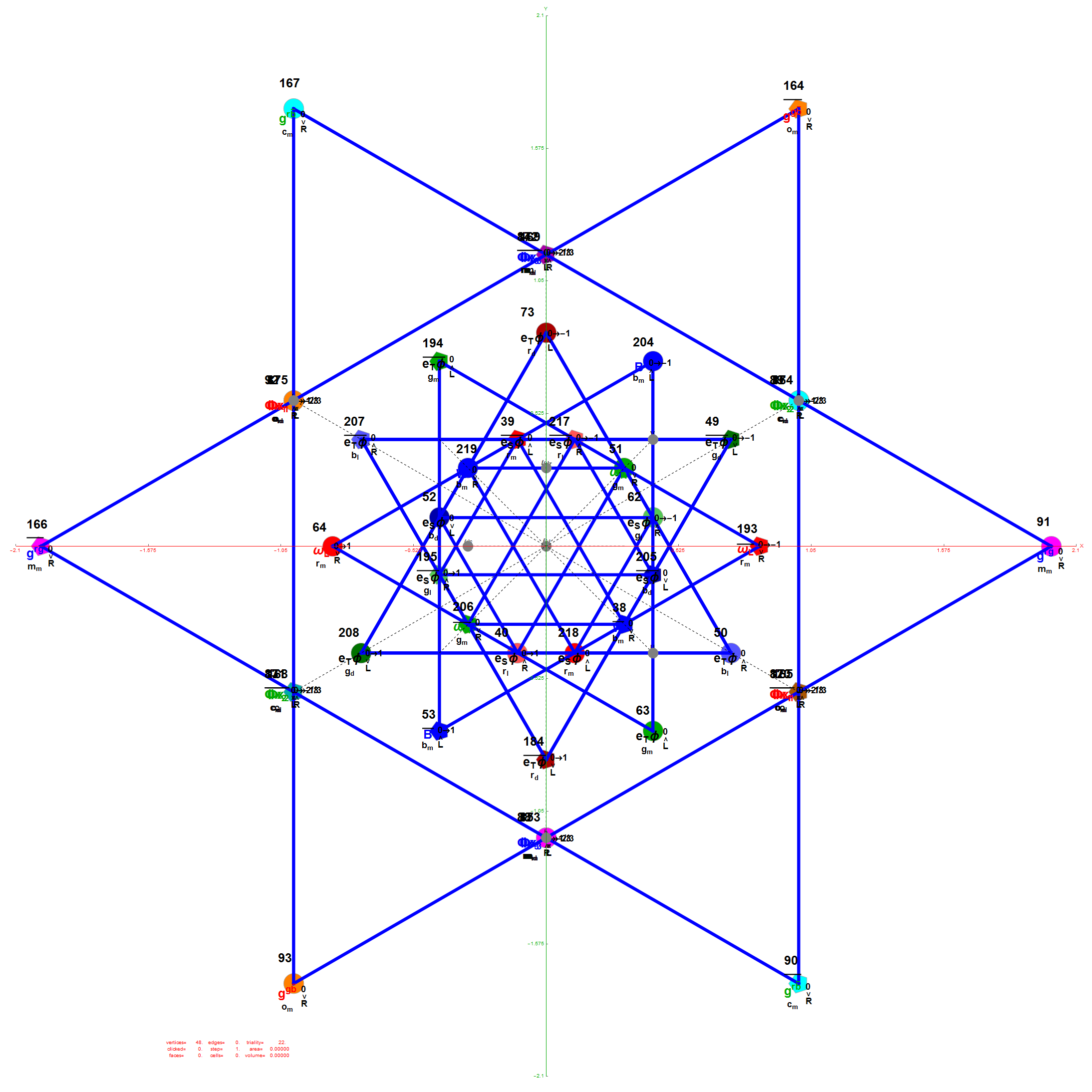
Another related fact in the folding pattern of the 6-Cube emerges when we note that since E8 contains 128 1/2 integer BC8 (the 8 Demi-Cube). In addition, we note that the 6D complement of BC8 and the 6-Cube is the same set of vertices. This means we get the same projection using all 128 vertices of the 6D trimmed BC8 as we do with the 64 of the 6-Cube, except now there are 768 6D Norm’d unit length edges rather than 192. Interestingly, that means that similar to E8 containing simultaneous copies of 4 600-Cells (a left and right pair scaled at Φ), E8 contains 4 simultaneous copies of the rhombic triacontahedron after adding the Φ scaling on the two sets of 12 inner BC8 vertices).
Wow – that is nice! Remember, you heard it here first!
If we try this idea with the complement of the integer elements of E8, namely the 112 6D trimmed D8 vertices complemented with 60 D6 vertices, the 6D trimmed 52 vertex complement contains 4 identical copies of the excluded 16 generator vertices of E8 {+/-1,0,0,0,0,0,0,0} permutations (plus 4 {0,0,0,0,0,0,0,0} vertices).
As you can see, the folding of the integer elements of E8 do not fold the same as the 1/2 integer elements, and in retrospect, we probably should not expect them to.
It is because of the symmetric 4D left/right symmetry of E8=BC8+D8 that we get the wonderful folding of it into H4+H4Φ !