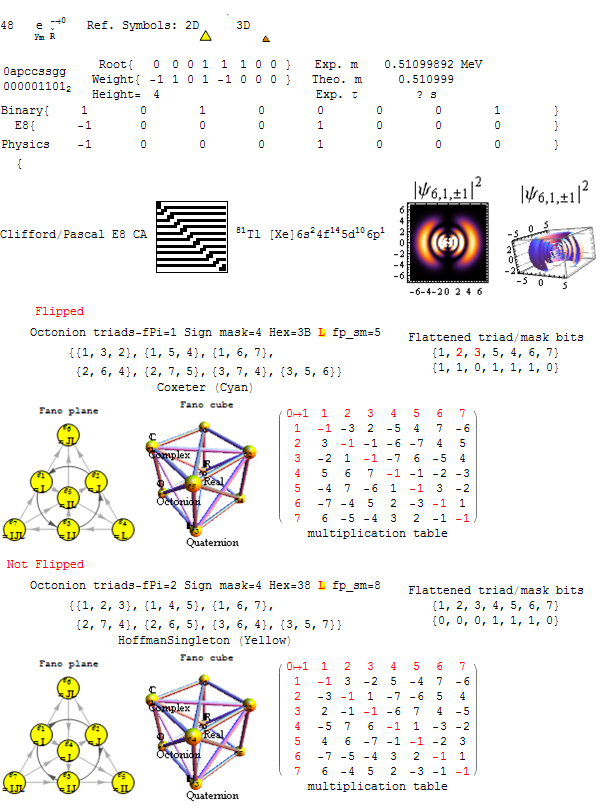
While it still needs some work – I’ve integrated the atomic elements to the Octonions, E8 and theoretical Lisi eSM model particle assignments (along with Wolfram’s NKS Cellular Automata linked to the Clifford Algebra/Pascal Triangle binary assignments). I have combined all these visualizations with the 2D/3D electron orbitals (based on the symmetry of the {n,l,m,s} quantum numbers (from the Stowe-Janet-Scerri Periodic Table. I totally understand this is not easy to dig into w/o some effort, but … it looks cool 😉
It is shown in an updated version of Fano.pdf. This is a very large and complex 30Mb file – with 241 pages. It shows the Lisi particle assignments, the E8 roots, split real even (SRE) E8 vertex and the Lisi “physics rotation”. It also shows two Fano plane and cubic derived from the symmetries of the E8 particle assignments (and all the relevant construction of it). See the interactive demo or the Mathematica Notebook for a more “navigational look” at the integration.