Here is a snapshot of the UI.

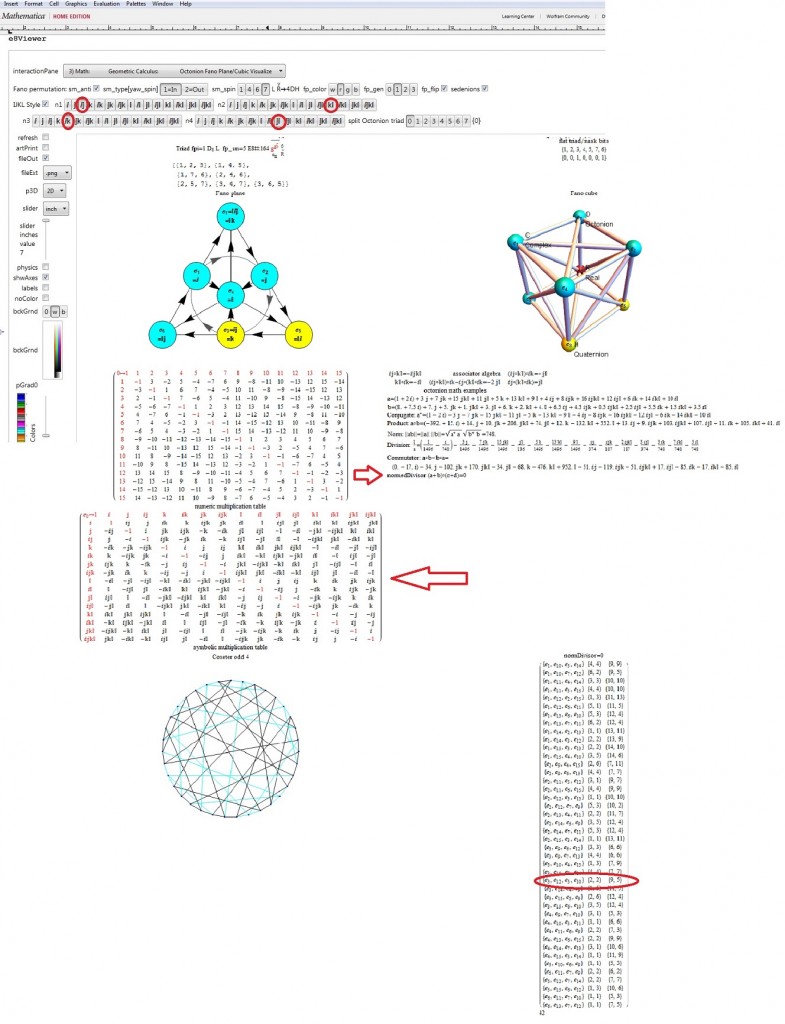
It is taken from an example given on this website: http://www.derivativesinvesting.net/article/307057068/a-few-hypercomplex-numbers/, which uses the harder to read IJKL style notation.

Compare the upper left quadrant of the multiplication table. It is the same as the octonion of E8 #164 (non-Flipped) used to generate the sedenion using the Cayley-Dickson doubling. It can be read off using the Fano Plane (or Fano Cube) mnemonic. My next post will show the Sedenion forms of these, namely the Fano Tetrahedron and Tesseract!

Notice the highlighting of the interesting aspect of sedenions, where some non-zero p=a+b and q=c+d give a product pq=0. These are given in a list of the {a,b,c,d} where p={a+b} and q={c+d} and pq=0 (along with the deltas between the indices), always 42 excluding trivial juxtapositions. In this case, it is the row entry with {3,12,5,10}.

Here is the computation of the same table in the format given in the Sedenion Wikipedia article.