Tag Archives: Math
E8 to H4 Folding Matrix work cited in the American Mathematical Society Blog
This blogs.ams.org/visualinsight article is an American Mathematical Society post based on some of my work.
This animated Gif from the article is from Greg Egan
Chaotic Attractor Animations
Hopf Fibration and Chaotic Attractors, etc.
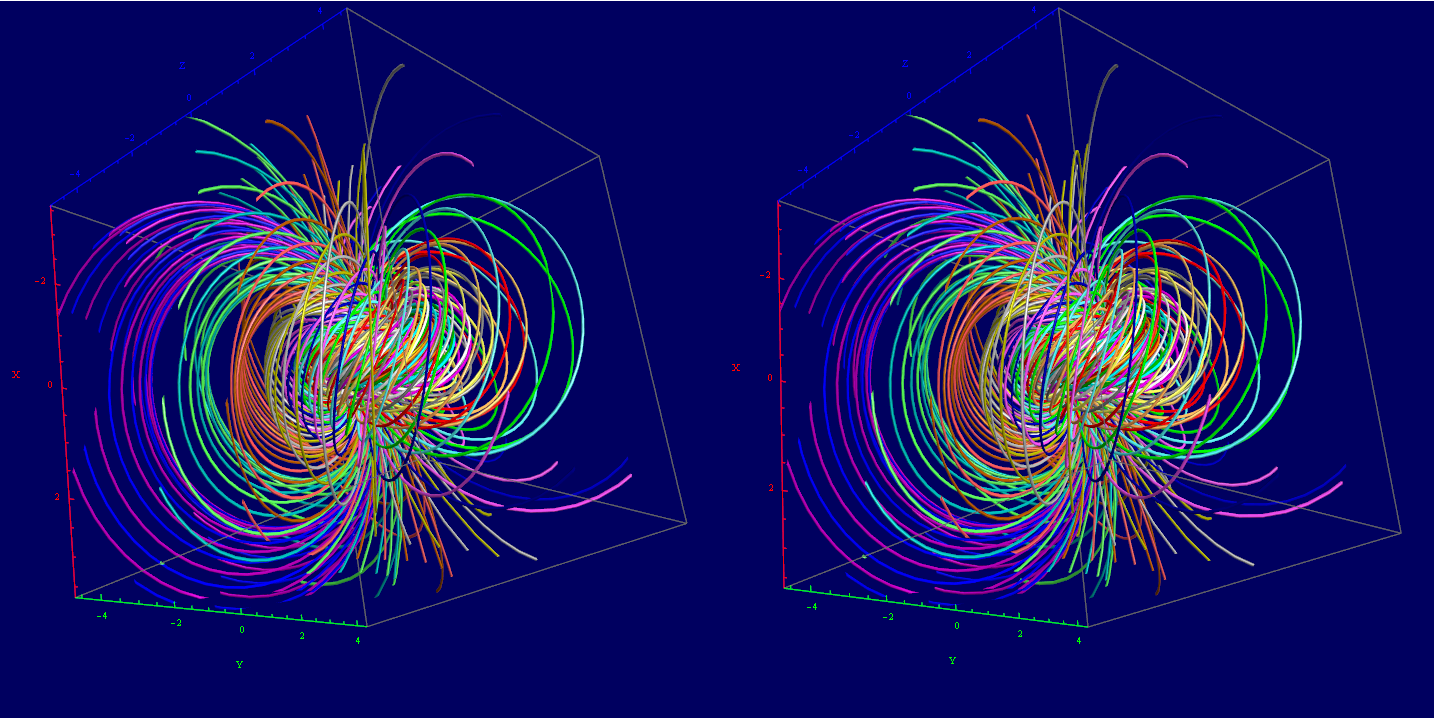
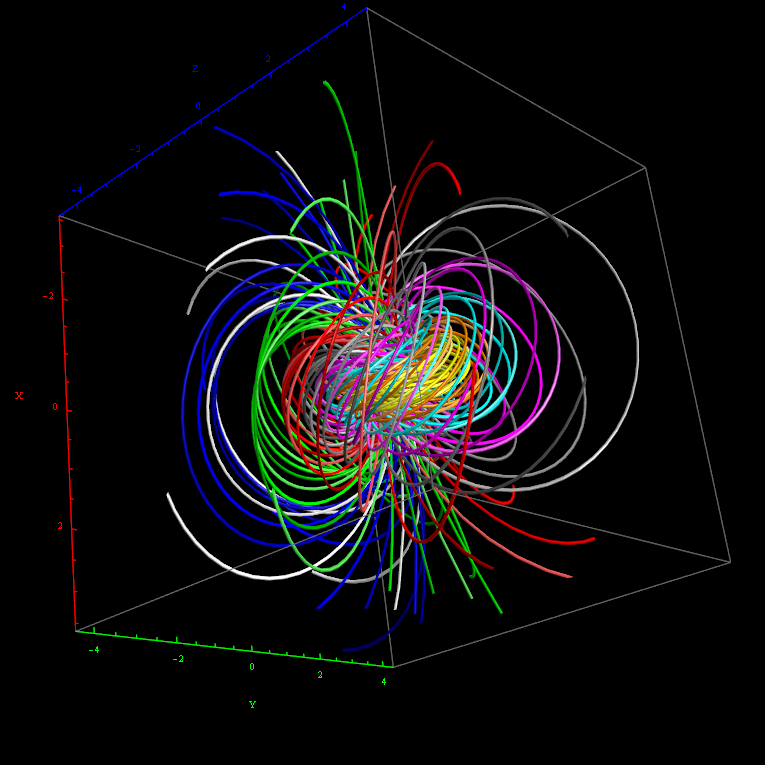
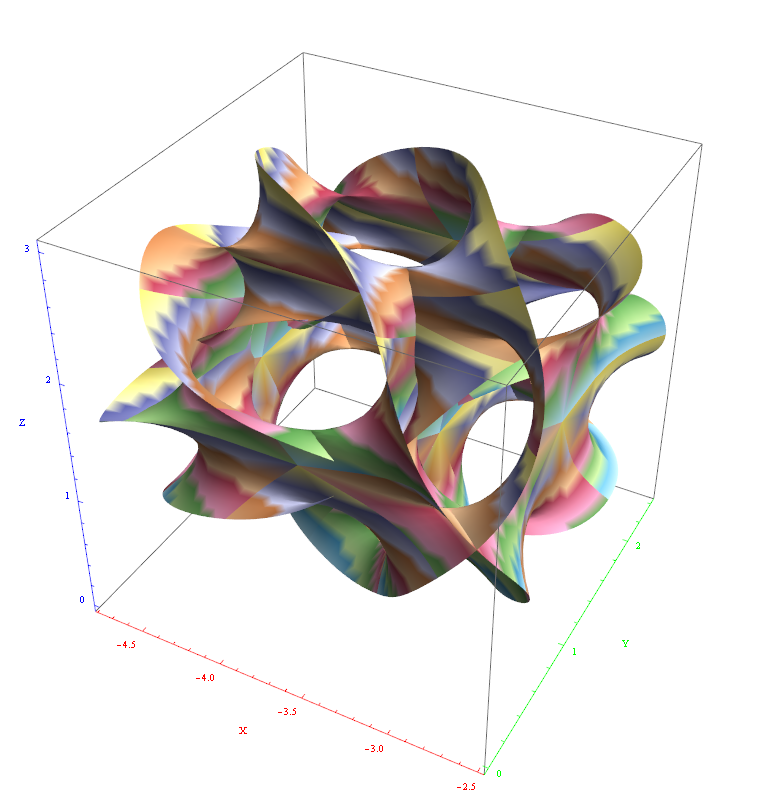
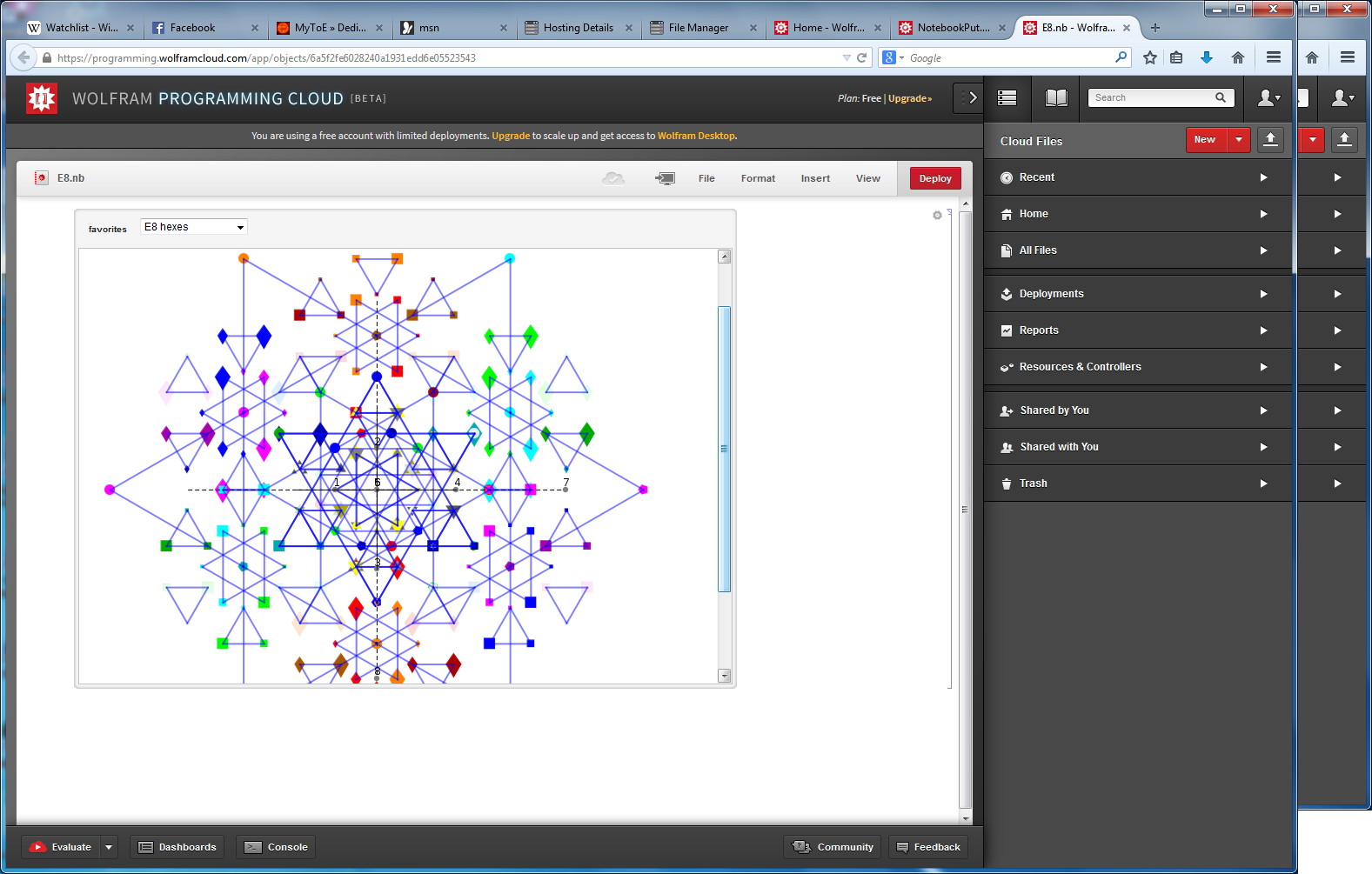
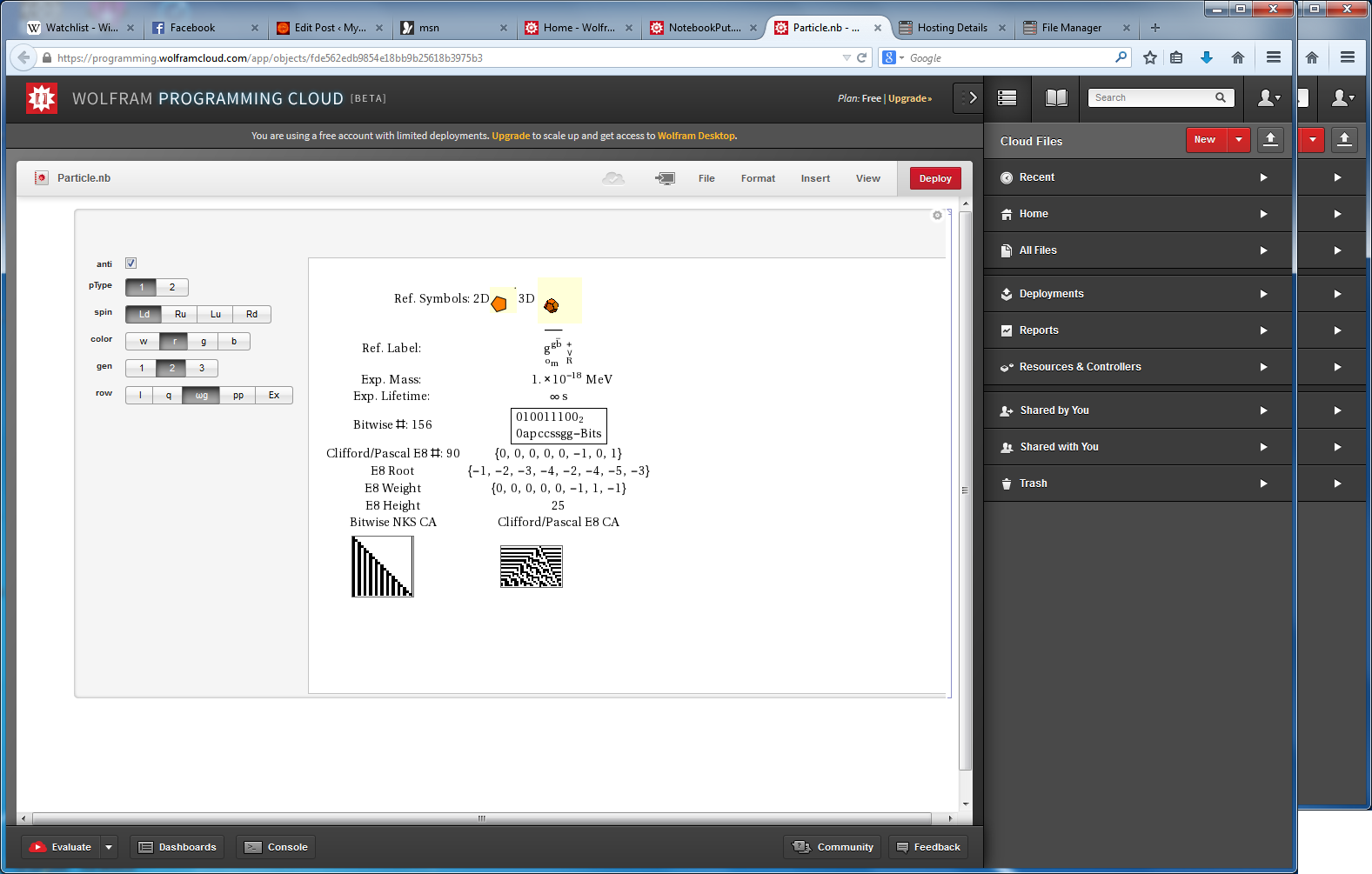
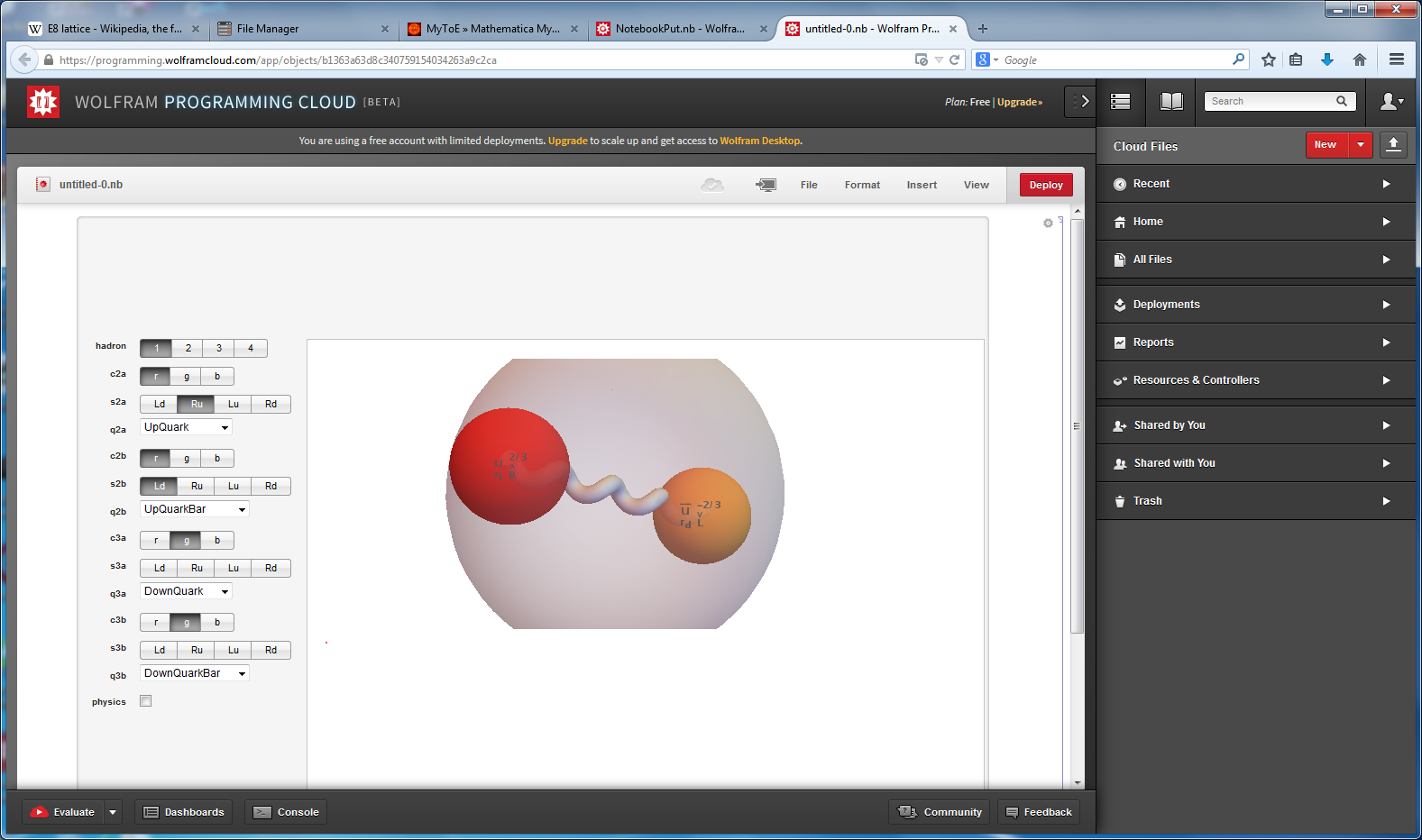
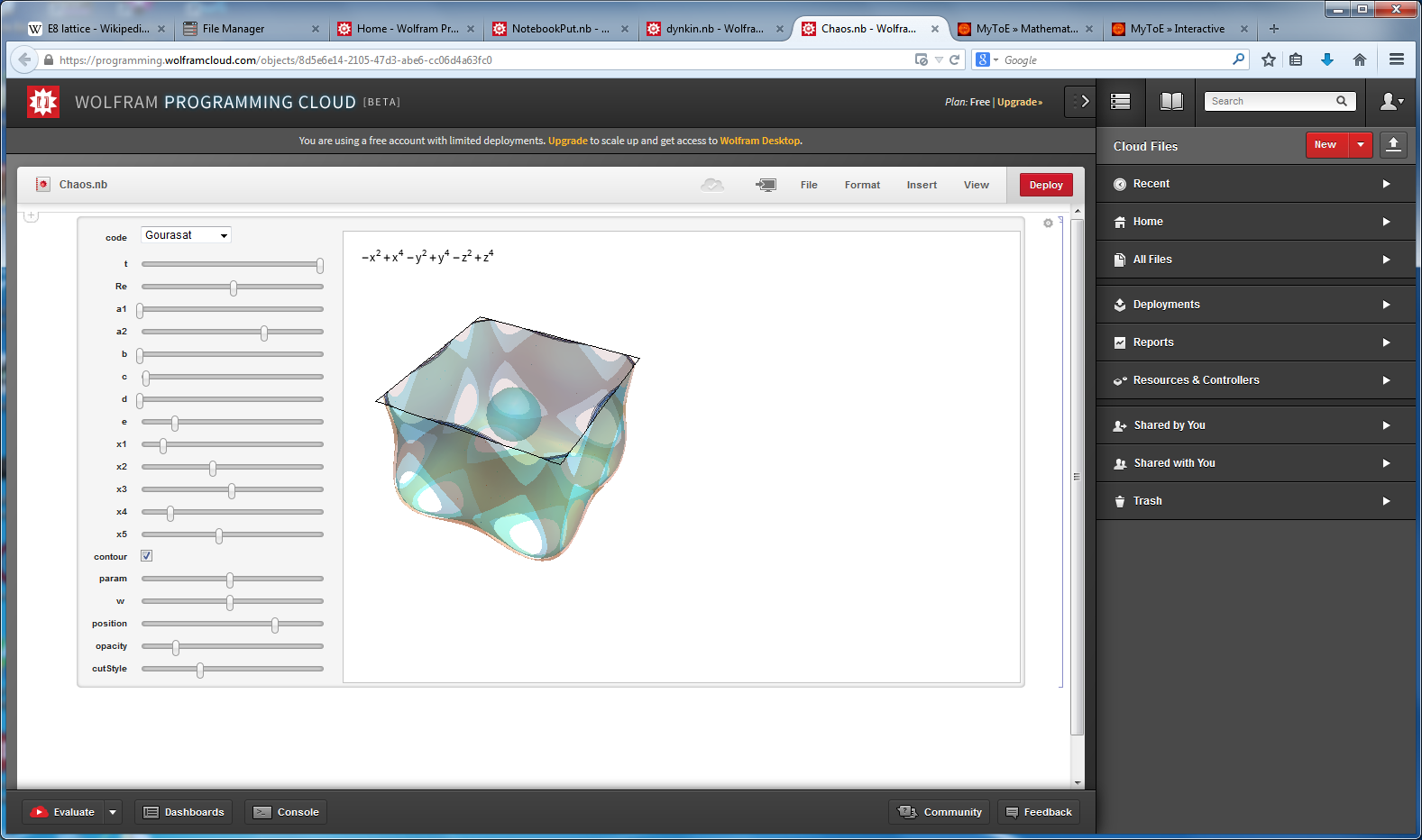
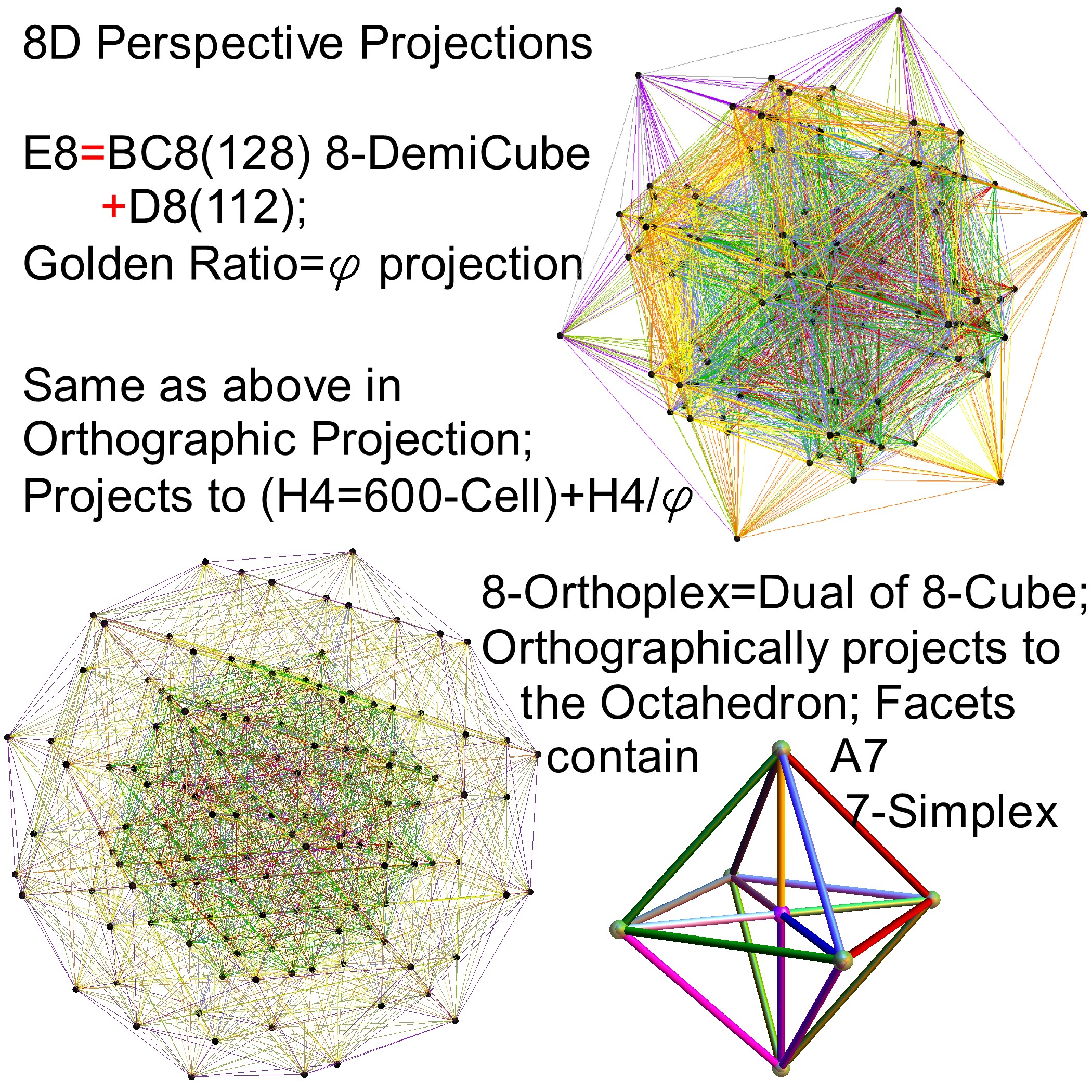
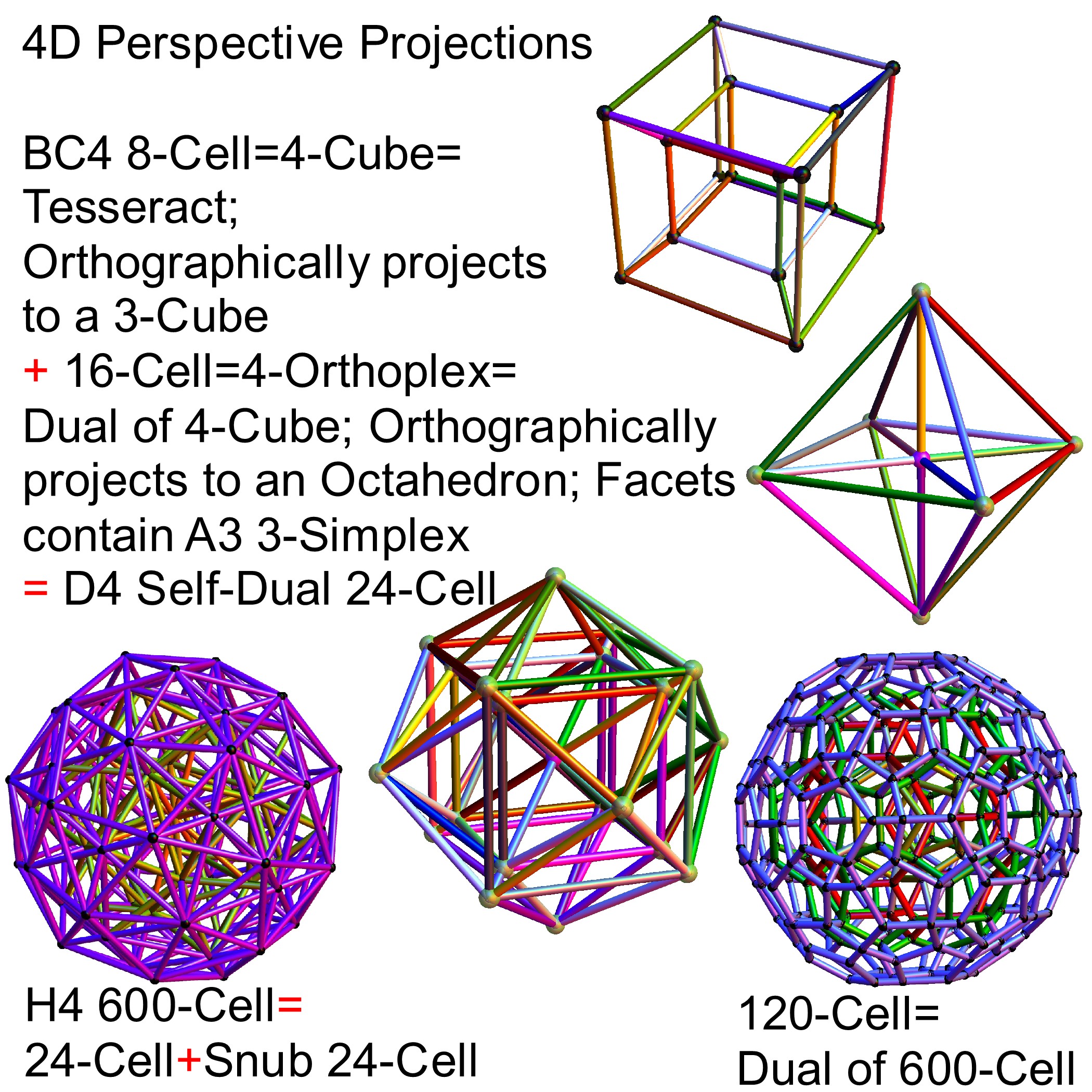
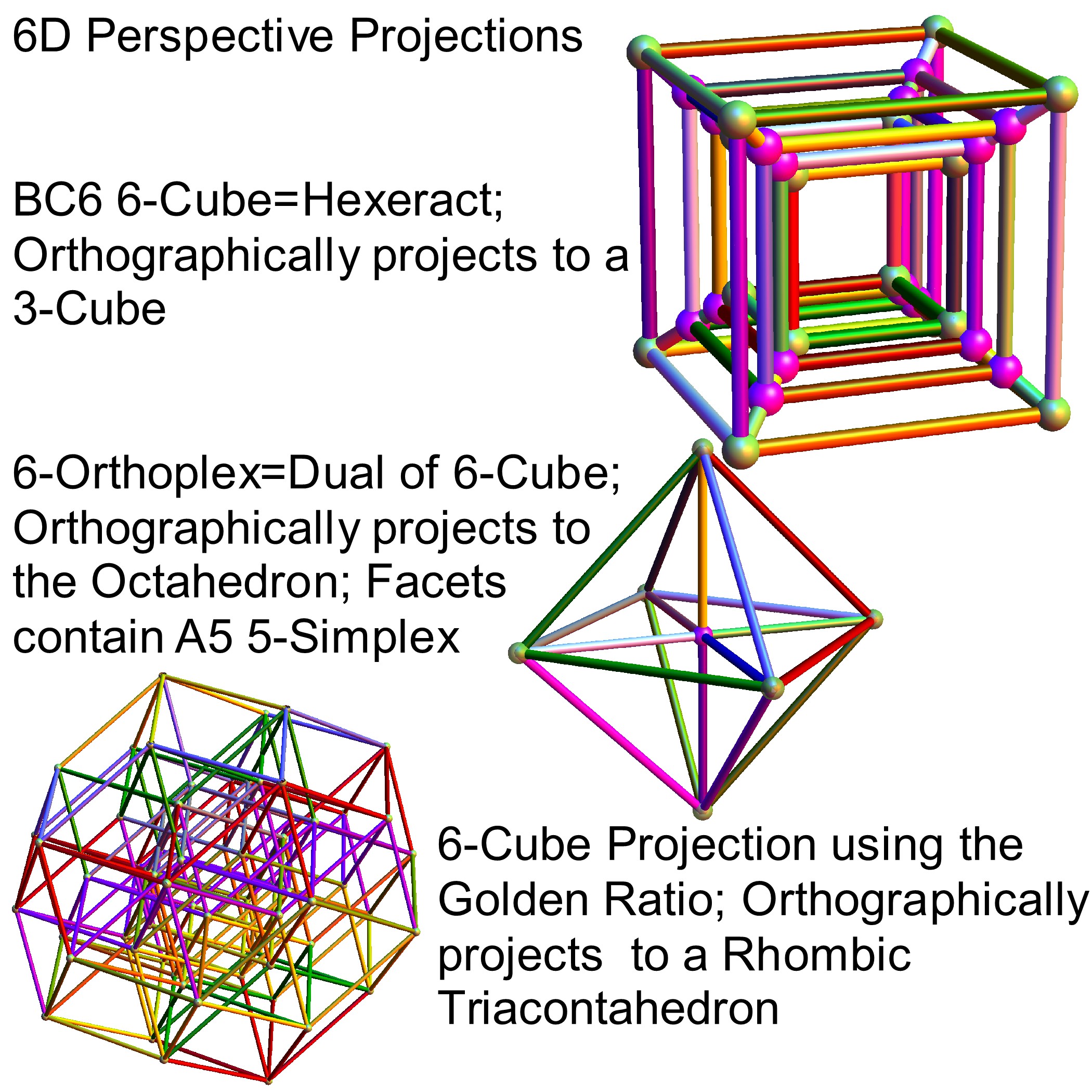
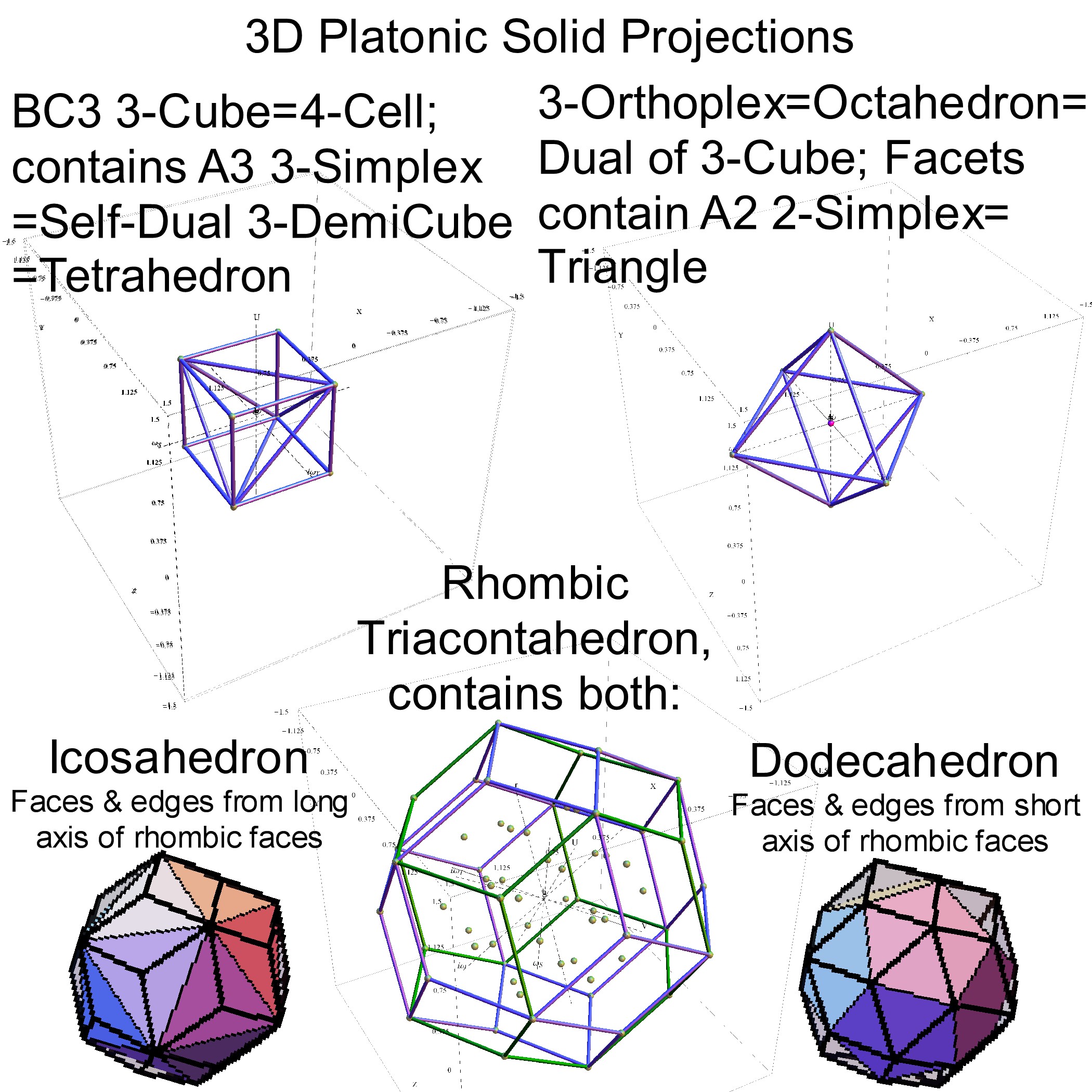
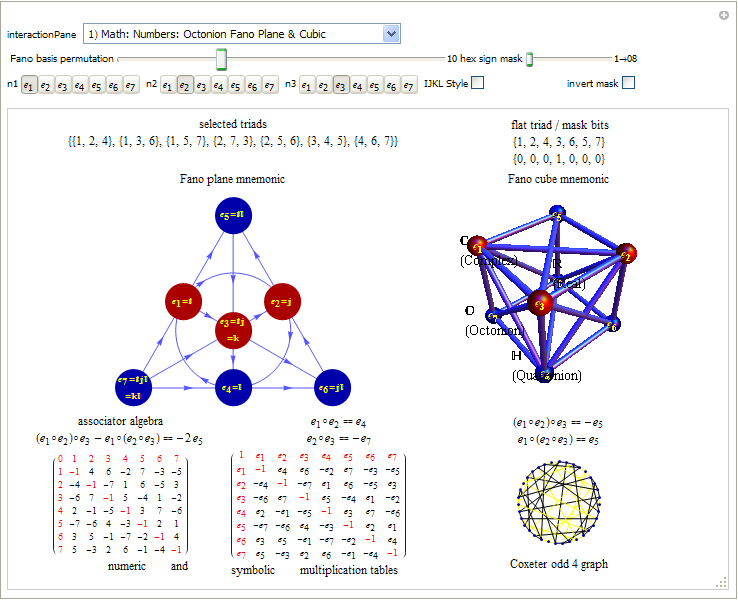
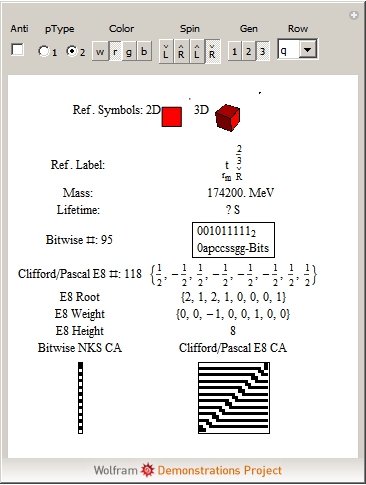
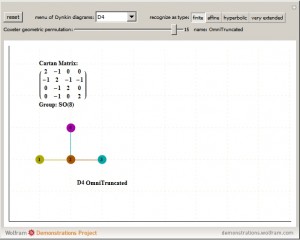
I’ve added some new features to my VisibLie_E8 ToE Demonstration. Some of it comes from Richard Hennigan’s Rotating The Hopf Fibration and Enrique Zeleny’s A Collection Of Chaotic Attractors . These are excellent demonstrations that I’ve now included with the features of my integrated ToE demonstration, since they are not only great visualizations, but relate to the high-dimensional physics of E8, octonions and their projections. This gives the opportunity to change the background and color schemes, as well as output 3D models or stereoscopic L/R and red-cyan anaglyph images.
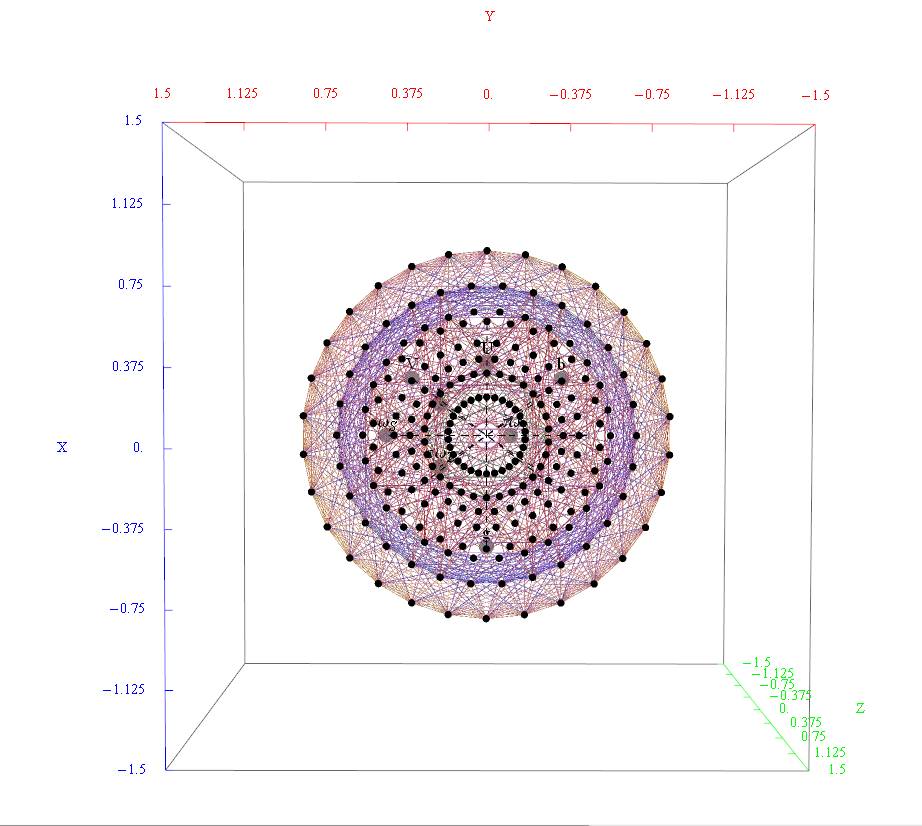
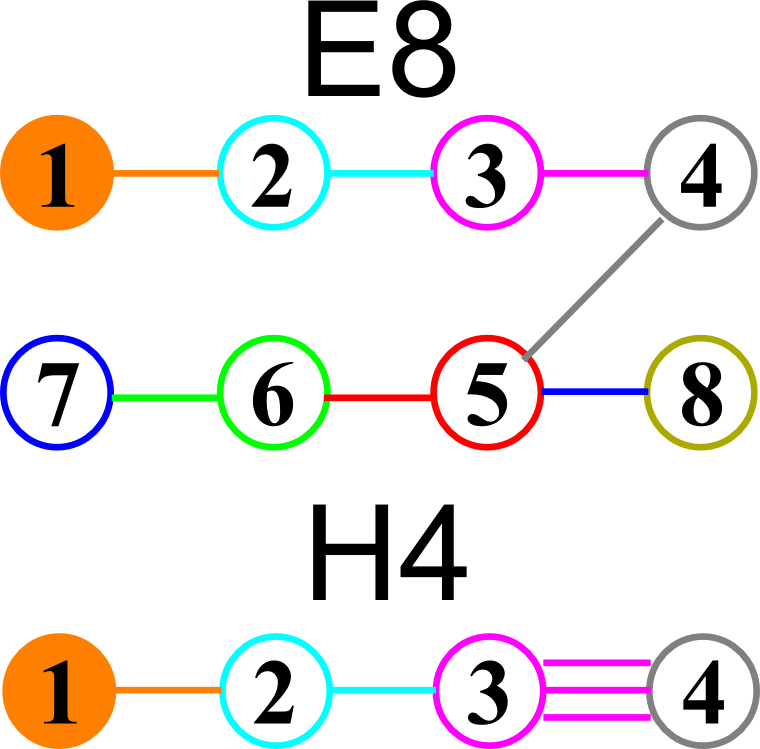
I’ve also used David Madore’s help to calculate the symbolic value of the E7 18-gon and 20-gon symmetries of E8. It uses the nth roots of unity (18 and 20, in this case) and applies a recursive dot product matrix based on the Weyl group centralizer elements of a given conjugacy class of E8. I ended up using a combination of Mathematica Group Theory built-in functions, SuperLie and also LieART packages. These symbolic projection values are:
Math only version of E8 to H4 projection
Mathematica MyToE on the Wolfram Cloud
I am playing around with the Wolfram Tweet-a-Program, and the Wolfram Language (i.e. Mathematica) on the Wolfram Cloud.
What’s really cool is that you can now interact with advanced math and HPC on your phone/tablet.
Here are a few results…
@Wolframtap
BTW – you will need a WolframID (and be logged into WolframCloud.com) to interact with these pages.
Octonions: The Fano Plane & Cubic
Navier-Stokes Chaos Theory, 6D Calabi-Yau and 3D/4D Surface visualizations
Solar System (from NBody Universe Simulator)
Added 3D and 4D Fractals and Surfaces (e.g. Calabi-Yau and Boy) to Pane 7
E8 folding to H4+H4/φ
I found the rotation matrix that shows the E8 Dynkin diagram can indeed be folded to H4+H4/φ.
The H4 and its 120 vertices make up the 4D 600 Cell. It is made up of 96 vertices of the Snub 24-Cell and the 24 vertices of the 24-Cell=[16 vertex Tesseract=8-Cell and the 8 vertices of the 4-Orthoplex=16-Cell]).
It can be generated from the 240 split real even E8 vertices using a 4×8 rotation matrix:
x = (1, φ, 0, -1, φ, 0, 0, 0)
y = (φ, 0, 1, φ, 0, -1, 0, 0)
z = (0, 1, φ, 0, -1, φ, 0, 0)
w = (0, 0, 0, 0, 0, 0, φ^2, 1/φ)
where φ=Golden Ratio=(1+Sqrt(5))/2
It is also interesting to note that the x, y, and z vectors project to a hull of the 3D Rhombic Triacontrahedron from the 6D 6 cube Hexaract (which then generates the hull of the Dodecahedron and Icosahedron Platonic solids).
Here’s a look at the Dynkin Diagram folding of E8 to H4+H4/φ:
I find in folding from 8D to 4D, that the 6720 edge counts split into two sets of 3360 from E8’s 6720 length Sqrt(2), but the combined edges and vertices recreate the E8 petrie diagram perfectly.
Some visualizations of this in 8D:
to 4D:
and also showing the Rhombic Triacontrahedron folding from 6D:
to 3D:
Complete Integration of Octonions with E8
I’ve updated all .CDF, .NB and older .NBP demonstration code with Mathematica v.9
This now includes the completed integration of octonions with E8 & the extended Stadard Model particle assignments. This means the 480 octonions are in fact in a 2:1 cover of E8’s 240 vertices (with their association to Lisi’s particle assignments). This creates the opportunity for a self-dual type of “super symmetry” where all three generations emerge from the octonions.
Octonions, Quaternions and the Fano plane mnemonic – Conquered!
See:
http://theoryofeverything.org/TOE/JGM/ToE_Demonstration.cdf
Of course, it requires the free Mathematica CDF plugin.