After significant peer review, my Dynkin Diagram Visualizer was published at Wolfram Demonstrations. Please see http://demonstrations.wolfram.com/DynkinDiagrams/
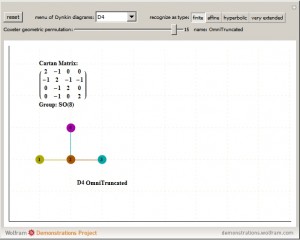
After significant peer review, my Dynkin Diagram Visualizer was published at Wolfram Demonstrations. Please see http://demonstrations.wolfram.com/DynkinDiagrams/

This free Mathematica Computable Document Format (.CDF) demonstration takes you on an integrated visual journey from the abstract elements of geometry, algebra, particle and nuclear physics, and on to the atomic elements of chemistry. http://theoryofeverything.org/TOE/JGM/ToE_Demonstration.cdf (0.5Mb)
It requires the free Mathematica CDF plugin.
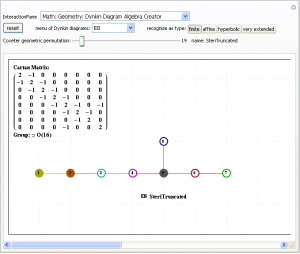
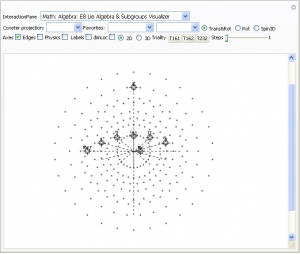

This is an image of the electron diffraction pattern of an icosahedral Zn-Mg-Ho quasicrystal with an overlay of a 5-Cube projection from the 240 vertices of the split real even E8 Lie Group.
The basis vectors for the E8 projection are shown (1:1 with the ring of gray vertices with the last 3 of 8 dimensions 0).
There are 2480 overlapping edge lines from the 240 E8 vertices. They have norm’d unit length calculated from the 5 non-zero projected dimensions of E8. Of these, 32 inner vertices and 80 edges belong to the 5D 5-Cube (Penteract) proper. Edges are shown with colors assigned based on origin vertex distance from the outer perimeter.
The vertex colors of the 5-Cube projection represent E8 vertex overlaps. These are:
InView vertices={color{overlap,count},…}Total
{LightGreen{1,20},Pink{5,20},Gray{10,10},Orange{20,1}}51
All vertices={color{overlap,count},…}Total
{LightGreen{1,20},Pink{5,100},Gray{10,100},Orange{20,20}}240
A related projection of a 6D 6-Cube (Hexeract) into a perspective 3D object using the Golden Ratio [Phi]. This particular projection is used to understand the structure of QuasiCrystals. The specific basis vectors are:
x = {1, [Phi], 0, -1, [Phi], 0}
y = {[Phi], 0, 1, [Phi], 0, -1}
z = {0, 1, [Phi], 0, -1, [Phi]}
There are 64 vertices and 192 unit length edges forming pentagonal symmetry along specific axis (as well as hexagonal symmetries on other axis).
I’ve just posted a new paper on using the simple roots of E8 to reduce the particle count of the Lisi model from 240 to 8. See DynkinParticleReductions.pdf
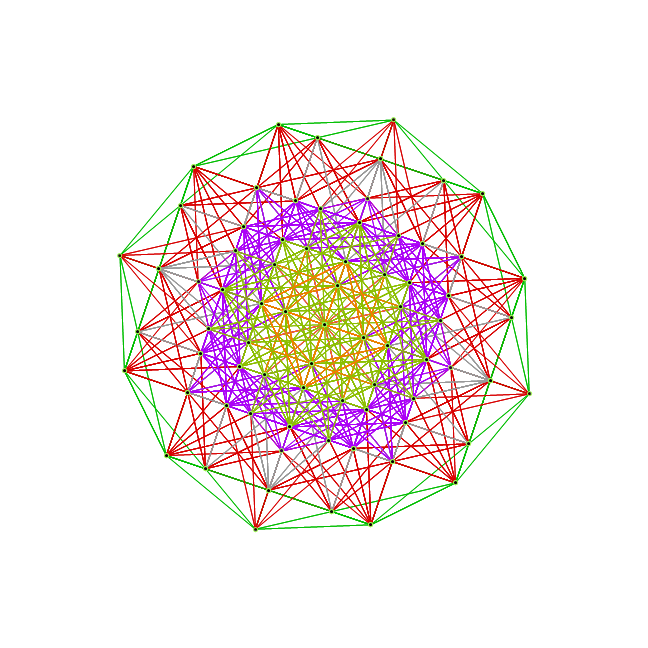 While the 3D model I used to create the 2D Van Oss projection isomorphic to E8 Petrie (and a beautiful pentagonal view), it was not the same as what was being used by Richter in his 3D “pre-Van-Oss” construction. Given my H (or x) and V (or y), the 3rd basis vector for this projections is most likely:
While the 3D model I used to create the 2D Van Oss projection isomorphic to E8 Petrie (and a beautiful pentagonal view), it was not the same as what was being used by Richter in his 3D “pre-Van-Oss” construction. Given my H (or x) and V (or y), the 3rd basis vector for this projections is most likely:
Z={0, -0.0801064, 0, 0.236818, 0, 0.0801064, 0, -0.236818}
which reproduces the Richter, Bathsheba and Wizzy’s 3D models. Interestingly, it produces one face (shown above) that is the same as all the orthonormal faces of 2 concentric 600 Cells (at the Golden Ratio). The 3rd unique face is:
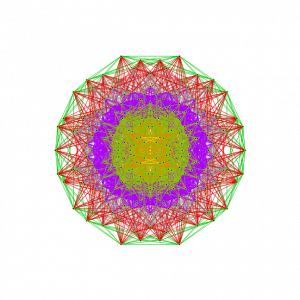
I replaced the 3D spin movie of this on my main page with this new projection.
This is constructed interactively using the mouse GUI (or manually through keyboard entry of the node / line tables) from VisibLie_Dynkin found on TheoryOfEverything.org.
The Lie group names are calculated based on the Dynkin topology. The geometric permutation names are calculated (to rank 8) based on the binary pattern of empty and filled nodes. The node and line colors can be used as indicators in Coxeter projections and/or Hasse diagrams.
This tool can be used to drive the visualizations in VisibLie_E8.
I have published my ToE.pdf to vixra.org http://vixra.org/abs/1006.0063 . While looking around vixra, I found a paper by Tony Smith on E8 http://vixra.org/pdf/0907.0006v1.pdf. It has much of the work on his website including references to Lisi and Bathsheba on their visualizations of E8. Some of the references are based on the 600 Cell set H4 & H4/Phi (shown by Richter to be isomorphic to E8). I can show the E8 Dynkin diagram can indeed be folded to H4.
The H4 and its 120 vertices make up the 4D 600 Cell (which is made up of 96 vertices of the snub-24 Cell and the 24 vertices of the 24 Cell=[16 vertex Tesseract=8-Cell and the 8 vertices of the 4-Orthoplex=16 Cell]). It can be generated from the 240 split real even E8 vertices using a 4×8 rotation matrix:
x = (1, φ, 0, -1, φ, 0, 0, 0)
y = (φ, 0, 1, φ, 0, -1, 0, 0)
z = (0, 1, φ, 0, -1, φ, 0, 0)
w = (0, 0, 0, 0, 0, 0, φ^2, 1/φ)
where φ=Golden Ratio=(1+Sqrt(5))/2
I find in folding from 8D to 4D, that the 6720 edge counts split into two sets of 3360 from E8’s 6720 length Sqrt(2).
I recreated here a E8 Petrie projection which is isomorphic to 2D split real even E8 Petrie projection (except it only produces half of the 6720 “shortest edge” counts, of different length). All of these use a single set of 3 projection basis vectors to produce a single 3D projected object with 3 unique faces. On one face, it has the famous E8 Petrie projection:
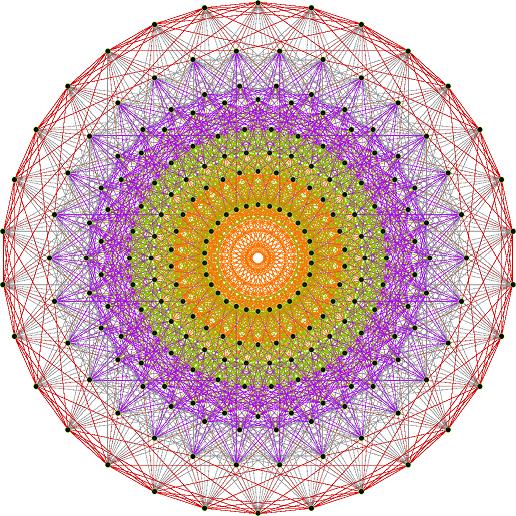
On another face it has a pentagonal projection:
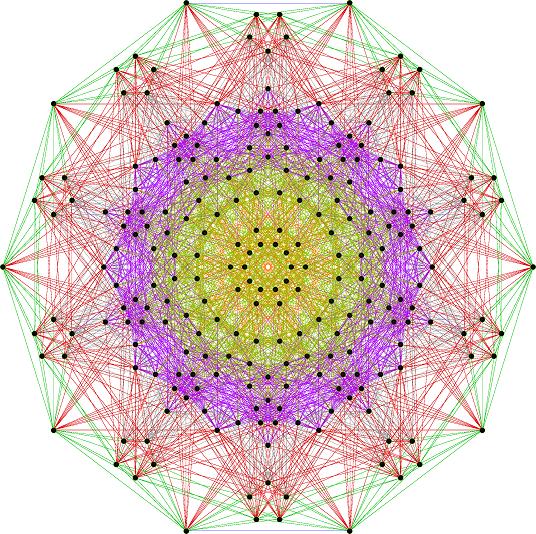
On the third unique face is the hexagonal projection:
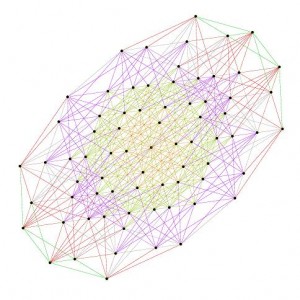
I created a movie (similar to those of Lisi) of the H4+H4/Phi 600 Cells that rotates the 2D H-V E8 face projection to the H-Z Pentagonal face (shown in the middle frames of the movie). This is an interesting rotation because this rotates through a square projection at around Pi/8.
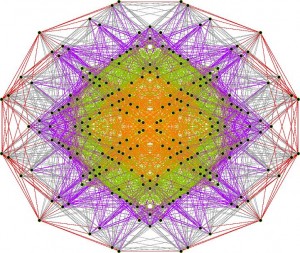
A lower quality YouTube is here: 600 Cells E8 to Pentagonal. Download and play the higher quality .avi: cell600E8pent
I also created a 3D perspective spin of that projection (two sets of mutually orthogonal cubic faces). On YouTube:600 Cells 3D Spin. Download the higher quality .avi: cell6003Dspin2
Similar to the work of other 3D artists like Bathsheba and Wizzy in Second Life (SL), this object can be created in Real Life (RL) as 3D laser etched crystal or rezzed as a 3000+ prim object in SL.
The 3 (H,V,Z) basis projection vectors are:

While these are 8D vectors for the 600 cells – they could just as well be 4D (setting the last 4 to zero, as they are simply negatives of the first 4).
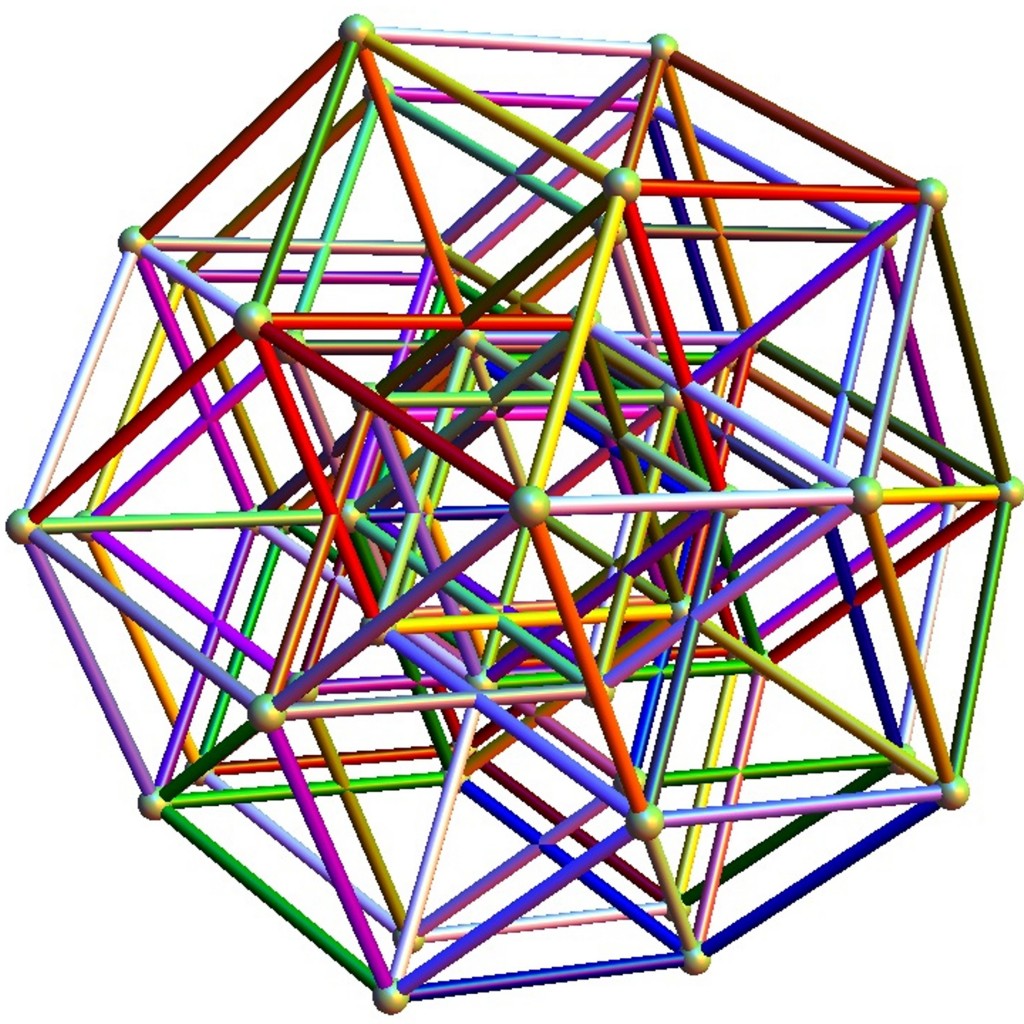
Orthogonally, the Zome like model from VisibLie_E8 shows: