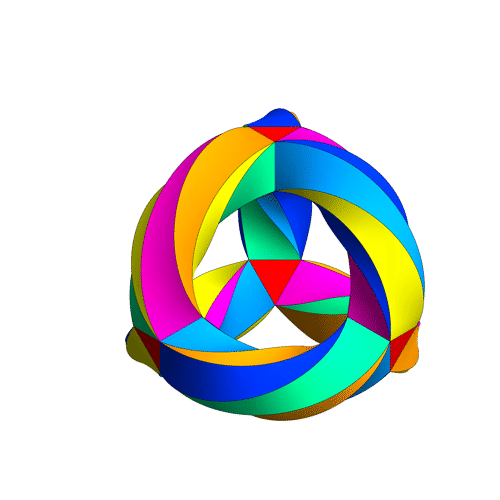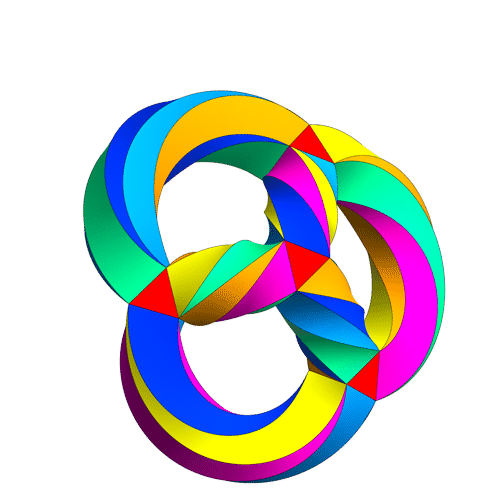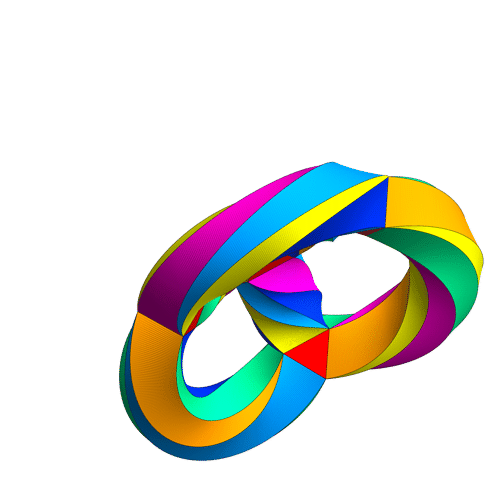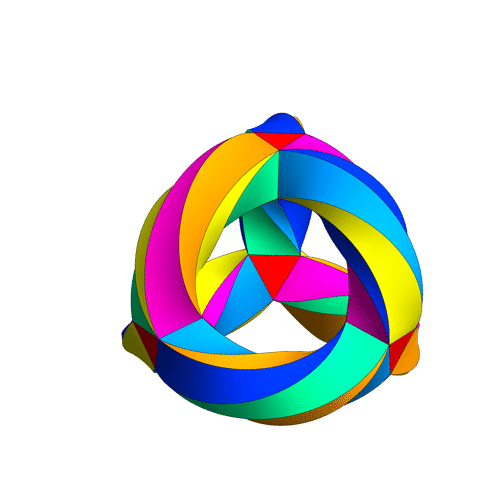Check out the new demonstrations using free interactive web plugin , .CDF, or .NB (for licensed Mathematica users) and social media integrations for comments, pages and posts.
Tag Archives: Physics
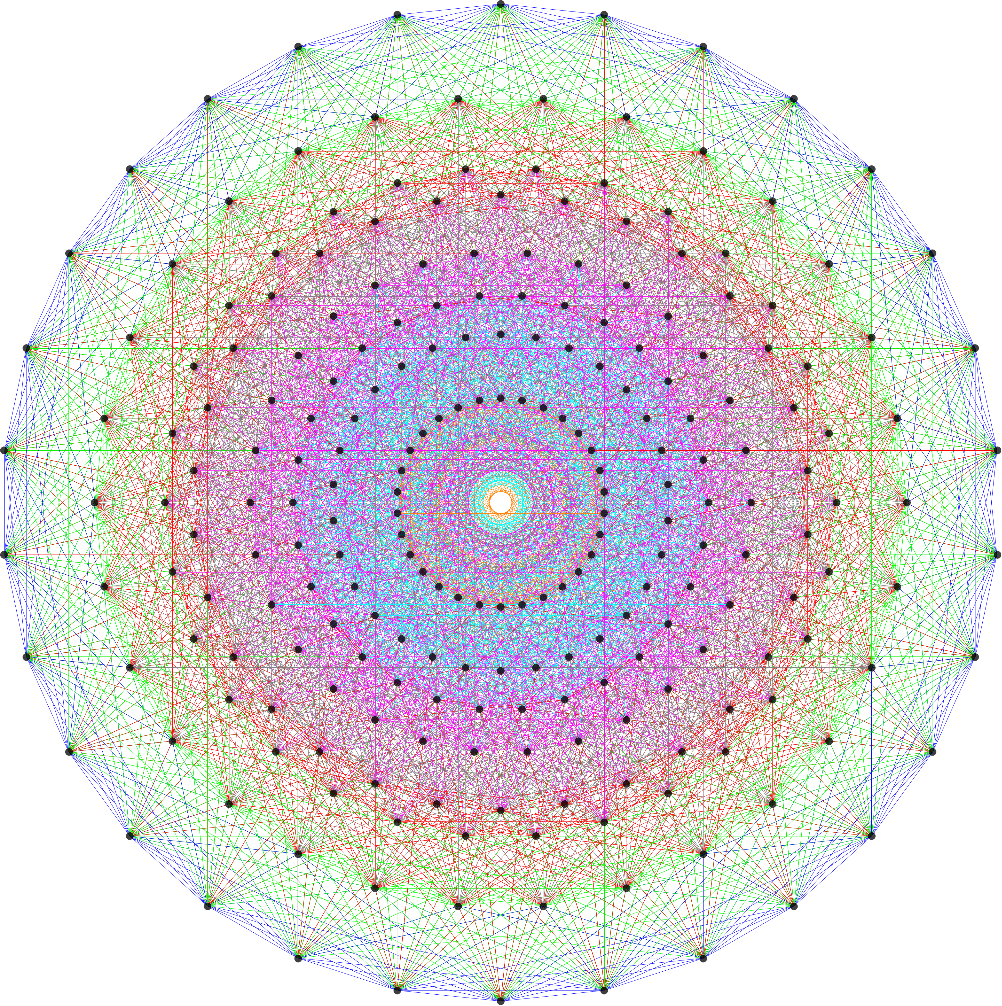
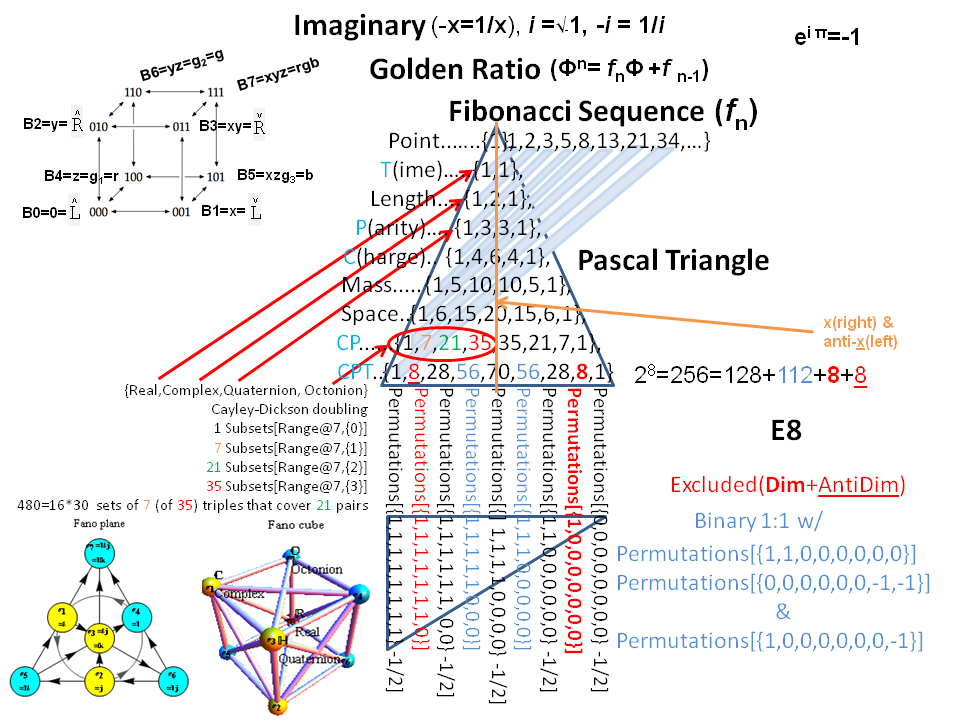
Another look at integrating the Pascal Triangle to Clifford Algebra, E8 Lie Algebra/Groups, Octonions and Particle Physics Standard Model
Modified Lisi split real even E8 particle assignment quantum bit patterns:
Assigning a specific mass, length, time, and charge metrics based on new dimensional relationships and the Planck constant (which defines Higgs mass).
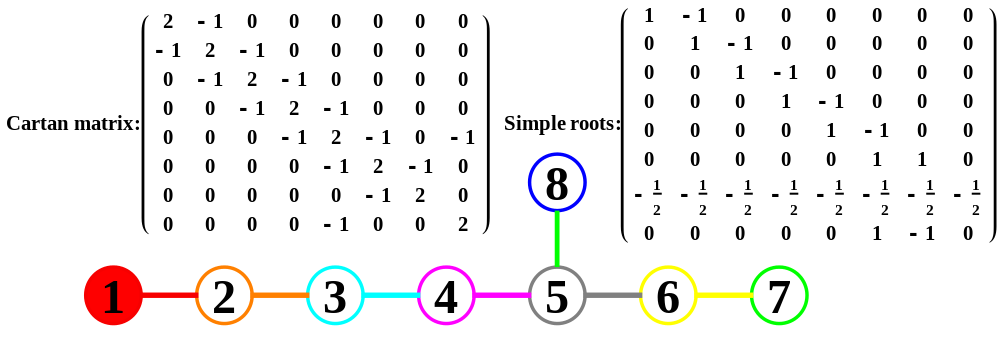
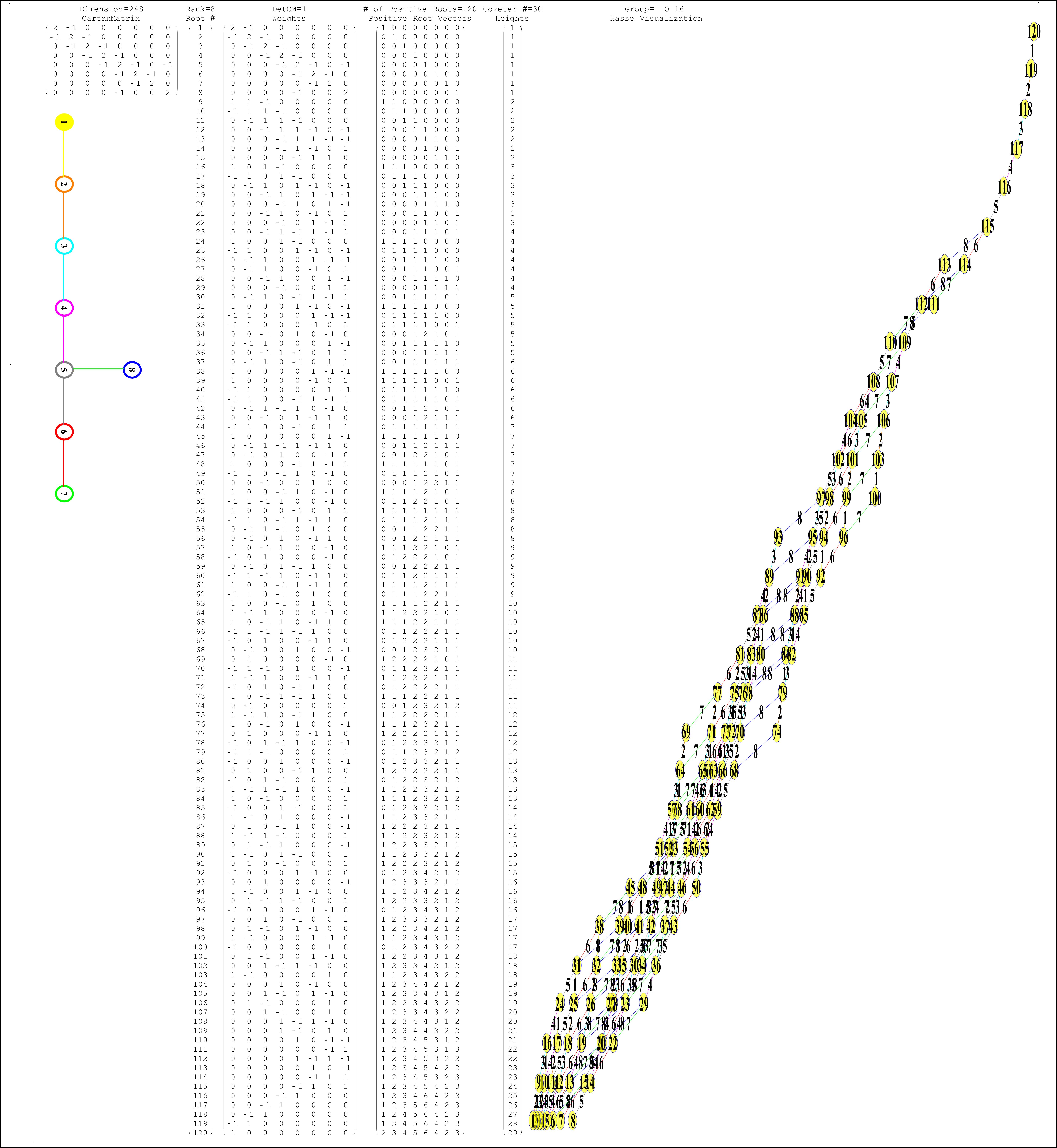
The split real even E8 group used has been determined from this simple root matrix (which gives the Cartan matrix upon dot product with a transpose of itself):
This Dynkin diagram builds the Cartan matrix and determines the root/weight/height with corresponding Hasse diagrams.
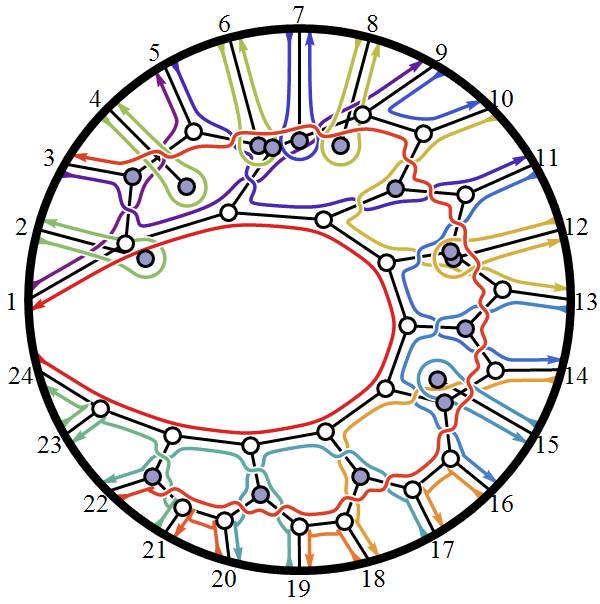
More amplituhedron capability (projected hull surface area and volume)
Getting more capability built into ToE_Demonstration.nb where it can now calculate the scattering amplitude by calculating the volume of the projected hull of selected edges in the n-Simplex Amplituhedron (based on a theory by Nima Arkani-Hamed, with some Mathematica code from J. Bourjaily for the positroid diagram). Of course, there is still much work to get this wrapped up…
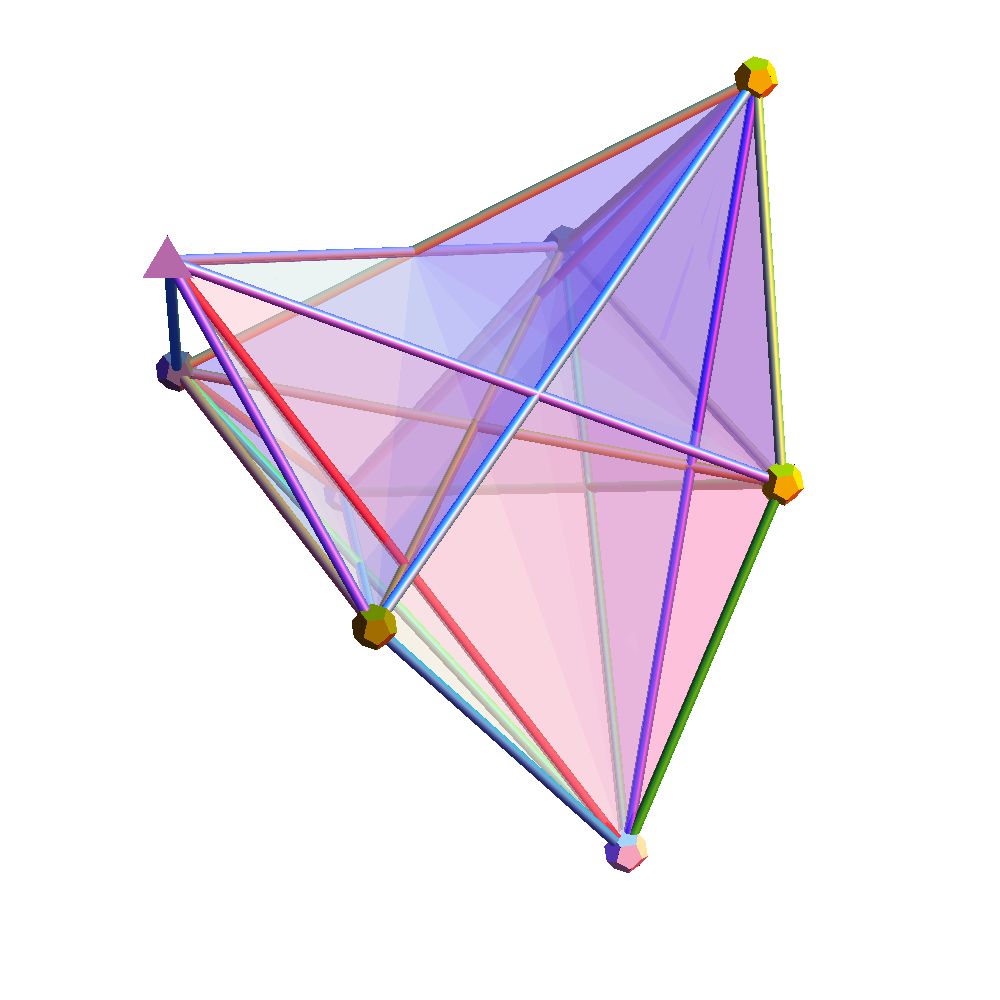
A few more pics of Positive Grassmannian Amplituhedrons…
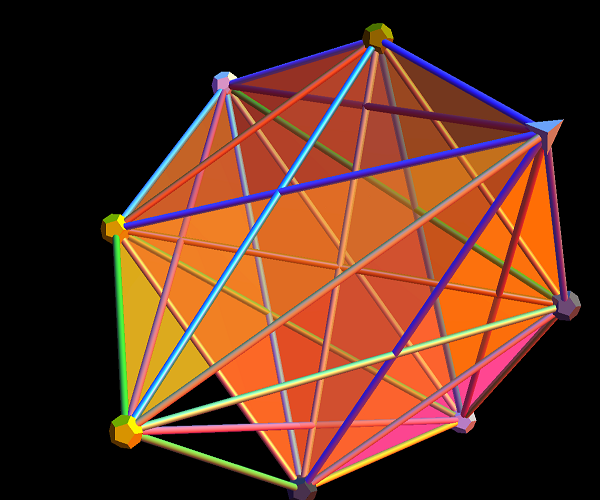
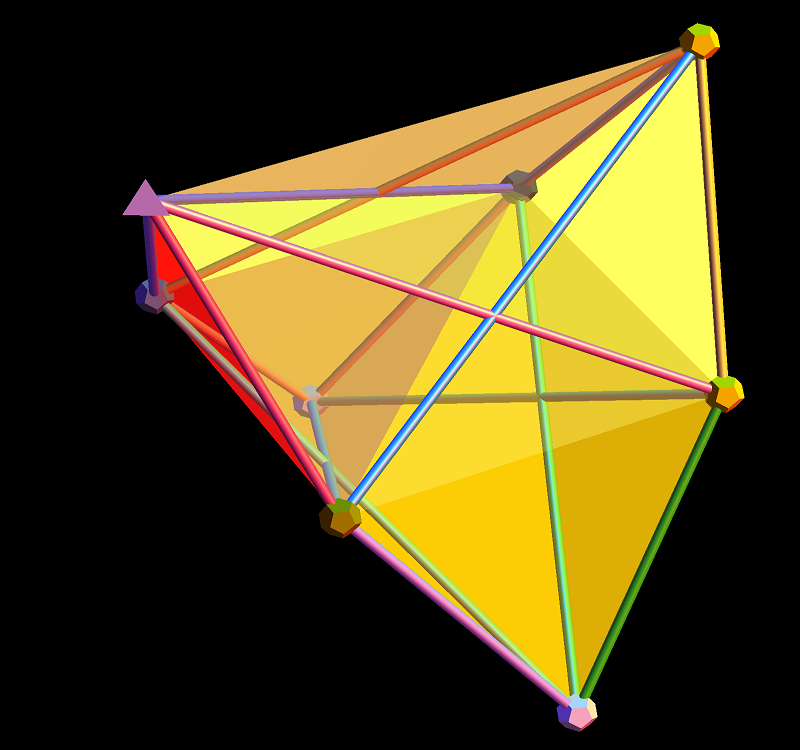
This last diagram is obtained using the following amplituhedron0.m as input to the ToE_Demonstration.nb (when using fully licensed Mathematica) as shown below:
* This is an auto generated list from ToE_Demonstration.nb *)
new := {
artPrint=True;
scale=0.1;
cylR=0.018;
range=2.;
pt={-0.3, 0.0, 0.6};
favorite=1;
showAxes=False;
showEdges=True;
showPolySurfaces=True;
eColorPos=False;
dimTrim=5;
ds=6;
pListName=”First8″;
dsName=”nSimplex”;
p3D=” 3D”;
edgeVals={{Sqrt[11/2], 8}, {Sqrt[9/2 – Sqrt[2]], 4}, {Sqrt[9/2 + Sqrt[2]], 4}};
};new;
Amplituhedron Visualizations!
Playing around trying to visualize the latest in the theoretical high energy particle physics (HEP/TH) determining how particle masses might be predicted from geometric principles (based on a theory by Nima Arkani-Hamed, with some Mathematica code from J. Bourjaily for the positroid diagram).
Positive Grassmannian Amplituhedrons
Compare this Mathematica(l) basis to the artistic representation by Andy Gilmore 
Updated demonstrations now include split octonions
I’ve updated the .NB, .CDF and interactive demonstrations to include the ability to visualize the split octonions.
Klein Quartic Curves
With some Mathematica source from Leon Lampret at math.stackexchange.com, I’ve been trying to understand the link between the bitangents of octonions and the Klein Quartic Curves.
Which seems to be closely related to Greg Egan’s wonderful visualization from
http://www.gregegan.net/SCIENCE/KleinQuartic/KleinQuartic.html
Detail explanation of E8 Integration with Octonions, Particles, and the Periodic Table
Please see Integrated E8, Binary, Octonion for a tutorial that explains the detail of the content of Fano.pdf. It outlines the relationships in the integration of E8 with Octonions, Binary, Particles, NKS, and the Periodic Table of Elements. Other formats are also available (.ppt or .pps and .pdf).
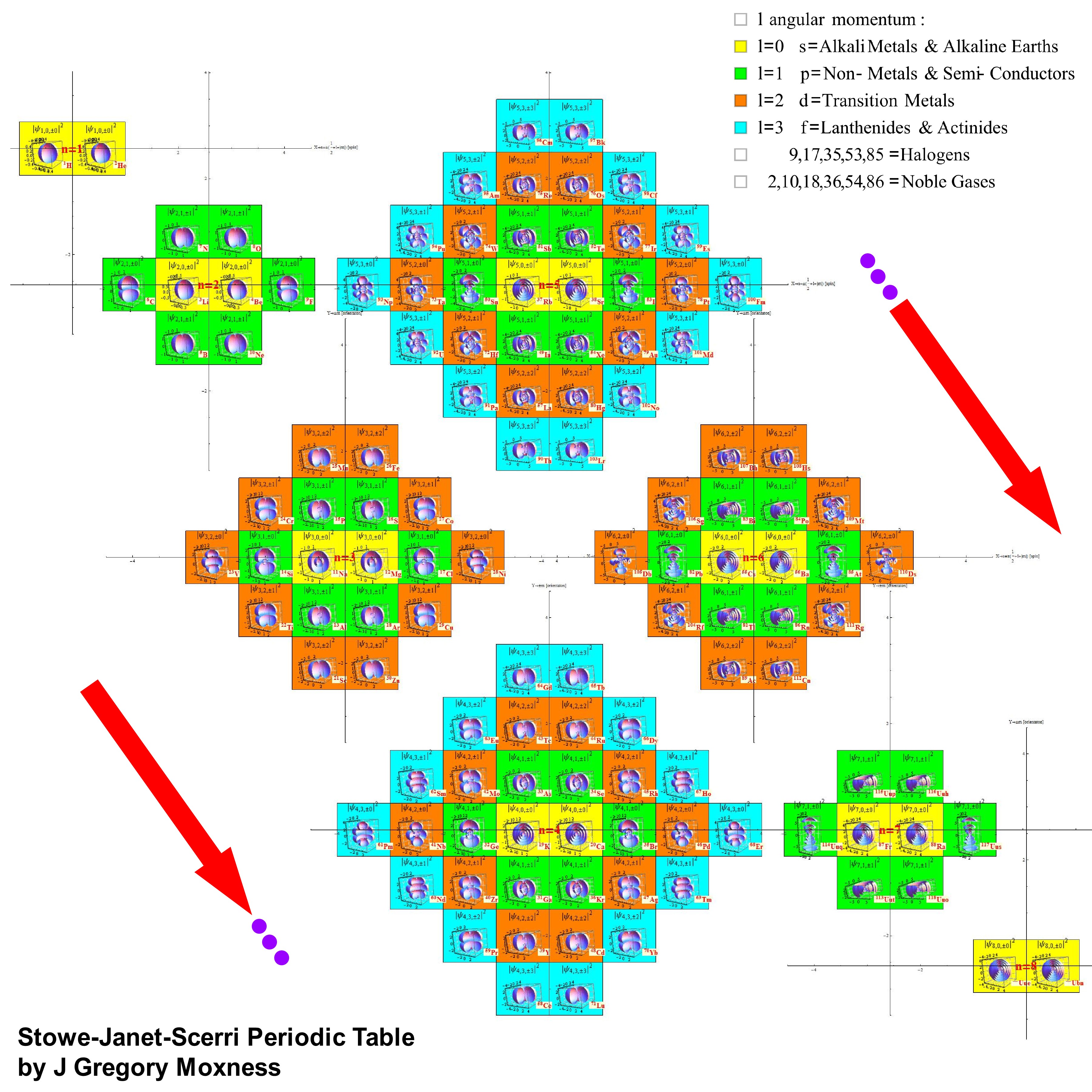
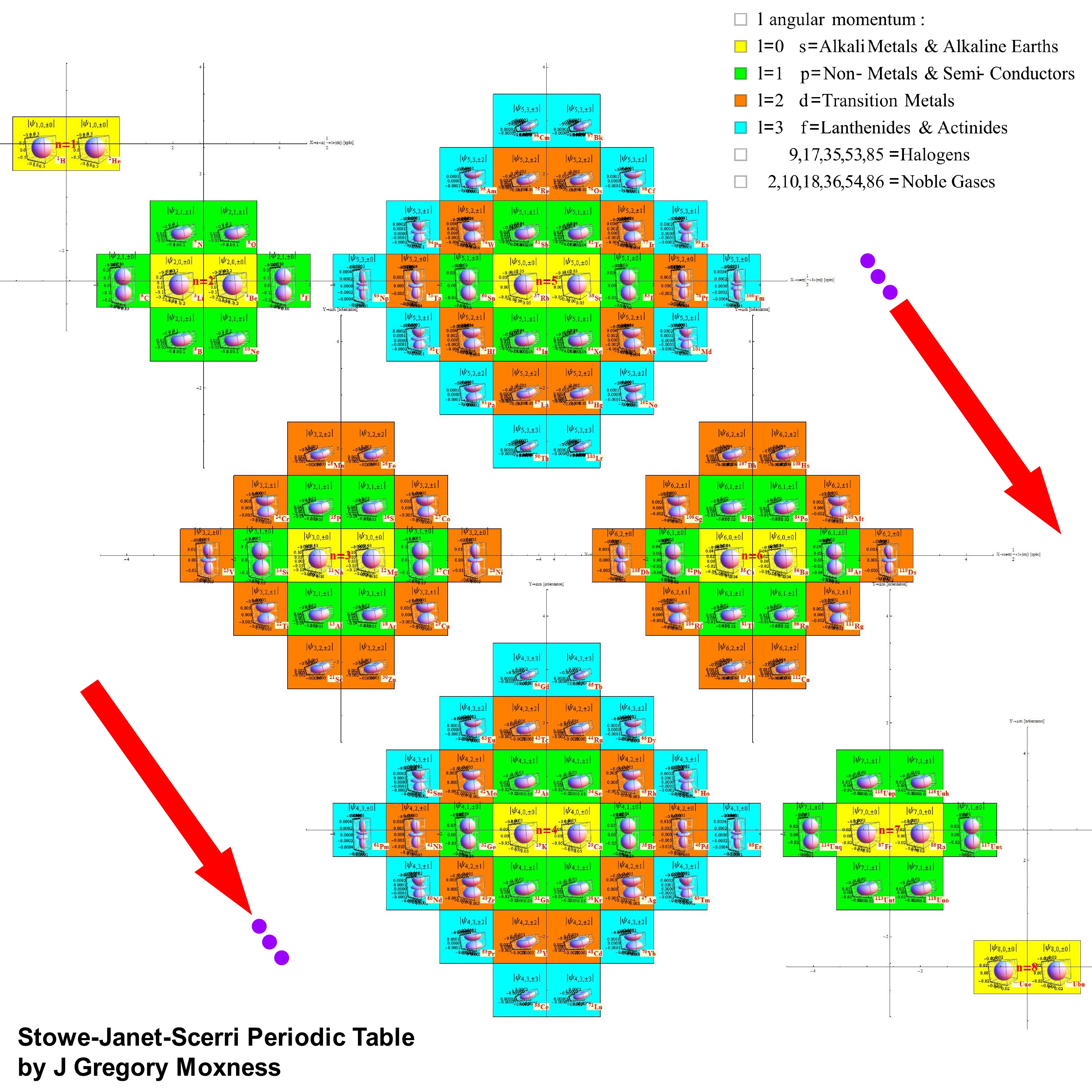
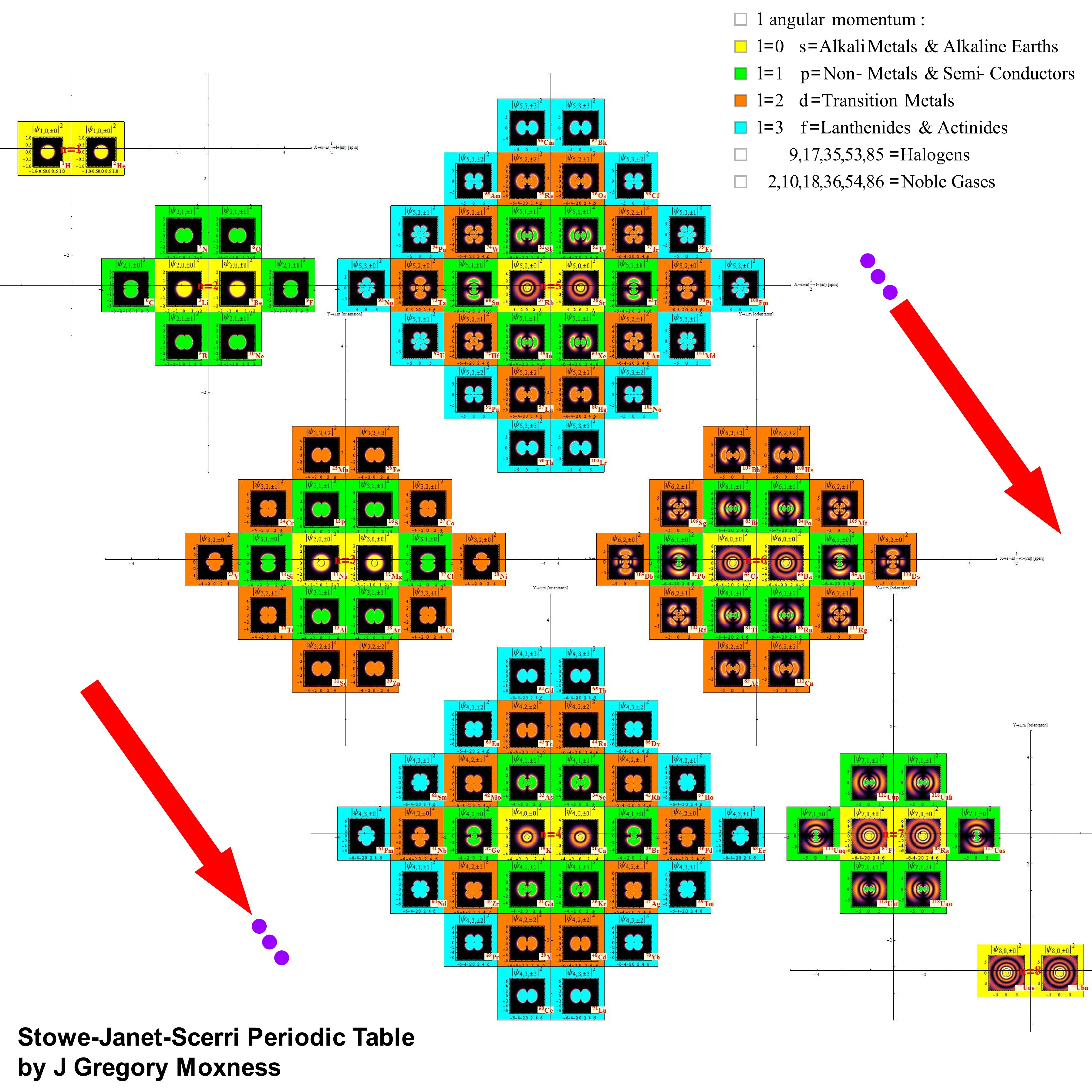
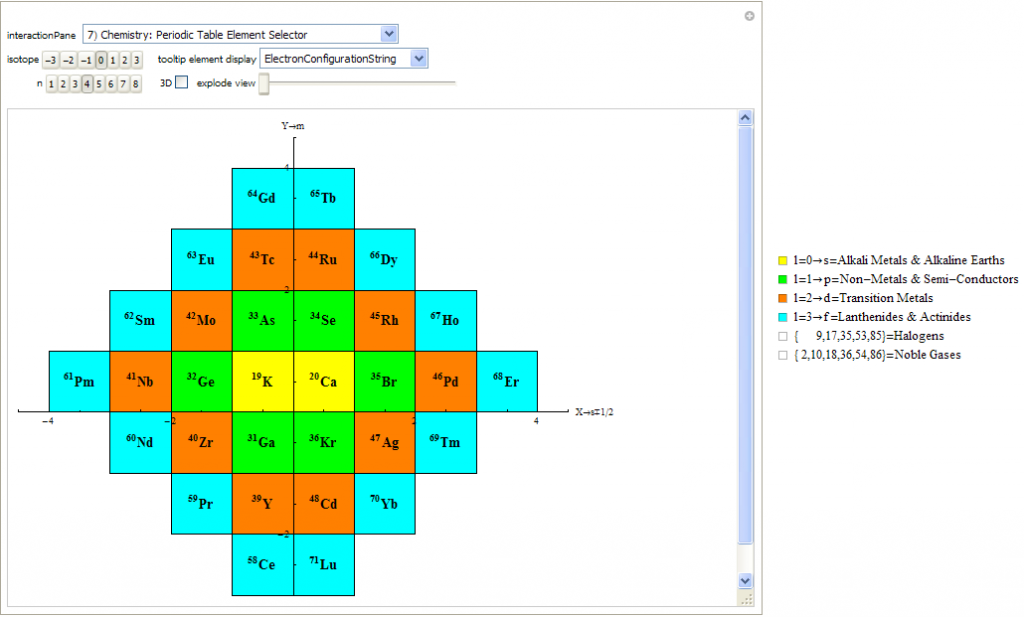
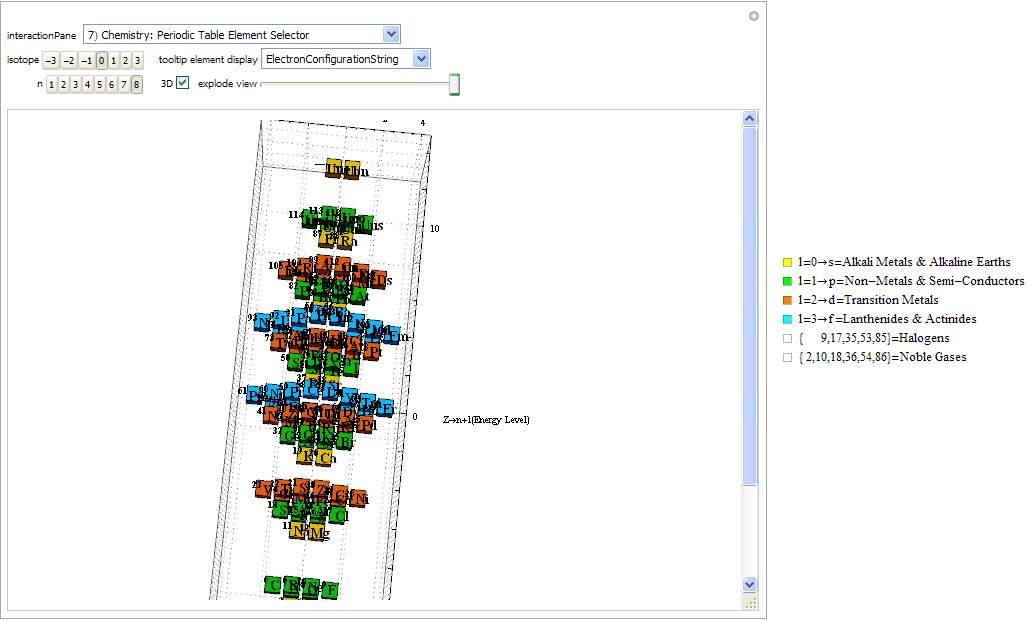
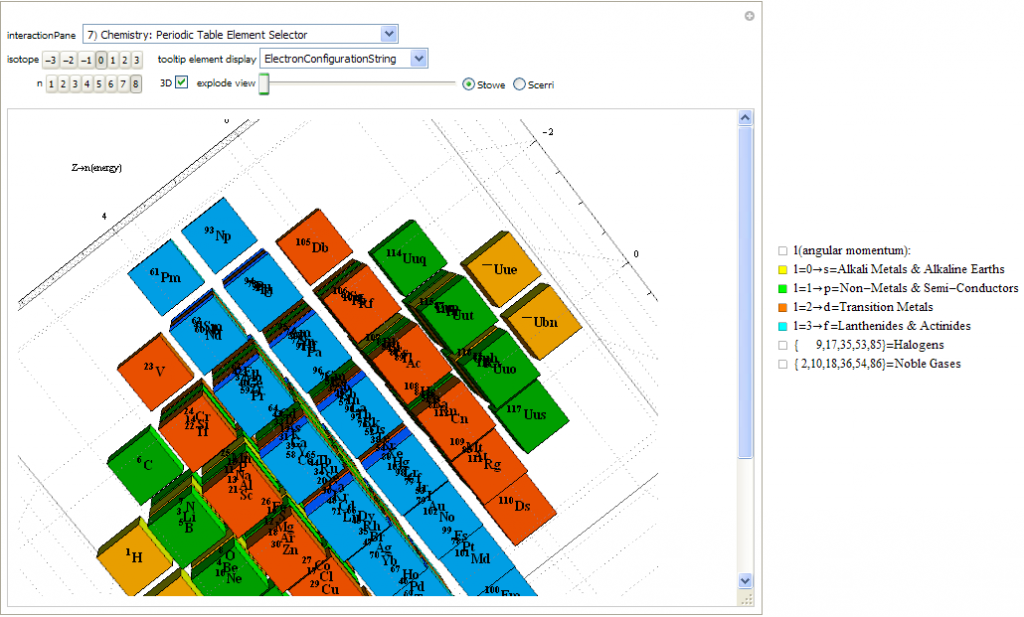
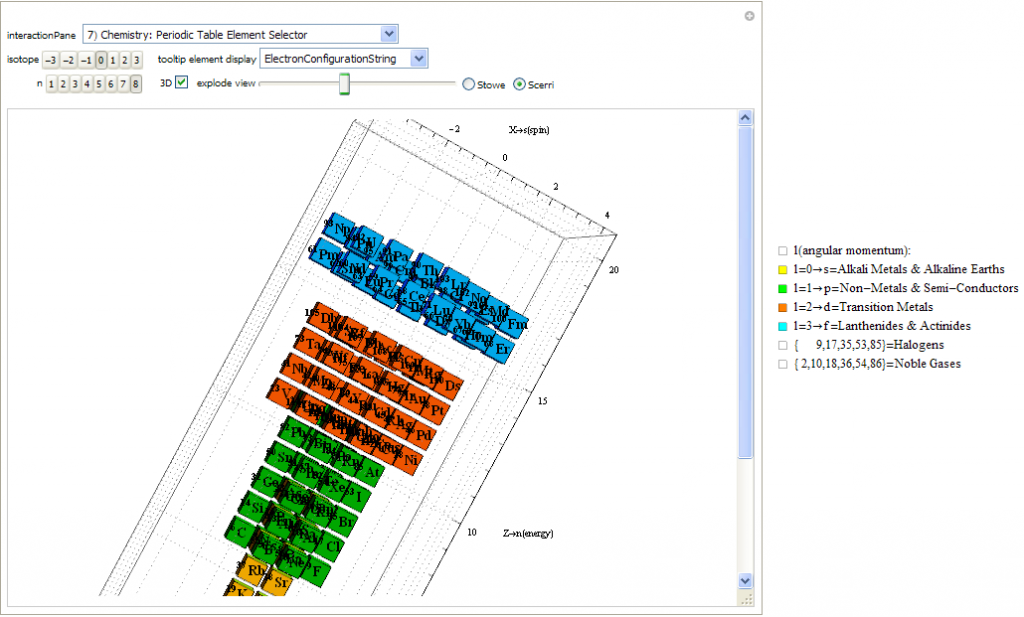
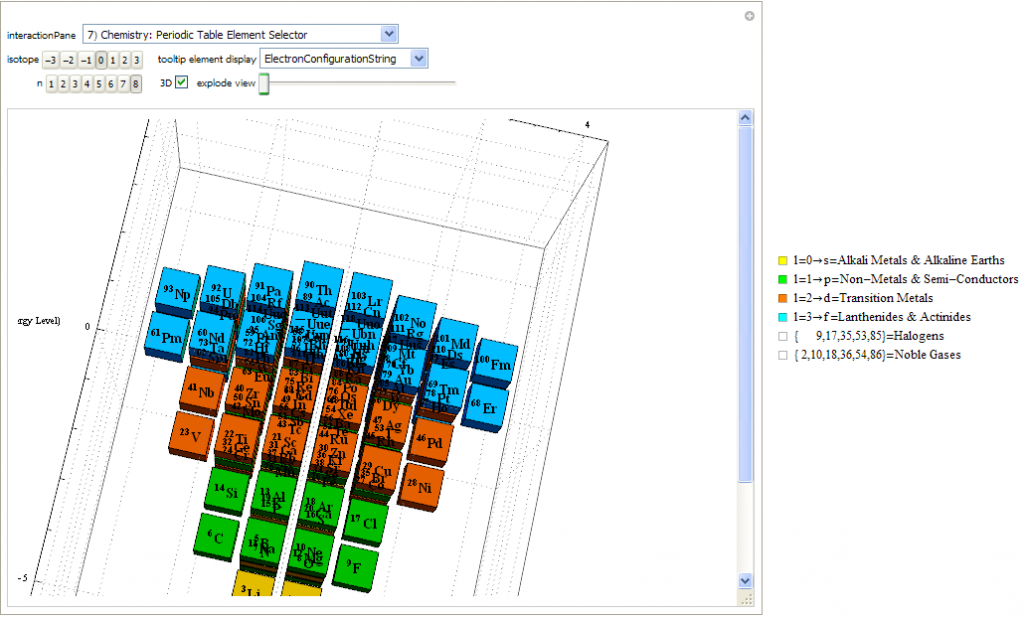
Created a new 4D Stowe-Janet-Scerri Periodic Table
I’ve replaced the standard periodic table in the 7th “Chemistry Pane” of my E8 visualizer with a 2D/3D/4D Stowe-Janet-Scerri version of the Periodic Table.
Interestingly, it has 120 elements, which is the number of vertices in the 600 Cell or the positive half of the 240 E8 roots. It is integrated into VisibLie_E8 so clicking on an element adds that particular atomic number’s E8 group vertex number to the 3rd E8 visualizer pane.
The code is a revision and extension of Enrique Zeleny’s Wolfram Demonstration
MyToE updated from 2013 Planck Spacecraft and 2012 LHC results
With the recent publication of results for the Planck spacecraft results and the recent LHC Higgs results for the discovery of a 125(+/-1.5)GeV Higgs boson, I thought I would publish the minor tweaks to my PDF ToE summary or see the Mathematica notebook here. Enjoy!
It is interesting to note that my original paper from ’98 (updated ’01) Constants-A_New_Look.pdf contains this new Planck CMB probe result for a Hubble constant of H0=67.133 km/s/Mpc, which is at odds with WMAP, COBE, and prior estimates.
This old paper has a Higgs mH=98.137 GeV, which is around the minima of the ChiSquared value for Higgs. This was quickly excluded by FermiLab results around that time. The basic Higgs prediction relies purely on the dimensionality of the model and the Planck constant. Adding a factor of 2^1/2 gave an aesthetically pleasing mH=147.98 in a ’07 paper here. This was close to a June ’11 FermiLab CDF bump at 148 GeV. Unfortunately D0 at FermiLab didn’t confirm it.
Interestingly between the ’01 and the ’07 papers, one of the Higgs mass models I used 2^1/4 (not 2^1/2) and puts mH=124.43 GeV – right where LHC ATLAS and CMS seem to have found it. This same model also (fairly) accurately integrates this to the Fermi Constant and vacuum expecation (VEV).
The bottom line, my model describes results that are within the most current and accurate experimentally measured data, including the LHC Higgs and Planck CMB probes.
ToE Summary
The 480 octonions, their Fano planes and multiplication tables
I am pleased to announce the availability of Fano.pdf, a 241 page pdf file with the 480 octonion permutations (with Fano planes and multiplication tables). These are organized into “flipped” and “non-flipped” pairs associated with the 240 assigned particles to E8 vertices (sorted by Fano plane index or fPi). For each split real even E8 vertex, the algebra root, weight and height are listed along with the Clifford/Pascal binary and physics rotation coordinates. On each page, the E8 particle number, symbol, and assigned 2D/3D shape are shown along with the (a)nti, (p)Type, (s)pin, (c)olor, (g)eneration bitwise quantum assignments. Also included is the particle experimental mass and lifetime along with my ToE theoretically calculated mass. (30MB)
I believe this is the only comprehensive presentation of all 480 Fano planes with their multiplication tables available.