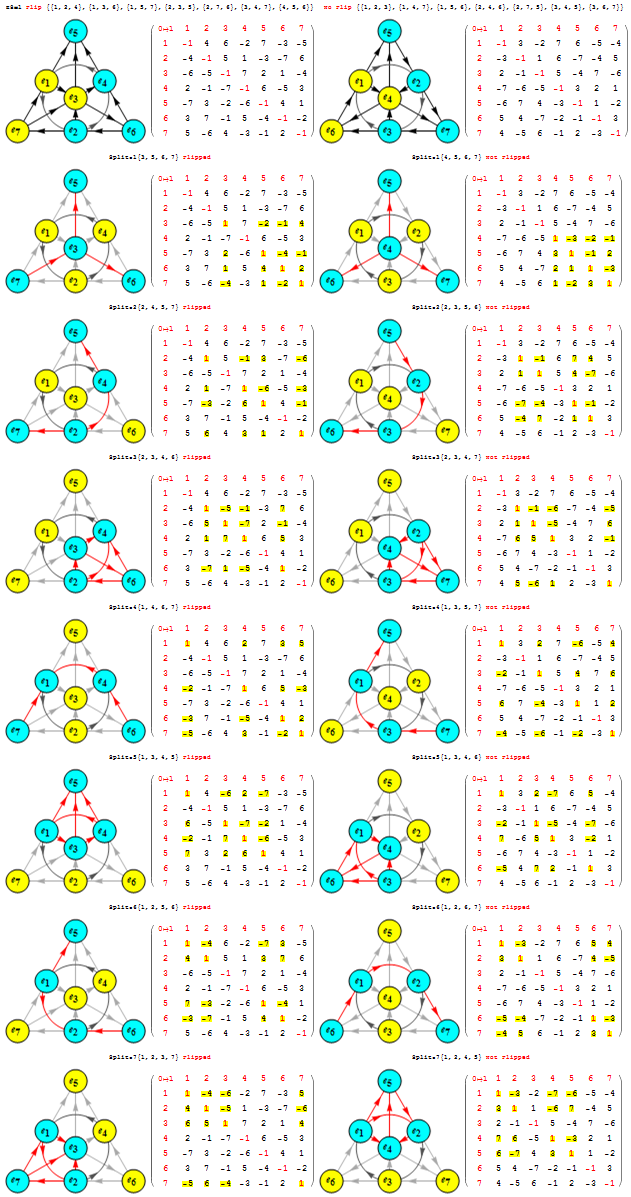
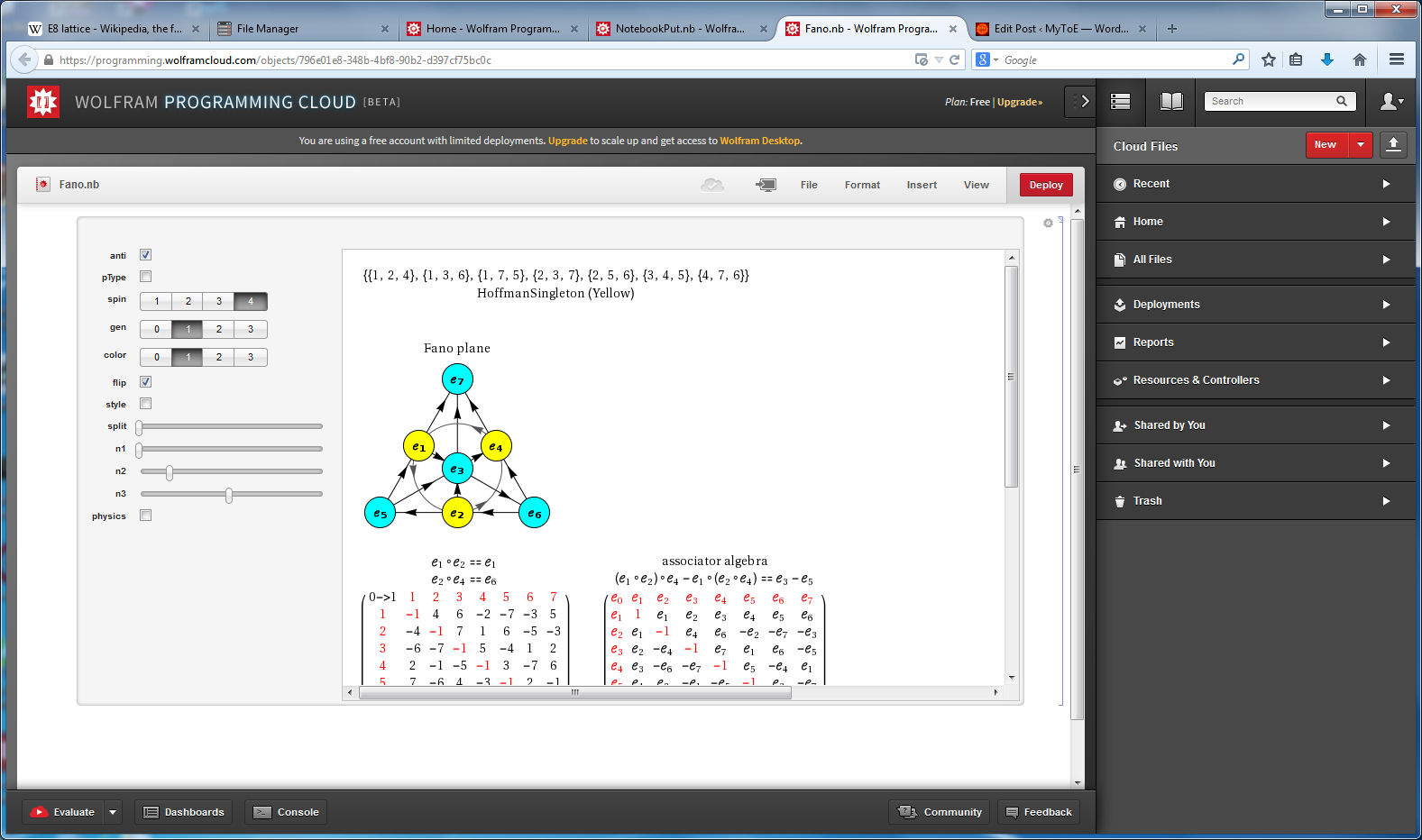
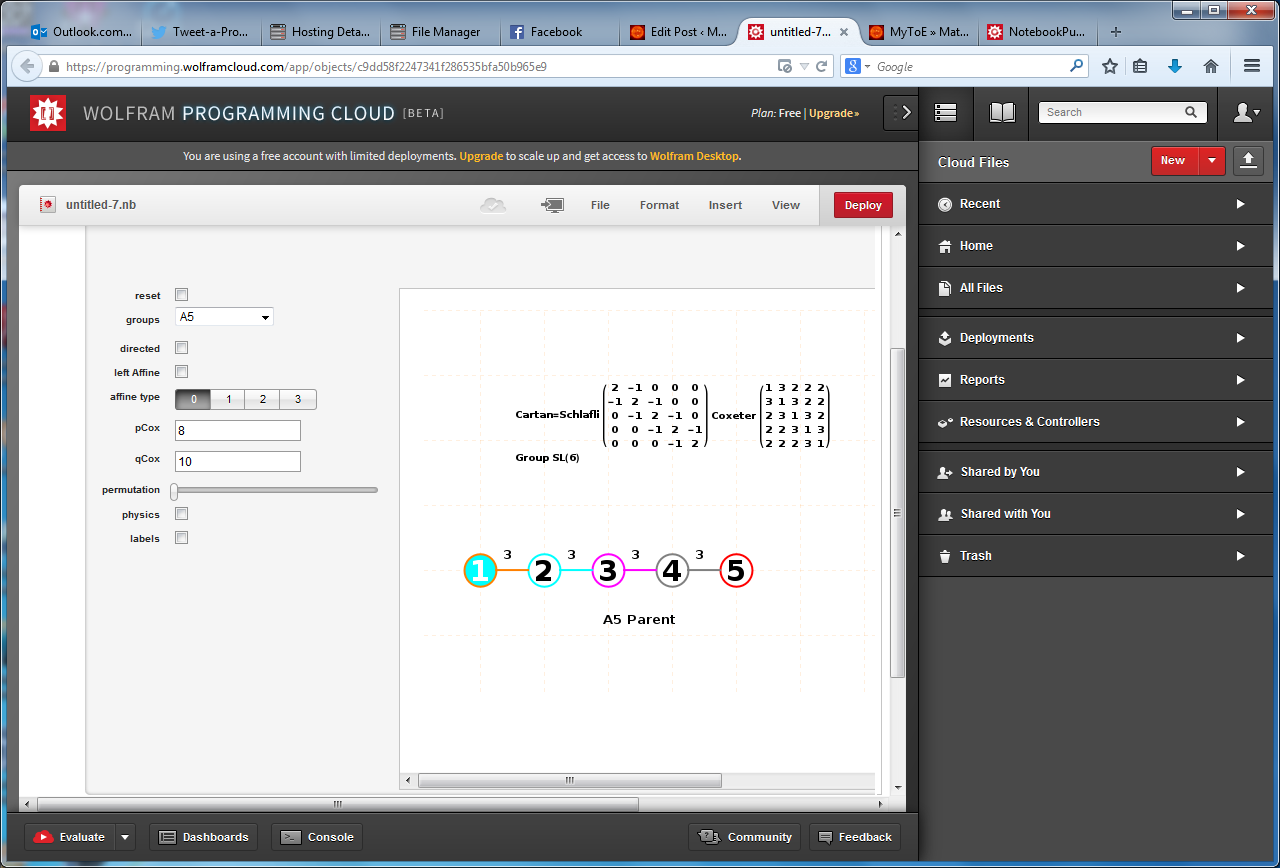
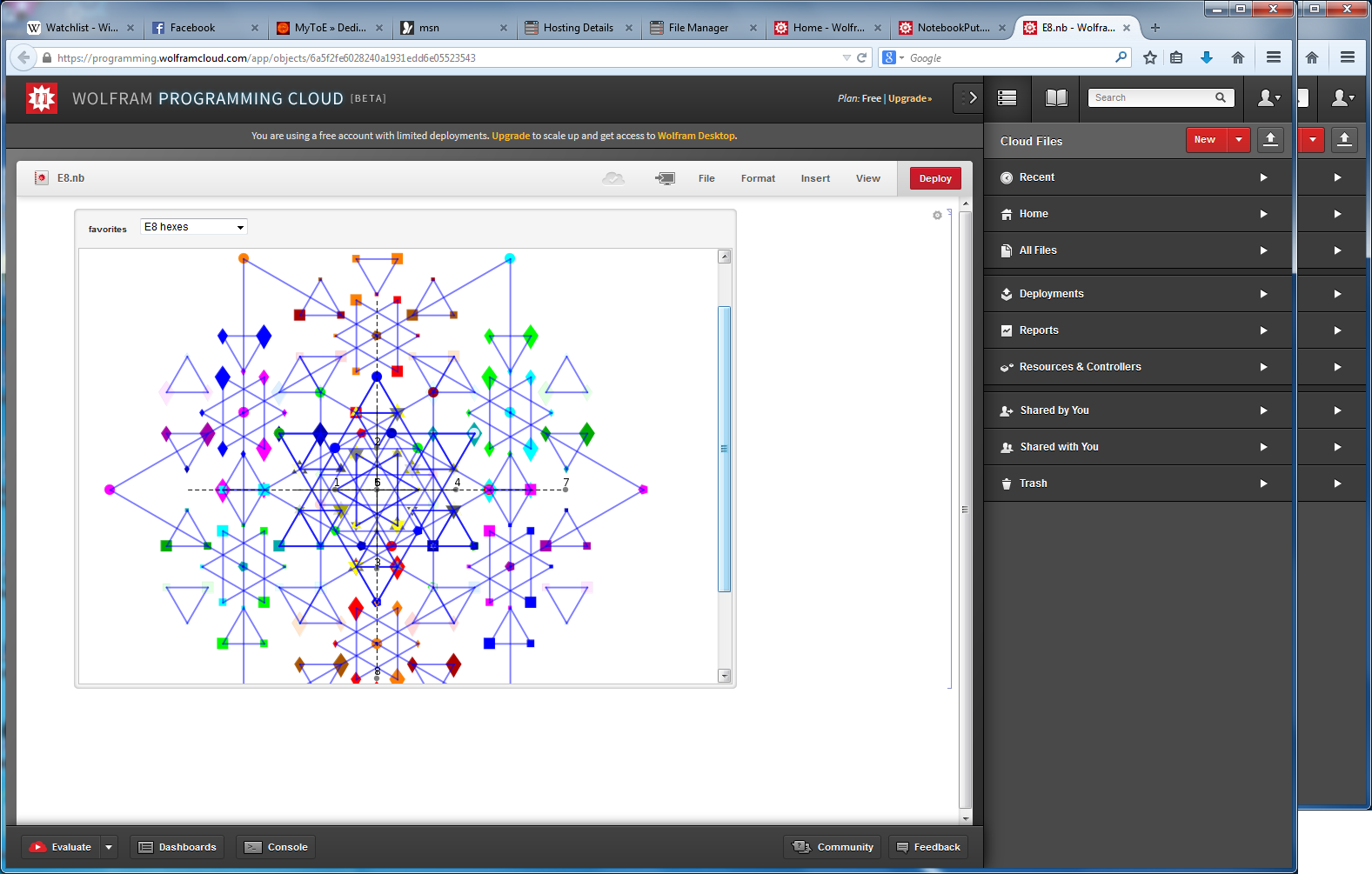
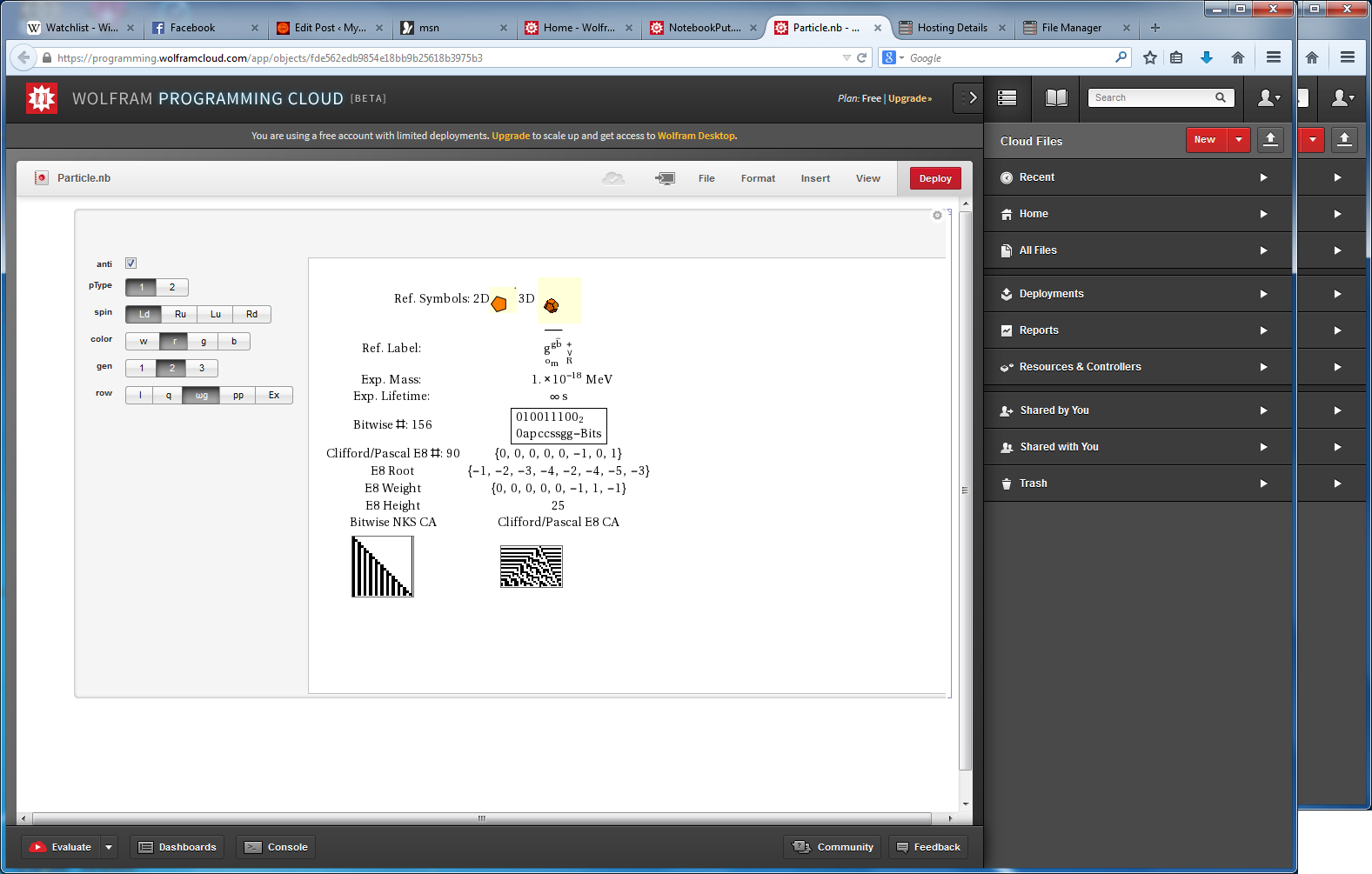
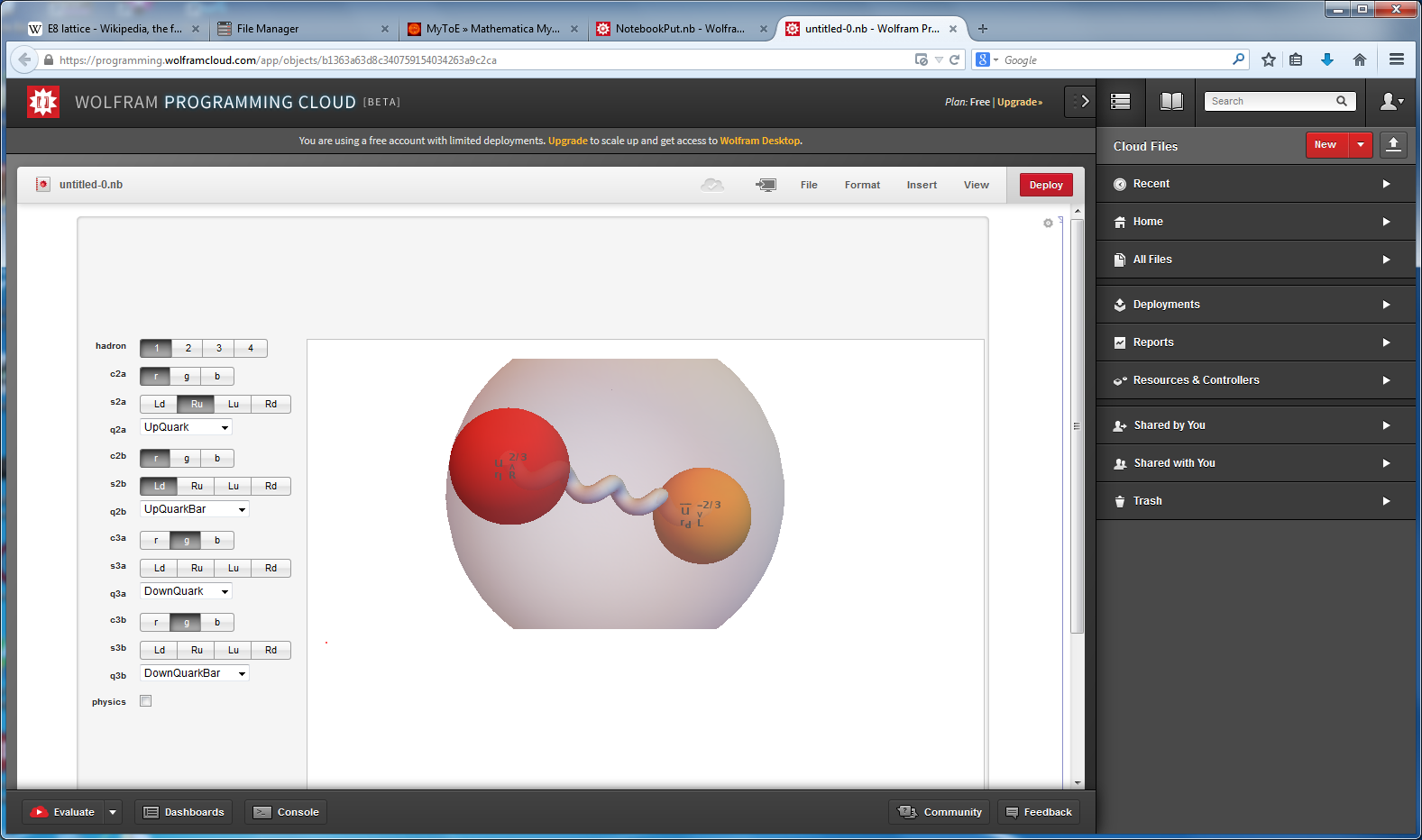
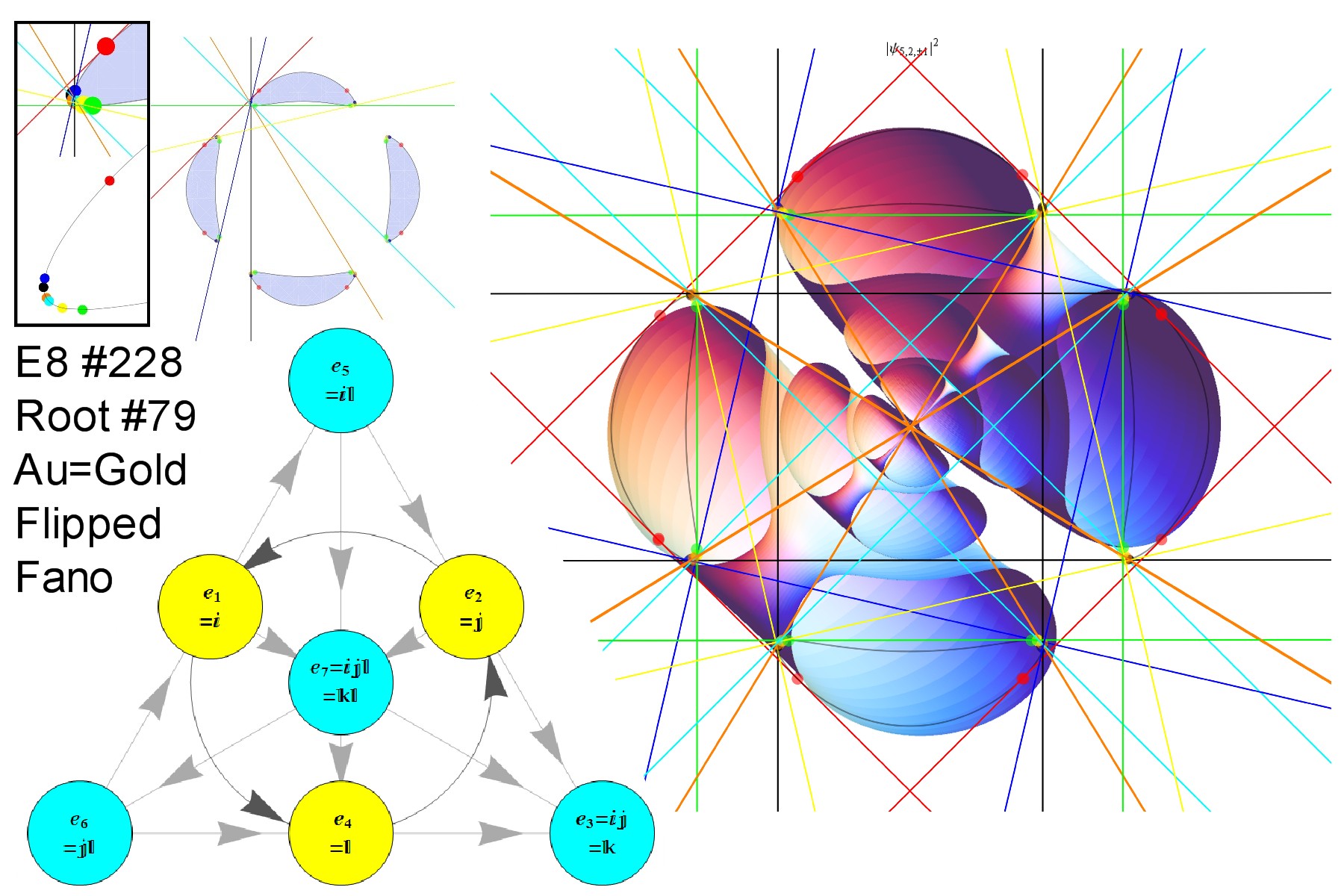
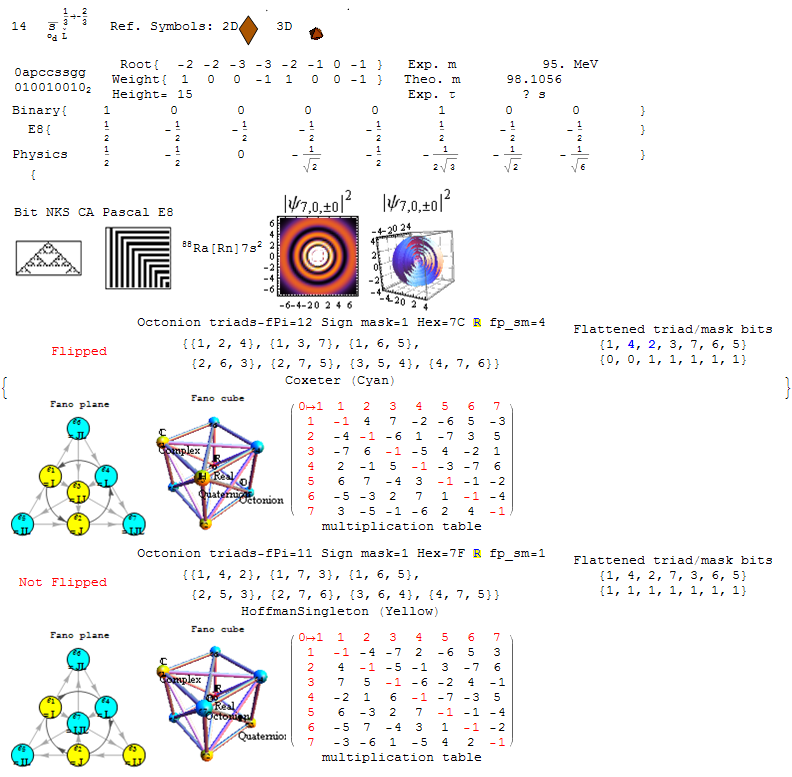
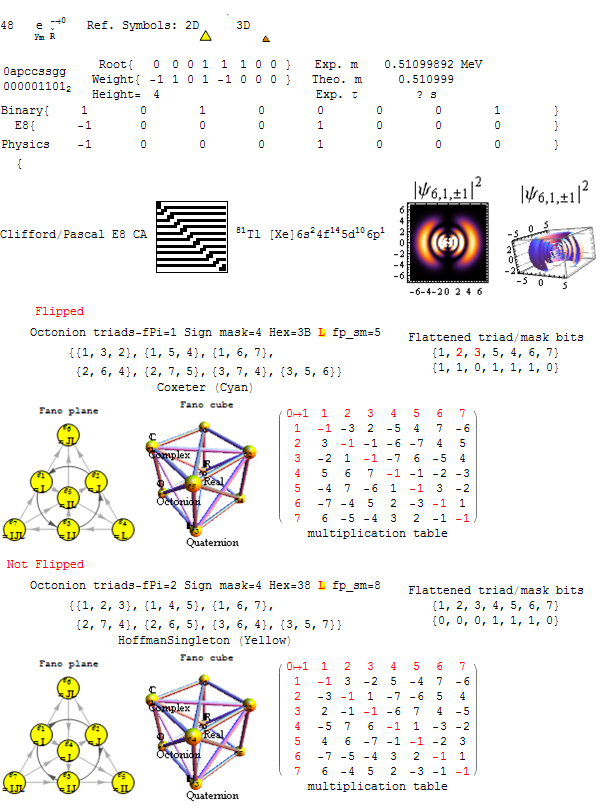
I am pleased to announce the availability of splitFano.pdf, a 321 page pdf file with the 3840=480*8 split octonion permutations (with Fano planes and multiplication tables). These are organized into “flipped” and “non-flipped” pairs associated with the 240 assigned particles to E8 vertices (sorted by Fano plane index or fPi).
There are 7 sets of split octonions for each of the 480 “parent” octonions (each of which is defined by 30 sets of 7 triads and 16 7 bit “sign masks” which reverse the direction of the triad multiplication). The 7 split octonions are identified by selecting a triad. The complement of {1,2,3,4,5,6,7} and the triad list leaves 4 elements which are the rows/colums corresponding to the negated elements in the multiplication table (highlighted with yellow background). The red arrows in the Fano Plane indicate the potential reversal due to this negation that defines the split octonions. The selected triad nodes are yellow, and the other 4 are cyan (25MB).
These allow for the simplification of Maxwell’s four equations which define electromagnetism (aka.light) into a single equation.
I believe this is the only comprehensive presentation of all 3840 Split Fano Planes with their multiplication tables available.
Below is the first page of the comprehensive split octonion list.