The following “paper with code” in viXra is a comprehensive analysis of Furey’s work on the hyper-complex algebra of RCHO. Please see the ancillary notebook, viewable using the free viewable Player, for the full detail.


The following “paper with code” in viXra is a comprehensive analysis of Furey’s work on the hyper-complex algebra of RCHO. Please see the ancillary notebook, viewable using the free viewable Player, for the full detail.


Please take a look here to view a paper I wrote about in a recent blog post here. The paper registered in arXiv is here and titled: The_Isomorphism_of_H4_and_E8.
As I like to provide more than just type-set text and graphics, I include in the arXiv the Mathematica notebooks with code snippets and actual output w/interactive 3D graphics. This gets attached in the ancillary files and is also linked as “Papers with Code” using my GitHub account here.
That caught the eye of the Wolfram editors who graciously offered to help with this post. My hats off to them. Enjoy the paper, with a follow-on paper: The_Isomorphism_of_3-Qubit_Hadamards_and_E8 here, including the notebook 😉
Click here for a PDF of my recent paper. This has been accepted by the arXiv as 2311.01486 (math.GR & hep-th) with an ancillary Mathematica Notebook here. These links have (and will continue to have) minor descriptive improvements/corrections that may not yet be incorporated into arXiv, so the interested reader should check back here for those. Another related follow-on paper on THE ISOMORPHISM OF 3-QUBIT HADAMARDS AND E8 is referenced in the blog post here.
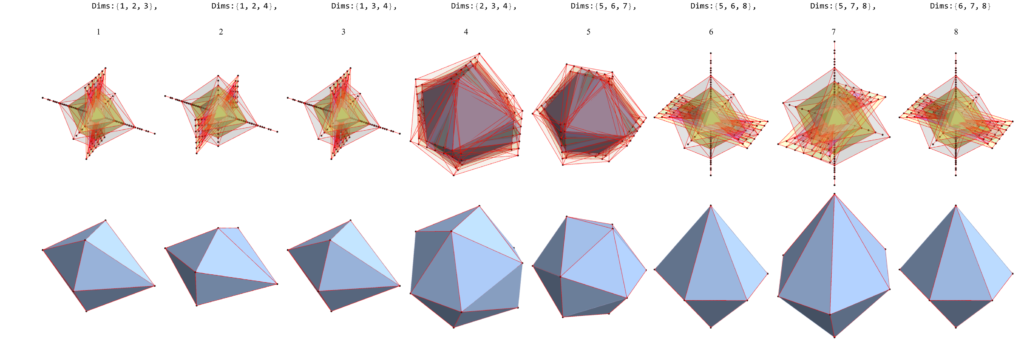
The abstract: This paper gives an explicit isomorphic mapping from the 240 real R^8 roots of the E8 Gossett 4_{21} 8-polytope to two golden ratio scaled copies of the 120 root H4 600-cell quaternion 4-polytope using a traceless 8×8 rotation matrix U with palindromic characteristic polynomial coefficients and a unitary form e^{iU}. It also shows the inverse map from a single H4 600-cell to E8 using a 4D<->8D chiral L<->R mapping function, phi scaling, and U^{-1}. This approach shows that there are actually four copies of each 600-cell living within E8 in the form of chiral H4L+phi H4L+H4R+phi H4R roots. In addition, it demonstrates a quaternion Weyl orbit construction of H4-based 4-polytopes that provides an explicit mapping between E8 and four copies of the tri-rectified Coxeter-Dynkin diagram of H4, namely the 120-cell of order 600. Taking advantage of this property promises to open the door to as yet unexplored E8-based Grand Unified Theories or GUTs.
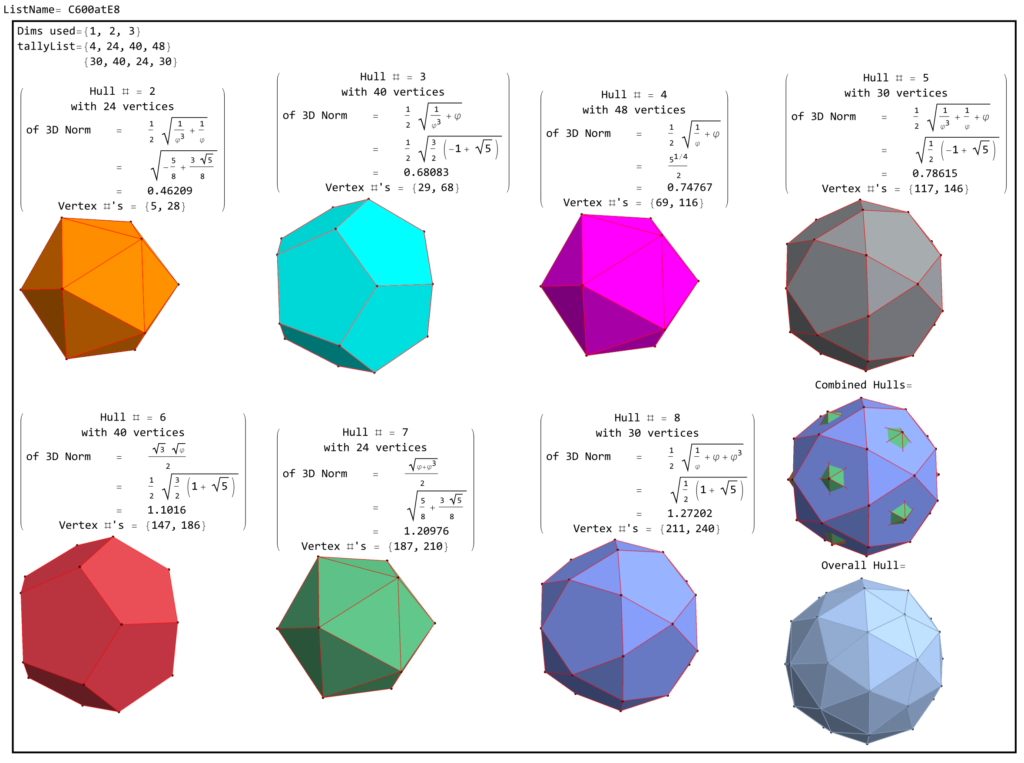
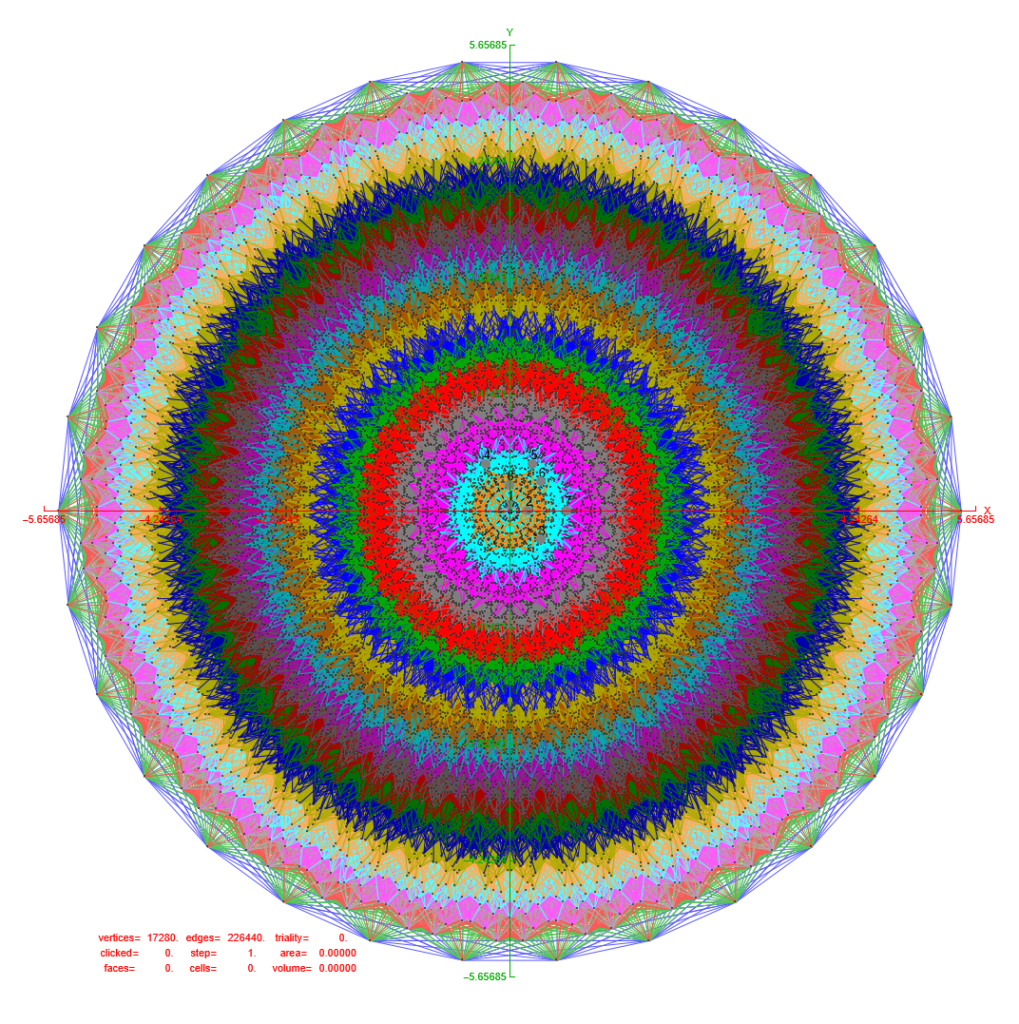
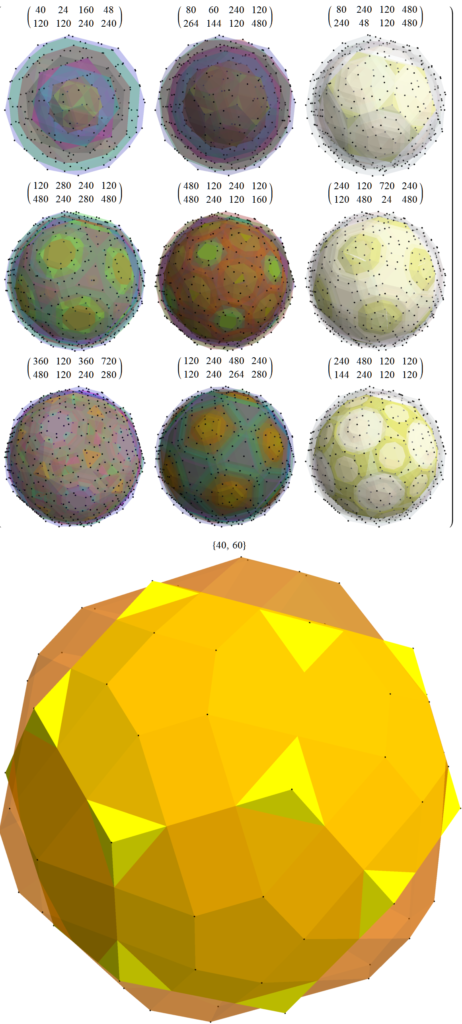




Below are SVG images of output from Pane 1 (Chaos) and Pane 17 (AI) of the VisibLie_E8 visualization tool:

Greg Moxness, Tucson AZ
This is constructed from VisibLie_E8 and uses the Mathematica package Mathgroup. A comprehensive PowerPoint/PDF that gives an overview of the underlying theory and VisibLie_E8 tool capability is in this post.
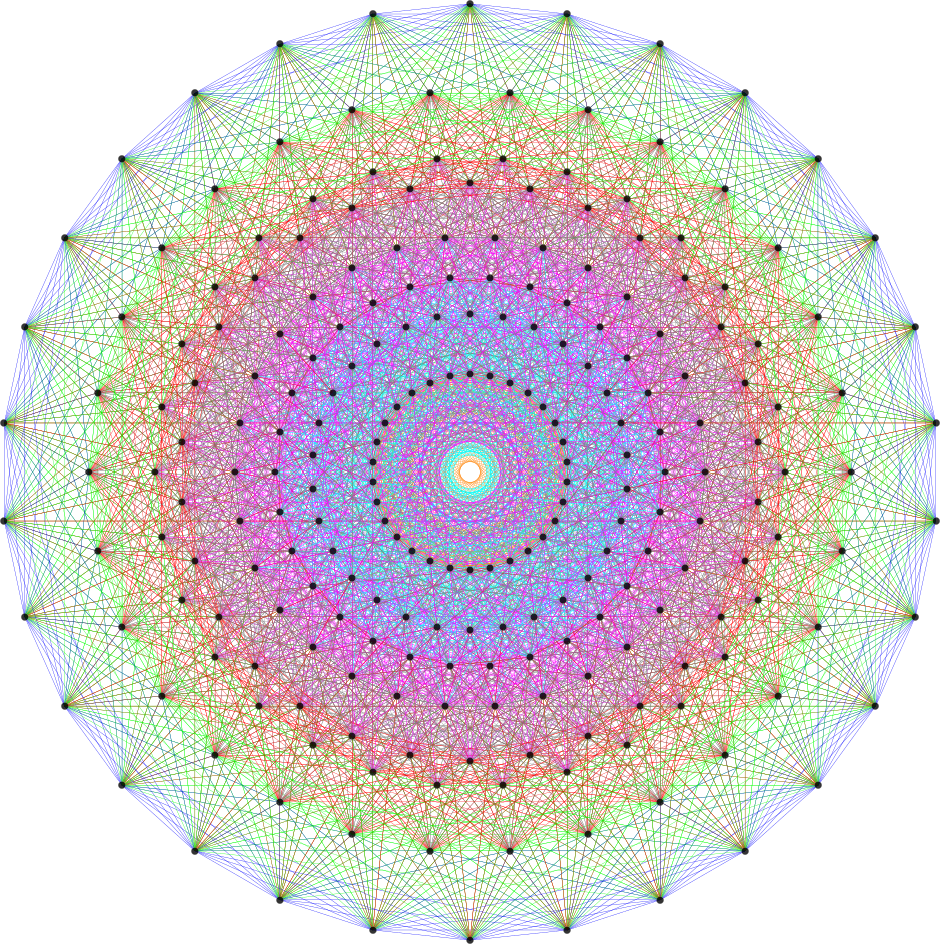
I think the most well-known (2D) image I’ve created so far (above) is found on Wikipedia’s (WP) math/geometry pages. It is what has been called the Public Relations (PR) or publicity photo for E8, which is an 8D (or 248 dimensional as the math guys count it) geometric object. It has been used in books, papers, math/science conference promotional materials, etc. That WP page also has what many used to consider “uninteresting” – my 3D versions of the same object. E8 is used in various theories to understand how the Universe operates way below the atomic level (i.e. the quantum stuff). I think it is responsible for what I call the shape of the Universe. As others have said, “who knew the Universe had a shape?”

In (very) layman’s terms, that 2D image of E8 looks sort-of-like how the lowly 4D Tesseract cube would look if it grew up into an 8D object, but a bit more interesting. The Tesseract was made (more) popular in the modern Avengers movies. In 2015 before I had ever seen any of those movies, I created a laser etched 3D projection of E8 within a jewel cut optical crystal cube and put a photo of that object lit from below by a blue LED on my website’s main homepage. Someone mentioned the resemblance and I was surprised at the likeness, motivating me to go see the movies.

Another of my more notable math/physics images has to do with the discovery of QuasiCrystals made by a guy, Dan Shechtman, who was ostracized from academia for the “impossible” idea of crystals having rotational symmetries beyond 2,3,4 and 6. He is now a Nobel Laureate. The WP image above is on that QuasiCrystal page as an overlay of part of E8 projected over a picture made from shooting a beam of x-rays at an icosahedral Ho-Mg-Zn quasicrystal. I didn’t actually do that experiment with the x-ray beams, but I did similar ones in my college days on a particle accelerator called the Cockroft-Walton Kevatron – see below for a picture of me (the one with the beard ;–) in the physics lab assembling a moon dust experiment. One of the professors had gotten the accelerator out of Germany after having worked on the Manhattan project.

E8 and its 4D children, the 600-cell and 120-cell (pages on which I have some work, amongst others) and its grandkids (2 of the 3D 5 Platonic Solids, one of which is the 3D version of the 2D Pentagon) are all related to the Fibonacci numbers and the Golden Ratio. So that kind of explains why most of my 2D art, 3D objects and sculptures (e.g. furniture like the dodecahedron table below), and 4D youtube animations all use the Golden Ratio theme.

Greg Moxness, Tucson AZ
I discovered an error in the WP article on the Disdyakis Triacontahedron. It seemed the scaling factor for determining the coordinates of the Icosidodecahedron hull was added and changed without any citation references. Since the factor seemed off, I analyzed it using the Koca, Mehmet’s paper and Weisstein, Eric W. “Disdyakis Triacontahedron.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/DisdyakisTriacontahedron.html
Please see this Mathematica Notebook for the results here or the PDF here.

Below is the SVG image of the notebook.
Greg Moxness, Tucson AZ
Updated: 05/11/2023
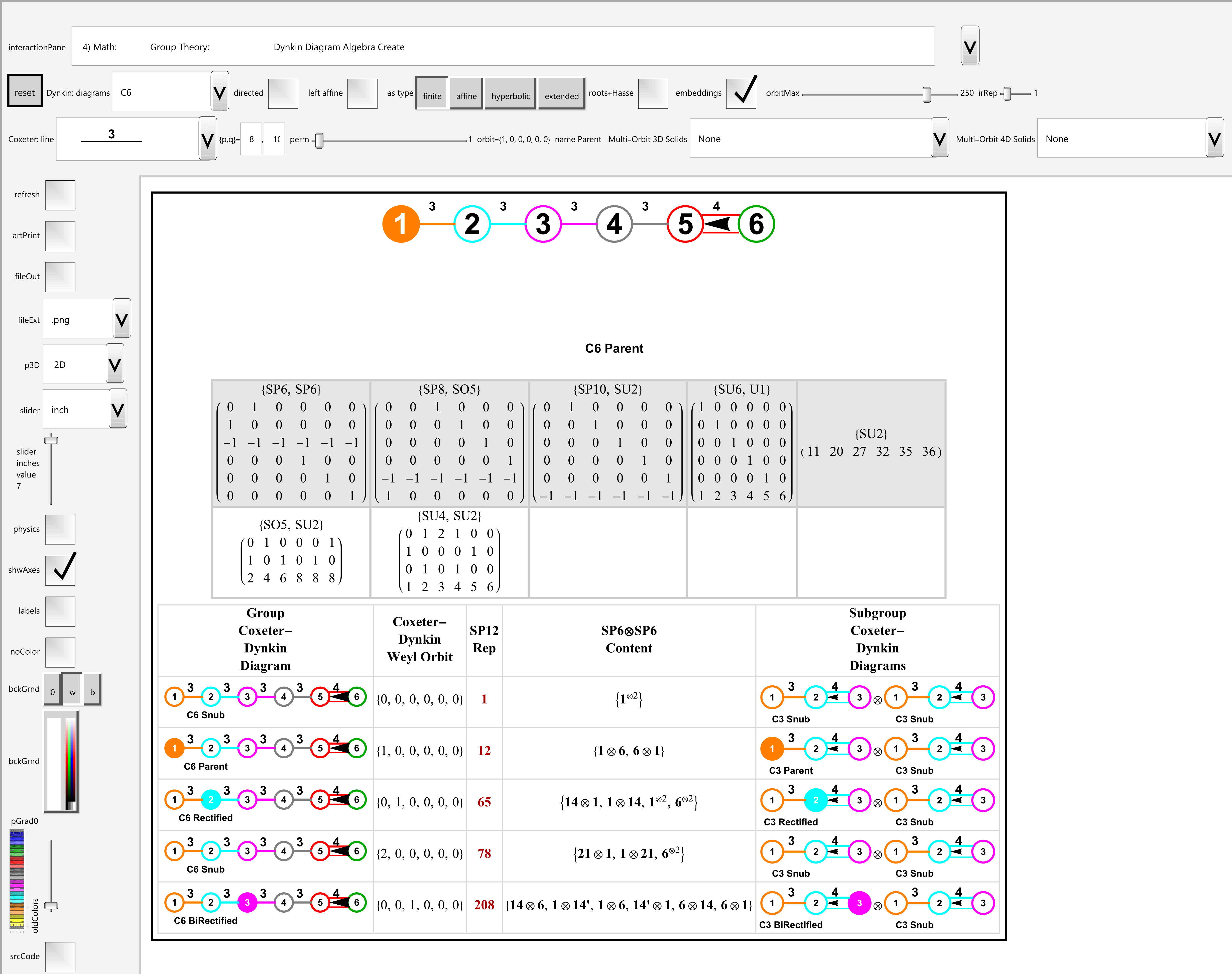
This post is a Mathematica evaluation of A4 Group Orbits & Their Polytope Hulls Using Quaternions and nD Weyl Orbits. This is a work-in-process, but the current results are encouraging for evaluating ToE’s.
Please see the this PDF or this Mathematica Notebook (.nb) for the details.
The paper being referenced in this analysis is here.
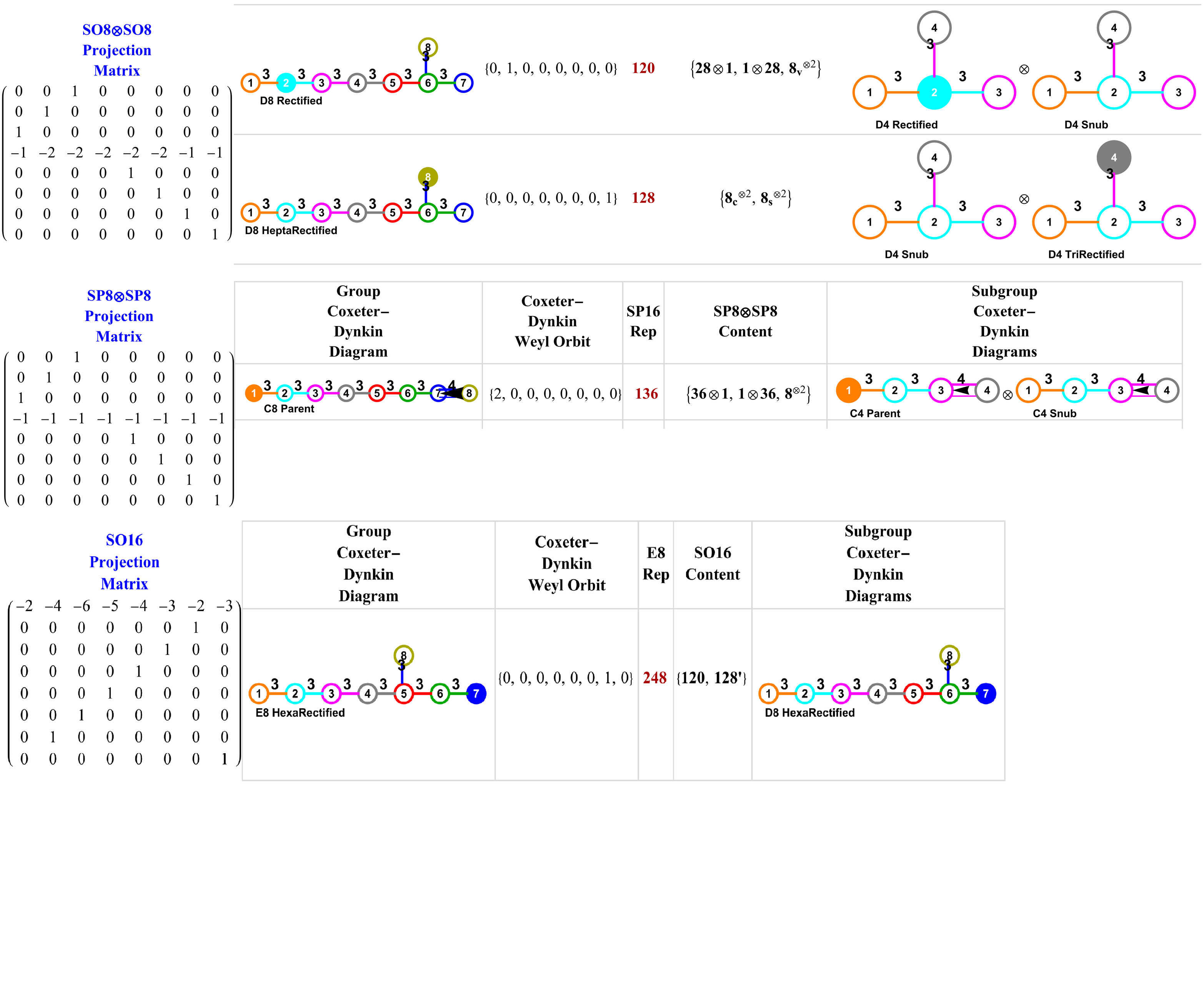
Of course, as in most cases, this capability has been incorporated into the VisibLie_E8 Demonstration codebase. See below for example screen shots:
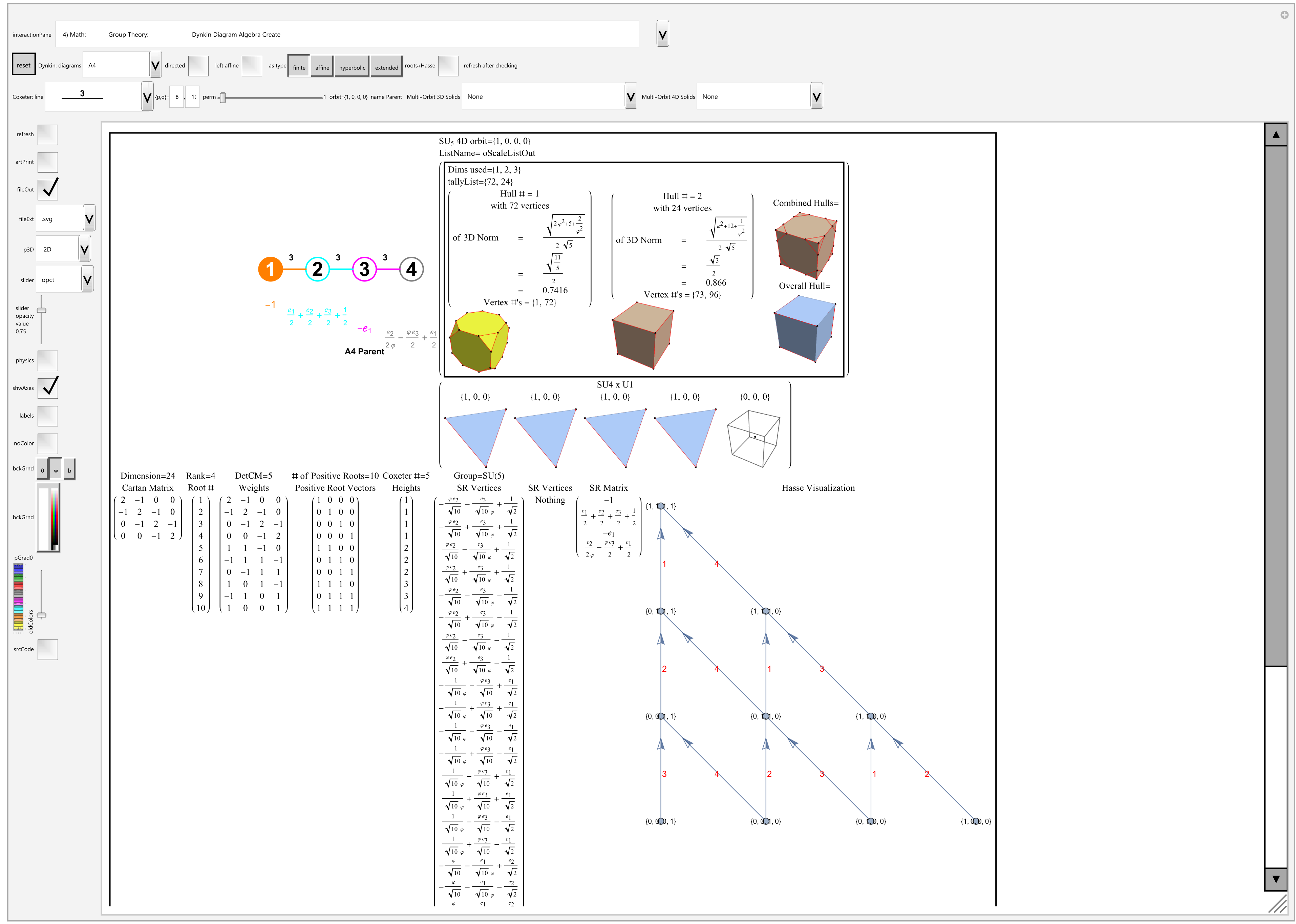
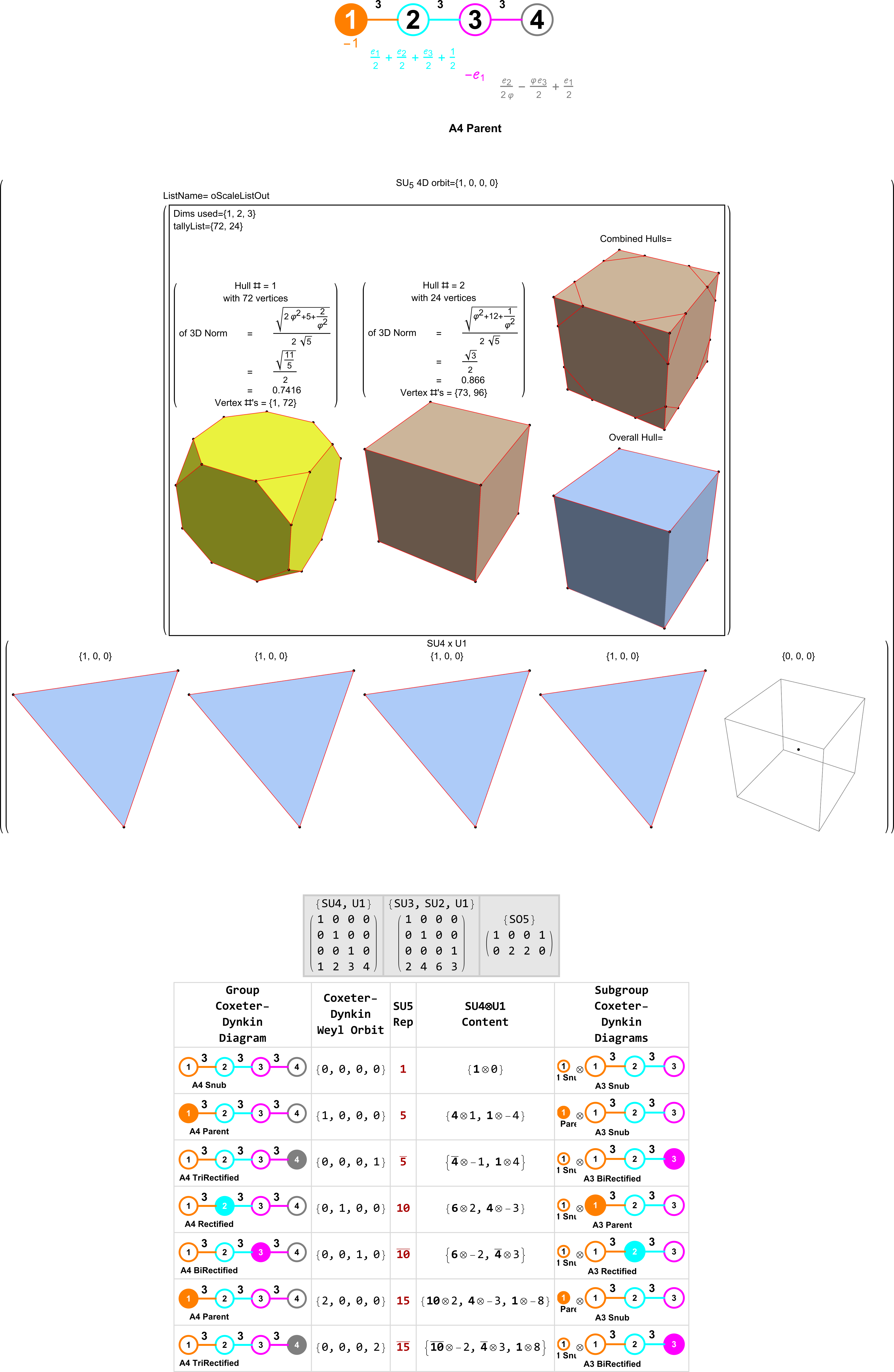
This is an example .svg file output from the same interactive demonstration:
More code and output images below: