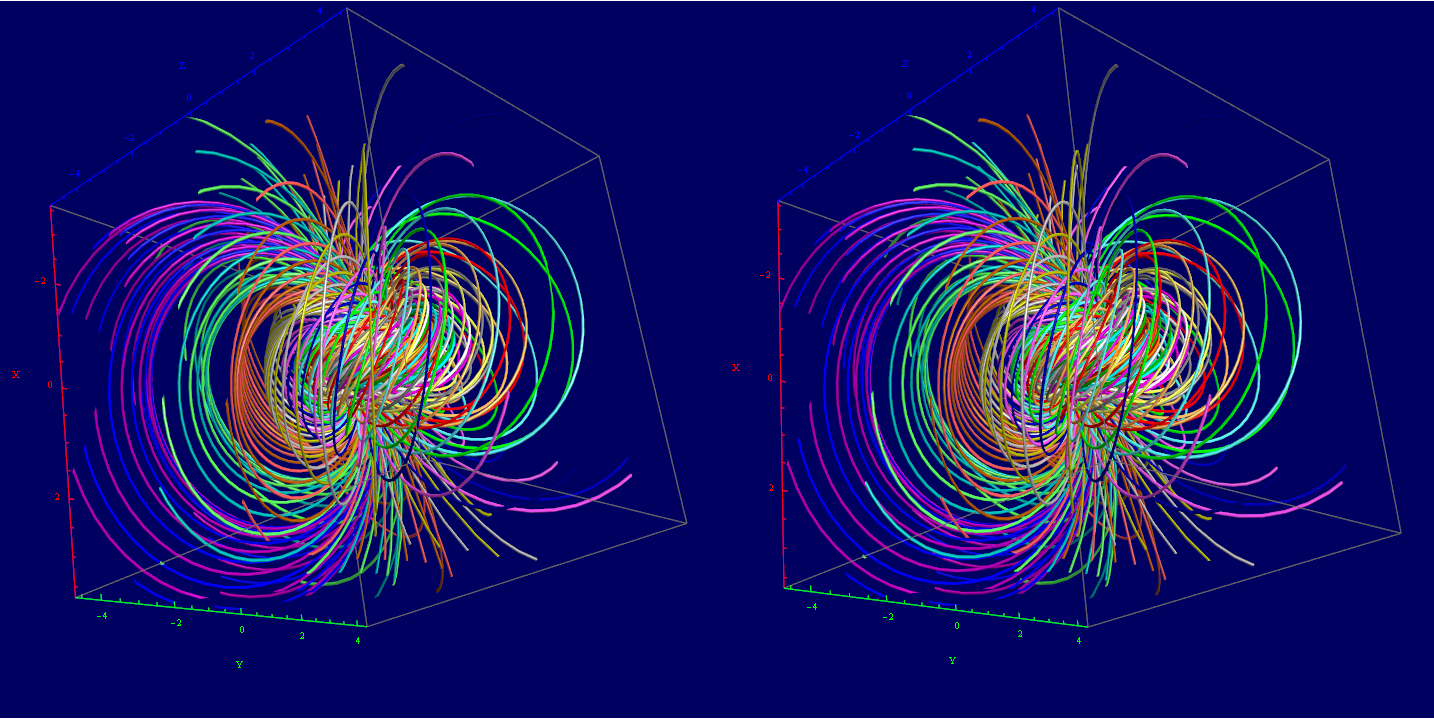
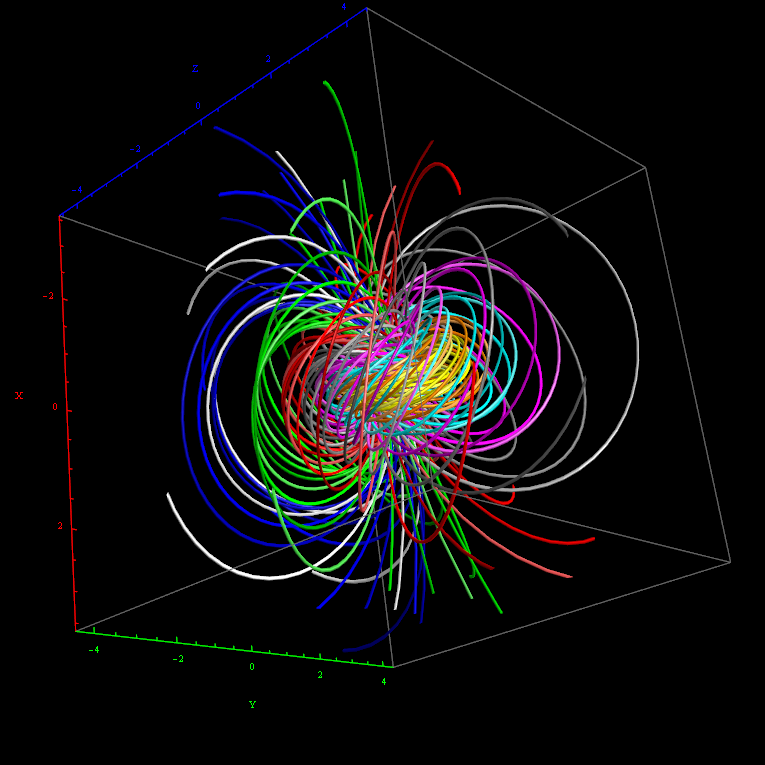
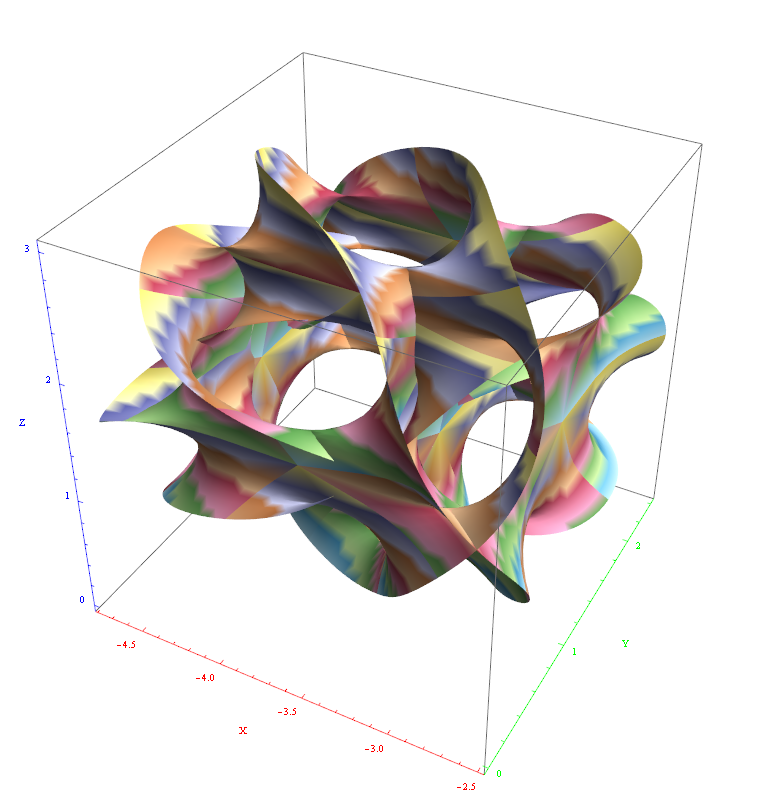
I’ve added some new features to my VisibLie_E8 ToE Demonstration. Some of it comes from Richard Hennigan’s Rotating The Hopf Fibration and Enrique Zeleny’s A Collection Of Chaotic Attractors . These are excellent demonstrations that I’ve now included with the features of my integrated ToE demonstration, since they are not only great visualizations, but relate to the high-dimensional physics of E8, octonions and their projections. This gives the opportunity to change the background and color schemes, as well as output 3D models or stereoscopic L/R and red-cyan anaglyph images.
I’ve also used David Madore’s help to calculate the symbolic value of the E7 18-gon and 20-gon symmetries of E8. It uses the nth roots of unity (18 and 20, in this case) and applies a recursive dot product matrix based on the Weyl group centralizer elements of a given conjugacy class of E8. I ended up using a combination of Mathematica Group Theory built-in functions, SuperLie and also LieART packages. These symbolic projection values are: