Tag Archives: Math
The Isomorphism of H4 and E8
Click here for a PDF of my recent paper. This has been accepted by the arXiv as 2311.01486 (math.GR & hep-th) with an ancillary Mathematica Notebook here. These links have (and will continue to have) minor descriptive improvements/corrections that may not yet be incorporated into arXiv, so the interested reader should check back here for those. Another related follow-on paper on THE ISOMORPHISM OF 3-QUBIT HADAMARDS AND E8 is referenced in the blog post here.
The abstract: This paper gives an explicit isomorphic mapping from the 240 real R^8 roots of the E8 Gossett 4_{21} 8-polytope to two golden ratio scaled copies of the 120 root H4 600-cell quaternion 4-polytope using a traceless 8×8 rotation matrix U with palindromic characteristic polynomial coefficients and a unitary form e^{iU}. It also shows the inverse map from a single H4 600-cell to E8 using a 4D<->8D chiral L<->R mapping function, phi scaling, and U^{-1}. This approach shows that there are actually four copies of each 600-cell living within E8 in the form of chiral H4L+phi H4L+H4R+phi H4R roots. In addition, it demonstrates a quaternion Weyl orbit construction of H4-based 4-polytopes that provides an explicit mapping between E8 and four copies of the tri-rectified Coxeter-Dynkin diagram of H4, namely the 120-cell of order 600. Taking advantage of this property promises to open the door to as yet unexplored E8-based Grand Unified Theories or GUTs.
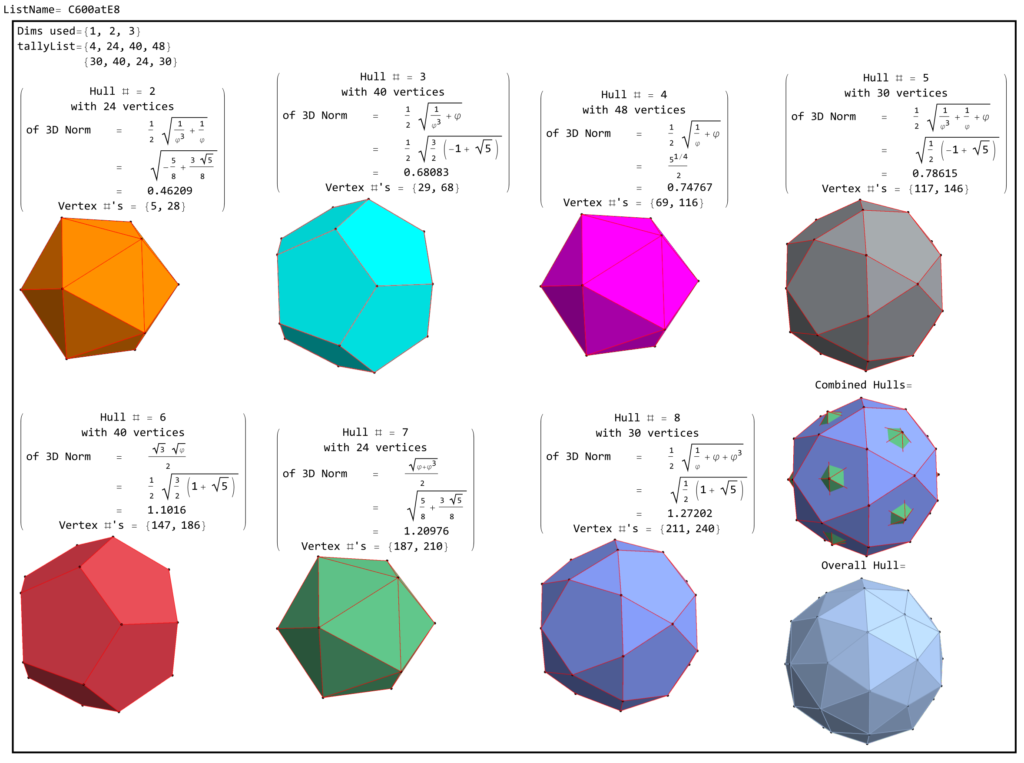

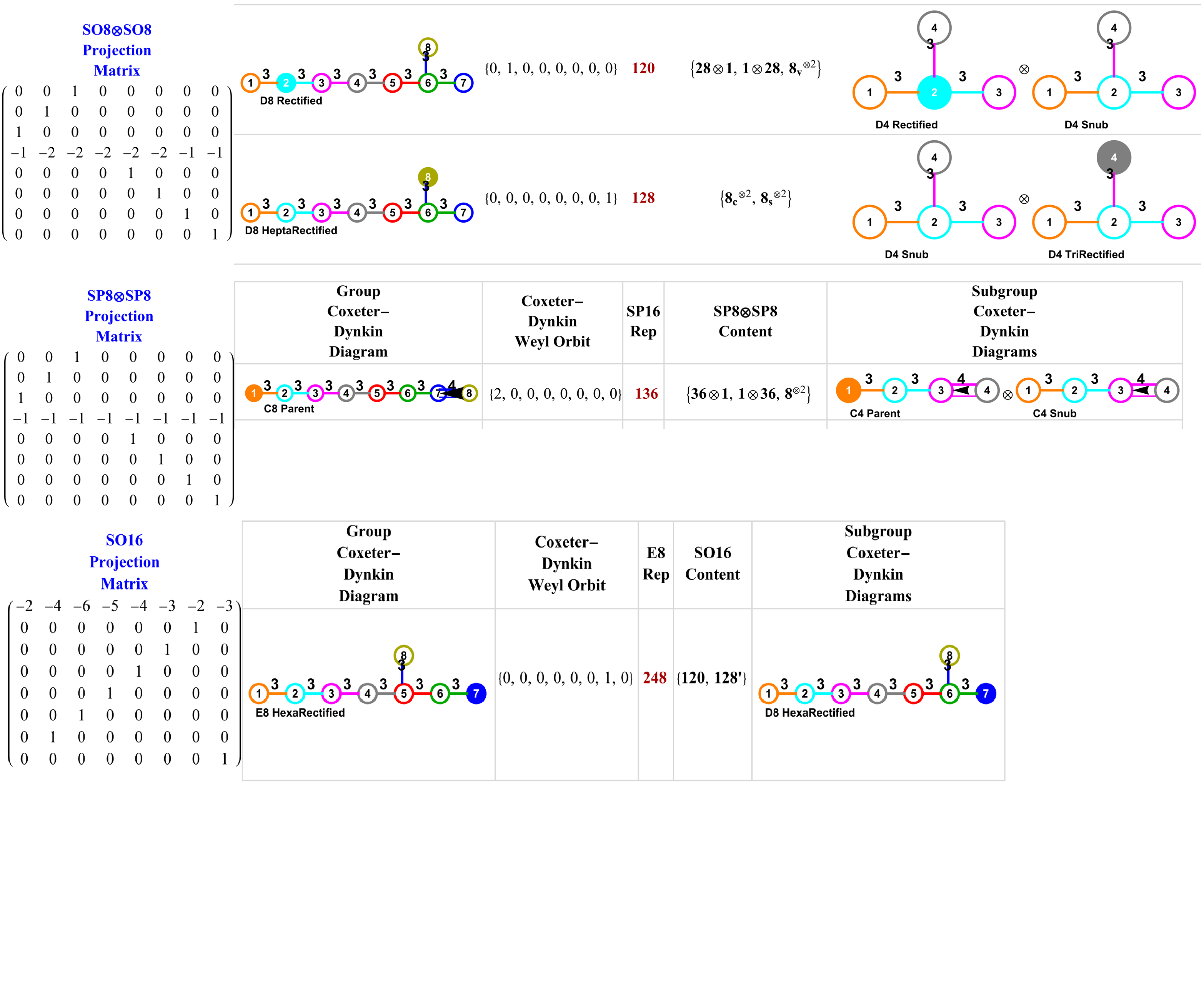


These include the specified 3D quaternion Weyl orbit hulls for each subgroup identified

Collections of 3D Surfaces, 3D Chaotic Attractors, 2D/3D Fractals, and 3D Cellular Automaton
Below are SVG images of output from Pane 1 (Chaos) and Pane 17 (AI) of the VisibLie_E8 visualization tool:
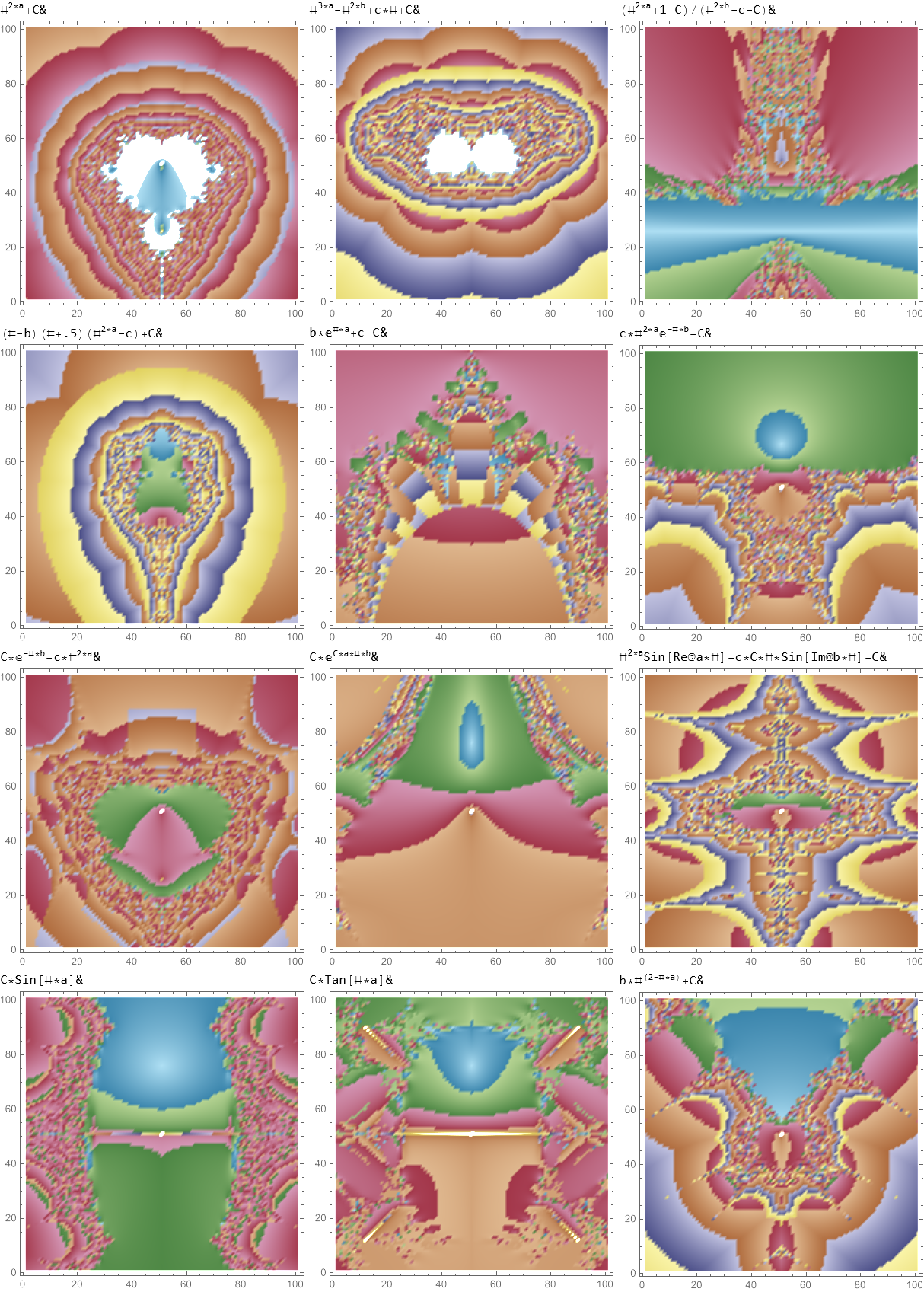

Greg Moxness, Tucson AZ
Added visualization of the embeddings of the maximal subgroups with associated projection matrices of Lie Algebras in the Dynkin Diagram pane (#4) of VisibLie_E8
This is constructed from VisibLie_E8 and uses the Mathematica package Mathgroup. A comprehensive PowerPoint/PDF that gives an overview of the underlying theory and VisibLie_E8 tool capability is in this post.
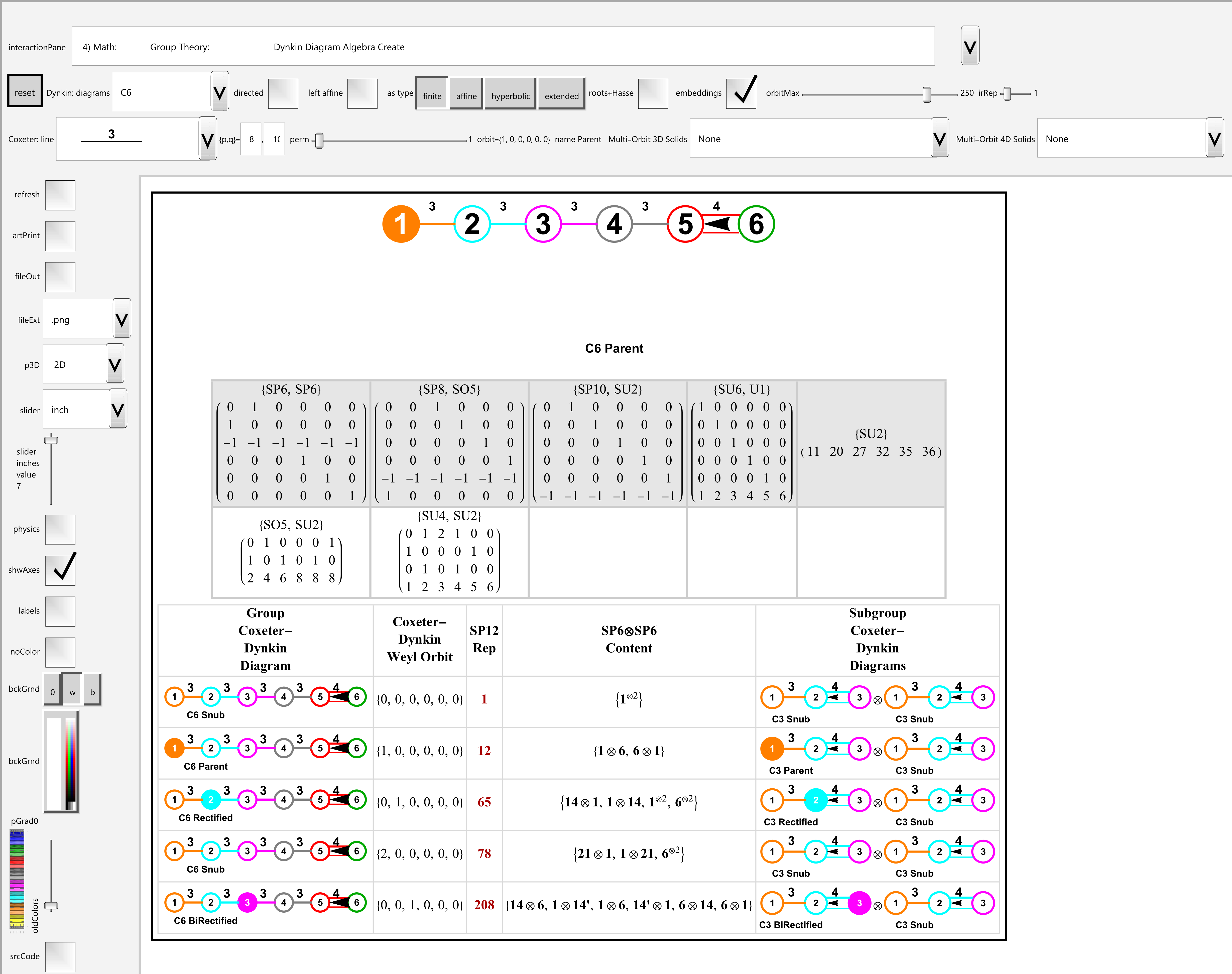
Greg Moxness, Tucson AZ
Info about my creative work: The Universe, Math, Physics, & Art
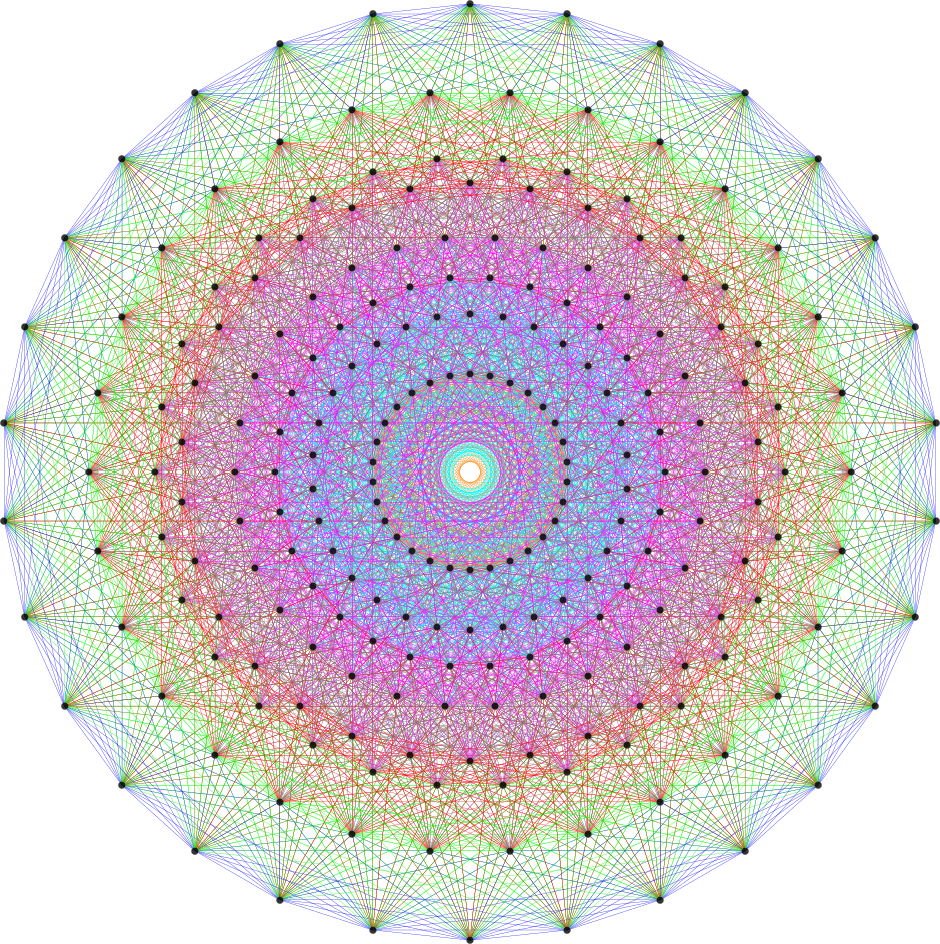
I think the most well-known (2D) image I’ve created so far (above) is found on Wikipedia’s (WP) math/geometry pages. It is what has been called the Public Relations (PR) or publicity photo for E8, which is an 8D (or 248 dimensional as the math guys count it) geometric object. It has been used in books, papers, math/science conference promotional materials, etc. That WP page also has what many used to consider “uninteresting” – my 3D versions of the same object. E8 is used in various theories to understand how the Universe operates way below the atomic level (i.e. the quantum stuff). I think it is responsible for what I call the shape of the Universe. As others have said, “who knew the Universe had a shape?”

In (very) layman’s terms, that 2D image of E8 looks sort-of-like how the lowly 4D Tesseract cube would look if it grew up into an 8D object, but a bit more interesting. The Tesseract was made (more) popular in the modern Avengers movies. In 2015 before I had ever seen any of those movies, I created a laser etched 3D projection of E8 within a jewel cut optical crystal cube and put a photo of that object lit from below by a blue LED on my website’s main homepage. Someone mentioned the resemblance and I was surprised at the likeness, motivating me to go see the movies.

Another of my more notable math/physics images has to do with the discovery of QuasiCrystals made by a guy, Dan Shechtman, who was ostracized from academia for the “impossible” idea of crystals having rotational symmetries beyond 2,3,4 and 6. He is now a Nobel Laureate. The WP image above is on that QuasiCrystal page as an overlay of part of E8 projected over a picture made from shooting a beam of x-rays at an icosahedral Ho-Mg-Zn quasicrystal. I didn’t actually do that experiment with the x-ray beams, but I did similar ones in my college days on a particle accelerator called the Cockroft-Walton Kevatron – see below for a picture of me (the one with the beard ;–) in the physics lab assembling a moon dust experiment. One of the professors had gotten the accelerator out of Germany after having worked on the Manhattan project.

E8 and its 4D children, the 600-cell and 120-cell (pages on which I have some work, amongst others) and its grandkids (2 of the 3D 5 Platonic Solids, one of which is the 3D version of the 2D Pentagon) are all related to the Fibonacci numbers and the Golden Ratio. So that kind of explains why most of my 2D art, 3D objects and sculptures (e.g. furniture like the dodecahedron table below), and 4D youtube animations all use the Golden Ratio theme.

Greg Moxness, Tucson AZ
A4 Group Orbits & Their Polytope Hulls Using Quaternions
Updated: 05/11/2023
This post is a Mathematica evaluation of A4 Group Orbits & Their Polytope Hulls Using Quaternions and nD Weyl Orbits. This is a work-in-process, but the current results are encouraging for evaluating ToE’s.
Please see the this PDF or this Mathematica Notebook (.nb) for the details.
The paper being referenced in this analysis is here.
Of course, as in most cases, this capability has been incorporated into the VisibLie_E8 Demonstration codebase. See below for example screen shots:
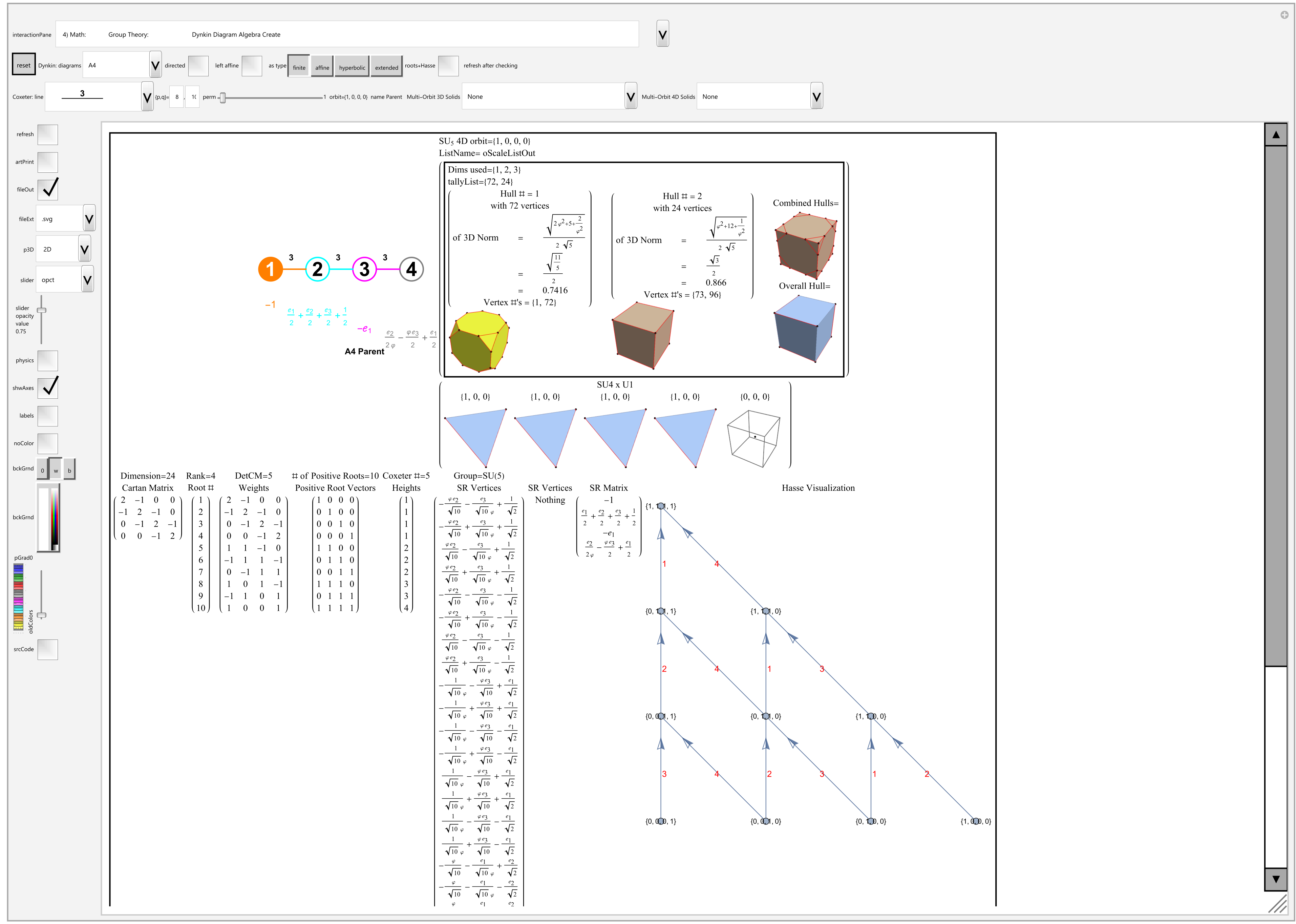
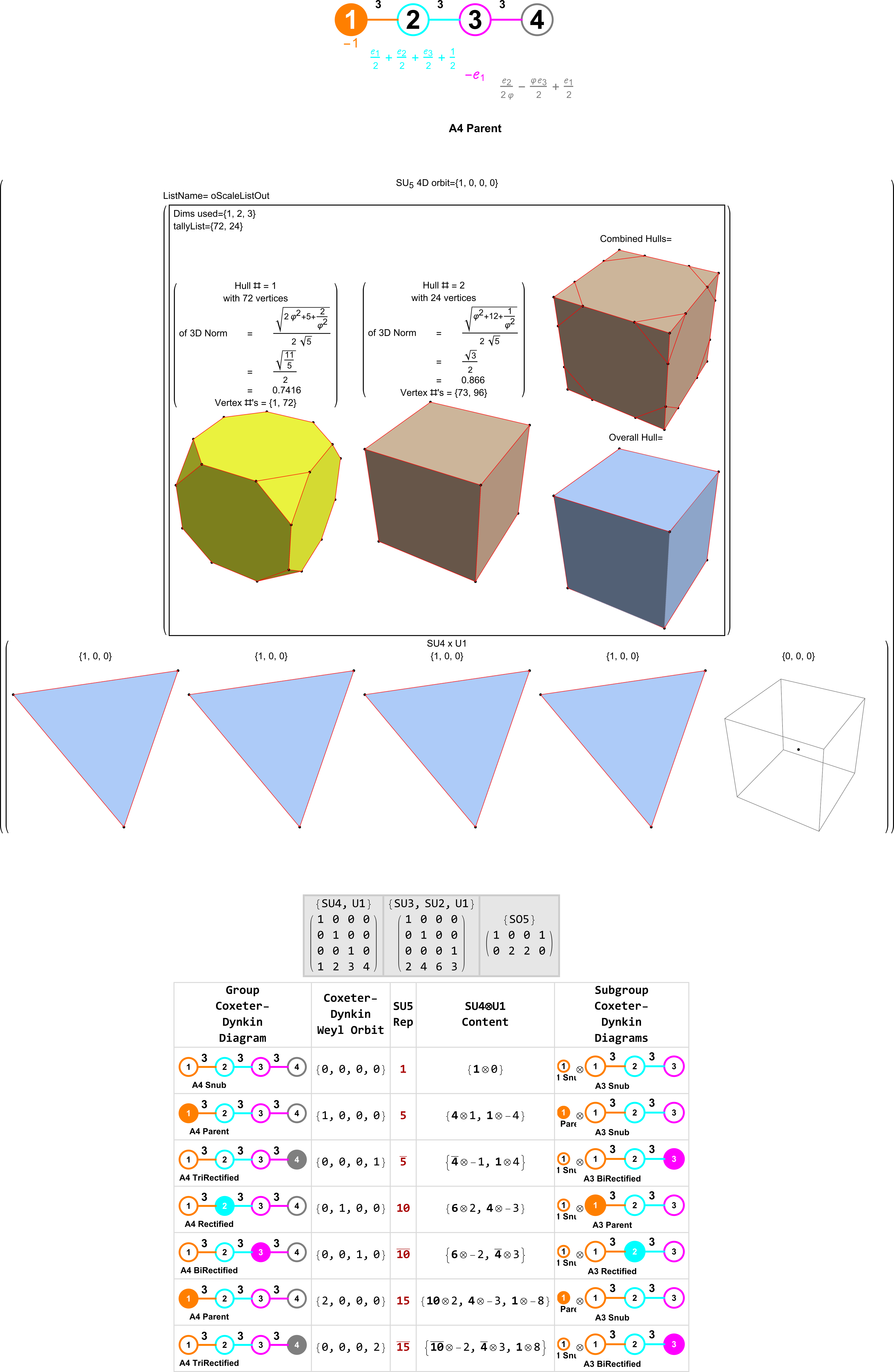
This is an example .svg file output from the same interactive demonstration:
More code and output images below:
Comparing two different 5-Cell Cartesian Coordinate sets
A New and Improved E8 Hasse Visualization
This uses the latest Mathematica version 13.2 with code tweaks to better understand what is being presented, including the E8 Algebra roots, weights, and heights. This is used on the E8 group theory page of WikiPedia.
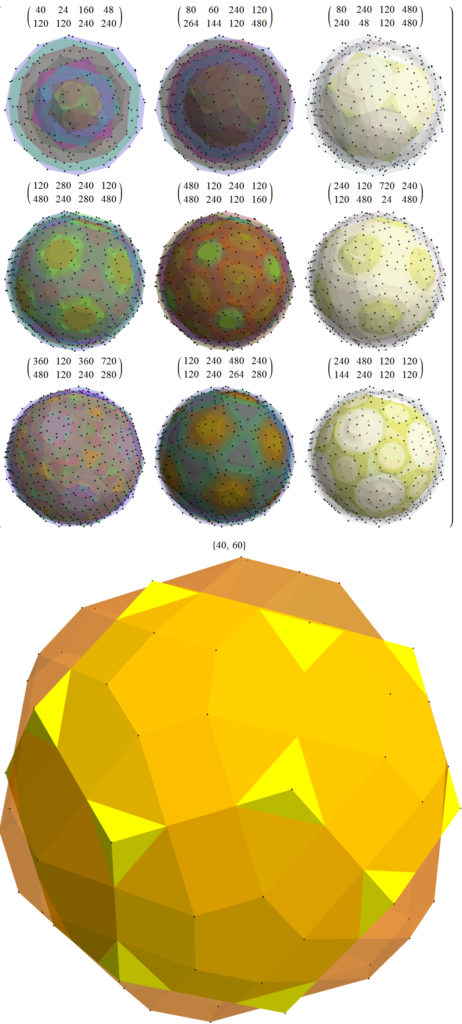
Visualizing the Quaternion Generated Dual to the Snub 24 Cell
I did a Mathematica (MTM) analysis of several important papers here and here from Mehmet Koca, et. al. The resulting MTM output in PDF format is here and the .NB notebook is here.
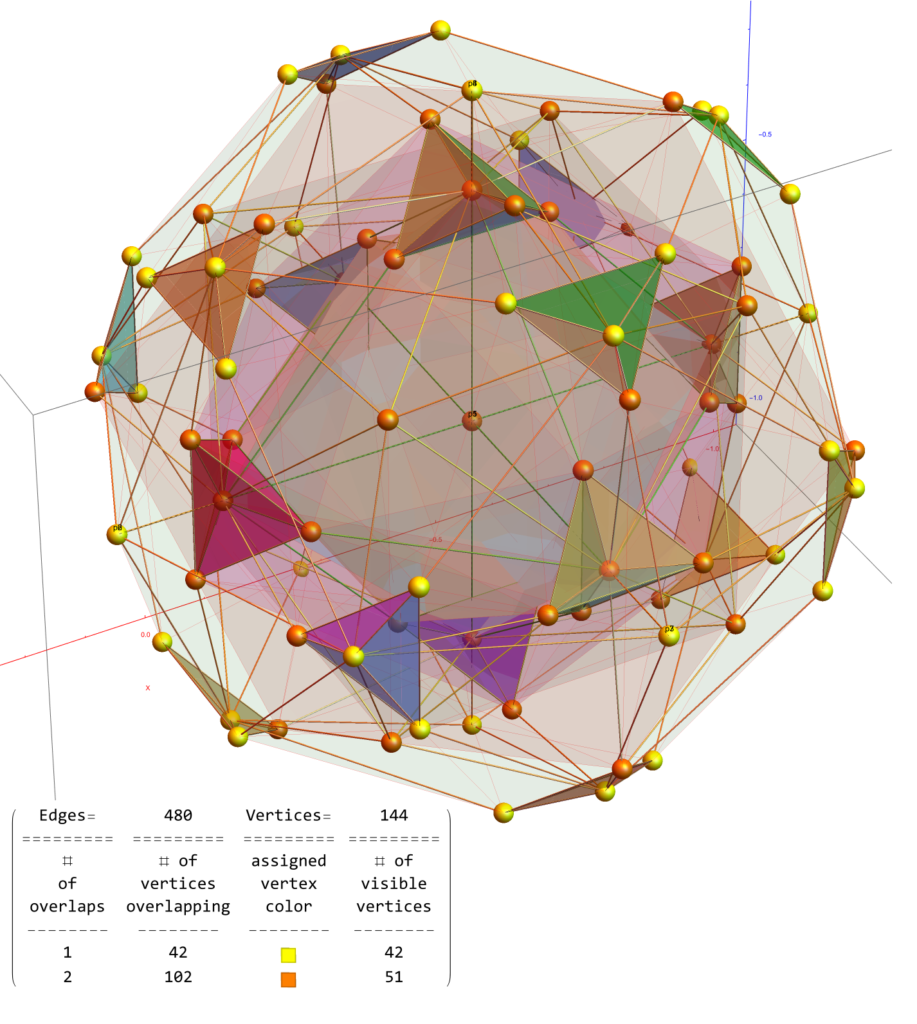
* The (42) yellow have no overlaps.
* The (51) orange have 2 overlaps.
* The (18) tetrahedral hull surfaces are uniquely colored.

What is really interesting about this is the method to generate these 3D and 4D structures is based on Quaternions (and Octonions with judicious selection of the first triad={123}). This includes both the 600 Cell and the 120 Cell and its group theoretic orbits. The 144 vertex Dual Snub 24 Cell is a combination of those 120 Cell orbits, namely T'(24) & S’ (96), along with the D4 24 Cell T(24).

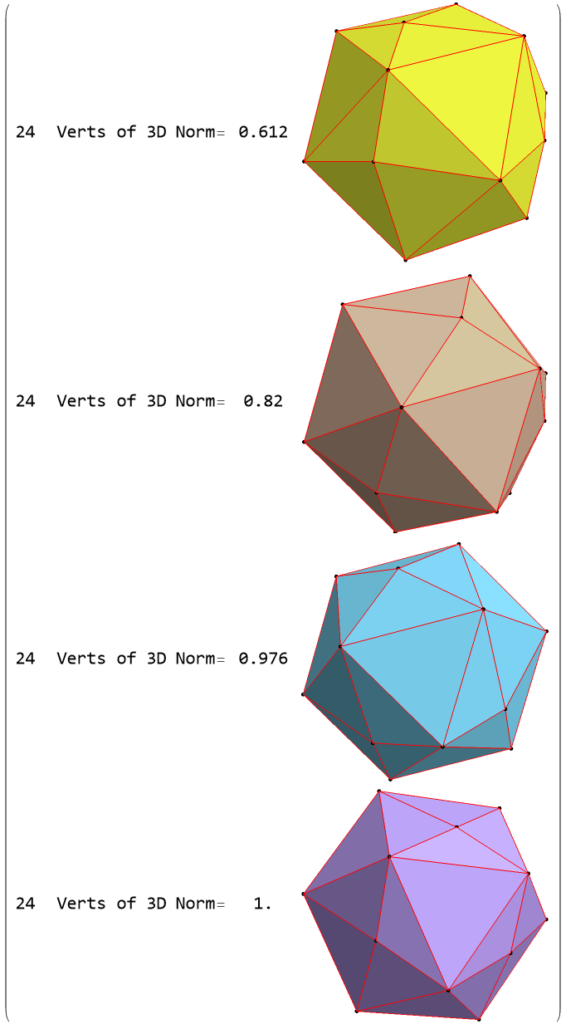
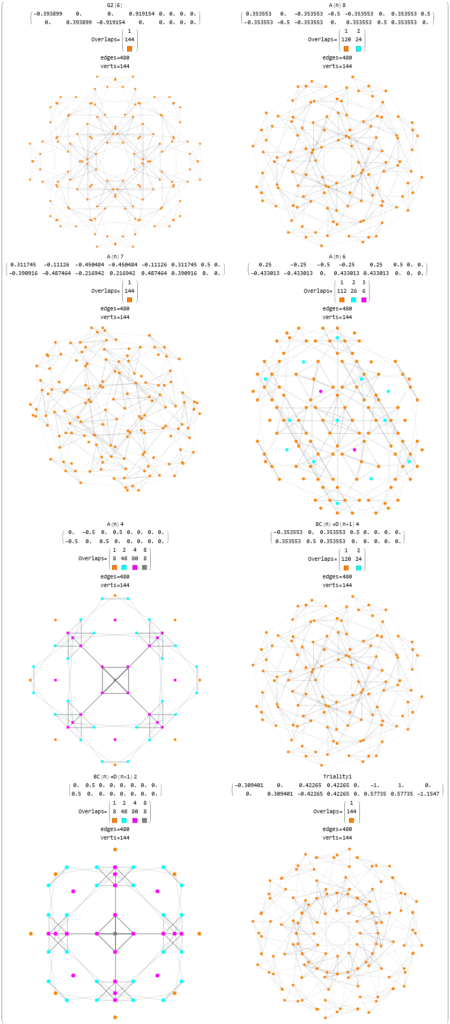
the W(D4) C3 orbits T'(24)+S'(96)+M (192)
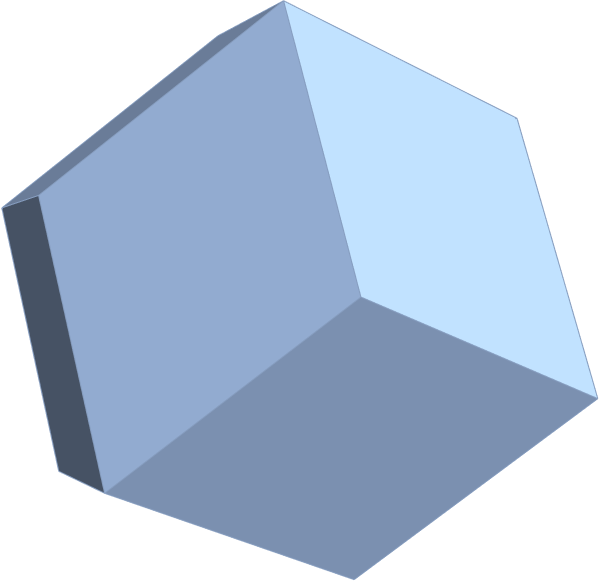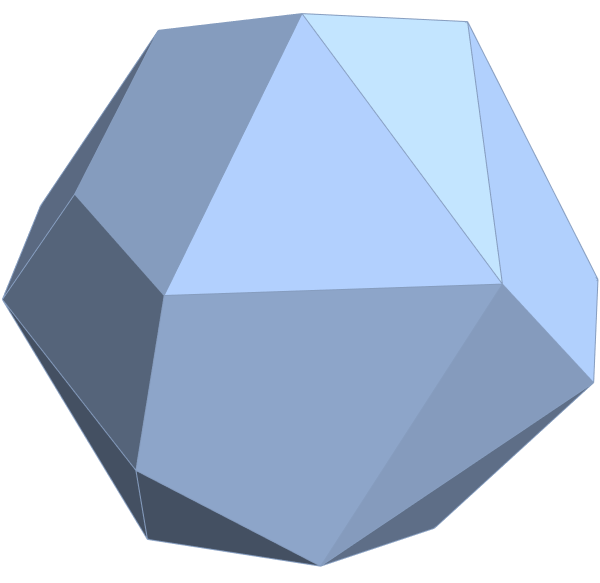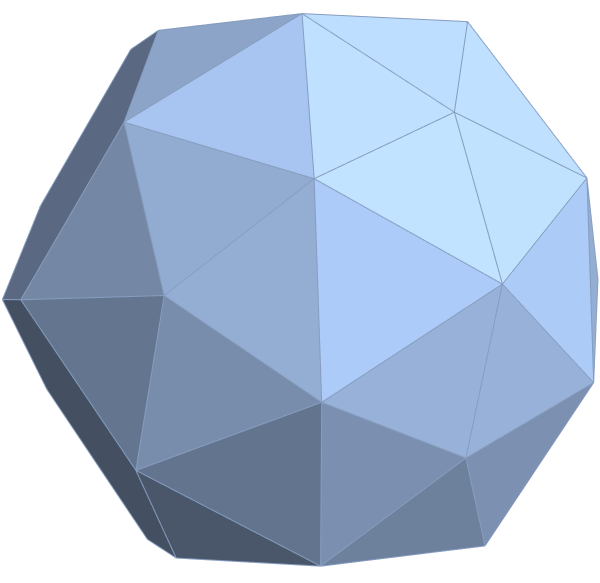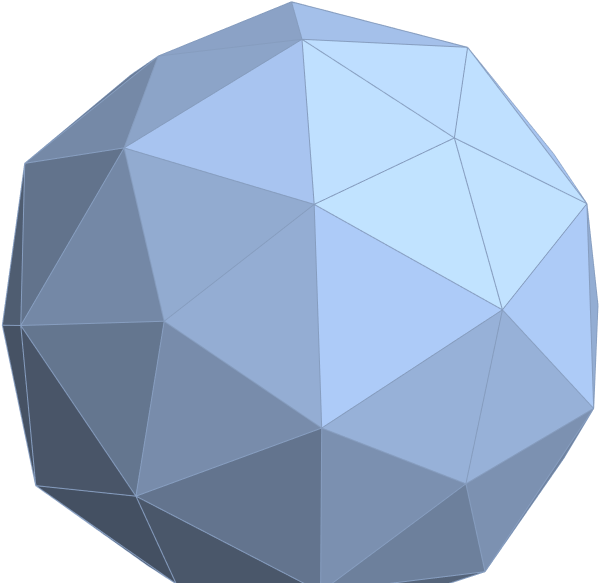

VisibLie E8: 3D Perfect Sri Yantra & 2D I-Ching Cloud Demonstrations
I’ve published a version of these demonstrations in the cloud, so no Mathematica installation is needed.
Please click here for the interactive Hindu Sri Yantra demonstration shown below.
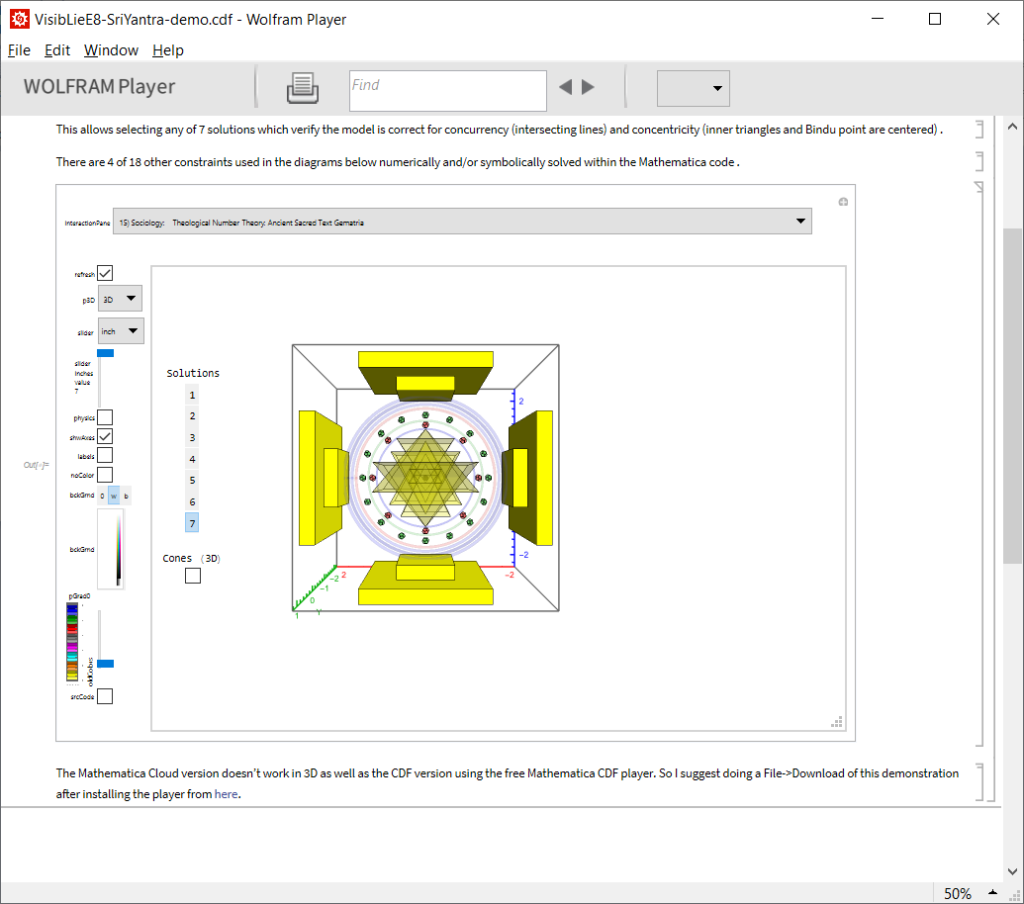
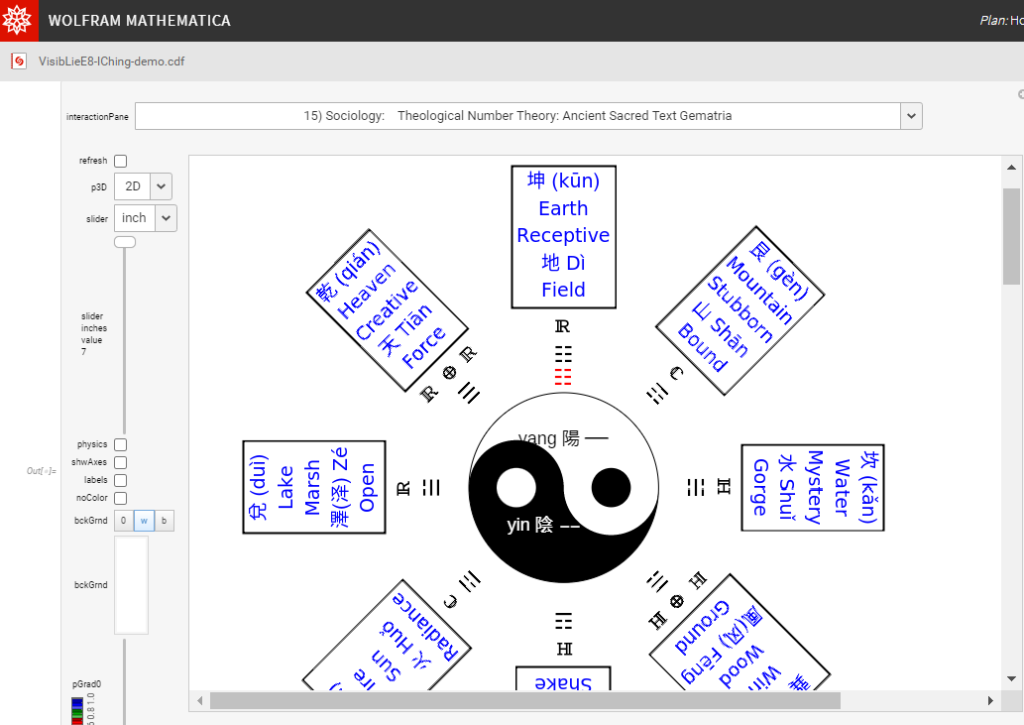
Please click here for the interactive Buddhist (Tao/Confucian) I-Ching demonstration shown below.
The Mathematica Cloud version doesn’t work in 3D as well as using a local .NB version with the free Mathematica CDF player. You can File->Download the local demonstration and use it after installing the CDF player found here.
Of course, the full licensed Mathematica Notebook works the best for this. See this file here for the Hindu 3D Sri Yantra and here for the Buddhist 2D I-Ching notebooks.
There is even a full pane 15) Sociology: Theological Number Theory: Ancient Sacred Text Gematria here.
Here is a list of other Interactive Demonstrations within my VisibLie-E8 package:
A Theory of Everything Visualizer, with links to free Cloud based Interactive Demonstrations:
1) Math: Chaos/Fibr/Fractal/Surface: Navier Stokes/Hopf/MandelBulb/Klein
2) Math: Number Theory: Mod 2-9 Pascal and Sierpinski Triangle
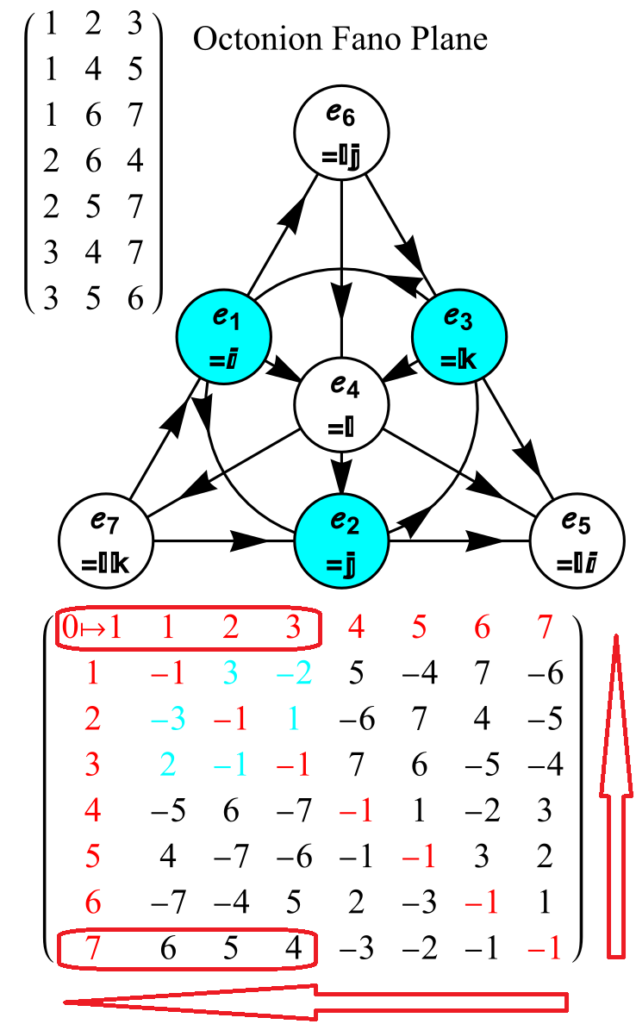
3) Math: Geometric Calculus: Octonion Fano Plane-Cubic Visualize
4) Math: Group Theory: Dynkin Diagram Algebra Create
5) Math: Representation Theory: E8 Lie Algebra Subgroups Visualize
6) Physics: Quantum Elements: Fundamental Quantum Element Select
7) Physics: Particle Theory: CKM(q)-PMNS(ν) Mixing_CPT Unitarity
8) Physics: Hadronic Elements: Composite Quark-Gluon Select Decays
9) Physics: Relativistic Cosmology: N-Body Bohmian GR-QM Simulation
10) Chemistry: Atomic Elements: 4D Periodic Table Element Select
11) Chemistry: Molecular Crystallography: 4D Molecule Visualization Select
12) Biology: Genetic Crystallography: 4D Protein/DNA/RNA E8-H4 Folding
13) Biology: Human Neurology: OrchOR Quantum Consciousness
14) Psychology: Music Theory & Cognition: Chords, Lambdoma, CA MIDI,& Tori
15) Sociology: Theological Number Theory: Ancient Sacred Text Gematria
16) CompSci: Quantum Computing: Poincare-Bloch Sphere/Qubit Fourier
17) CompSci: Artificial Intelligence: 3D Conway’s Game Of Life
18) CompSci: Human/Machine Interfaces: nD Human Machine Interface


