Click here for a PDF of my recent paper. This has been accepted by the arXiv as 2311.01486 (math.GR & hep-th) with an ancillary Mathematica Notebook here. These links have (and will continue to have) minor descriptive improvements/corrections that may not yet be incorporated into arXiv, so the interested reader should check back here for those. Another related follow-on paper on THE ISOMORPHISM OF 3-QUBIT HADAMARDS AND E8 is referenced in the blog post here.
The abstract: This paper gives an explicit isomorphic mapping from the 240 real R^8 roots of the E8 Gossett 4_{21} 8-polytope to two golden ratio scaled copies of the 120 root H4 600-cell quaternion 4-polytope using a traceless 8×8 rotation matrix U with palindromic characteristic polynomial coefficients and a unitary form e^{iU}. It also shows the inverse map from a single H4 600-cell to E8 using a 4D<->8D chiral L<->R mapping function, phi scaling, and U^{-1}. This approach shows that there are actually four copies of each 600-cell living within E8 in the form of chiral H4L+phi H4L+H4R+phi H4R roots. In addition, it demonstrates a quaternion Weyl orbit construction of H4-based 4-polytopes that provides an explicit mapping between E8 and four copies of the tri-rectified Coxeter-Dynkin diagram of H4, namely the 120-cell of order 600. Taking advantage of this property promises to open the door to as yet unexplored E8-based Grand Unified Theories or GUTs.
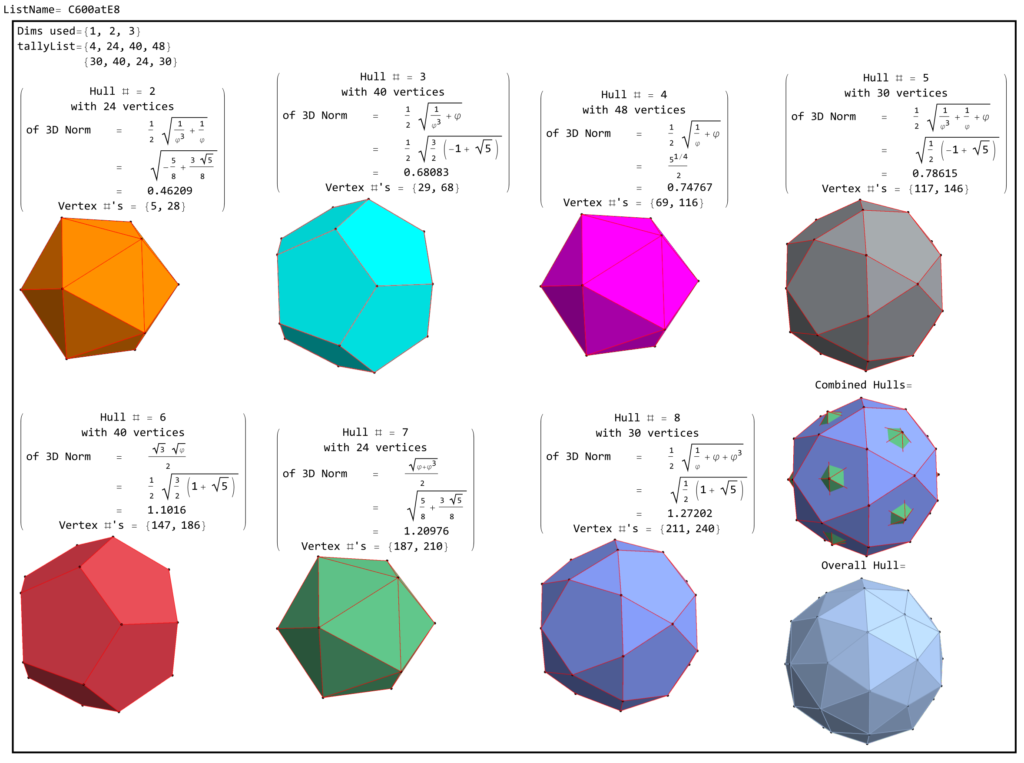
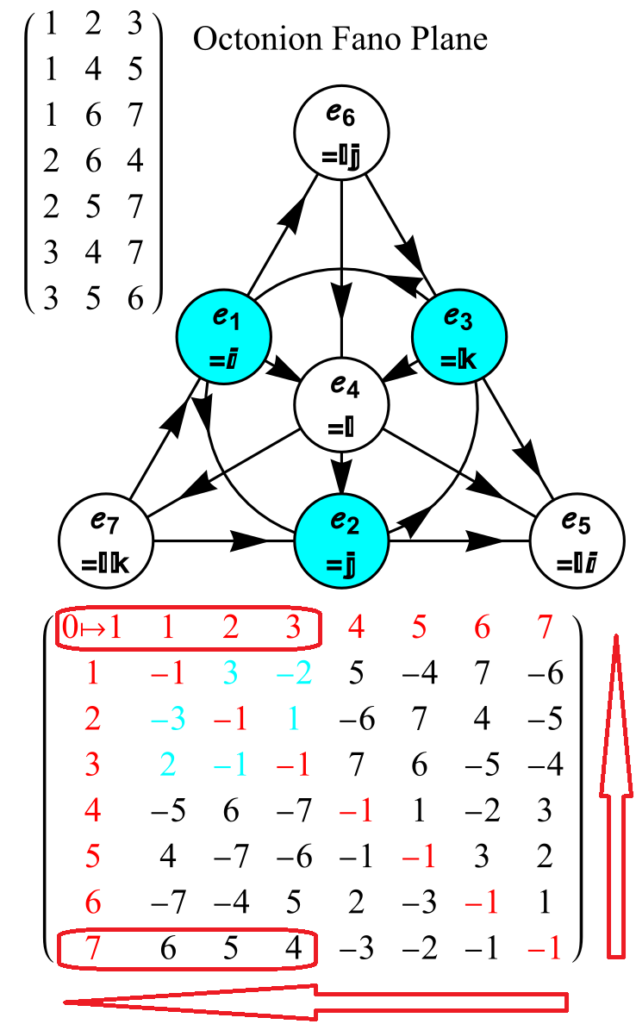
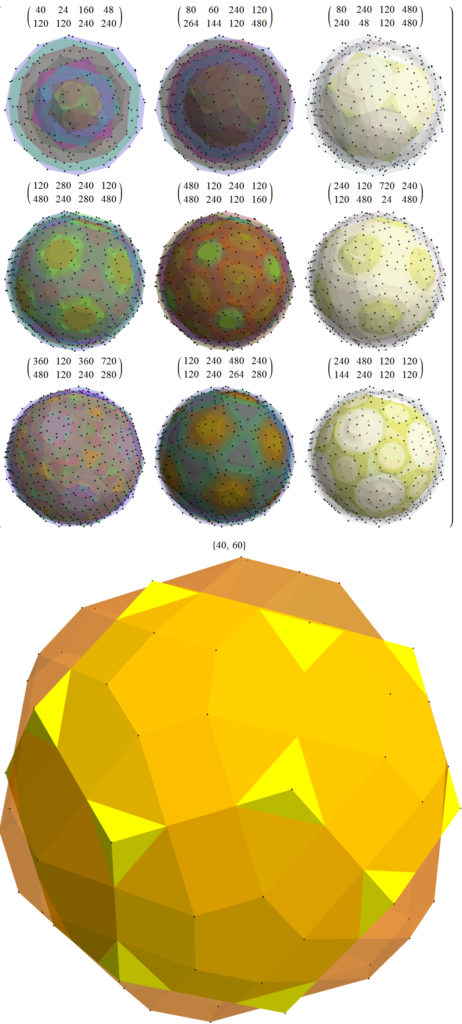

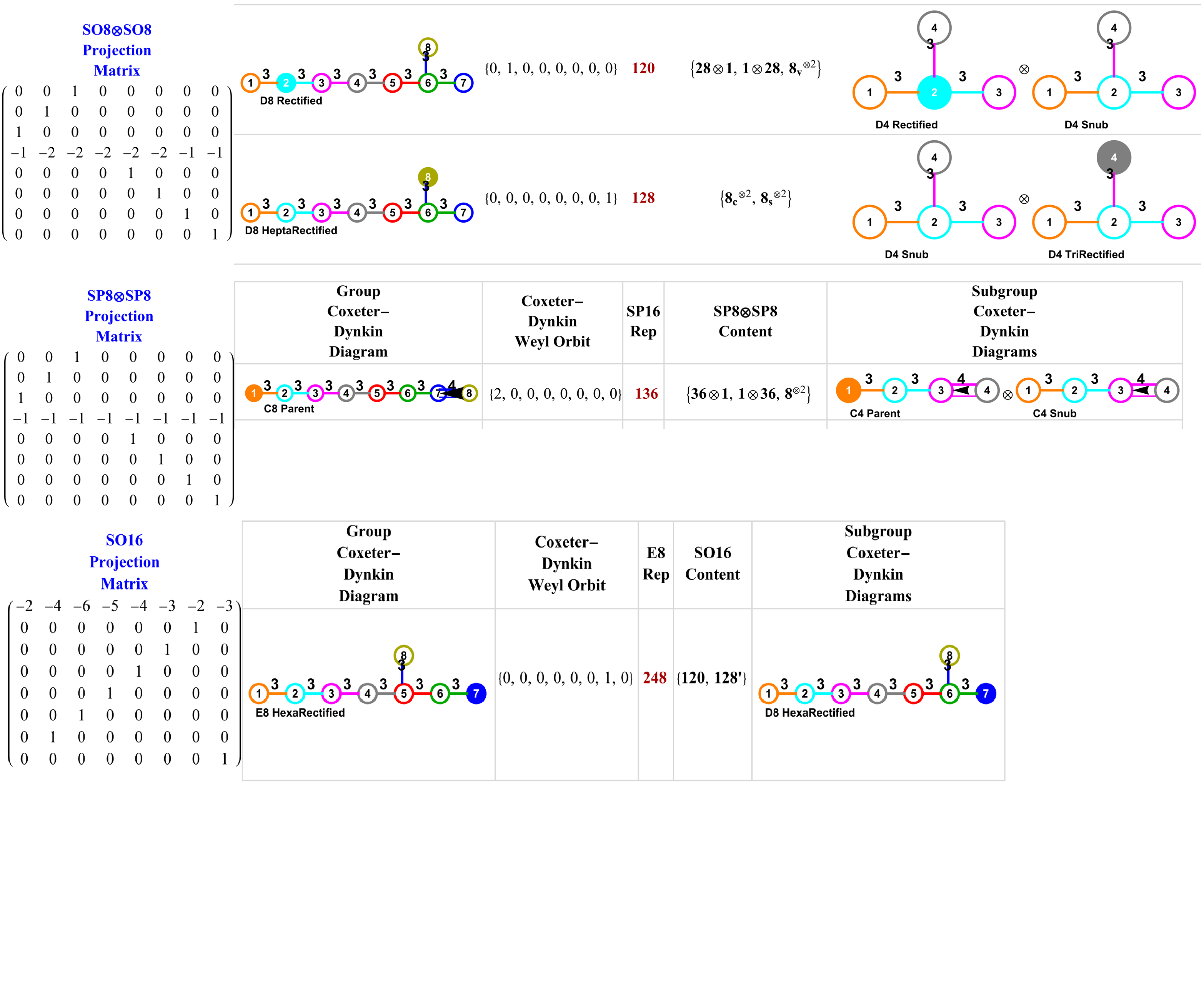


These include the specified 3D quaternion Weyl orbit hulls for each subgroup identified


