More recent related developments are here.

For more information on this, please see this Wolfram MathSource page.

This post describes the derivation of G2 automorphisms for each of the 480 unique octonion multiplication tables, as well as each of the 7 split octonions (created from negating the 4 row/column entries which are not members of the split #, which is an index to one of the 7 triads that make up the octonion).

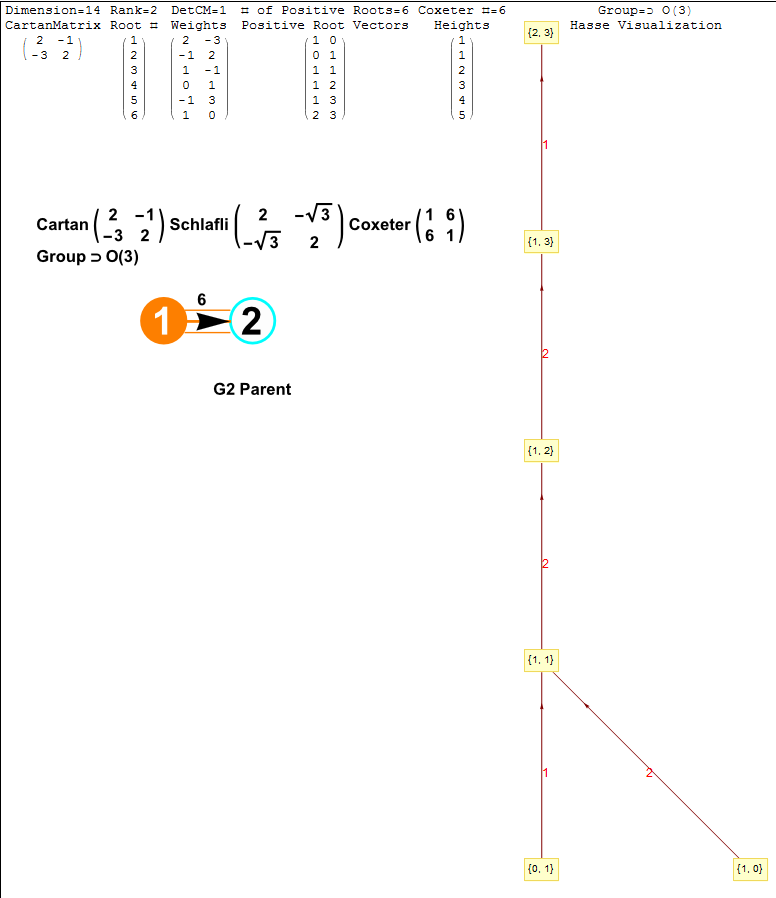
The Exceptional Lie Algebra/Group G2 is identified by its Dynkin diagram and/or associated Cartan Matrix (also shown here with its Hasse diagram):

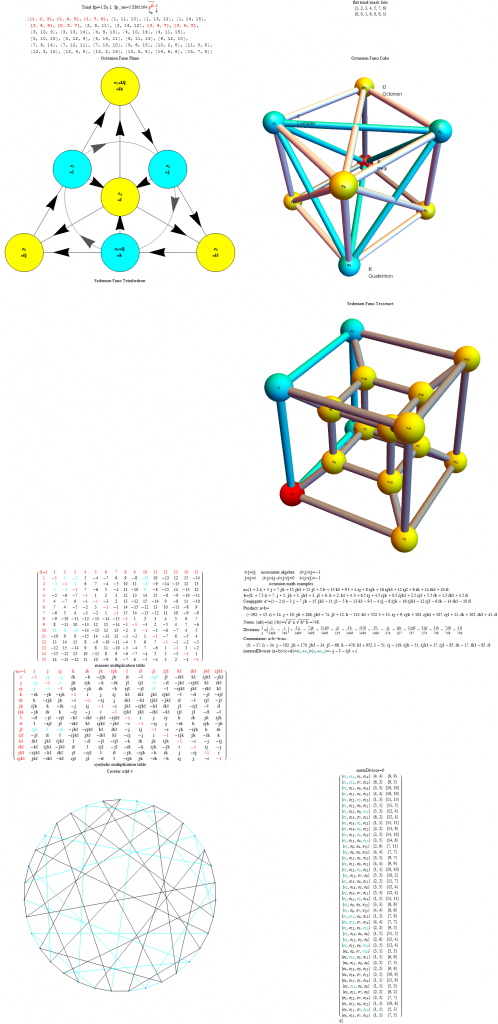
The particular octonion multiplication table selected in the example referenced above is associated in my model as a “Non Flipped E8 #164”. The multiplication table in various formats (IJKL, e_n, and Numeric) is:

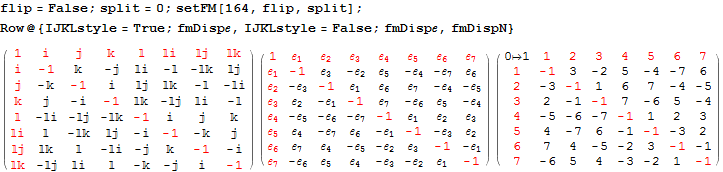
The selected multiplication table (fm) is the basis for the following octonion symbolic math:
[wlcode](* Octonion math from the matrix using 8D vector representations for x and y, this has the Subscript[\[ScriptE], 0]=1 first *)
octProduct[a_, b_] := Block[{c3 = Array[0 &, 8]},
Do[c3[[If[i != j, Abs@fm[[i, j]] + 1, 1]]]+=Sign@fm[[i, j]] a[[i]] b[[j]],
{i, 8}, {j, 8}];
Chop@c3];

(* Complex, quaternion and octonian multiplication Subscript[\[ScriptE], a]\[SmallCircle]Subscript[\[ScriptE], b] *)
quat2oct@in_ := Block[{a3},
If[QuaternionQ@in,
a3 = FromQuaternion@in;
Switch[Length@a3,
0, Re@a3 + Im@a3 Subscript[\[ScriptE], 1],
2, If[Length@a[[1]] > 0, a3,
If[Head@a3 === Times, a3[[1]] a3[[2]],
1\[SmallCircle](Re@a3[[1]] +
Im@a3[[1]] Subscript[\[ScriptE], 1]) + a3[[2]]]],
3, Re@a3[[1]] + Im@a3[[1]] Subscript[\[ScriptE], 1] +
a3[[2 ;;]]],
“not Quaternion”] /. Most@Thread[octIJKL -> oct]];

(* Octonion math with conversions, leave final as octonion *)
SmallCircle[a_List, b_List] := octonion@octProduct[a, b];
SmallCircle[a_, b_Quaternion] := a\[SmallCircle]quat2oct@b;
SmallCircle[a_Quaternion, b_] := quat2oct@a\[SmallCircle]b;
SmallCircle[a_, b_Complex] := a\[SmallCircle]ToQuaternion@b;
SmallCircle[a_Complex, b_] := ToQuaternion@a\[SmallCircle]b;
SmallCircle[a_, b_] := oct2List@a\[SmallCircle]oct2List@b;

associator[a_List, b_List,c_List] := (a\[SmallCircle]b)\[SmallCircle]c-a\[SmallCircle](b\[SmallCircle]c);
associator[a_, b_, c_] :=associator[oct2List@a, oct2List@b, oct2List@c];[/wlcode]

Each set of 21 upper triangle pairs of octonion elements (utOct) has 14 “derivations” which are null
(alternatively, the NullSpace of the derivation vectors of utOct has 7 which are NOT null…)

A derivation pair D_{x, y} is defined by:
[wlcode](* Commutator *)
commutator[x_,y_]:=x\[SmallCircle]y-y\[SmallCircle]x;
CircleDot[x_,y_]:=commutator[x, y];

(* Commutator matrix *)
comMat[x_, y_] := x.y – y.x;
comMat[{x_, y_}] := comMat[x, y];

(* Derivation matrix and vector *)
derivation[x_,y_][a_]:=(x\[CircleDot]y)\[CircleDot]a-3 associator[x,y,a];
Square[{x_, y_, a_}] := derivation[x, y][a];
derMatrix[x_,y_]:=Table[Coefficient[\[Square]{x,y,oct[[i]]},oct[[j]]], {j, 7}, {i,7}];
derVector[x_,y_]:=derMatrix[x, y]//Flatten;[/wlcode]
The 14 null pairs define G2 for a SPECIFIC octonion multiplication matrix.

For each of 7 non-null derivations there is a triple of D_{x1, y1}=D_{x2, y2}+D_{x3, y3} related derivations.

There is a 7×21 matrix describing the non-NullSpace for the octonion given in the Wolfram MathSource reference above along with the 7 non-null triples. This is generated by g2Null:
[wlcode]g2Null:=NullSpace[derVector[Subscript[\[ScriptE], #1], Subscript[\[ScriptE],#2]]&@@@utOct//Transpose];

(* Formatting all non-Null upper triangle pairs derivation entries *)
outG2Null := MatrixForm[parallelMap[Grid[{
{Row[
Subscript[D, Row@Flatten@##] & /@
Partition[Flatten@{utOct[[Flatten@Position[#, -1]]]}, 2]]},{“==”},
{Row[
Subscript[D, Row@Flatten@##] & /@
Partition[Flatten@{utOct[[Flatten@Position[#, 1]]]}, 2]]}(*),
{“\[LongDash]\[LongDash]\[LongDash]\[LongDash]”}**)}] &,
g2Null]];[/wlcode]

getG2Null (below) retrieves two octonion multiplication matrices for the flipped and non-flipped index on one of 240 E8 particles.
[wlcode]formG2Null := MatrixForm@{
Row@{Style[Row@{“flip=”, flip}, Blue],
Style[” split # \[DownArrow],”, Red]},
g2NullTbl = Table[{
split,
setFM[#, flip, split];
outG2Null},
{split, 0, 7}];
Row@triads,
MatrixForm[Column[#, Center] & /@ noNull@# & /@ Table[
(* Color the common Der in each column *)
cmnD =first@Select[g2NullTbl[[All,2,1,i,1,3,1,1,All]],
Length@# == 1 &];
cmnDclr = Style[cmnD, Magenta];
If[j == 1, {“”, Row@{
(* Highlight the missing index in the triple D_{x,y} for each row *)
Style[Complement[Range@7,Union@Flatten@g2NullTbl[[All,2,1,i,1,3,1,1,All,2,1]]][[1]],Darker@Green],
g2NullTbl[[1, 2, 1, i]] /. cmnD -> cmnDclr}},
(* Display only non-null derivations from the splits if not the same as the base octonion *)
If[g2NullTbl[[1,2,1,i]] =!= g2NullTbl[[j,2,1,i]],
{Style[g2NullTbl[[j, 1]], Red],
g2NullTbl[[j,2,1,i]] /. cmnD -> cmnDclr}]],
{i,7},{j,8}]]} &;

getG2Null := ColumnForm[{
Style[Row@{“E8#=”, #}, Darker@Green],
Row@{flip = False; formG2Null@#, flip = True; formG2Null@#}},
Center] &;[/wlcode]

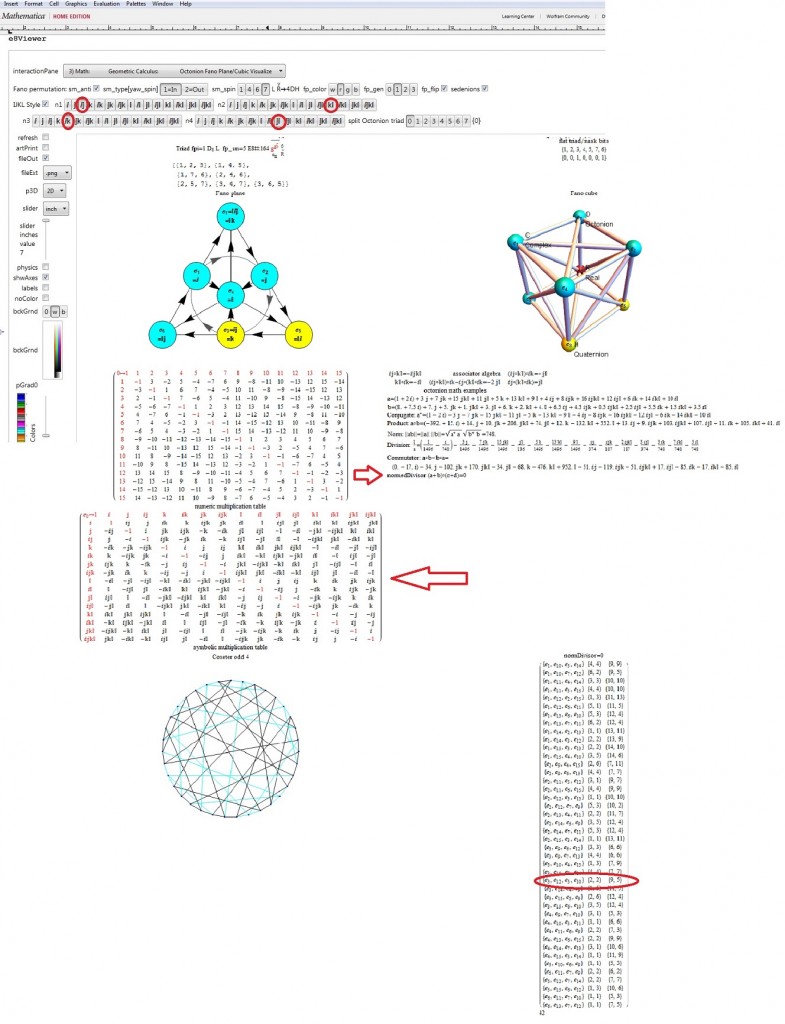
Here we show the output of getG2Null for the example non-Flipped E8 #164):

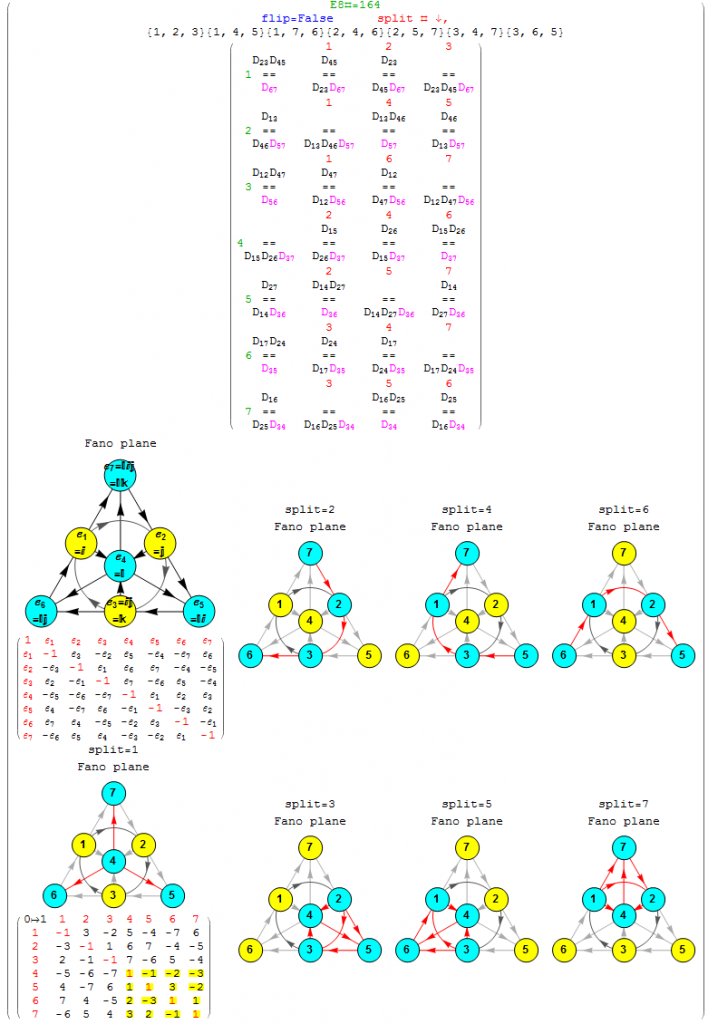
Emergent patterns:

1. For each of the 7 non-null derivation triples (the first column of the 7 rows), there are precisely 3 (of the 7) split octonions that don’t share the exact same non-null triple derivation pair as the parent (non-split) octonion (these deviations are shown in column 2 thru 4, along with the associated Fano plane diagrams for the parent and 7 split octonions of E8 #164).
2. Each non-null derivation triple contains 6 of 7 indices, and each row is missing a different index (highlighted in green before the column 1 triple). The sequence of missing element numbers in each row of the given example follows the row number.
3. It is only the equality relationship (signs) of the non-Null triple that change in 3 of the 7 splits, not the D_{x,y} itself.
4. There are always 2 pairs of 2 D_{x,y} which are negative (i.e. with a -1 entry in the NullSpace matrix located above the “==”) that occur across the row.
5. There is always a common positive D_{x,y} (i.e. with a +1 entry in the NullSpace matrix located below the “==”) in each entry of the row (colored magenta). The common positive entries in the 7 rows suggest a “distinguished” non-null indicator for the 14=21-7 G2 automorphism.
6. All octonion multiplication matrices have the first 3 rows of distinguished entries of {6,7},{5,7} and {5,6} in that order (i.e. the last 2 rows of utOct).
7. There are several possible choices for G2 automorphism sets of 14 elements within each of 480 octonions based on the 7 non-Null entries. Interestingly, there are the 4 sets of rows in utOct which sum to 14 elements, specifically rows {{1, 2, 4}, {1, 2, 5, 6}, {1, 2, 4, 6}, {2, 3, 4, 5}}). The distinguished entries of the flipped E8 #164 example below (as in the MathSource post referenced above) suggests a G2 created by rows {1,2,4} of utOct. Although, not all G2 sets must use complete rows as in this example.

This is octonionG2-nonNull, a 480 page (15 MB) which lists each of the 7 non-Null parent octonion derivations (and for each of those, the 3 other split octonion non-null derivations) which are NOT a member of the 14 null derivations for each of 480 octonion multiplication matrices and 7 splits for each (480*8=3840). It includes the Fano plane mnemonics for the parent and 7 split octionions. This is a smaller 240 page (1MB) version of octonionG2-nonNull.pdf without the Fano plane mnemonics.