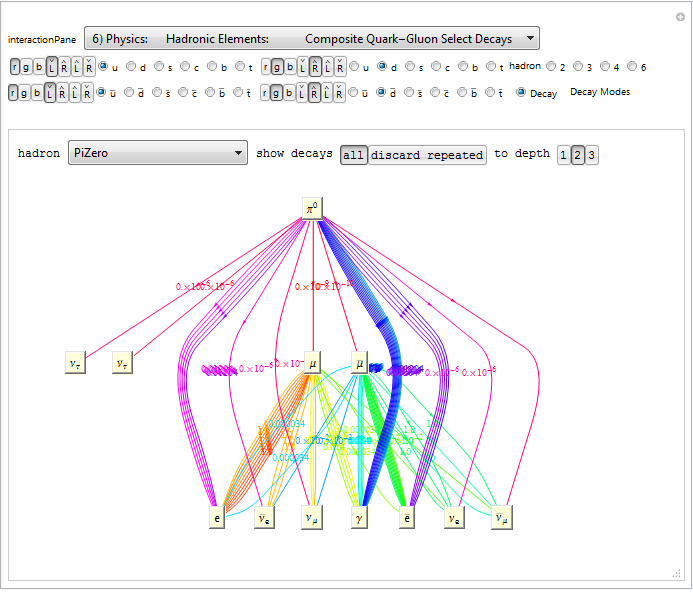
I’ve published a version of these demonstrations in the cloud, so no Mathematica installation is needed.
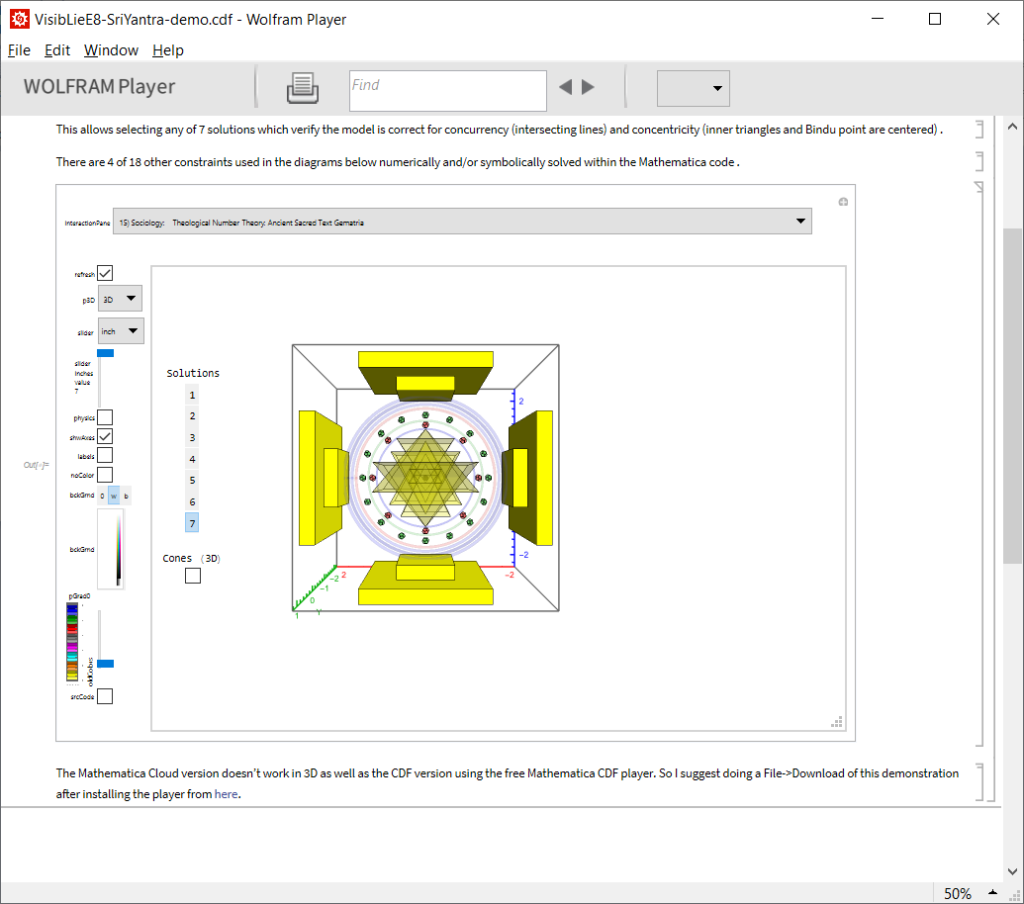
Please click here for the interactive Hindu Sri Yantra demonstration shown below.
Please click here for the interactive Buddhist (Tao/Confucian) I-Ching demonstration shown below.
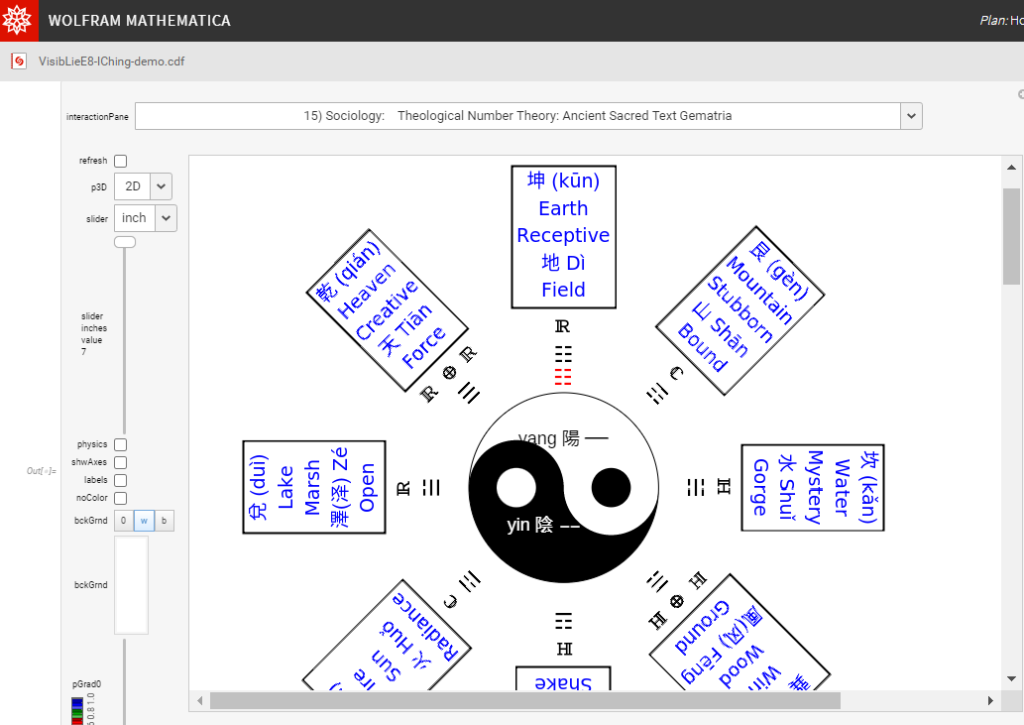
The Mathematica Cloud version doesn’t work in 3D as well as using a local .NB version with the free Mathematica CDF player. You can File->Download the local demonstration and use it after installing the CDF player found here.
Of course, the full licensed Mathematica Notebook works the best for this. See this file here for the Hindu 3D Sri Yantra and here for the Buddhist 2D I-Ching notebooks.
There is even a full pane 15) Sociology: Theological Number Theory: Ancient Sacred Text Gematria here.
Here is a list of other Interactive Demonstrations within my VisibLie-E8 package:
A Theory of Everything Visualizer, with links to free Cloud based Interactive Demonstrations:
1) Math: Chaos/Fibr/Fractal/Surface: Navier Stokes/Hopf/MandelBulb/Klein
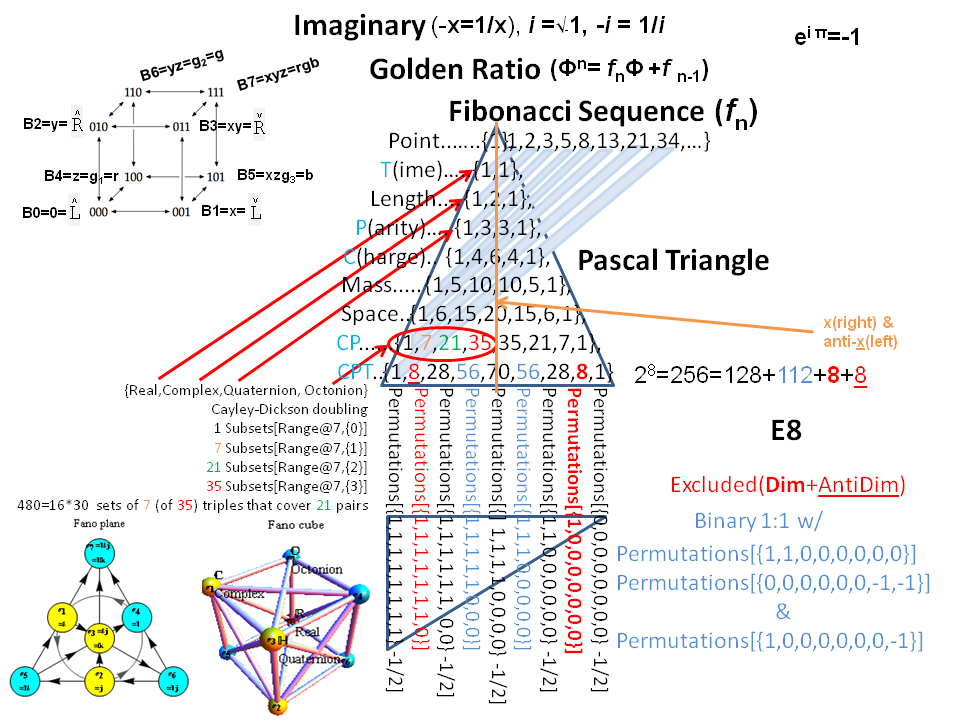
2) Math: Number Theory: Mod 2-9 Pascal and Sierpinski Triangle
3) Math: Geometric Calculus: Octonion Fano Plane-Cubic Visualize
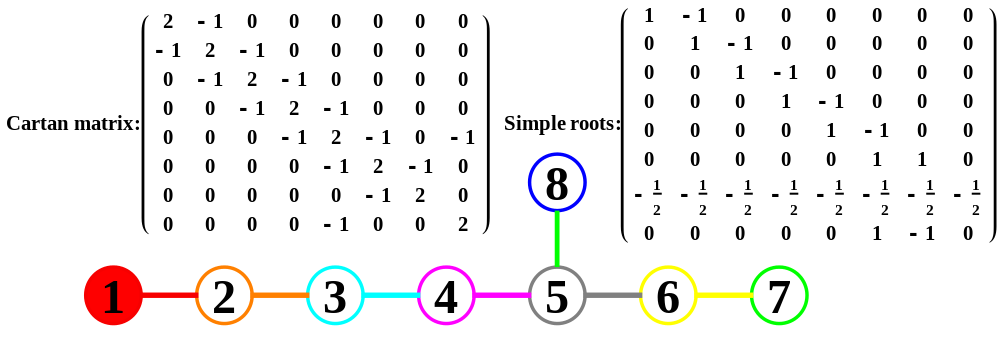
4) Math: Group Theory: Dynkin Diagram Algebra Create
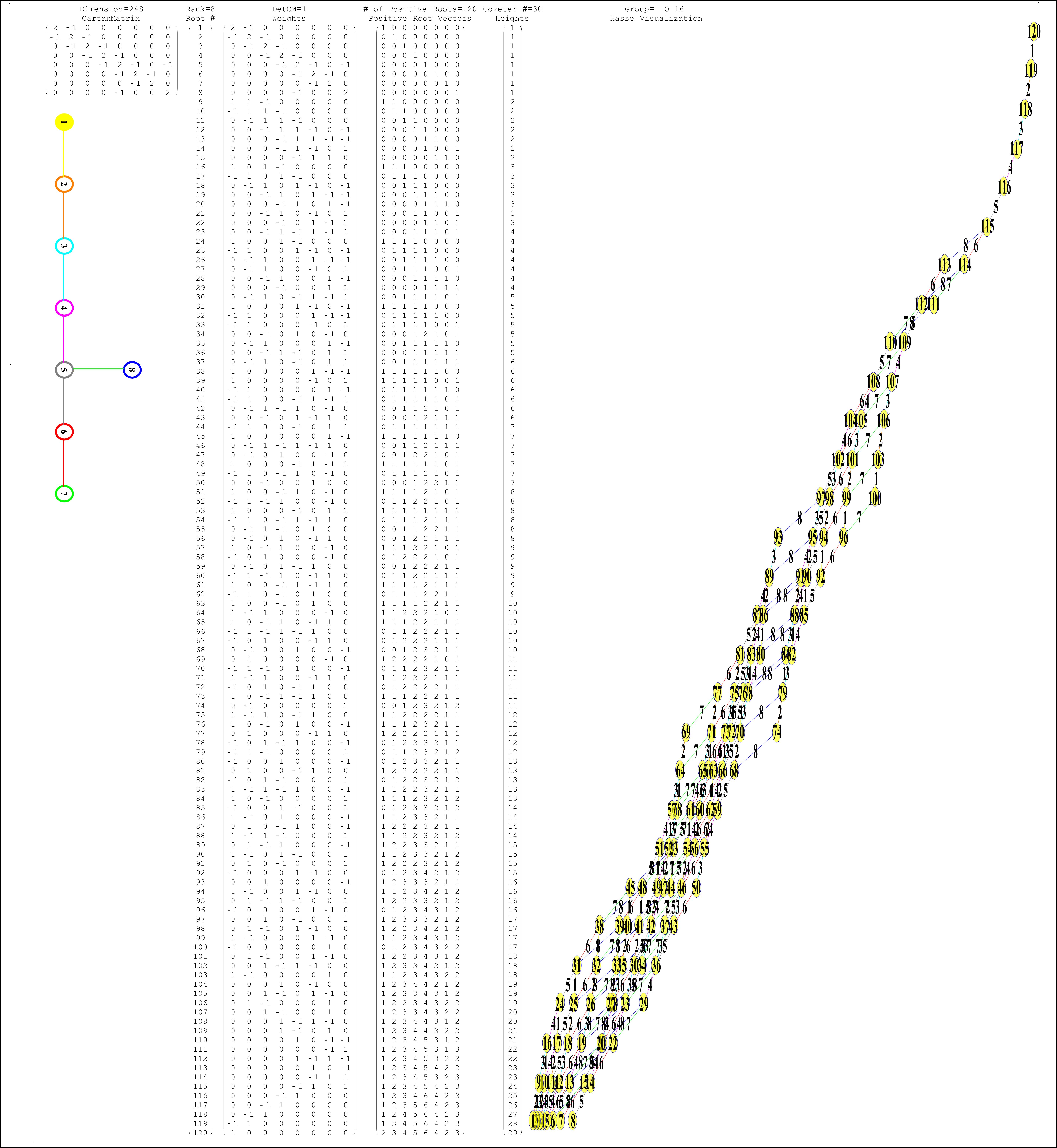
5) Math: Representation Theory: E8 Lie Algebra Subgroups Visualize
6) Physics: Quantum Elements: Fundamental Quantum Element Select
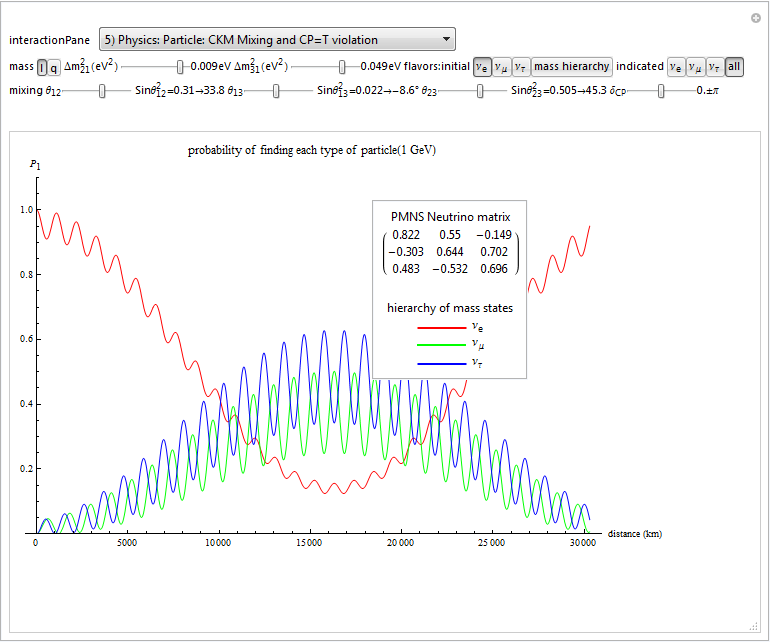
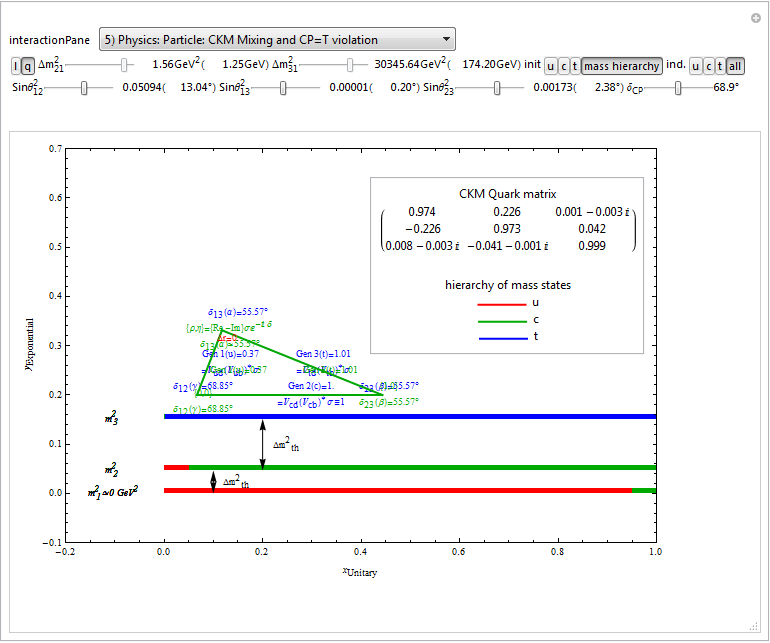
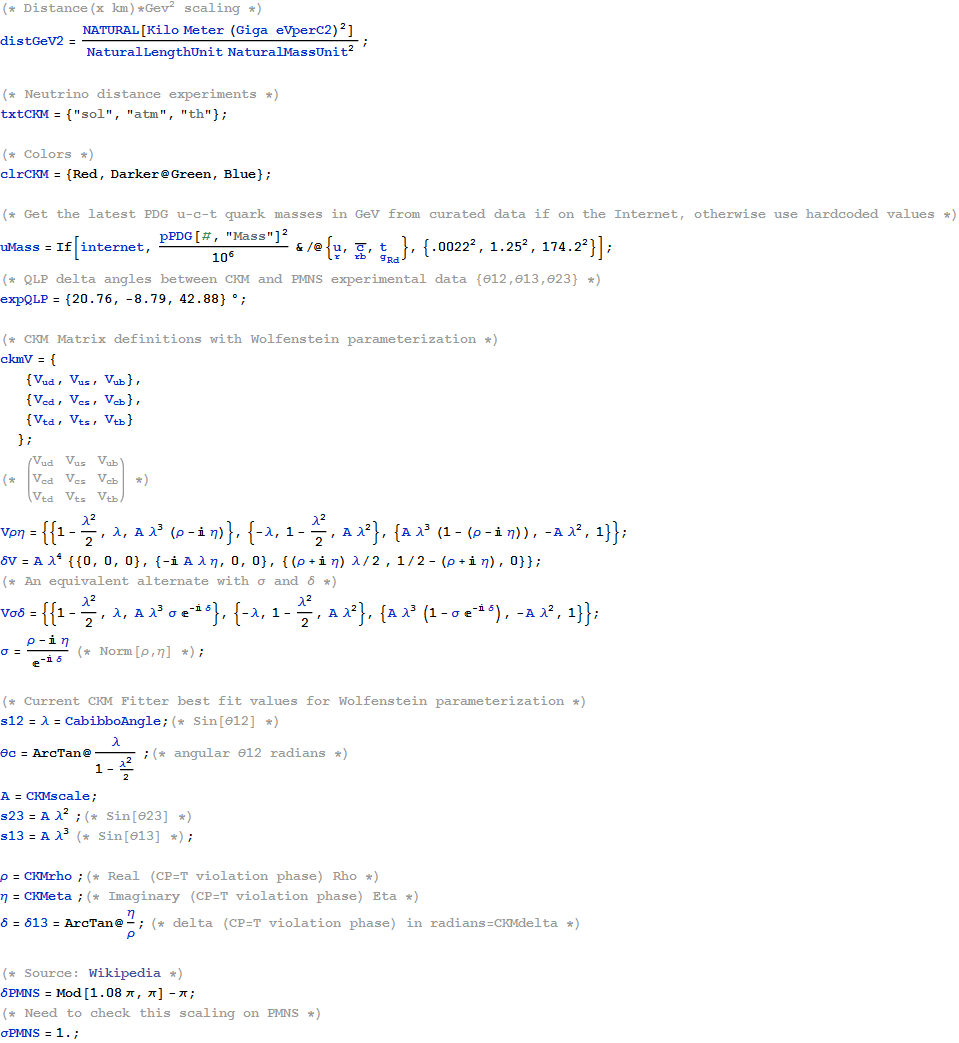
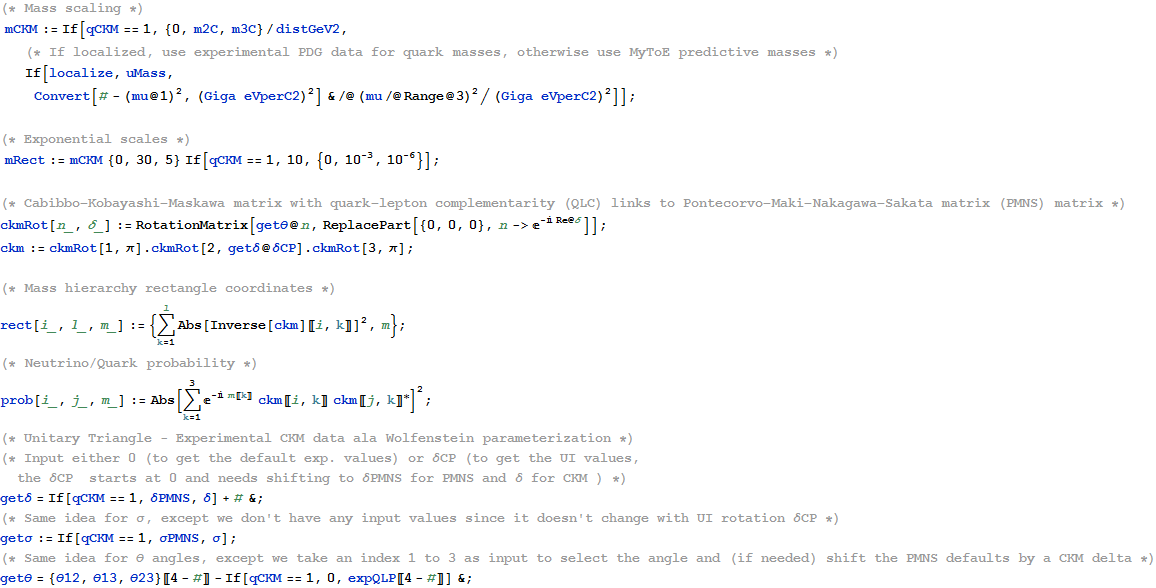
7) Physics: Particle Theory: CKM(q)-PMNS(ν) Mixing_CPT Unitarity
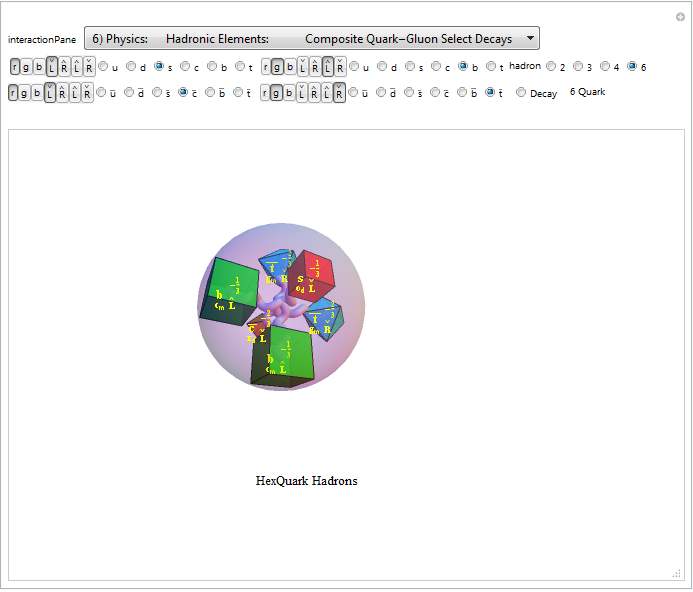
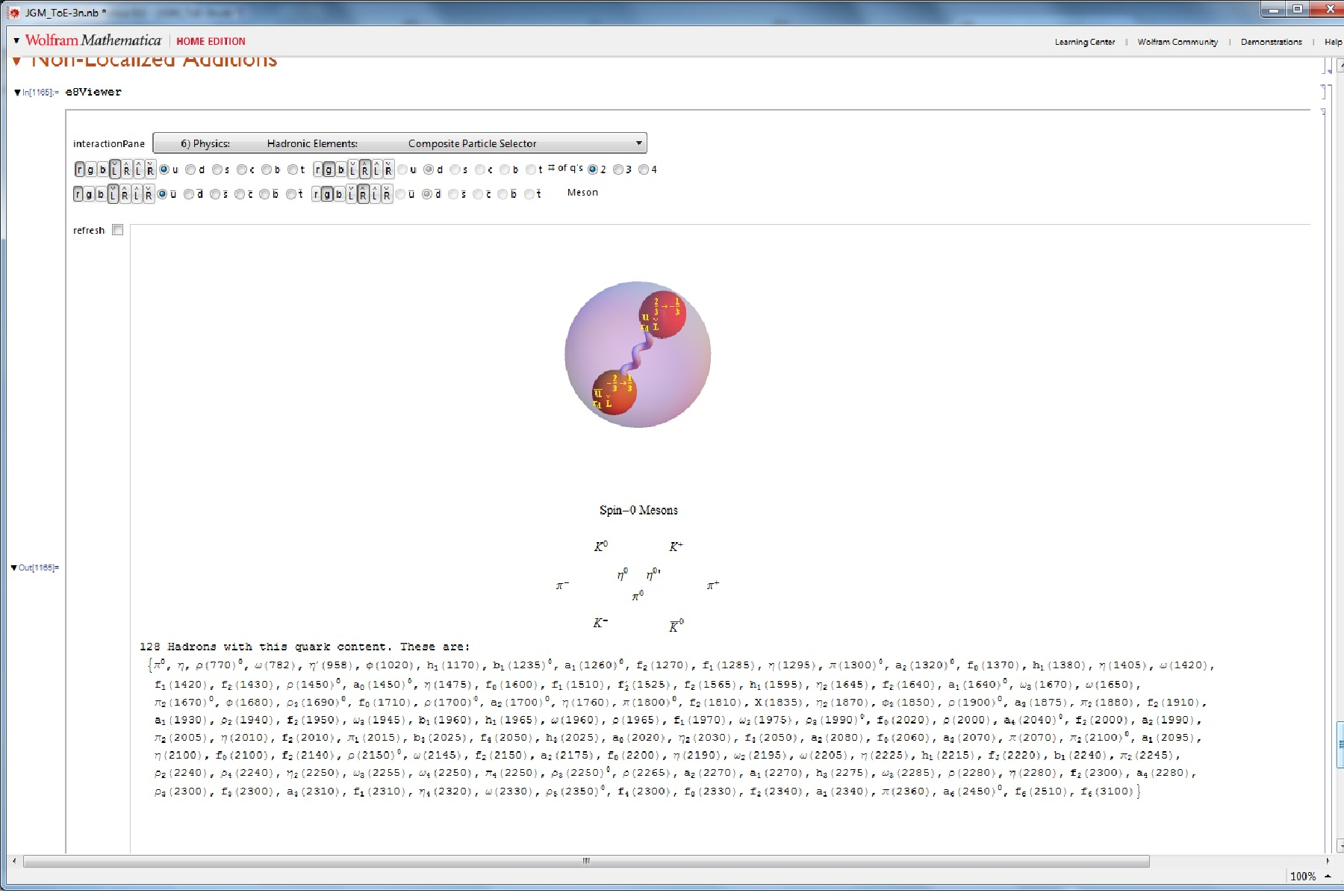
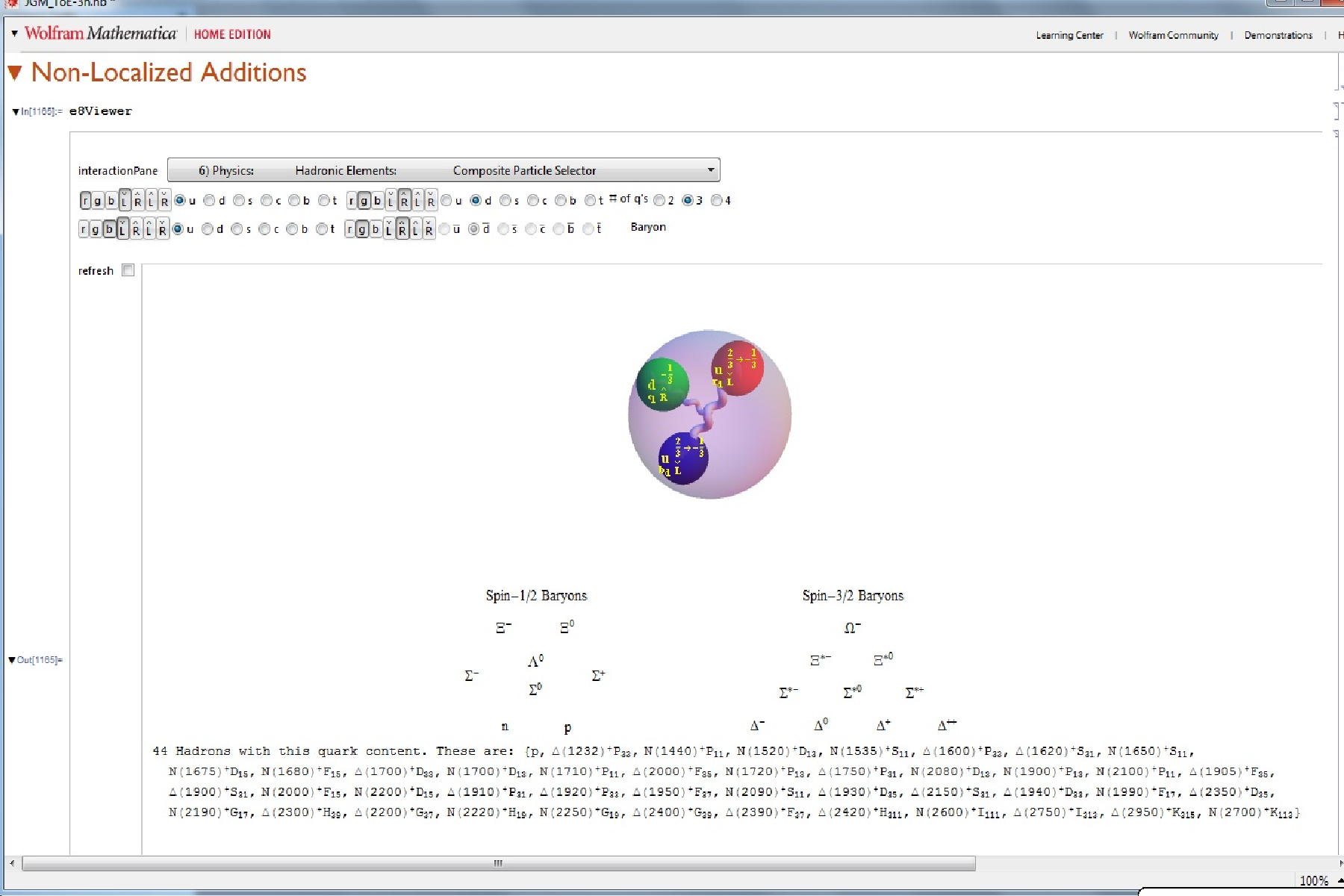
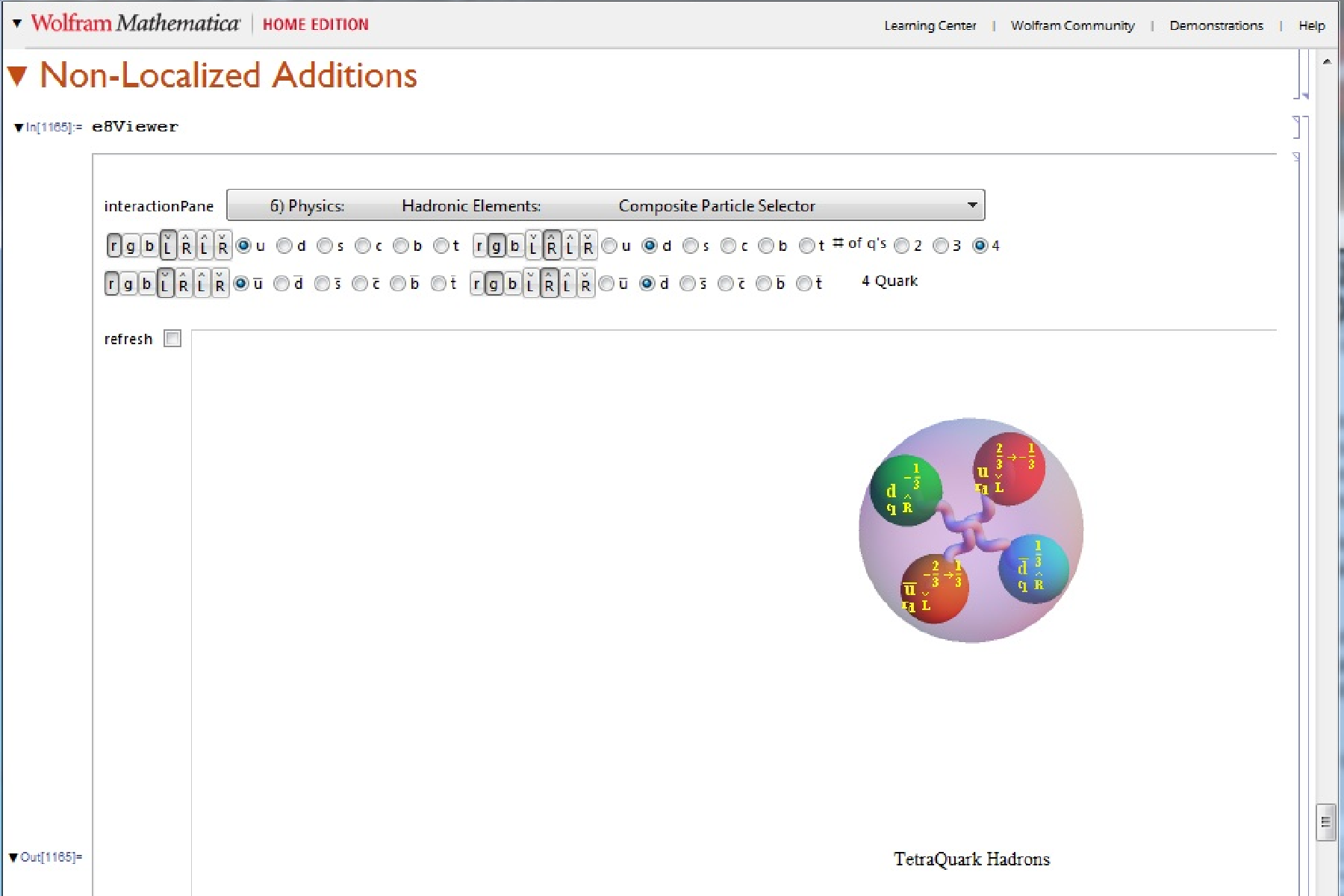
8) Physics: Hadronic Elements: Composite Quark-Gluon Select Decays
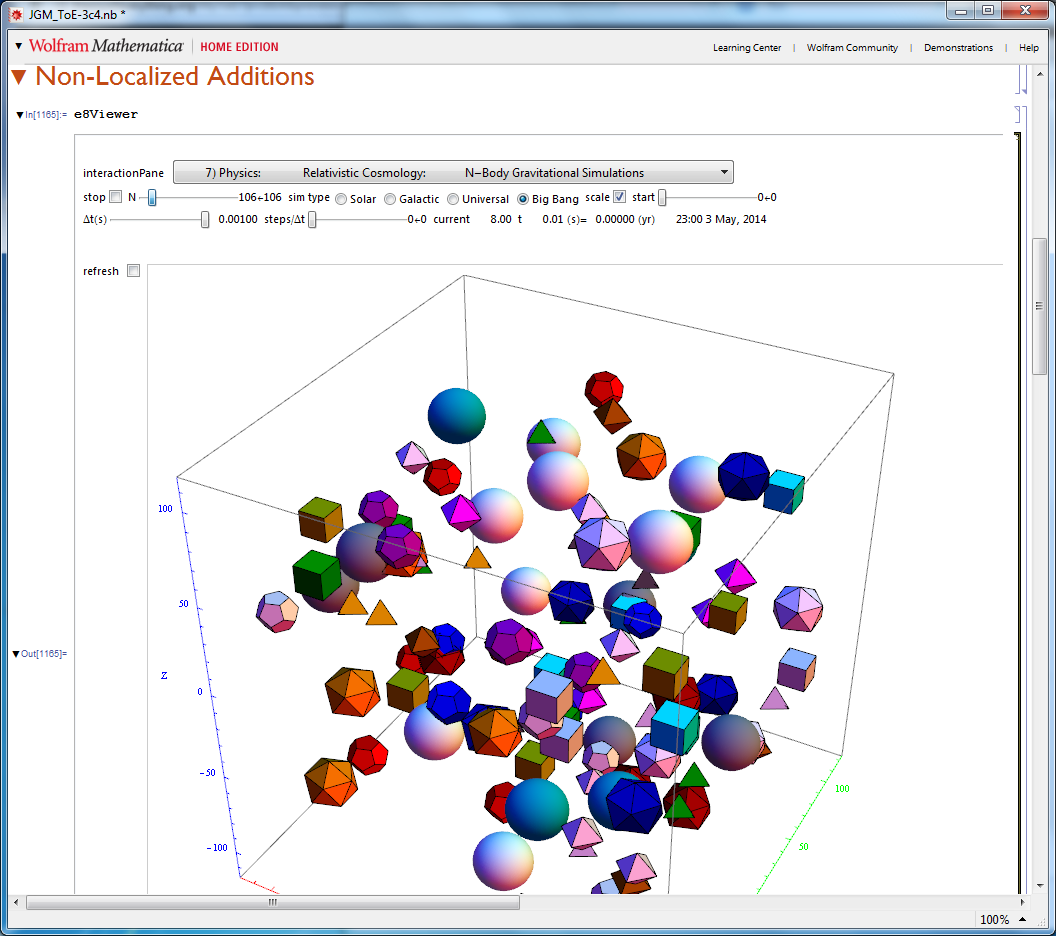
9) Physics: Relativistic Cosmology: N-Body Bohmian GR-QM Simulation
10) Chemistry: Atomic Elements: 4D Periodic Table Element Select
11) Chemistry: Molecular Crystallography: 4D Molecule Visualization Select
12) Biology: Genetic Crystallography: 4D Protein/DNA/RNA E8-H4 Folding
13) Biology: Human Neurology: OrchOR Quantum Consciousness
14) Psychology: Music Theory & Cognition: Chords, Lambdoma, CA MIDI,& Tori
15) Sociology: Theological Number Theory: Ancient Sacred Text Gematria
16) CompSci: Quantum Computing: Poincare-Bloch Sphere/Qubit Fourier
17) CompSci: Artificial Intelligence: 3D Conway’s Game Of Life
18) CompSci: Human/Machine Interfaces: nD Human Machine Interface