Tag Archives: 2D

Physics

Improved SVG E8 Petrie and Hexagonal Triality Representations

Leave a comment

Stay tuned for more images. I think I will use this post to place my more beautiful works!

E8 in Petrie projection with 3D theoretically assigned physics particles

These use a better combination of specularity and opacity with both math and physics (theoretical assigned) 3D vertices. This is accomplished by actually projecting into 3D but using only X-Y basis vectors with Z={0,0,0,0,0,0,0,0} and the (virtual) camera at XYZ={0,0,∞}.

Some images use color coding for vertices that indicate overlaps (e.g. when in the spherical (math) vertices E8 hexagonal basis). The overlap number data may then be presented in the lower left. This data can be removed using SVG editors such as Inkscape.

Some images also show the 3D technical axes (basis) projection vectors as well as the vertex, edge, and other data. Also, bear in mind that the PNG images shown below (so they are visible in Google Images after being crawled) tend to show pixelation artifacts and can present with black background vs. white. The SVG presentation (obtained by clicking the embedded image link) will be correct and the transparent background can be modified easily (e.g. with Inkscape).

Please note, these are provided under Creative Commons CC BY-SA 4.0 Attribution-ShareAlike 4.0 International license, so if you use them please cite me at this site (or me on the Wikipedia (WP) article or WP commons source):

Below is the well known PR photo for E8 in Petrie projection with basis vector axes and data presented (click the image for the downloadable SVG):

E8 in Petrie projection with axes and other data

Below is the E8 hexagonal (aka. as the “E6/D4 Mox [6]” in Wikipedia) projection:

E8 hexagonal (aka. as the “E6/D4 Mox [6]” basis in Wikipedia) projection

The E8 hexagonal with the 3D assigned theoretical physics vertices:

E8 with the 3D assigned theoretical physics vertices in hexagonal projection

The E8 hexagonal projection with 6720 edges:

E8 with edges in hexagonal projection

The Rectified E8 in hexagonal projection with 6720 vertices:

Rectified E8 with edges in hexagonal projection

E8142 in hexagonal projection with 17280 vertices:

E8142 in hexagonal projection

E8142 in Petrie projection with 17280 vertices:

E8142 in Petrie projection

The periodic table with orbitals in 2D:

The periodic table with orbitals in 2D

The periodic table with orbitals in 3D:

The periodic table with orbitals in 3D

Kneser neighborhood graph of Niemeier lattices with associated Mathematica Notebook here:

Kneser neighborhood graph of Niemeier lattices with associated Mathematica Notebook here.

The E8 subgroup tree:

E8 Subgroup Tree with associated Mathematica Notebook here.
Physics

E8 and H4 Gram Matrix Visualizations

Leave a comment

Beautiful MatrixPlot’s of E8 and H4.

This is not the typical E8 Gram matrix representation as the Cartan matrix using only the simple roots (shown at the end of this post).

It uses all 240 E8 vertices (+120/-120 roots) of the E8 Split Real Even (SRE) vertices to produce the Gram matrix (with vertices sorted in simple numeric order):

Full E8 Split Real Even (SRE) vertex Gram matrix in vertex numeric sort order

The same 240 E8 vertices (+120/-120 roots) below are sorted by the 9th row of the binary structure Pascal Triangle, excluding the 2nd & 2nd to last entries of -/+ 8 (i.e. {-1,-8,-28,-56,70=(-35/35),56,28,8,1}, where the 112 integer D8 are -56/56 and the 128 half-integer BC8 are {-1,-28,-35,35,28,1}).

Full E8 Split Real Even (SRE) vertex E8 Gram matrix in Pascal Triangle order

As above, but with H4+H4φ 8D Gram matrix created using the dot product of E8 against the 8×8 E8 to H4 folding matrix U:

H4+H4φ 8D Gram matrix

Now with only the H4φ 4D Gram matrix created as 120 H4 4D vertices:

H4φ 4D Gram matrix

Compare this to the Gram matrix using the root weights of E8 (in Pascal triangle order vs. sorted into root and/or weight order):

E8 Gram Weights (in Pascal Triangle order)

Then compare to the Cartan matrix produced as the Gram matrix of only the 8 E8 simple roots:

E8 Cartan matrix from 8 simple roots
Personal, Sculpture and Art

Info about my creative work: The Universe, Math, Physics, & Art

Leave a comment

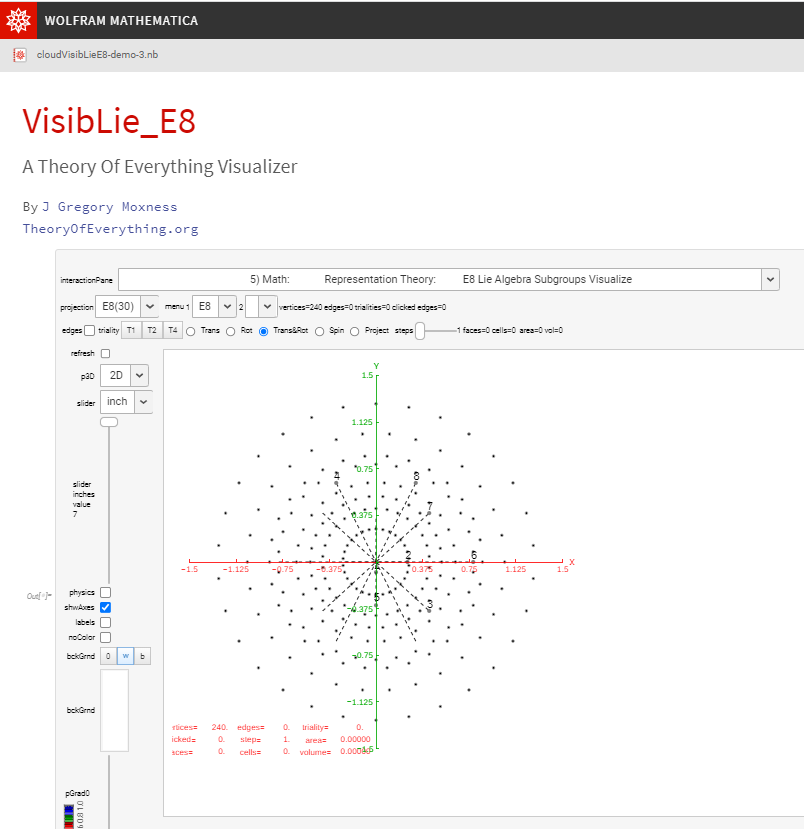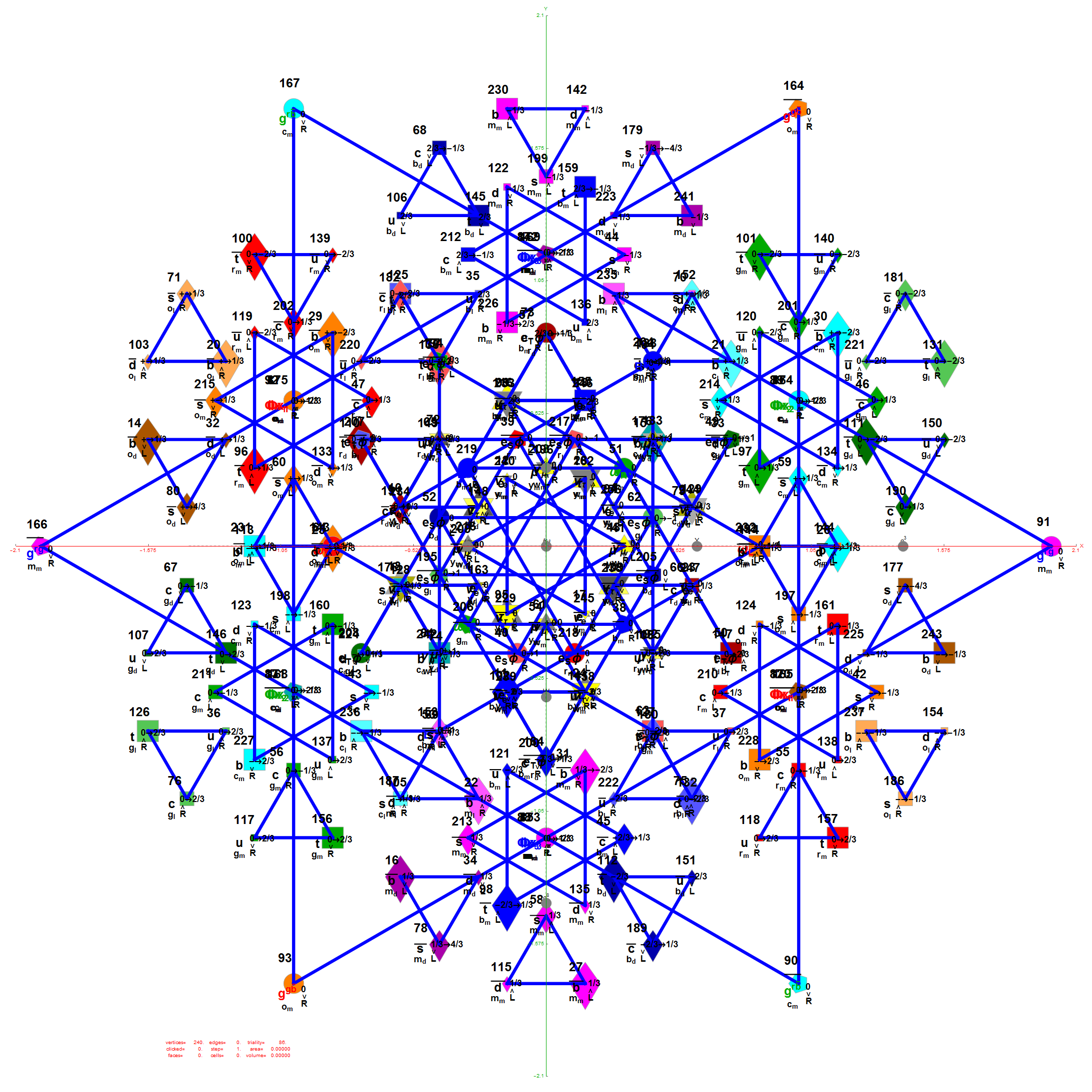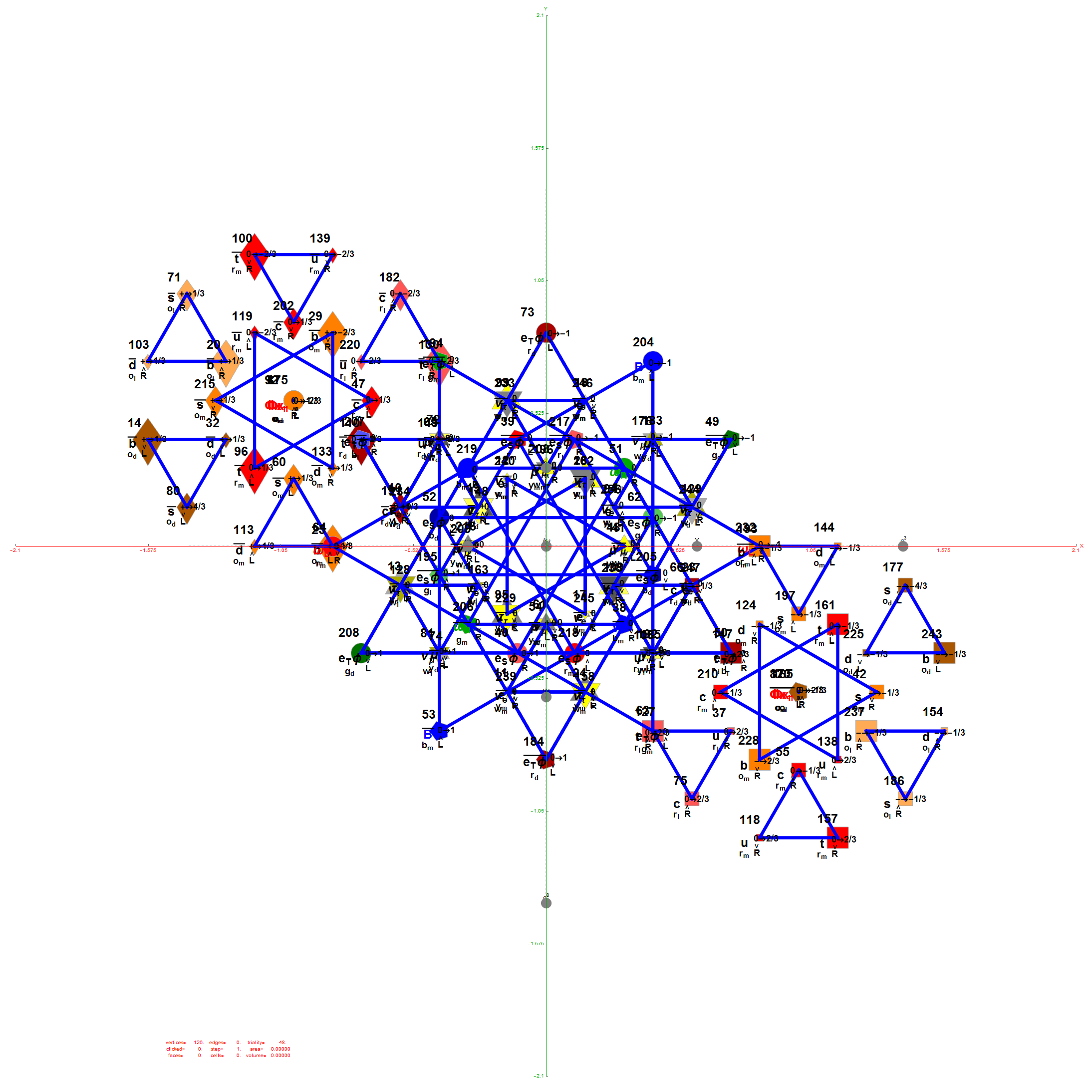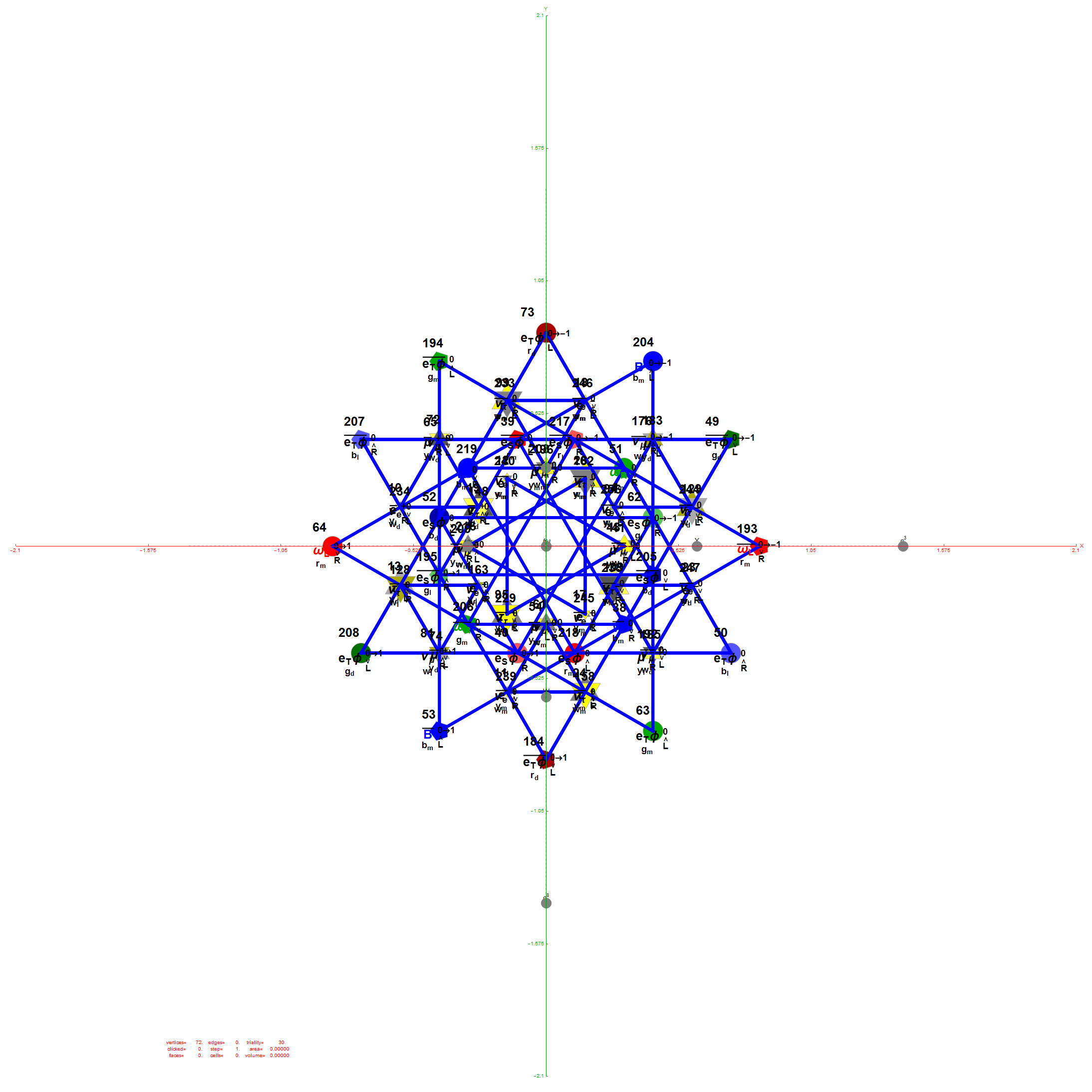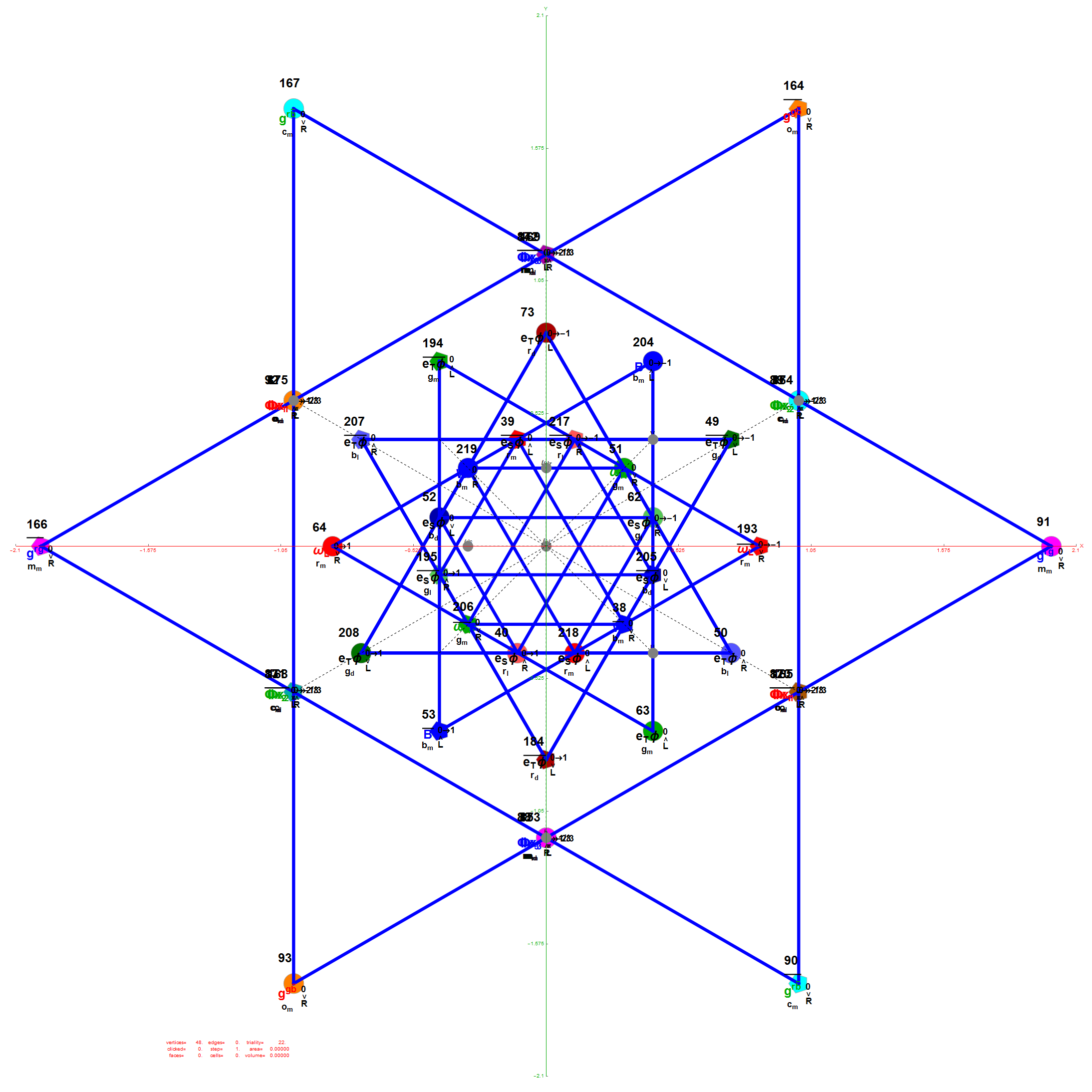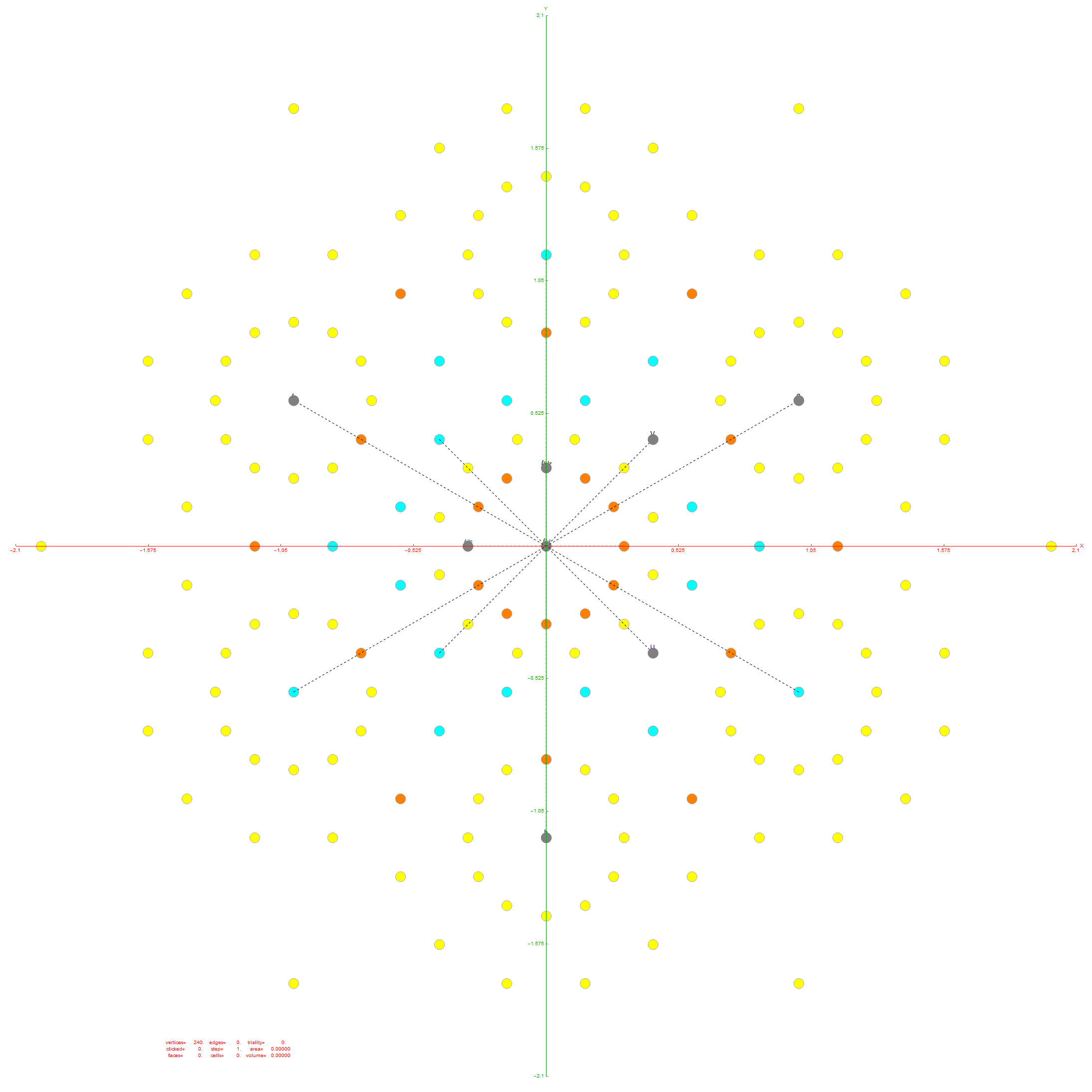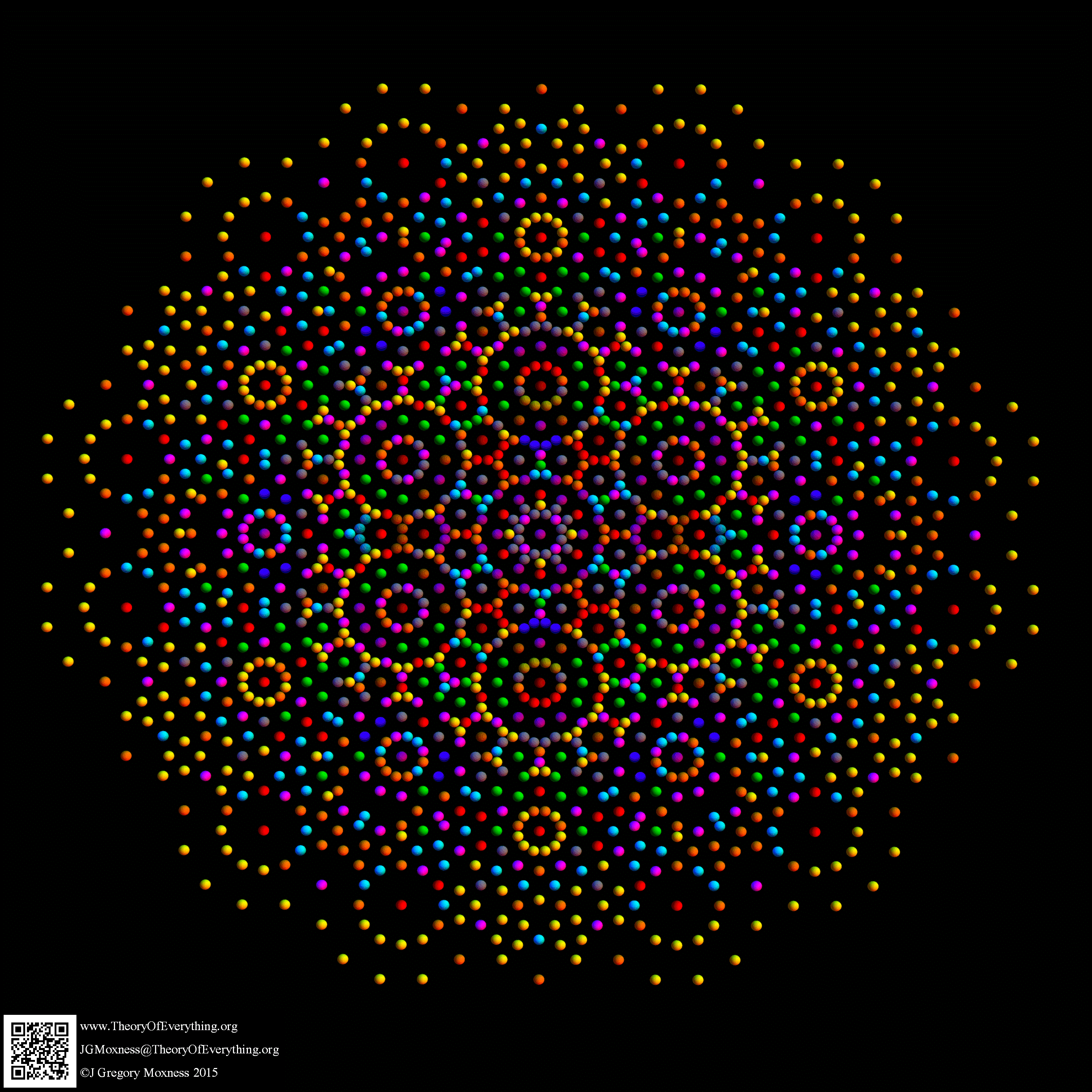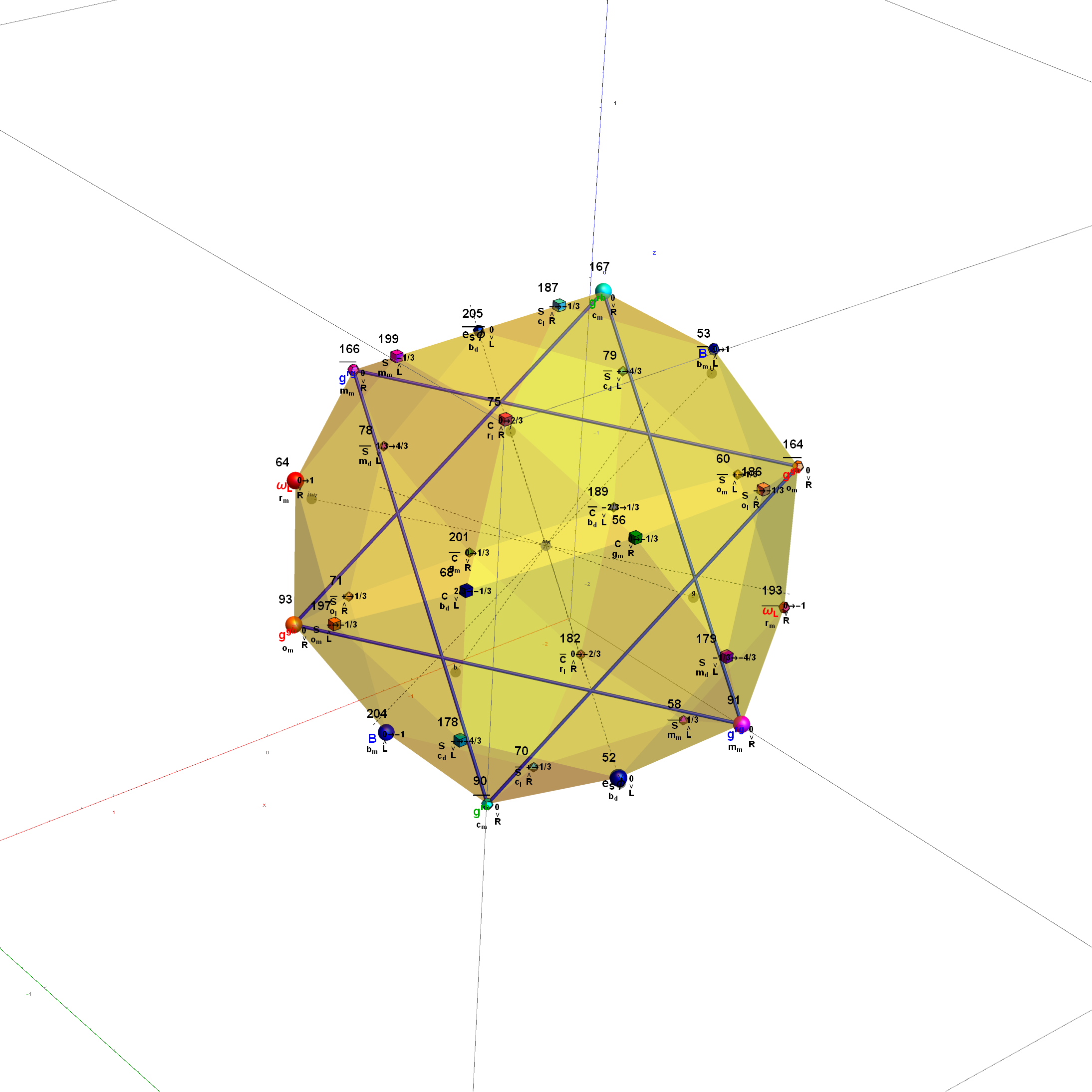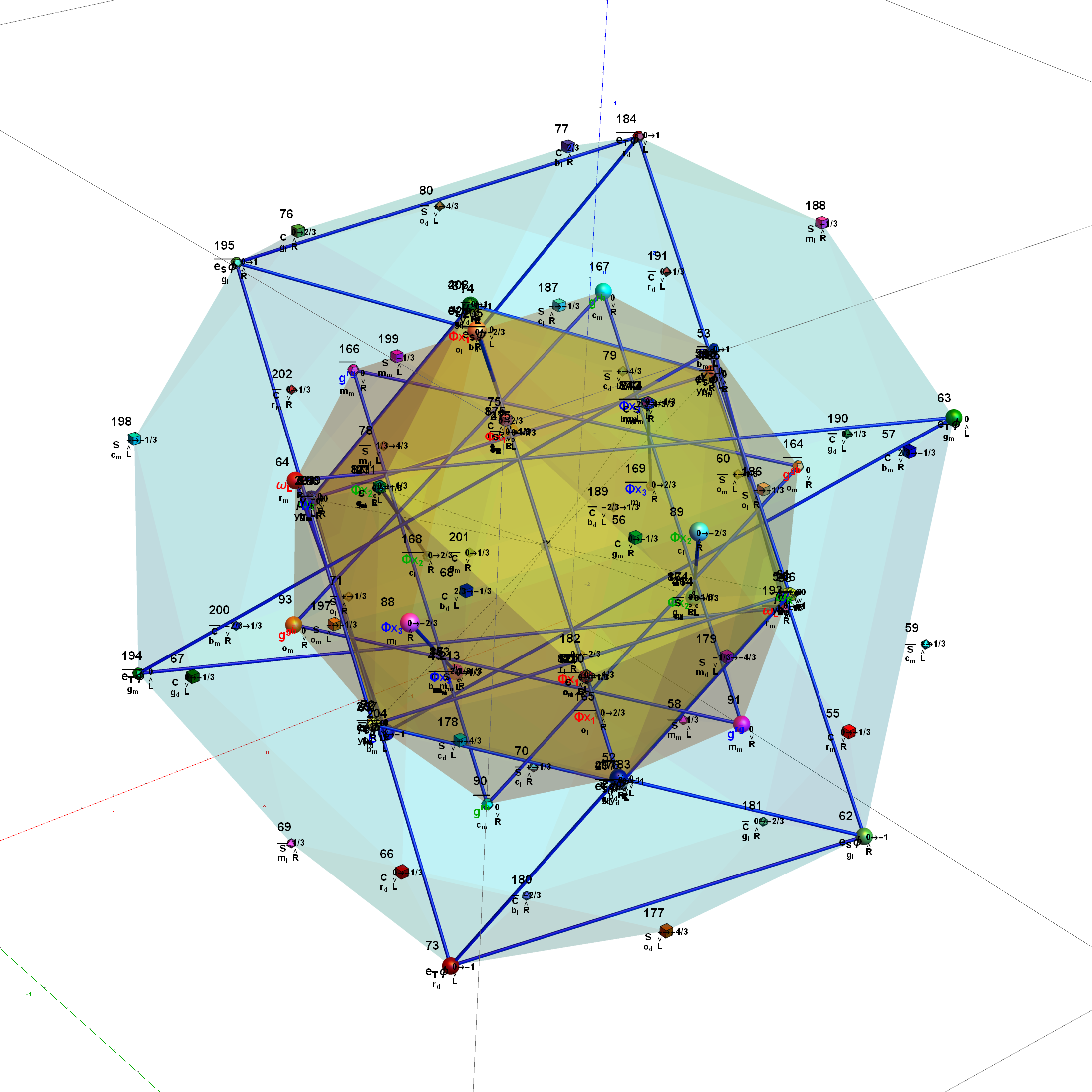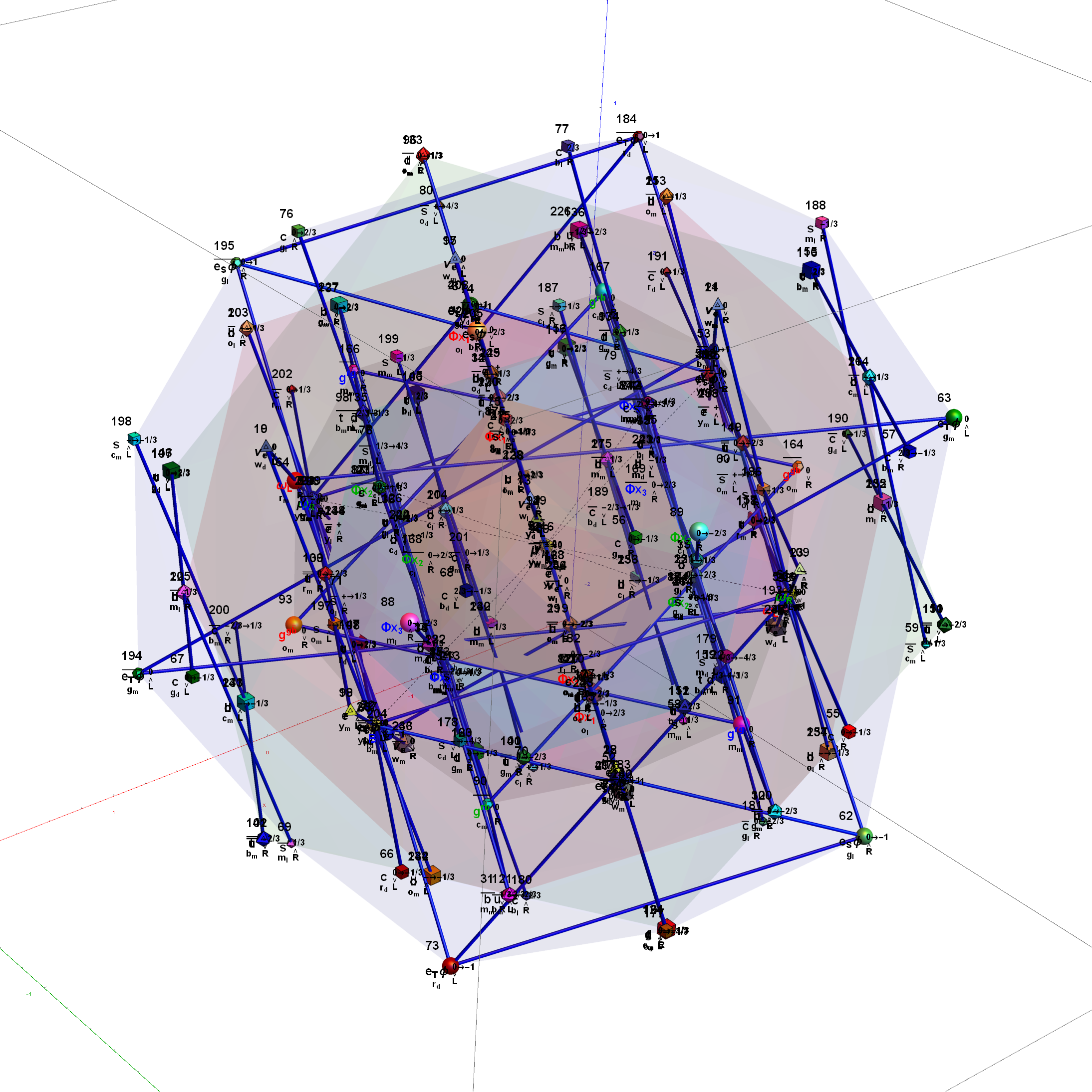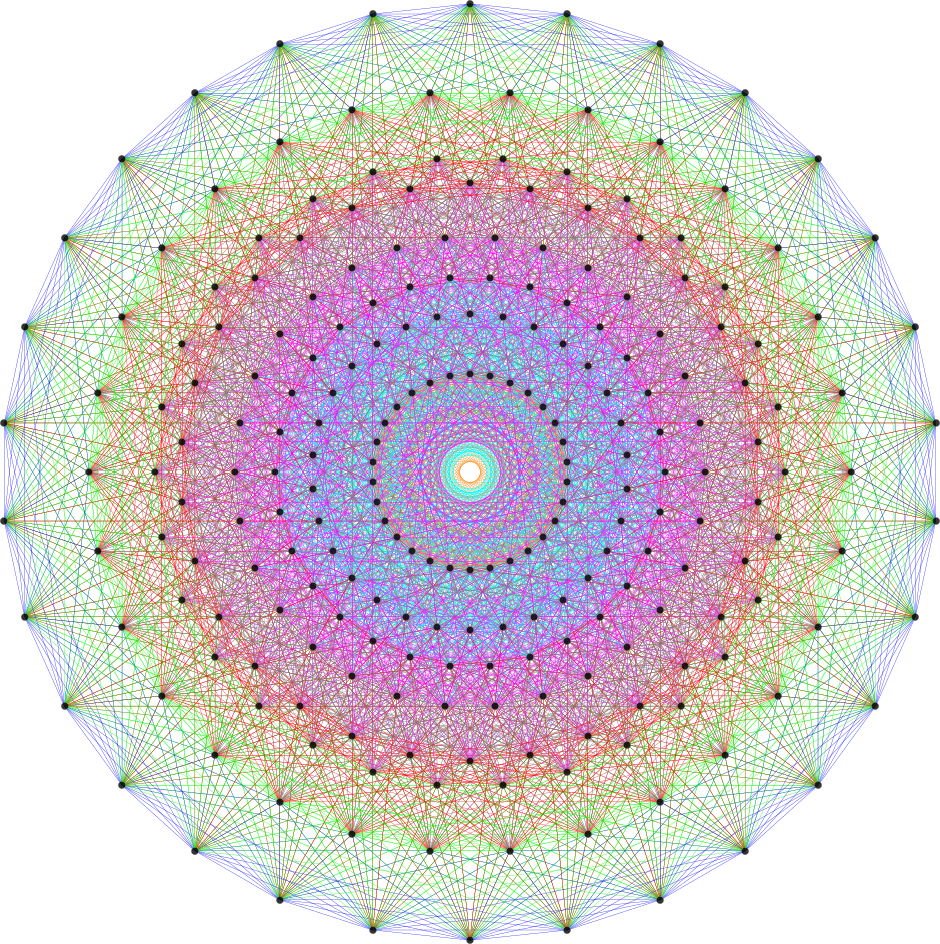
I think the most well-known (2D) image I’ve created so far (above) is found on Wikipedia’s (WP) math/geometry pages. It is what has been called the Public Relations (PR) or publicity photo for E8, which is an 8D (or 248 dimensional as the math guys count it) geometric object. It has been used in books, papers, math/science conference promotional materials, etc. That WP page also has what many used to consider “uninteresting” – my 3D versions of the same object. E8 is used in various theories to understand how the Universe operates way below the atomic level (i.e. the quantum stuff). I think it is responsible for what I call the shape of the Universe. As others have said, “who knew the Universe had a shape?”

In (very) layman’s terms, that 2D image of E8 looks sort-of-like how the lowly 4D Tesseract cube would look if it grew up into an 8D object, but a bit more interesting. The Tesseract was made (more) popular in the modern Avengers movies. In 2015 before I had ever seen any of those movies, I created a laser etched 3D projection of E8 within a jewel cut optical crystal cube and put a photo of that object lit from below by a blue LED on my website’s main homepage. Someone mentioned the resemblance and I was surprised at the likeness, motivating me to go see the movies.

Another of my more notable math/physics images has to do with the discovery of QuasiCrystals made by a guy, Dan Shechtman, who was ostracized from academia for the “impossible” idea of crystals having rotational symmetries beyond 2,3,4 and 6. He is now a Nobel Laureate. The WP image above is on that QuasiCrystal page as an overlay of part of E8 projected over a picture made from shooting a beam of x-rays at an icosahedral Ho-Mg-Zn quasicrystal.  I didn’t actually do that experiment with the x-ray beams, but I did similar ones in my college days on a particle accelerator called the Cockroft-Walton Kevatron – see below for a picture of me (the one with the beard ;–)  in the physics lab assembling a moon dust experiment. One of the professors had gotten the accelerator out of Germany after having worked on the Manhattan project.

E8 and its 4D children, the 600-cell and 120-cell (pages on which I have some work, amongst others) and its grandkids (2 of the 3D 5 Platonic Solids, one of which is the 3D version of the 2D Pentagon) are all related to the Fibonacci numbers and the Golden Ratio. So that kind of explains why most of my 2D art, 3D objects and sculptures (e.g. furniture like the dodecahedron table below), and 4D youtube animations all use the Golden Ratio theme.

Greg Moxness, Tucson AZ

Physics

Cloud Based VisibLie_E8 Demonstration

Leave a comment

The cloud deployments don’t have all the needed features as the fully licensed Mathematica notebooks, so I included a few of the panes that seem to work for the most part. Some 3D and animation features won’t work, but it is a start. Bear in mind that the response time is slow.

Link to the demonstration.

A Theory of Everything Visualizer, with links to free Cloud based Interactive Demonstrations:

1) Math: Chaos/Fibr/Fractal/Surface: Navier Stokes/Hopf/MandelBulb/Klein

2) Math: Number Theory: Mod 2-9 Pascal and Sierpinski Triangle

3) Math: Geometric Calculus: Octonion Fano Plane-Cubic Visualize

4) Math: Group Theory: Dynkin Diagram Algebra Create

5) Math: Representation Theory: E8 Lie Algebra Subgroups Visualize

6) Physics: Quantum Elements: Fundamental Quantum Element Select

7) Physics: Particle Theory: CKM(q)-PMNS(ν) Mixing_CPT Unitarity

8) Physics: Hadronic Elements: Composite Quark-Gluon Select Decays

9) Physics: Relativistic Cosmology: N-Body Bohmian GR-QM Simulation

10) Chemistry: Atomic Elements: 4D Periodic Table Element Select

11) Chemistry: Molecular Crystallography: 4D Molecule Visualization Select

12) Biology: Genetic Crystallography: 4D Protein/DNA/RNA E8-H4 Folding

13) Biology: Human Neurology: OrchOR Quantum Consciousness

14) Psychology: Music Theory & Cognition: Chords, Lambdoma, CA MIDI,& Tori

15) Sociology: Theological Number Theory: Ancient Sacred Text Gematria

16) CompSci: Quantum Computing: Poincare-Bloch Sphere/Qubit Fourier

17) CompSci: Artificial Intelligence: 3D Conway’s Game Of Life

18) CompSci: Human/Machine Interfaces: nD Human Machine Interface

Physics

The free Wolfram CDF Player v. 13 works with my VisibLie E8 ToE demonstration on Win10

Leave a comment

In case you’re interested, I just verified the demo works on the free Mathematica CDF player v.13 for Win10.

Just go to https://www.wolfram.com/player/ install, download and open the app:

https://theoryofeverything.org/TOE/JGM/ToE_Demonstration.nb

There is a ton of other cool interactive stuff in there. FYI – Some features don’t work without a full Mathematica license.

Enjoy.

Physics

Working with E8+++

Leave a comment

I wanted to confirm some work being done with E11 (or more specifically the Extended E8+++), so I used my “VisibLie” notebook (which includes the “SuperLie” package for analyzing Lie Algebras) to get the following information:

I first created the Dynkin diagram which produces the Cartan Matrix:

This allows the evaluation of the EigenSystem of the Cartan matrix as follows:

As well as using the SuperLie package to evaluate the Positive Roots, Weights and Heights of the E8+++ (The first 80 are shown. For the full list in .pdf click here or click on the image below):

The 4870 positive roots up to height 47 generate a Hasse diagram as follows (with 3 sections zoomed in):

I am working on replication of the Petrie projection by A.G. Lisi based on his prescription using his basis vectors for 2D projection and a Simple Roots Matrix:

Adjusting this E11 Simple Roots Matrix (srmE11) to match the Dynkin diagram above and then verifying it creates the same Cartan matrix, we have:

To get the 9740 E8+++ vertices, we simply use the dot product of the transpose of srmE11 against the positive and negative root vectors (first 50 shown):

A first cut at plotting these involves projecting them to a 2D using the dot product of the 2 basis vectors provided, which gives the following ListPlot:

The limited results from SuperLie are consistent with the image given by Lisi on the Bee’s BackReaction blog, after eliminating the vertical “levels” in my raw plot.

Email me if you want more detail, see errors, or would like to help.

Greg
JGMoxness@theoryofeverything.org