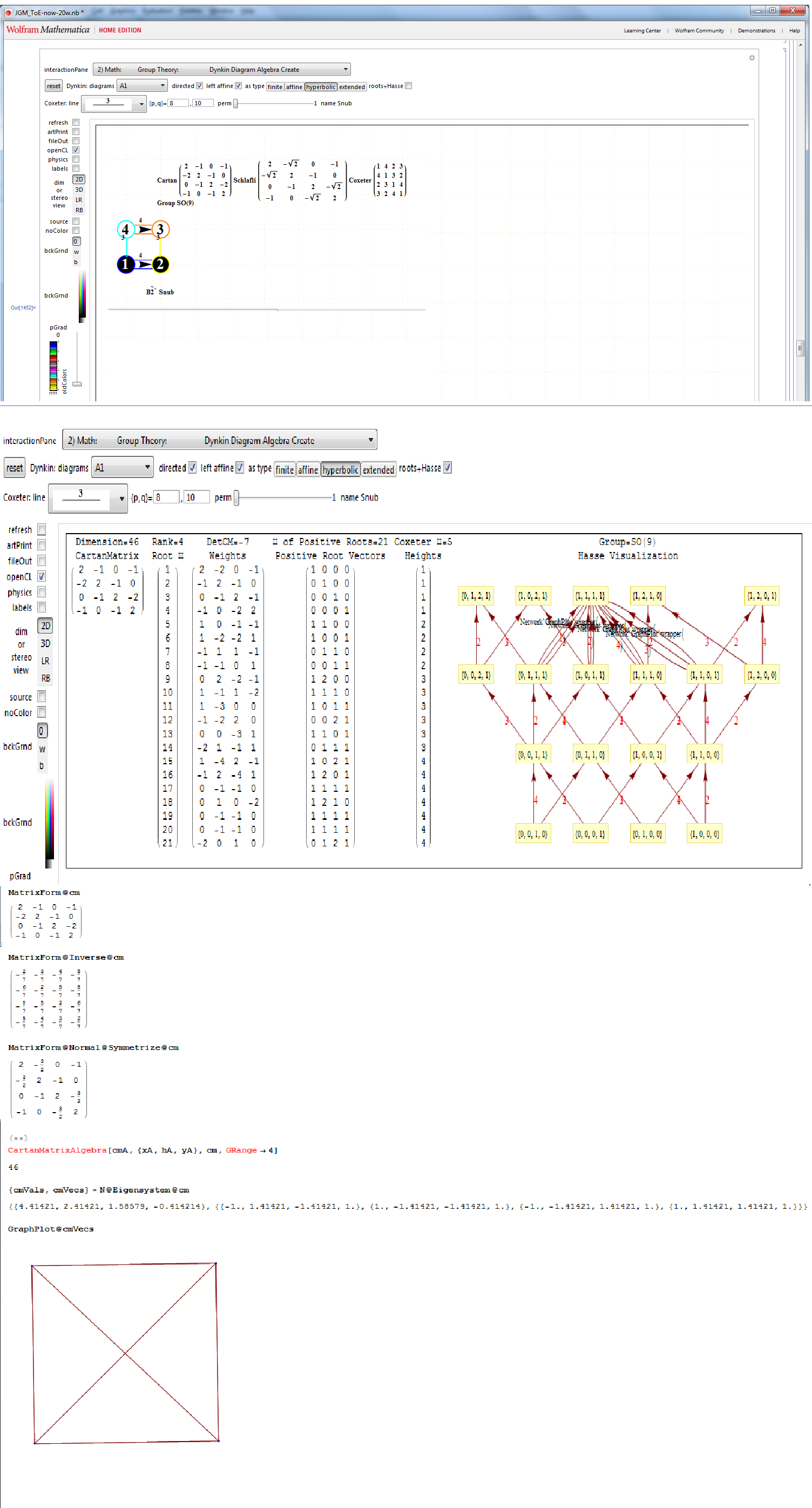
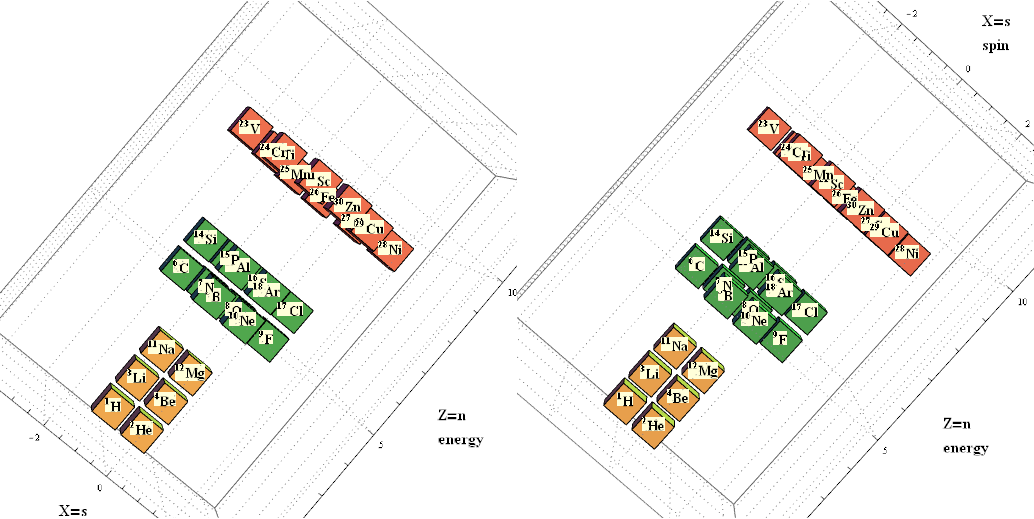
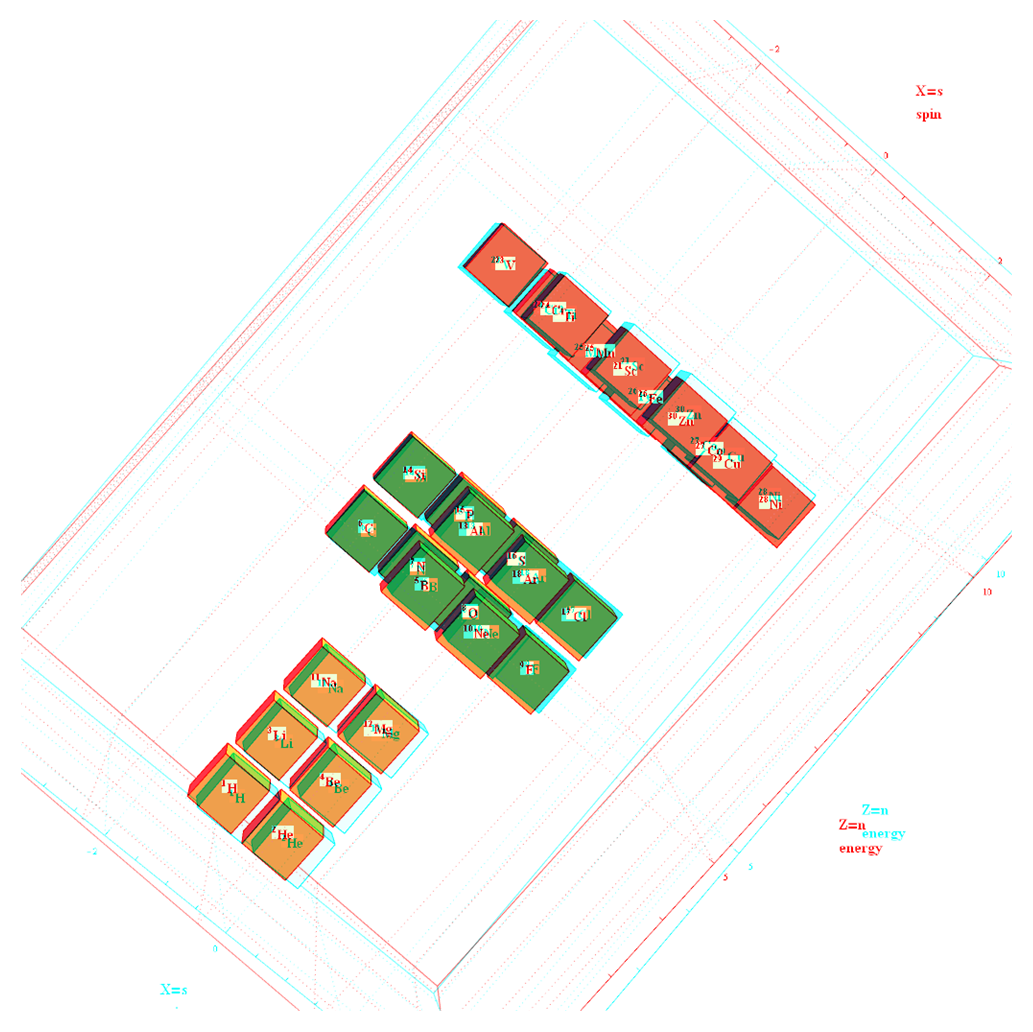
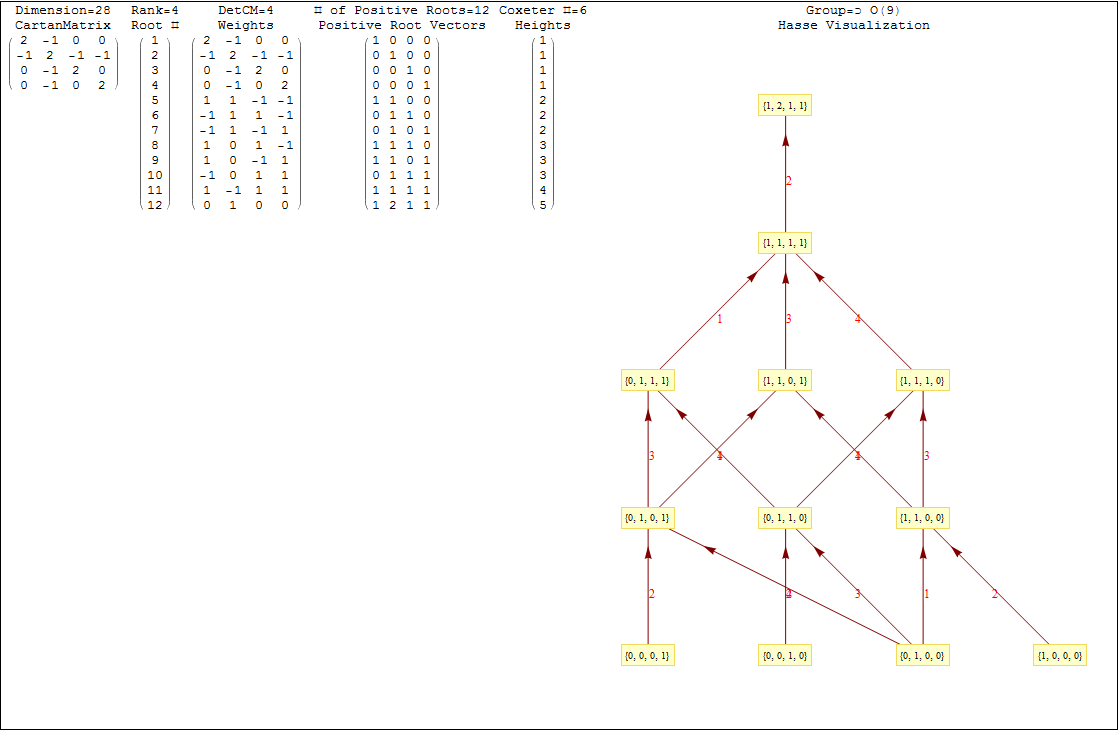
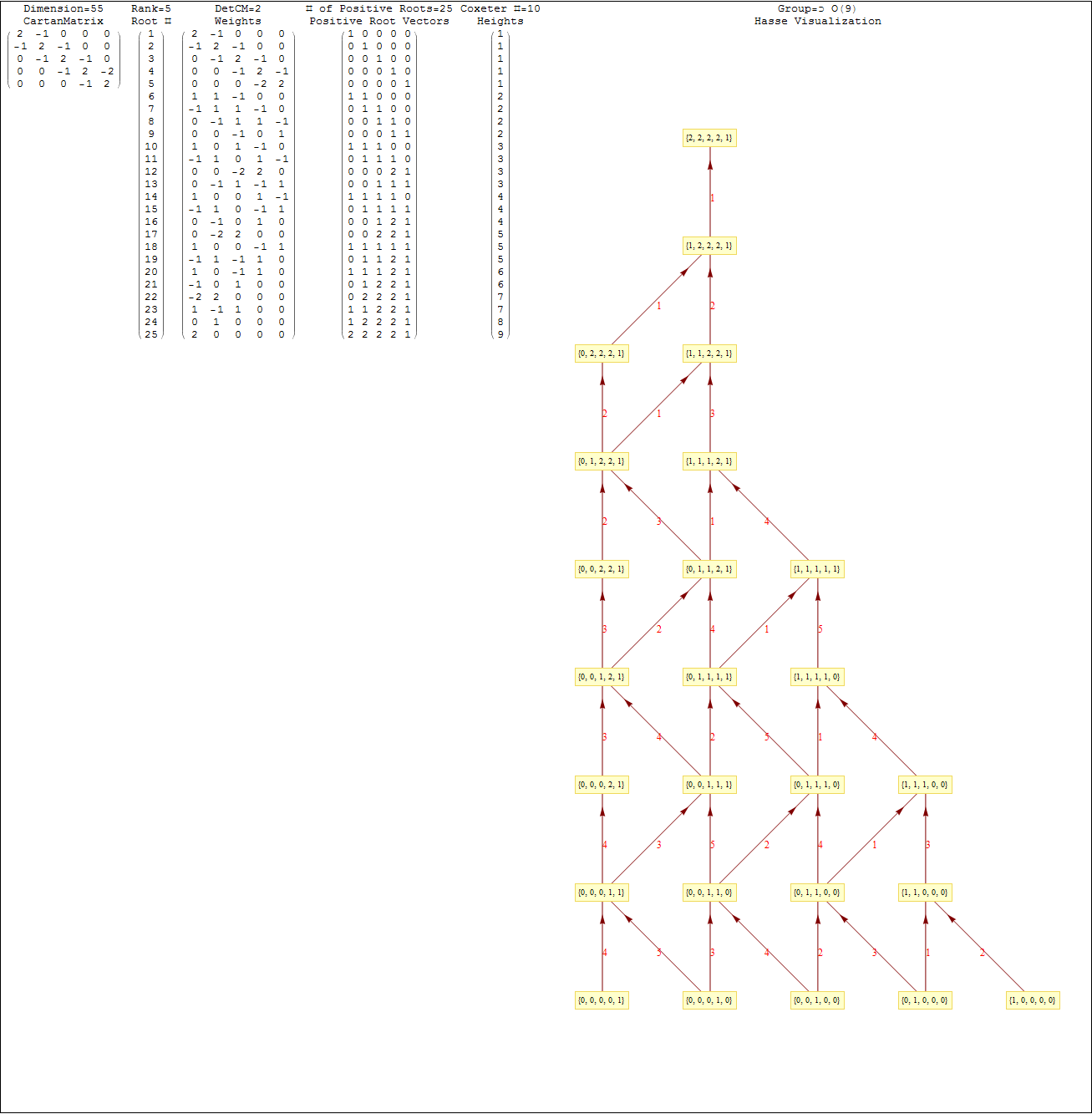
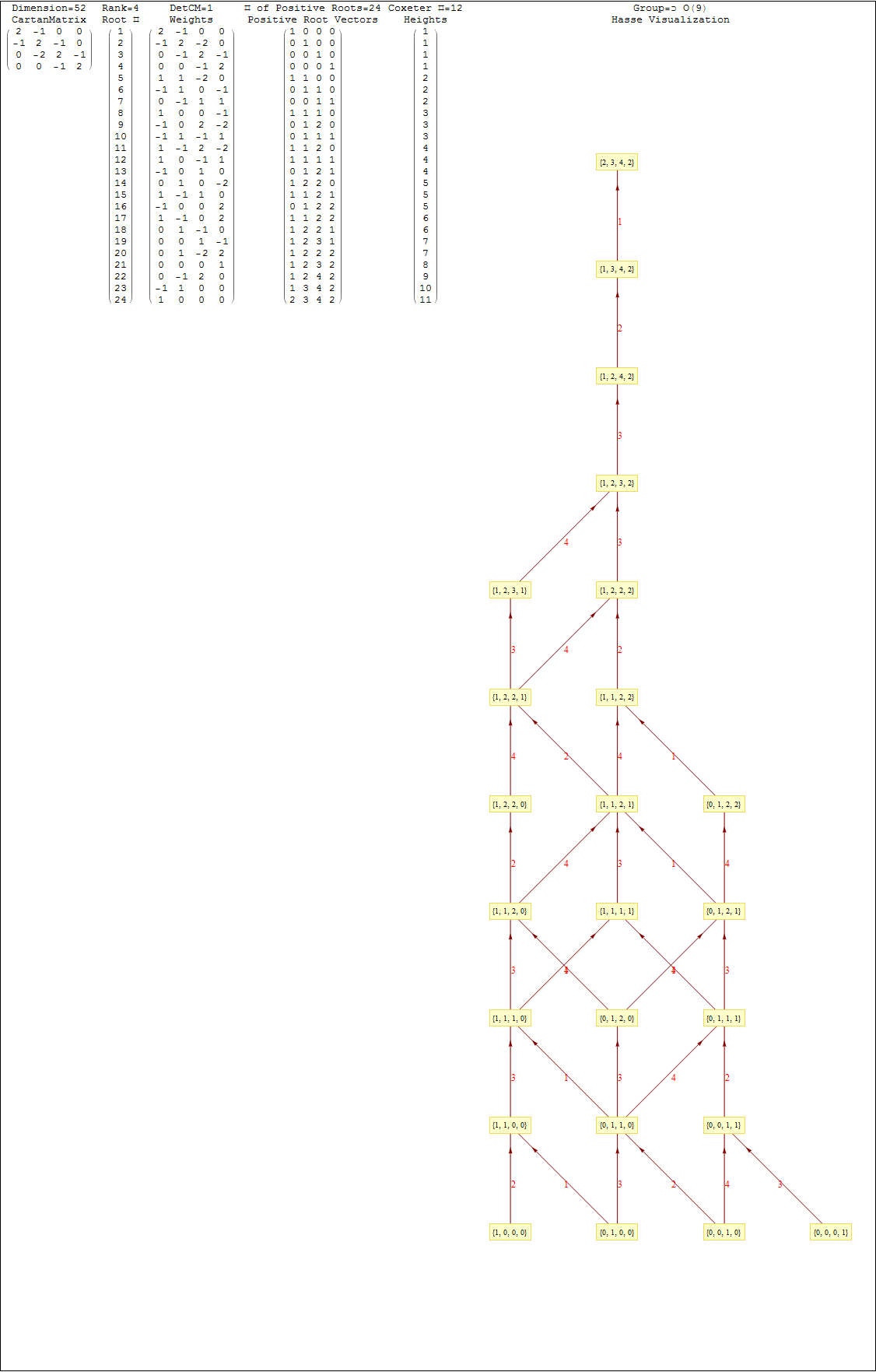
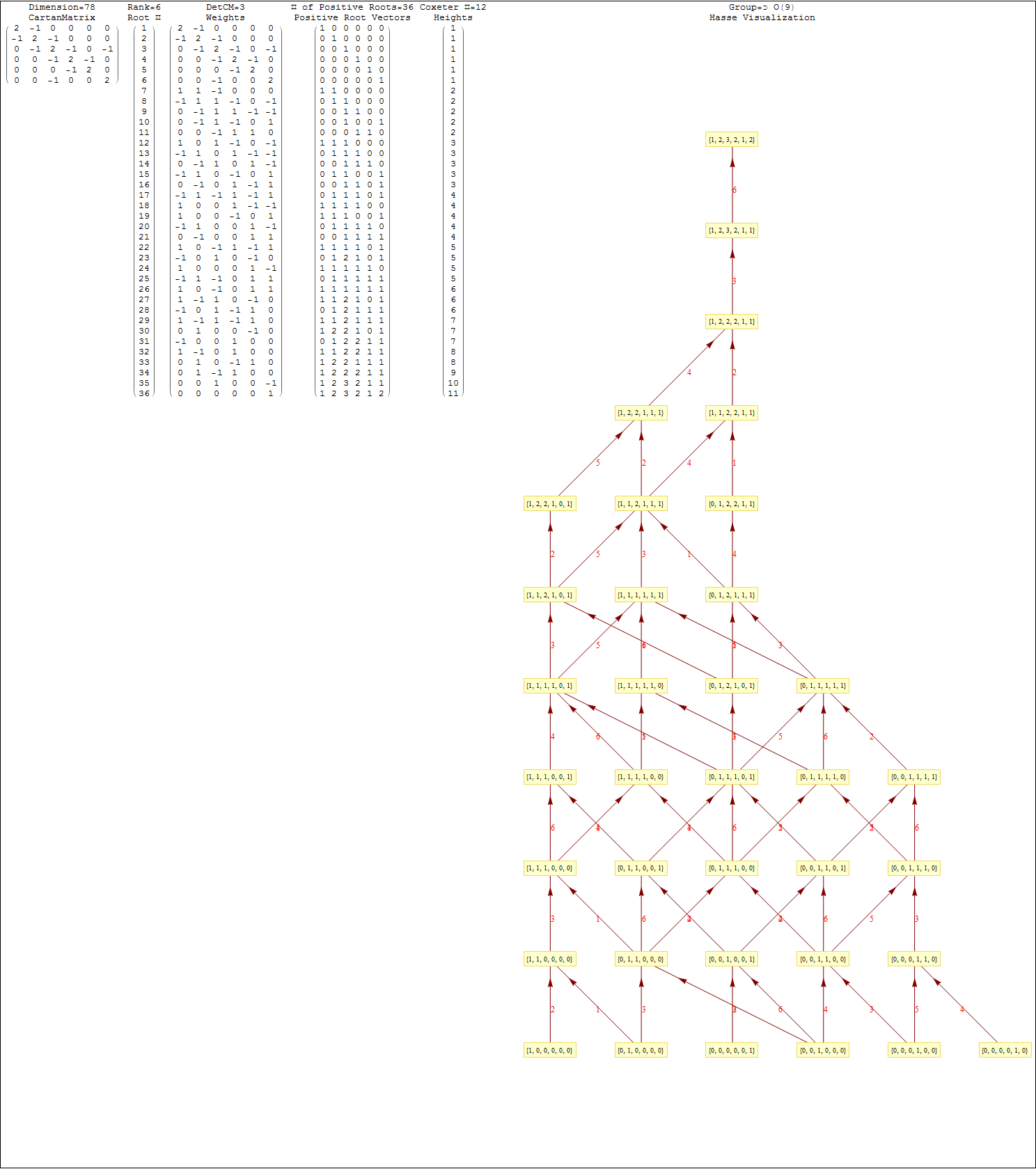
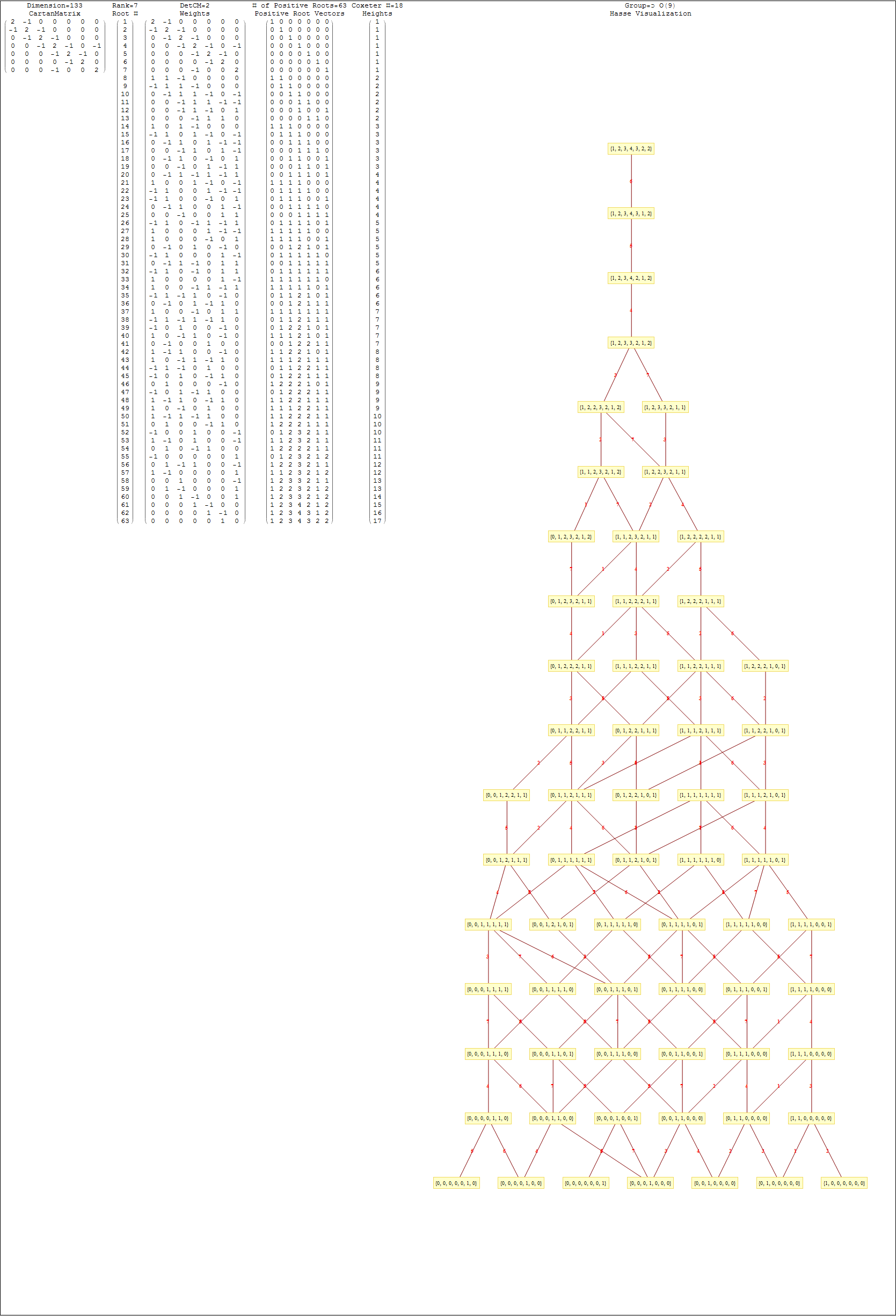
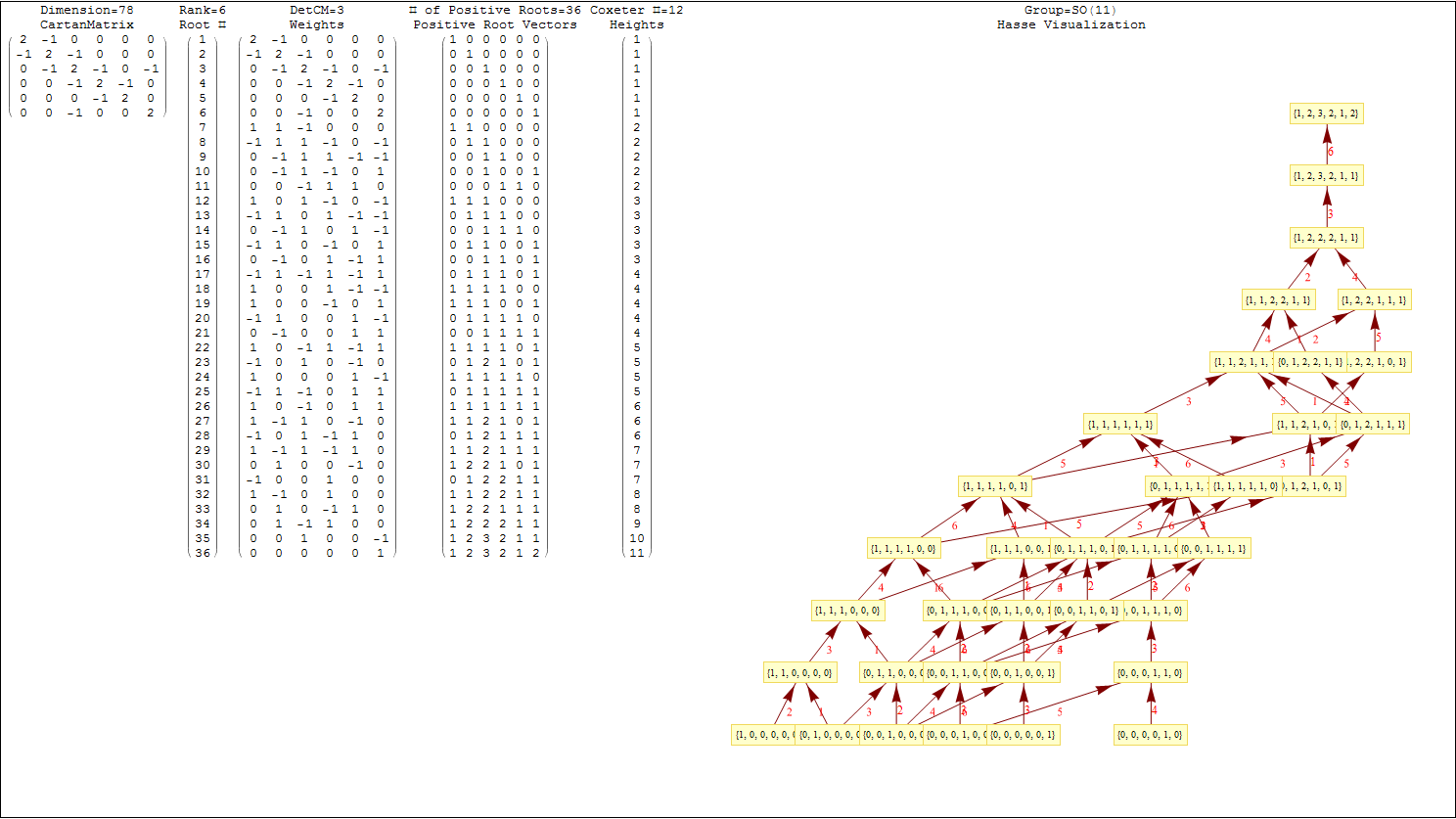
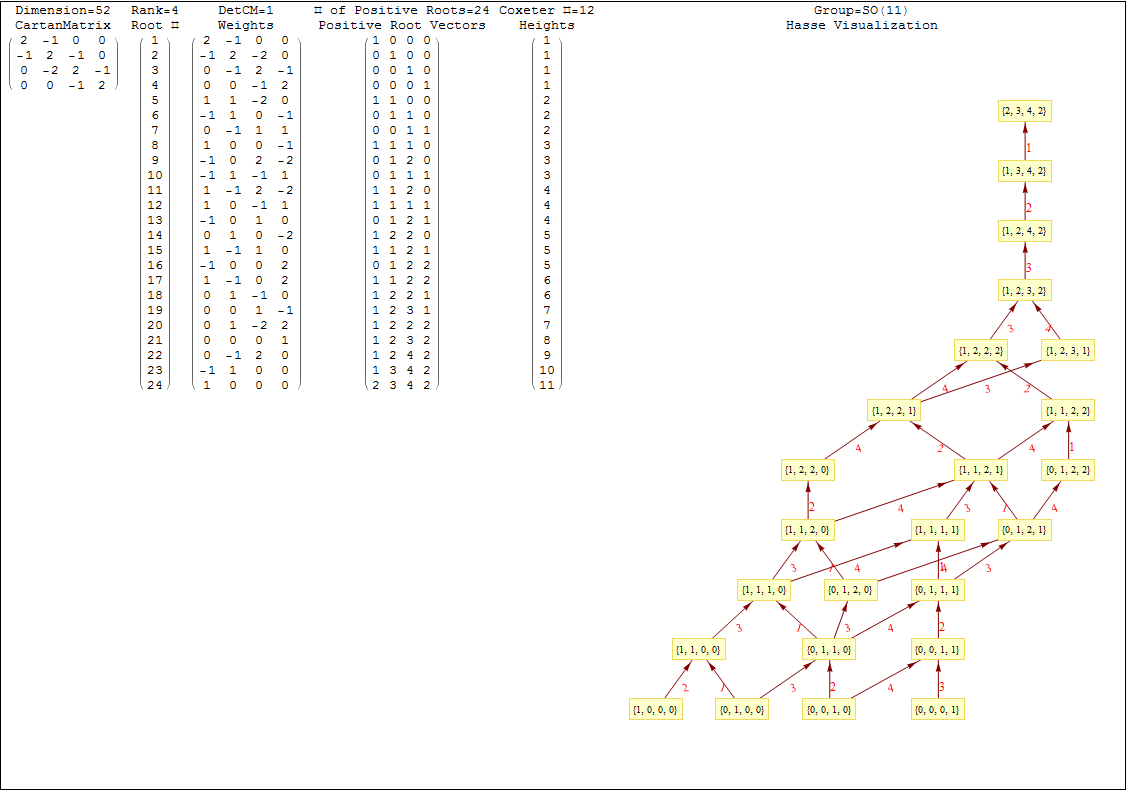
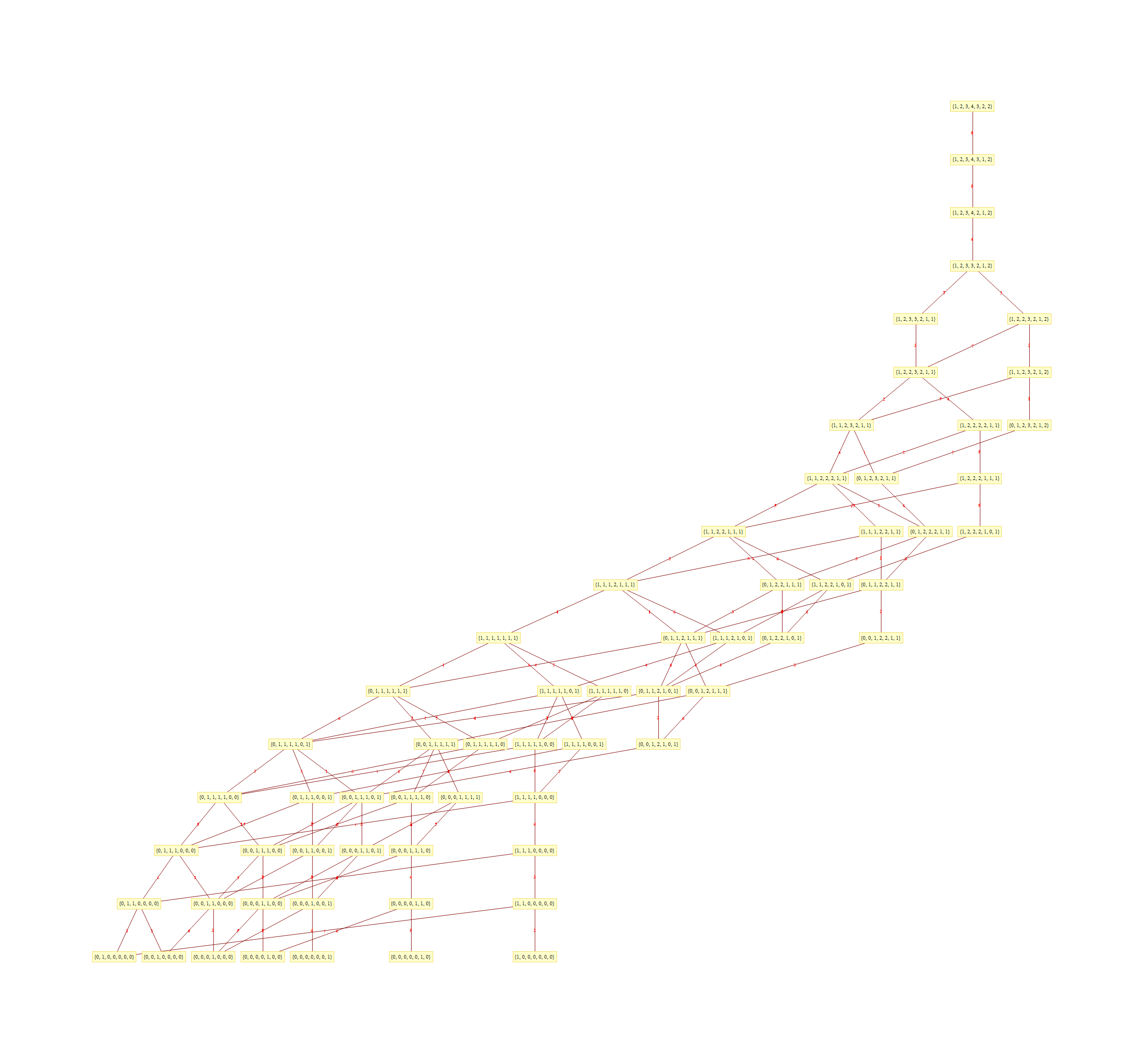
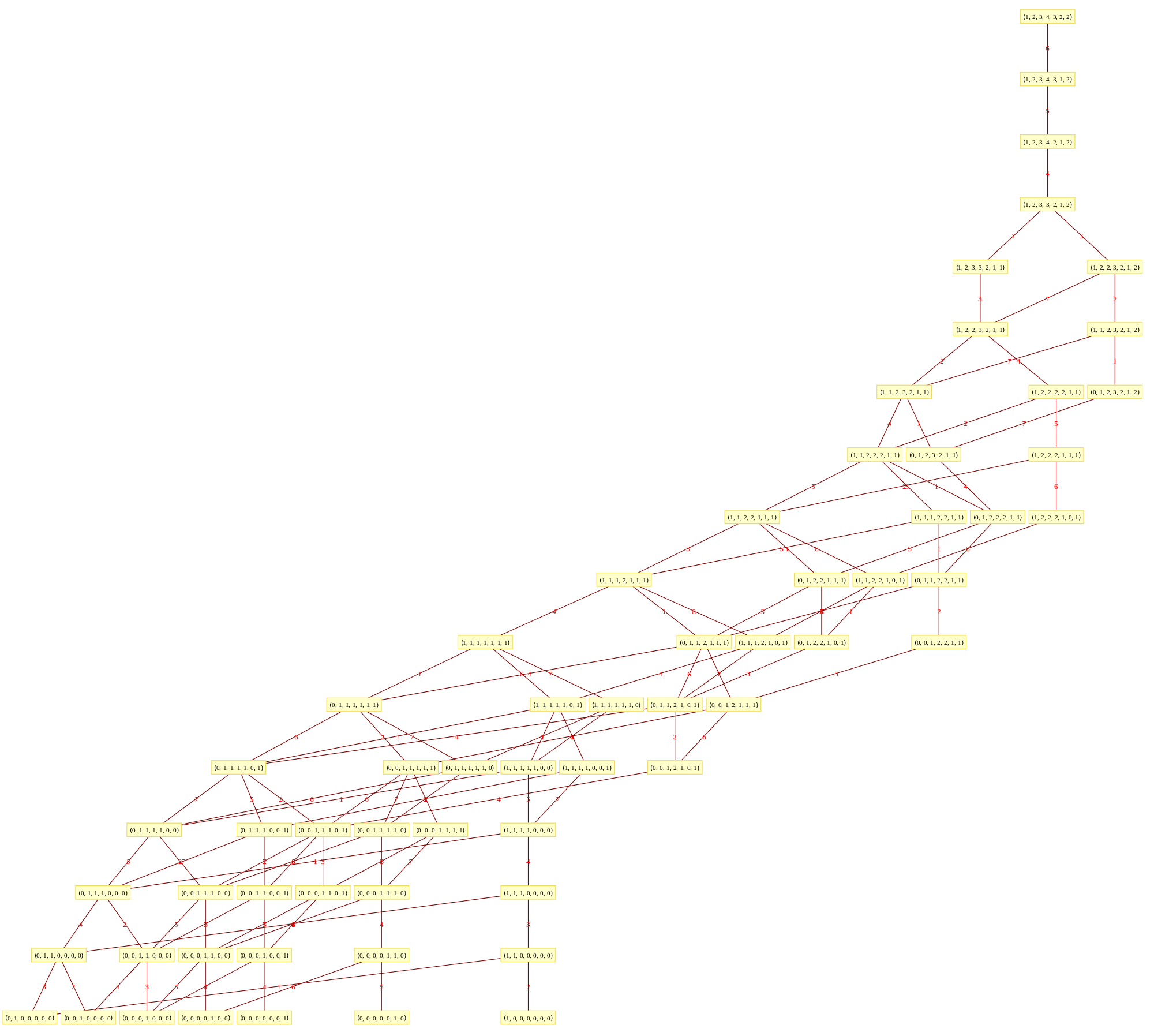
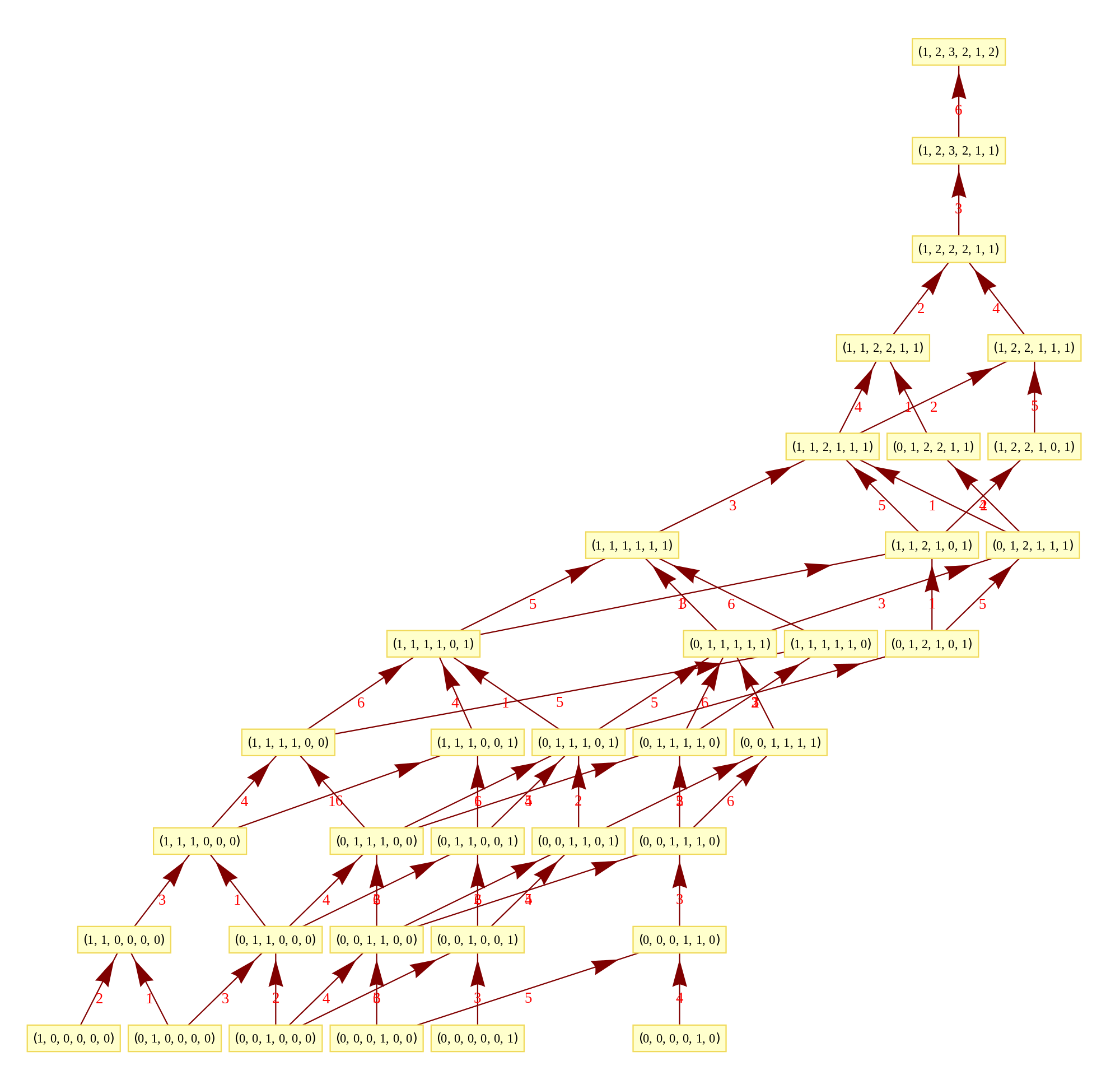
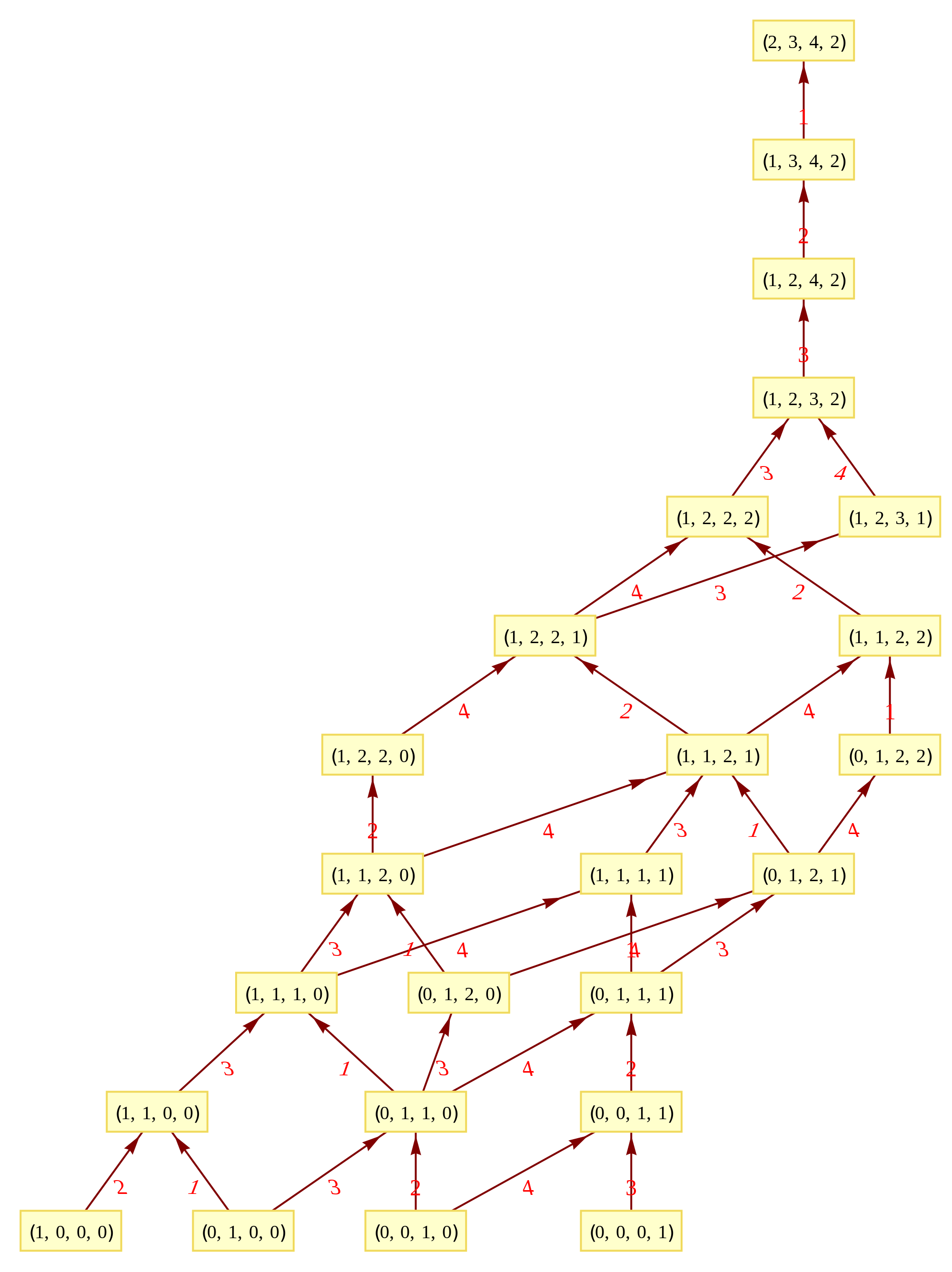
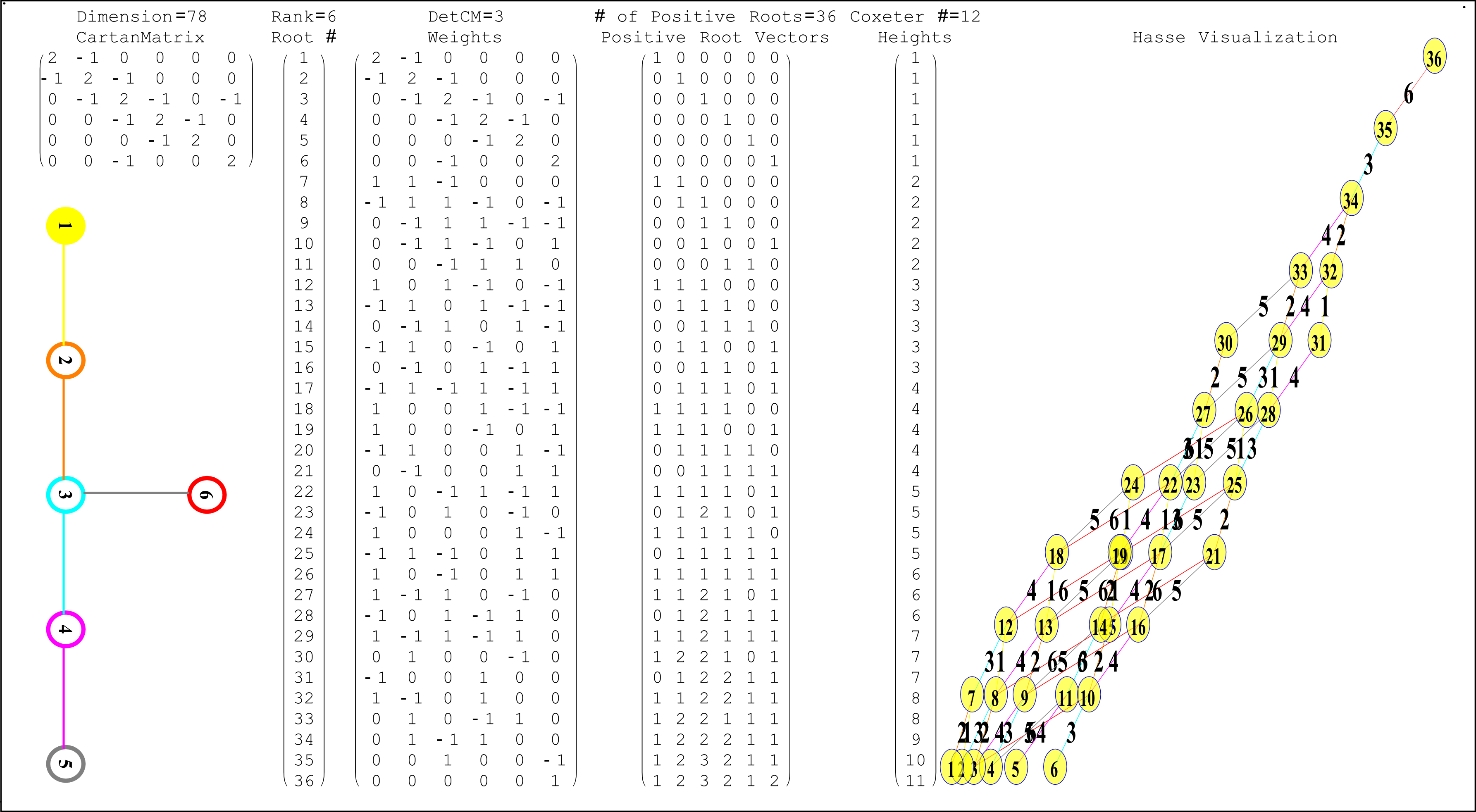
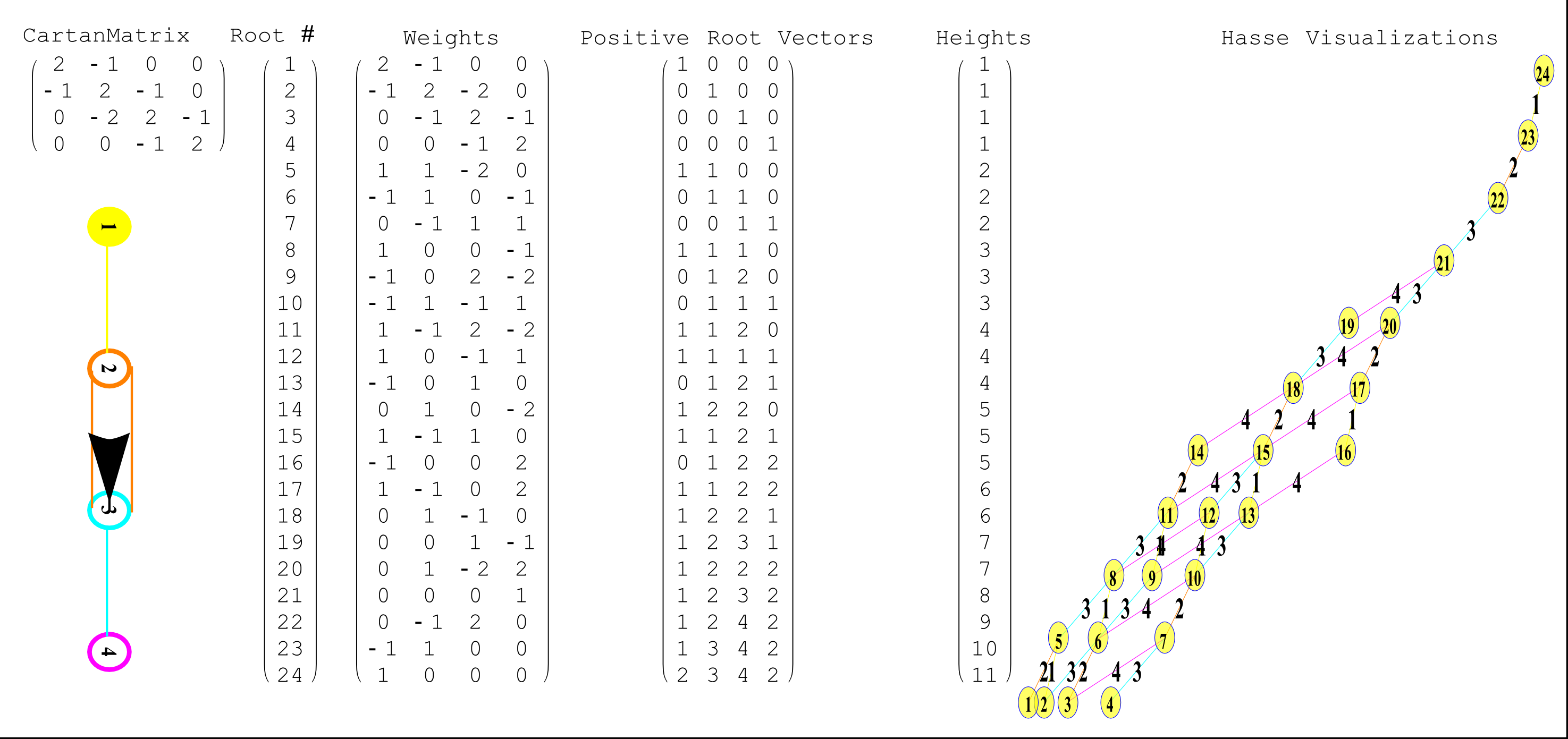
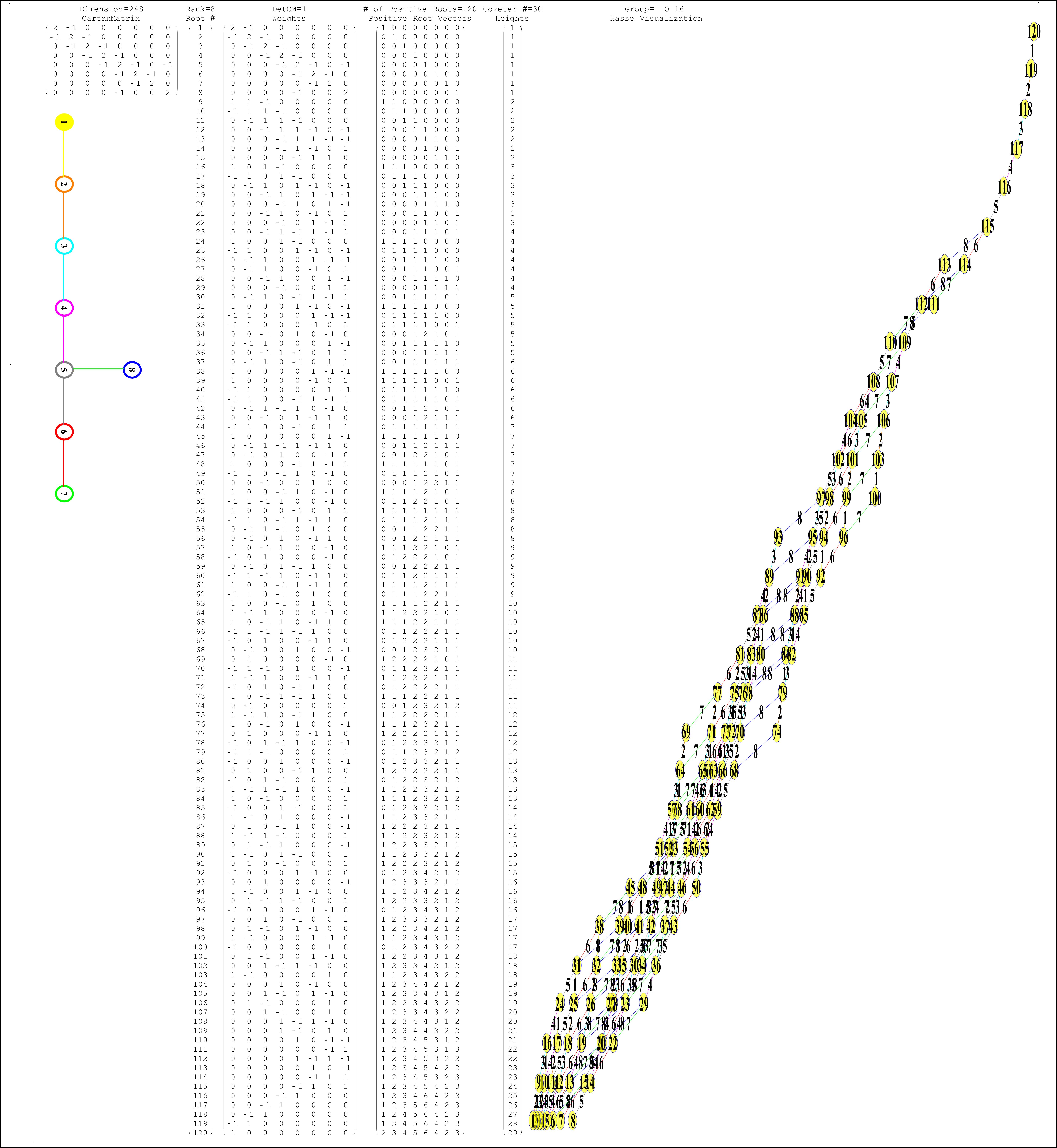
This uses the latest Mathematica version 13.2 with code tweaks to better understand what is being presented, including the E8 Algebra roots, weights, and heights. This is used on the E8 group theory page of WikiPedia.
Tag Archives: Hasse
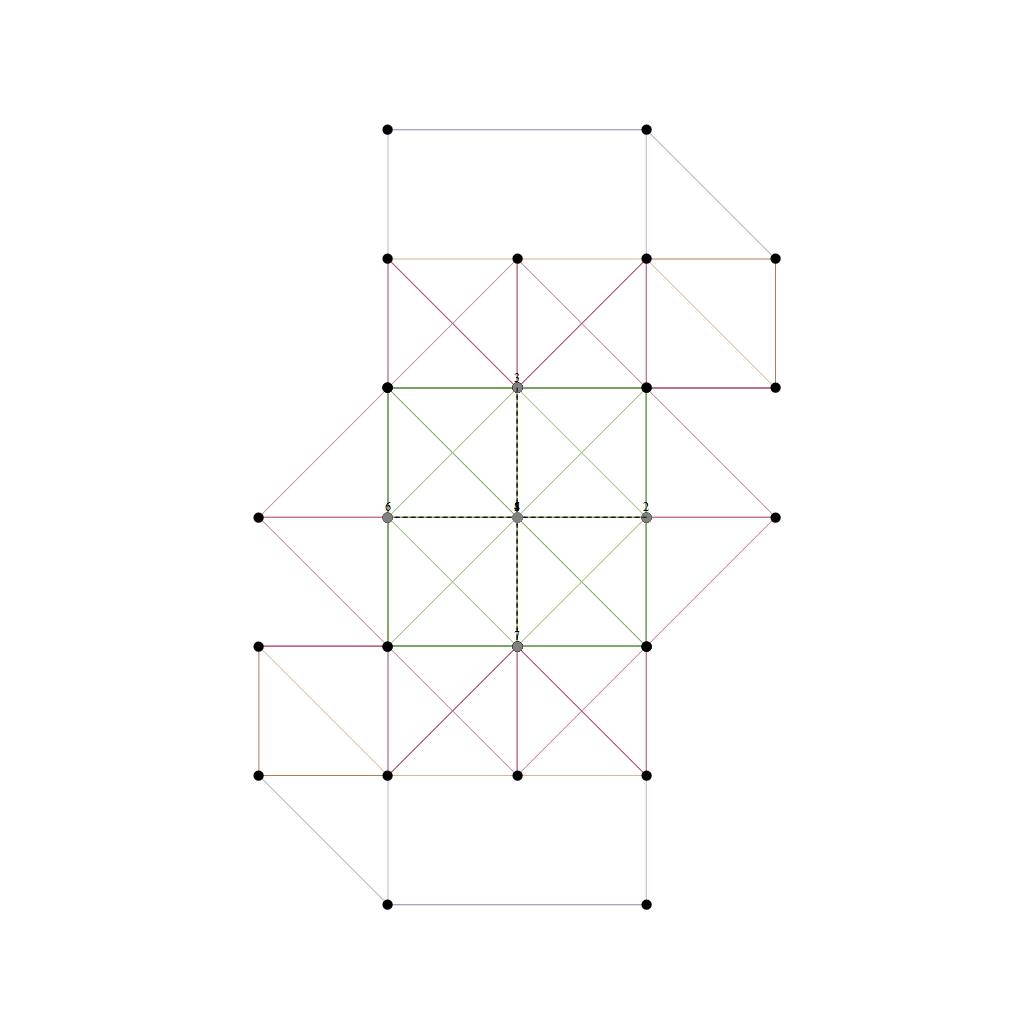
Hyperbolic Dynkin #136 Detail
In followup to John Baez’ G+ thread on Hyperbolic Dynkin diagrams, specifically on the only rank 4 compact symmetrizable diagram 136, I used my “VisibLie” notebook (which includes the “SuperLie” package for analyzing Lie Algebras) to get the following information:
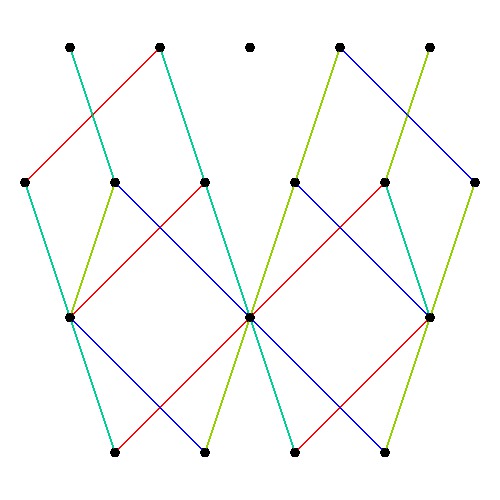
Using the “SimpLie” Google Code OpenSource software, we get Hasse diagram of:
Symmetrized Cartan matrix:
1 -1 0 -1/2
-1 2 -1 0
0 -1 2 -1
-1/2 0 -1 1
One possible set of basis vectors for this is:
srH136={{0,2,0,0},{0,-1,1,0},{0,0,-1,1},{Sqrt[-7],-1,-1,-3}};
with 4D angles between each node of:
{{1->2,135.},{2->3,120.},{3->4,135.},{4->1,120.},{1->3,90.},{2->4,90.}}
Norm’d Length between nodes is:
{2, Sqrt[2], Sqrt[2], 2}
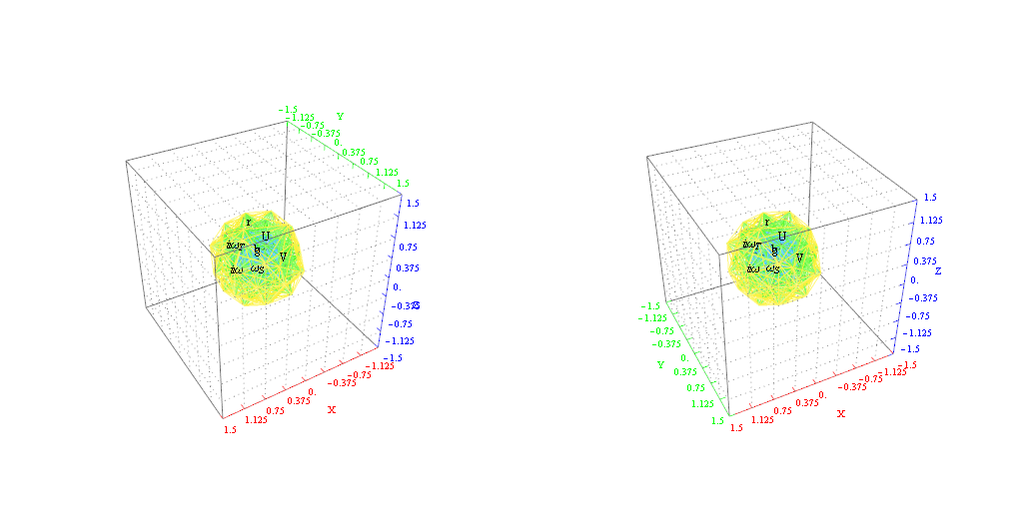
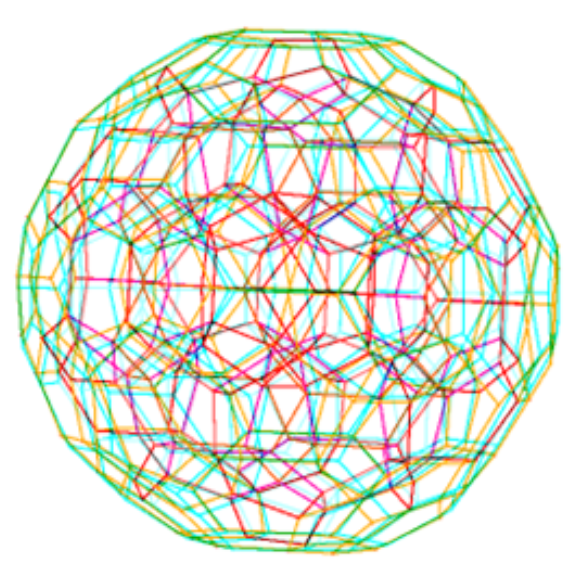
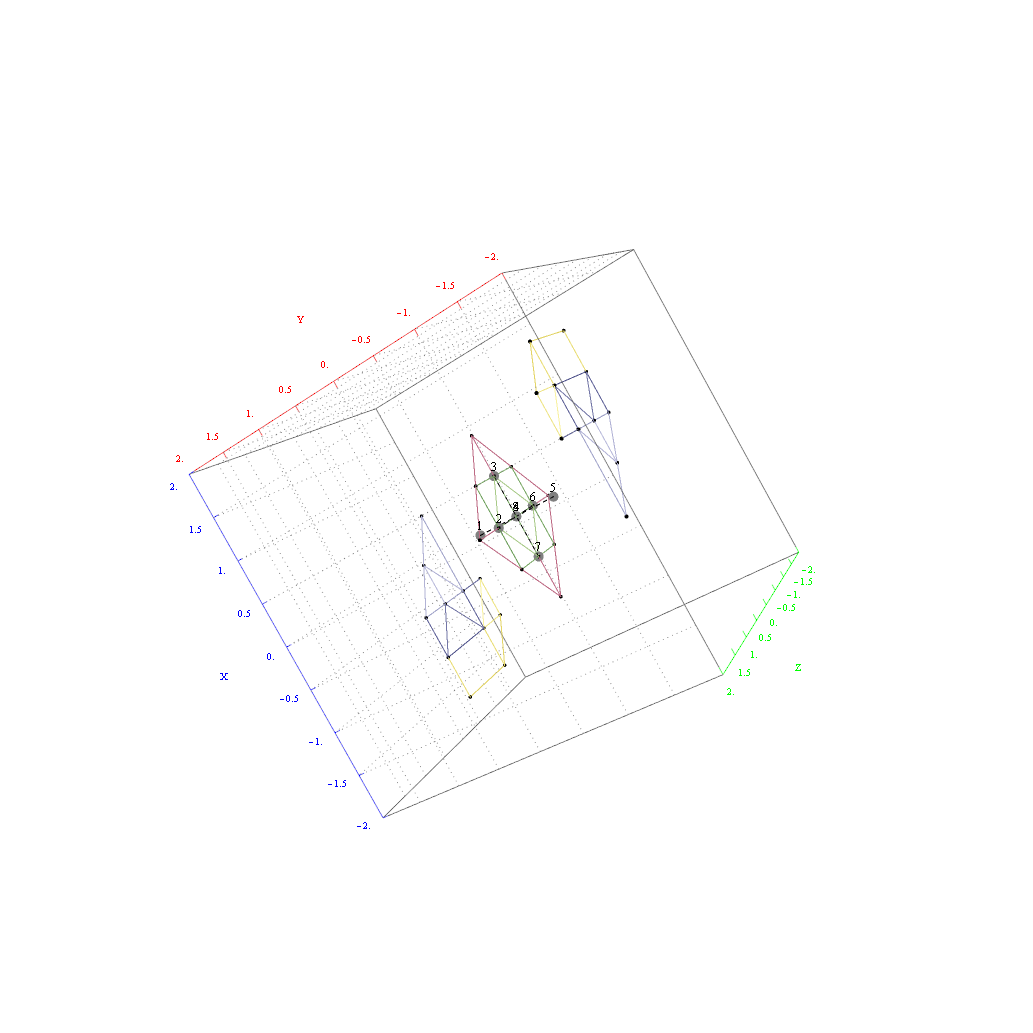
as visualized in 2D and 3D, with 42 vertices and 26 edges of Norm’d 4D length of 2 and 94 at Sqrt[2]:
Interactive Hasse Visualizations and StereoScopic viewing
Along with added options for Left-Right and Red-Cyan Anaglyph stereoscopic outputs on the left side control panel…
I’ve added Interactive Hasse Visualizations to the #2 Dynkin Demonstration Pane. There is now a checkbox for showing the detail root vector data and Hasse visualizations (instead of the default interactive Dynkin pane). This is done from an integration of SuperLie 2.07 by P. Grozman.
If you have a full licensed Mathematica, use ToE_Demonstration.nb. For use with the free CDF Player, use ToE_Demonstration.cdf or as an interactive web page.