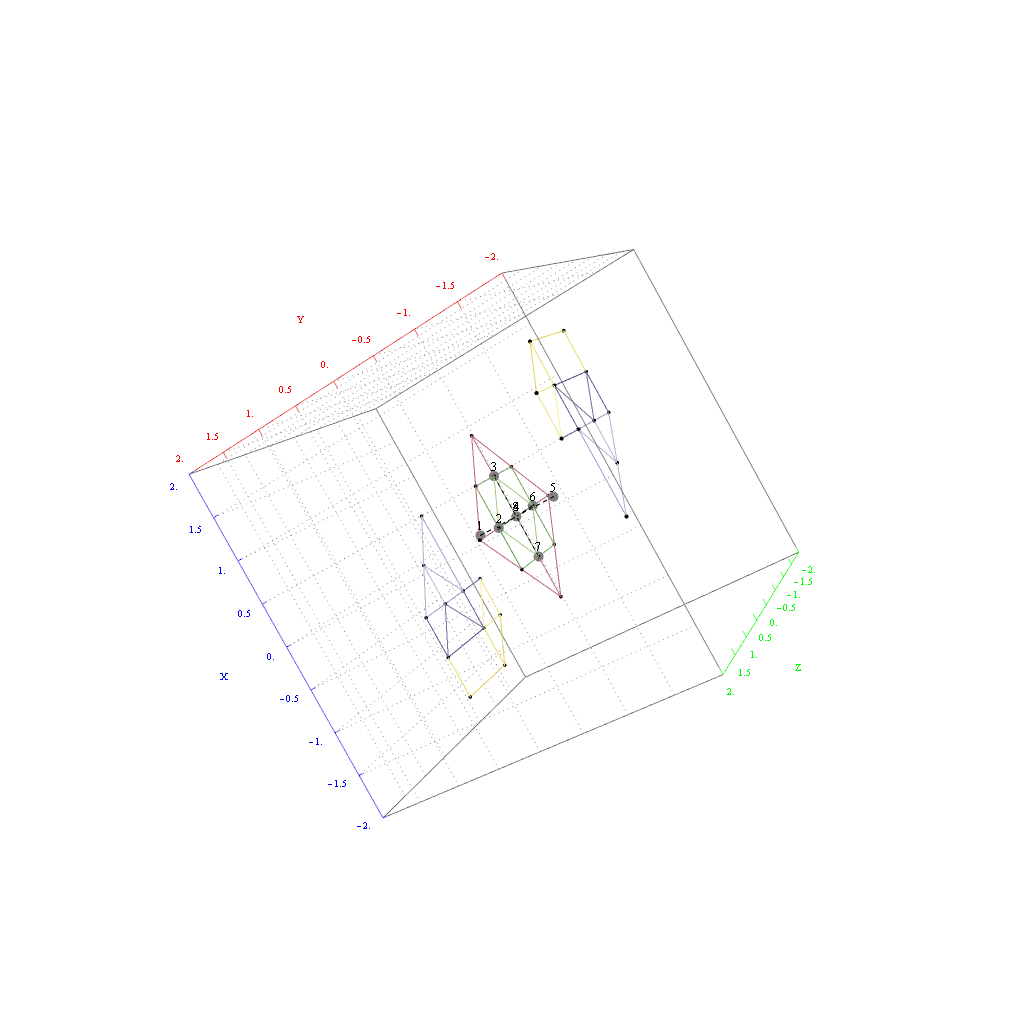
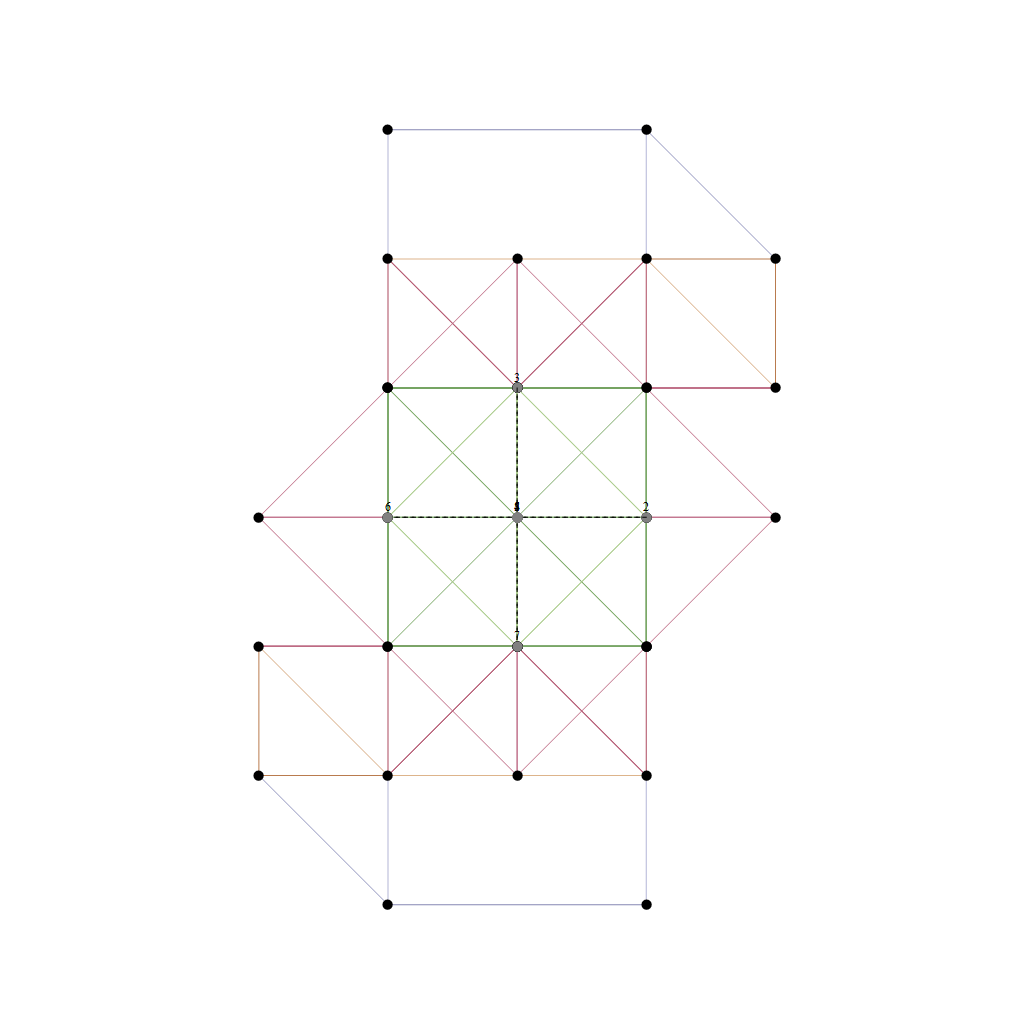
In followup to John Baez’ G+ thread on Hyperbolic Dynkin diagrams, specifically on the only rank 4 compact symmetrizable diagram 136, I used my “VisibLie” notebook (which includes the “SuperLie” package for analyzing Lie Algebras) to get the following information:
Using the “SimpLie” Google Code OpenSource software, we get Hasse diagram of:
Symmetrized Cartan matrix:
1 -1 0 -1/2
-1 2 -1 0
0 -1 2 -1
-1/2 0 -1 1
One possible set of basis vectors for this is:
srH136={{0,2,0,0},{0,-1,1,0},{0,0,-1,1},{Sqrt[-7],-1,-1,-3}};
with 4D angles between each node of:
{{1->2,135.},{2->3,120.},{3->4,135.},{4->1,120.},{1->3,90.},{2->4,90.}}
Norm’d Length between nodes is:
{2, Sqrt[2], Sqrt[2], 2}
as visualized in 2D and 3D, with 42 vertices and 26 edges of Norm’d 4D length of 2 and 94 at Sqrt[2]: