The original post is here. The update is in the form of a PowerPoint here or in PDF form here. Or click each image below:


Greg Moxness, Tucson AZ
I’ve published a version of these demonstrations in the cloud, so no Mathematica installation is needed.
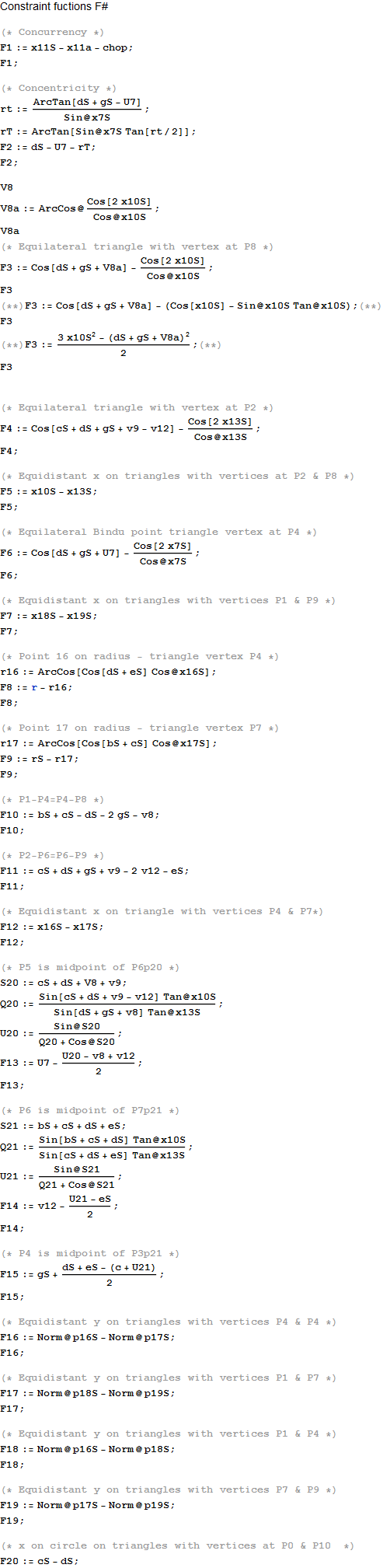
Please click here for the interactive Hindu Sri Yantra demonstration shown below.
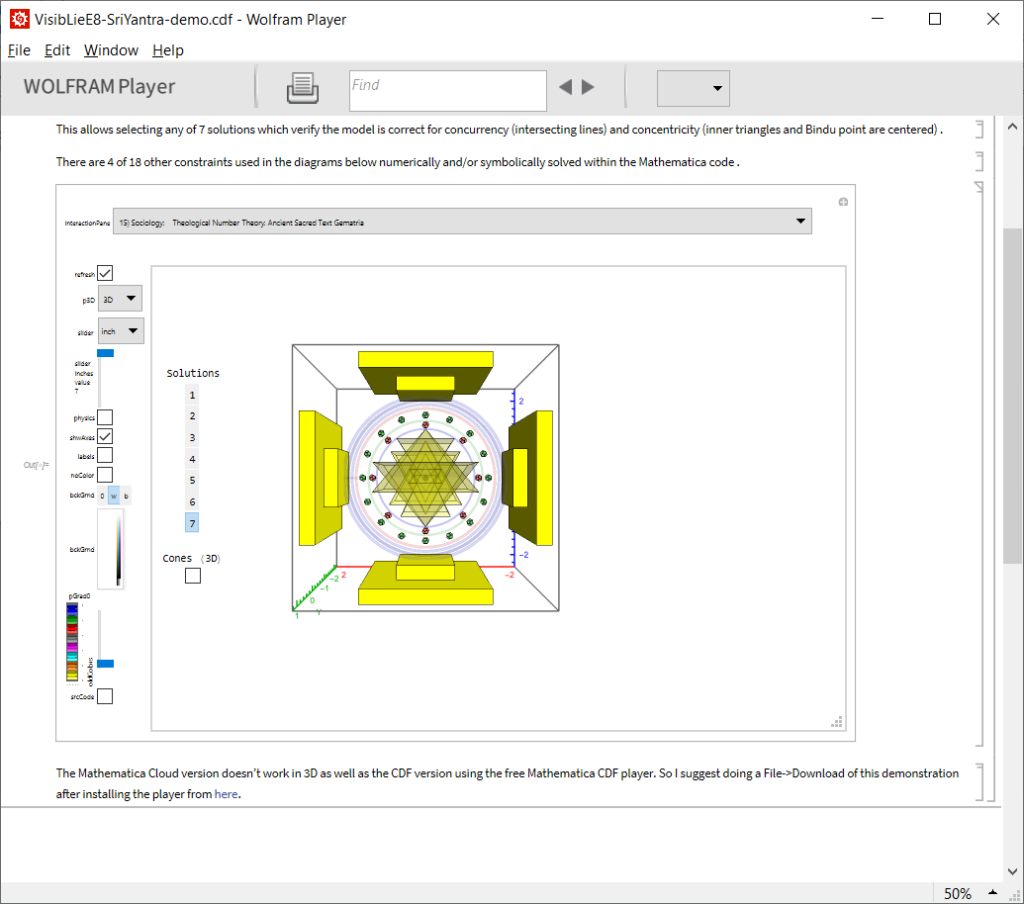
Please click here for the interactive Buddhist (Tao/Confucian) I-Ching demonstration shown below.
The Mathematica Cloud version doesn’t work in 3D as well as using a local .NB version with the free Mathematica CDF player. You can File->Download the local demonstration and use it after installing the CDF player found here.
Of course, the full licensed Mathematica Notebook works the best for this. See this file here for the Hindu 3D Sri Yantra and here for the Buddhist 2D I-Ching notebooks.
There is even a full pane 15) Sociology: Theological Number Theory: Ancient Sacred Text Gematria here.
Here is a list of other Interactive Demonstrations within my VisibLie-E8 package:
A Theory of Everything Visualizer, with links to free Cloud based Interactive Demonstrations:
1) Math: Chaos/Fibr/Fractal/Surface: Navier Stokes/Hopf/MandelBulb/Klein
2) Math: Number Theory: Mod 2-9 Pascal and Sierpinski Triangle
3) Math: Geometric Calculus: Octonion Fano Plane-Cubic Visualize
4) Math: Group Theory: Dynkin Diagram Algebra Create
5) Math: Representation Theory: E8 Lie Algebra Subgroups Visualize
6) Physics: Quantum Elements: Fundamental Quantum Element Select
7) Physics: Particle Theory: CKM(q)-PMNS(ν) Mixing_CPT Unitarity
8) Physics: Hadronic Elements: Composite Quark-Gluon Select Decays
9) Physics: Relativistic Cosmology: N-Body Bohmian GR-QM Simulation
10) Chemistry: Atomic Elements: 4D Periodic Table Element Select
11) Chemistry: Molecular Crystallography: 4D Molecule Visualization Select
12) Biology: Genetic Crystallography: 4D Protein/DNA/RNA E8-H4 Folding
13) Biology: Human Neurology: OrchOR Quantum Consciousness
14) Psychology: Music Theory & Cognition: Chords, Lambdoma, CA MIDI,& Tori
15) Sociology: Theological Number Theory: Ancient Sacred Text Gematria
16) CompSci: Quantum Computing: Poincare-Bloch Sphere/Qubit Fourier
17) CompSci: Artificial Intelligence: 3D Conway’s Game Of Life
18) CompSci: Human/Machine Interfaces: nD Human Machine Interface
An interesting post re:qualifications for a ToE prompted me to jot down my initial list of requirements. A ToE should inform, expand on, or rationalize, in a mathematically self consistent and rigorous way, the state of the current SM & GR confirmed experimental data:
1) Prescription (aka prediction, retrodiction or specific rationalization) for 3 generations of fundamental fermion and boson particles (and their resulting composite particles), including: charge, spin, color, mass, lifetime, branching ratio, and scattering amplitudes (aka. S-Matrix)
2) Prescription for CKM and PMNS unitary matrices and CPT conservation
3) Framework for the integration of QM and GR, including e/m, weak, strong and gravitational forces
4) Explanation for dark energy and dark matter in proportion to visible matter
5) Solution to the hierarchy problem
6) Provide a realistic computational model based on the above for the evolution of the Universe from BB to present
7) Explain an arrow of time that is consistent with GR and QM CPT conservation symmetries
…
Non-specific general appeals to the anthropic principle, landscapes, and/or multiverses tend to excuse or avoid prescription and thus become a benign point (or possibly even meta-physical or philosophical), such that they are not considered supportive of an actually verifiable (aka. scientific) theory.
If the theory says “we can’t know” or “we can’t measure” or “it just is that way” – it isn’t science or part of a ToE. again – my opinion and definition of “science”.
There is redundancy in this list, that is expected (even required). Of course, the beauty of the theory would be in conclusively demonstrating that throughout!
Until we can study an actual ToE that is put on the table – the list is only a guide to what might be needed. I am working on a ToE, but it doesn’t yet meet all the criteria (it’s hard work 😉
IF we have a ToE and really understand it, we should, as Feynman suggested, be able to explain it in plain language to anyone. But in the current state of physics, a completed ToE does not yet exist.
IMO, a ToE is about knowing the Universal Laws of Physics (ULPs). It isn’t, in detail, involved in knowing the Universal Initial Conditions UICs).
If you believe that the laws of “climate science” are known (don’t get me started…), then the only problem with predicting the weather is not so much about NOT knowing the laws – it is about not knowing with sufficient accuracy the initial conditions (location & momentum) of enough particles in the system. We’re missing the “butterfly flapping its wings in the Pacific” data points.
The Copenhagen interpretation of QM suggests that is impossible in principle to know any quantum system ICs (vs. the deterministic formulation of QM by DeBroglie-Bohm). Either way, my view is ToE=ULP.s w/o UICs. So prediction of all long term events specifically (like what I will think about next) is NOT the goal.
We just need enough of an idea about the UICs to initiate the computer model so it comes out close enough to get Earth like planets with weather and life forms thinking about this topic.
Easier, but NOT easy!
Last year I posted this on Pascal Triangle Modulo 2 thru 9 and their Sierpinski Maps.
I just saw an interesting post by Lucien Khan on some Theological numerology (gematria) as it relates to the Modulo 10 patterns of Fibonacci here.
I verified the pattern and added a few more as it relates to the repeating Modulo 9 and 10 patterns, Pascal Triangle and E8 (as in my original post).
Numbers are highlighted when divisible by:
60 are in red
30 are in green
15 are in blue
12 are in magenta
This is all tied to the Pascal Triangle with its 2^n binary (Clifford Algebra) representation, E8 and the number 4!=24 and Octonions.
All of these structures, including the 3 dimensional geometry of the Platonic solids (and its big brother, the 4D non-crystallographic H4 group geometry) are related to E8 via a folding matrix I determined a few years ago here.
For some related interesting reading from John Baez regarding the number 24 and its link to String Theory (M-Theory) updated from last week! (see also related info on his other favorite numbers 5 and 8).
Please note, this is about the GEOMETRY used in what has come to be called “Sacred Geometry”. Upon further investigation, along with the Kabbalah’s “Tree of Life”, it seems even the Jewish “Star of David” (Solomon) is medieval and may not be sourced in authentic ancient Abrahamic theology.
As it stands, the so-called “sacred” origin of these, including the pentagon that shows up in the icosahedral/dodecahedral Platonic solids due to the Sqrt(5) Golden Ratio (Phi) relationship within my E8 to H4 folding, is likely medieval and mostly pagan. I am merely pointing out that E8 contains the geometry that many find “interesting” for whatever reason, and am not promoting the underlying cults that use them.
Video (Best in HD):
My E8 F4 projection w/blue triality edges and physics particle assignments:
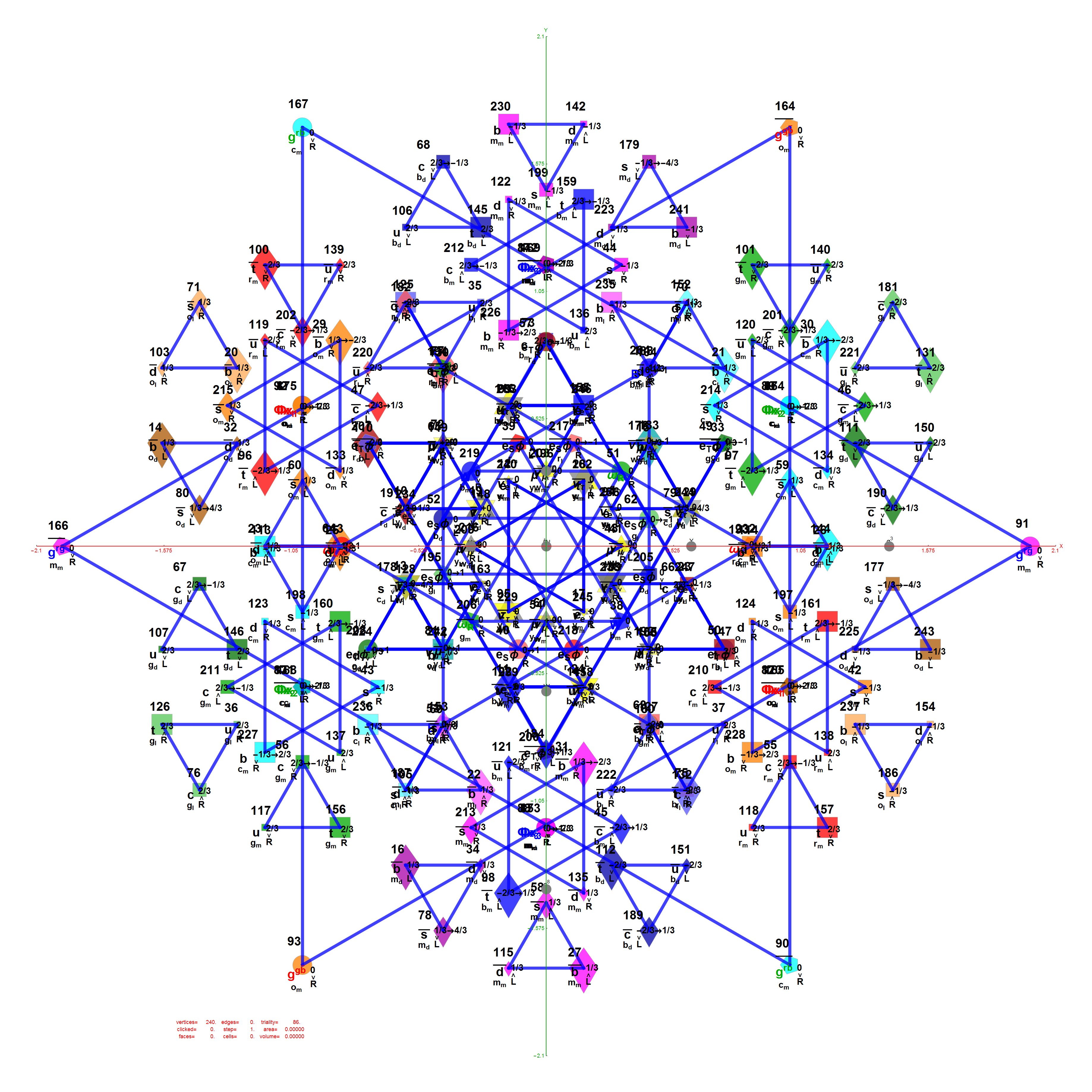
My E8 F4 projection with 6720 edge lines:

My E8 F4 projection rectified:

Kabbalah Tree of Life Overlay:

Copyright J Gregory Moxness 2015
Rectified E8 and F4 Triality (Original Work)
WikiMedia Commons source images:
Metatron’s Cube (User:Barfly2001)
Flower of Life (User:Life_of_Riley)
Tree of Life (User:AnonMoos)
Based on an excellent 1998 paper by C.S. Rao I’ve modeled the Sri Yantra in Mathematica and incorporated it into the VisibLie_E8 demonstrations (I will upload that soon).
This is a reference figure to verify the model is correct for concurrency (intersecting lines) and concentricity (inner triangles and Bindu point are centered). There are 4 of 18 other constraints used in the diagrams below numerically and/or symbolically solved within the Mathematica code.
Here are 7 of many possible solutions using the 20 constraint rules to produce optimal spherical and plane forms of the Sri Yantra.
Solution 1: Solving constraints (* 1,2,3,4,8 *)
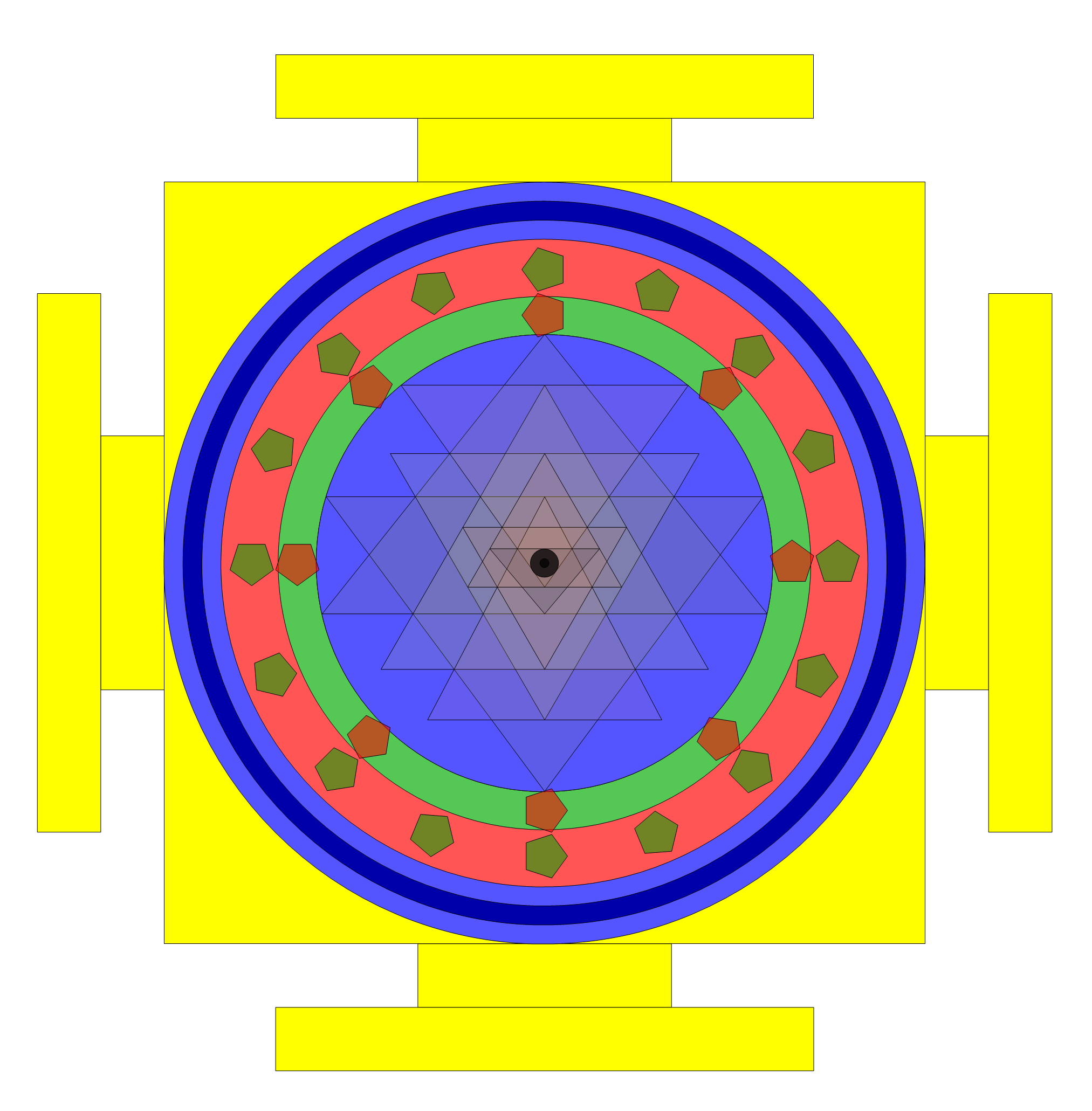
Solution 2: Solving constraints (* 1,2,3,10,15 *)
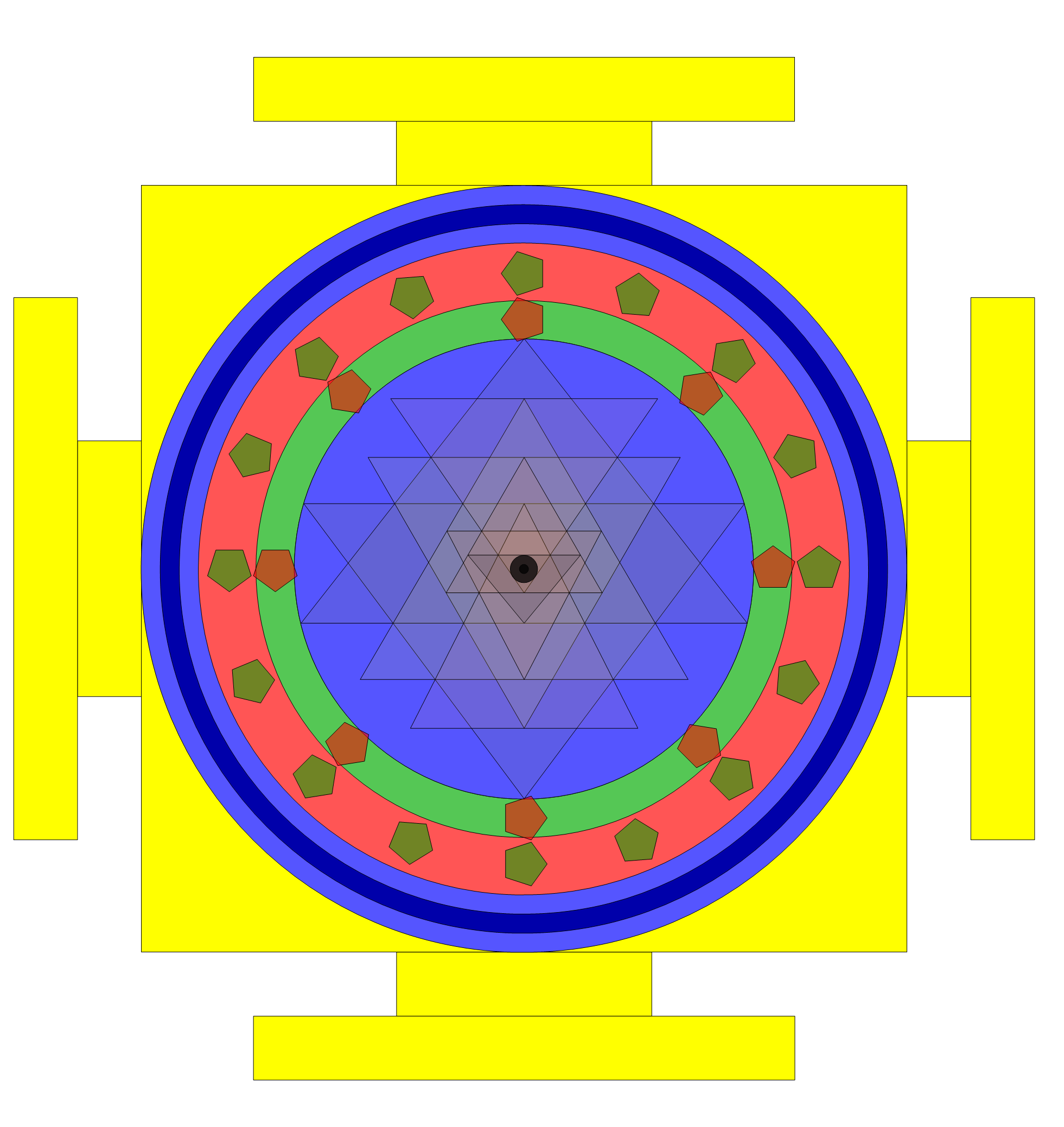
Solution 3: Solving constraints(* 1,2,4,5,10 *)
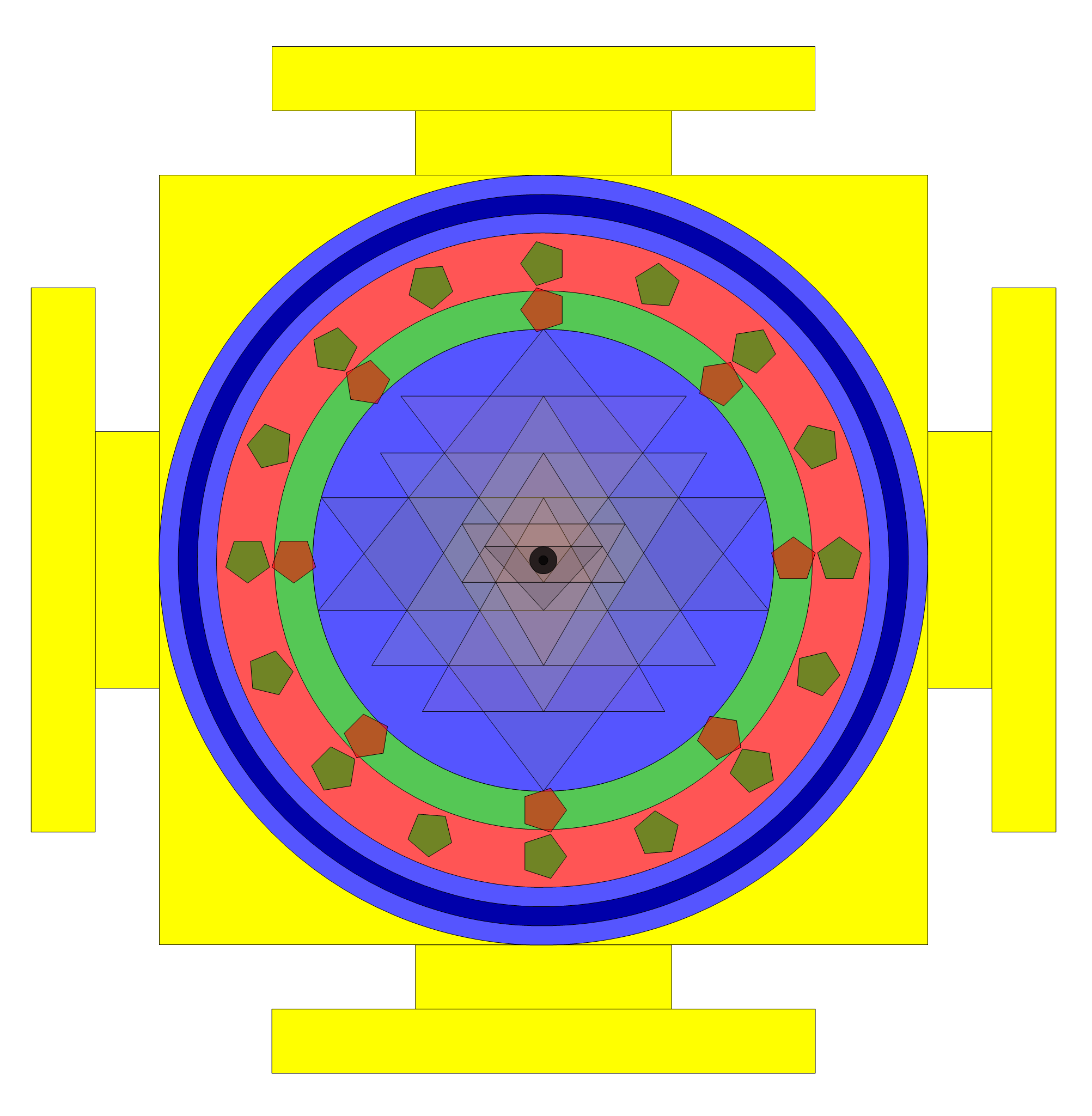
Solution 4: Solving constraints (* 1,2,5,6,19 *)
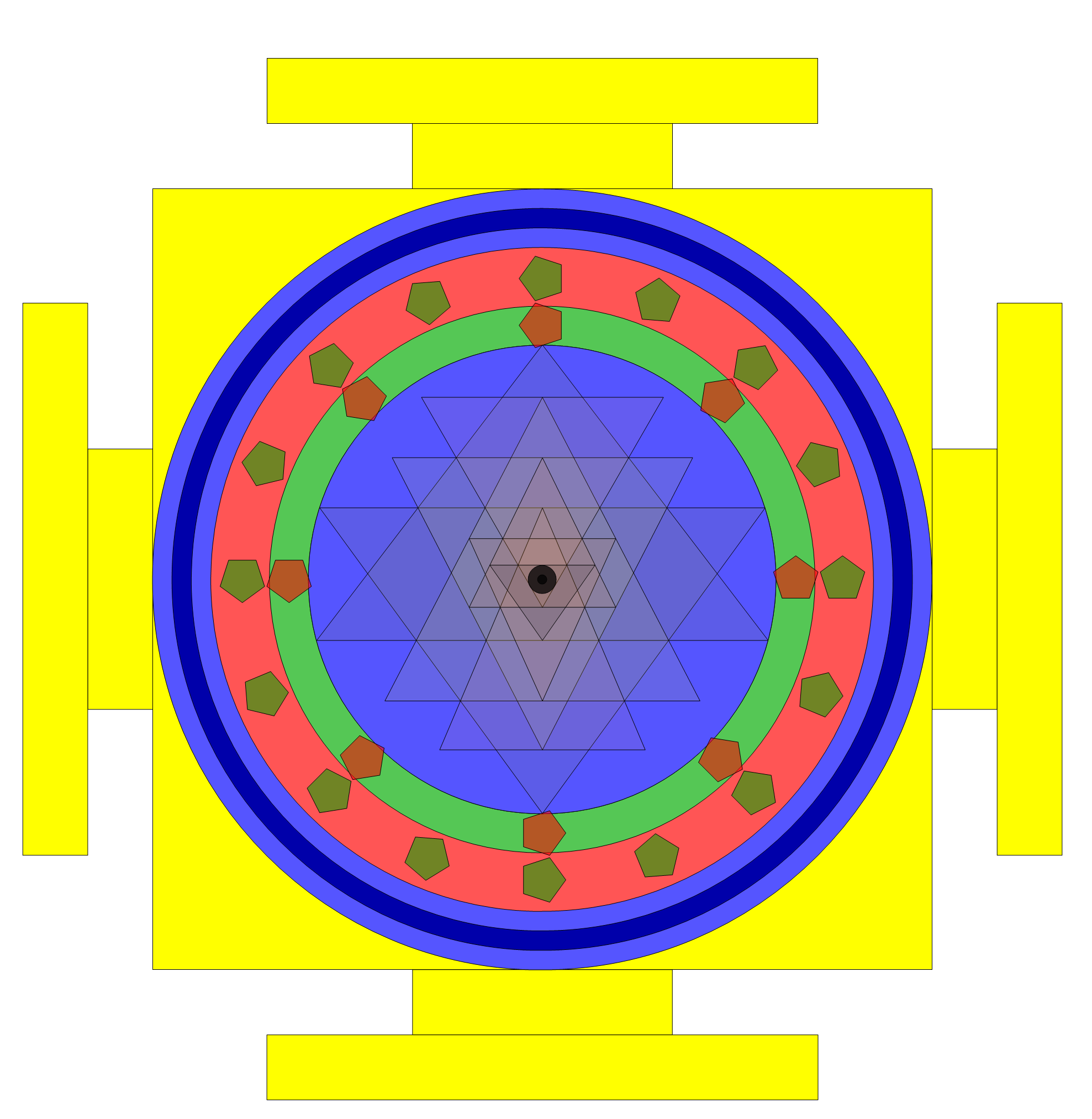
Solution 5: Solving constraints (* 1,2,6,14,19 *)
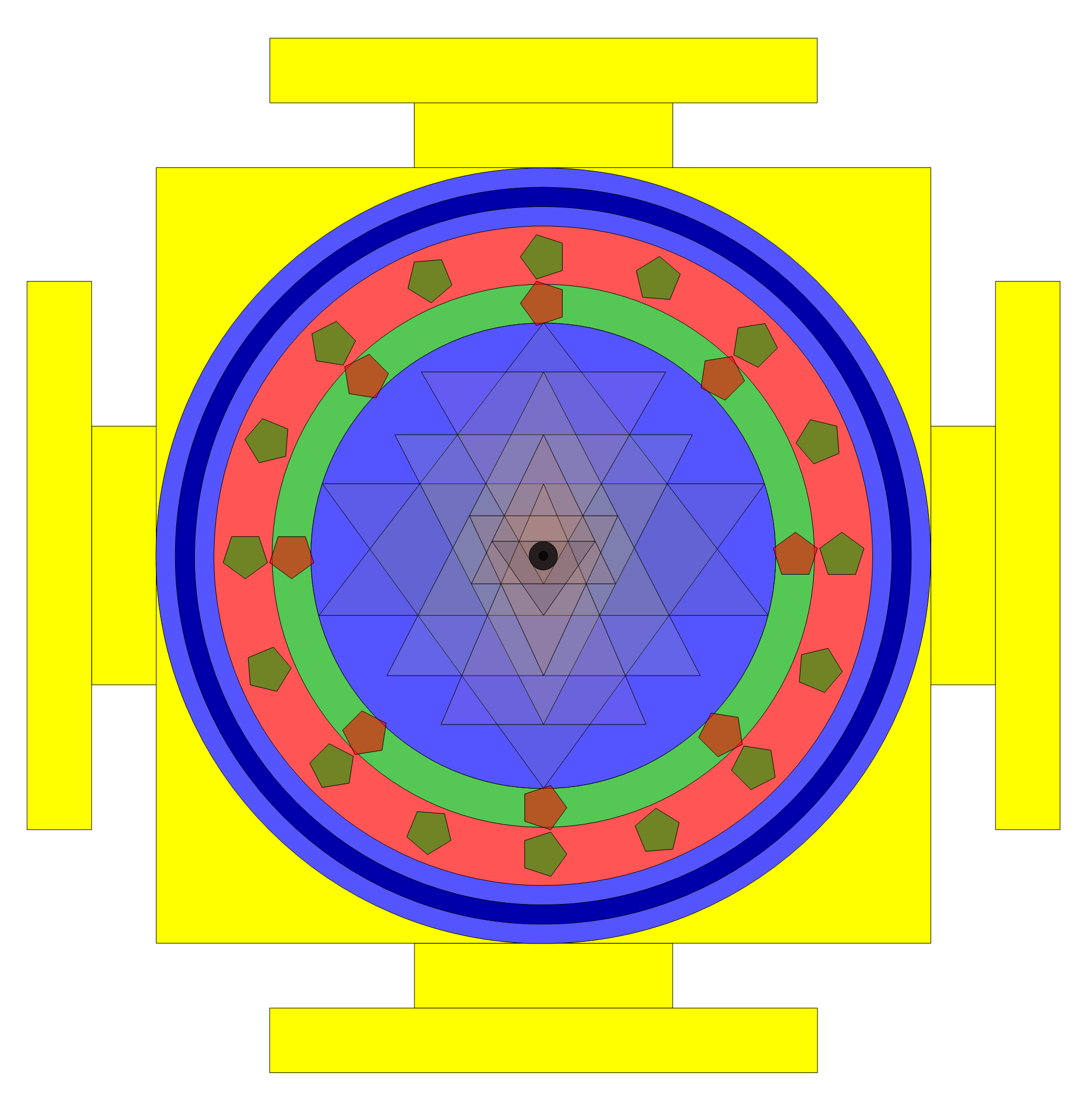
Solution 6: Solving constraints (* 1,2,8,9,20 *)
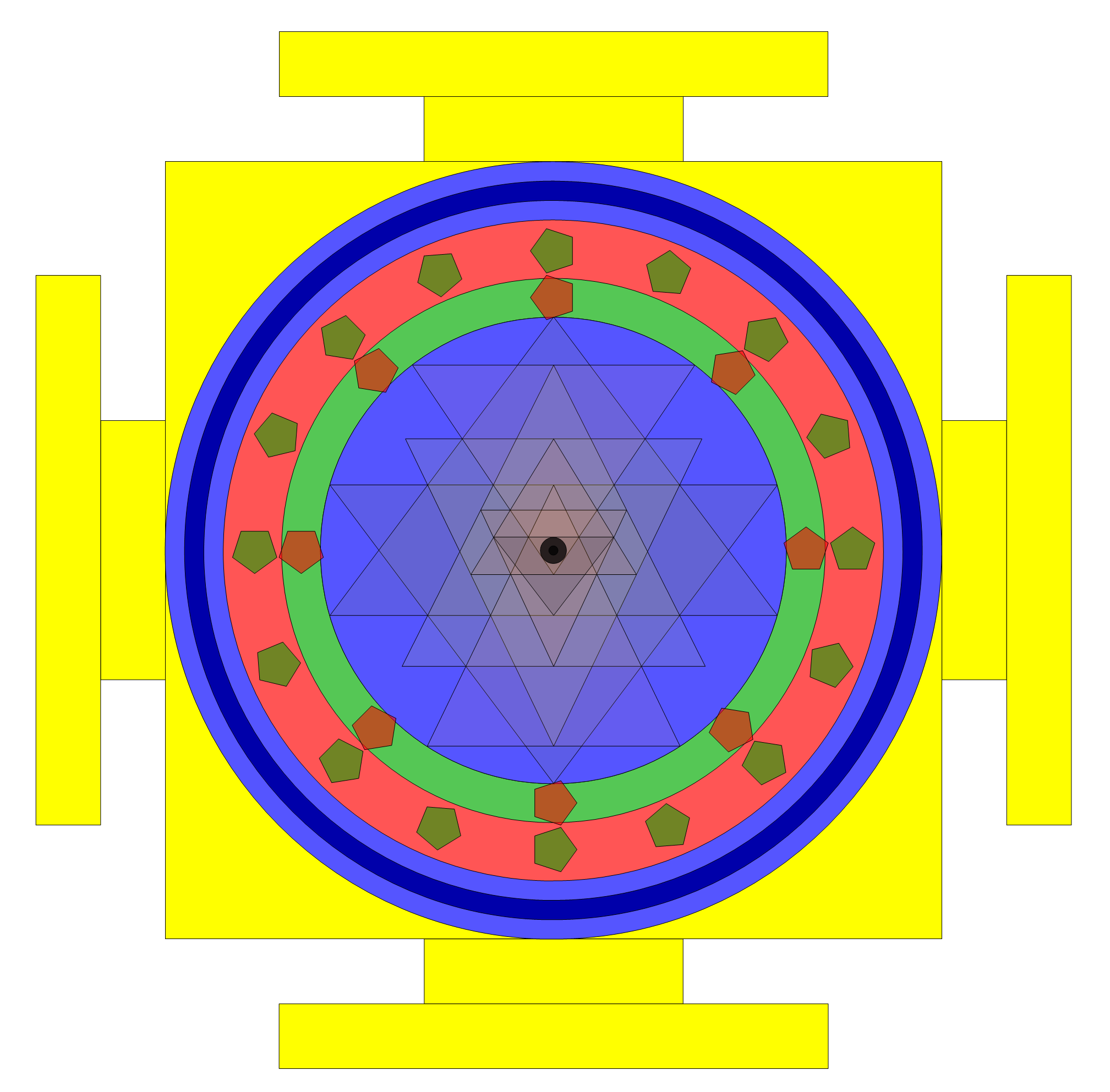
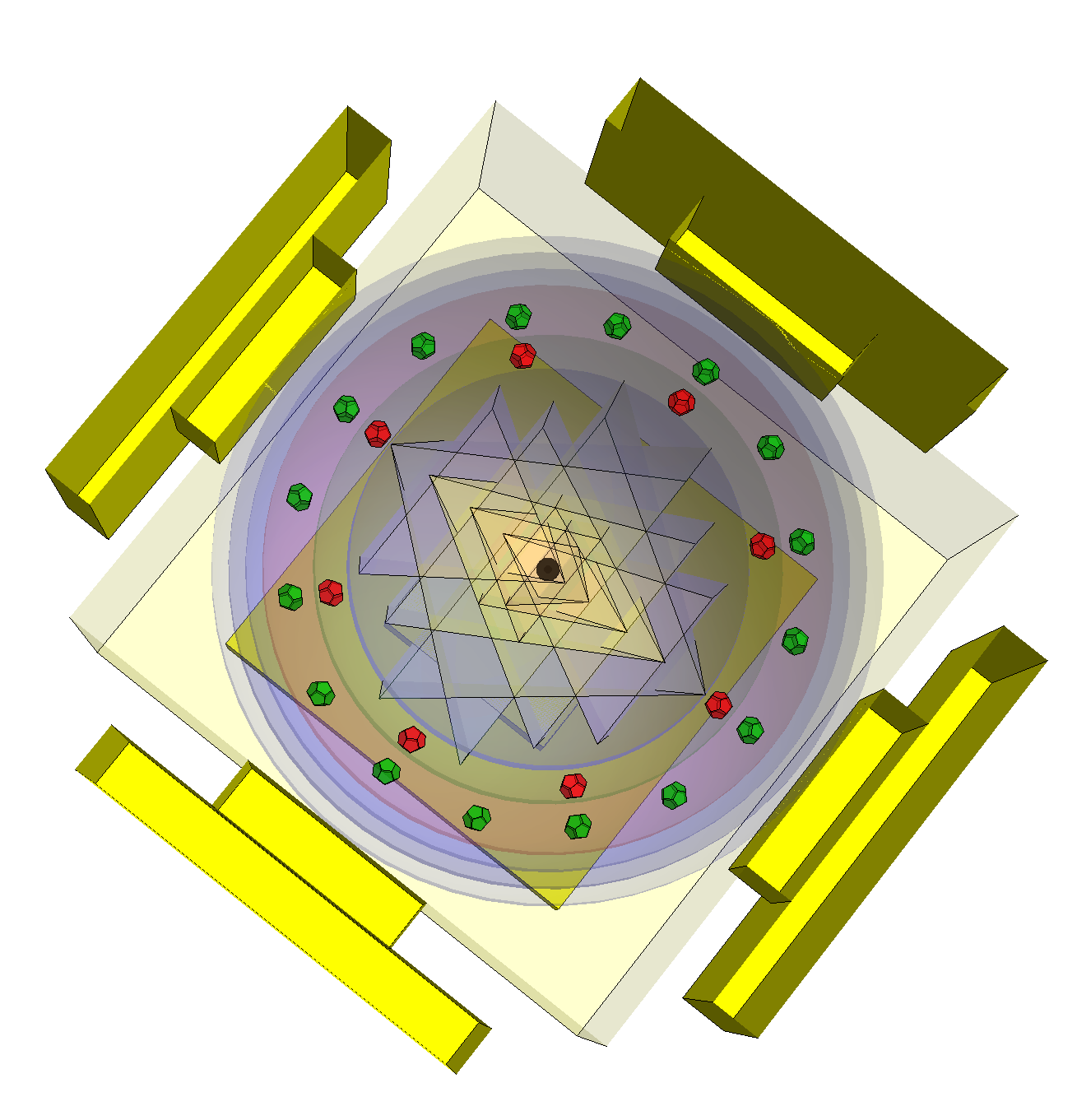
3D using pyramids and new clipping and slicing functions to take off the front (and back) portions of the symmetric 3D object.
I will produce a version option with conical shapes just for fun (soon).
This is a list of the details behind each constraint function Fn