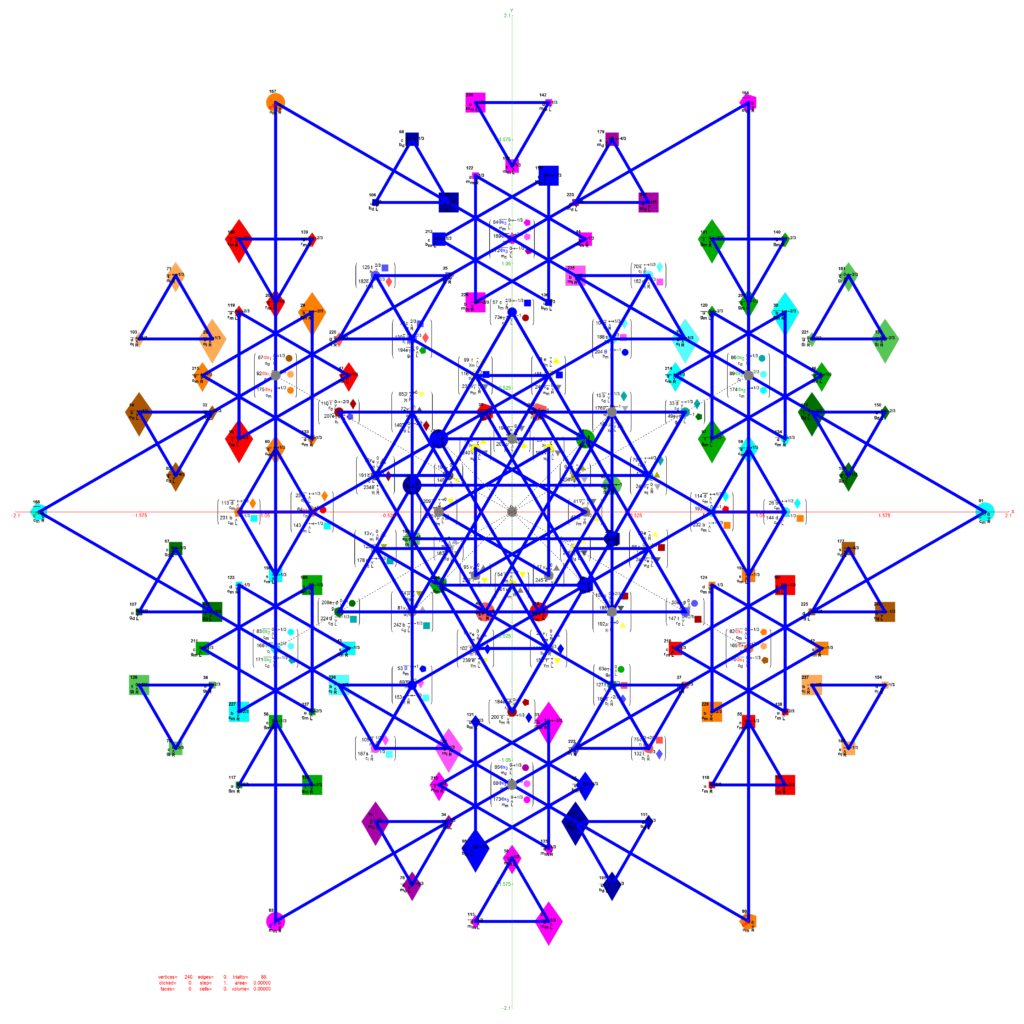
I’ve had a number of related posts on this topic, but I wanted to present a few new pictures and PDF documents that combine the 7 concentric hulls forming Platonic solid related sets of E8 vertices projected to 3D with vertices of five pairs of 24-cell objects.
These break down the E8 structure into familiar 3D objects, such as the icosahedron with its dual the dodecahedron, the icosidodecahdron, and the 16-cell with its dual the 8-cell (aka. Tesseract) combined to create the self-dual 24-cell.
You can see that 6 of the yellow vertices connect to the 24-cell. Rotating that 24-cell four times in 3-space by π/5 gives the connections to the rest of the vertices in H4Φ and completes the 30 vertex icosidodecahedron . The same is true for the 120 vertices of H4 using the corresponding 24-cell in H4.
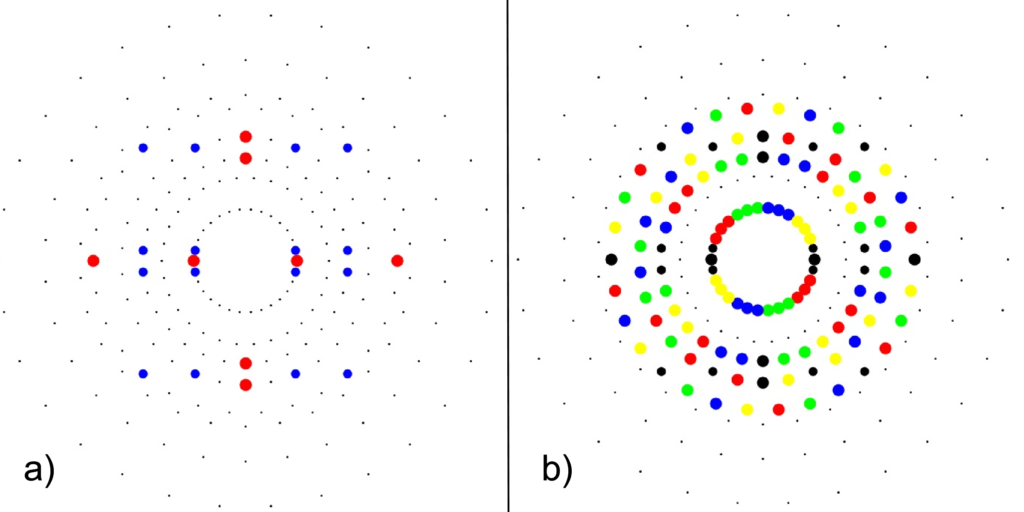
b) Snub 24-cell highlighting four π/5 rotations of the 24-cell (black) in red, green, blue, yellow.
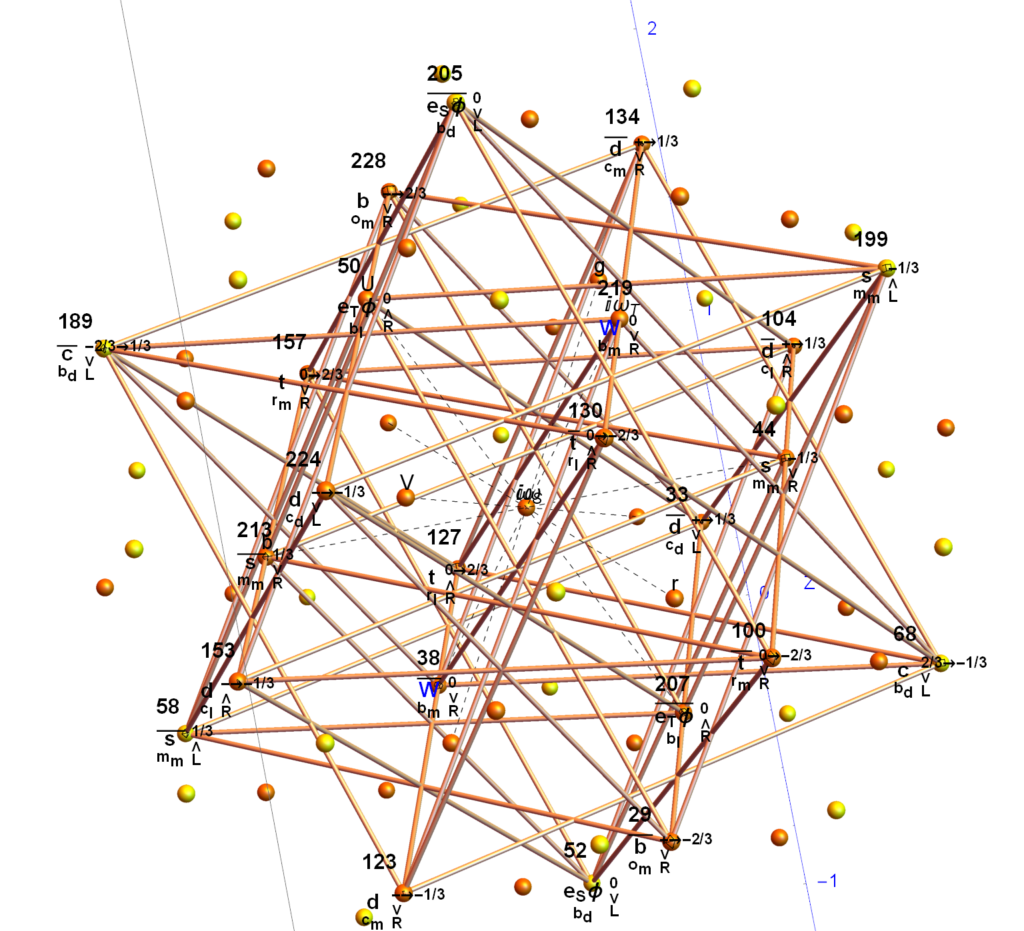
The following paper hulls-24cells-combined.pdf (13MB) & interactive Mathematica Notebook hulls-24cells-combined.nb (34MB) contains a comprehensive set of images that show the contents of the 7 concentric hulls of Platonic solid related shapes as well as their integration with one of the rotations of 24-cells in H4 and H4Φ in E8 (the same one used in the image above).
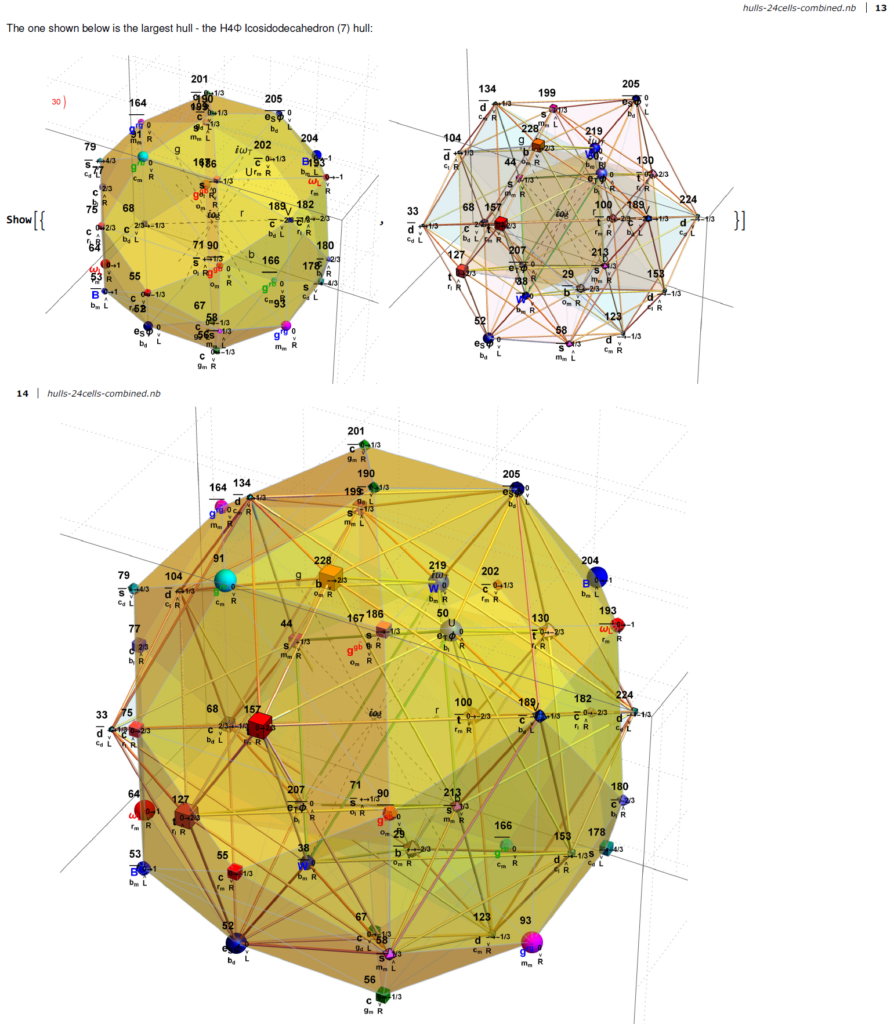
In the E8 Petrie projection, every hull (each with 2 or 4 overlapping vertices) pair into left/right patterns. See the set of four icosahedrons that occupy the 3rd hull in both 2D and 3D (the yellow edge sets belongs to the H4Φ and the blue sets belong to H4) :
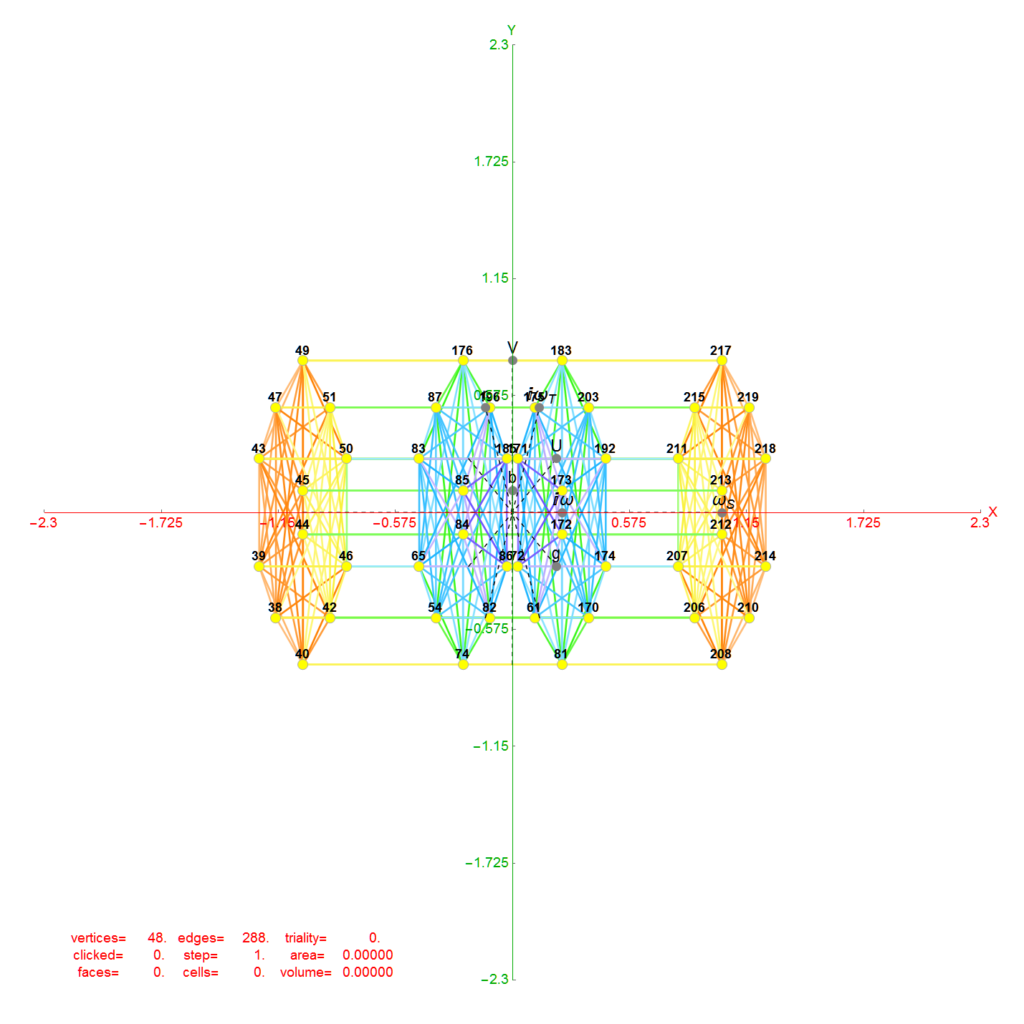
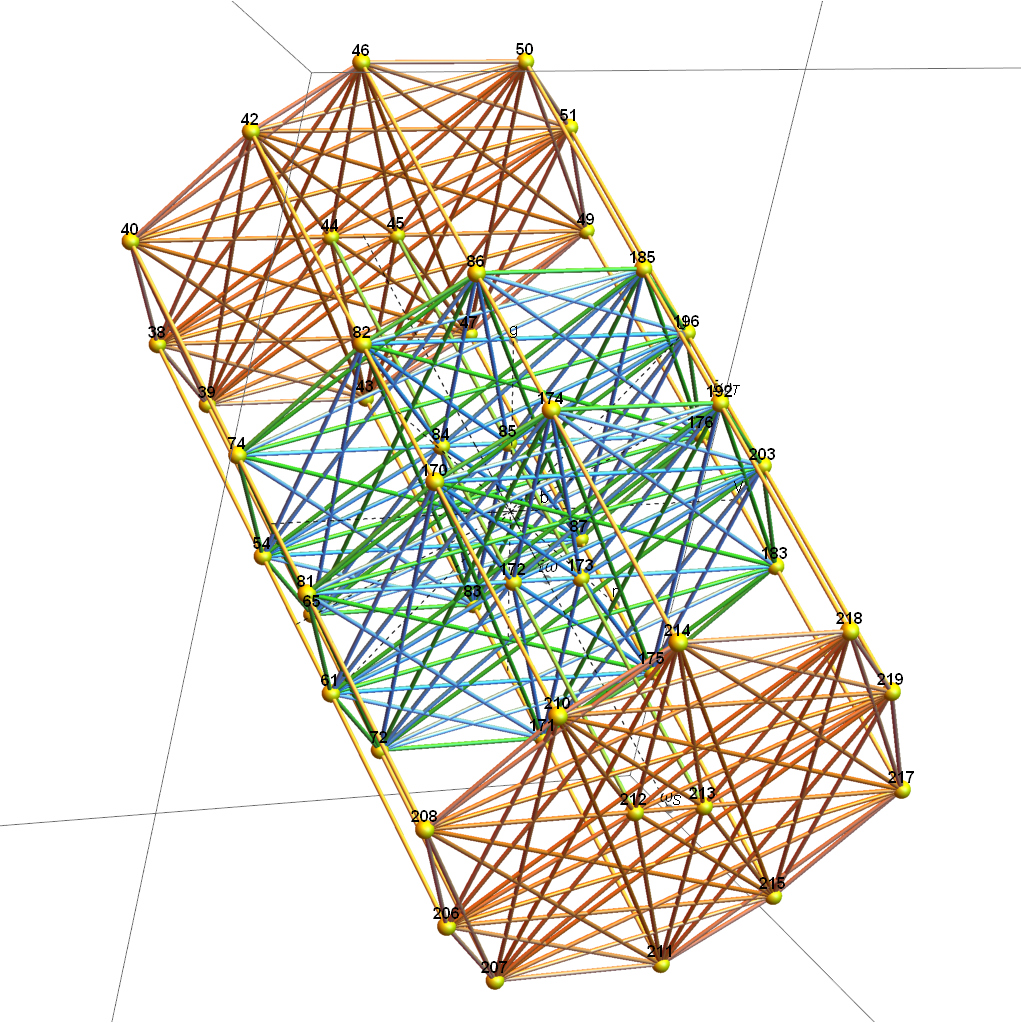
The pair of dodecahedrons that occupy the 5th hull in both 2D and 3D (the yellow edge set belongs to the H4Φ and the blue belong to H4) :
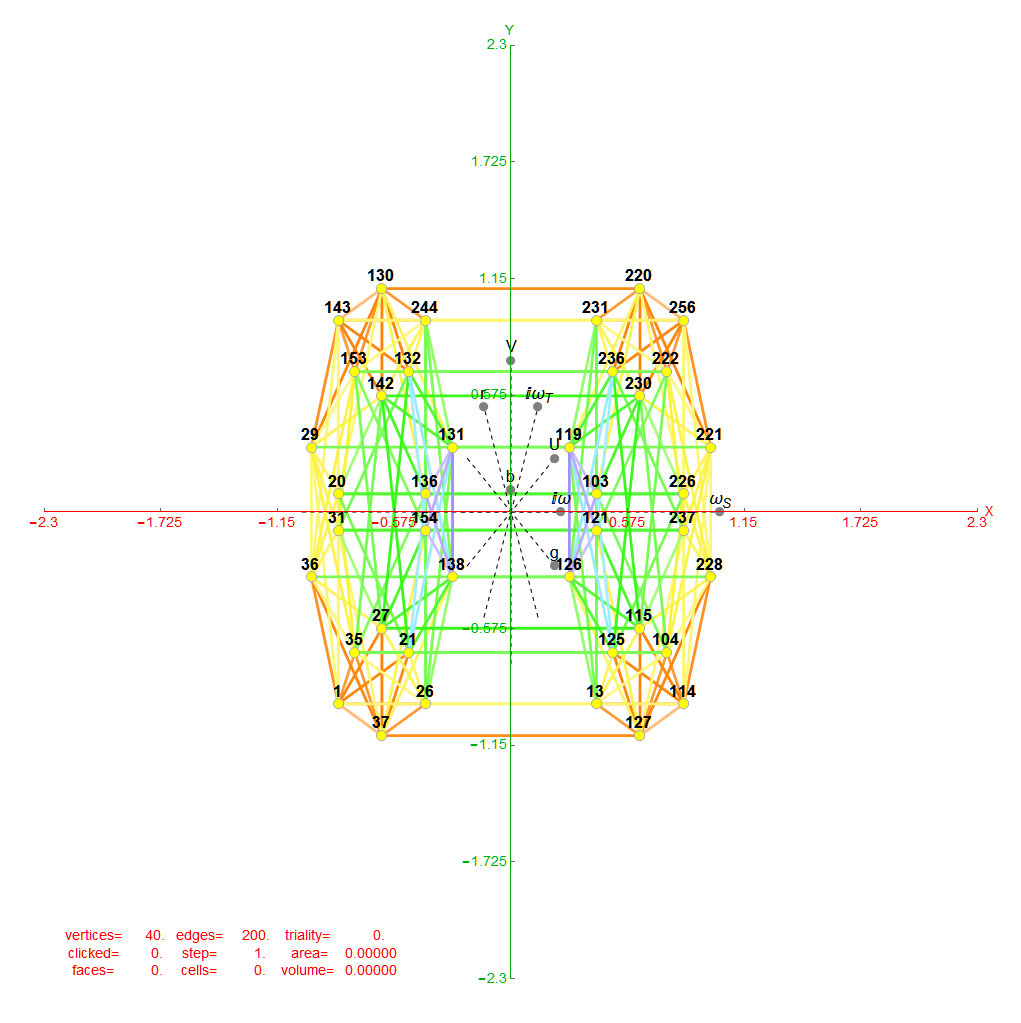
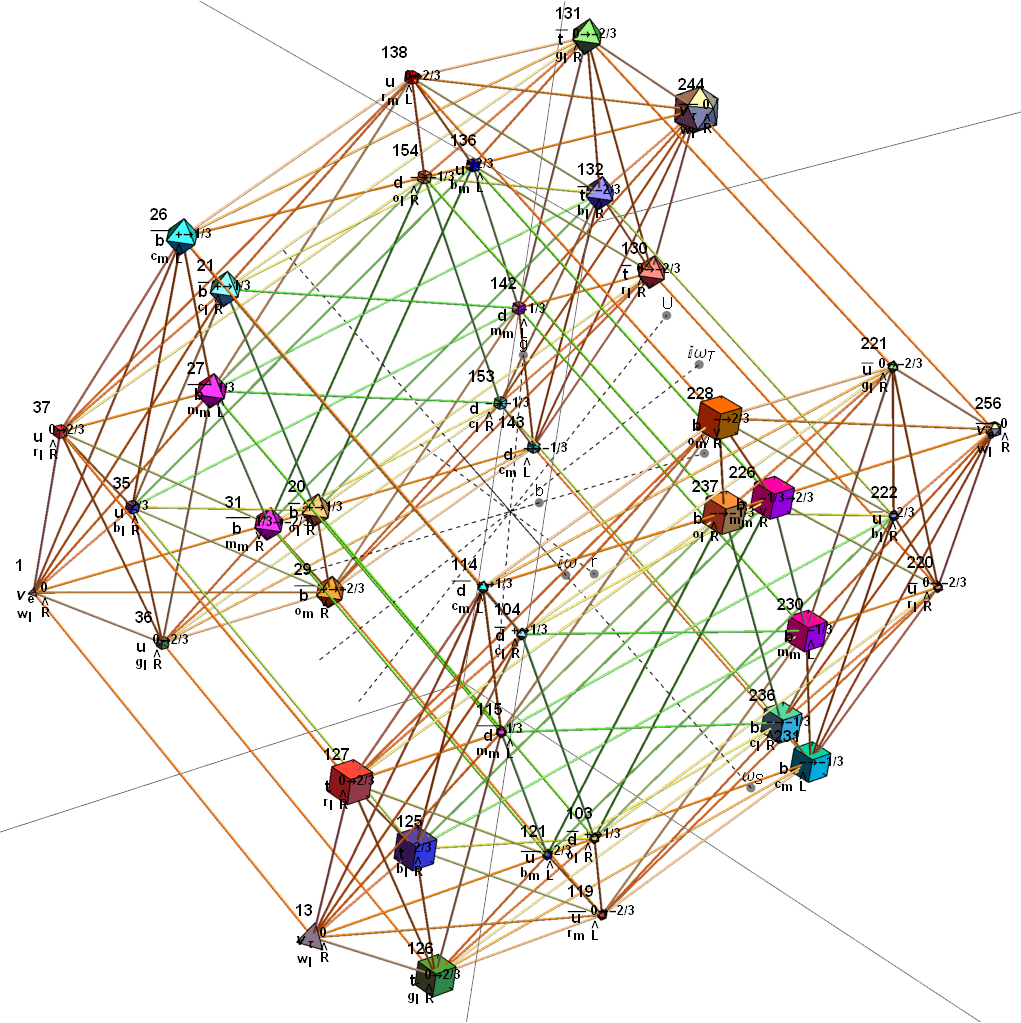
Below is an animation that cycles through the sequence of 2D Petrie Projections of the pairs of hulls. One cycle shows each frame individually and the other builds the E8 Petrie from the previous 2D hull.
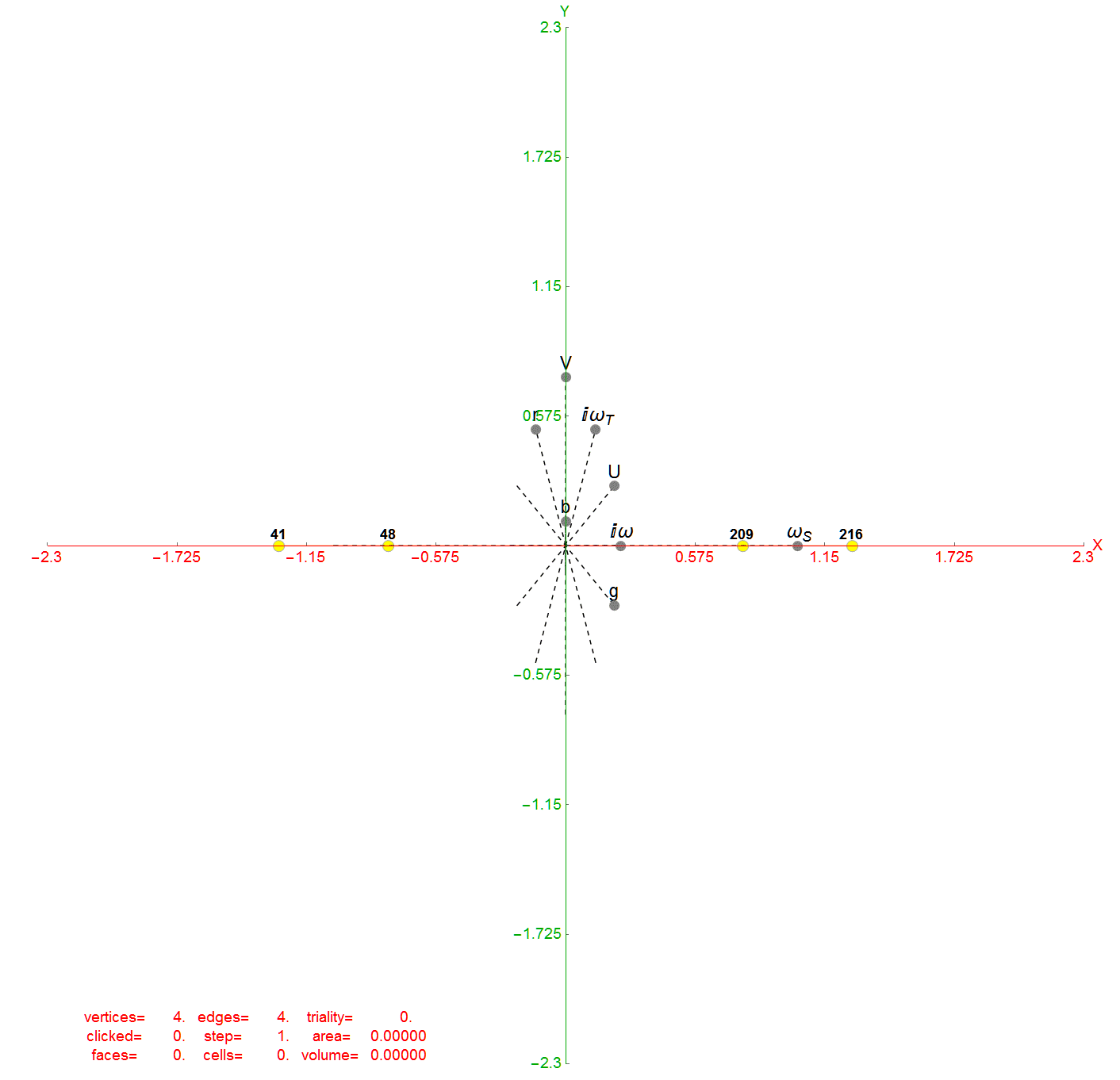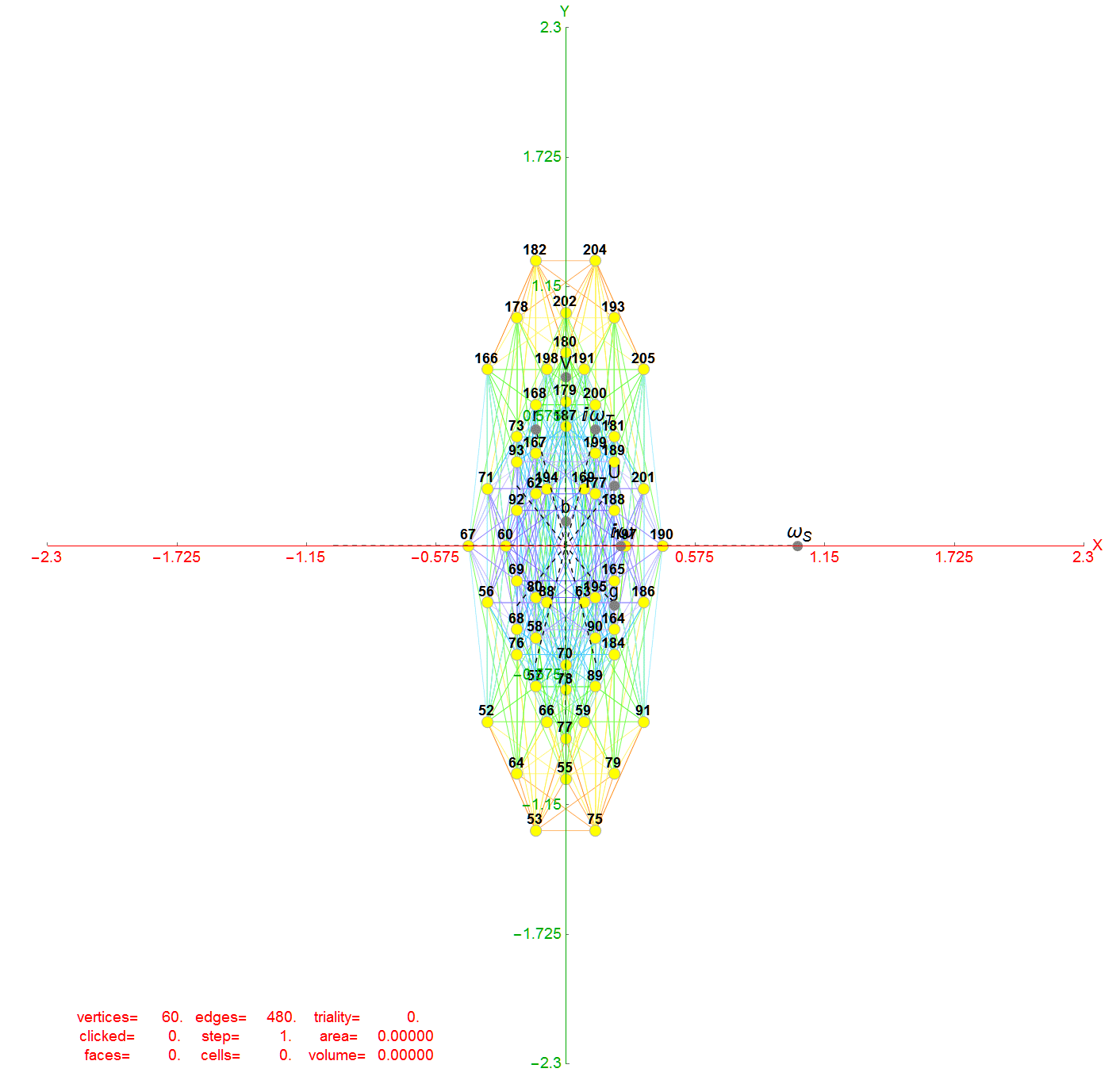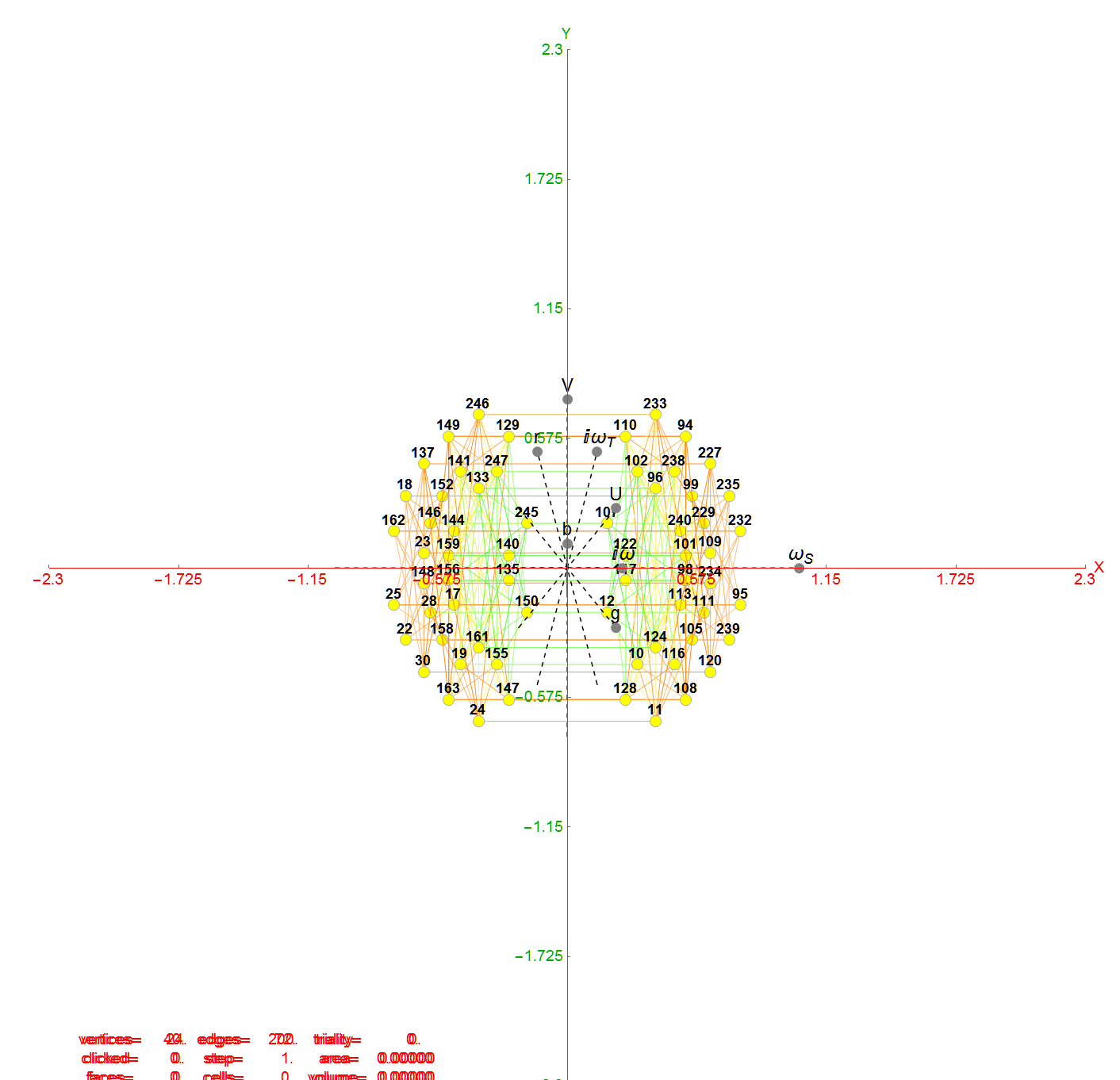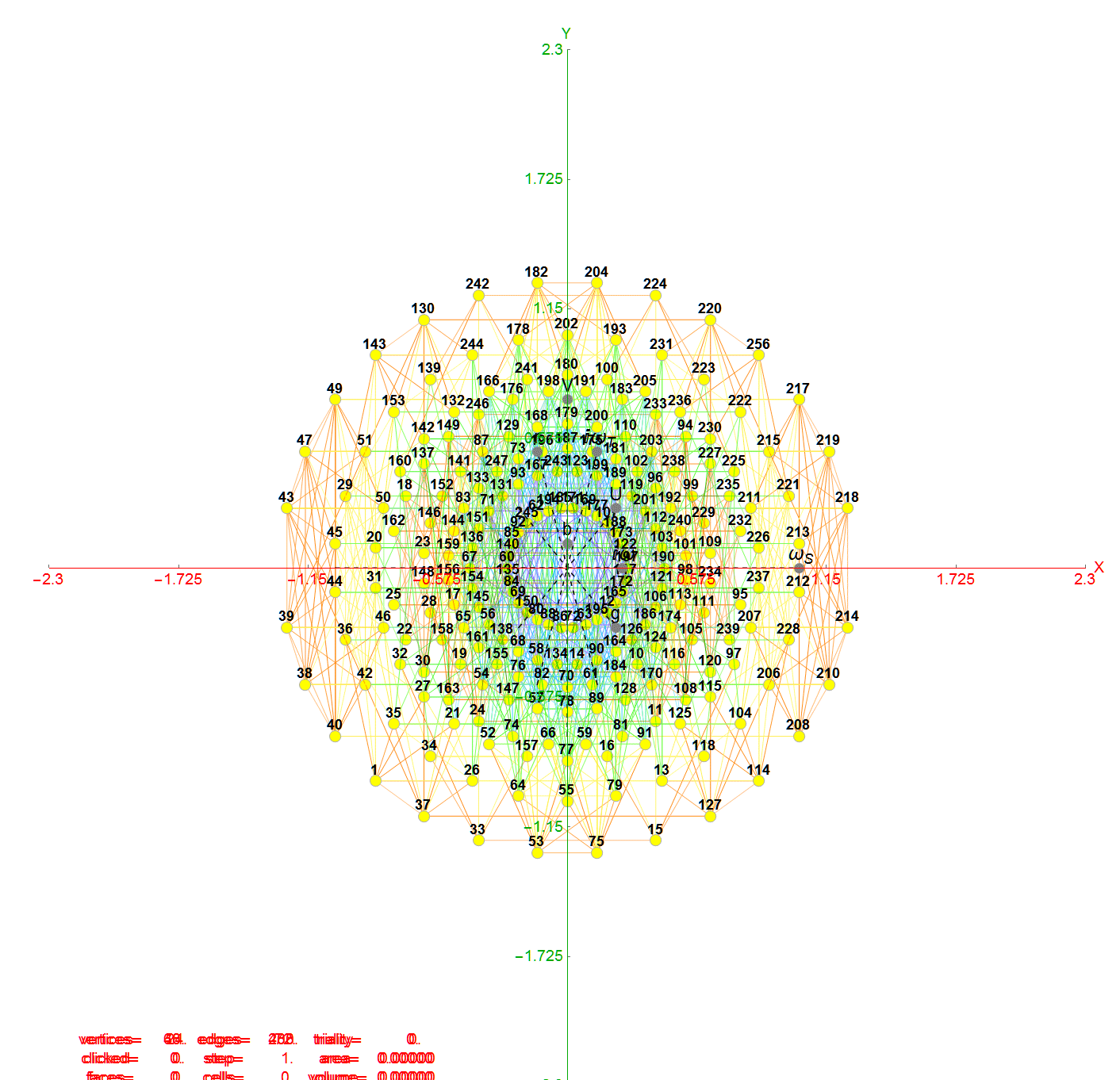
Below are images of the left (H4) and right (H4Φ) 2D Petrie projections of the hulls (which are defined by the Norm’s of 3D projected vertices using the E8->H4 folding matrix rows 2-4 as basis vectors). The two 30 vertex 4 & 7 Icosidodecahedron hulls and four 0th hull (points) are omitted leaving the gaps in the diagram. When these gap vertices are combined with the 48 3rd hull Icosahedrons (above), they make up the 112 integer D8 group assigned to the Bosons (48) and 2nd generation Fermions (64) in the physics model described below.
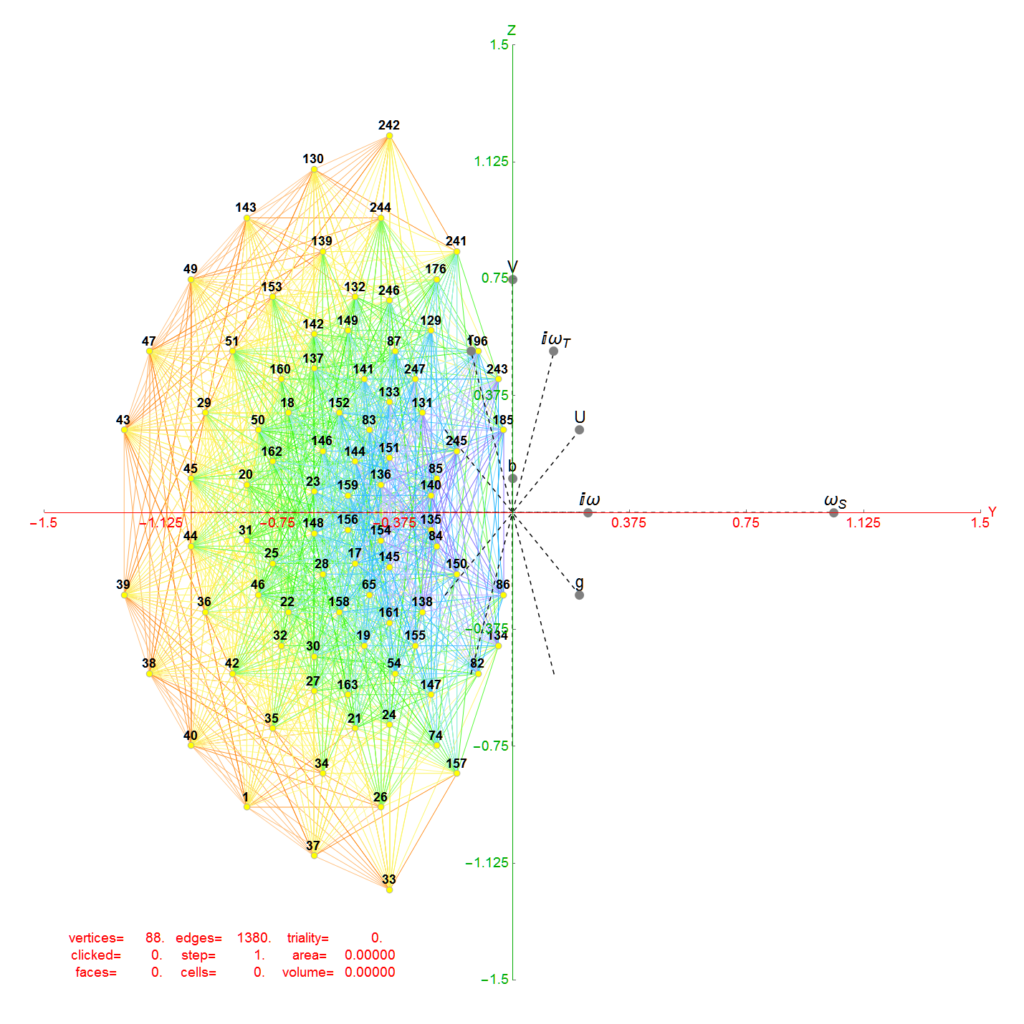
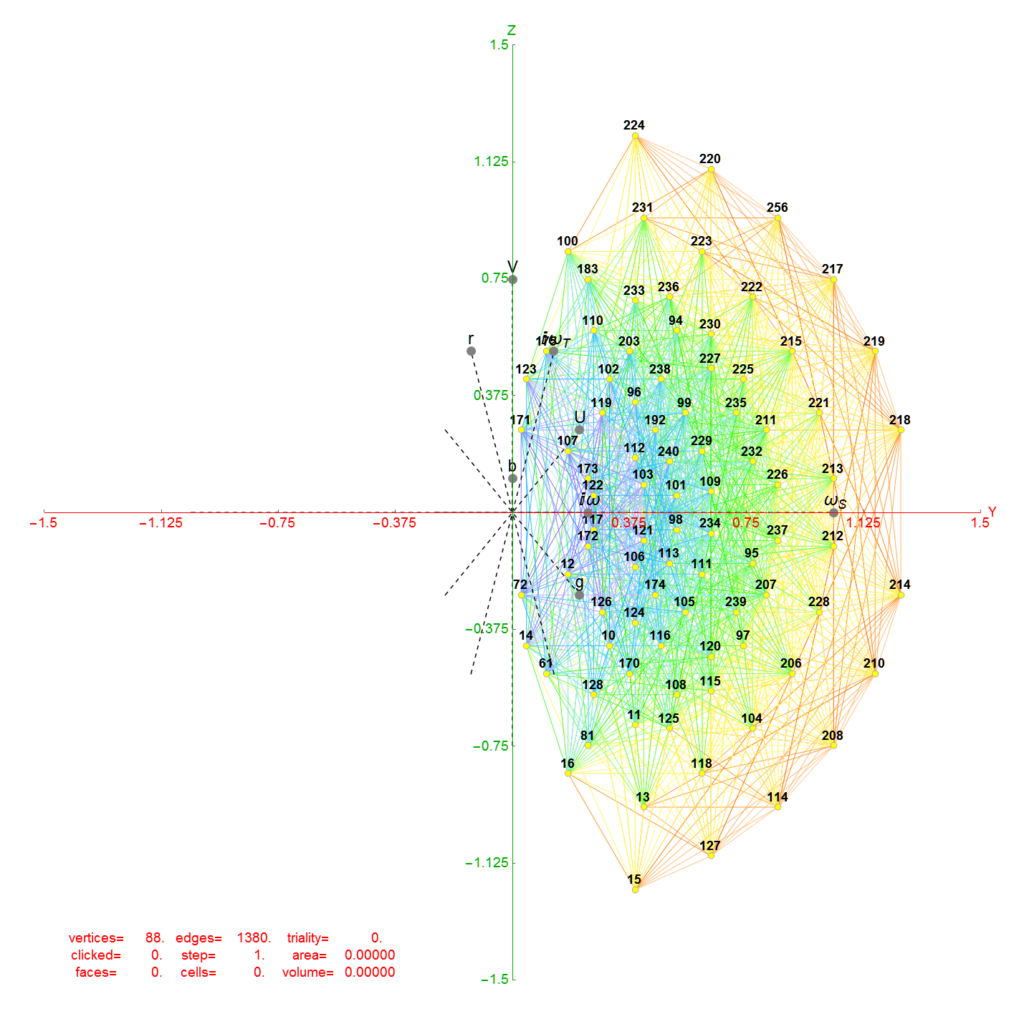
The combined set of hulls projected using the rows of the folding matrix as basis vectors is shown below from previous work:
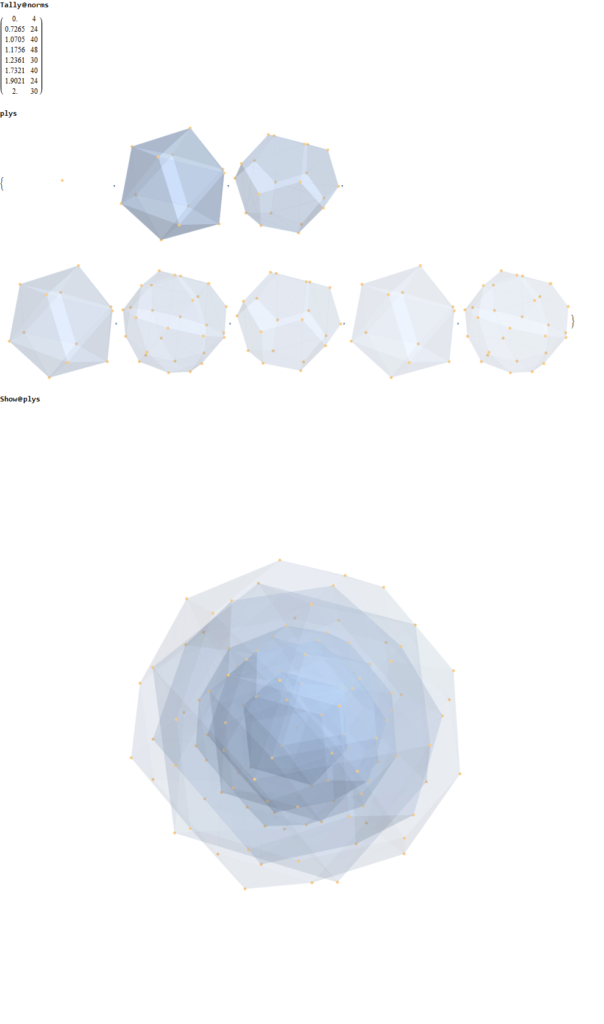
This paper hull-list-3b.pdf (4MB) & interactive Mathematica Notebook hull-list-3b.nb (20MB) contains the visualizations and detail E8 vertices associated with each Platonic solid related concentric hulls. This paper 24cell-list-3b.pdf (6MB) & interactive Mathematica Notebook 24cell-list-3b.nb (20MB) contains the visualizations and detail for the five 24-cells in each H4 & H4Φ. Both of these papers also have detail information about its assigned physics particle based on a modified A.G. Lisi model (shown below). This paper describes these particle assignment symmetries in more detail.