Based on an excellent 1998 paper by C.S. Rao I’ve modeled the Sri Yantra in Mathematica and incorporated it into the VisibLie_E8 demonstrations (I will upload that soon).
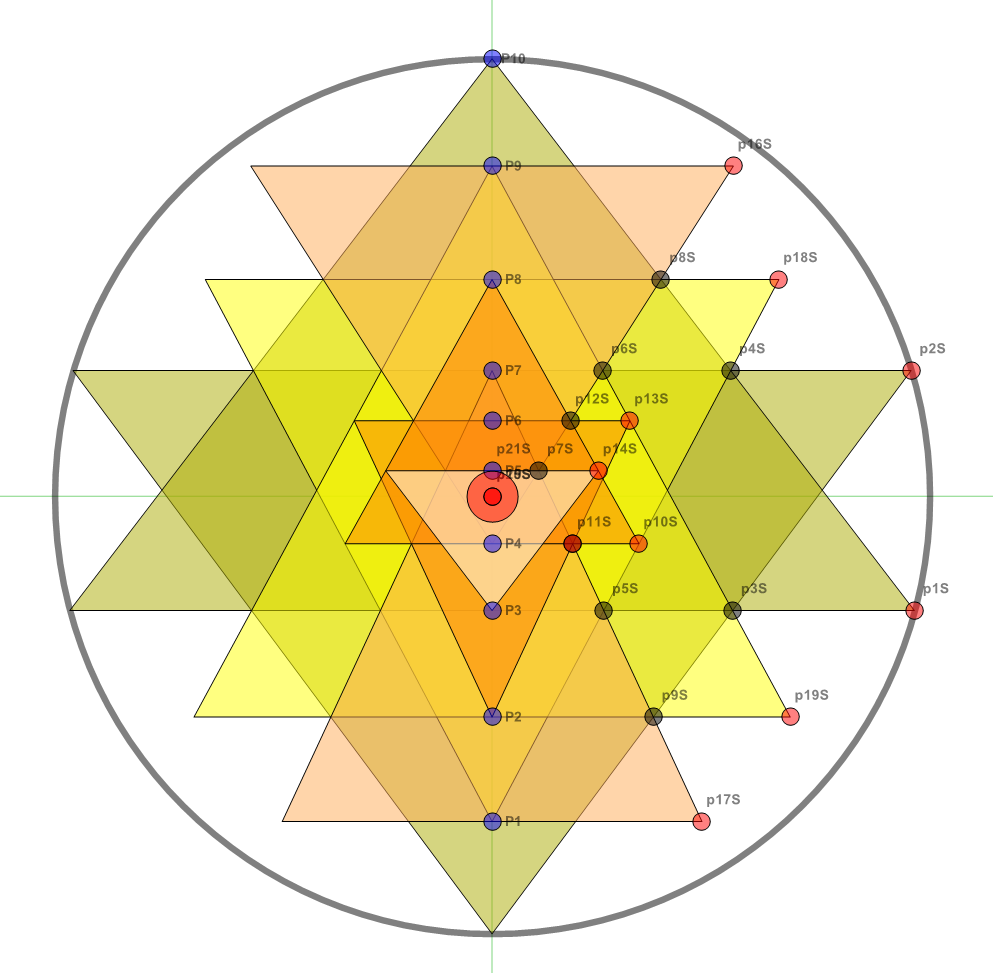
This is a reference figure to verify the model is correct for concurrency (intersecting lines) and concentricity (inner triangles and Bindu point are centered). There are 4 of 18 other constraints used in the diagrams below numerically and/or symbolically solved within the Mathematica code.
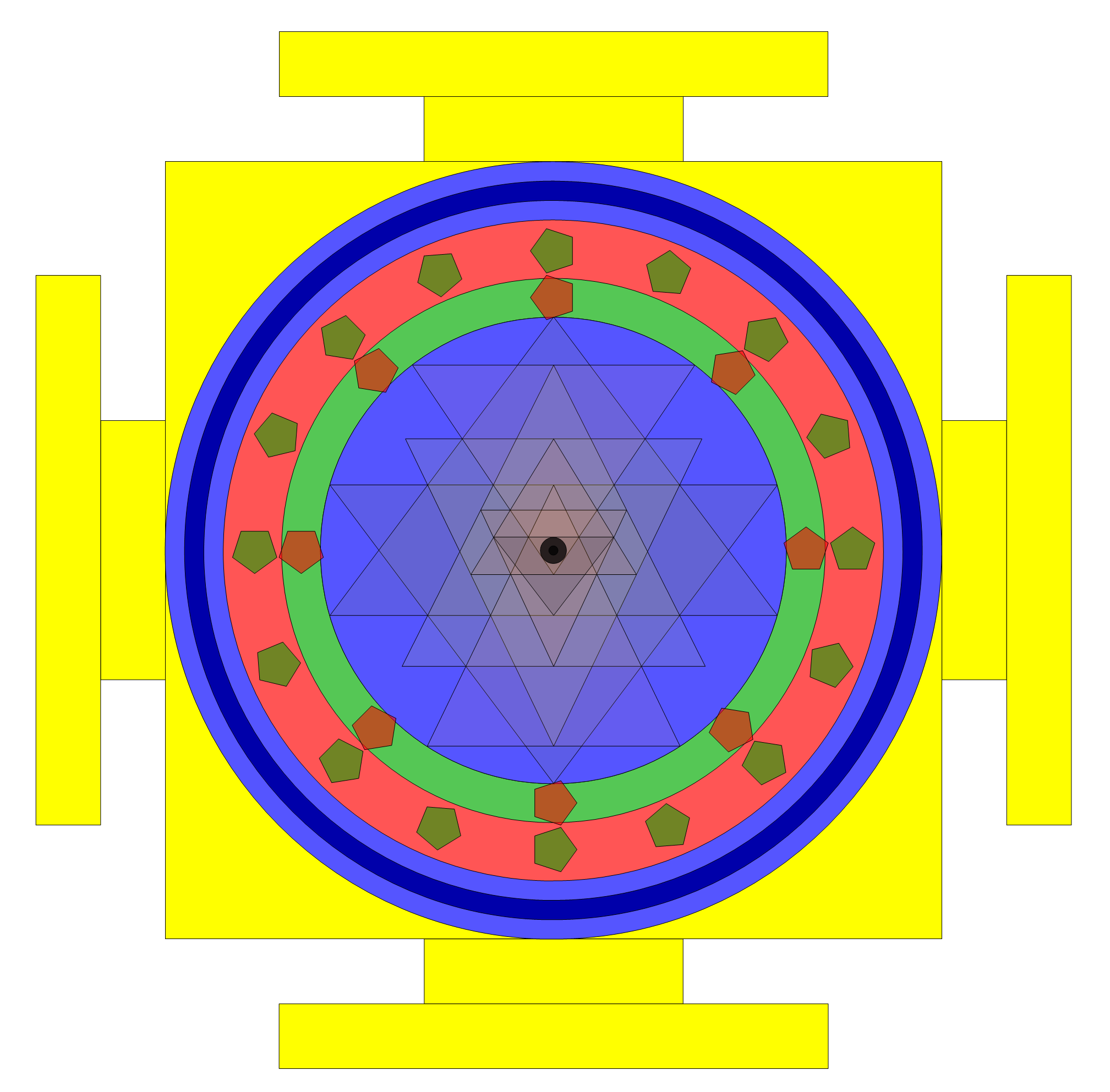
Here are 7 of many possible solutions using the 20 constraint rules to produce optimal spherical and plane forms of the Sri Yantra.
Solution 1: Solving constraints (* 1,2,3,4,8 *)
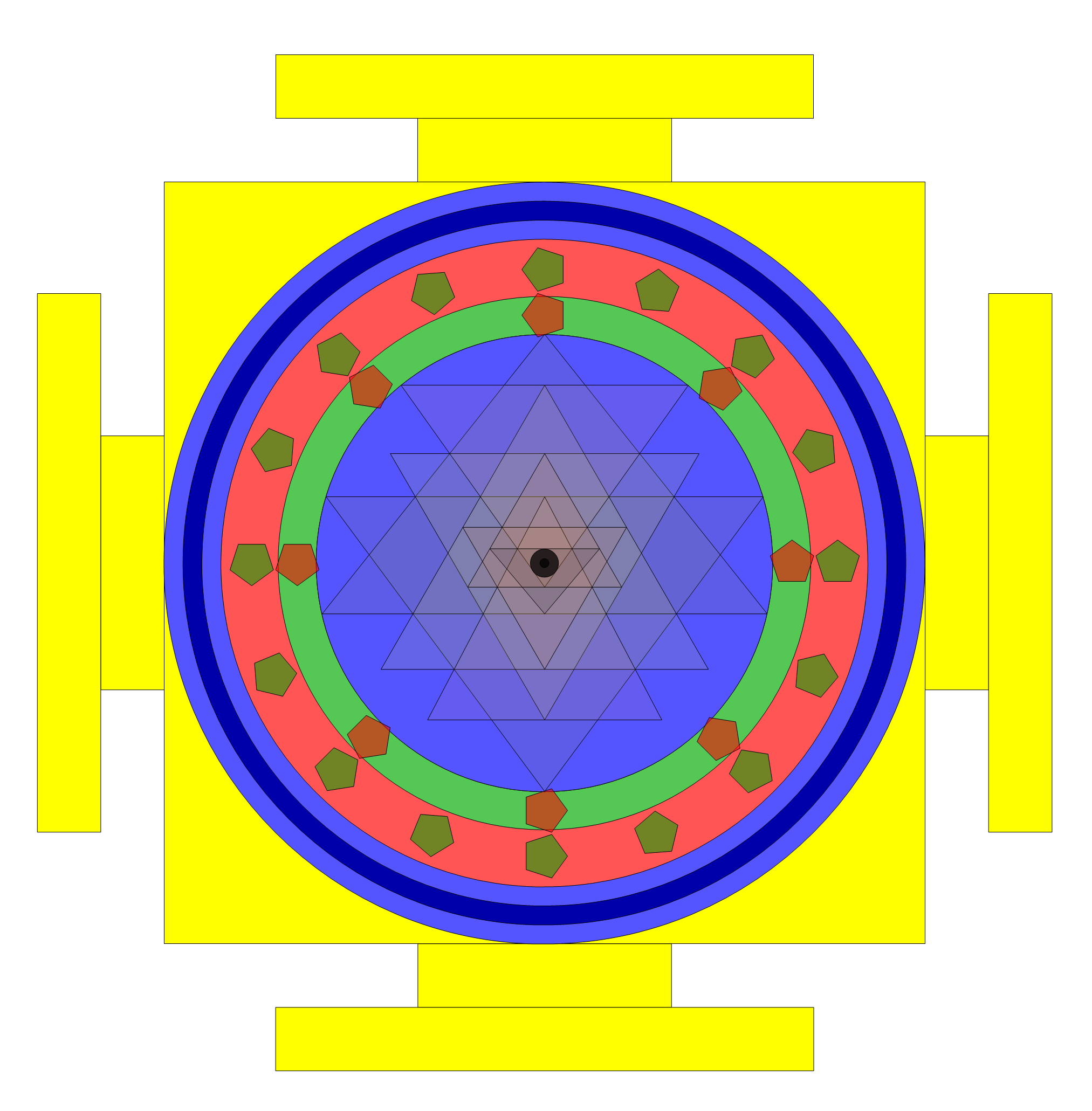
Solution 2: Solving constraints (* 1,2,3,10,15 *)
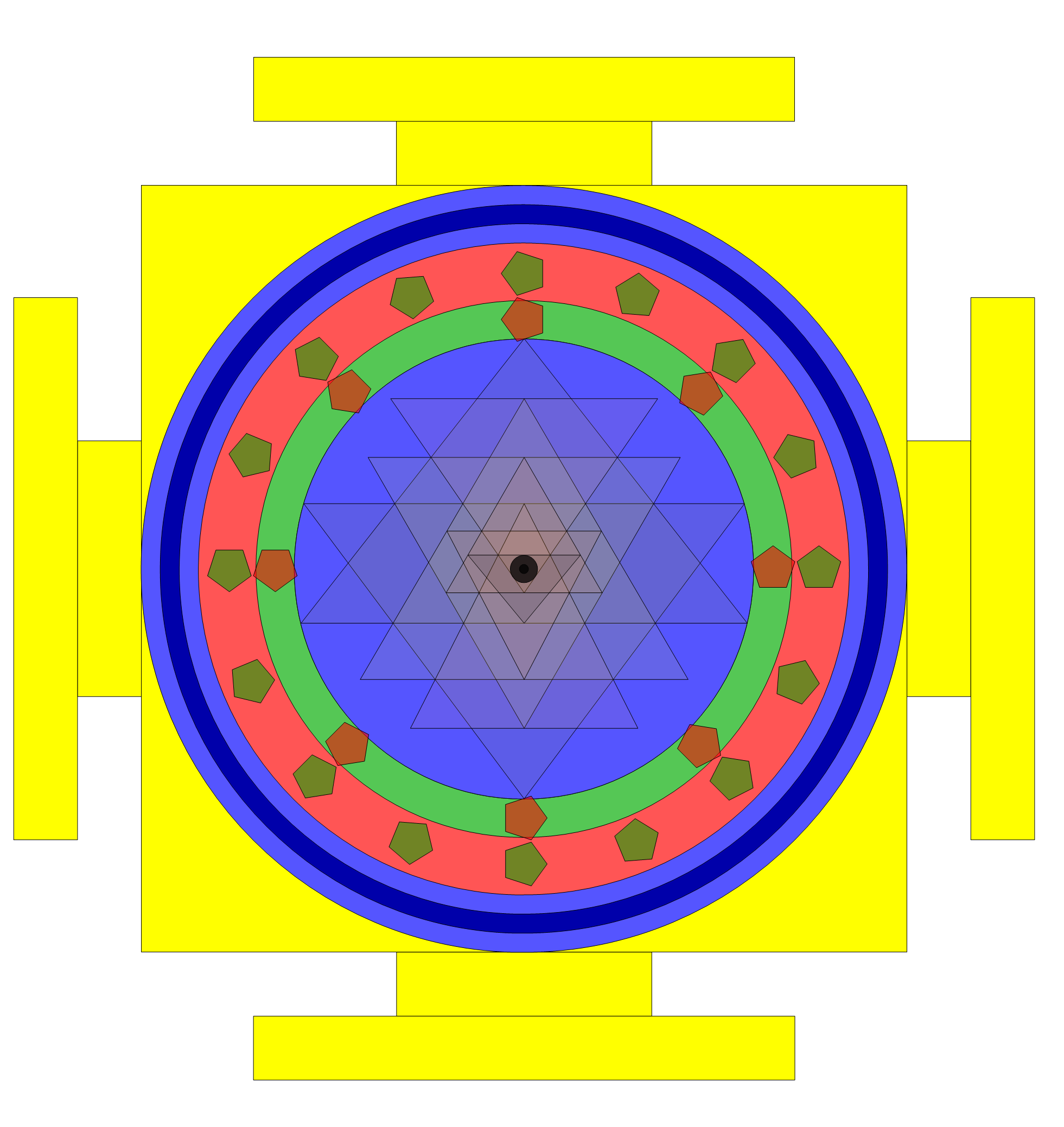
Solution 3: Solving constraints(* 1,2,4,5,10 *)
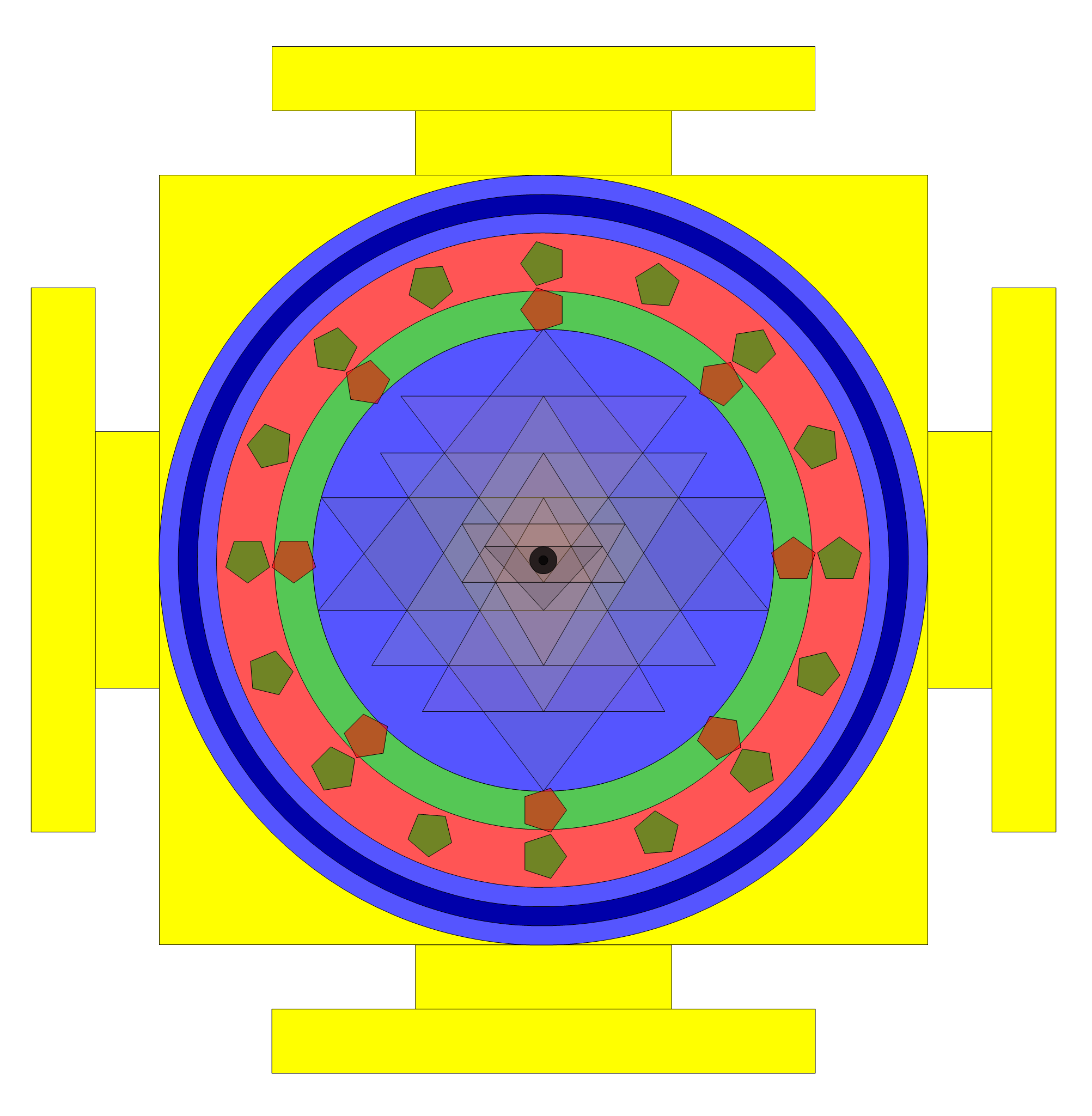
Solution 4: Solving constraints (* 1,2,5,6,19 *)
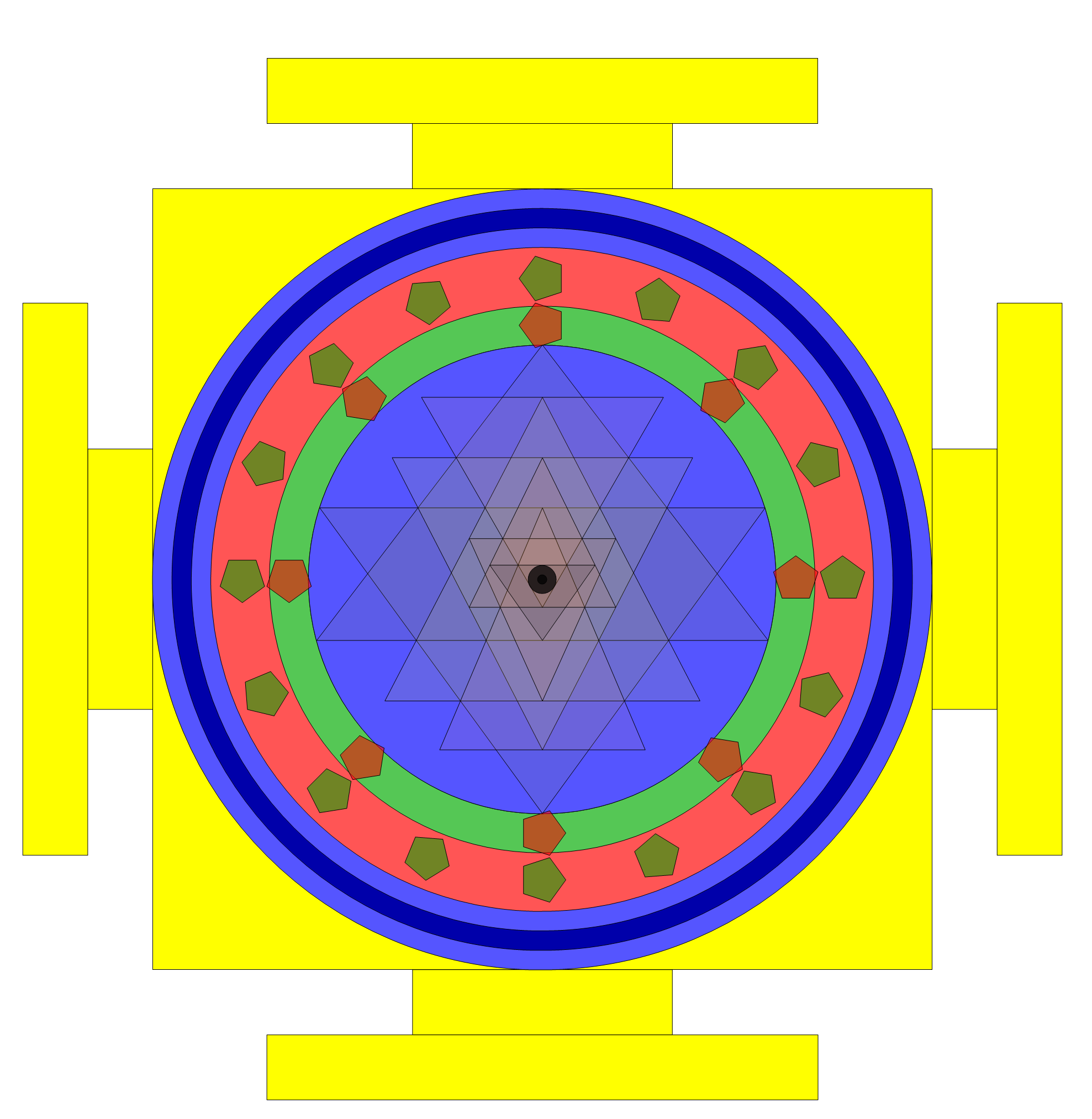
Solution 5: Solving constraints (* 1,2,6,14,19 *)
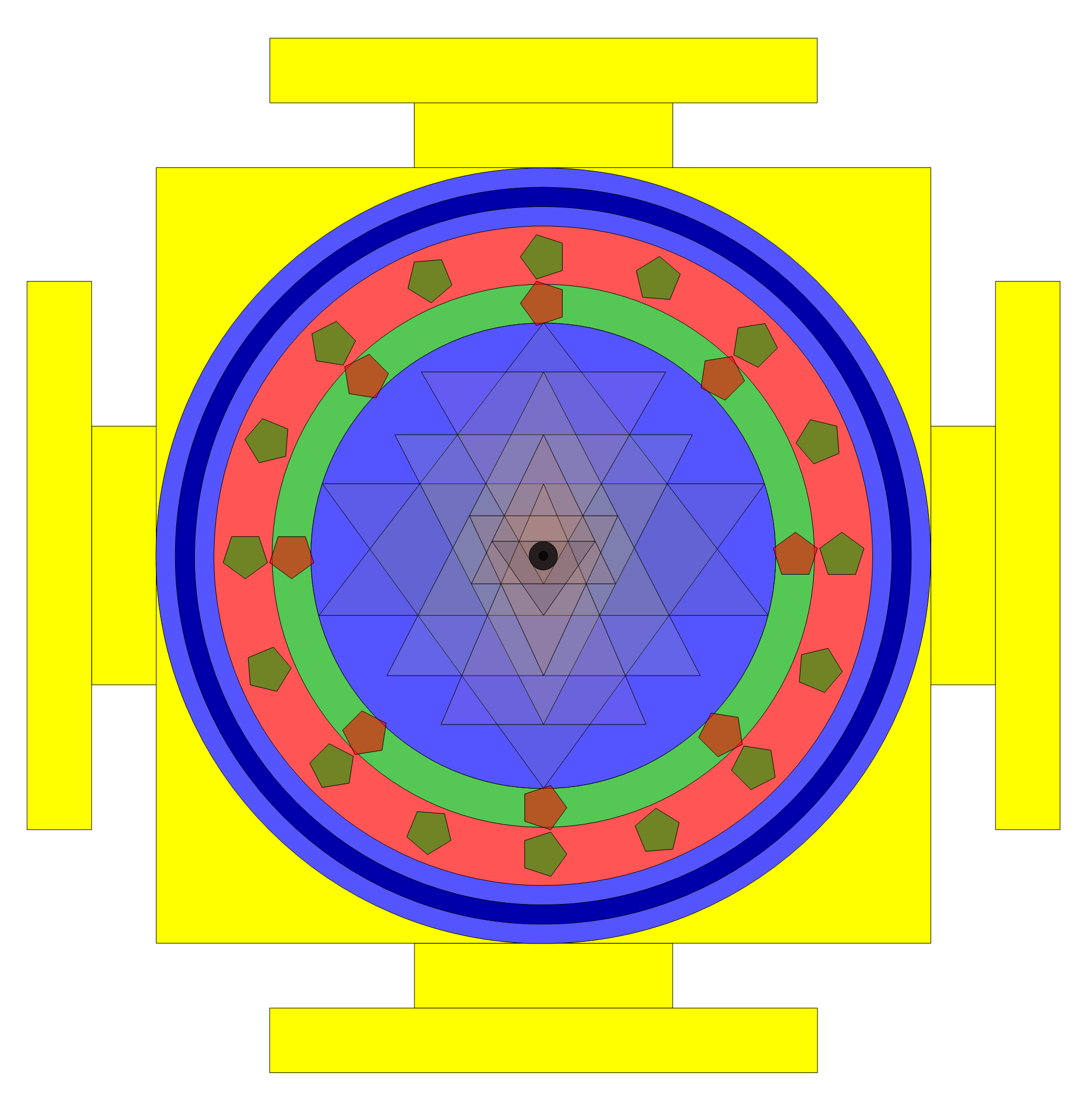
Solution 6: Solving constraints (* 1,2,8,9,20 *)
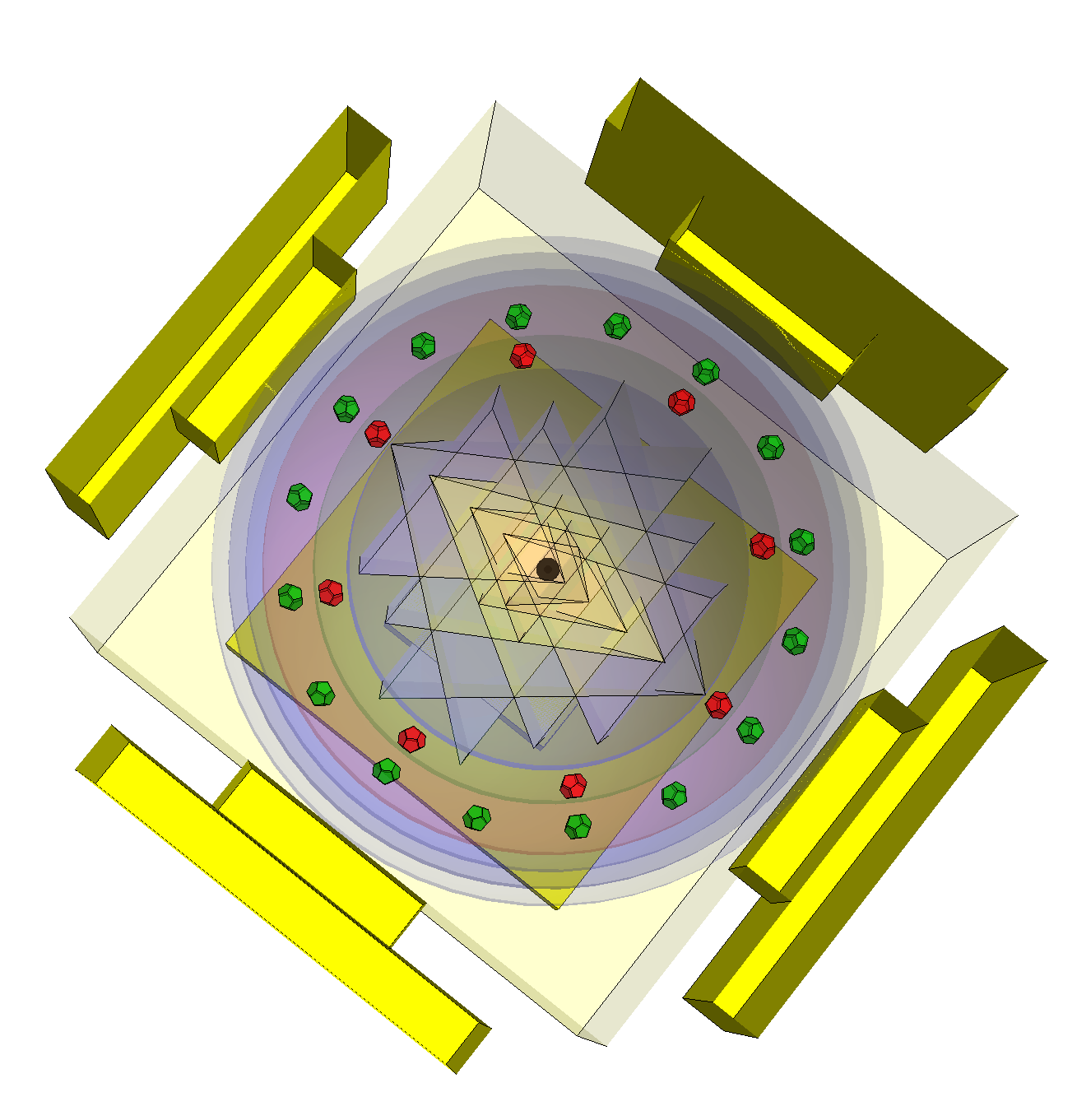
3D using pyramids and new clipping and slicing functions to take off the front (and back) portions of the symmetric 3D object.
I will produce a version option with conical shapes just for fun (soon).
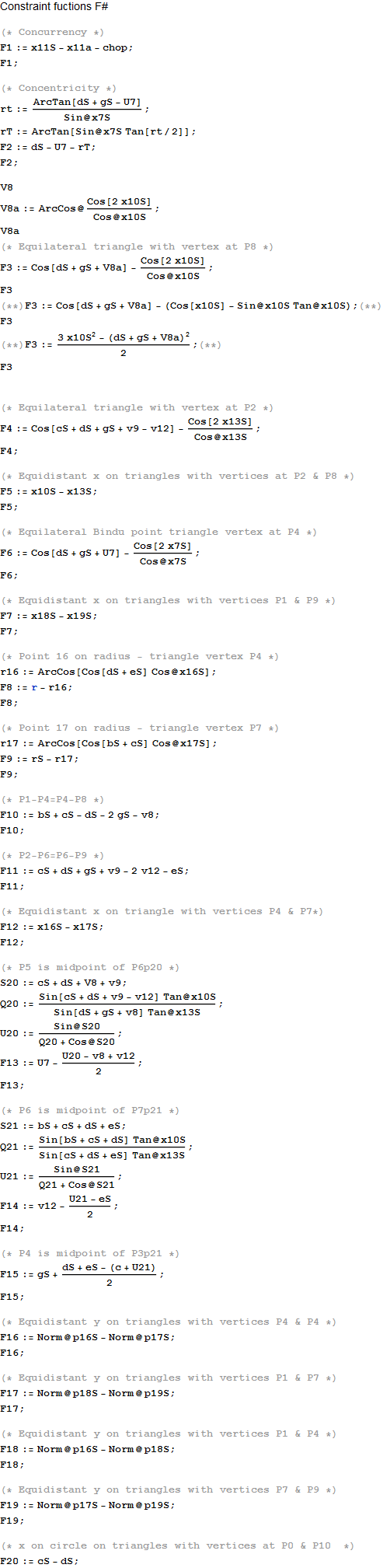
This is a list of the details behind each constraint function Fn

hi…great work ive stumbled upon here after 2 years of check on the net…of the 7, the one with constraints 1,2,4,5,10 seem to be closest to perfection…Since the horizontal axis crosses the intersection points of outer three inverted traingles…however it doesnt cut the central dot and is slightly up..can you redo the math to have the horizontal axis piercing the intersetions of the outer three triangles and the center? warm rgds
Thanks. I am working on an unrelated paper, so this type of change may be some time away. It may not be possible to make that change without breaking the constraints involved. These are precise mathematical solutions to the geometry – make any change and it breaks something.
many thanks…can you possibly help me by listing out the constraints so that i can map them?
The best place to get the constraints is to read the paper my model is based off of (the link near the top of the post).
http://sriyantraresearch.com/References/Rao.pdf
It’s a fairly intensive paper.