This page presents the comprehensive 15 permutations of the six 4D polychora (i.e. 5, 16/8, 24, 600/120 cells) in full SVG format for convenient use in high quality academic papers on the topic (e.g. simply save the SVG and edit in Inkscape or other tool to produce PDF or PNG, etc.). You are free to use these under Creative Commons Attribution-ShareAlike 4.0 International CC BY-SA 4.0 with appropriate attribution. Drop me an email if you find anything that needs correction.

My cell-first and vertex-first {5,3,3} 120-cell section visualizations with subgroup sections (when the inscribed solid has more than one permutation in its orbit) are available in Wikipedia Commons here and here. Let me know if you need customized hyper-complex and/or hyper-dimensional group-theoretic projection/section visualizations, as my extensive Mathematica code-base may be able to generate it.

The content below uses a 6×15 matrix of 4D to 3D projections of the convex hulls, each with a link to a page with that objects Coxeter section decomposition. I want to give a shout-out (cite) qfbox.info  and polytope.miraheze.org for providing vertex coordinates used in the creation of the objects. The Vertex-Edge-Face-Cell first sections are in another one of my posts here.

There is also another 6×15 table with links to video animations of the sections in the 4D to 3D flatlander from Left/Right (or minus to plus). This is an analog of 3D objects passing through the 2D planar world of flatlanders.

Also available is a Mathematica notebook (360Mb) with code to produce the 4D vertex data as well as the visualized interactive 3D objects. See also an overview of these lists explained in a this Powerpoint presentation, which covers the isomorphisms between them due to the symmetries in the A4, BC4, and H4 Coxeter-Dynkin diagrams that represent them.

Below are some screenshots from a PPT I created to explain the organization. Some of this content is now on Wikipedia from my updates to those pages. The PPT is available here (in PDF here) or you can click on the PNG images (below) to get the SVG versions:

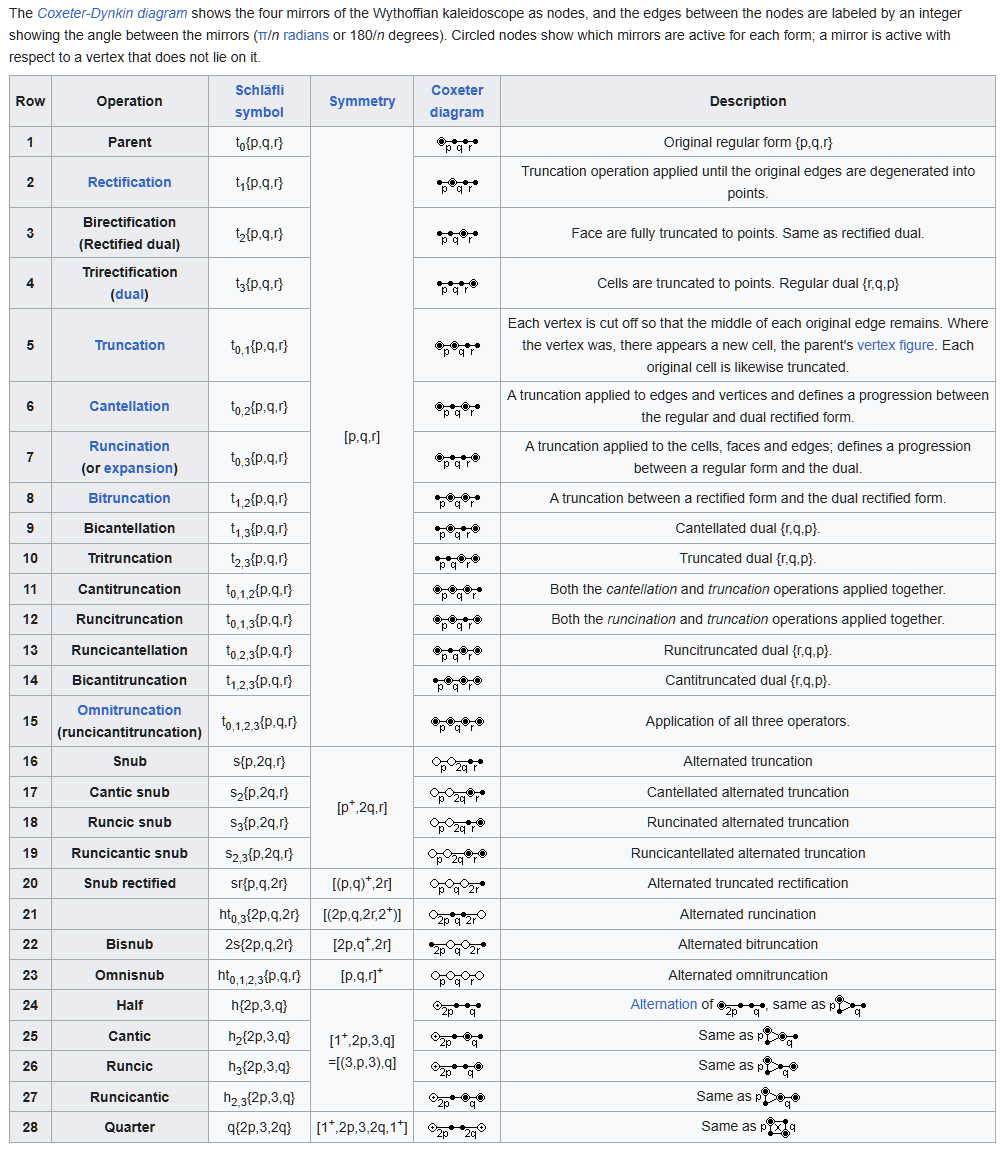
The chart below is here on Wikipedia (WP):

I took screenshots of a few qfbox.info pages to annotate the differences in layout below. Please note the palindromic binary Weyl group orbits and operation equivalences between them:

The Coxeter-Dynkin diagram relationships between the BC4, D4, and F4 are as follows (my apologies to those who might be irritated by my use of filled nodes instead of the “ringed” nodes):

The Coxeter-Dynkin diagram relationship between the D4 (dual 24-cell parent) + D4 Snub 24-cell = H4 are:

But let’s not forget the larger symmetry of these 4-polytopes, as they are related to the largest exceptional algebra and group of E8. Indeed, E8 is isomorphic to H4+H4φ through a simple rotation (folding) matrix.

Links to the SVG Section Files:

Links to Sectioning MP4 Video Animations (i.e. 4D to 3D Flatlander):

For completeness, I am also including a table of 3D polyhedra, namely the Platonic, Archimedean, and Catalan Solids including
their irregular and chiral forms. These were created using
quaternion Weyl orbits directly from the A3, B3, and H3 group
symmetries

.

Another post with more detail on the 5-cell (A4) SU(5)->SU(4) maximal subgroup content generated via quaternions is here.