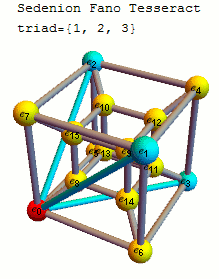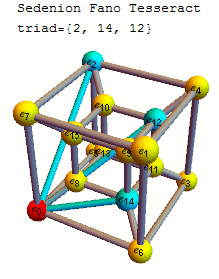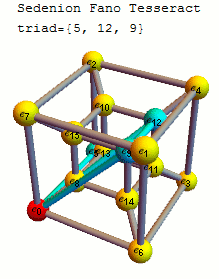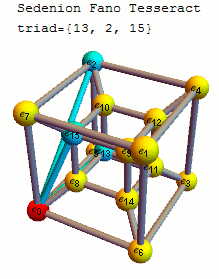In order to better visualize the sedenion Fano Tesseract, I’ve created an animation that steps through highlighting the vertices and edges of the triads that make up its multiplication table.
I start by showing the simpler octonion version – an 8 dimensional (8D) “Fano Cube” projection. The example octonion is the one (of 480) shown on the octonion Wikipedia article.
[wlcode]{{1, 2, 3}, {1, 4, 5}, {1, 7, 6}, {2, 4, 6}, {2, 5, 7}, {3, 4, 7}, {3, 6, 5}}[/wlcode]
The Fano Cube (as introduced by John Baez here) is created from the ubiquiteous “Fano Plane” by keeping the Real component (e_0) of octonions and requiring that each line of the plane be shown as a hyper-plane through e_0. Each animation step is one of 7 triads representing the triality of 3 vertices in that particular octonion multiplication table:
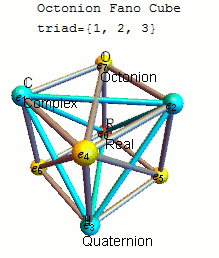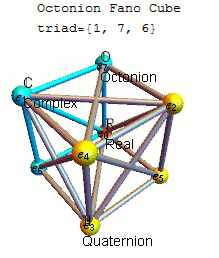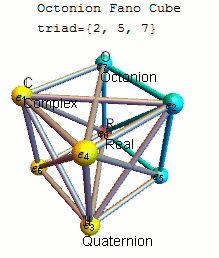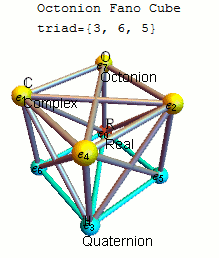
The 16D sedenion (one of many possible) used in this post uses the Cayley-Dickson doubling procedure on the “parent octonion” (above). The Fano Tesseract is created in the same manner as the octonion visualization, which uses the 16 vertex tesseract to show the sedenon’s 35 triads (with the triads from the “parent octonion” highlighted in red):