Tag Archives: Math
Interactive Reimann Zeta Function Zeros Demonstration
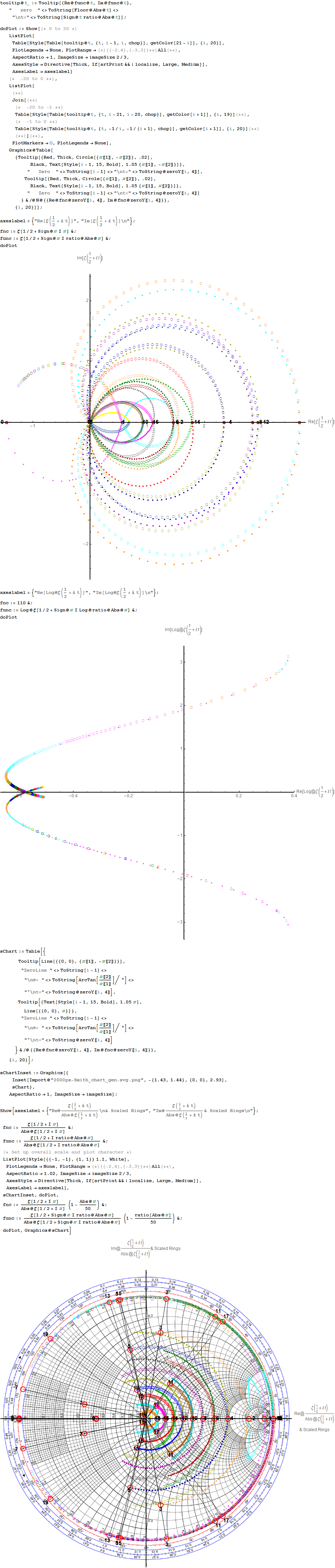
This web enabled demonstration shows a polar plot of the first 20 non-trivial Riemann zeta function zeros (including Gram points) along the critical line Zeta(1/2+it) for real values of t running from 0 to 50. The consecutively labeled zeros have 50 red plot points between each, with zeros identified by concentric magenta rings scaled to show the relative distance between their values of t. Gram’s law states that the curve usually crosses the real axis once between zeros.
A downloadable copy is available ZetaZeros-local-art-50.cdf Latest: 05/23/2016.
Note: The interactive CDF plug-in as required below does not currently work on Chrome browsers.
A Snapshot picture for those w/o Wolfram CDF interactivity:
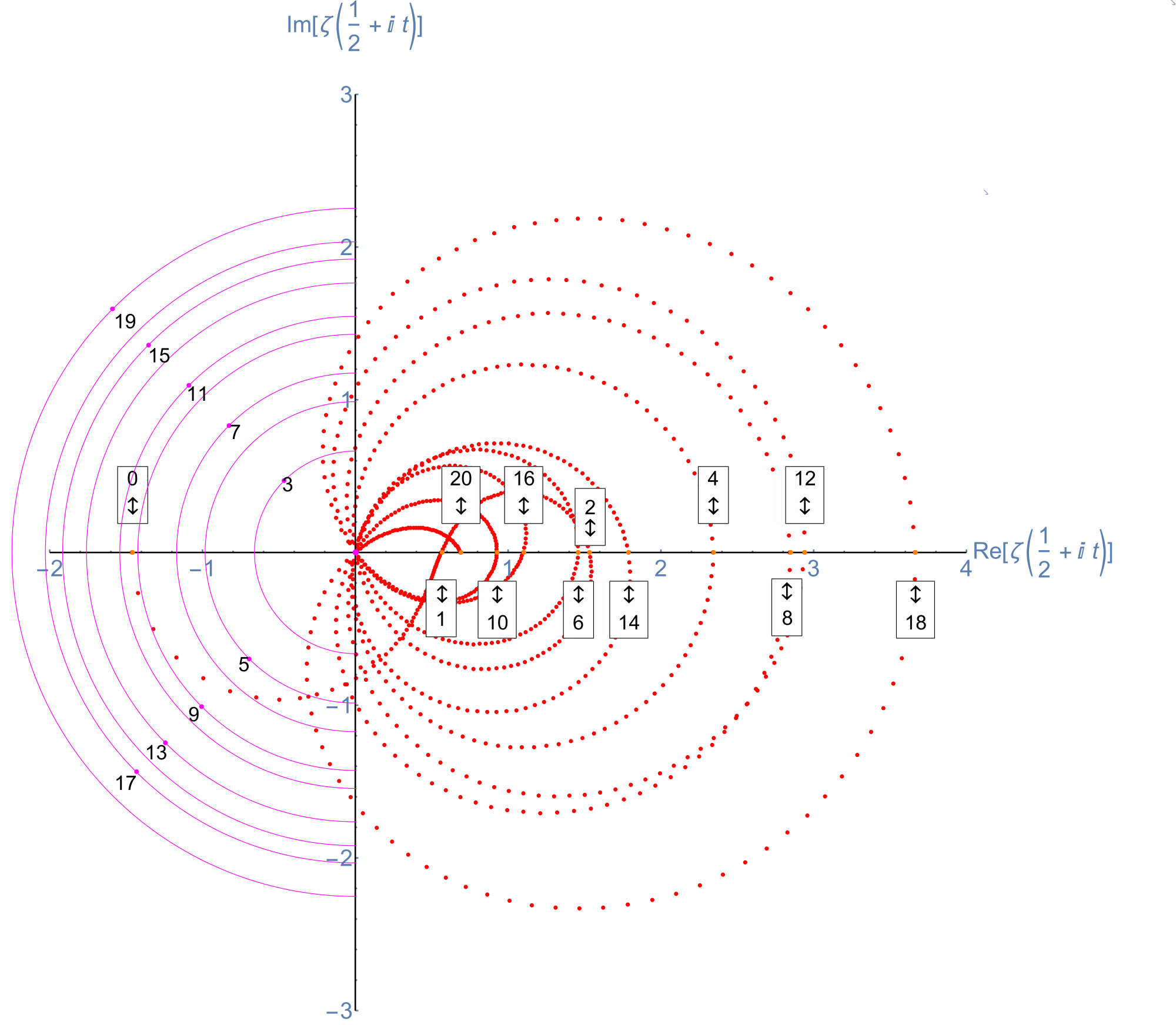
Selectable example code snippet:
[wlcode]Show[ListPlot[Style[pts2, Red], PlotRange -> {{-2, 4}, {-3, 3}},
AspectRatio -> 1, ImageSize -> imageSize,
AxesStyle ->
Directive[Thick, If[artPrint && ! localize, Large, Medium]],
Graphics[{PointSize@.01,
tttxt := If[artPrint && ! localize, tttxt1, ttxt0];
If[ttxt0 = ToString[# – 1];
Abs@zeroY[[#, 1]] < 10 chop,
(* Magenta Critical Line Zeta Zeros *)
tttxt1 =
Column[{ToString[# - 1], "t=" <> ToString@zeroY[[#, 4]]},
Center];
ttLoc =
zeroY[[#, 4]] If[artPrint && ! localize, 1, 2] imagesize/40000;
(* Flip Point Labels above/below the X axis *)
ttLoc1 = {-1, (-1)^Round[#/2]} ttLoc/Sqrt[2];
{Magenta, Point@ttLoc1,
Circle[zeroY[[#, ;; 2]], ttLoc, {1, 3} \[Pi]/2],
Black,
Tooltip[Text[
Style[tttxt, If[artPrint && ! localize, Large, Medium, Bold]],
(* Shift the Labels off the Point *)
ttLoc1 (1 – (-1)^Round[#/2] .05)], tttxt1]},
(* Orange Critical Line Imaginary zeros w/Real>0 *)
tttxt1 =
Column[{ToString[# – 1], “x=” <> ToString@zeroY[[#, 1]],
“t=” <> ToString@zeroY[[#, 4]]}, Center];
{Tooltip[{Orange, Point@zeroY[[#, ;; 2]], Text[Style[
Column[If[EvenQ[Round[(# – 1)/2]], Prepend,
Append][{“\[UpDownArrow]”}, tttxt], Center,
Frame -> True],
Black, If[artPrint && ! localize, Large, Medium],
Background -> White],
(* Flip Point Labels above/below the X axis *)
zeroY[[#, ;; 2]] + {0, (-1)^Round[(# – 1)/2]} If[
artPrint && ! localize, 1,
If[artPrint, 4/1, 3]] imagesize/5000]},
Column[{ToString[# – 1], “x=” <> ToString@zeroY[[#, 1]],
“t=” <> ToString@zeroY[[#, 4]]}, Center]]}] & /@
Range@Length@zeroY,
Magenta, Disk[{0, 0}, .03]}]][/wlcode]
More plots with various scaling functions and multi-color coding along with Tooltip on mouse-over. Bear in mind the last Smith Chart with a division by Abs@Zeta indicates where the increments go exponential near the 0.
The Imaginary, Irrational and Transcendental in Linear Algebra and Trigonometry
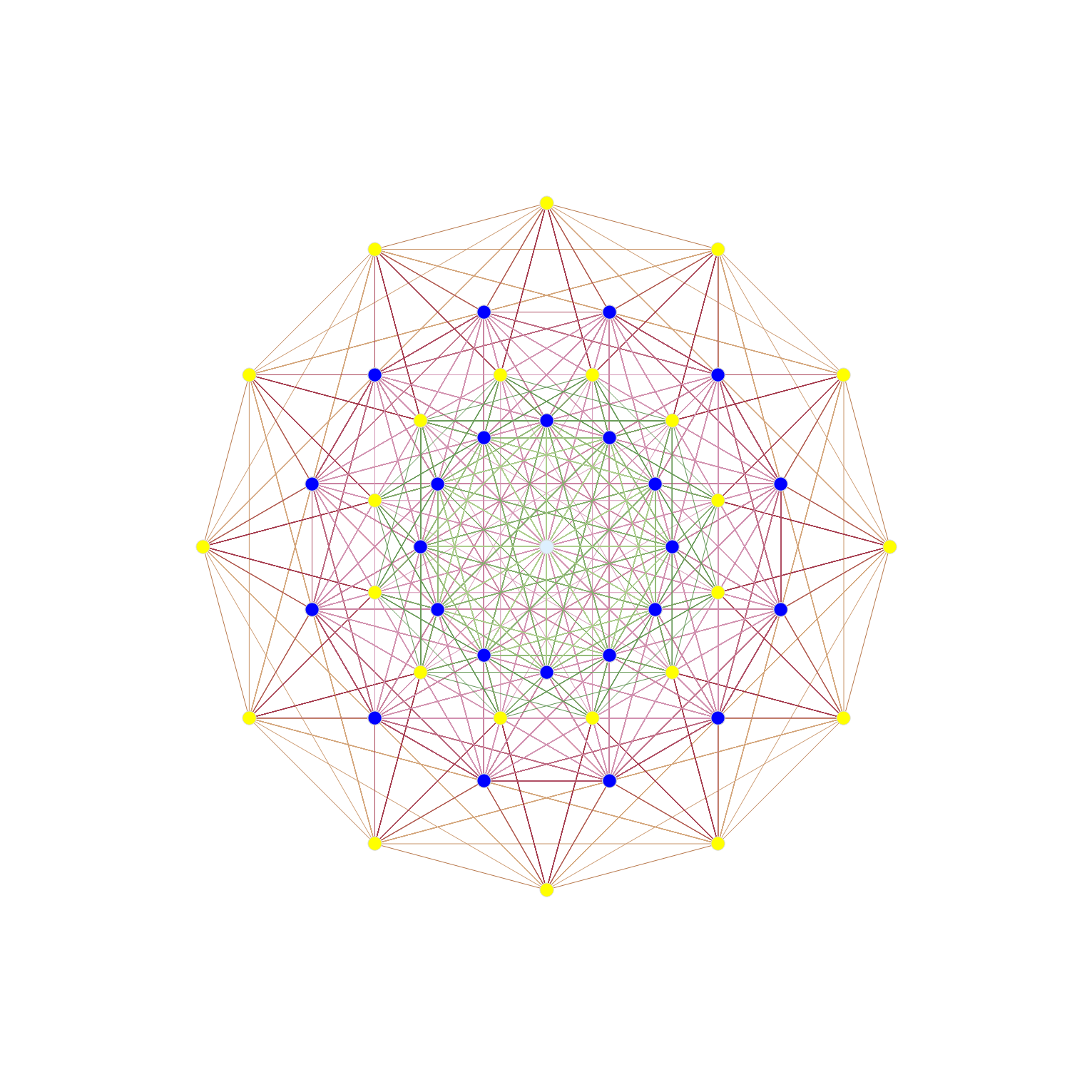
E8 in E6 Petrie Projection
An article (interview) with John Baez used an E8 projection which I introduced to Wikipedia in Feb of 2010 here. Technically, it is E8 projected to the E6 Coxeter plane.
The projection uses X Y basis vectors of:
X = {-Sqrt[3] + 1, 0, 1, 1, 0, 0, 0, 0};
Y = {0, Sqrt[3] – 1, -1, 1, 0, 0, 0, 0};
Resulting in vertex overlaps of:
24 Yellow with 1 overlap
24 Dark Blue each with 8 overlaps (192 vertices)
1 Light Blue with 24 overlaps (24 vertices)
After doing this for a few example symmetries, Tom took my idea of projecting higher dimensional objects to the 2D (and 3D) symmetries of lower dimensional subgroups – and ran with it in 2D – producing a ton of visualizations across WP. 🙂
It was one of those that was subsequently used that article from the 4_21 E8 WP page.
Here is a representation of E6 in the E6 Coxeter plane:
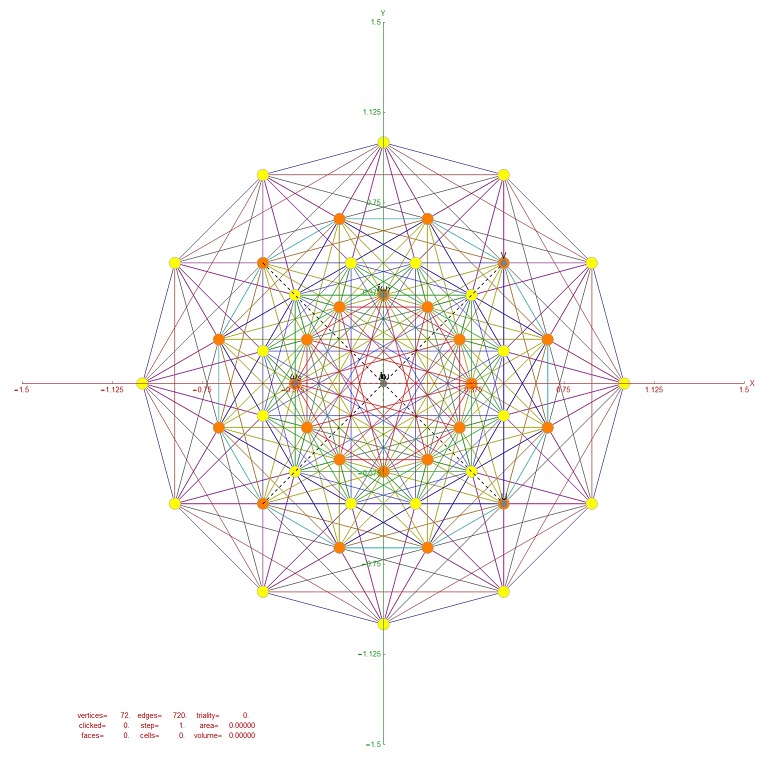
Resulting in vertex overlaps of:
24 Yellow with 1 overlap
24 Orange each with 2 overlaps (48 vertices)
G2 as the automorphism group of the (split) octonion algebra
For more information on this, please see this Wolfram MathSource page.
This post describes the derivation of G2 automorphisms for each of the 480 unique octonion multiplication tables, as well as each of the 7 split octonions (created from negating the 4 row/column entries which are not members of the split #, which is an index to one of the 7 triads that make up the octonion).
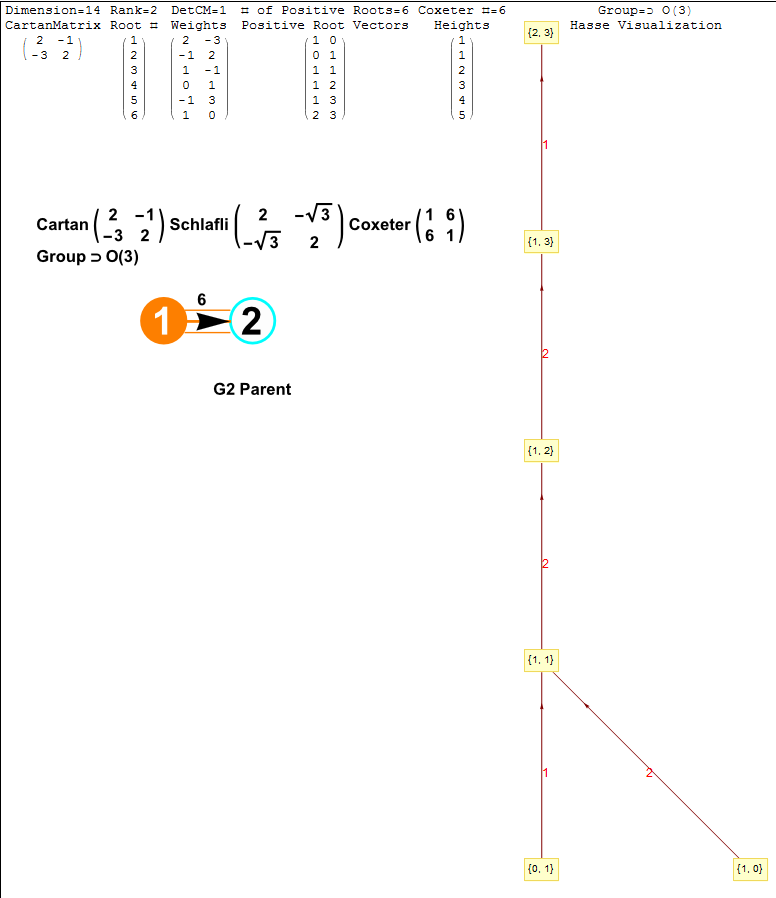
The Exceptional Lie Algebra/Group G2 is identified by its Dynkin diagram and/or associated Cartan Matrix (also shown here with its Hasse diagram):
The particular octonion multiplication table selected in the example referenced above is associated in my model as a “Non Flipped E8 #164”. The multiplication table in various formats (IJKL, e_n, and Numeric) is:
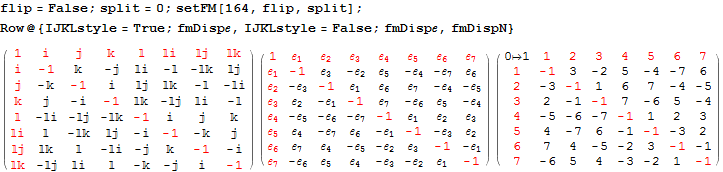
The selected multiplication table (fm) is the basis for the following octonion symbolic math:
[wlcode](* Octonion math from the matrix using 8D vector representations for x and y, this has the Subscript[\[ScriptE], 0]=1 first *)
octProduct[a_, b_] := Block[{c3 = Array[0 &, 8]},
Do[c3[[If[i != j, Abs@fm[[i, j]] + 1, 1]]]+=Sign@fm[[i, j]] a[[i]] b[[j]],
{i, 8}, {j, 8}];
Chop@c3];
(* Complex, quaternion and octonian multiplication Subscript[\[ScriptE], a]\[SmallCircle]Subscript[\[ScriptE], b] *)
quat2oct@in_ := Block[{a3},
If[QuaternionQ@in,
a3 = FromQuaternion@in;
Switch[Length@a3,
0, Re@a3 + Im@a3 Subscript[\[ScriptE], 1],
2, If[Length@a[[1]] > 0, a3,
If[Head@a3 === Times, a3[[1]] a3[[2]],
1\[SmallCircle](Re@a3[[1]] +
Im@a3[[1]] Subscript[\[ScriptE], 1]) + a3[[2]]]],
3, Re@a3[[1]] + Im@a3[[1]] Subscript[\[ScriptE], 1] +
a3[[2 ;;]]],
“not Quaternion”] /. Most@Thread[octIJKL -> oct]];
(* Octonion math with conversions, leave final as octonion *)
SmallCircle[a_List, b_List] := octonion@octProduct[a, b];
SmallCircle[a_, b_Quaternion] := a\[SmallCircle]quat2oct@b;
SmallCircle[a_Quaternion, b_] := quat2oct@a\[SmallCircle]b;
SmallCircle[a_, b_Complex] := a\[SmallCircle]ToQuaternion@b;
SmallCircle[a_Complex, b_] := ToQuaternion@a\[SmallCircle]b;
SmallCircle[a_, b_] := oct2List@a\[SmallCircle]oct2List@b;
associator[a_List, b_List,c_List] := (a\[SmallCircle]b)\[SmallCircle]c-a\[SmallCircle](b\[SmallCircle]c);
associator[a_, b_, c_] :=associator[oct2List@a, oct2List@b, oct2List@c];[/wlcode]
Each set of 21 upper triangle pairs of octonion elements (utOct) has 14 “derivations” which are null
(alternatively, the NullSpace of the derivation vectors of utOct has 7 which are NOT null…)
A derivation pair D_{x, y} is defined by:
[wlcode](* Commutator *)
commutator[x_,y_]:=x\[SmallCircle]y-y\[SmallCircle]x;
CircleDot[x_,y_]:=commutator[x, y];
(* Commutator matrix *)
comMat[x_, y_] := x.y – y.x;
comMat[{x_, y_}] := comMat[x, y];
(* Derivation matrix and vector *)
derivation[x_,y_][a_]:=(x\[CircleDot]y)\[CircleDot]a-3 associator[x,y,a];
Square[{x_, y_, a_}] := derivation[x, y][a];
derMatrix[x_,y_]:=Table[Coefficient[\[Square]{x,y,oct[[i]]},oct[[j]]], {j, 7}, {i,7}];
derVector[x_,y_]:=derMatrix[x, y]//Flatten;[/wlcode]
The 14 null pairs define G2 for a SPECIFIC octonion multiplication matrix.
For each of 7 non-null derivations there is a triple of D_{x1, y1}=D_{x2, y2}+D_{x3, y3} related derivations.
There is a 7×21 matrix describing the non-NullSpace for the octonion given in the Wolfram MathSource reference above along with the 7 non-null triples. This is generated by g2Null:
[wlcode]g2Null:=NullSpace[derVector[Subscript[\[ScriptE], #1], Subscript[\[ScriptE],#2]]&@@@utOct//Transpose];
(* Formatting all non-Null upper triangle pairs derivation entries *)
outG2Null := MatrixForm[parallelMap[Grid[{
{Row[
Subscript[D, Row@Flatten@##] & /@
Partition[Flatten@{utOct[[Flatten@Position[#, -1]]]}, 2]]},{“==”},
{Row[
Subscript[D, Row@Flatten@##] & /@
Partition[Flatten@{utOct[[Flatten@Position[#, 1]]]}, 2]]}(*),
{“\[LongDash]\[LongDash]\[LongDash]\[LongDash]”}**)}] &,
g2Null]];[/wlcode]

getG2Null (below) retrieves two octonion multiplication matrices for the flipped and non-flipped index on one of 240 E8 particles.
[wlcode]formG2Null := MatrixForm@{
Row@{Style[Row@{“flip=”, flip}, Blue],
Style[” split # \[DownArrow],”, Red]},
g2NullTbl = Table[{
split,
setFM[#, flip, split];
outG2Null},
{split, 0, 7}];
Row@triads,
MatrixForm[Column[#, Center] & /@ noNull@# & /@ Table[
(* Color the common Der in each column *)
cmnD =first@Select[g2NullTbl[[All,2,1,i,1,3,1,1,All]],
Length@# == 1 &];
cmnDclr = Style[cmnD, Magenta];
If[j == 1, {“”, Row@{
(* Highlight the missing index in the triple D_{x,y} for each row *)
Style[Complement[Range@7,Union@Flatten@g2NullTbl[[All,2,1,i,1,3,1,1,All,2,1]]][[1]],Darker@Green],
g2NullTbl[[1, 2, 1, i]] /. cmnD -> cmnDclr}},
(* Display only non-null derivations from the splits if not the same as the base octonion *)
If[g2NullTbl[[1,2,1,i]] =!= g2NullTbl[[j,2,1,i]],
{Style[g2NullTbl[[j, 1]], Red],
g2NullTbl[[j,2,1,i]] /. cmnD -> cmnDclr}]],
{i,7},{j,8}]]} &;
getG2Null := ColumnForm[{
Style[Row@{“E8#=”, #}, Darker@Green],
Row@{flip = False; formG2Null@#, flip = True; formG2Null@#}},
Center] &;[/wlcode]
Here we show the output of getG2Null for the example non-Flipped E8 #164):
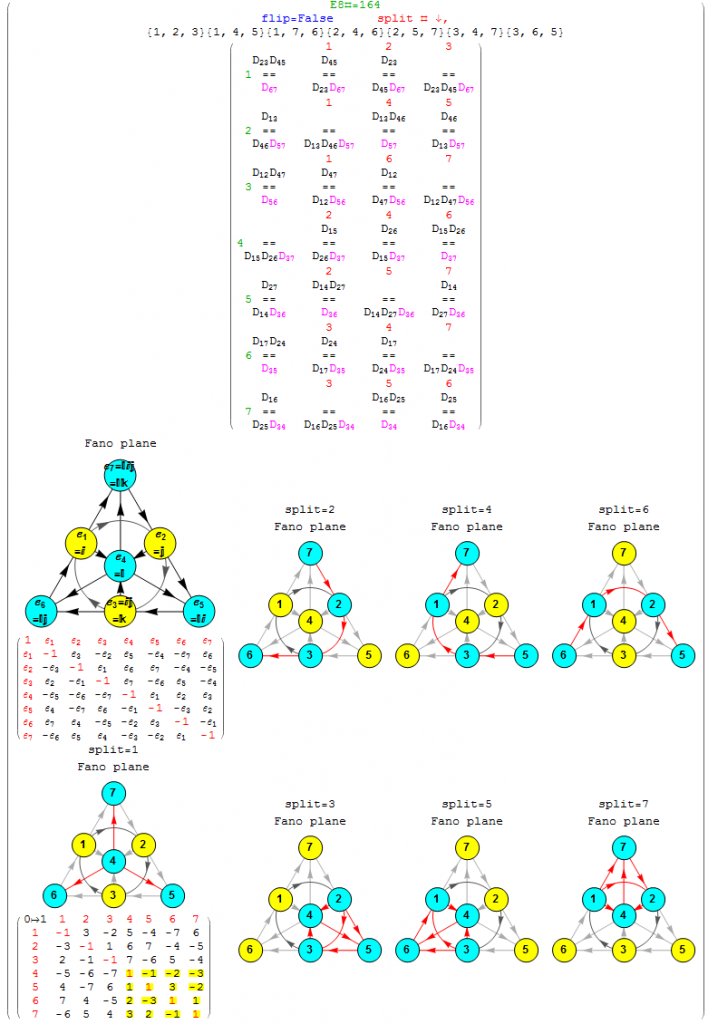
Emergent patterns:
- For each of the 7 non-null derivation triples (the first column of the 7 rows), there are precisely 3 (of the 7) split octonions that don’t share the exact same non-null triple derivation pair as the parent (non-split) octonion (these deviations are shown in column 2 thru 4, along with the associated Fano plane diagrams for the parent and 7 split octonions of E8 #164).
- Each non-null derivation triple contains 6 of 7 indices, and each row is missing a different index (highlighted in green before the column 1 triple). The sequence of missing element numbers in each row of the given example follows the row number.
- It is only the equality relationship (signs) of the non-Null triple that change in 3 of the 7 splits, not the D_{x,y} itself.
- There are always 2 pairs of 2 D_{x,y} which are negative (i.e. with a -1 entry in the NullSpace matrix located above the “==”) that occur across the row.
- There is always a common positive D_{x,y} (i.e. with a +1 entry in the NullSpace matrix located below the “==”) in each entry of the row (colored magenta). The common positive entries in the 7 rows suggest a “distinguished” non-null indicator for the 14=21-7 G2 automorphism.
- All octonion multiplication matrices have the first 3 rows of distinguished entries of {6,7},{5,7} and {5,6} in that order (i.e. the last 2 rows of utOct).
- There are several possible choices for G2 automorphism sets of 14 elements within each of 480 octonions based on the 7 non-Null entries. Interestingly, there are the 4 sets of rows in utOct which sum to 14 elements, specifically rows {{1, 2, 4}, {1, 2, 5, 6}, {1, 2, 4, 6}, {2, 3, 4, 5}}). The distinguished entries of the flipped E8 #164 example below (as in the MathSource post referenced above) suggests a G2 created by rows {1,2,4} of utOct. Although, not all G2 sets must use complete rows as in this example.
This is octonionG2-nonNull, a 480 page (15 MB) which lists each of the 7 non-Null parent octonion derivations (and for each of those, the 3 other split octonion non-null derivations) which are NOT a member of the 14 null derivations for each of 480 octonion multiplication matrices and 7 splits for each (480*8=3840). It includes the Fano plane mnemonics for the parent and 7 split octionions. This is a smaller 240 page (1MB) version of octonionG2-nonNull.pdf without the Fano plane mnemonics.
Octonion triality testing
I am working on validating some theoretical work on the triality automorphisms of the split octonions. This is a post with preliminary work on that… for those who are interested 🙂
BTW – It requires the here.
An addendum to the original post (below):

[WolframCDF source=”http://theoryofeverything.org/TOE/JGM/octonion triality checks.cdf” width=”900″ height=”8000″ altimage=”http://theoryofeverything.org/TOE/JGM/octonion triality checks.png” altimagewidth=”900″ altimageheight=”8000″]
Updated VisibLie_E8 demonstrations to the latest Mathematica 10.2
2D Fourier Transforms on E8 Vertex Projections
Interesting stuff as it relates to QuasiCrystals and non-Crystallographic analysis.
Original source demonstration from John Holland modified and integrated into my VisibLie_E8 viewer…Cool!
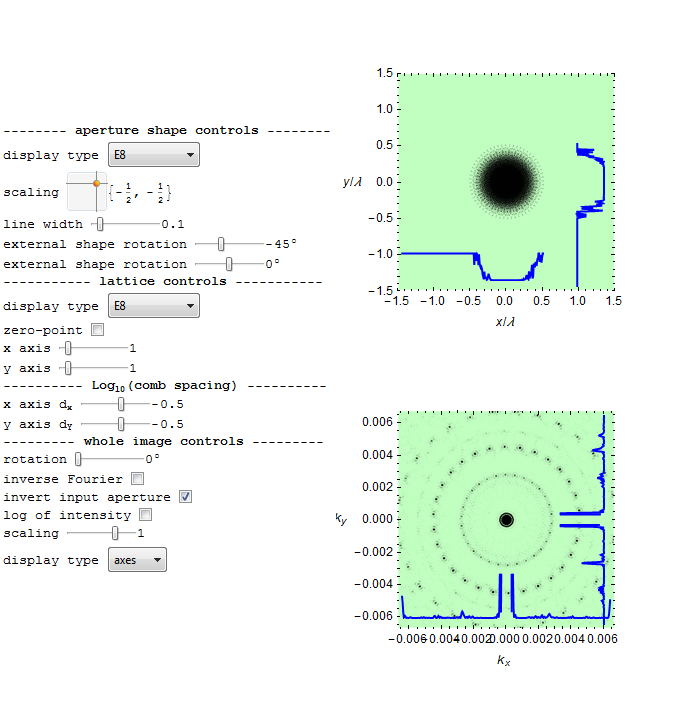
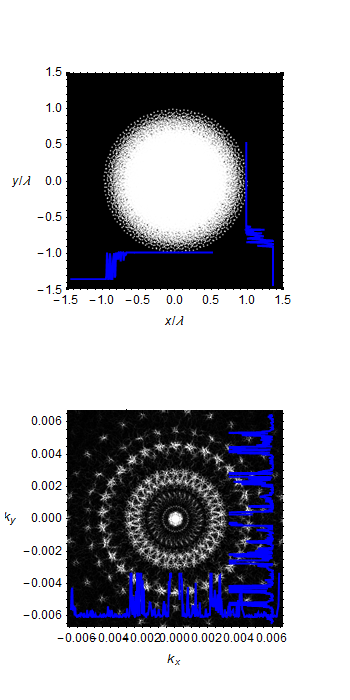
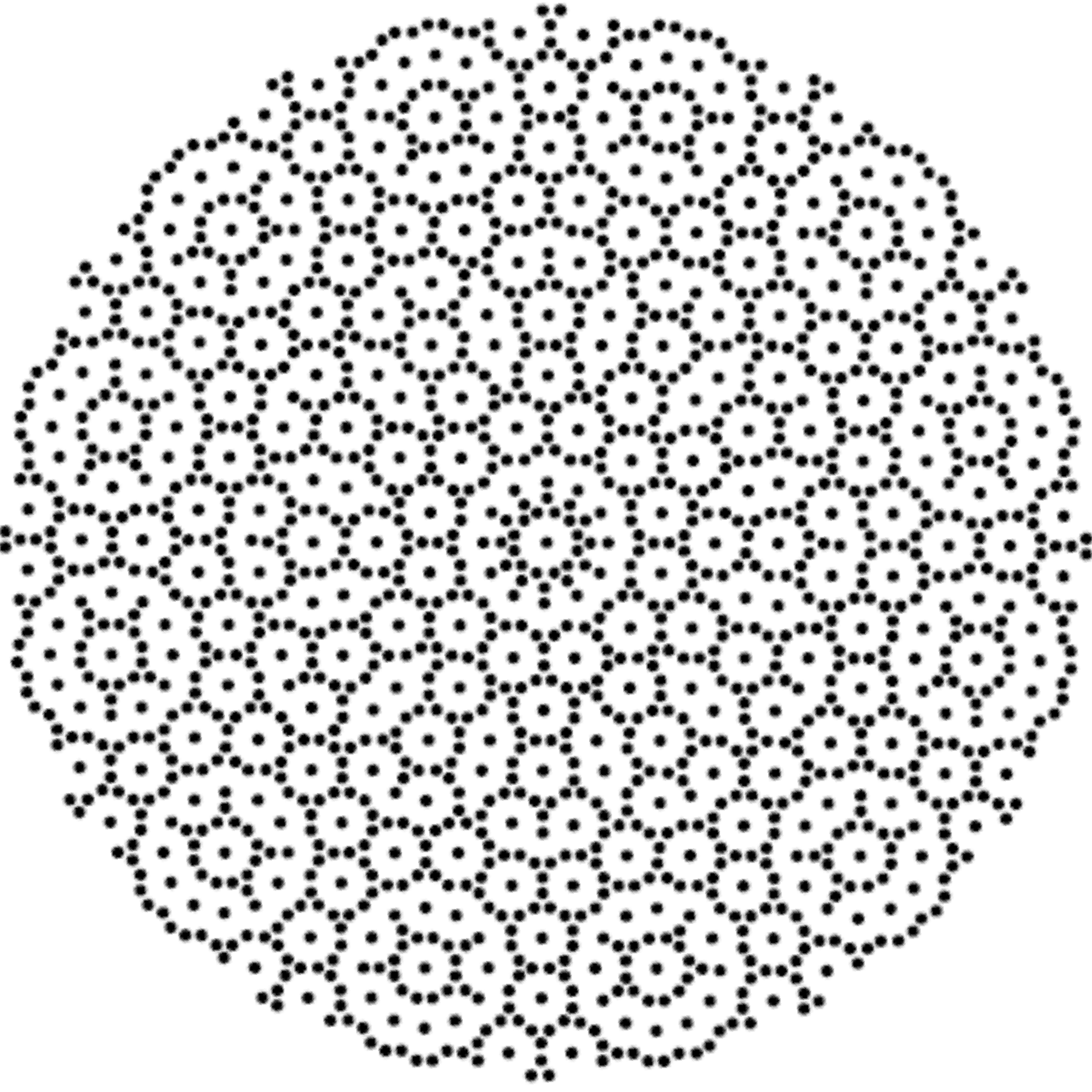
QuasiCrystals and Geometry
I found a 1995 book (PDF online) “QuasiCrystals and Geometry” by Marjorie Senechal. There were some very nice diffraction patterns that match rectified 4_21 E8 Polytope 12,18, and 30-gon projections. See my overlays below:
12-gon Rectified E8
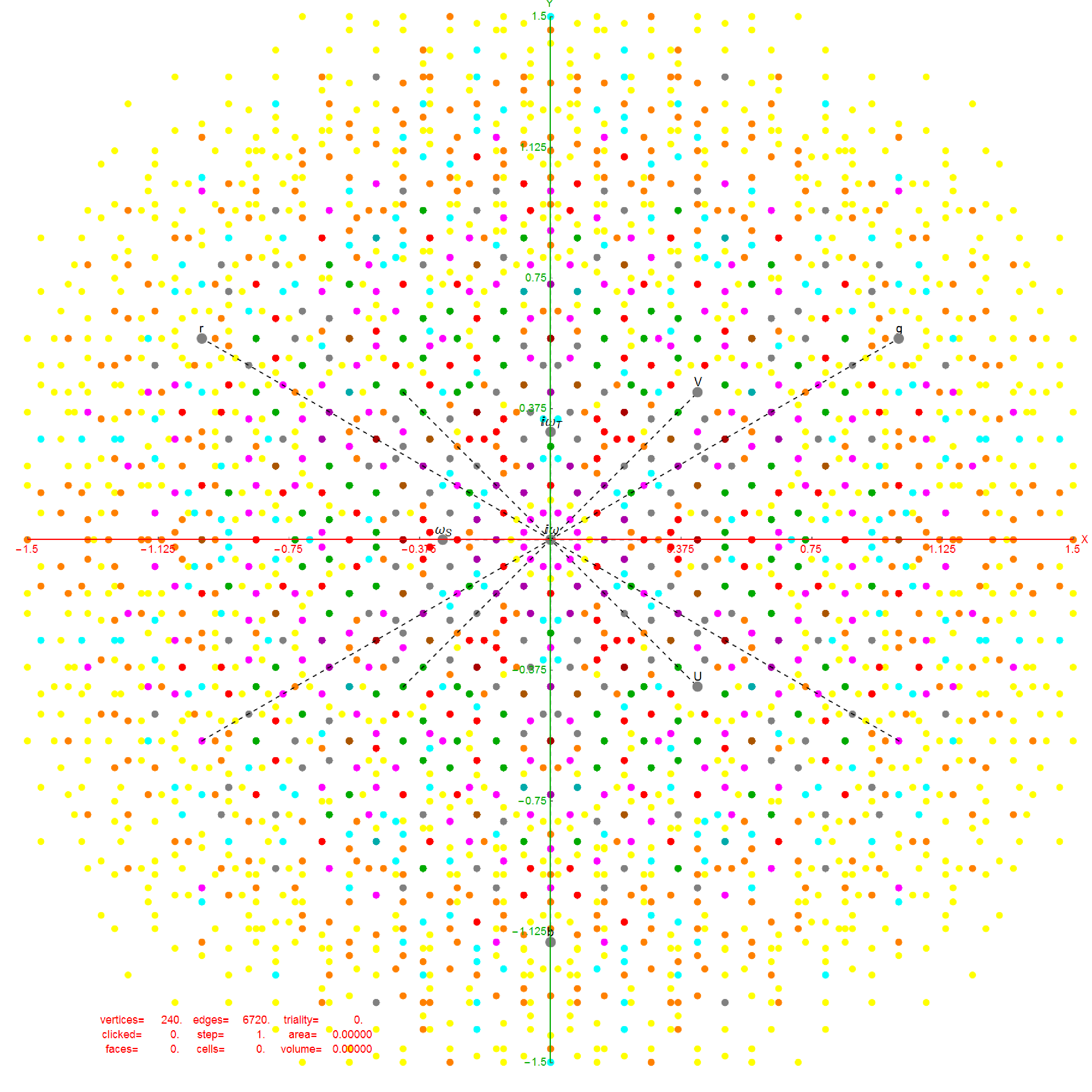
Diffraction

Overlay
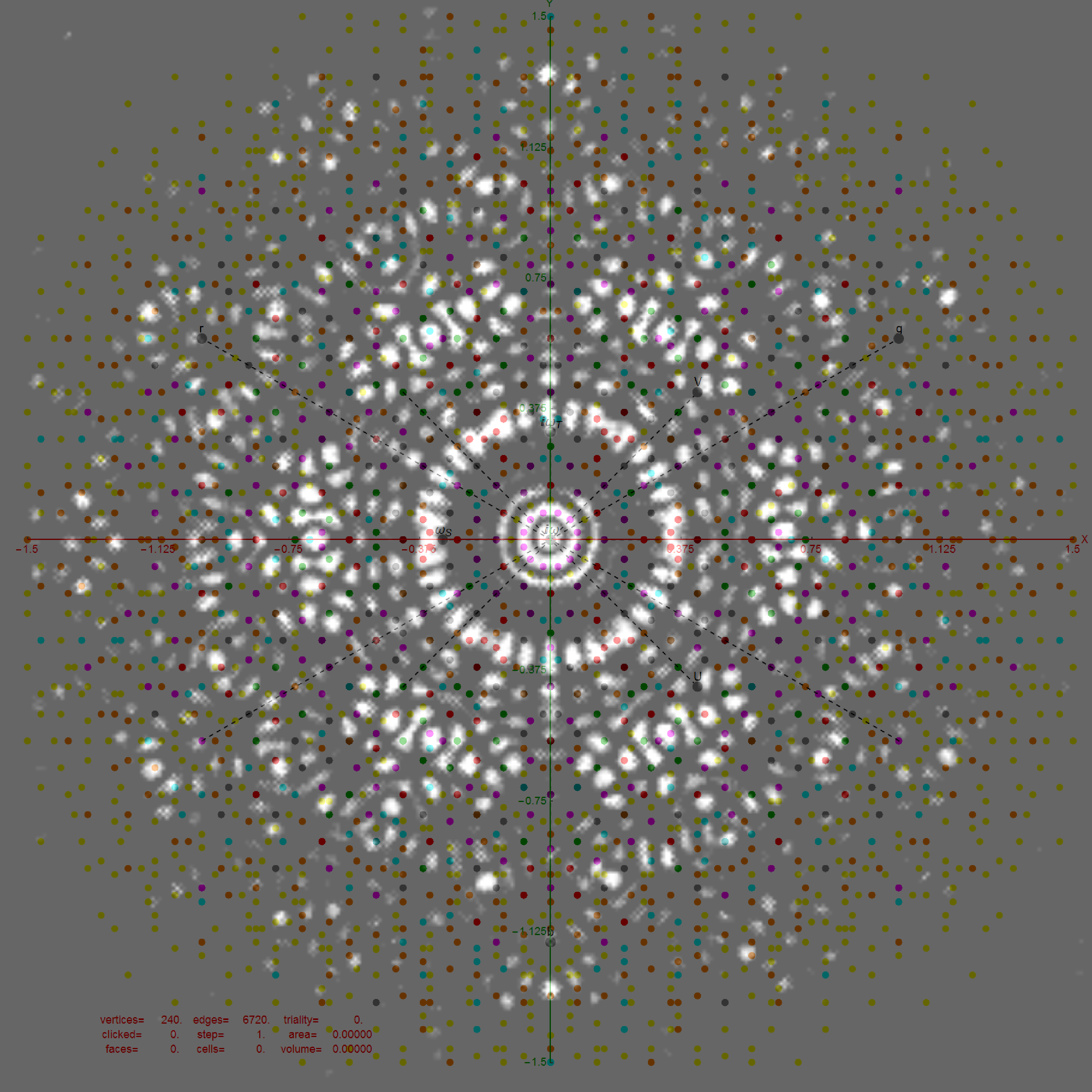
18-gon Rectified E8

Diffraction

Overlay

30-gon Rectified E8
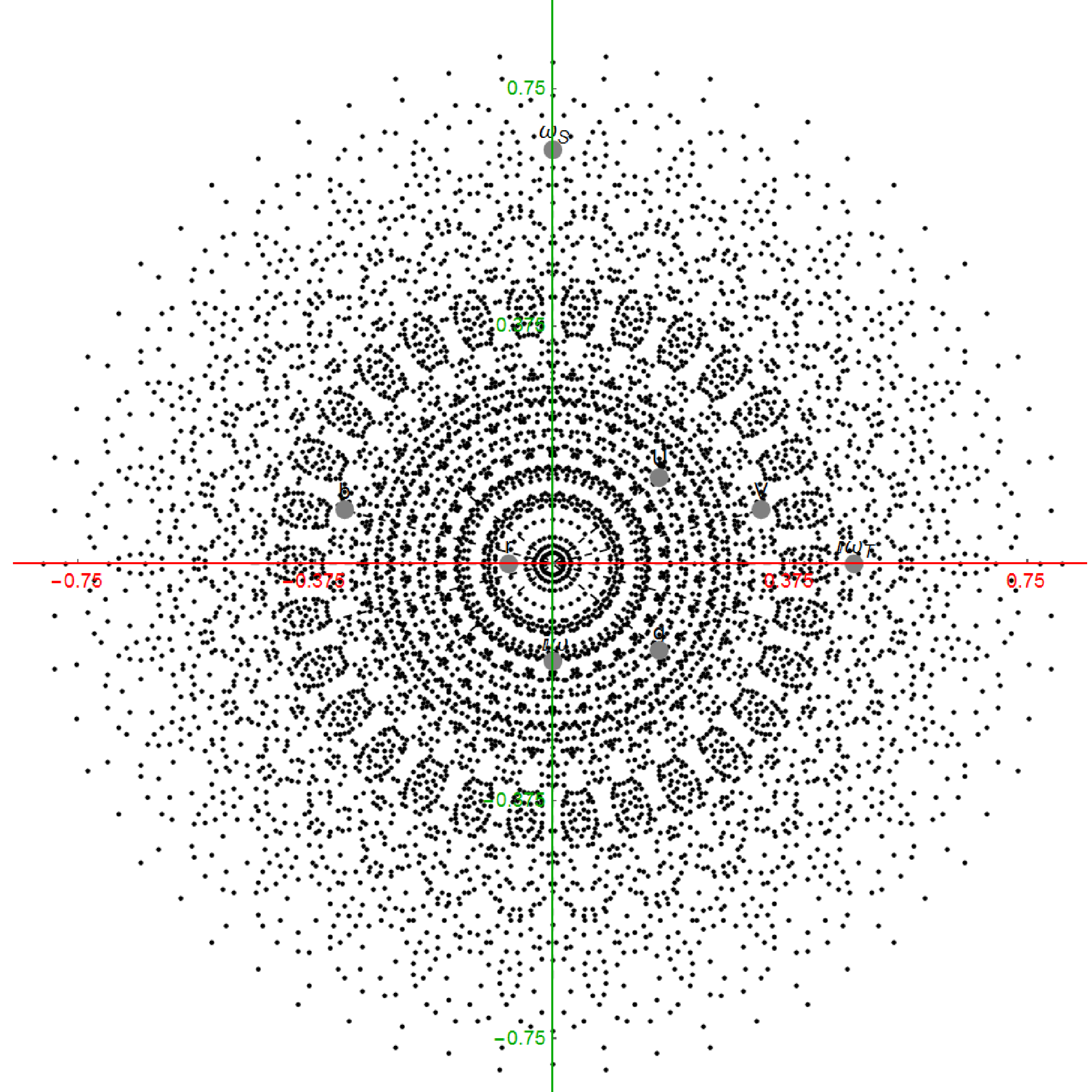
Diffraction

Overlay
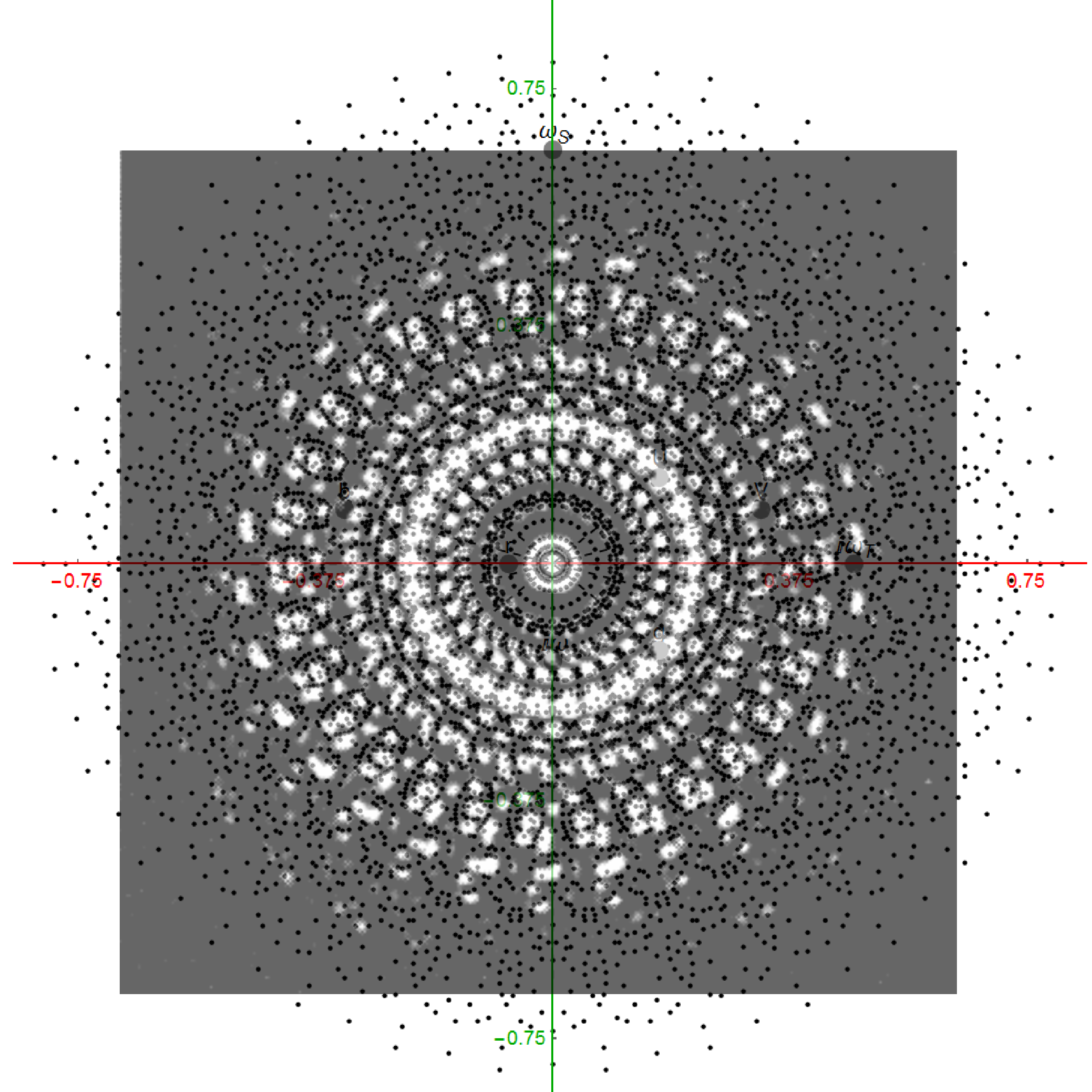
and another 12-gon rectified E8 pattern overlay from M. & N. Koca’s in “12-fold Symmetric Quasicrystallography from affine E6, B6, and F4”:

Fun with Tutte-Coxeter, Beordijk-Coxeter, E8 and H4
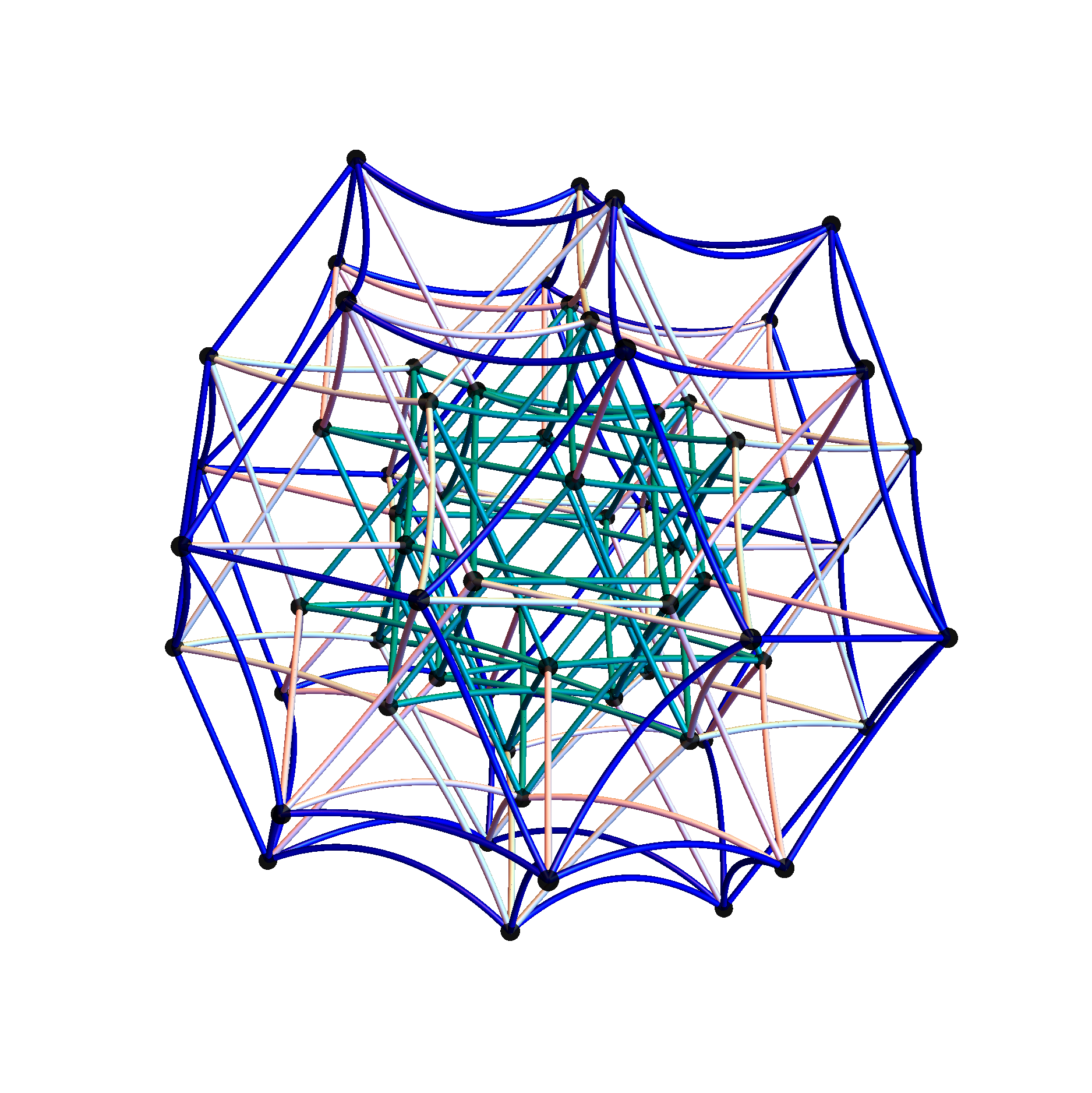
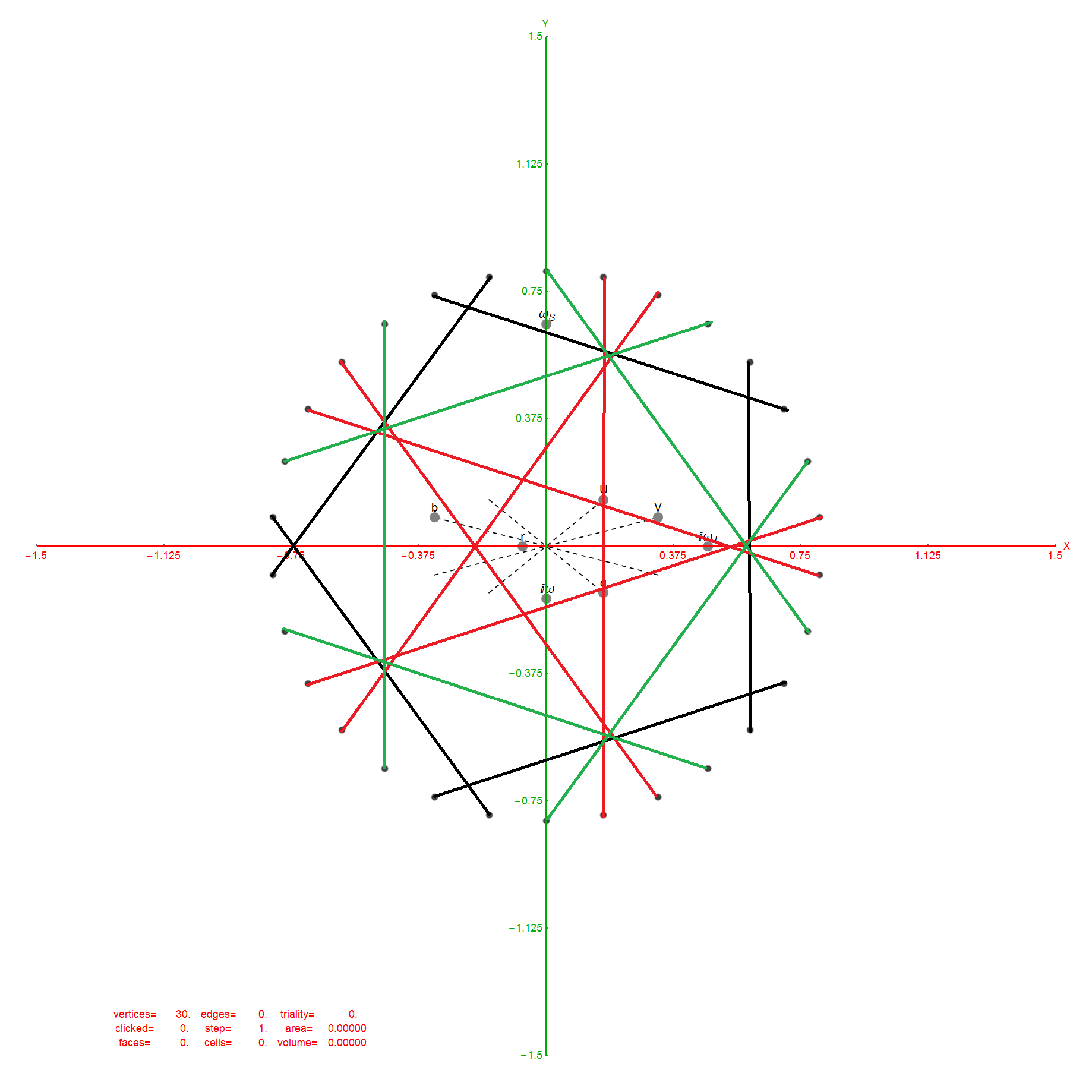
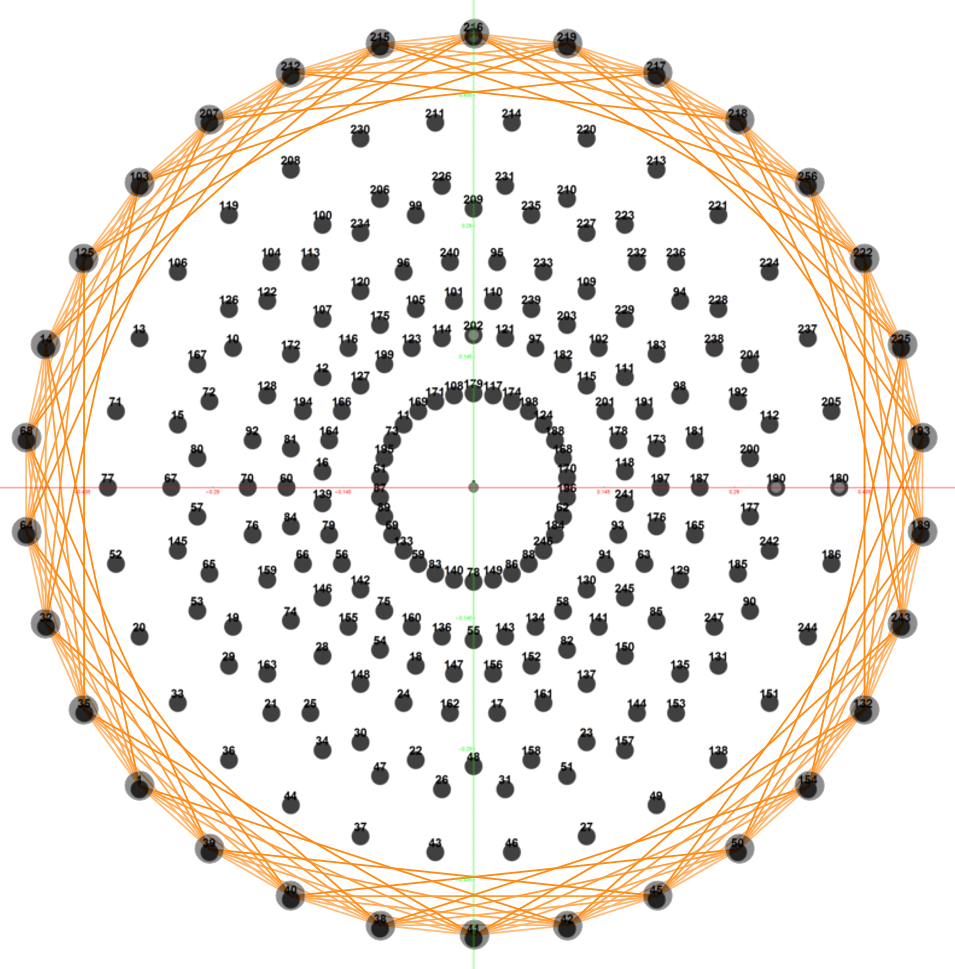
In reference to a G+ post by Baez (w/Greg Egan), it’s interesting to note the link to E8’s outer ring of the Petrie projection of a split real even E8, which creates a Beordijk-Coxeter helix.
Beordijk-Coxeter helix in 2D
Beordijk-Coxeter helix in 3D
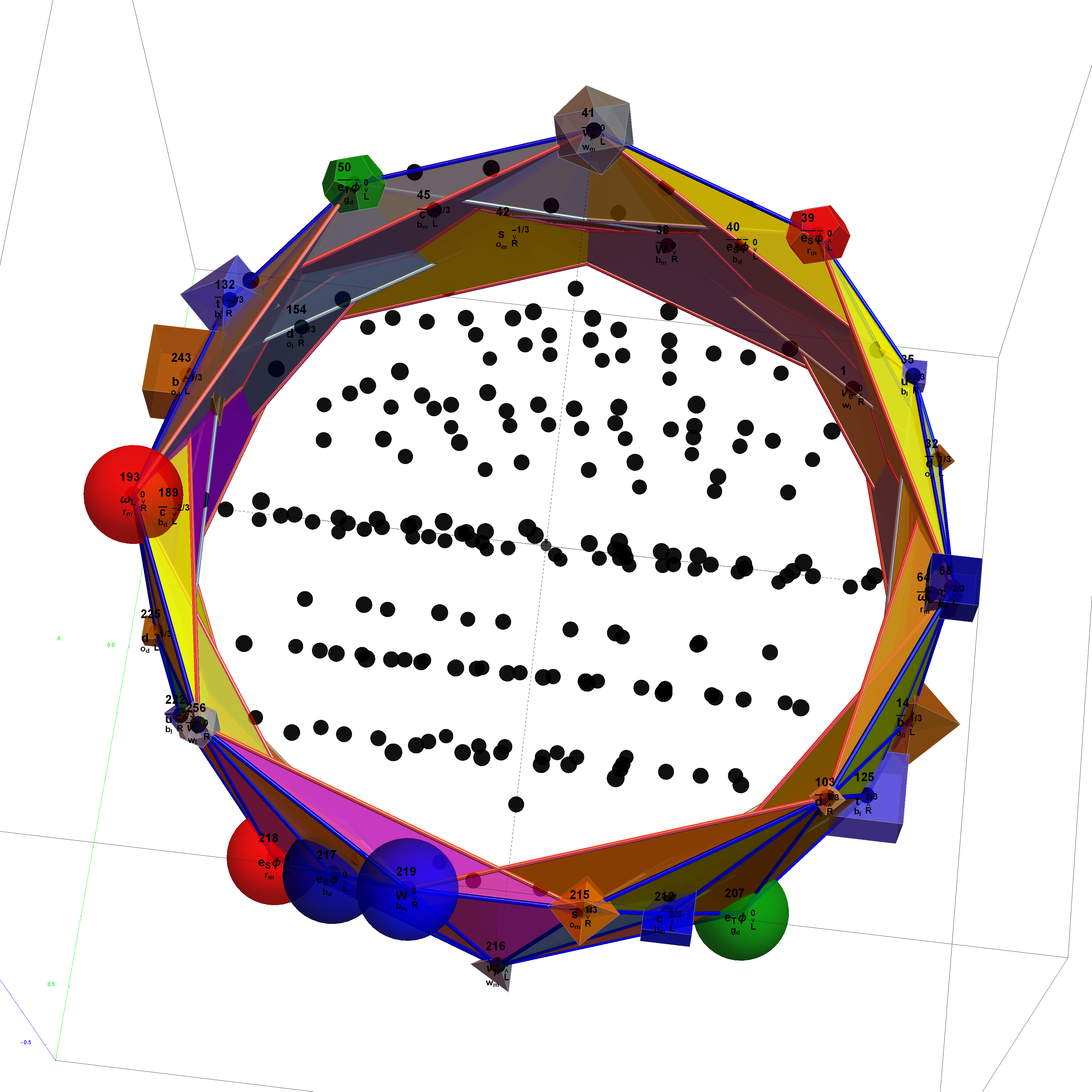
The Beordijk-Coxeter helix connects the nearest 6 vertices on the outer ring. The Tutte-Coxeter graph is created in 3 (blk,grn,red) sets of edges by taking the (outer) ring and skipping (6,8,12) or counting (7,9,13) vertices. It shows there are 2 perfect pentagons and 1 pentagram (with different radii due to the difference in distance between the sets of vertices used).
Of course, the crystallographic E8 is manifestly related to the 5 fold symmetry of the pentagon, with its integral relationship to the non-crystallographic H4 group (and its Coxeter-Dynkin diagram) through E8 to H4 folding using the Golden ratio Phi.
It is interesting to note that the skipping of 5+(1,3,7) vertices is similar to the creation of the 120 (240) vertex positions of H4 (E8) Petrie projection by adding to the 24 vertices of the 8-cell and 16-cell (which make up the self-dual 24-cell) the 96 vertices of the Snub 24-cell. This is done through 4 rotations skipping 5 vertices.
Also notice the (1,3,7) are the number of the imaginary parts of Complex, Quaternion, and Octonion numbers, also integrally related to E8.