Best viewed in HD mode…

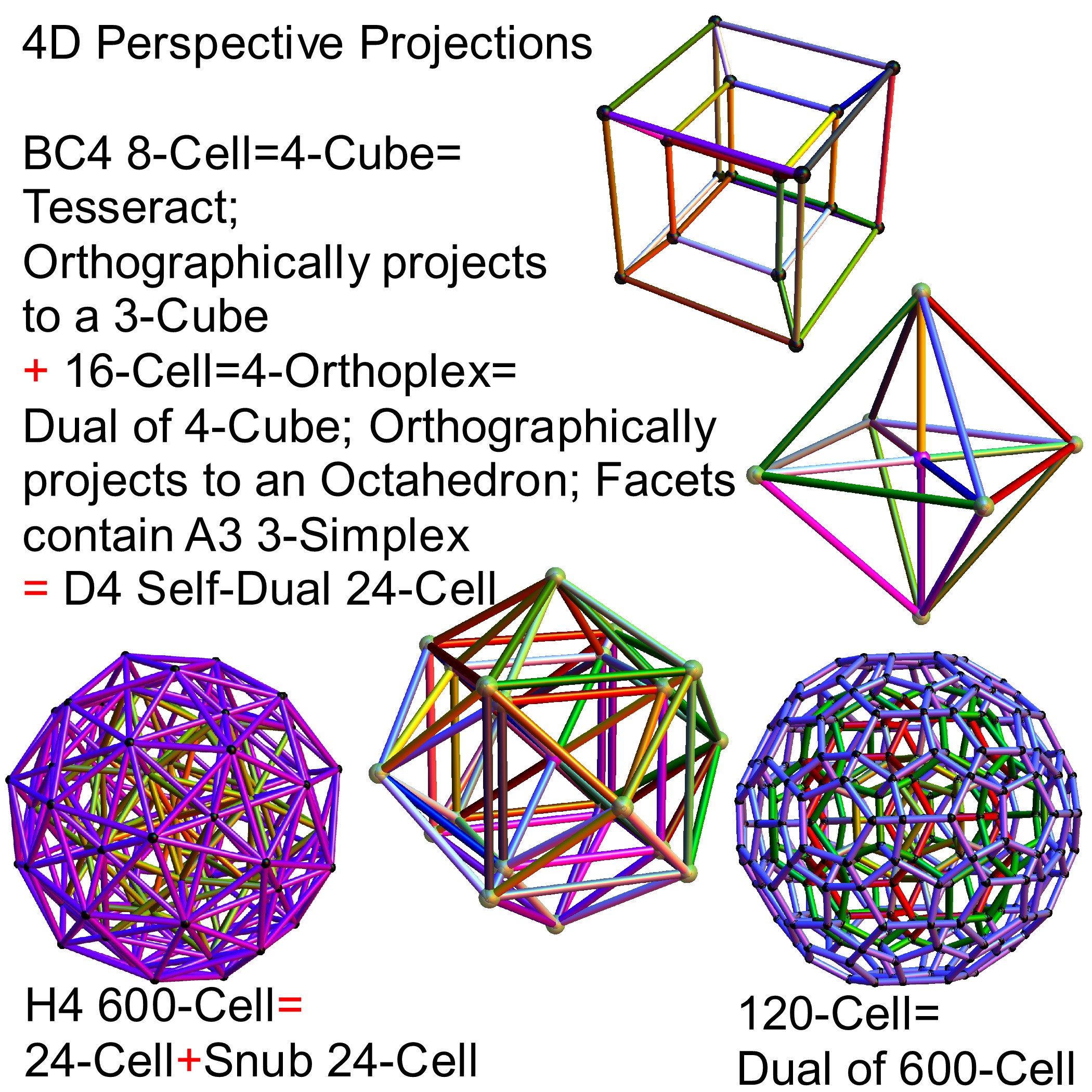
Last year I showed that the Dynkin diagram of the Lie Algebra, Group and Lattice of E8 is related to the Coxeter-Dynkin of the 600 Cell of H4 through a folding of their diagrams:

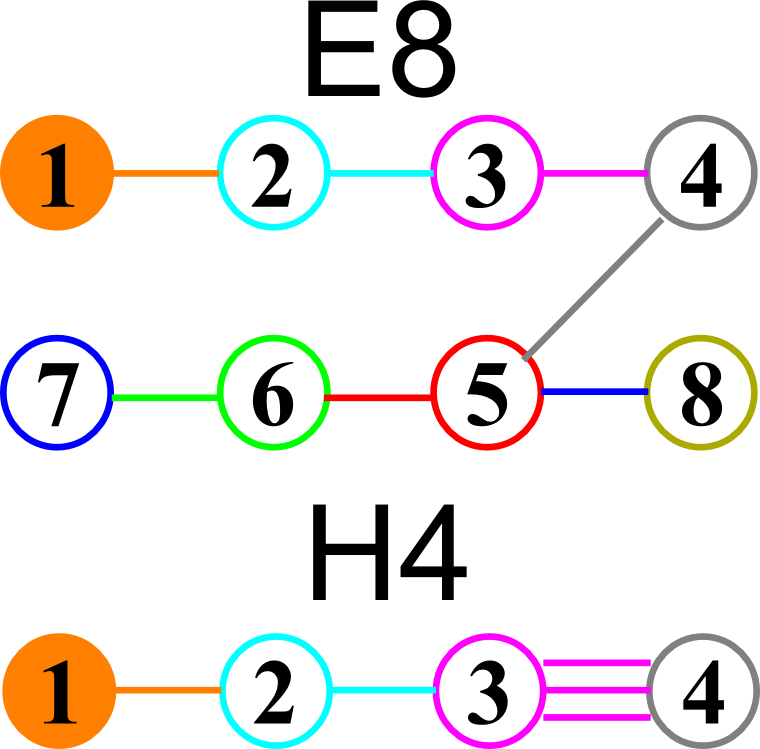
I had found the E8 to H4 folding matrix several years ago after reading several papers by Koca and another paper by Dechant, on the topic. The matrix I found is:

Notice that C600=Transpose[C600] and the Quaternion–Octonion like structure (ala. Cayley-Dickson) within the folding matrix. Only the first 4 rows are needed for folding, but I use the 8×8 matrix to rotate 8D vectors easily.

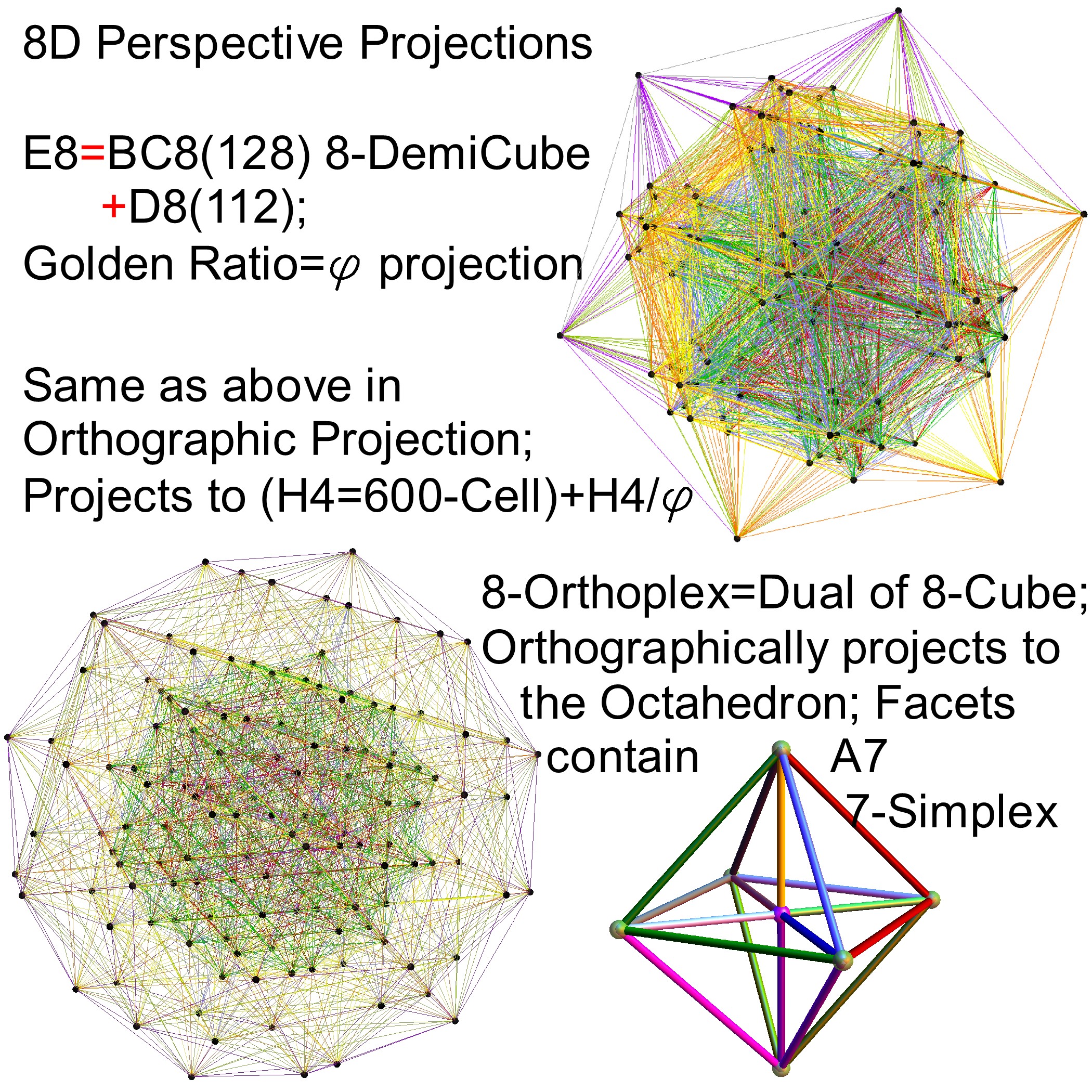
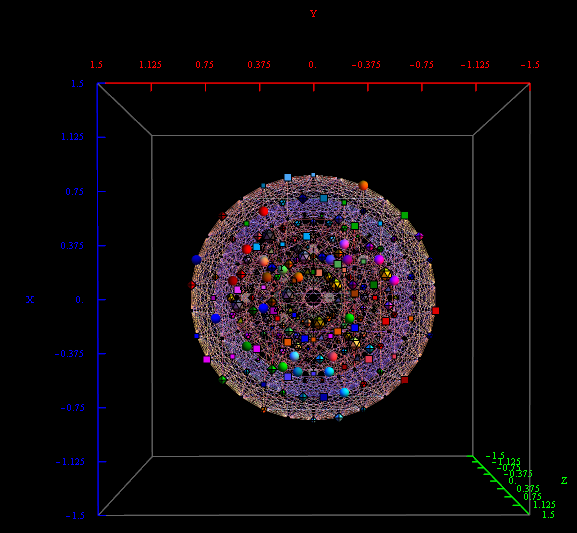
The following x,y,z vectors project E8 to its Petrie projection on one face (or 2 of 6 cubic faces, which are the same).

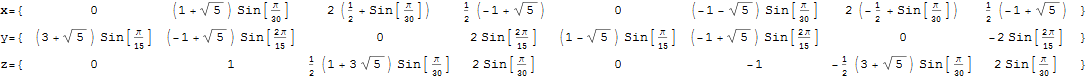
On another face are the orthonormal H4 600 cell and the concentric H4/Phi. There are 6720 edges with 8D Norm’d length of Sqrt[2], but I only show 1220 in order to prevent obscuring the nodes.

These values were calculated using the dot product of the Inverse[4*C600] with the following H4 Petrie projection vertices (aka. the Van Oss projection), where I’ve added the z vector for the proper 3D projection. Notice I am still using 8D basis vectors with the last 4 zero, as this maintains scaling due to the left-right symmetries in C600).

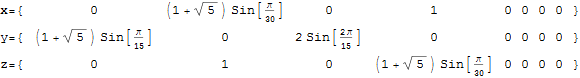
The Split Real Even (SRE) E8 vertices are generated from the root system for the E8 Dynkin diagram and its resulting Cartan matrix:

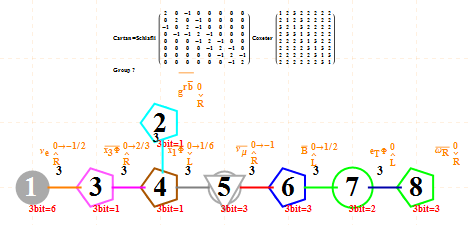
This is input from my Mathematica “VisibLie” application. It is shown with the assigned physics particles that make up the simple roots matrix entries:
.
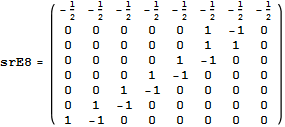Please note, the Cartan matrix can also be generated by srE8.Transpose[srE8]

It takes Transpose[srE8] and applies the dot product against the 120 positive and 120 negative algebra roots generated by the Mathematica “SuperLie” package (shown along with its Hasse diagram, which I generate in the full version of my Mathematica notebook):

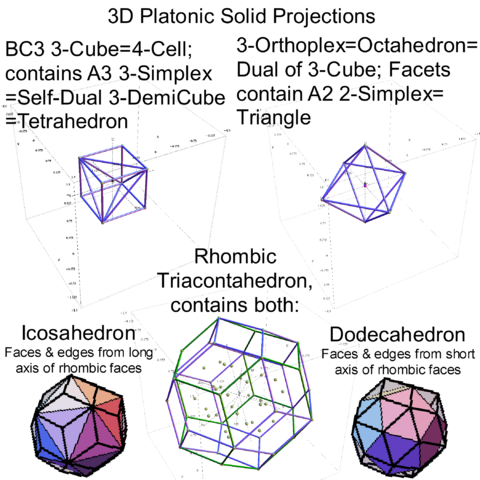
Interestingly, E8 in addition to containing the 8D structures D8 and BC8 and the 4D Polychora, contains the 7D E7, as well as the 6D structures of the Hexeract or 6 Cube. I also showed several years ago that this projects down to the 3D as the Rhombic Triacontahedron. The Rhombic Triacontahedron (of Quasicrystal fame) contains the Platonic Solids including the Icosahedron and Dodecahedron! This is shown to be done through folding of the 6-Cube using rows 2 through 4 of the E8 to H4 folding matrix!!