Tag Archives: E8
E8 to 3D projection using my H4 folding matrix
Best viewed in HD mode…
Last year I showed that the Dynkin diagram of the Lie Algebra, Group and Lattice of E8 is related to the Coxeter-Dynkin of the 600 Cell of H4 through a folding of their diagrams:
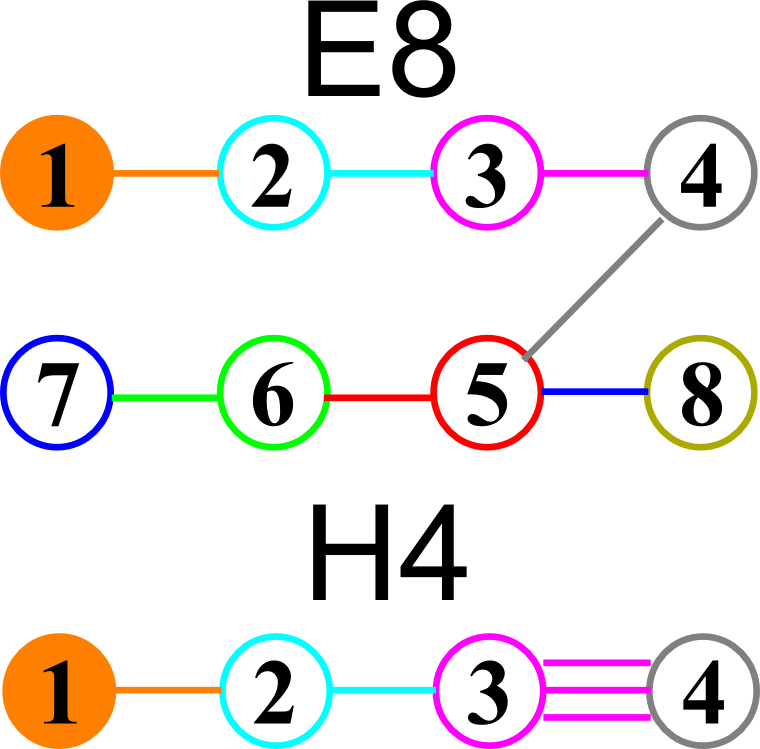
I had found the E8 to H4 folding matrix several years ago after reading several papers by Koca and another paper by Dechant, on the topic. The matrix I found is:
Notice that C600=Transpose[C600] and the Quaternion–Octonion like structure (ala. Cayley-Dickson) within the folding matrix. Only the first 4 rows are needed for folding, but I use the 8×8 matrix to rotate 8D vectors easily.
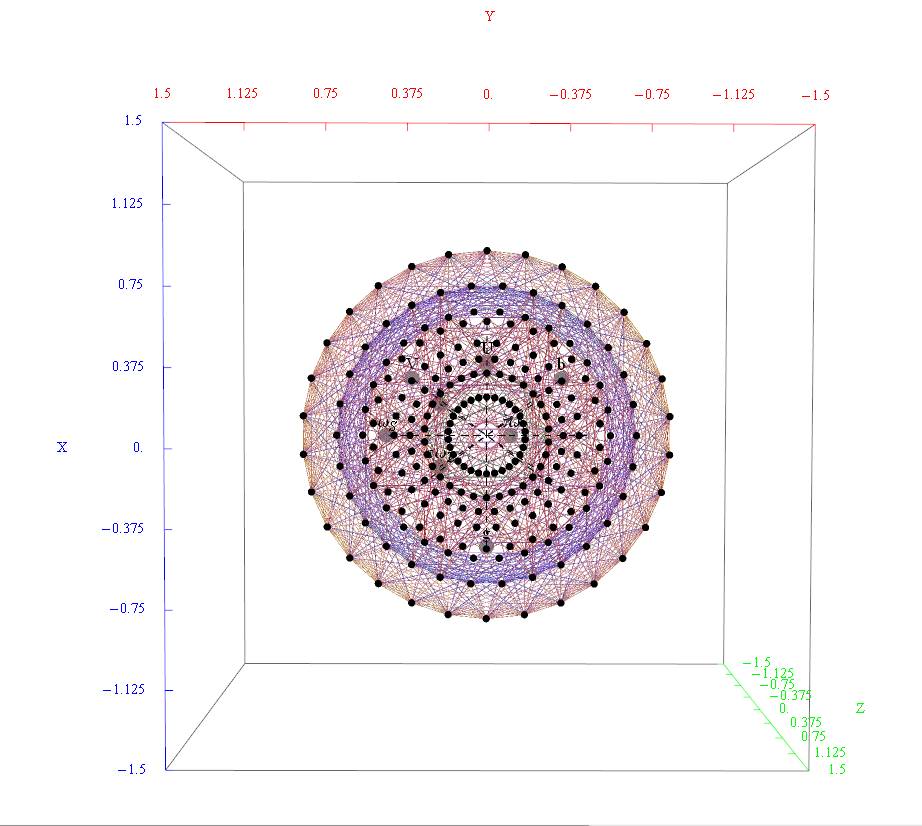
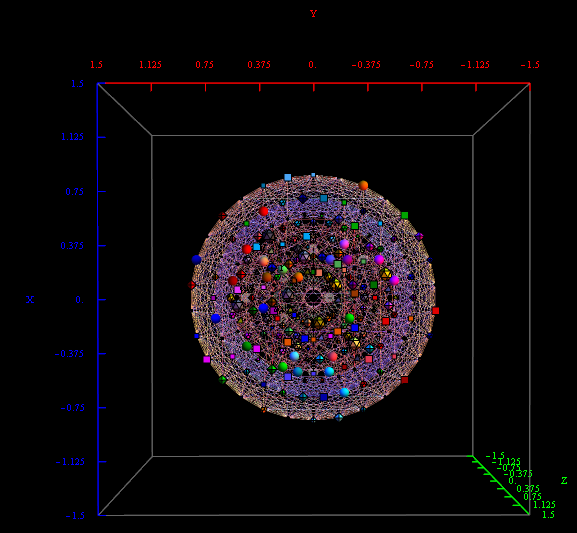
The following x,y,z vectors project E8 to its Petrie projection on one face (or 2 of 6 cubic faces, which are the same).
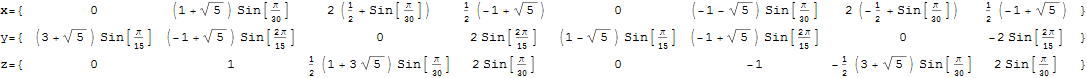
On another face are the orthonormal H4 600 cell and the concentric H4/Phi. There are 6720 edges with 8D Norm’d length of Sqrt[2], but I only show 1220 in order to prevent obscuring the nodes.
These values were calculated using the dot product of the Inverse[4*C600] with the following H4 Petrie projection vertices (aka. the Van Oss projection), where I’ve added the z vector for the proper 3D projection. Notice I am still using 8D basis vectors with the last 4 zero, as this maintains scaling due to the left-right symmetries in C600).
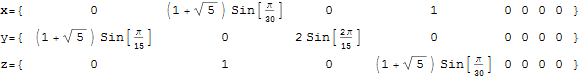
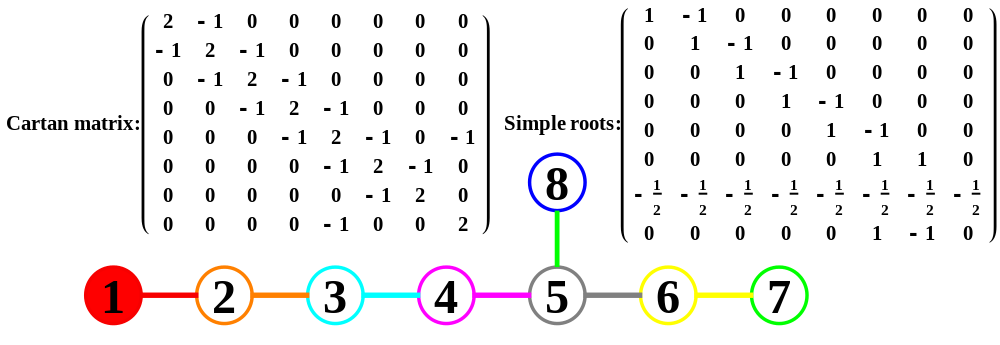
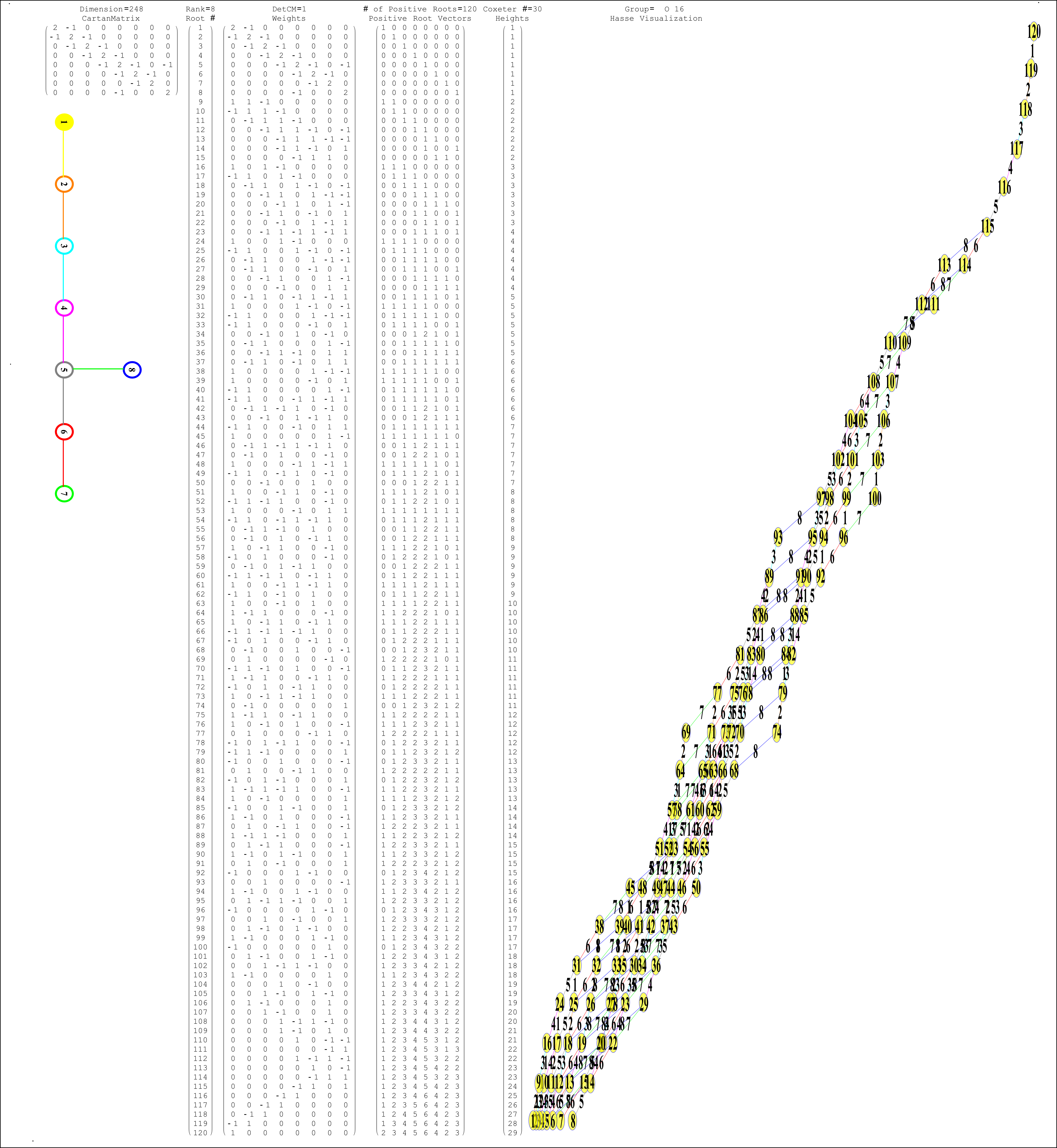
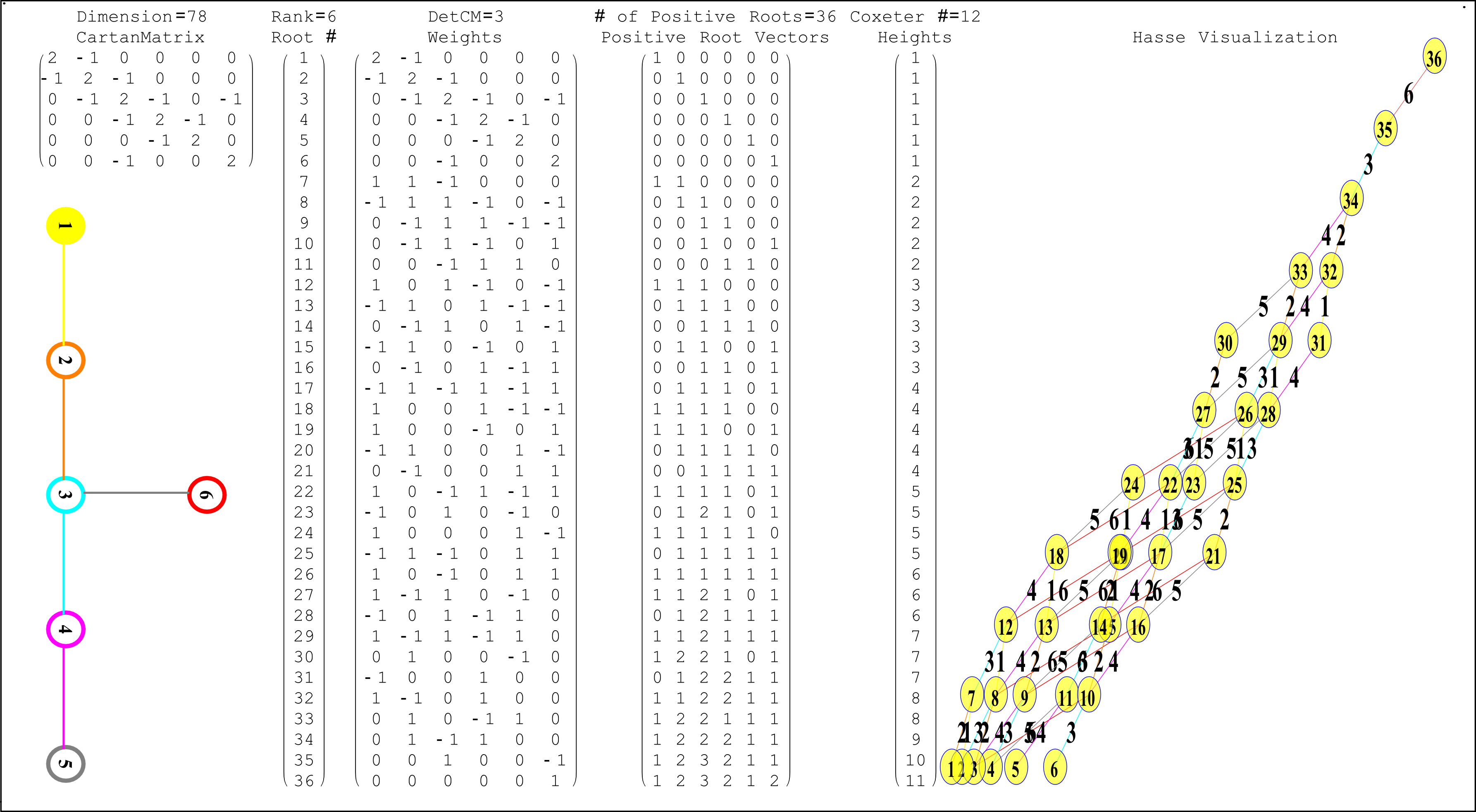
The Split Real Even (SRE) E8 vertices are generated from the root system for the E8 Dynkin diagram and its resulting Cartan matrix:
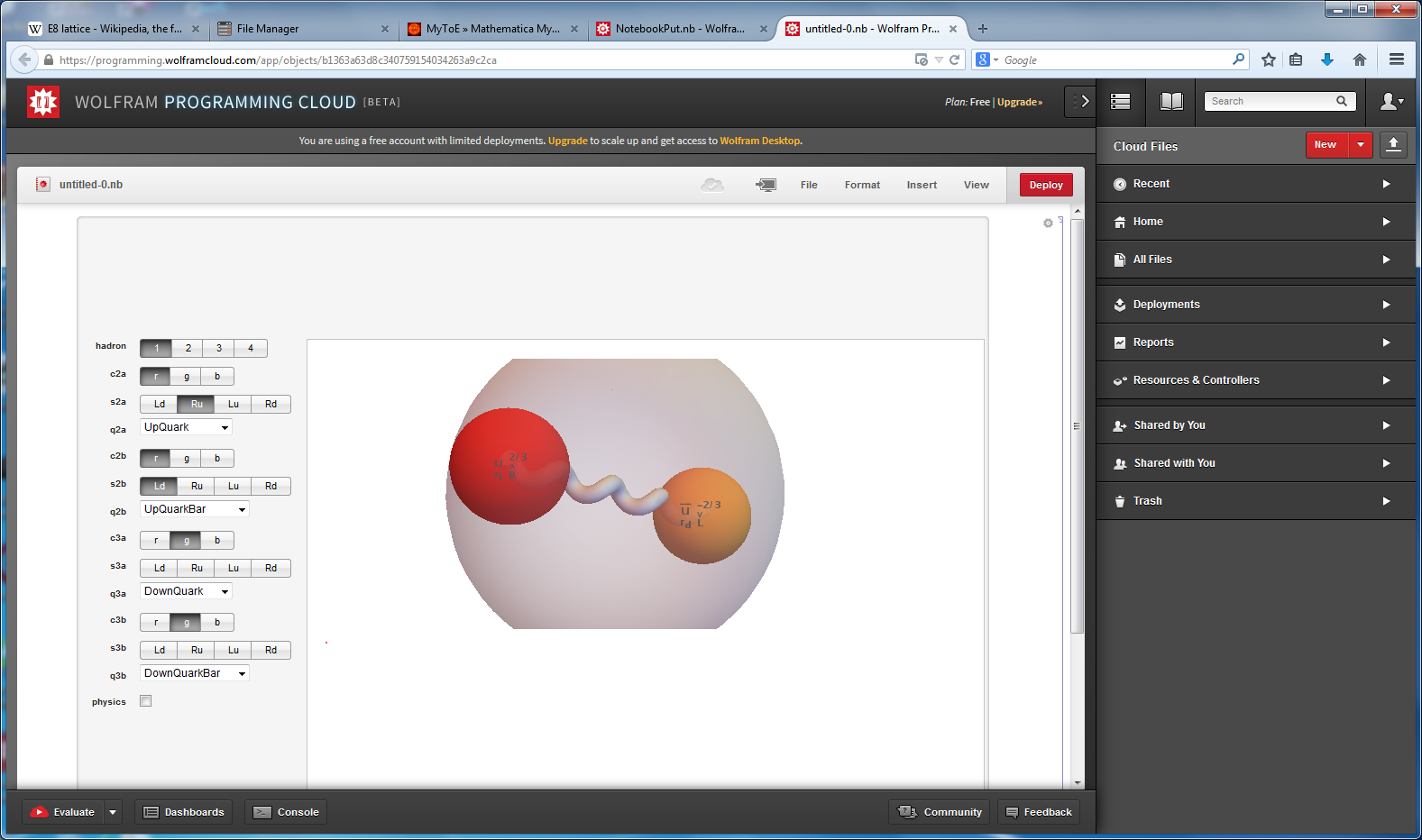
This is input from my Mathematica “VisibLie” application. It is shown with the assigned physics particles that make up the simple roots matrix entries:
.
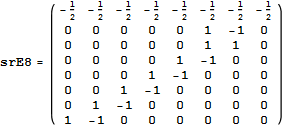Please note, the Cartan matrix can also be generated by srE8.Transpose[srE8]
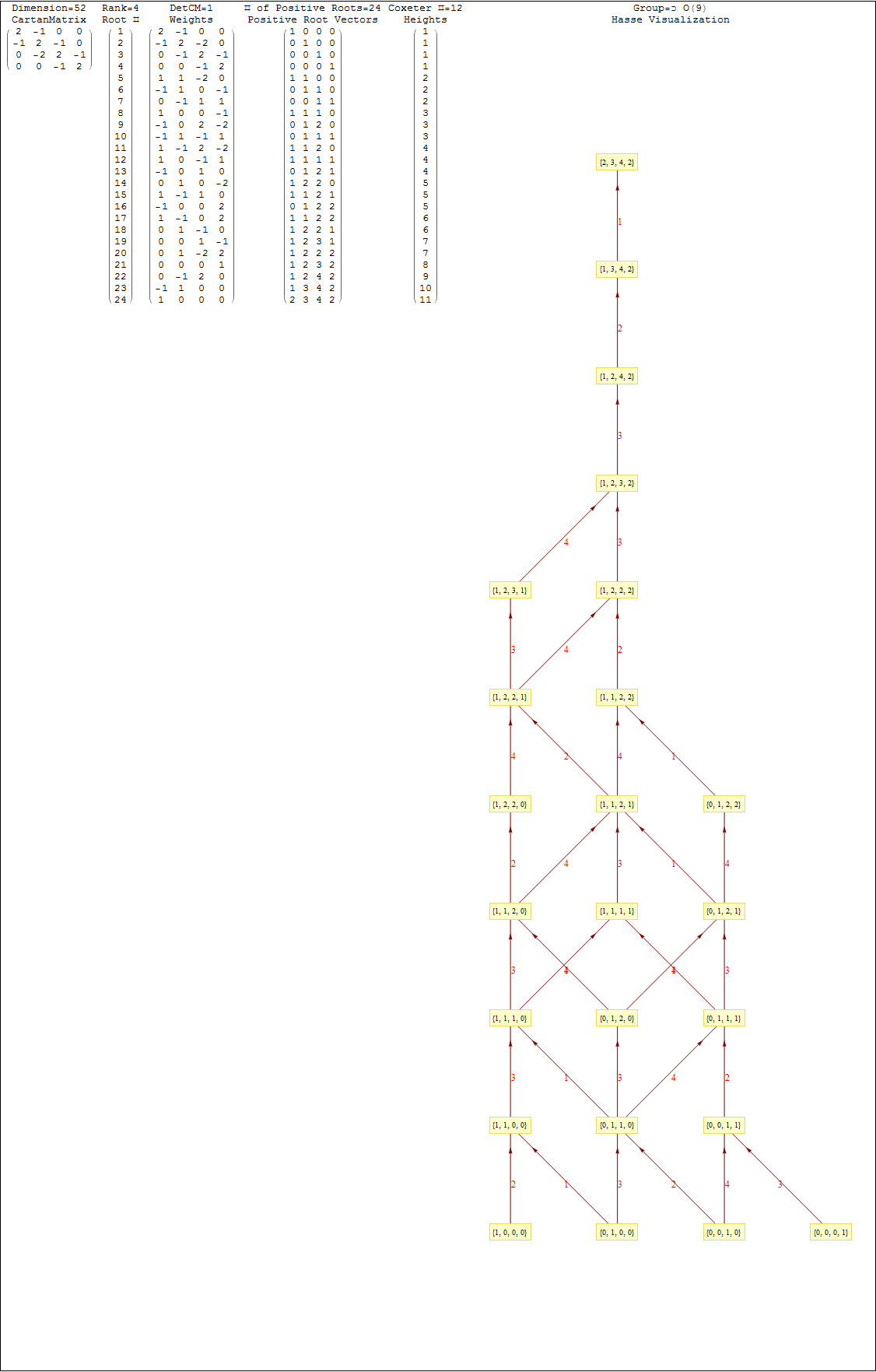
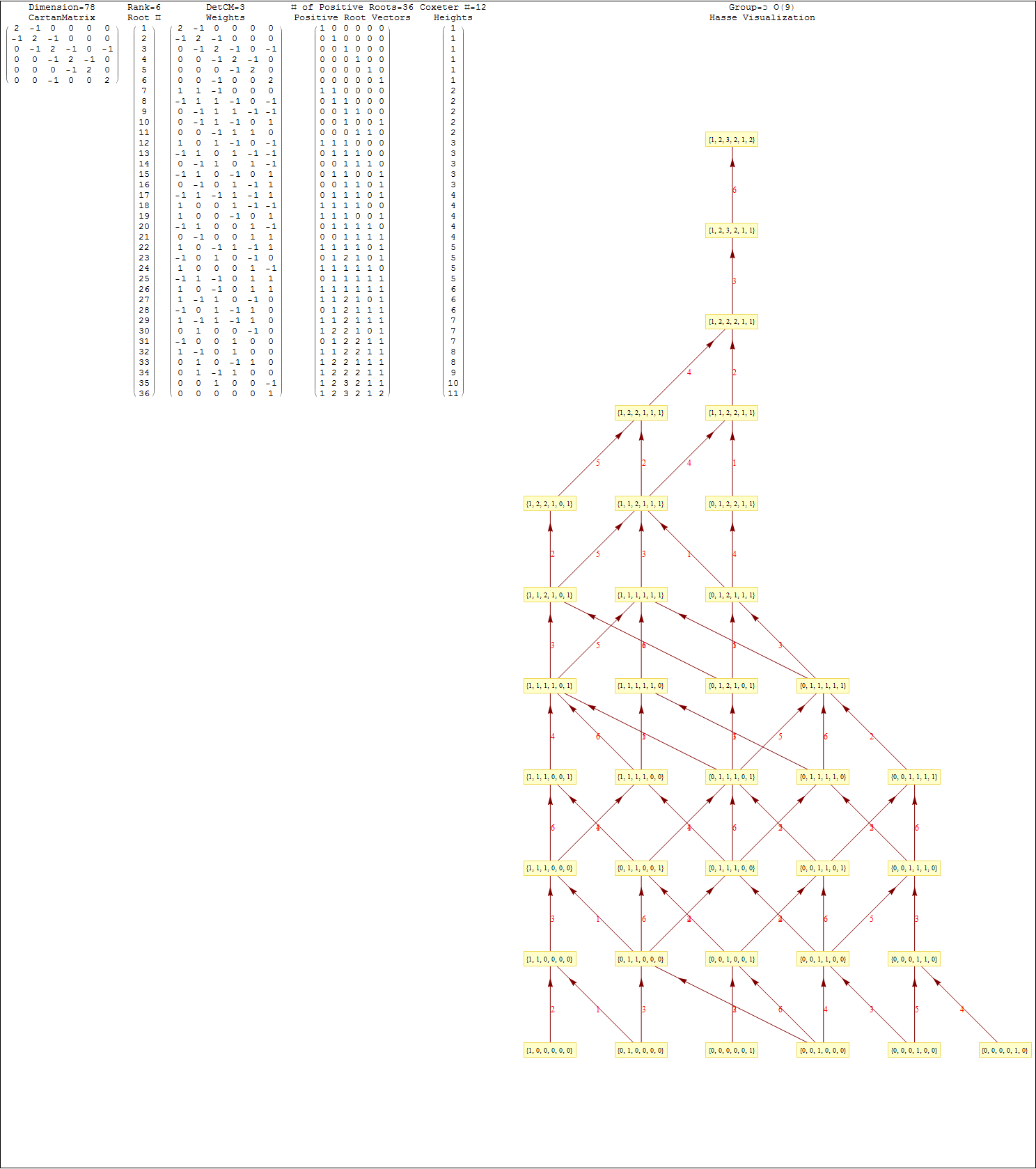
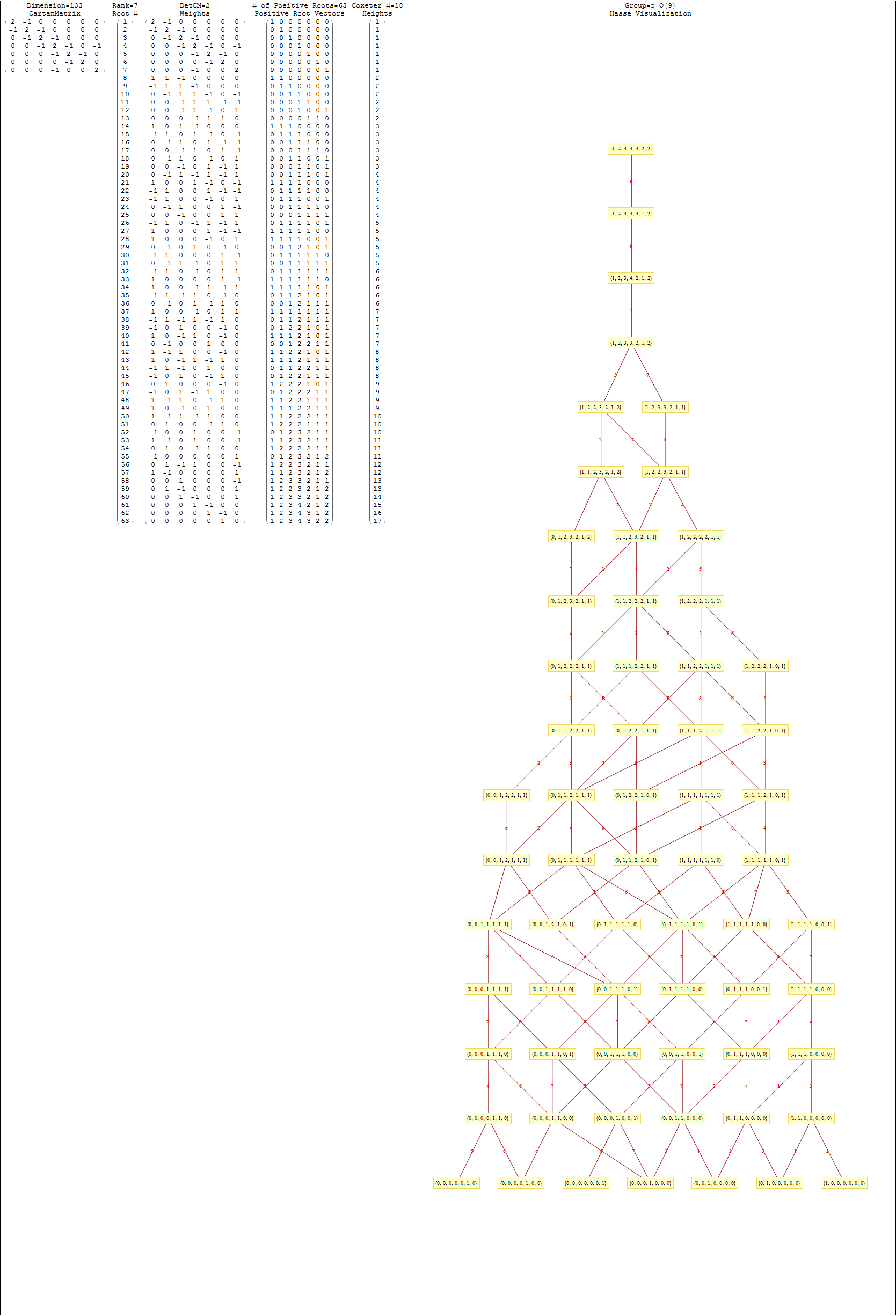
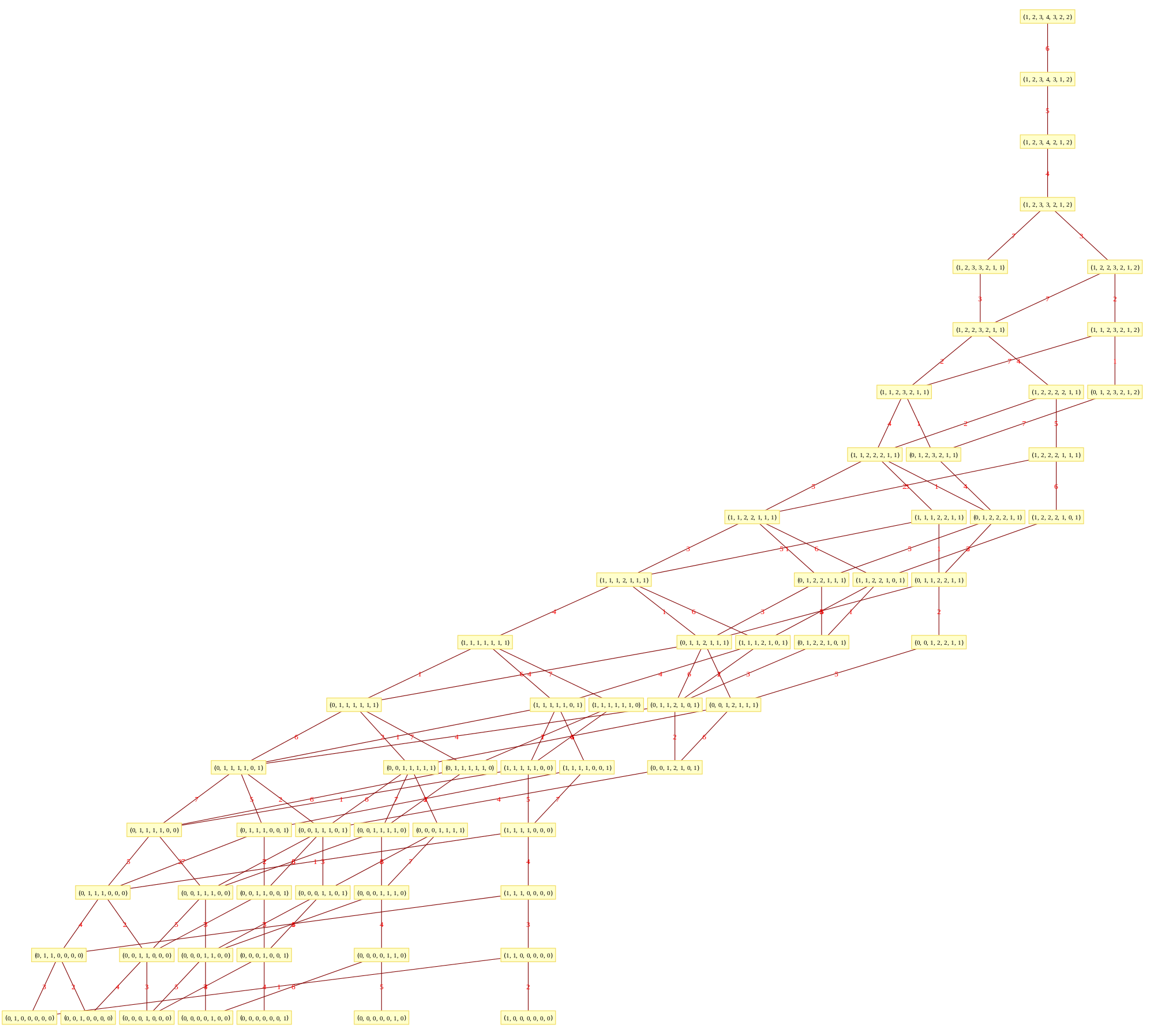
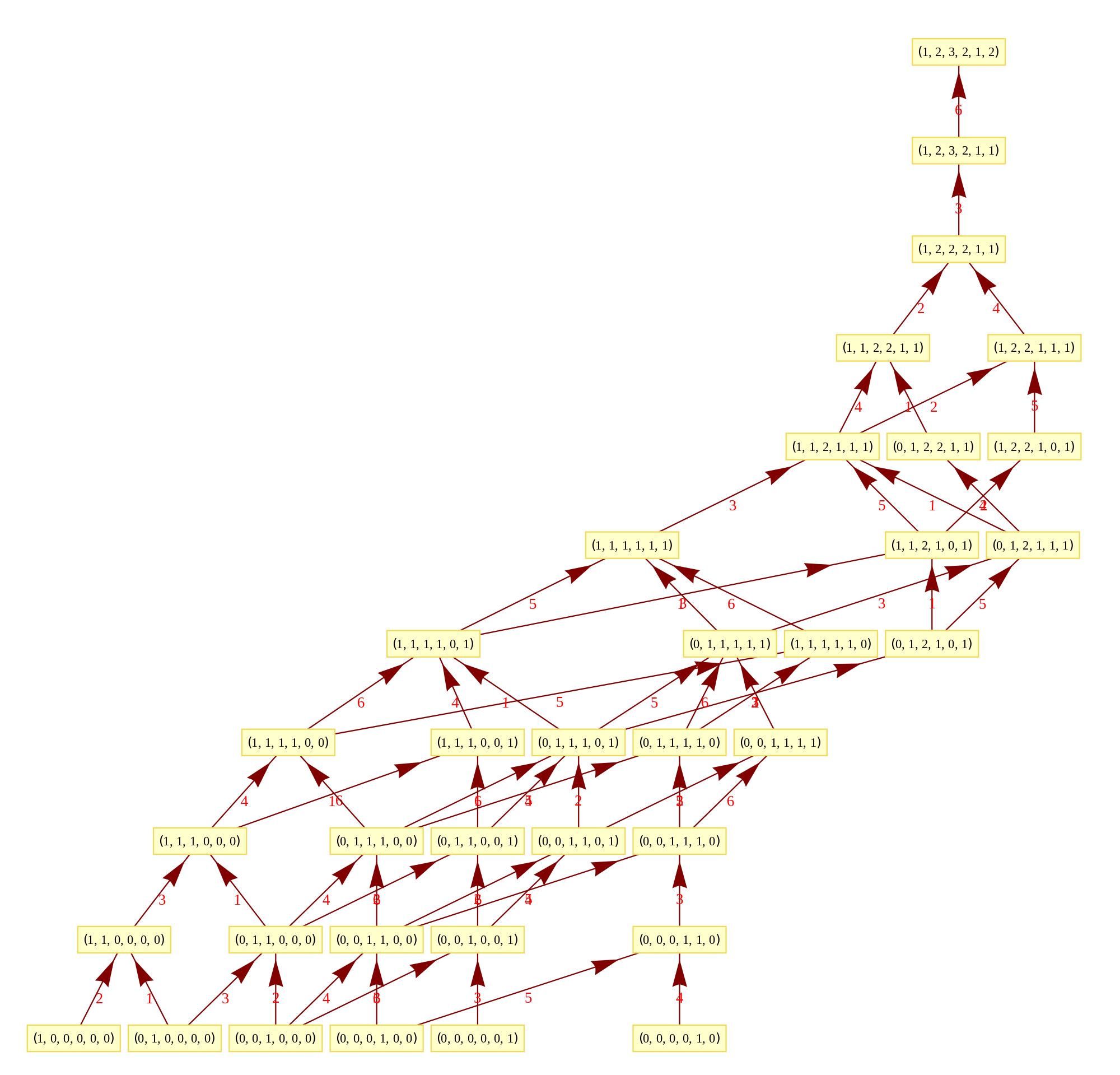
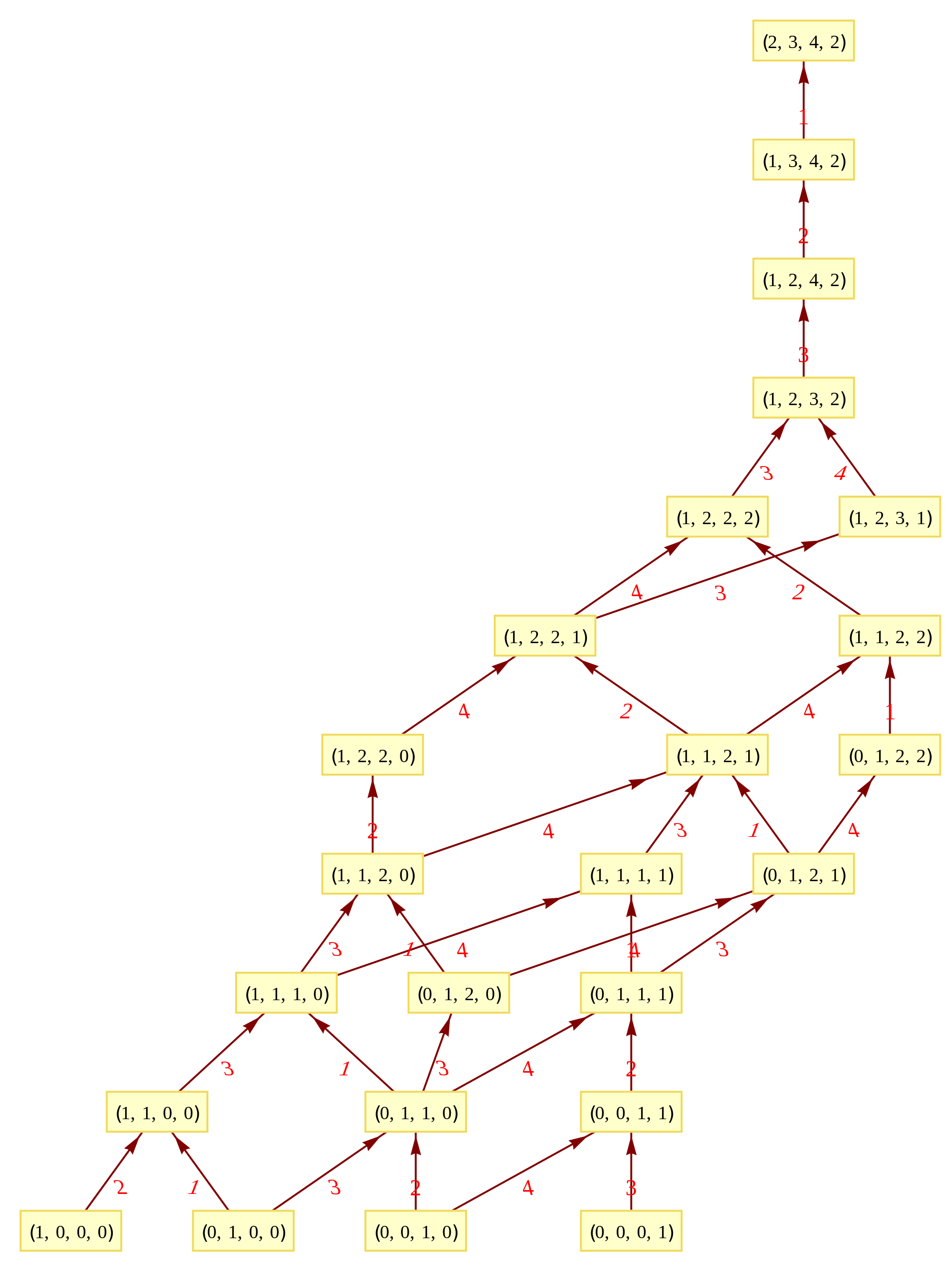
It takes Transpose[srE8] and applies the dot product against the 120 positive and 120 negative algebra roots generated by the Mathematica “SuperLie” package (shown along with its Hasse diagram, which I generate in the full version of my Mathematica notebook):
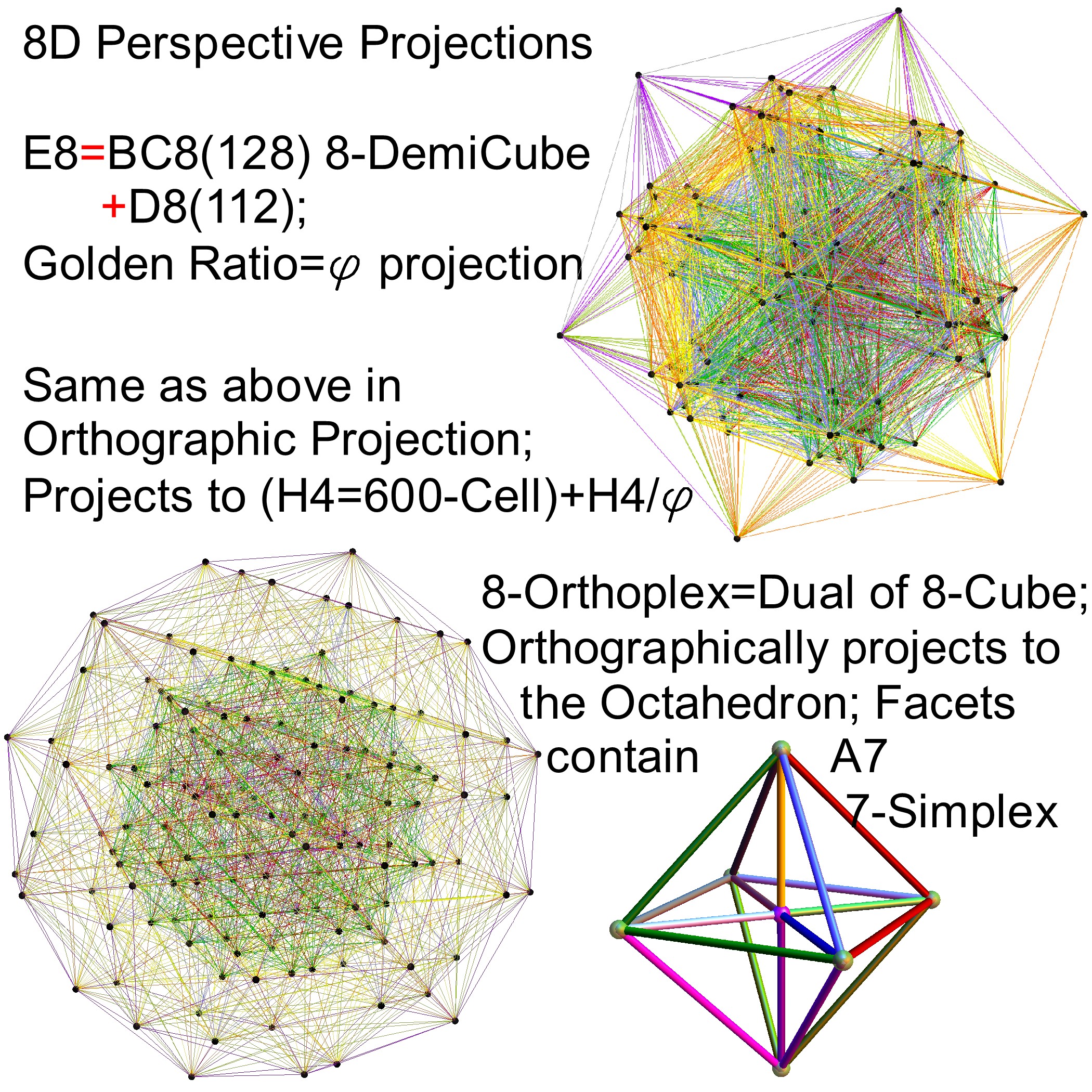
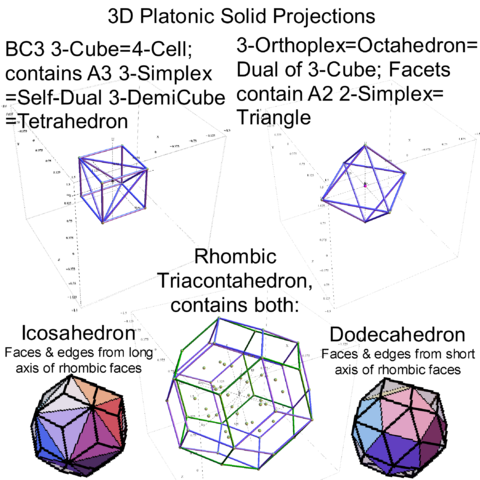
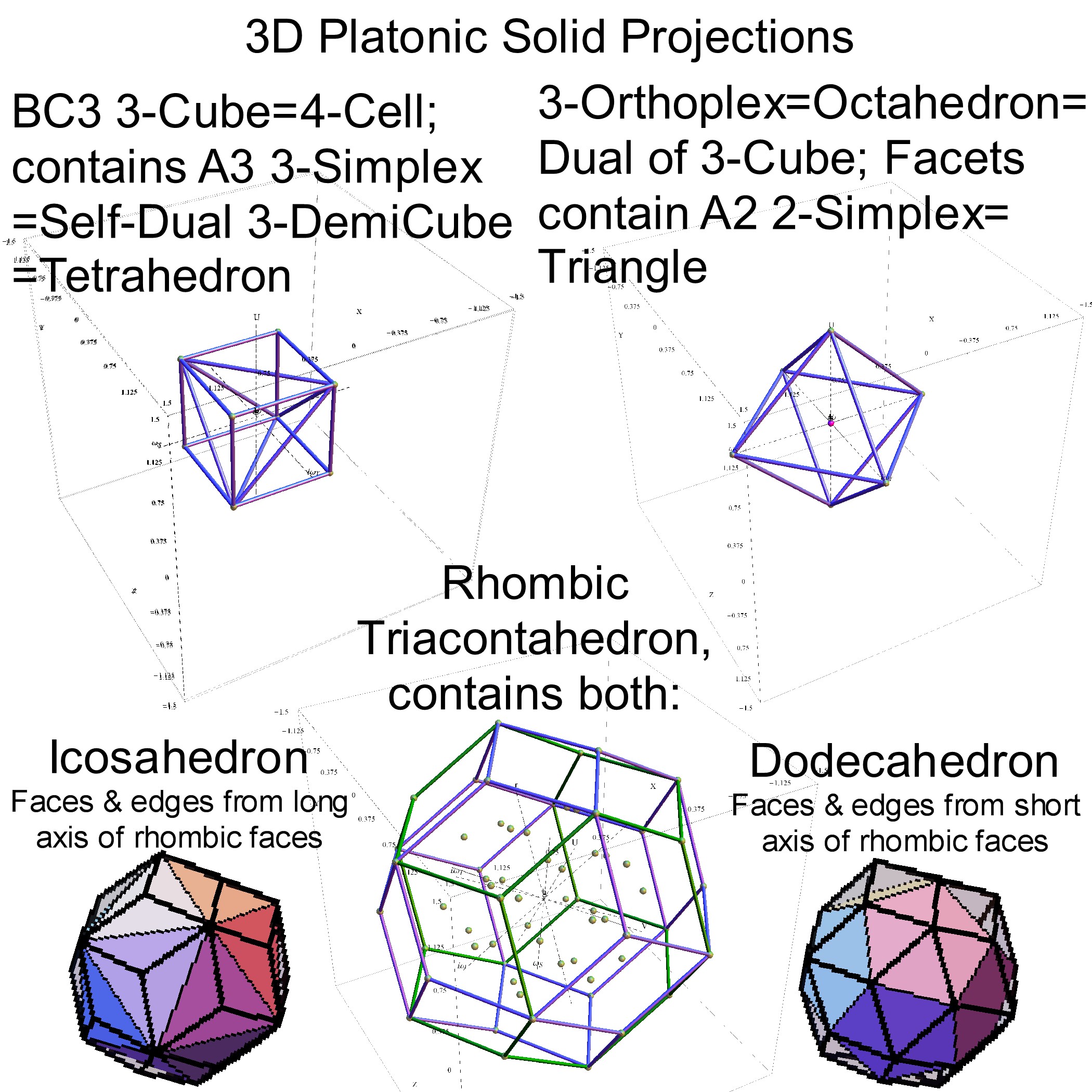
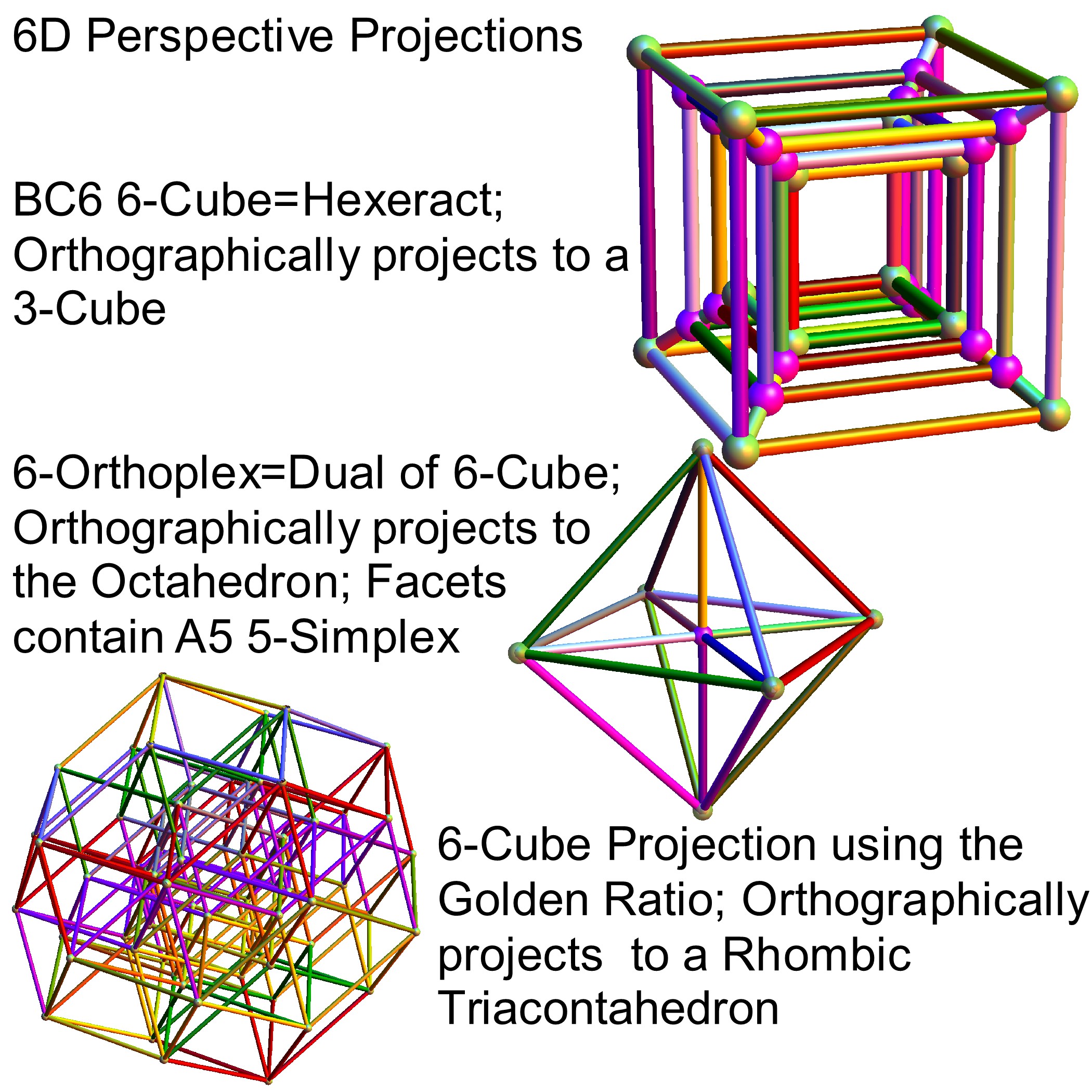
Interestingly, E8 in addition to containing the 8D structures D8 and BC8 and the 4D Polychora, contains the 7D E7, as well as the 6D structures of the Hexeract or 6 Cube. I also showed several years ago that this projects down to the 3D as the Rhombic Triacontahedron. The Rhombic Triacontahedron (of Quasicrystal fame) contains the Platonic Solids including the Icosahedron and Dodecahedron! This is shown to be done through folding of the 6-Cube using rows 2 through 4 of the E8 to H4 folding matrix!!
Mathematica MyToE on the Wolfram Cloud
I am playing around with the Wolfram Tweet-a-Program, and the Wolfram Language (i.e. Mathematica) on the Wolfram Cloud.
What’s really cool is that you can now interact with advanced math and HPC on your phone/tablet.
Here are a few results…
@Wolframtap
BTW – you will need a WolframID (and be logged into WolframCloud.com) to interact with these pages.
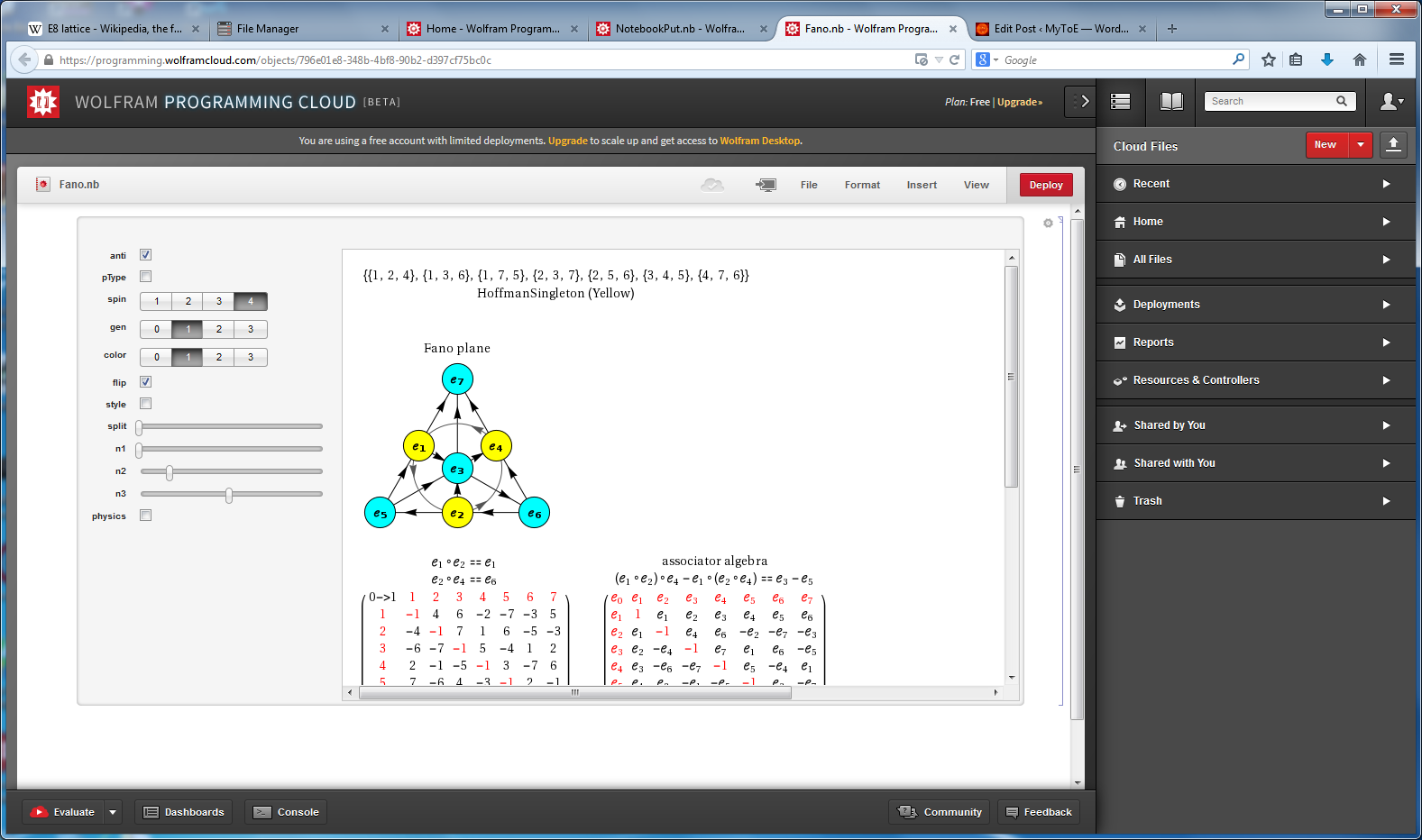
Octonions: The Fano Plane & Cubic
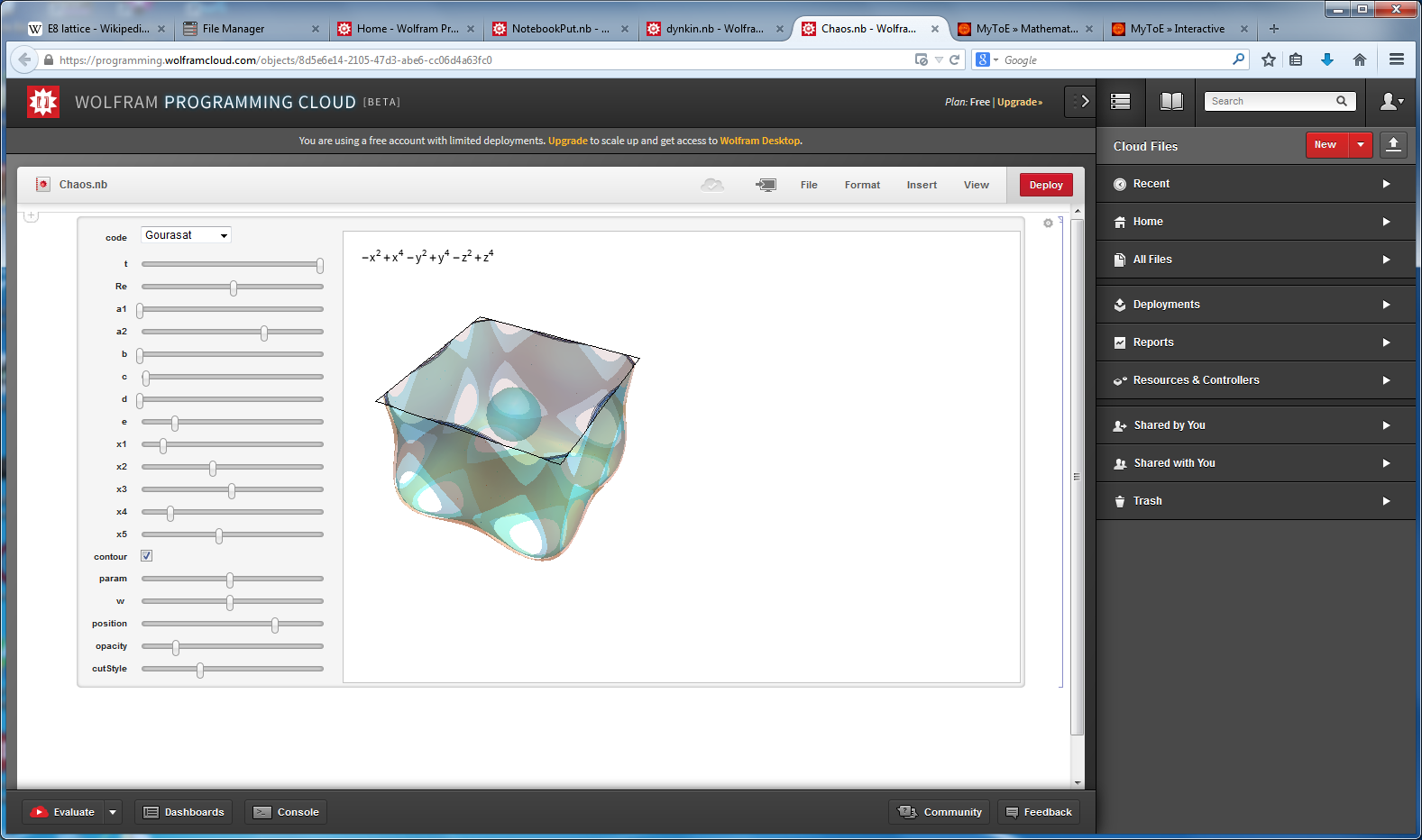
Navier-Stokes Chaos Theory, 6D Calabi-Yau and 3D/4D Surface visualizations
Solar System (from NBody Universe Simulator)
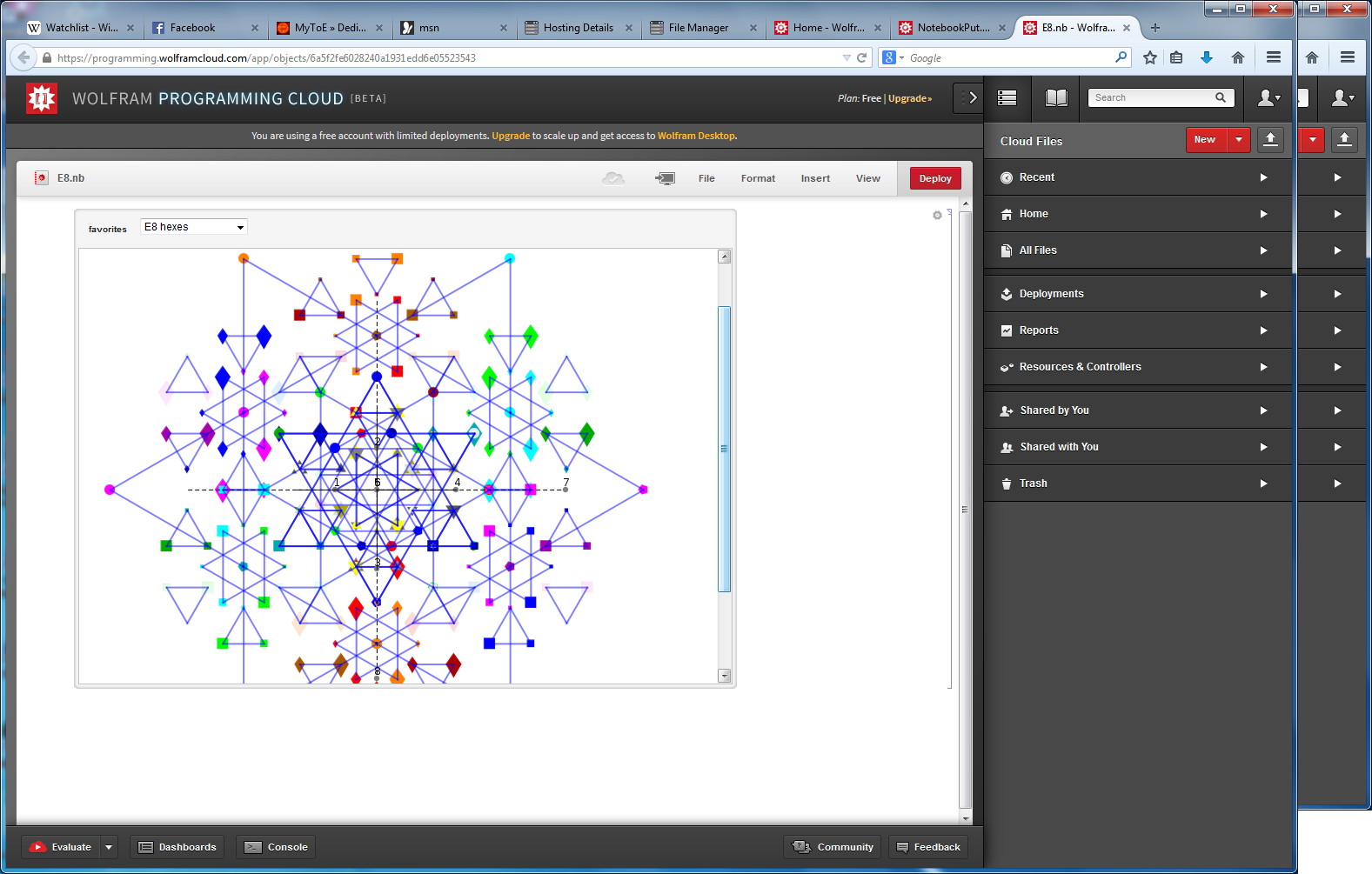
My 2D Petrie projection of E8 with Sqrt(6) edges as a Mandala
E8 projected
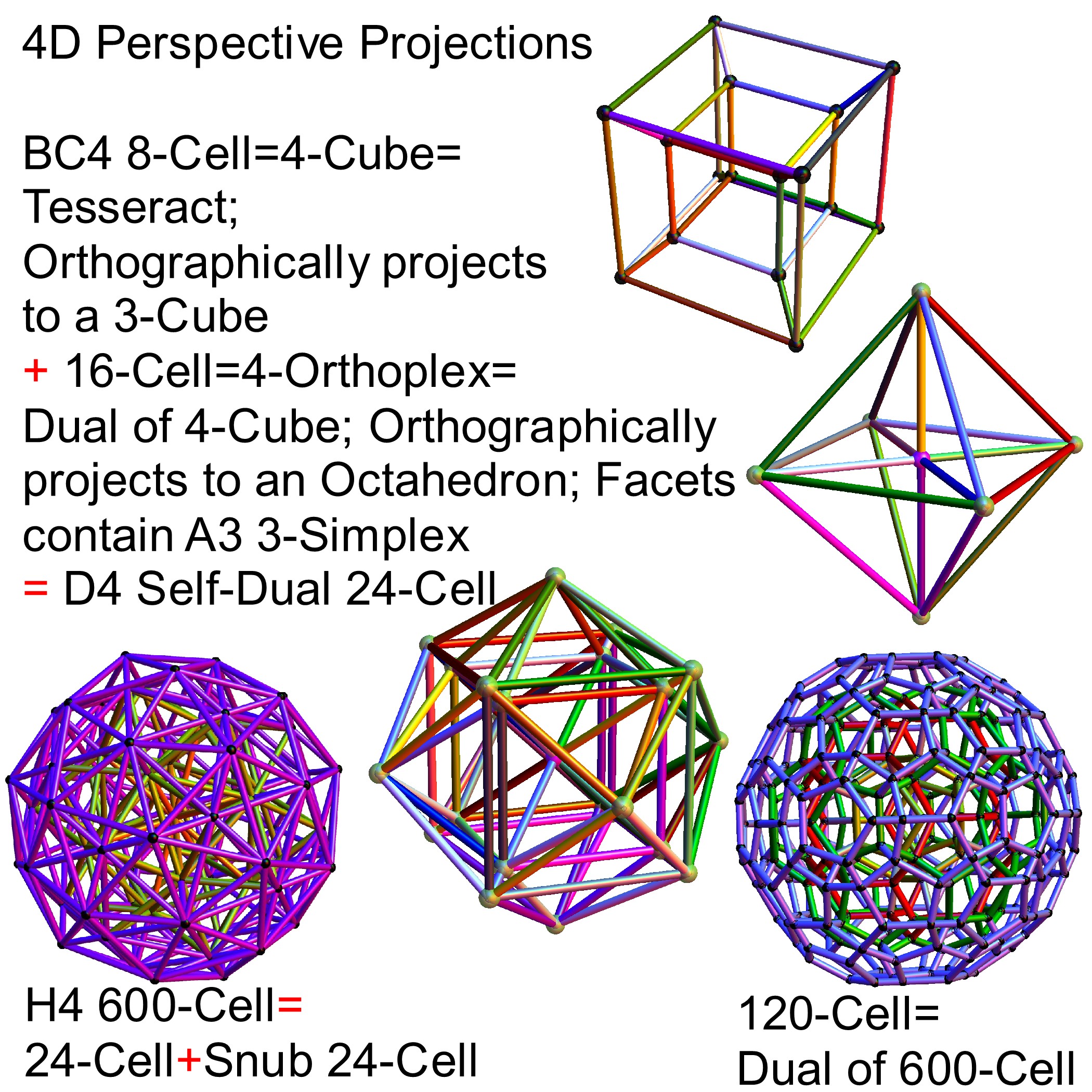
E8 folding to H4+H4/φ
I found the rotation matrix that shows the E8 Dynkin diagram can indeed be folded to H4+H4/φ.
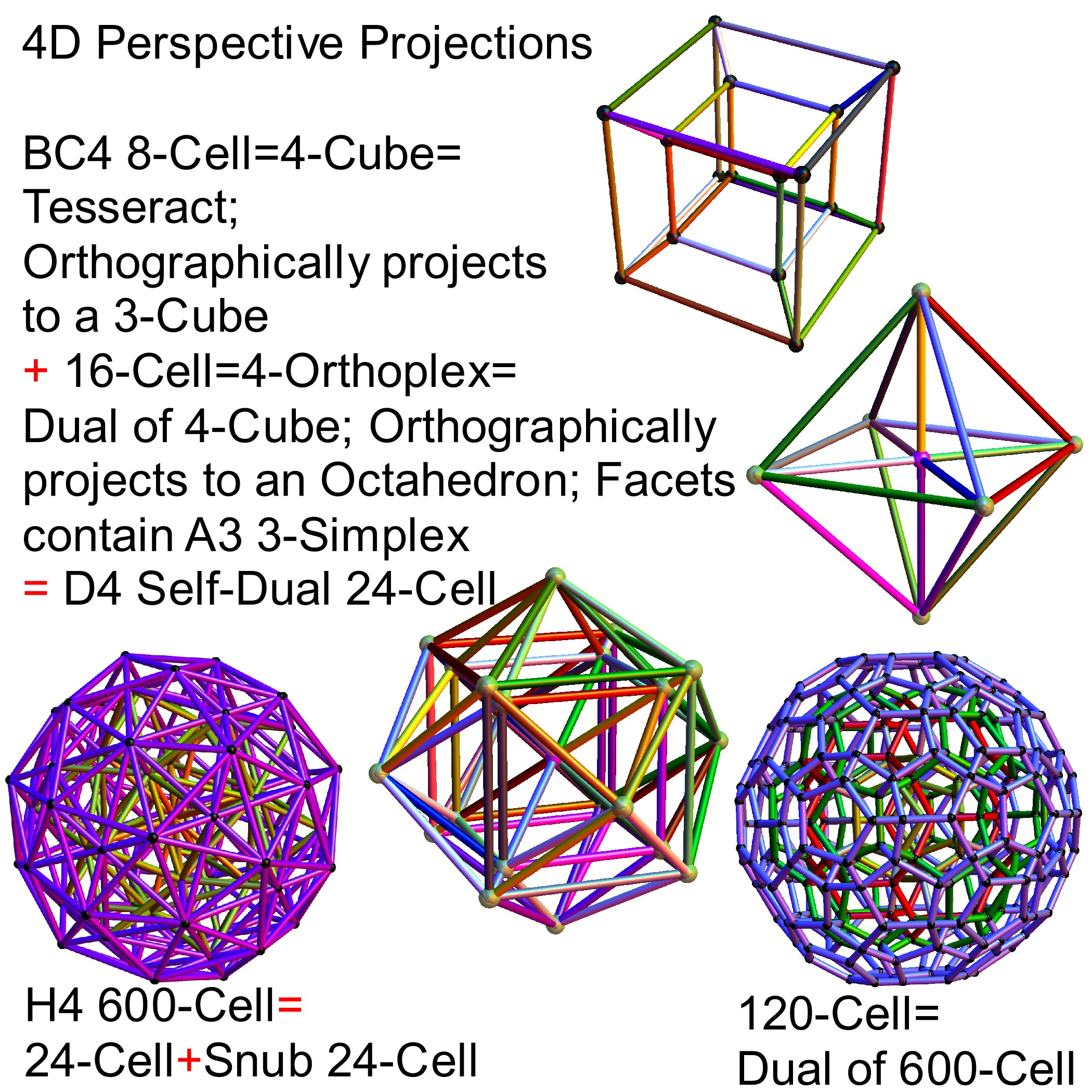
The H4 and its 120 vertices make up the 4D 600 Cell. It is made up of 96 vertices of the Snub 24-Cell and the 24 vertices of the 24-Cell=[16 vertex Tesseract=8-Cell and the 8 vertices of the 4-Orthoplex=16-Cell]).
It can be generated from the 240 split real even E8 vertices using a 4×8 rotation matrix:
x = (1, φ, 0, -1, φ, 0, 0, 0)
y = (φ, 0, 1, φ, 0, -1, 0, 0)
z = (0, 1, φ, 0, -1, φ, 0, 0)
w = (0, 0, 0, 0, 0, 0, φ^2, 1/φ)
where φ=Golden Ratio=(1+Sqrt(5))/2
It is also interesting to note that the x, y, and z vectors project to a hull of the 3D Rhombic Triacontrahedron from the 6D 6 cube Hexaract (which then generates the hull of the Dodecahedron and Icosahedron Platonic solids).
Here’s a look at the Dynkin Diagram folding of E8 to H4+H4/φ:
I find in folding from 8D to 4D, that the 6720 edge counts split into two sets of 3360 from E8’s 6720 length Sqrt(2), but the combined edges and vertices recreate the E8 petrie diagram perfectly.
Some visualizations of this in 8D:
to 4D:
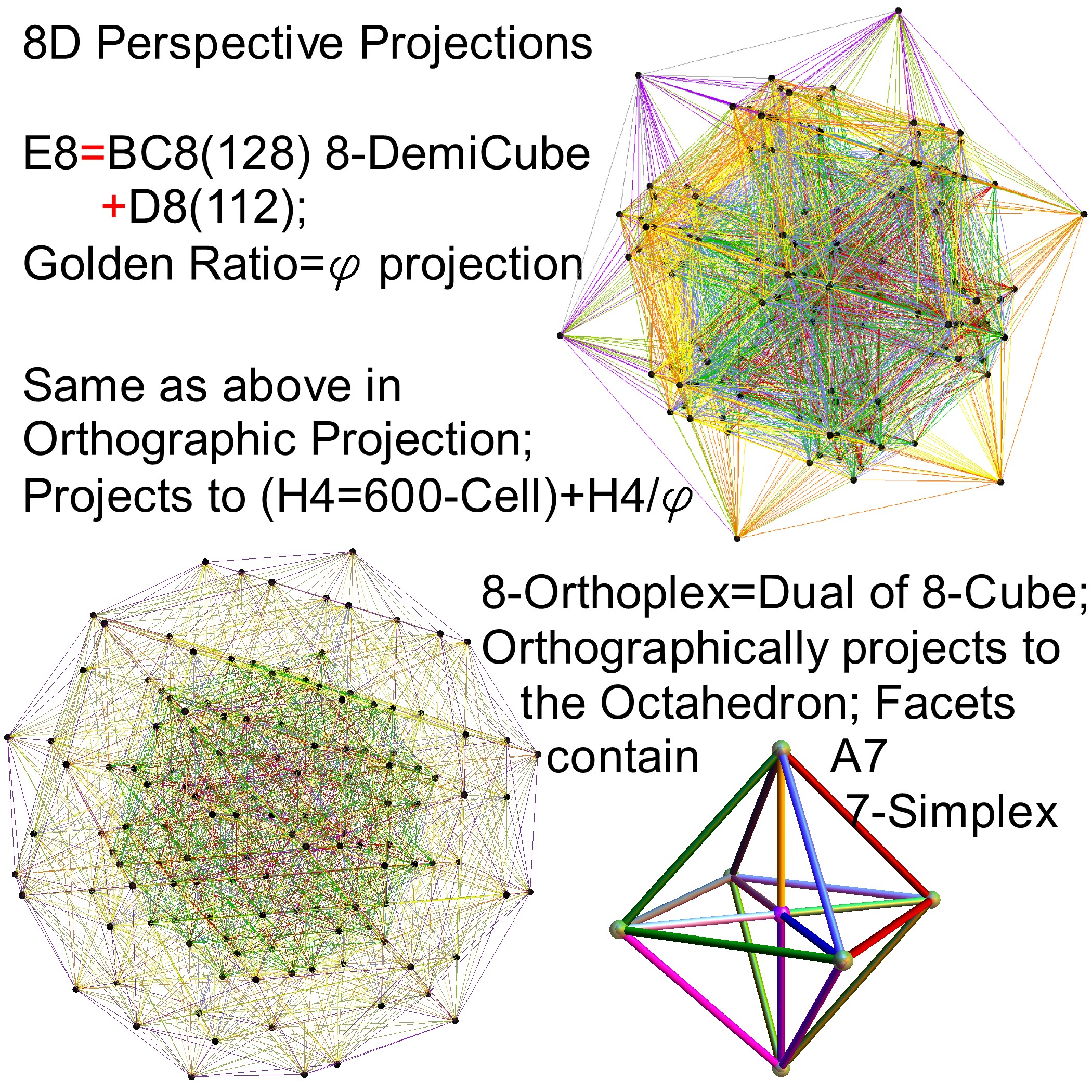
and also showing the Rhombic Triacontrahedron folding from 6D:
to 3D:
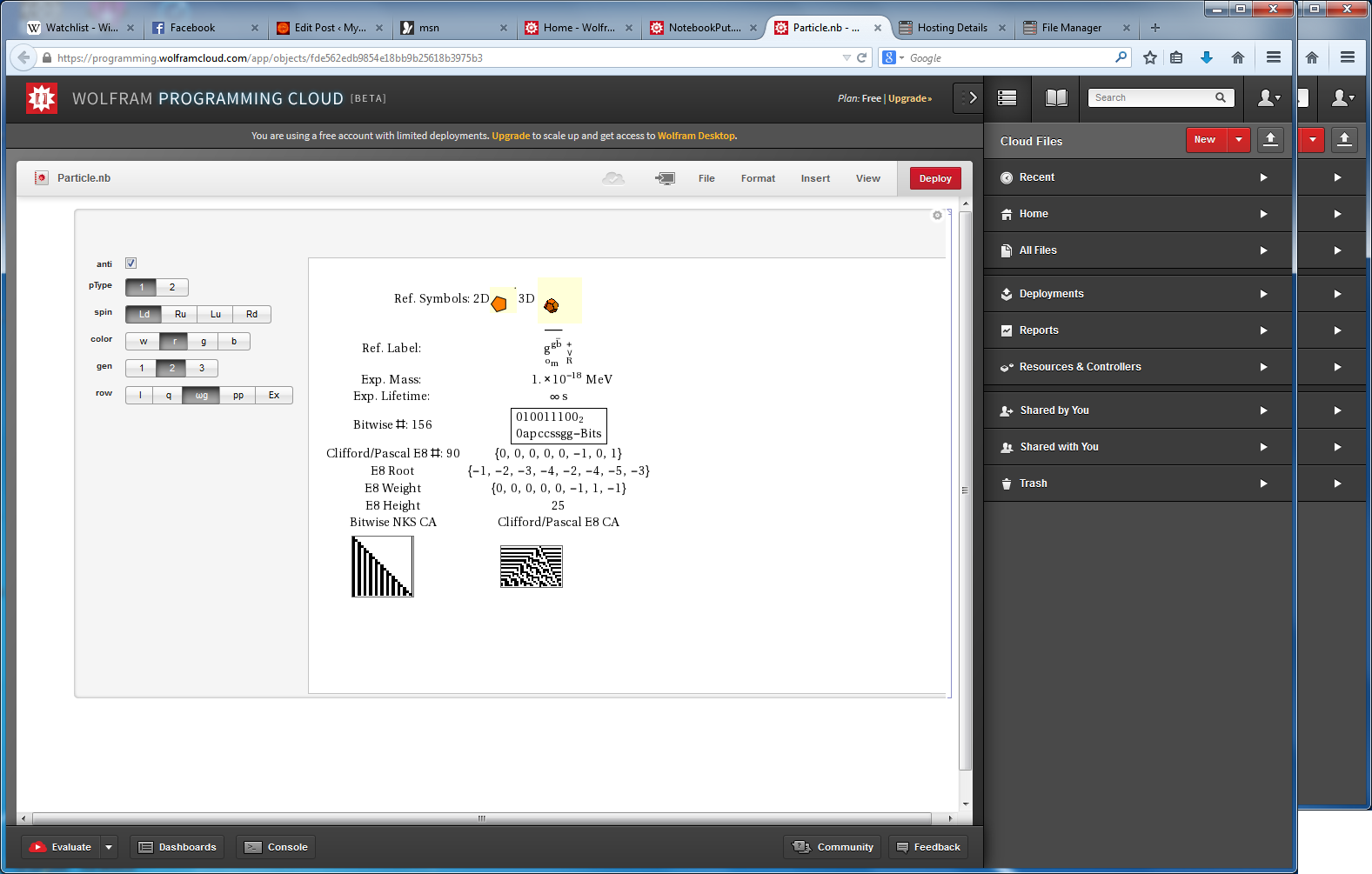
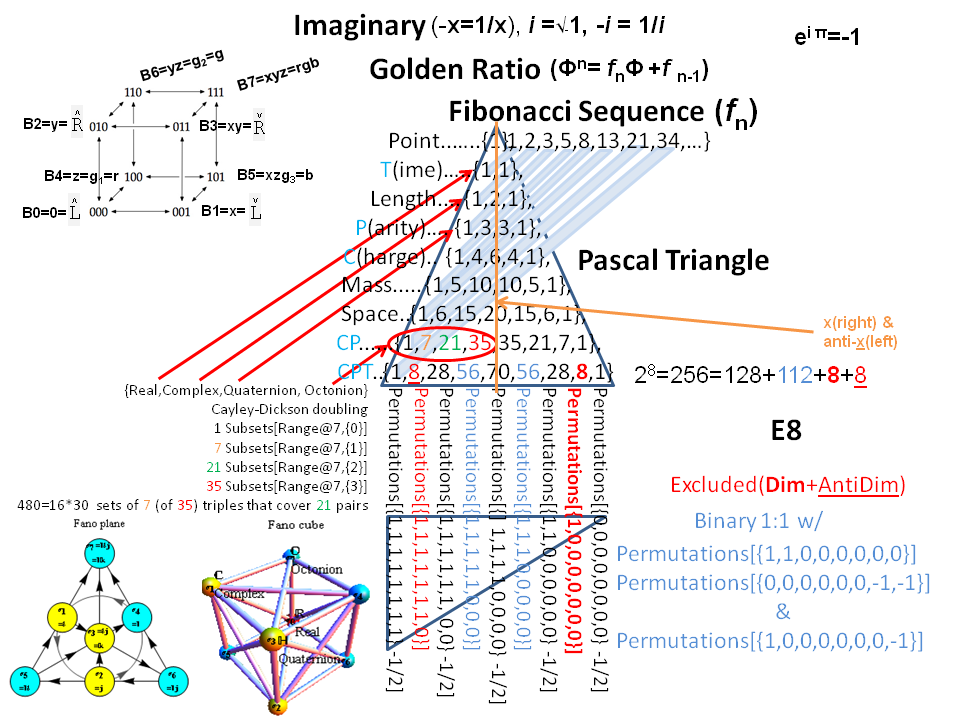
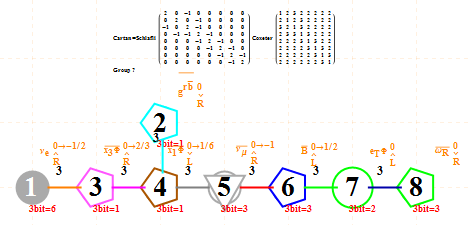
Another look at integrating the Pascal Triangle to Clifford Algebra, E8 Lie Algebra/Groups, Octonions and Particle Physics Standard Model
Modified Lisi split real even E8 particle assignment quantum bit patterns:
Assigning a specific mass, length, time, and charge metrics based on new dimensional relationships and the Planck constant (which defines Higgs mass).
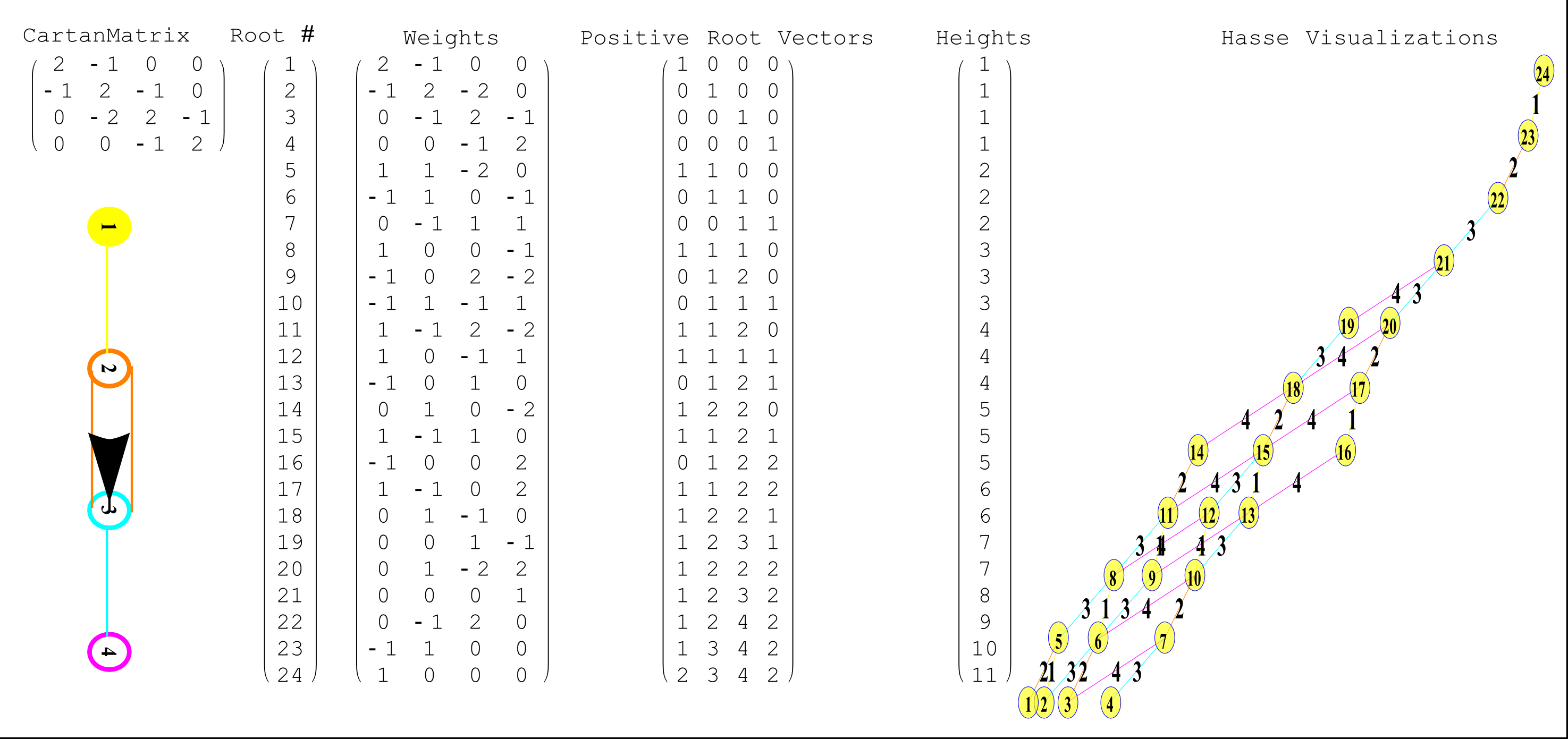
The split real even E8 group used has been determined from this simple root matrix (which gives the Cartan matrix upon dot product with a transpose of itself):
This Dynkin diagram builds the Cartan matrix and determines the root/weight/height with corresponding Hasse diagrams.
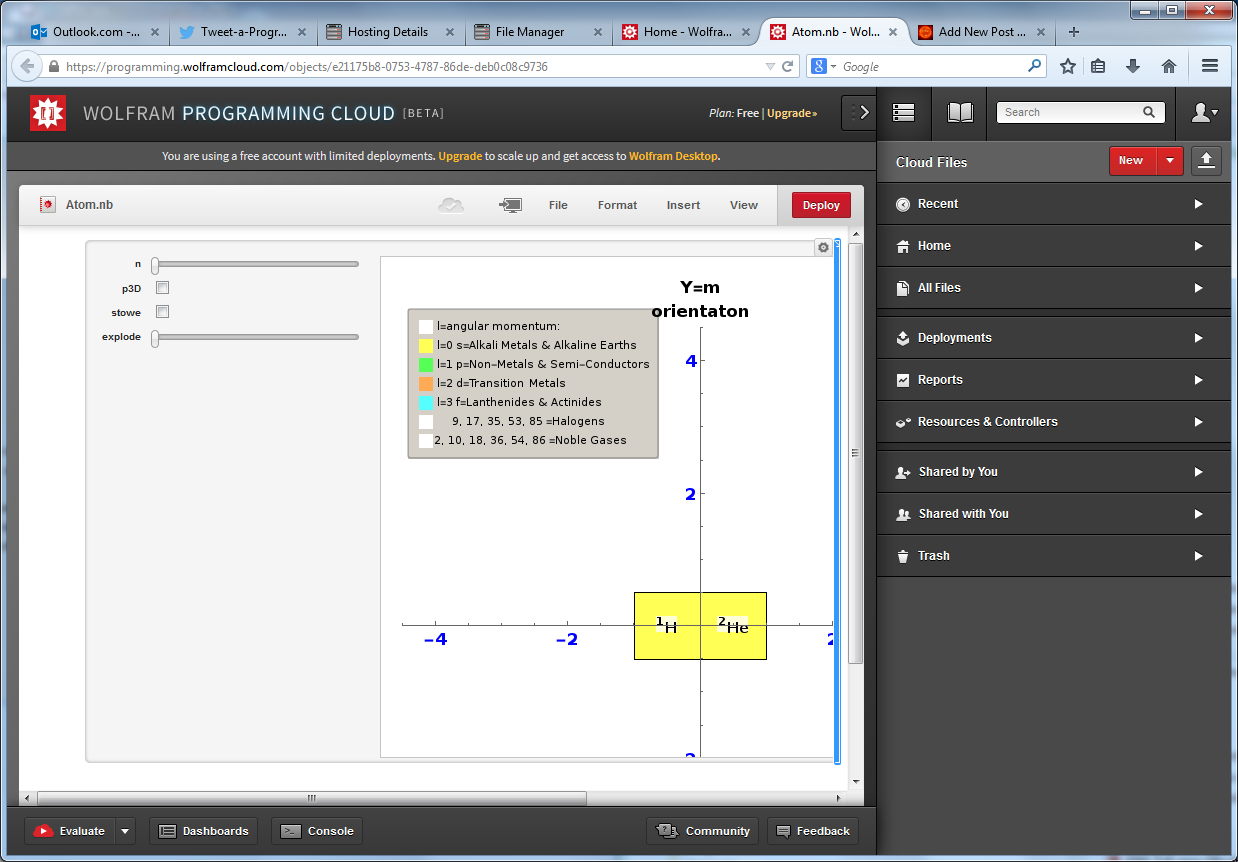
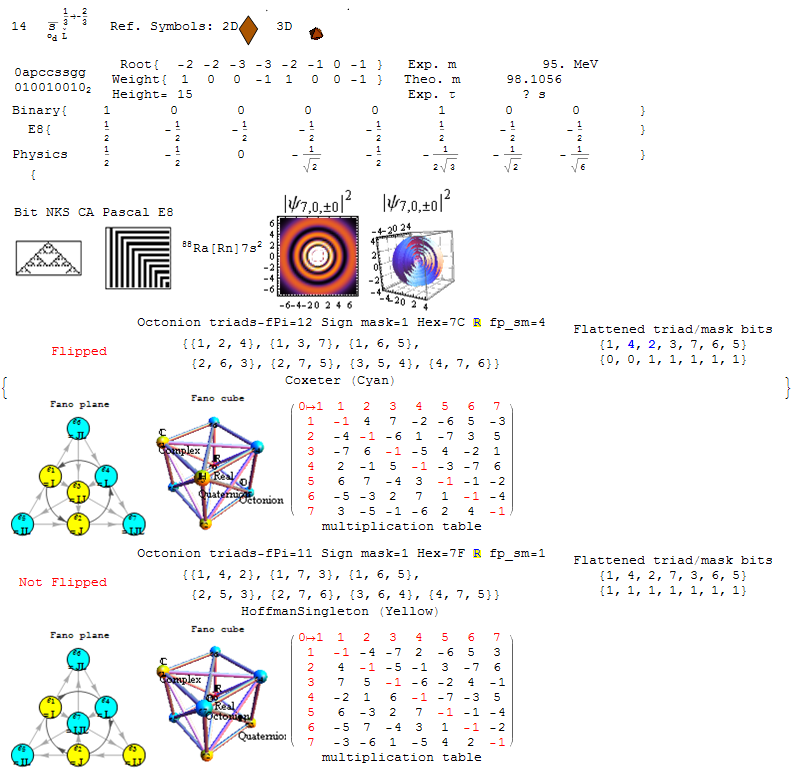
Detail explanation of E8 Integration with Octonions, Particles, and the Periodic Table
Please see Integrated E8, Binary, Octonion for a tutorial that explains the detail of the content of Fano.pdf. It outlines the relationships in the integration of E8 with Octonions, Binary, Particles, NKS, and the Periodic Table of Elements. Other formats are also available (.ppt or .pps and .pdf).
Improved complete index of E8, Binary, Octonions, Particles, NKS CA & Periodic Table
The main change was an improved association of the 120 periodic table elements to the 120 root vectors weighted by their simple root grading. See the full 241 page reference here.
Improved the Hasse Visualizations
I’ve added better edge coloring and added edge root vector information (for the added simple root used).
