The Leech lattice is a sub-quotient of the largest of the sporadic finite simple groups, namely the Monster group. It is related to (and can be constructed by) E₈ and the 23rd Niemeier lattice of E₈³. The 24D Leech lattice is interesting to the physics of sphere packing, error-correcting codes, and possibly unifying General Relativity (GR) with Quantum Mechanics (QM). String theory was founded on the ideas related to its relationship to the Monster group and how 24 dimensions relate to the bosonic energy levels of the partition function on a torus. For more on the Monster and Group Theory, see my post here.

But taking things down a 8D (Bott periodic) notch, roughly speaking the 16D Barnes-Wall lattice is related to E₈ in the same way by BW₁₆=E₈².

I found some very nice recent visualizations on the BW₁₆ WP article by Misaki Ohta with related arXiv papers. He provided links to related code and data here. Below are my renderings using that provided information.

It is interesting to note that if one projects the 61440 2nd shortest 16D vectors of BW₁₆  using orthogonal projection mapping ℝ¹⁶ → ℝ² (i.e. to B₈ basis vectors [x=Cos, y=Sin]@(0-15)π/8 used for E₈ below vs. the proper (0-15)π/16 B₁₆ as done above), we get a similar result as projecting the 2nd shortest 8D vectors of E₈ using the same basis shown as grey vertices in Fig 2 of arXiv:2506.11725:

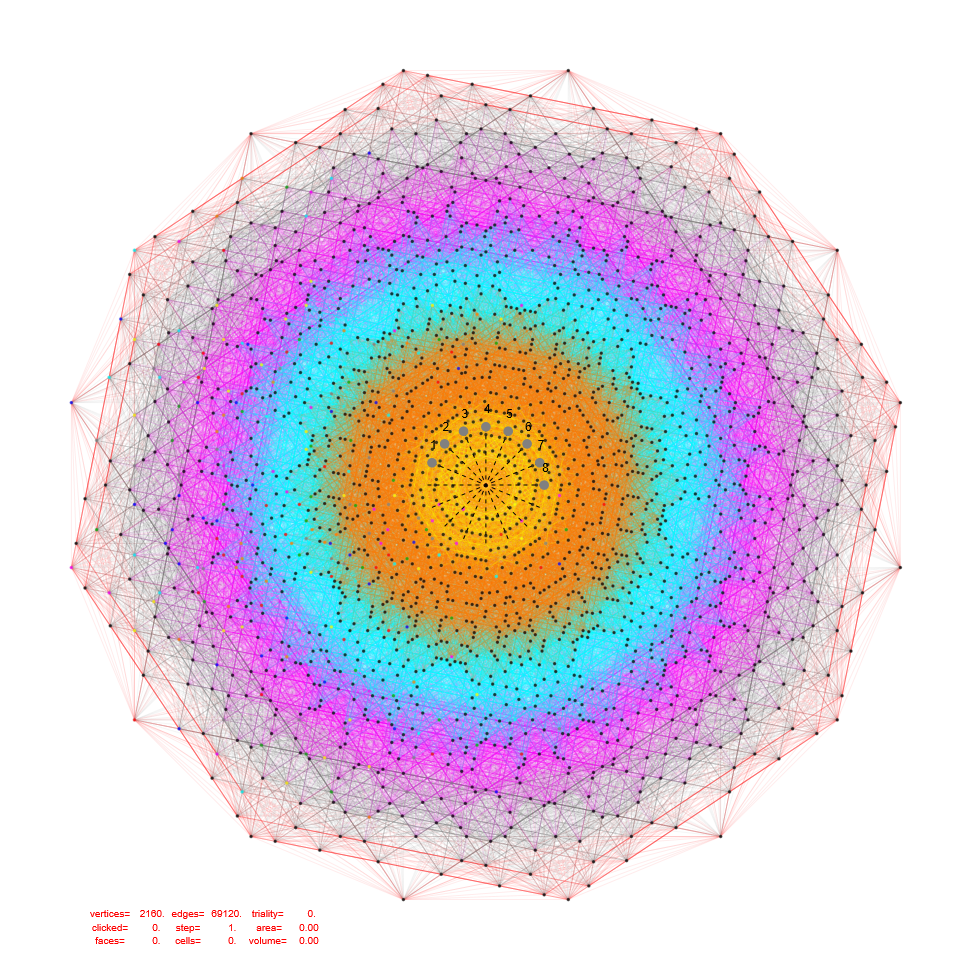
Projecting the 2160 2nd shortest 8D vectors of E₈ using the B₈ basis vectors including 69120 edges of 8D norm=√8 with colors assigned by projected edge length (notice the similarity in the vertex locations of the figure above):

Projecting the 4320 shortest 16D vectors of BW₁₆  using orthogonal projection mapping ℝ¹⁶ → ℝ² using the B₈ basis vectors [x=Cos, y=Sin]@(0-15)π/8 gives the results shown in Fig. 2 as red and blue vertices:

This time with edges colored by projected edge lengths:

Now, getting creative with the 16D projections of the 4230 BW₁₆, if we double the E8 Petrie basis vectors we get a similar result with 480+1 visible vertices with one at the origin w/240 overlapping vertices. There are 240 yellow with no overlaps and 240 blue with 16 overlaps each. There are 604800 norm=4 edges using roughly the same color pallet as my WP E₈ Petrie image. This makes it easier to see the difference between the 4230 BW₁₆ and the normal E₈ Petrie projection, which seem to share the grid-like pattern of the 24-cells within the folded E₈ = H₄ + φ H₄ :

This is the same as above, but using the 61440 vertex BW₁₆ with no edges (given there are millions of them). Please note that the number of visible vertices is the same as E8₂₄₁ at 2160!