Please see my latest paper here.

It adds information related to my previous blog post here.

Abstract: Previously, a determination of the relationship between the Natural numbers (N) and the n’th odd fibbinary number has been made using a relationship with the Golden ratio phi=(Sqrt[5]+1}/2 and tau=1/phi. Specifically, if the n’th odd fibbinary equates to the j’th N, then j=Floor[n phi^2 – 1]. This note documents the completion of the relationship for the even fibbinary numbers, such that if the n’th even fibbinary equates to the j’th N, then j=Floor[n phi]-1, starting at j=0 for n=1. Alternatively, starting at j=2 for n=1, then j=Floor[n phi + tau].

Title:Even FibBinary Numbers and the Golden Ratio
Authors: J Gregory Moxness
Comments: Dec 31 2018, 5 pages, 4 Figures.
Subjects: Combinatorics

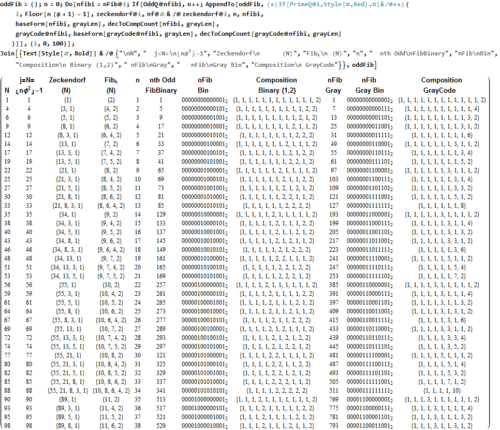
Below is a listing of the N integers represented by their 38 odd FibBinaries, along with the binary and Gray code Compositions.

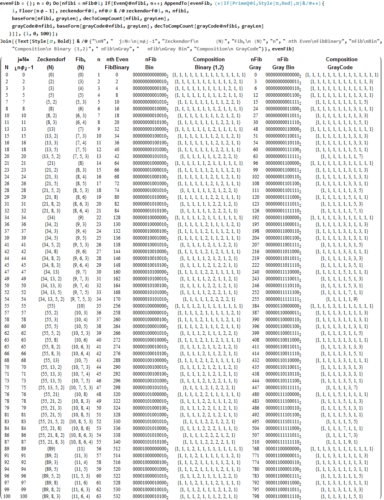
Below is a listing of the first 63 N integers represented by their even FibBinaries, along with the binary and Gray code Compositions.

Code output examples:

Mathematica Code Snippets:

I was prompted by Chris Birke to take a look at this very interesting paper by Linus Lindroos. Chris is working with my E8 to H4 Folding Matrix for optimizing computation using network theory and hyper-dimensional geometric structures.

I was able to validate the paper with some quick Mathematica code.

Below is the code that sets up the generation of the tables, including various binary, numeric, and symbolic (graph) Compositions.

Notice the last statement (above) lists the odd FibBinaries (up to N=200) as related to the Floor of the n*Phi^2-1, with n=1 to 77.

Below is a listing of the first 100 N integers represented by their odd and even FibBinaries, along with the binary and Gray code Compositions.