Tag Archives: 4D

Physics

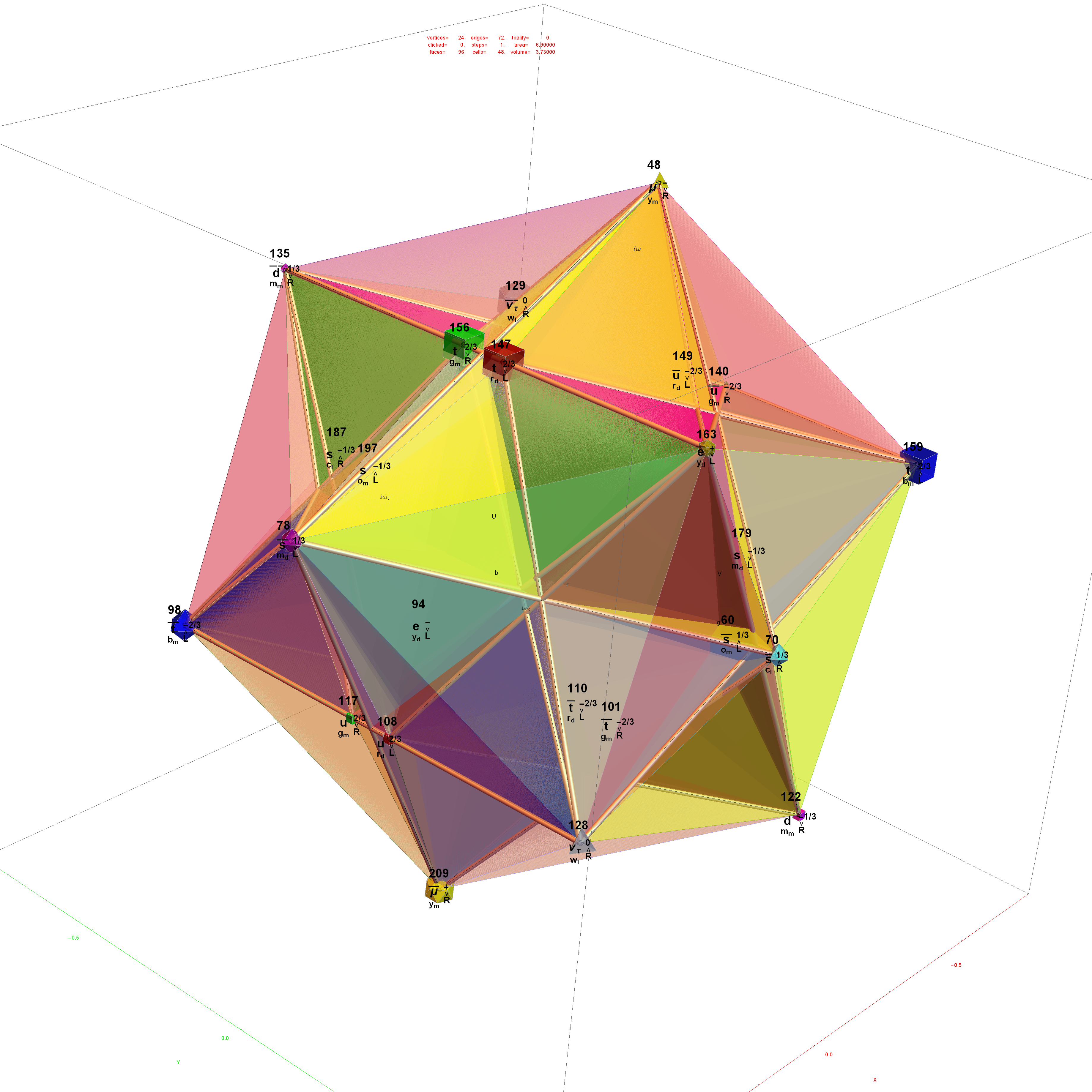
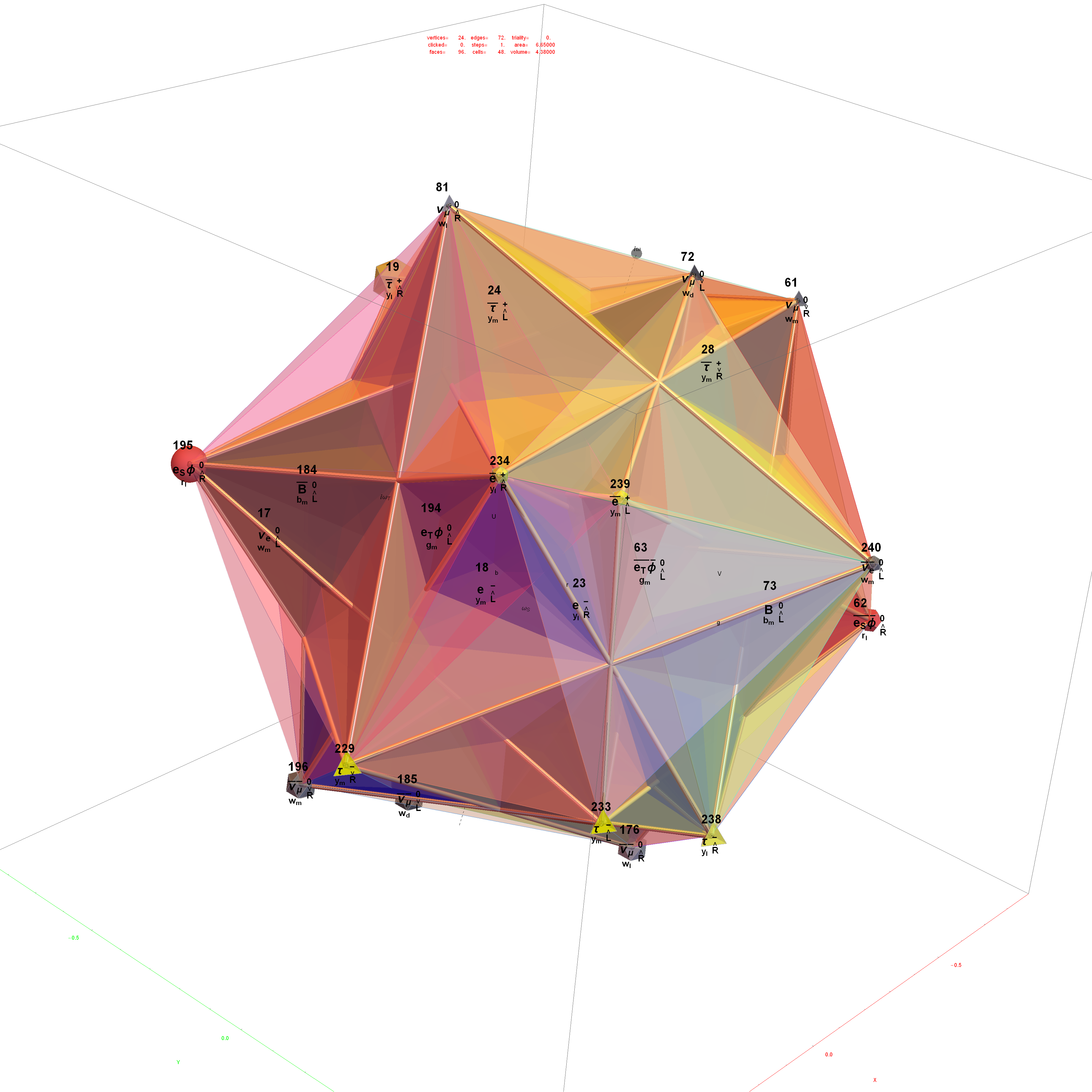
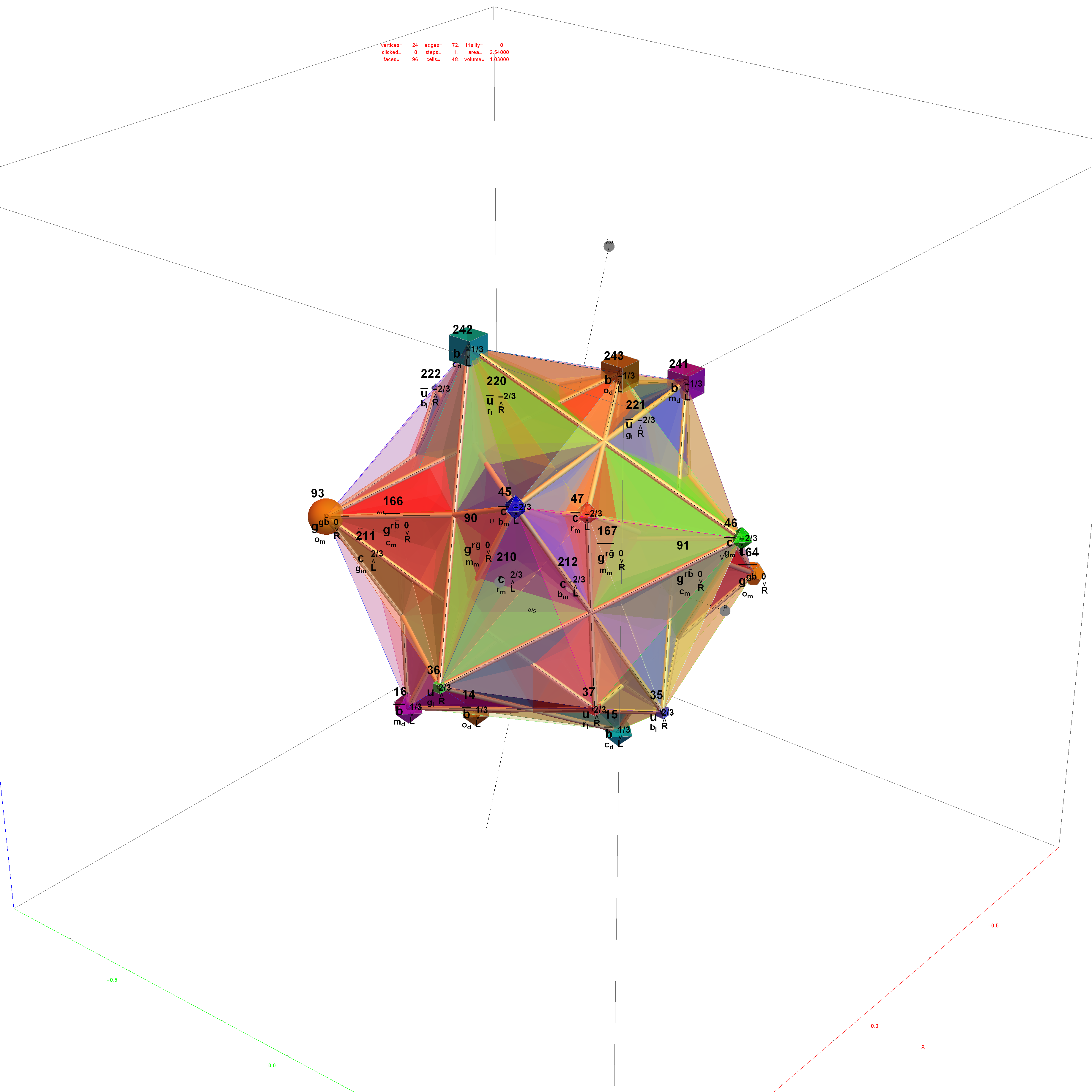
Comparing nearest edges between Split Real Even (SRE) E8

Leave a comment

I have been intrigued with Richter’s arXiv 0704.3091 “Triacontagonal Coordinates for the E8 root system” paper.

Comparing nearest edges between Split Real Even (SRE) E8 and Richter’s Complex 4D Golden Ratio Petrie Projection Model:

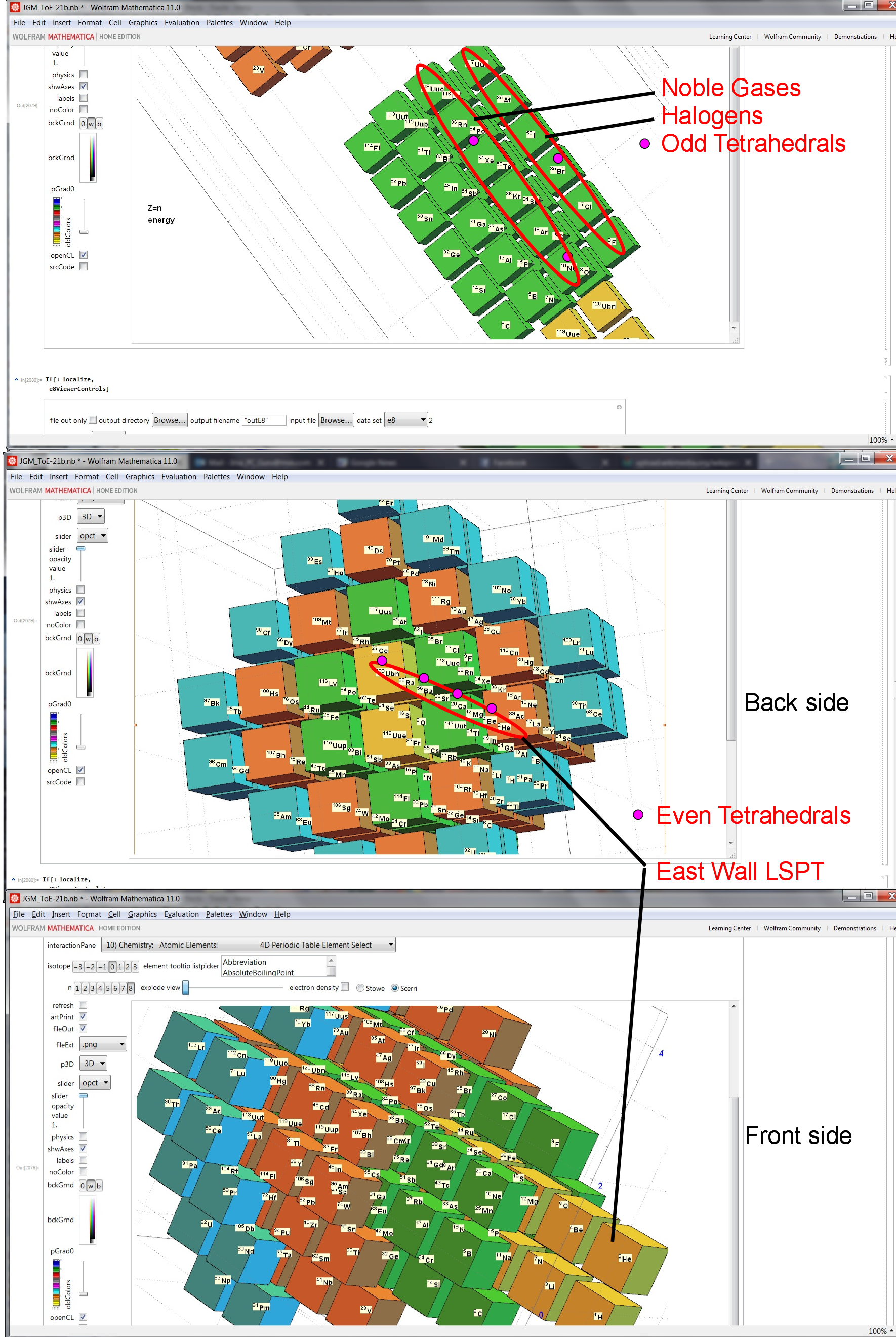
Please note, the vertex numbers are reordered from Richter’s paper in order to be consistent with ArXiv quant-ph 1502.04350 “Parity Proofs of Kochen-Specker theorem based on the Lie Algebra E8” by Aravind and Waegell. This paper uses the beautiful symmetries of E8 as a basis for proof sets related to the Bell inequalities of quantum mechanics. Below is a graphic showing that vertex number ordering:

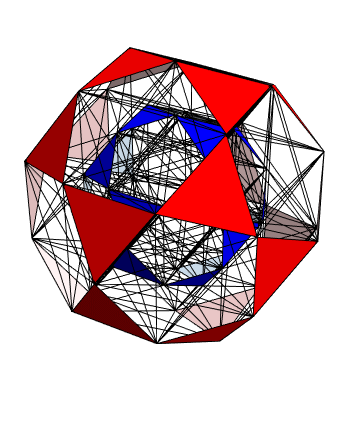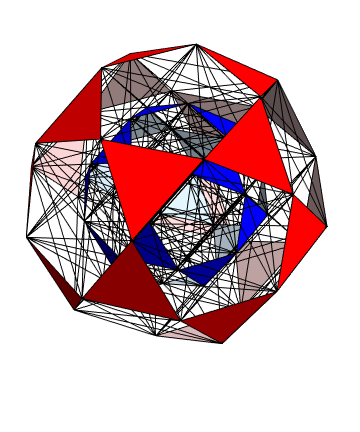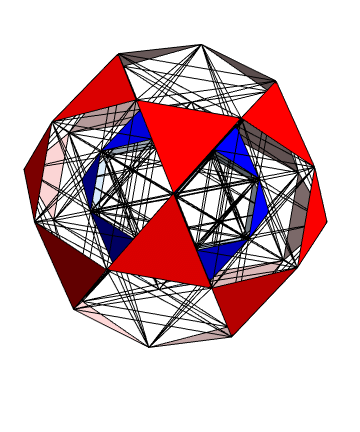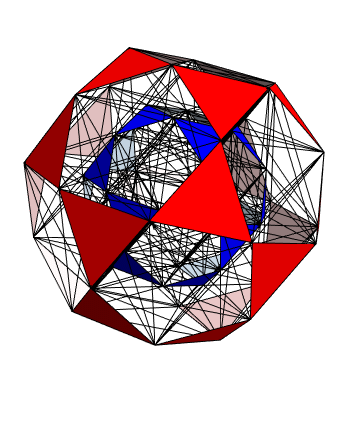
Richter’s model with 74 nearest edges per vertex (Complex 4D Norm’d length Sqrt[2], with 8880 total):

Richter’s model with only 26 nearest edges per vertex (Complex 4D Norm’d length 1, 3120 total):

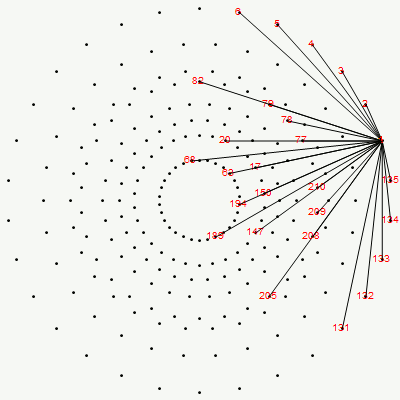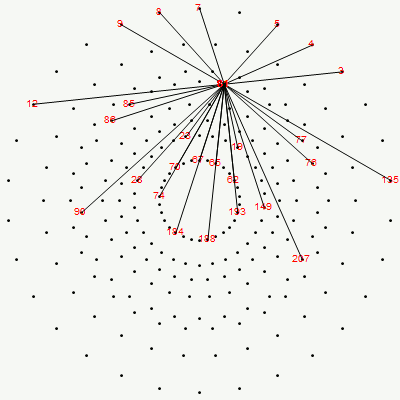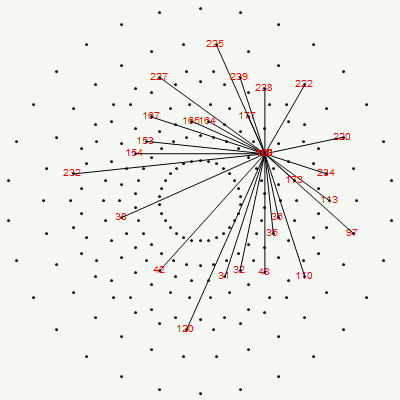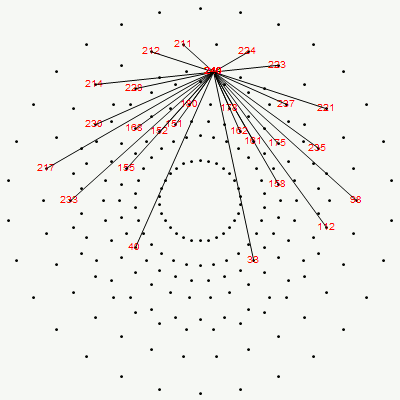
The above unity length edge pattern has is more consistent with the SRE E8 below.

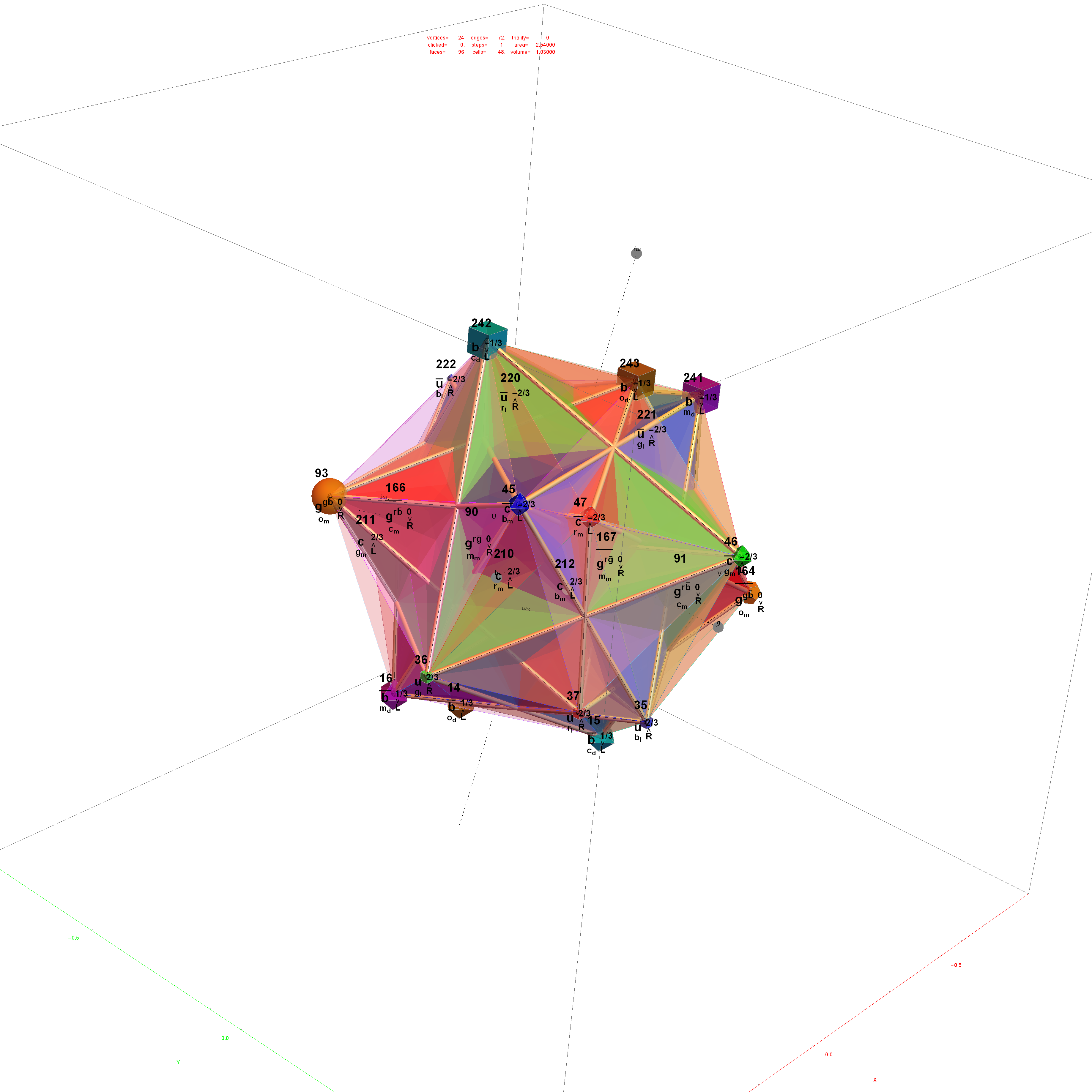
The SRE E8 Petrie Projection (with 56 Norm’d edge length Sqrt[2] for each vertex, 6720 total). This is equivalent to folding E8 to H4 with an 8×8 rotation matrix which creates a 4D-left H4+H4*Phi and a 4D-right H4+H4*Phi.

Please note, the vertex number is that of the E8 vertices rotated (or “folded”) to H4 in 2D Petrie projection. The vertex numbers are in canonical binary order from E8’s 1:1 correspondence with the 9th row of the Pascal Triangle (eliminating the 16 generator/anti-generator vertices of E8 found in the 2nd and 8th column of the Pascal Triangle). The graphic below shows the vertex number ordering:

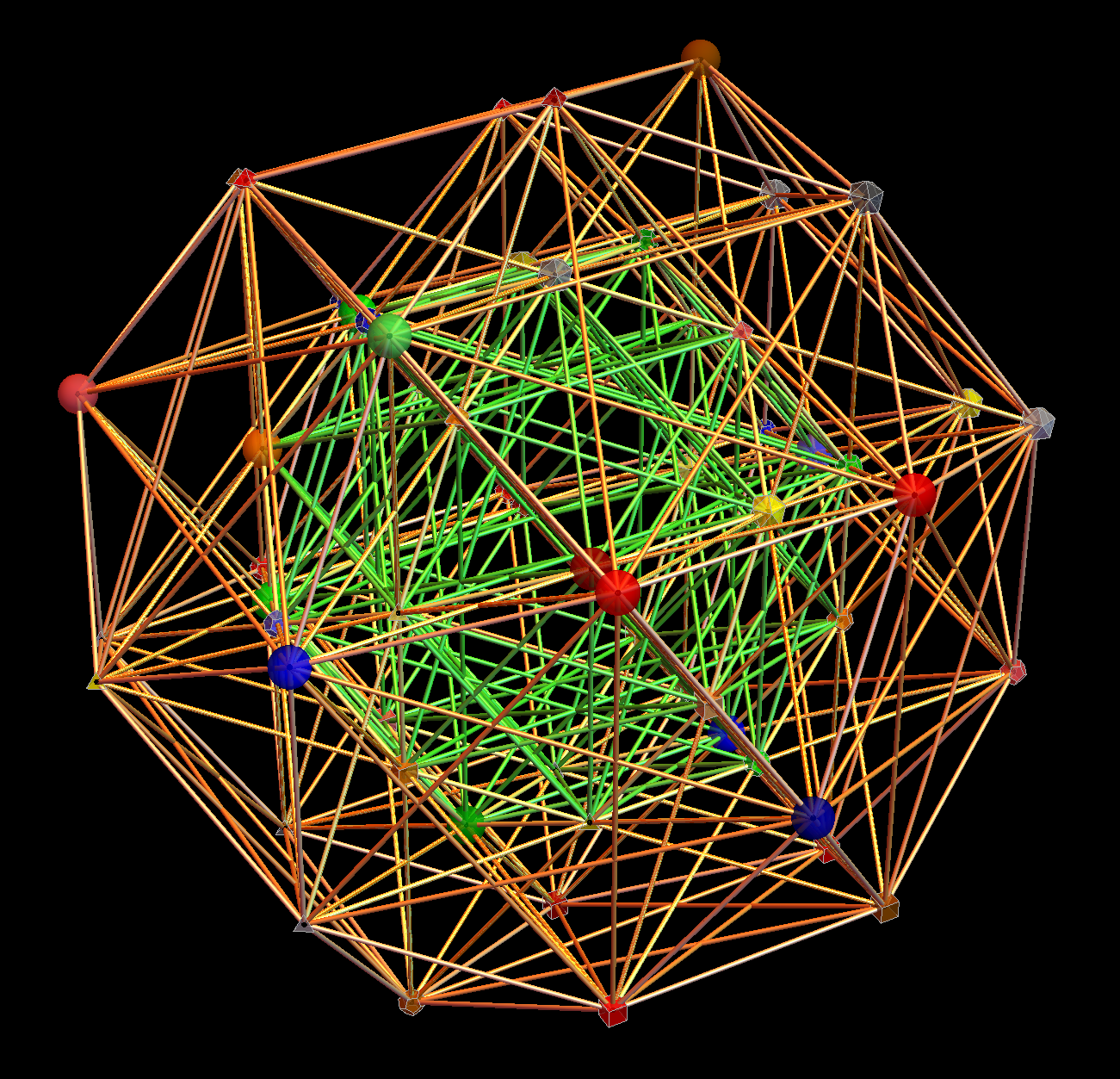
Here we take the 4D-left half and project to two concentric rings of H4 and H4 Phi (Golden Ratio) with 56 nearest edges per vertex (Norm’d length of unity or Phi for each vertex):

The animation frames are sorted by the ArcTan[y/x] of the vertex position in each ring (sorted H4*Phi outer to inner, then H4 outer to inner).

BTW – if you find this information useful, or provide any portion of it to others, PLEASE make sure you cite this post. If you feel a blog post citation would not be an acceptable form for academic research papers, I would be glad to clean it up and put it into LaTex format in order to provide it to arXiv (with your academic sponsorship) or Vixra. Just send me a note at:  jgmoxness@theoryofeverthing.org. 

Philosophy, Physics

Universal Time’s Arrow as a Broken Symmetry of an 8D Crystallographic E8 folding to self dual H4+H4φ 4D QuasiCrystal spacetime

Leave a comment

Animations of Wolfram’s Cellular Automaton rule 224 in a 3D version of Conway’s Game of Life.

While this does not yet incorporate the E8 folding to 4D H4+H4φ construct, the notion of applying it, as the title suggests, to a fundamental particle physics simulation of a “Quantum Computational Universe” or an emergent (non)crystallographic genetic DNA (aka. Life) is an interesting thought…

Watch a few notional movies, some in left-right stereo 3D. Best viewed in HD mode.

More to come, soon!
outAI2

These are snapshots of all the different initial conditions on the rule 224. Each set of 25 has a different object style and/or color gradient selection.
AI 1-25

AI 26-50

AI 51-75

AI 76-100

AI 101-125

AI 126-150

AI 151-175

AI 176-200

AI 201-225

AI 226-250

AI 251-253

Physics

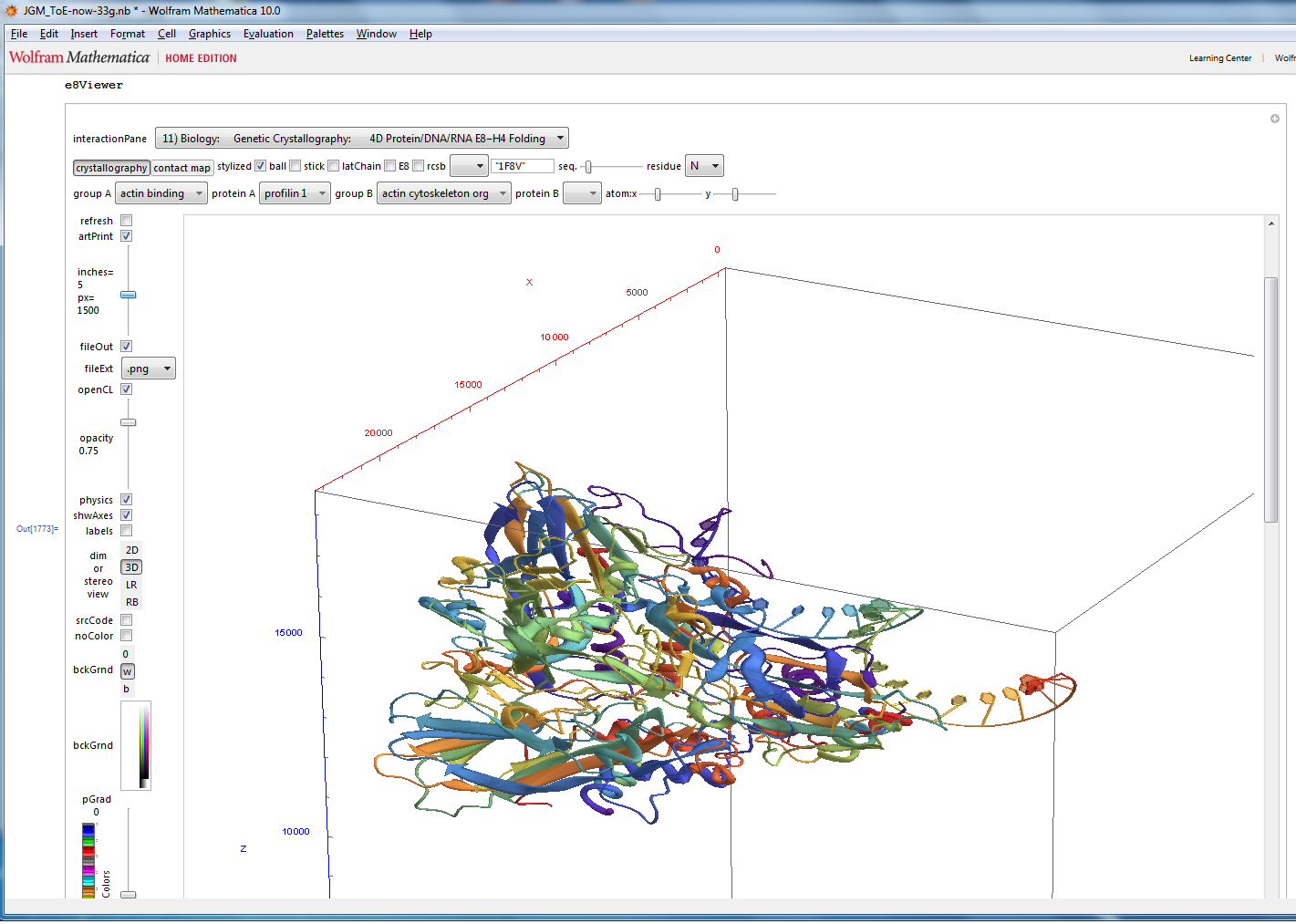
Playing around visualizing non-crystallographic DNA/RNA

Leave a comment

I’ve got interaction between the DNA/RNA protein visualizations (e.g. “1F8V- PARIACOTO VIRUS REVEALS A DODECAHEDRAL CAGE OF DUPLEX RNA) with the VisibLie_E8 projections of crystallographic E8 to non-crystallographic H4 (and to dodecahedral H3 in 3 dimensions, of course).

These pics are a simple (naive) merge of the D6 projected using the E8 to H4 folding matrix and the Protein DB at http://www.rcsb.org/ for 1F8V).

outE80prot

DNAscreen

outDNA

outDNAprot

Physics

D6 projected to 3D using the E8 to H4 Folding Matrix

Leave a comment

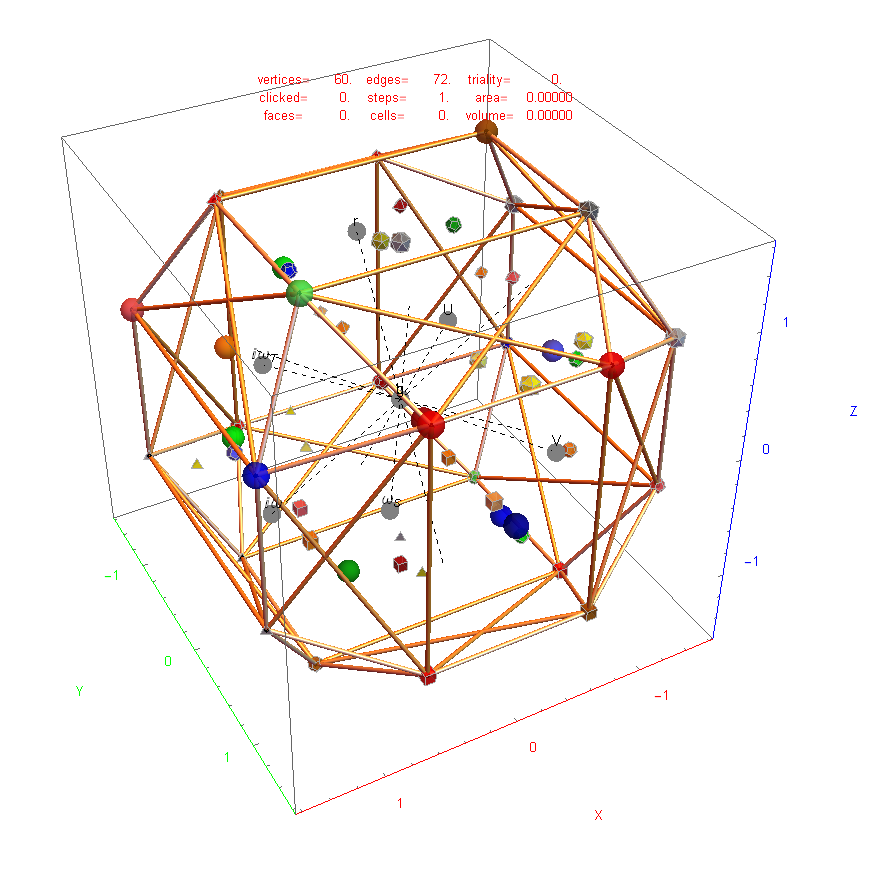
This blogs.ams.org/visualinsight article is an American Mathematical Society post based on some of my work. I’ve made an animation of the D6 polytope with 60 vertices and 480 edges of 6D length Sqrt(2). It is similar to the one in the article by Greg Egan. This version was made from my VisibLie E8 demonstration software.

Best viewed in HD mode.

The process for making this using the .nb version of VisibLie E8 ToE demonstration:
1) Side menu selections:

  • slide “inches” to 4 (lowers the px resolution)
  • select “3D”
  • set bckGrnd “b” (black)
  • uncheck the shwAxes box
  • check the physics box (to give it interesting vertex shapes/colors)
  • change the fileExt to “.avi” and check the fileOut box (to save the .avi)
  • check the artPrint box (to give it cylinder-like edges)

 

2) Go to the #9) HMI nD Human Interface pane:
2a) Top menu selections:

  • set pScale to .08 (to increase the vertex shape sizes)

2b) Inside the pane selections:

  • set “eRadius” to .01 (for thicker edge lines)

 

3) Go to the #2) Dynkin pane and interactively create (or select from the drop down menu) the D6 diagram.
BTW – this actually selects the subset of vertices from the E8 polytope that are in D6.
 

4) Go to the #3) E8 Lie Algebra pane:
4a) Top menu selections:

  • E8->H4 projection
  • check the edges box
  • “spin” animation
  • 30 animation “steps”

or simply upload this file or copy / paste the following into a file with extension of “.m” and select it from the “input file” button on the #9 HMI nD Human Interface pane.

(* This is an auto generated list from e8Flyer.nb *)
new :={
artPrint=True;
inches=4;
physics=True;
p3D=” 3D”;
bckGrnd=GrayLevel[0];
fileExt=”.avi”;
shwAxes=False;
scale=0.08;
selPrj=”E8->H4″;
lie=”D6″;
cylR=0.01;
showEdges=True;
steps=30;
pthRot=”Spin”;
selPrj=”E8->H4″;
p3D=” 3D”;
};new;

In the next version I will just make this another “MetaFavorite”, so it will be in the dropdown menu in all versions.
Enjoy!
D6-3Da

Physics

Fun with 8D rotations of E8

Leave a comment

This is a little clip containing three different 8 dimensional rotations of E8. While it may seem like a simple rotation of an object in 3-space, if you look carefully (especially the first rotation), you can see sets of vertices moving in different directions.

The object (the 240 vertices of E8 along with 1220 of 6720 edges of 8D length Sqrt[2]) is not “moving”. It is the camera that is moving in an 8 dimensional space.

Best when viewed in HD!

The previous 3D animations here and here are created by projecting the 8 dimensional object of E8 into 3 and simply rotating (spinning) that object around in 3-space. I like to call those animations 4D, since animation visualizes changes over time – a 4D space-time object if you will…