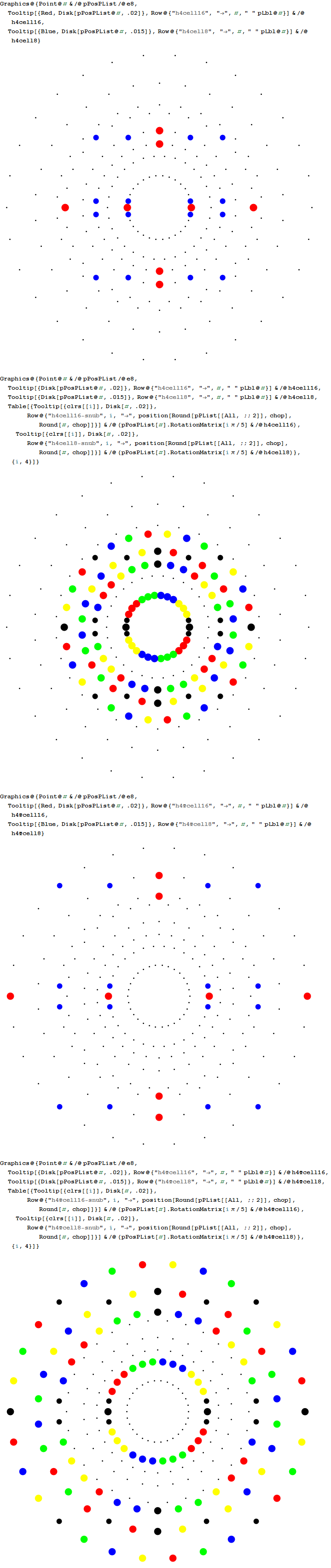
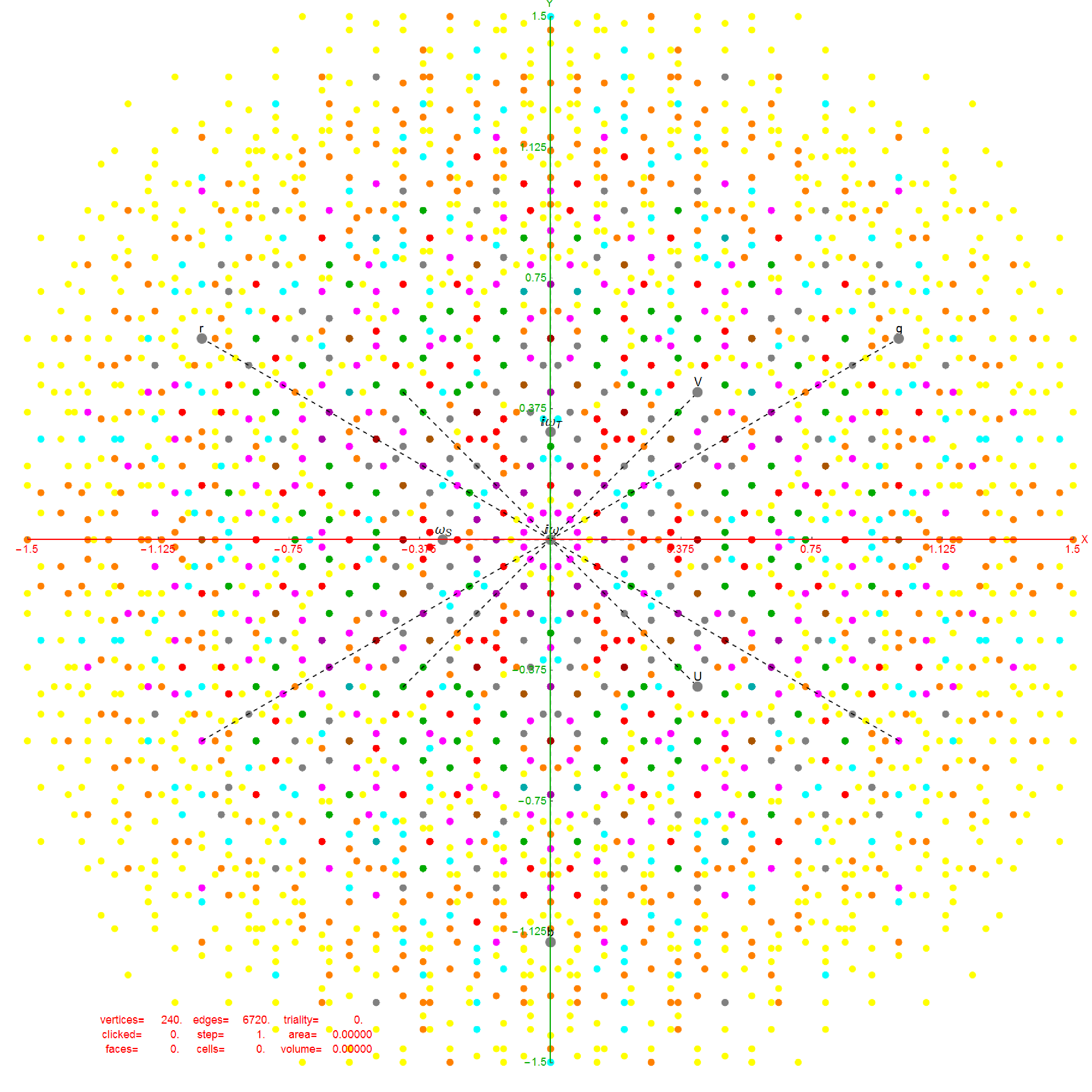
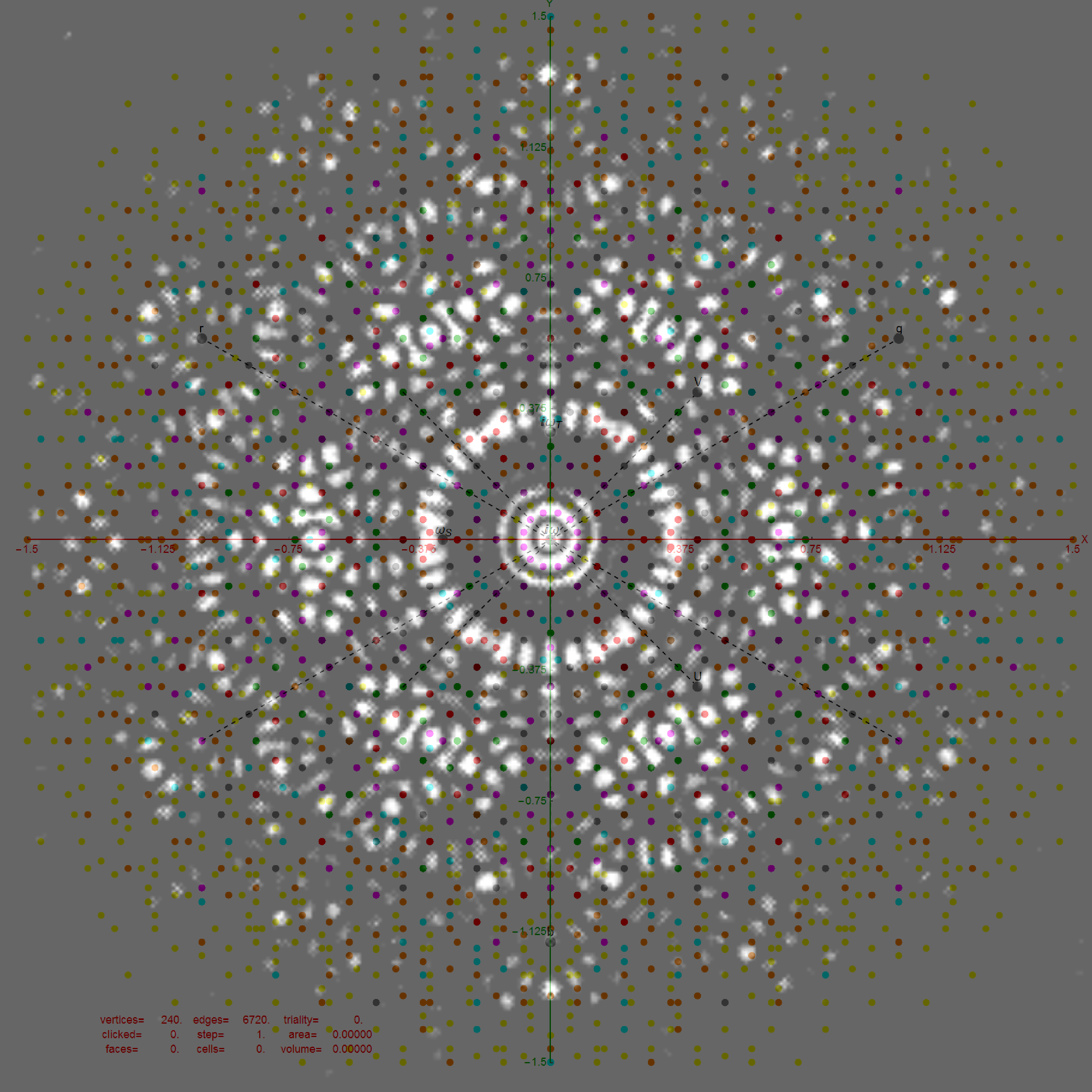
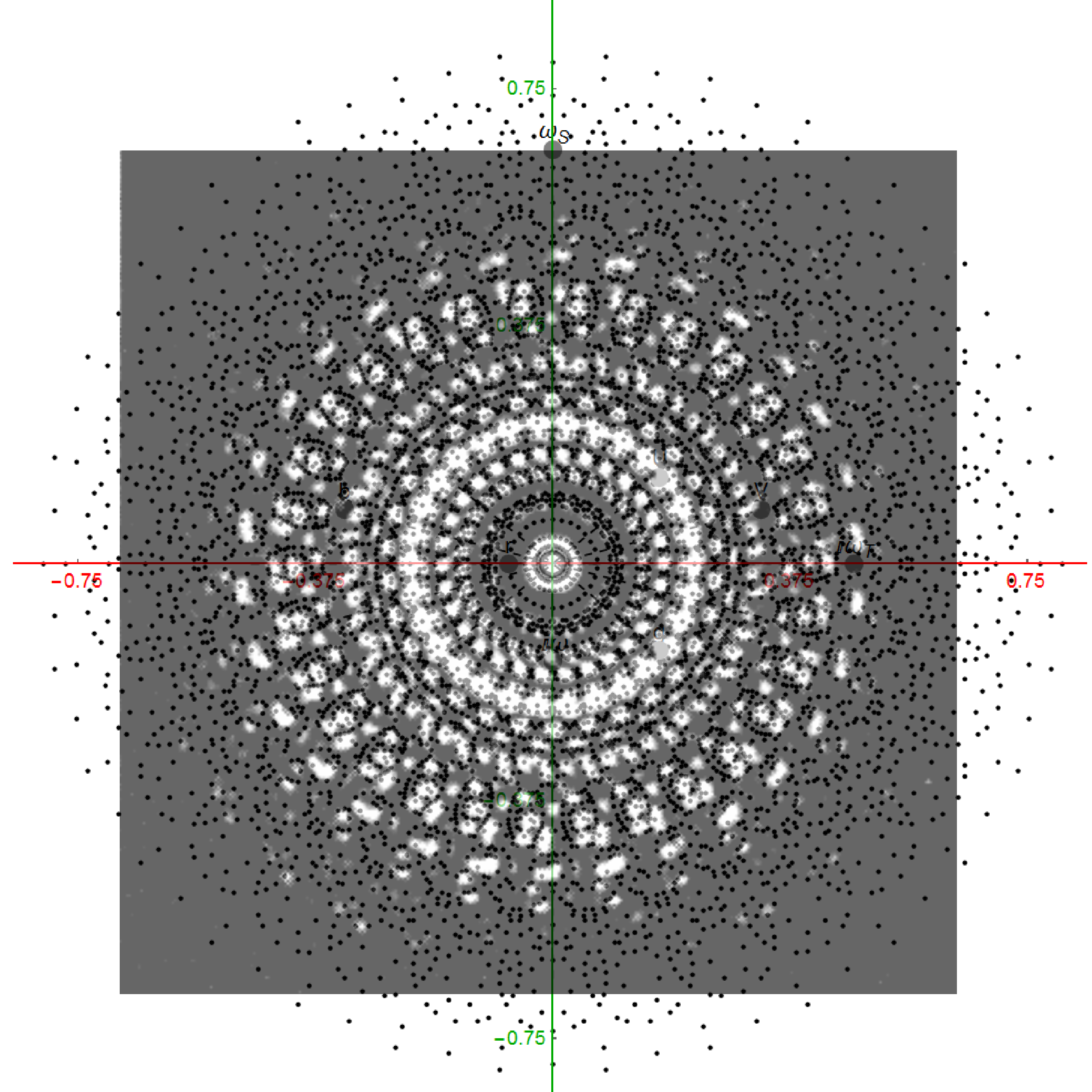
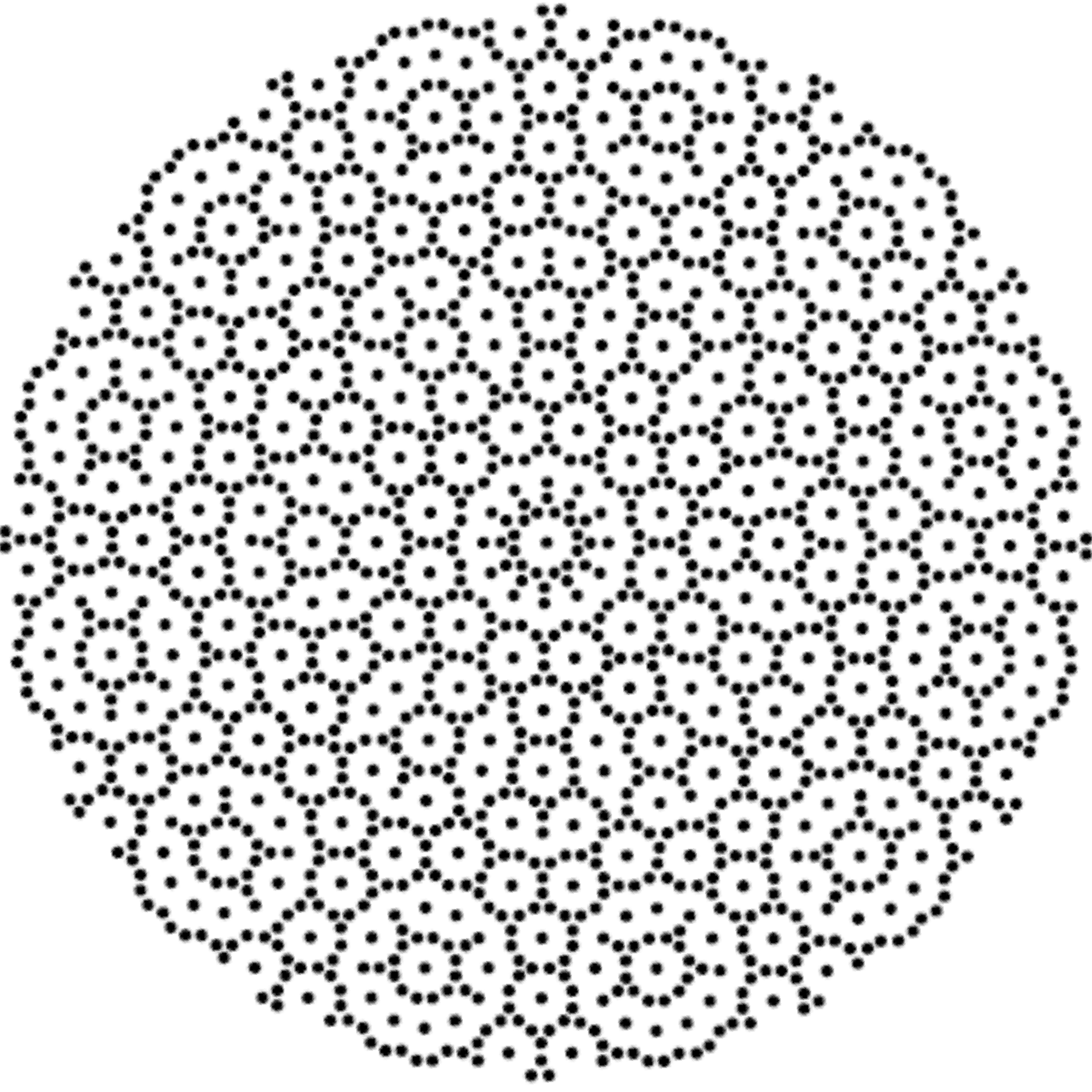
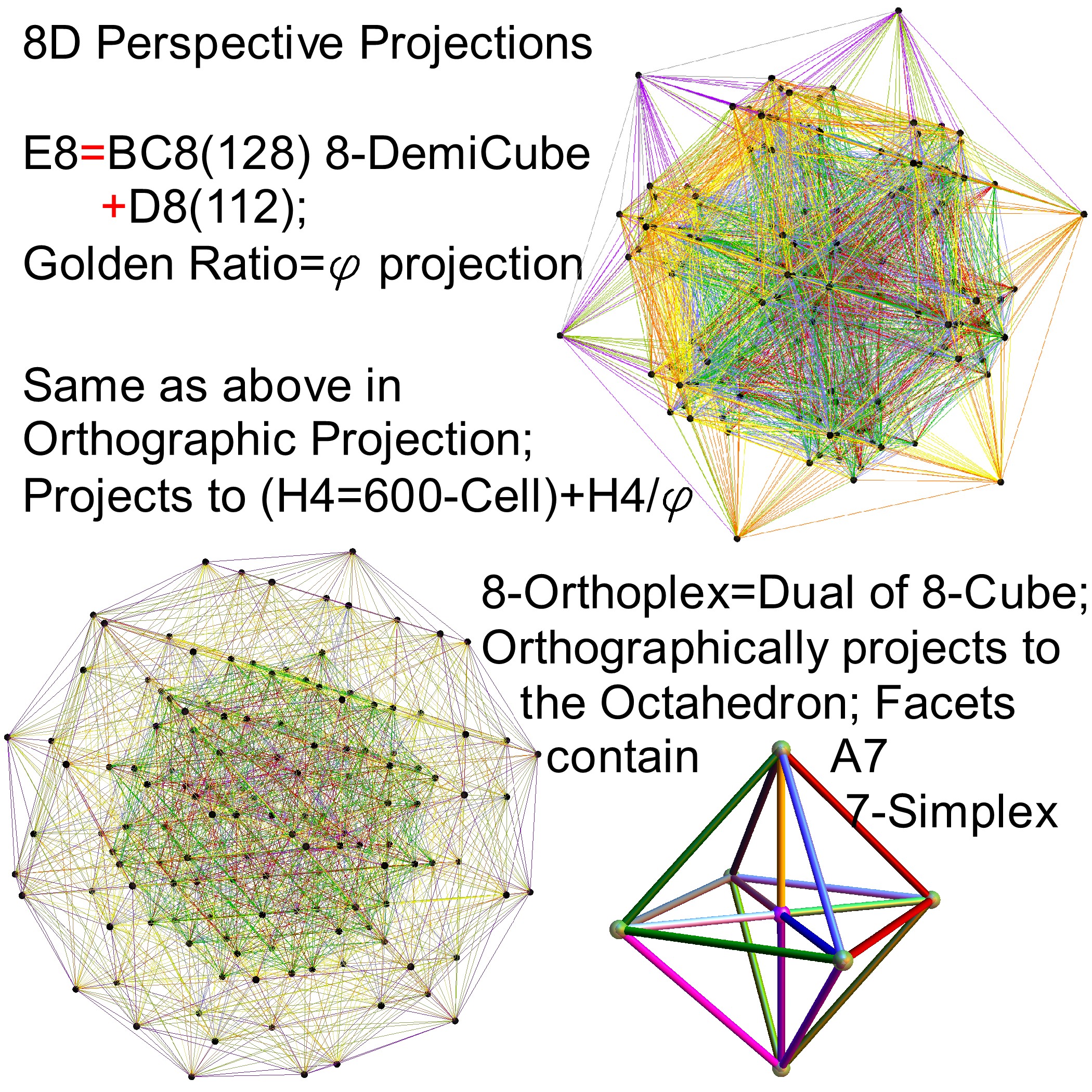
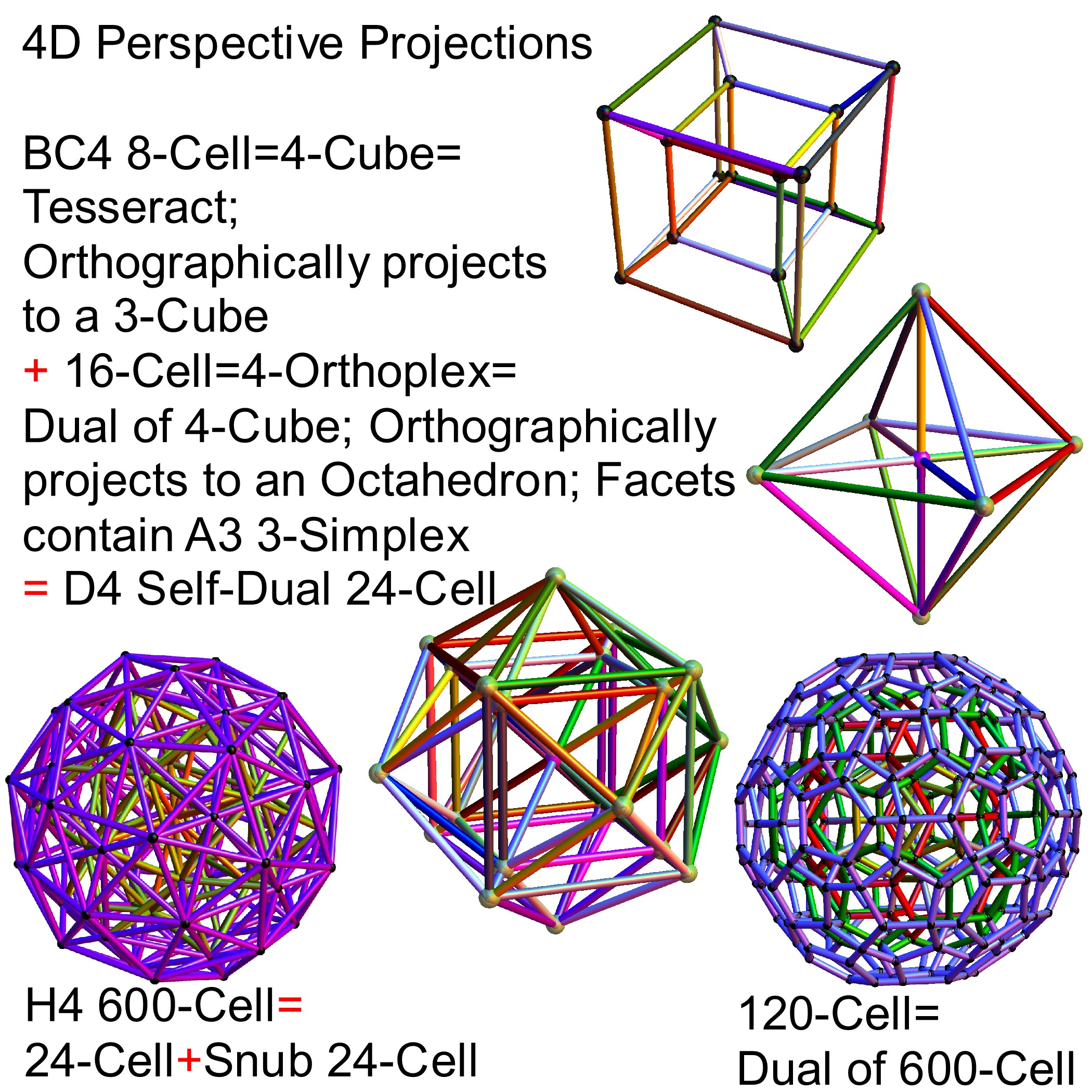
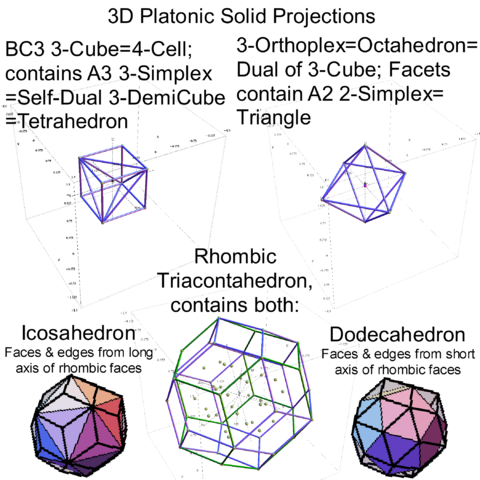
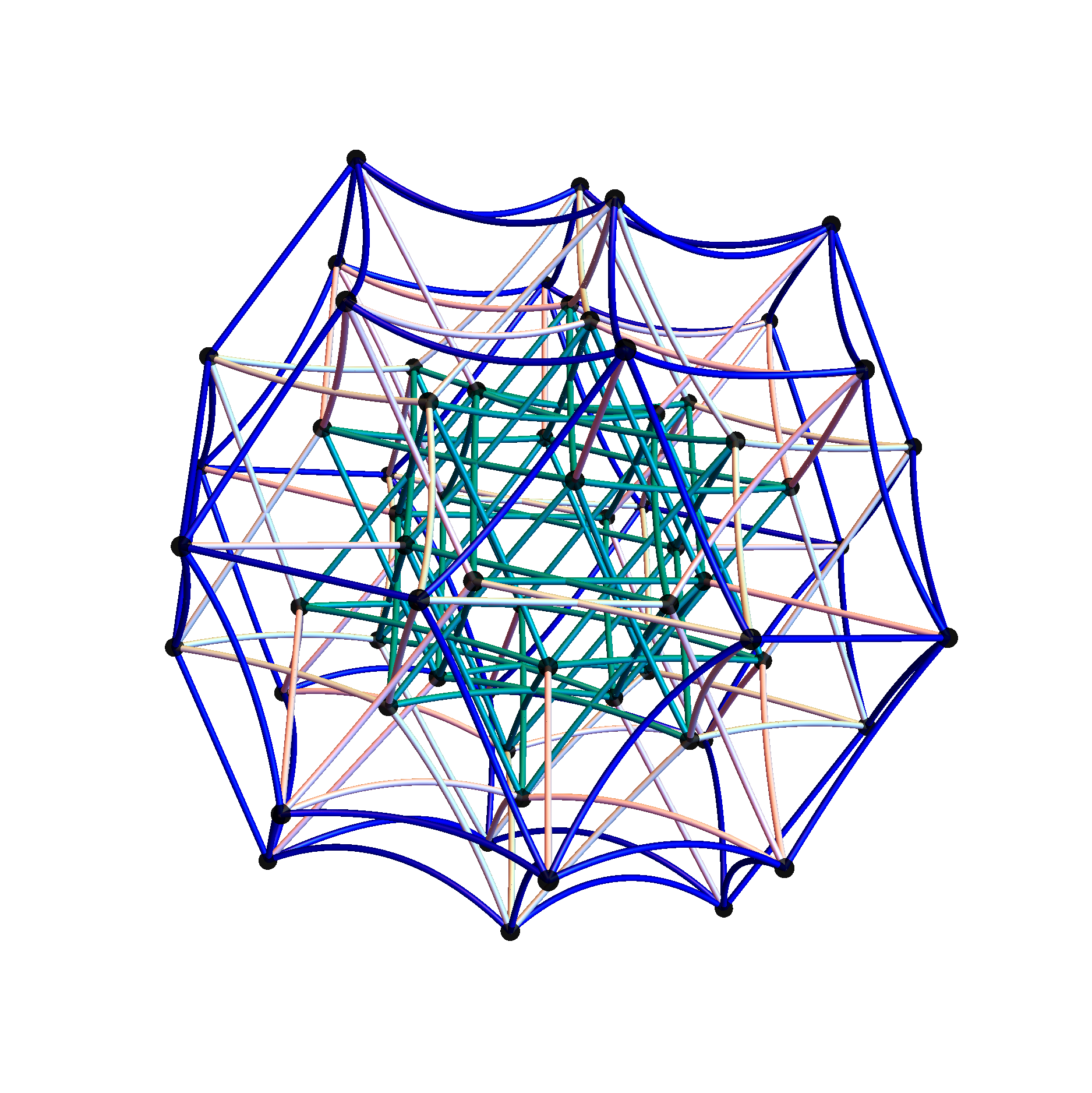
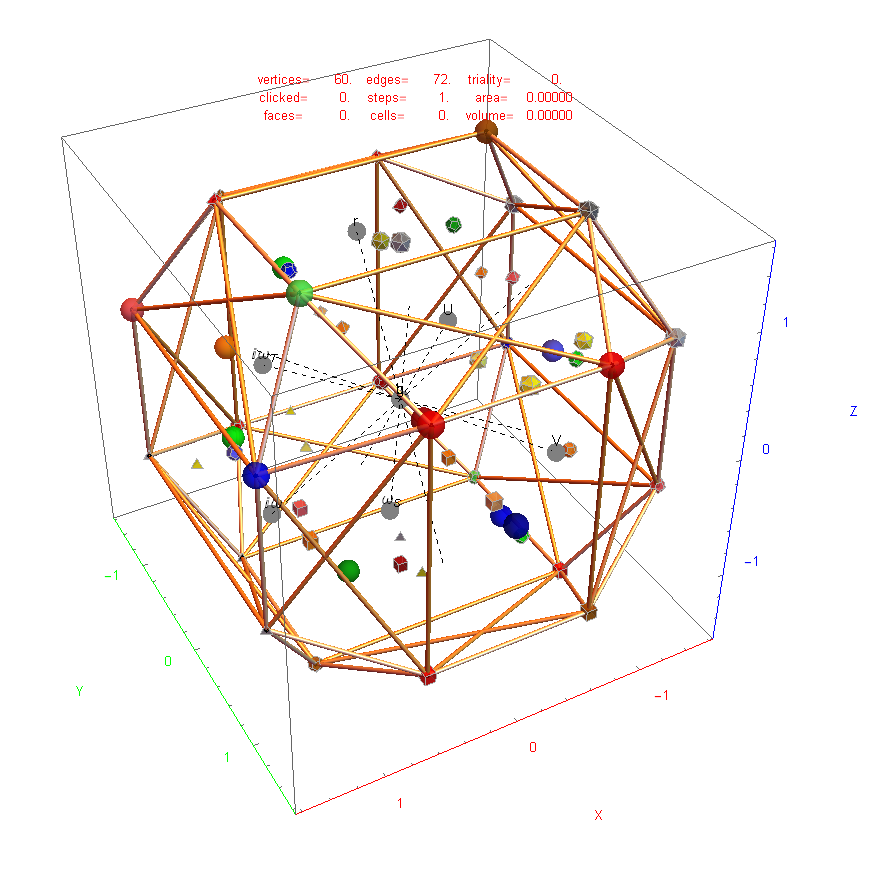
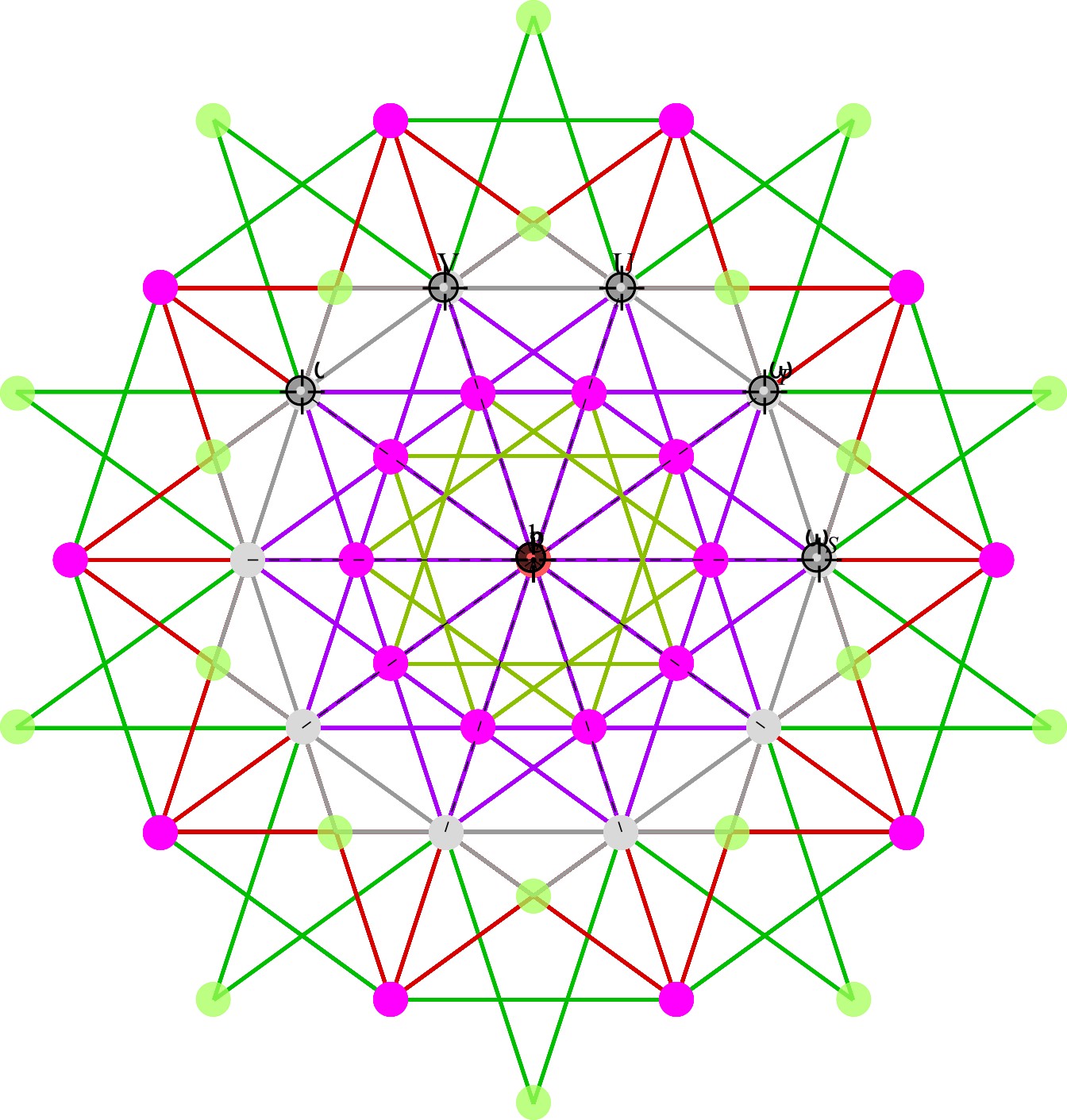
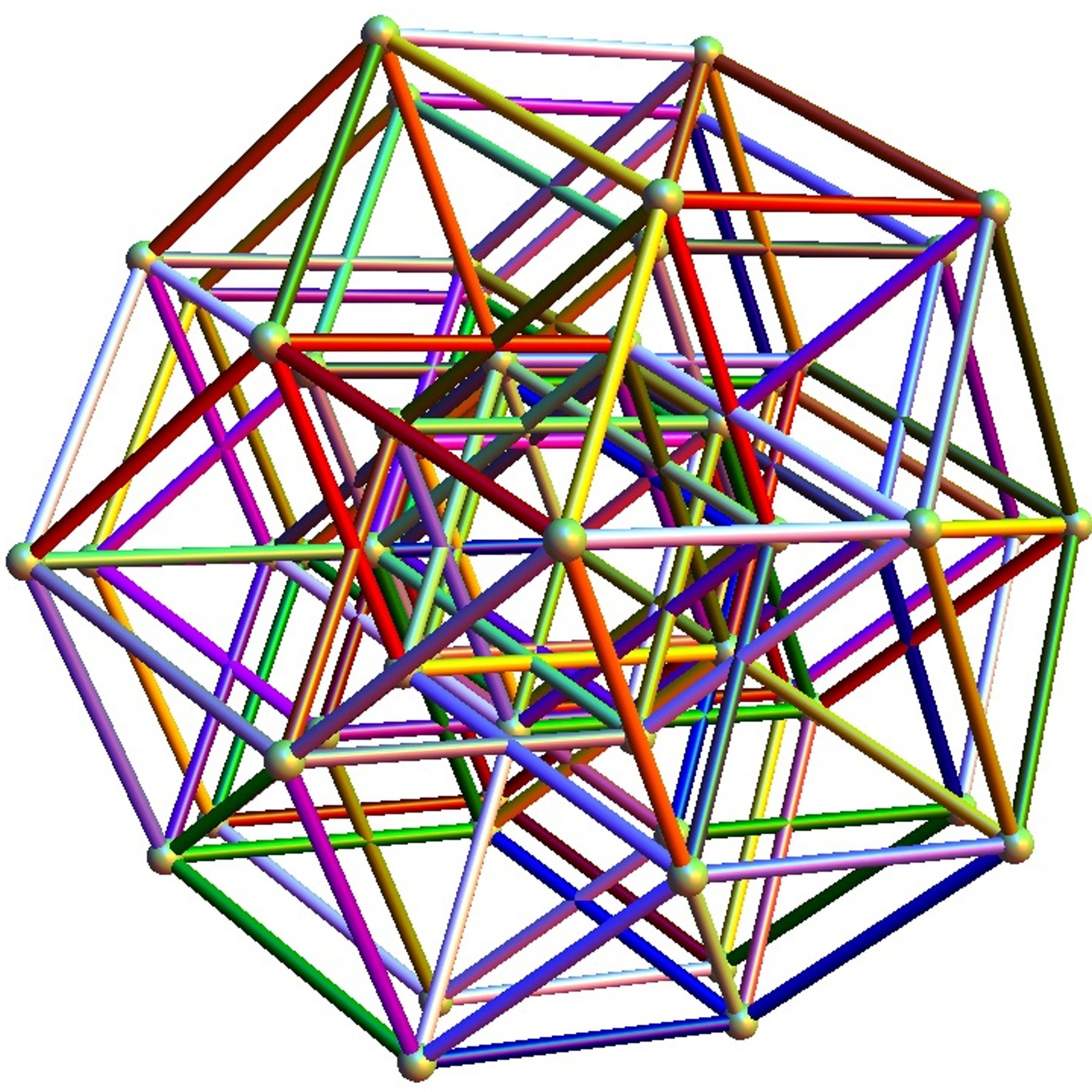
In reference to a G+ post by Baez (w/Greg Egan), it’s interesting to note the link to E8’s outer ring of the Petrie projection of a split real even E8, which creates a Beordijk-Coxeter helix.
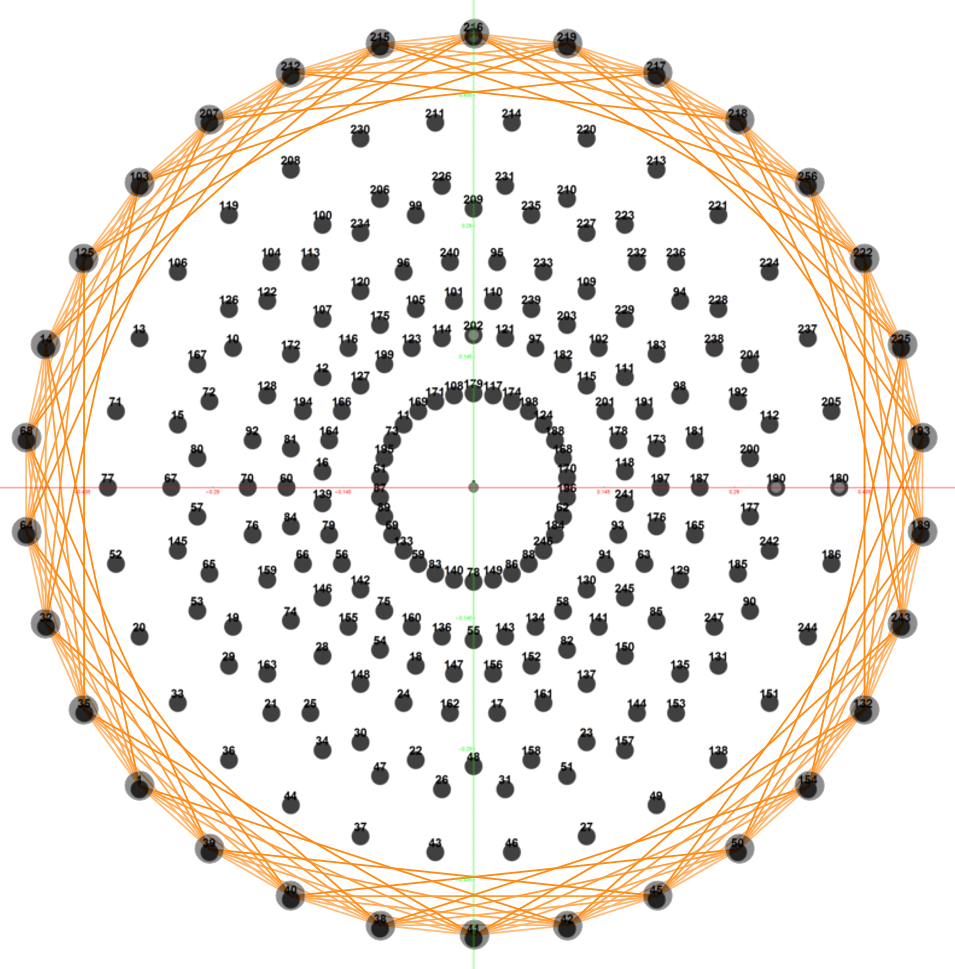
Beordijk-Coxeter helix in 2D
Beordijk-Coxeter helix in 3D
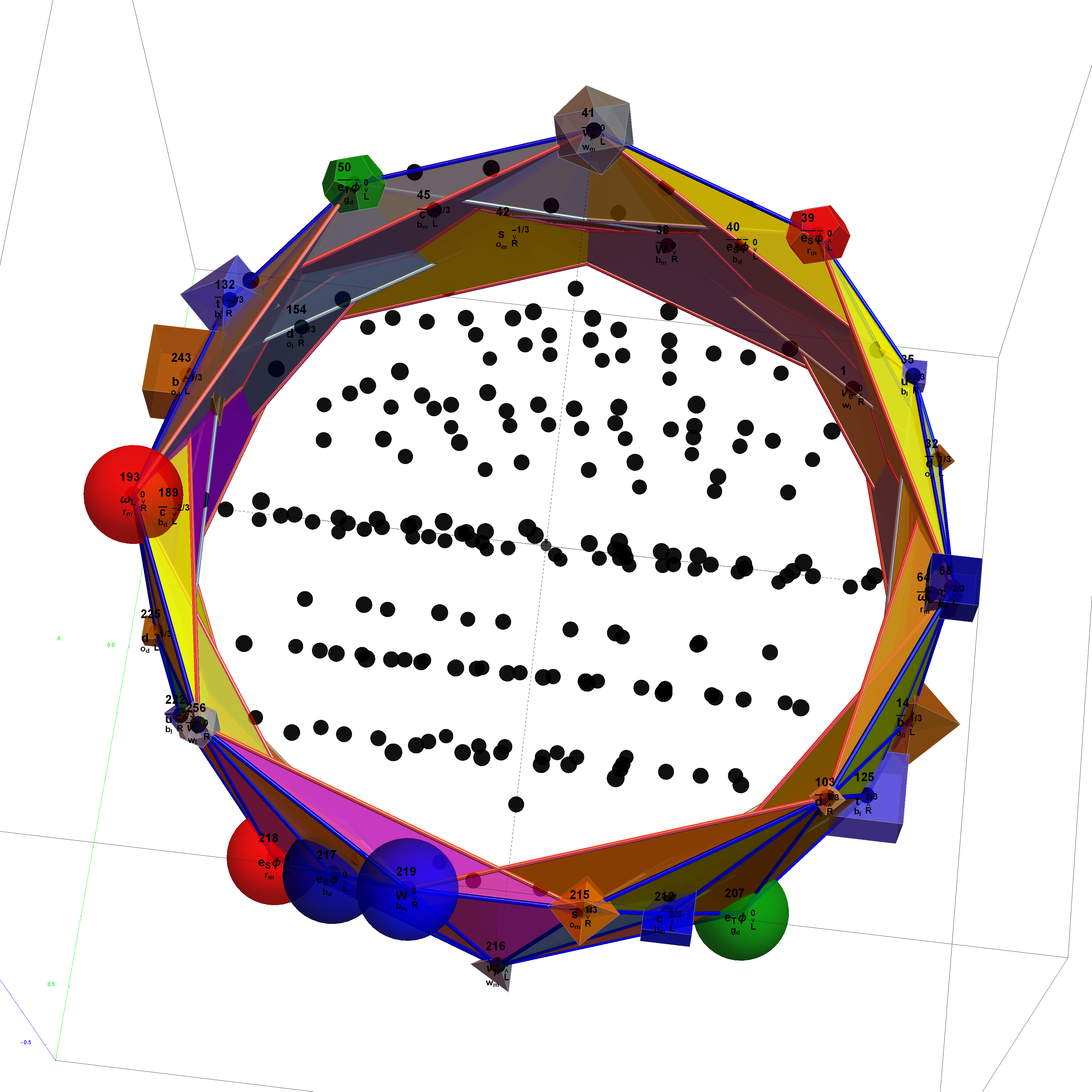
The Beordijk-Coxeter helix connects the nearest 6 vertices on the outer ring. The Tutte-Coxeter graph is created in 3 (blk,grn,red) sets of edges by taking the (outer) ring and skipping (6,8,12) or counting (7,9,13) vertices. It shows there are 2 perfect pentagons and 1 pentagram (with different radii due to the difference in distance between the sets of vertices used).
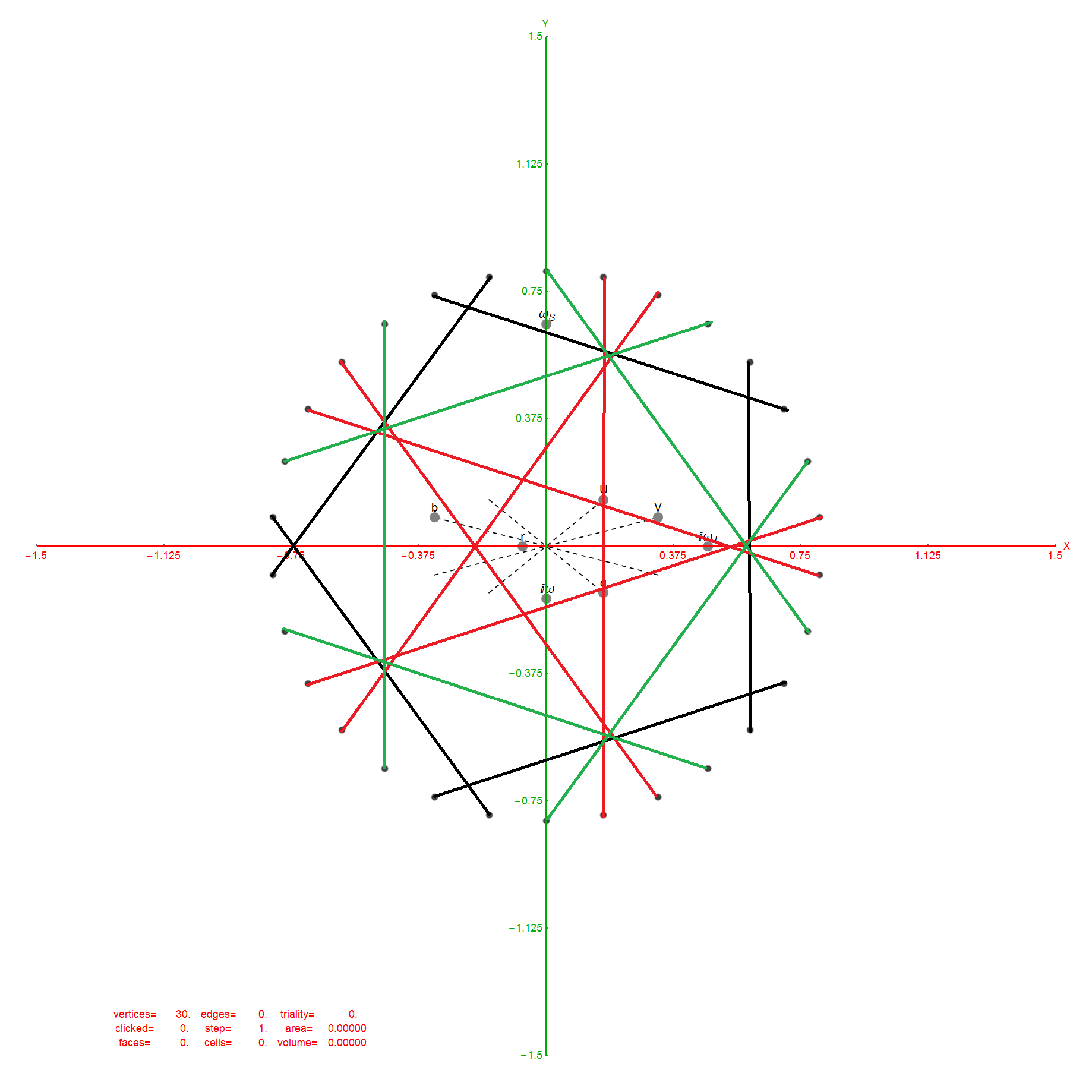
Of course, the crystallographic E8 is manifestly related to the 5 fold symmetry of the pentagon, with its integral relationship to the non-crystallographic H4 group (and its Coxeter-Dynkin diagram) through E8 to H4 folding using the Golden ratio Phi.
It is interesting to note that the skipping of 5+(1,3,7) vertices is similar to the creation of the 120 (240) vertex positions of H4 (E8) Petrie projection by adding to the 24 vertices of the 8-cell and 16-cell (which make up the self-dual 24-cell) the 96 vertices of the Snub 24-cell. This is done through 4 rotations skipping 5 vertices.
Also notice the (1,3,7) are the number of the imaginary parts of Complex, Quaternion, and Octonion numbers, also integrally related to E8.