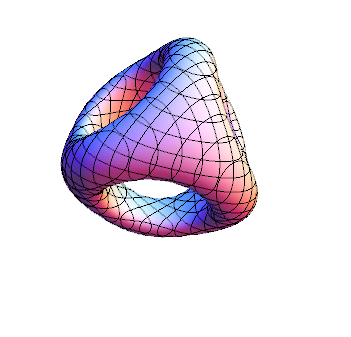
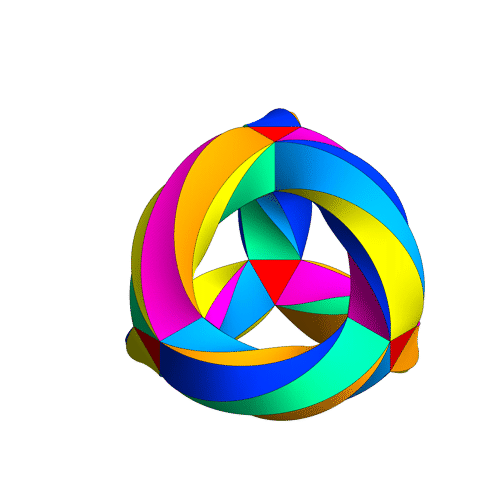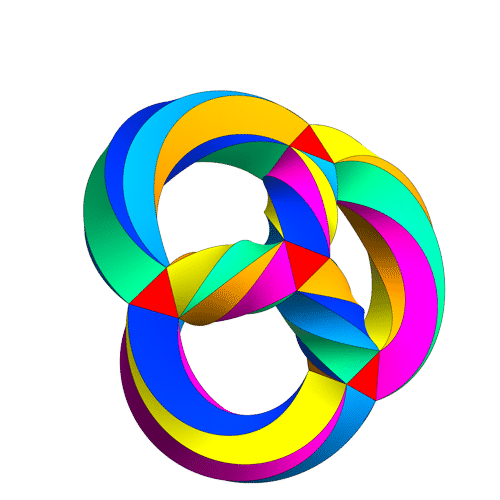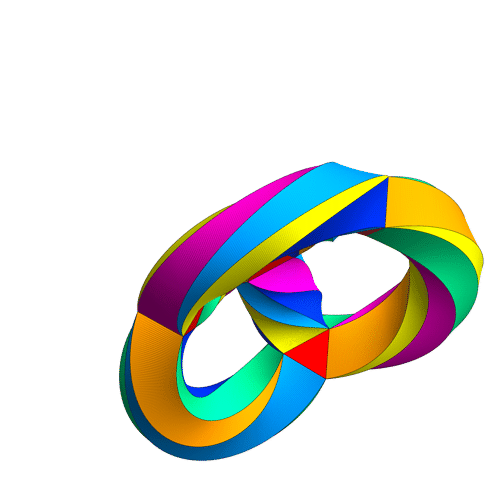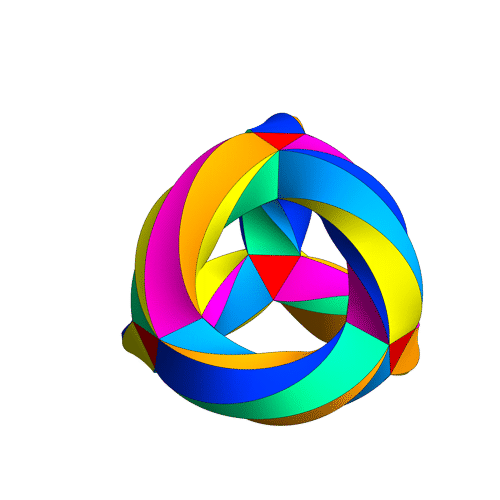I’ve updated the .NB, .CDF and interactive demonstrations to include the ability to visualize the split octonions.
Monthly Archives: June 2013
Klein Quartic Curves
With some Mathematica source from Leon Lampret at math.stackexchange.com, I’ve been trying to understand the link between the bitangents of octonions and the Klein Quartic Curves.
Which seems to be closely related to Greg Egan’s wonderful visualization from
http://www.gregegan.net/SCIENCE/KleinQuartic/KleinQuartic.html
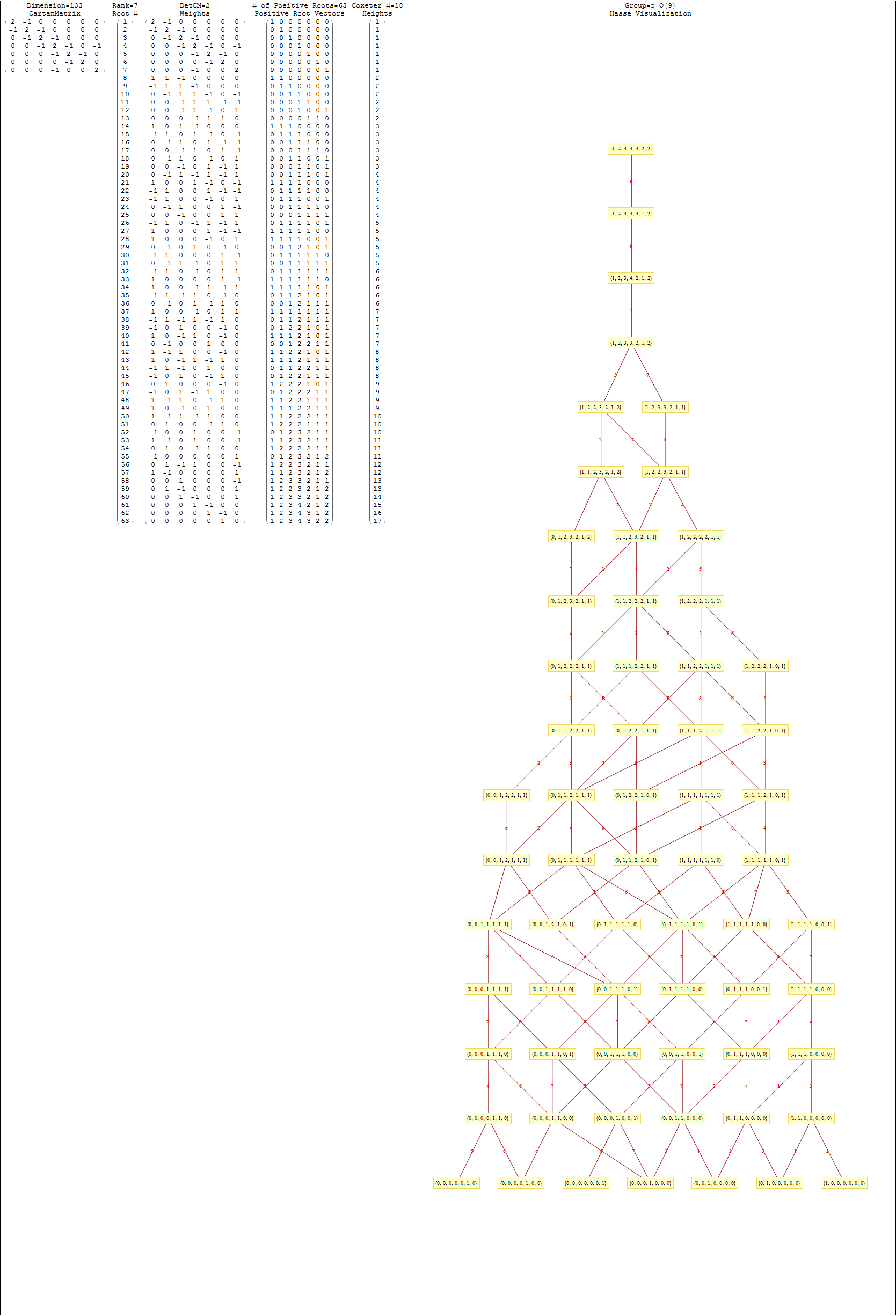
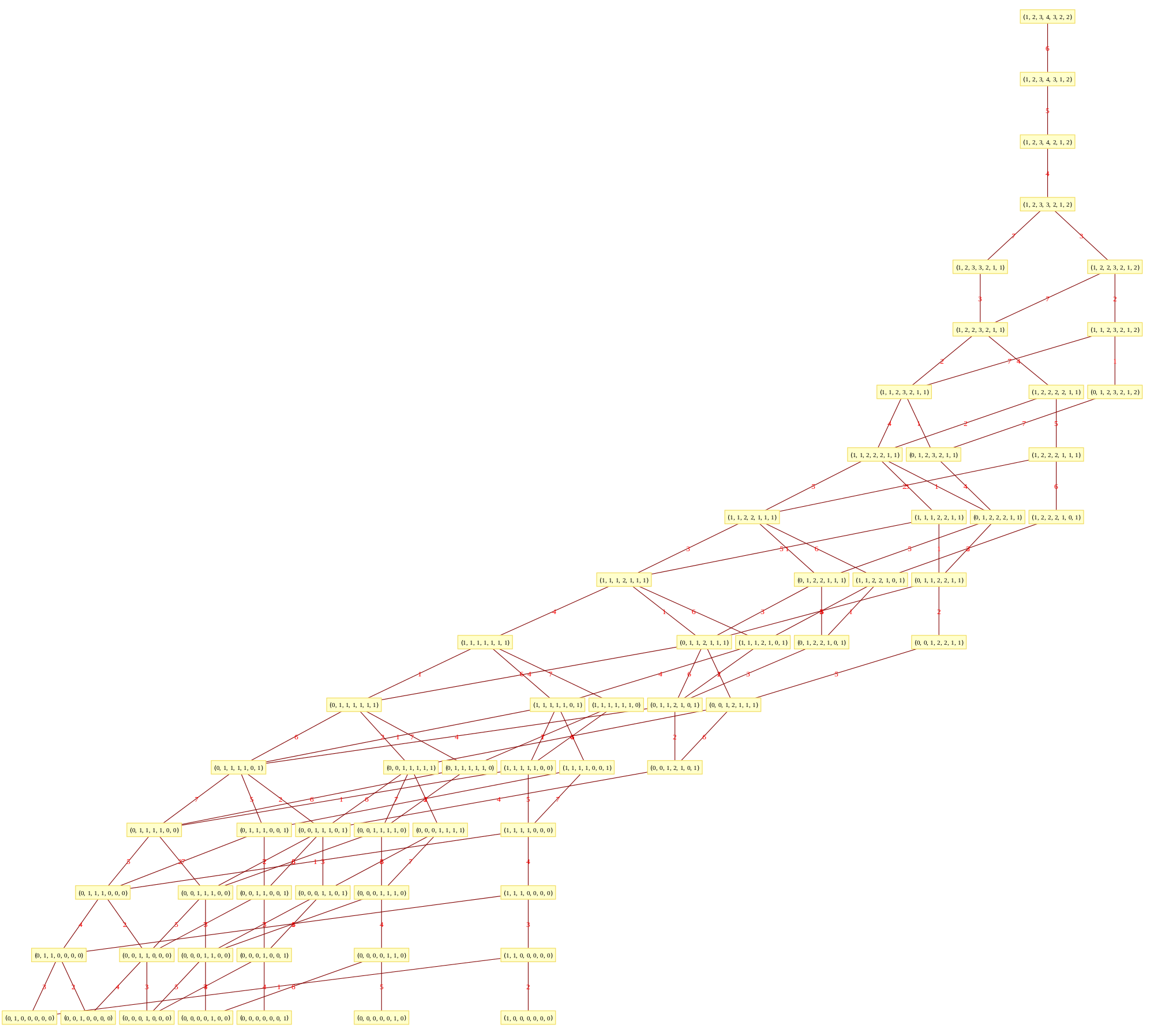
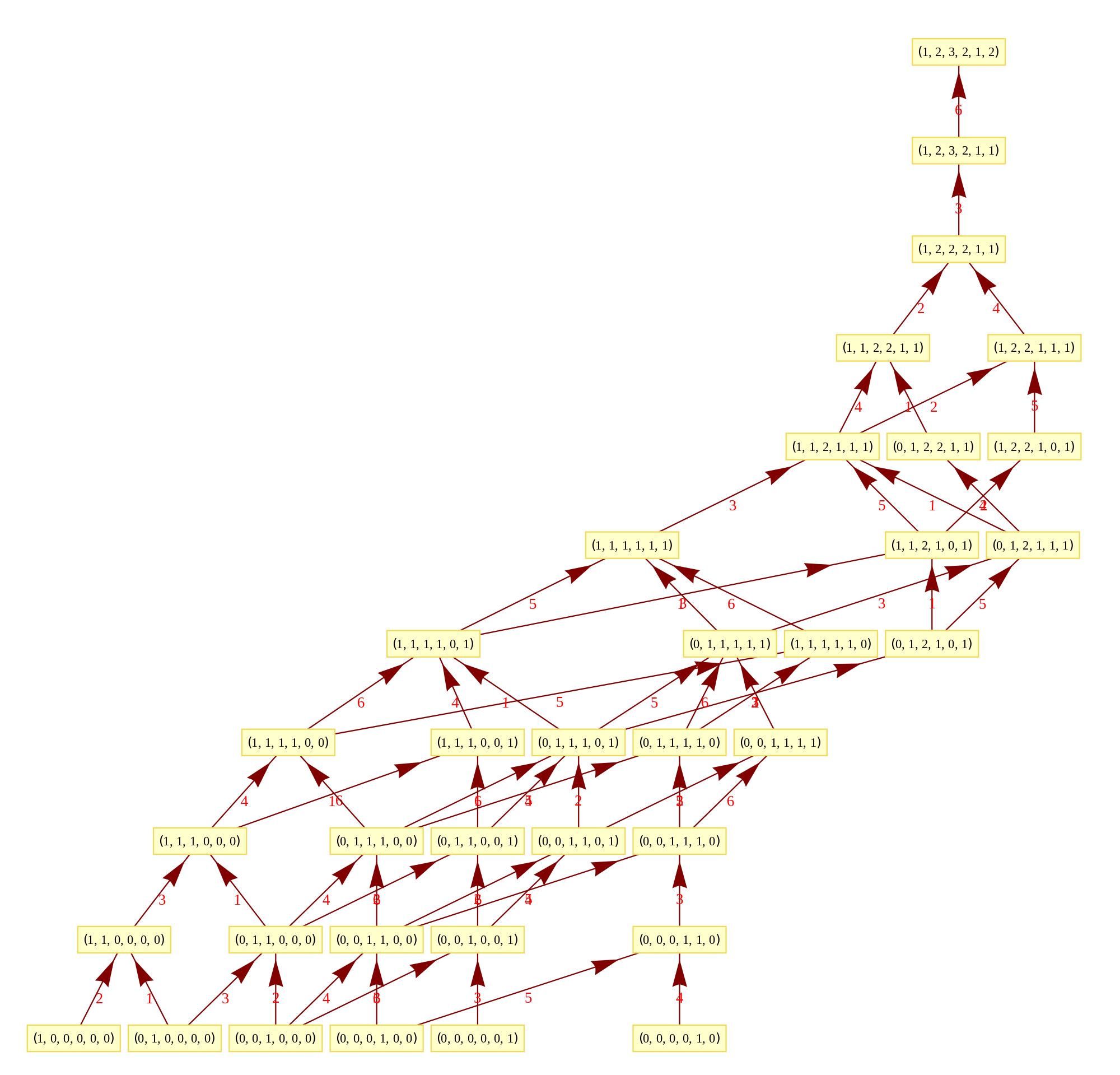
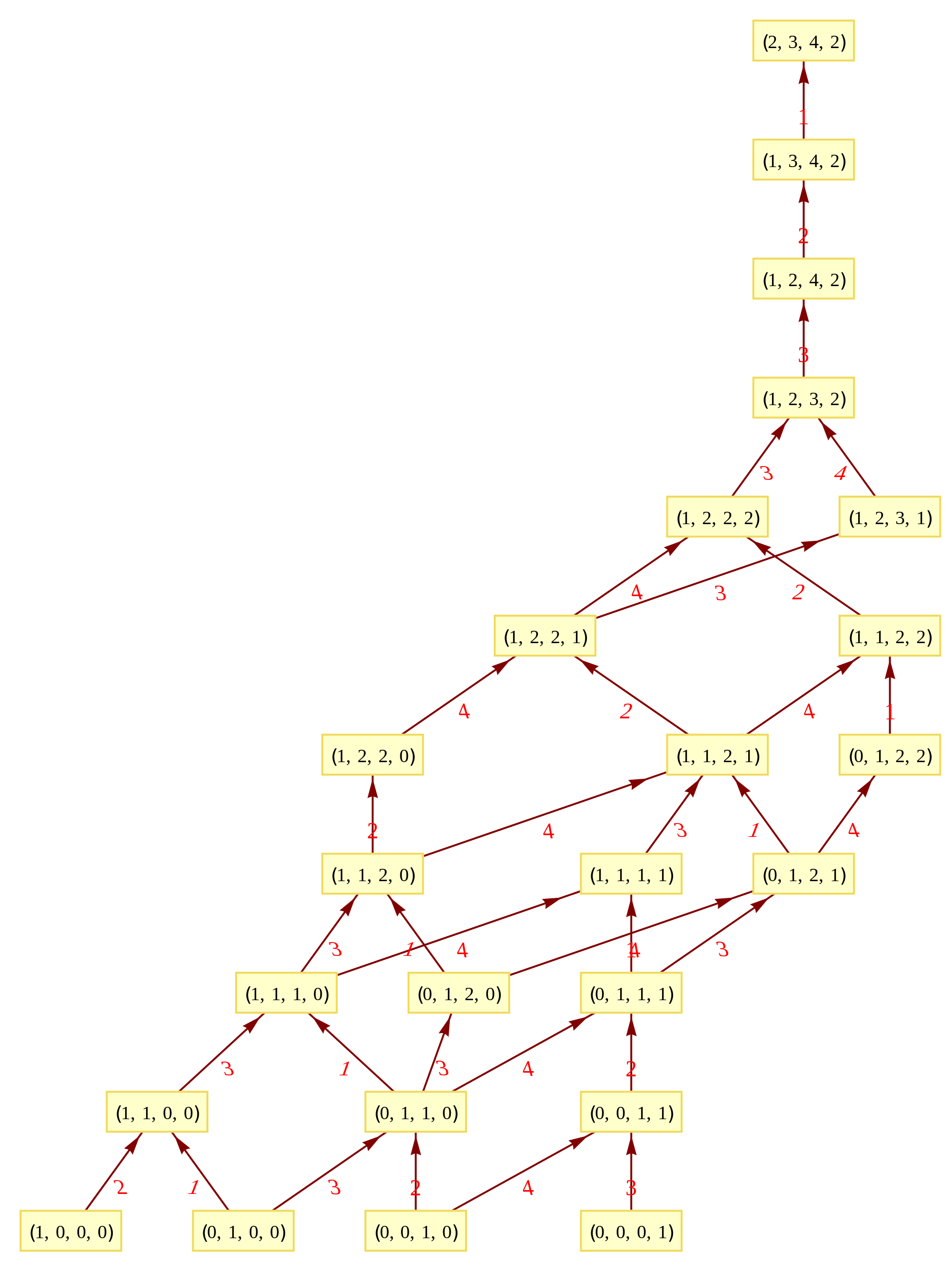
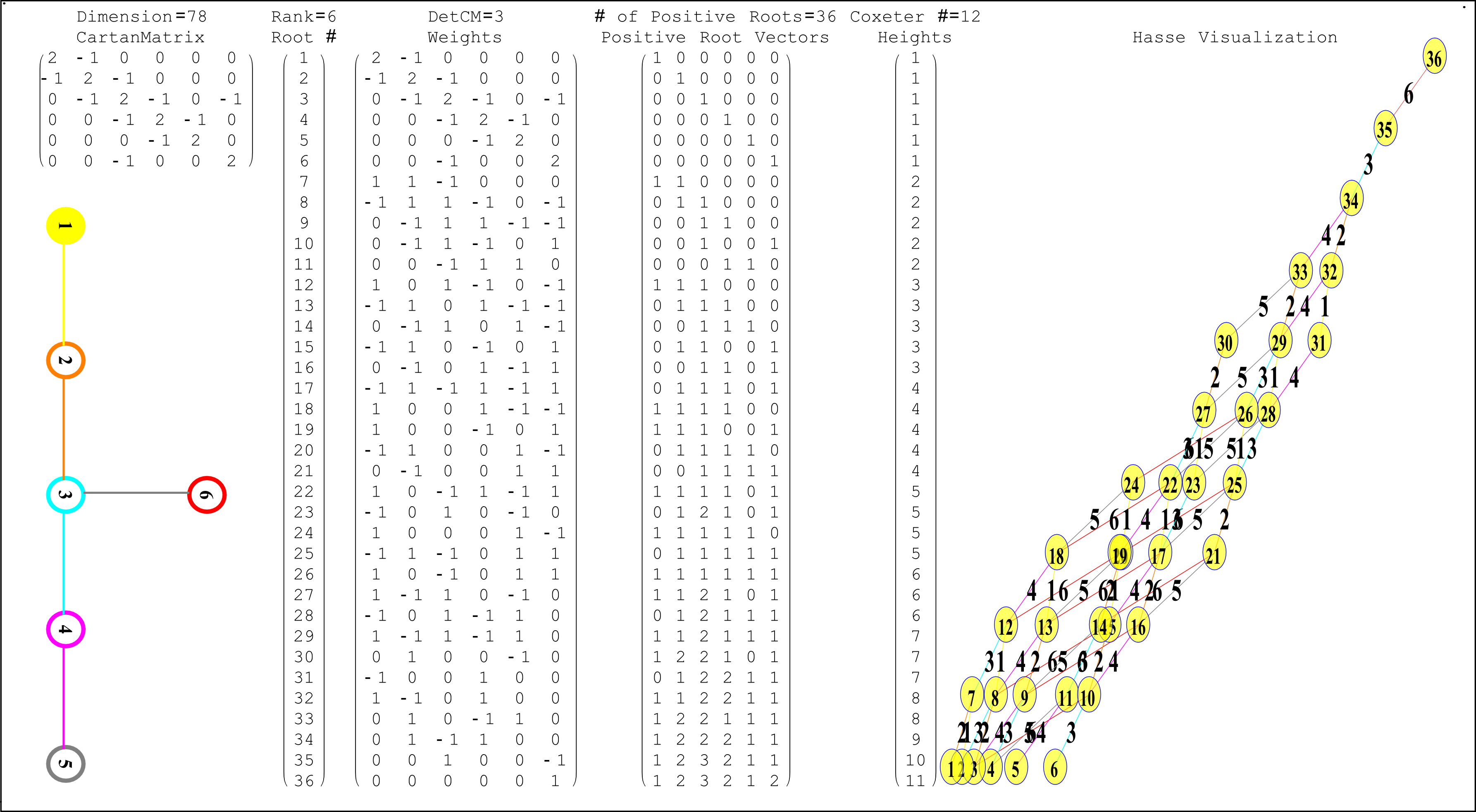
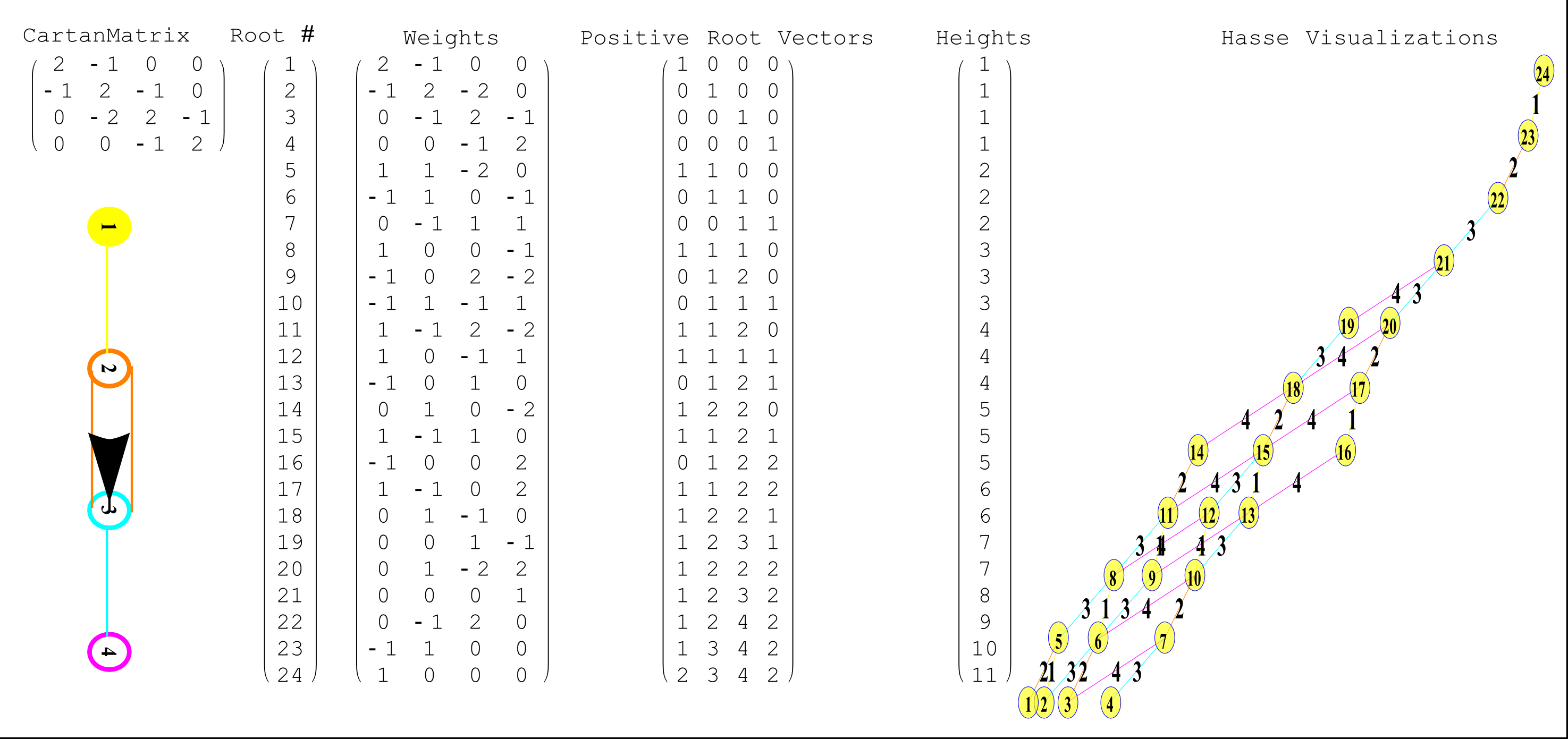
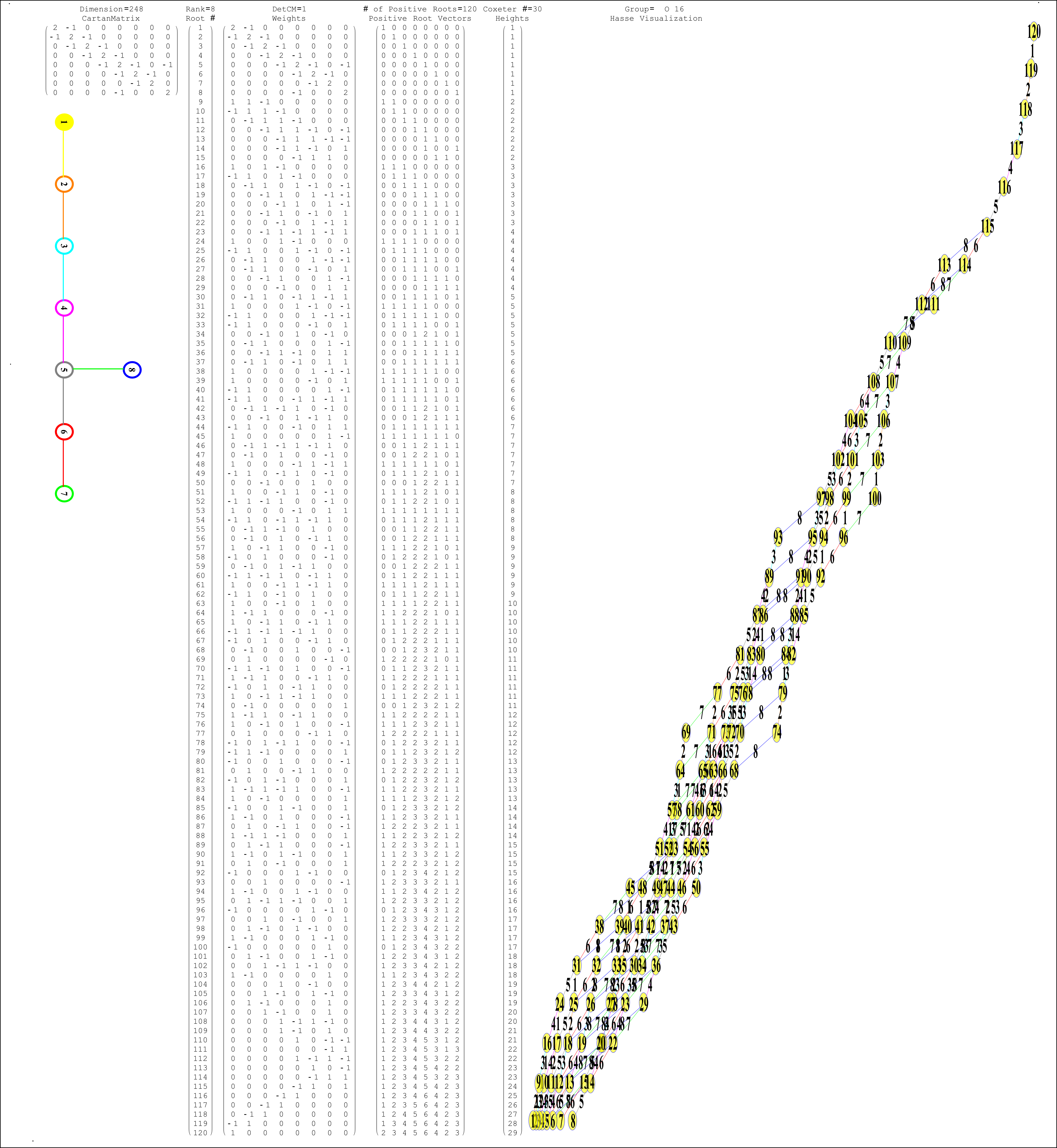
The Comprehensive Split Octonions and their Fano Planes
Please see this post for updates to these graphs.
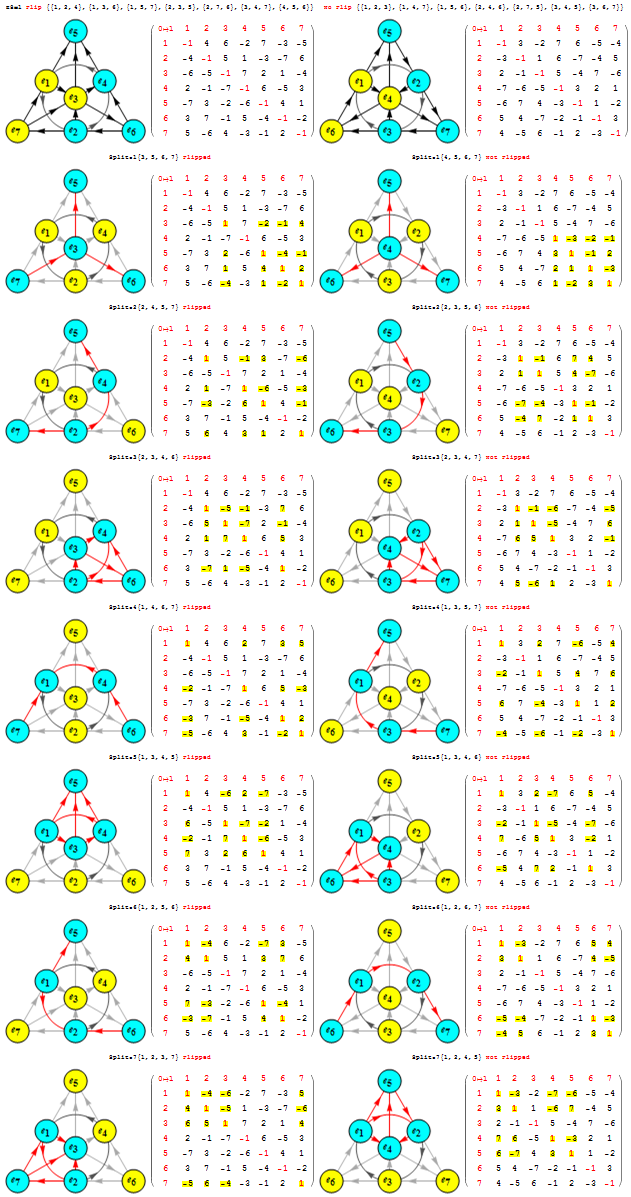
I am pleased to announce the availability of splitFano.pdf, a 321 page pdf file with the 3840=480*8 split octonion permutations (with Fano planes and multiplication tables). These are organized into “flipped” and “non-flipped” pairs associated with the 240 assigned particles to E8 vertices (sorted by Fano plane index or fPi).
There are 7 sets of split octonions for each of the 480 “parent” octonions (each of which is defined by 30 sets of 7 triads and 16 7 bit “sign masks” which reverse the direction of the triad multiplication). The 7 split octonions are identified by selecting a triad. The complement of {1,2,3,4,5,6,7} and the triad list leaves 4 elements which are the rows/colums corresponding to the negated elements in the multiplication table (highlighted with yellow background). The red arrows in the Fano Plane indicate the potential reversal due to this negation that defines the split octonions. The selected triad nodes are yellow, and the other 4 are cyan (25MB).
These allow for the simplification of Maxwell’s four equations which define electromagnetism (aka.light) into a single equation.
I believe this is the only comprehensive presentation of all 3840 Split Fano Planes with their multiplication tables available.
Below is the first page of the comprehensive split octonion list.
Connecting the Octonion Fano Plane to the Atomic Elements
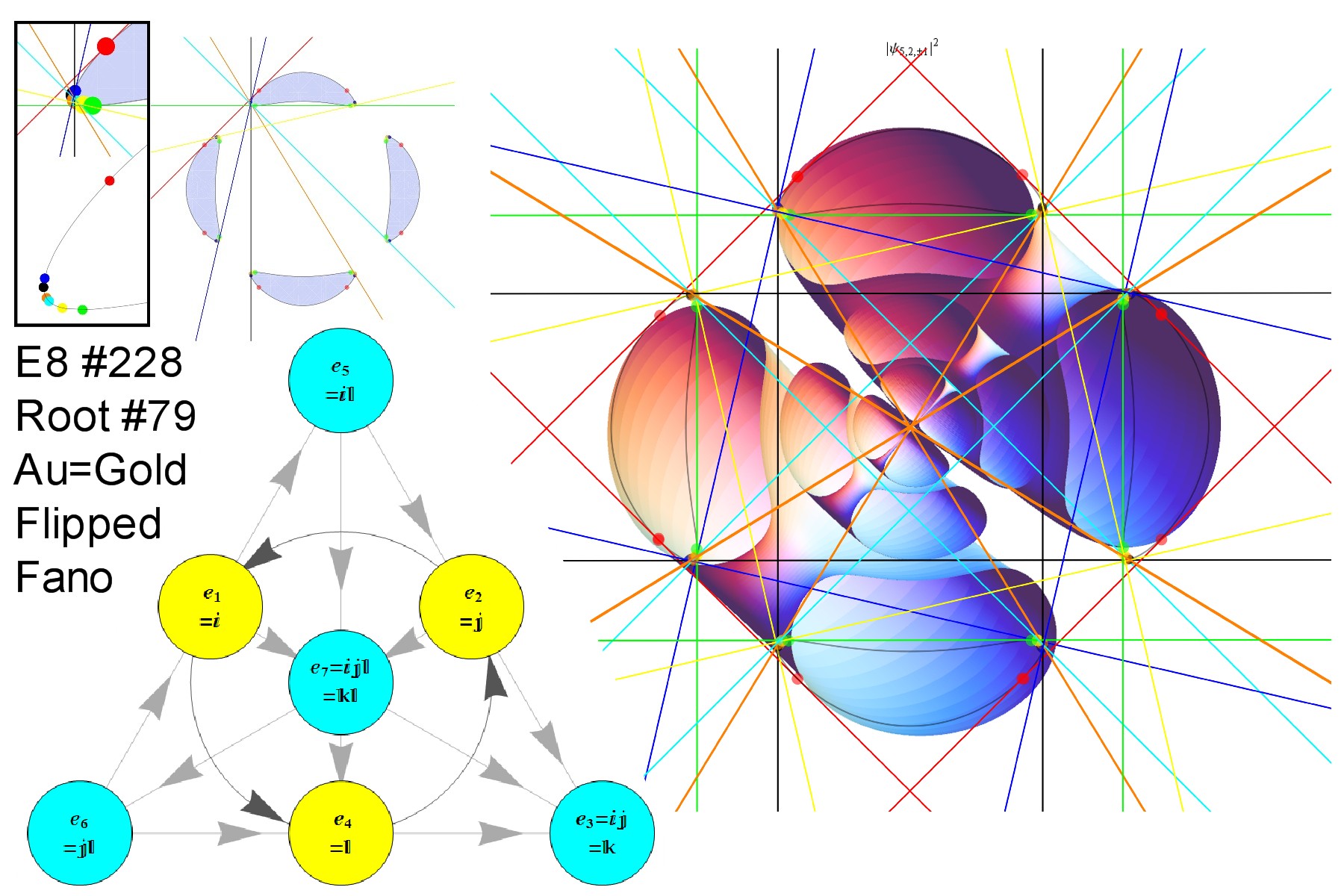
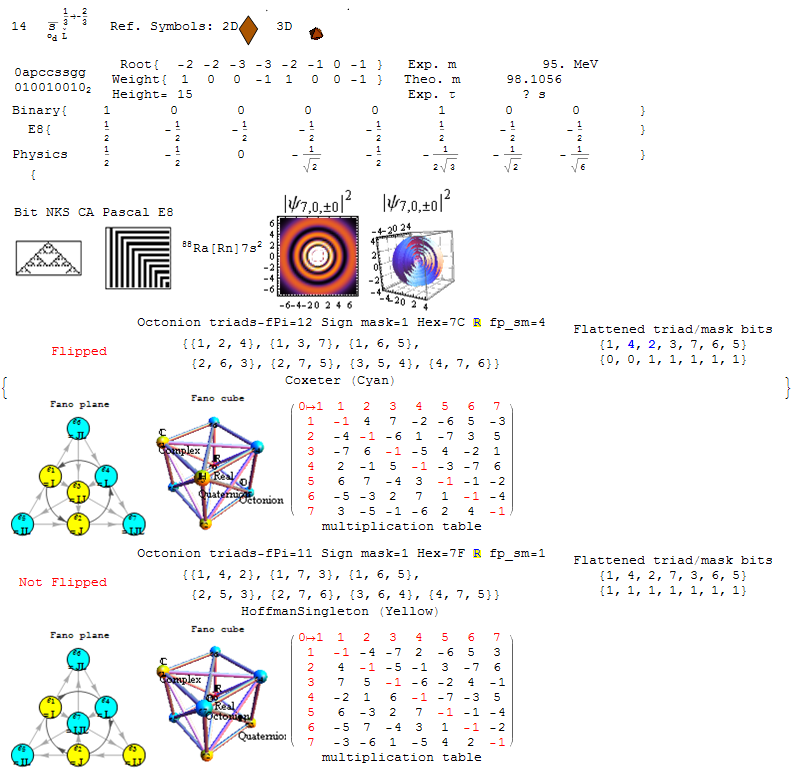
There are 28 octonion Fano plane triangles that correspond directly to the 28 Trott quartic curve bitangents. These bitangents are directly related to the Legendre functions used in the Shroedinger spherical harmonic electron orbital probability densities. Shown below is a graphic of these overlaid onto the n=5, l=2, m=1 element, which is assigned to gold (Au). When using an algorithm based on the E8 positive algebra root assignments, the “flipped” Fano plane has E8 algebra root number 79 (the atomic number of Au) and split real even group number of 228 (in Clifford/Pascal triangle order). For more information, please see the complete list of integrated Fano indices here with full explanation of the layout here.
Detail explanation of E8 Integration with Octonions, Particles, and the Periodic Table
Please see Integrated E8, Binary, Octonion for a tutorial that explains the detail of the content of Fano.pdf. It outlines the relationships in the integration of E8 with Octonions, Binary, Particles, NKS, and the Periodic Table of Elements. Other formats are also available (.ppt or .pps and .pdf).
Created a simpler Fano plane and cubic .pdf
A simpler version of Fano.pdf is here FanoOnly.pdf (15MB).
Improved complete index of E8, Binary, Octonions, Particles, NKS CA & Periodic Table
The main change was an improved association of the 120 periodic table elements to the 120 root vectors weighted by their simple root grading. See the full 241 page reference here.