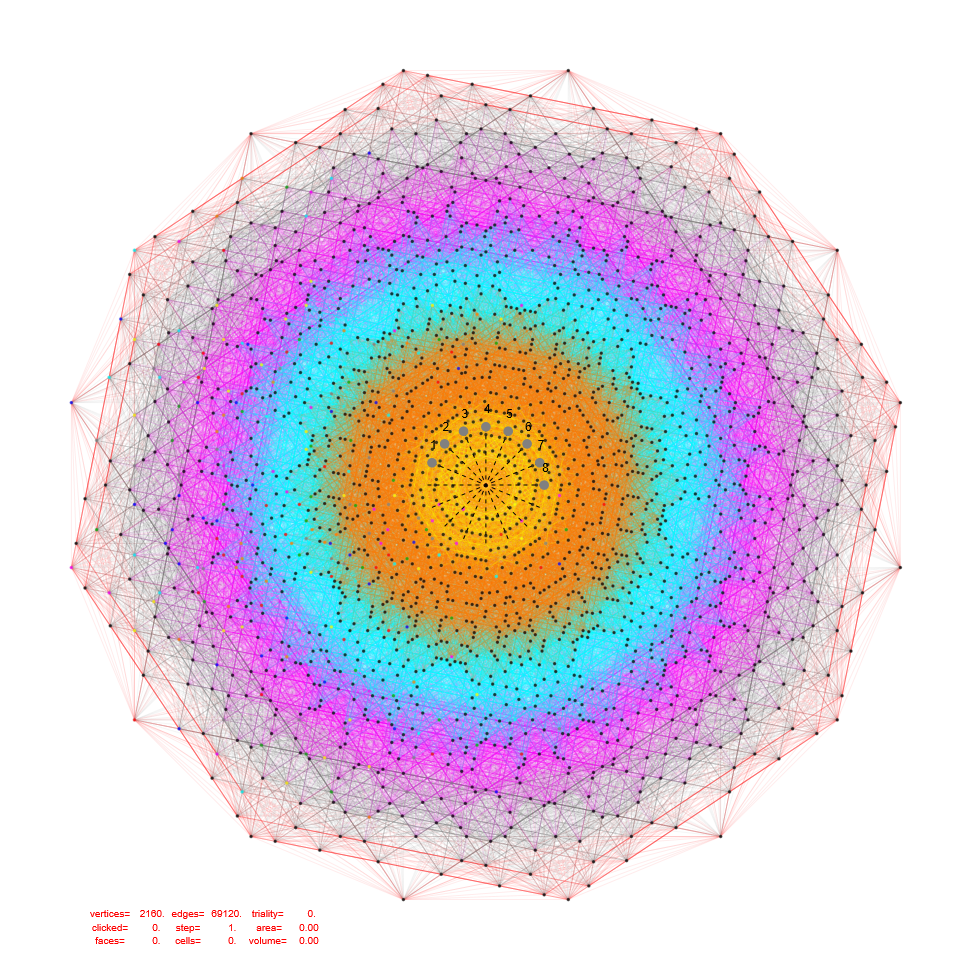
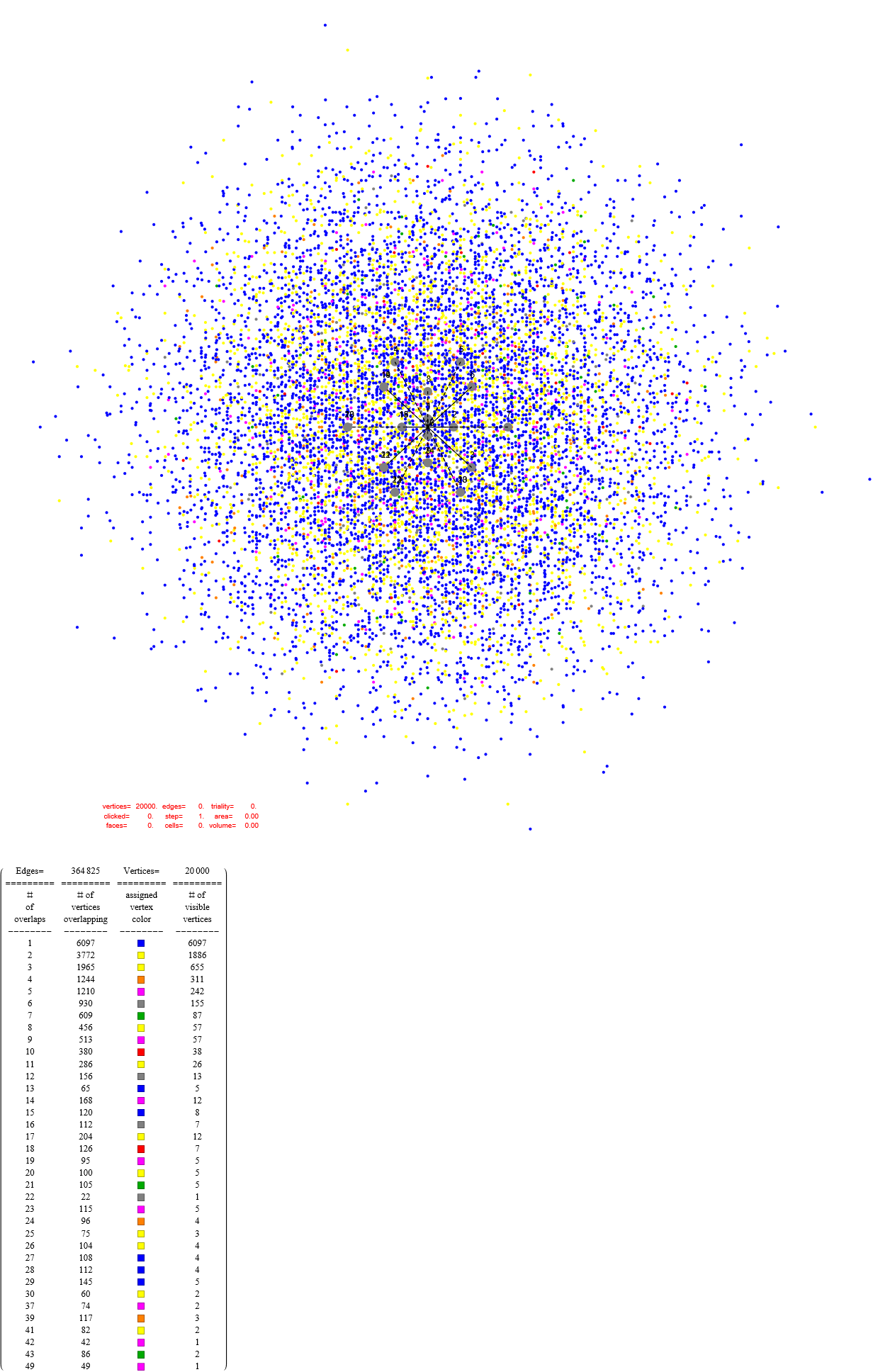
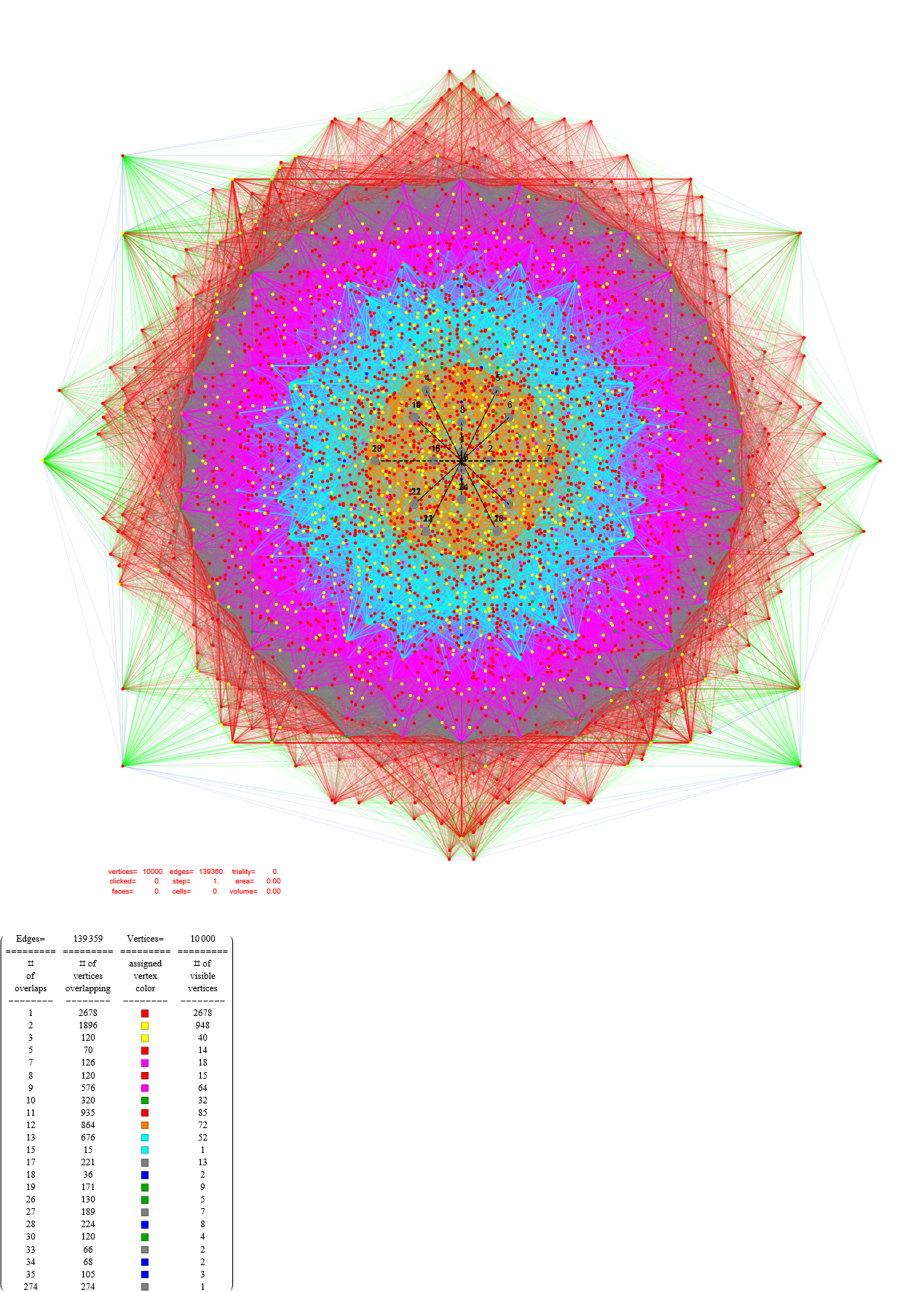
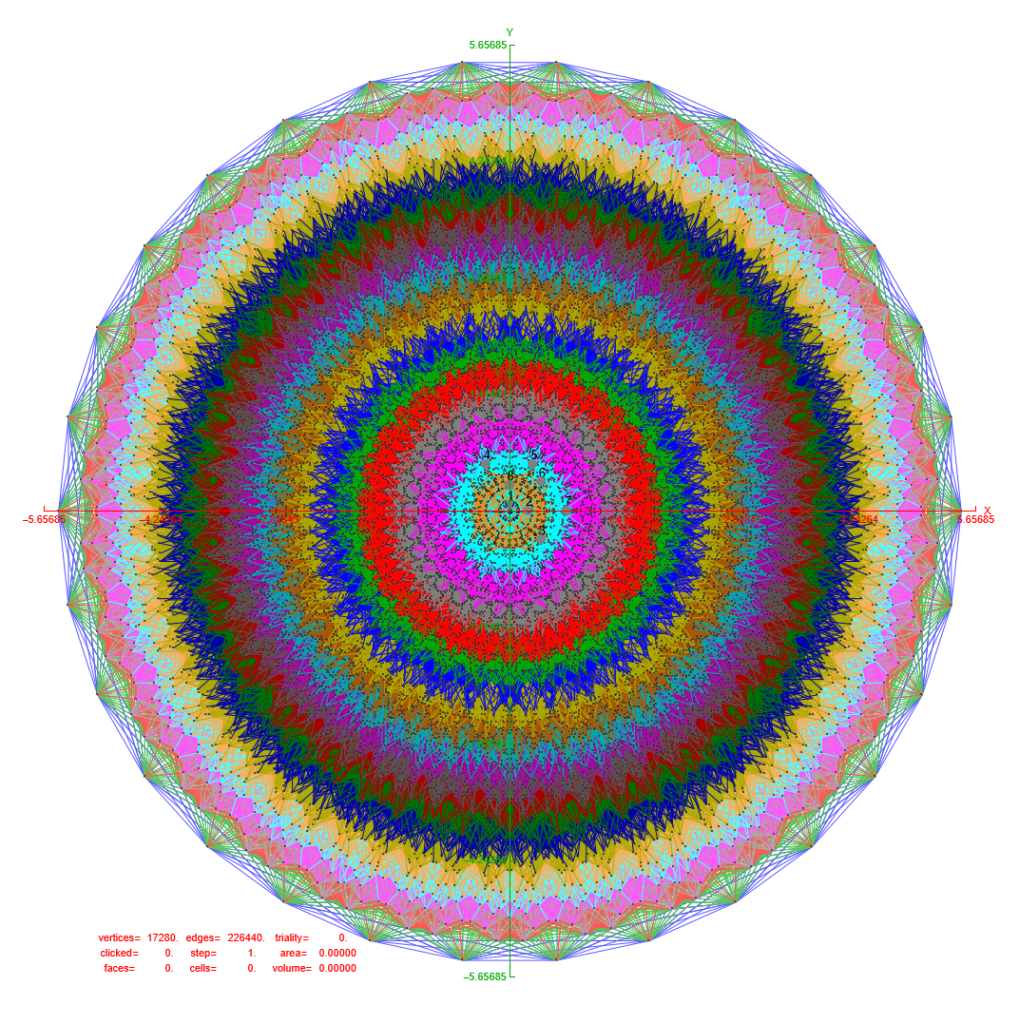
This post is a work in process, so check back for the latest visualizations and data. Today (Dec. 31 2025) I finally finished a major update to the section SVG files from the first update of 12/16/2025. Have a blessed New Year for 2026 and beyond!
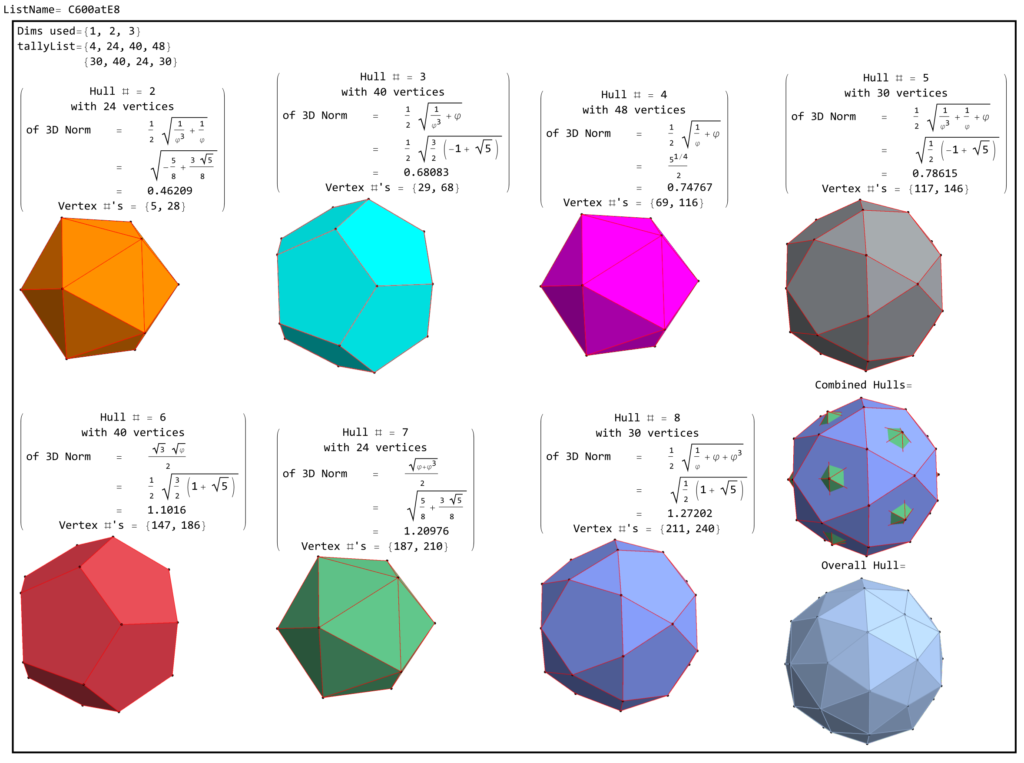
These were improved a bit on 01/04/2026 and on 01/06/2026 I added more informative Thumbnail icons in the matrix links that include the vertex-edge-face-cell OverallHull images. On 01/12/2026 I added the Snub 24-cell orientations.
So if you downloaded previous files, you may want to take another look, as some of the output had anomalous data that didn’t render, along with other errors (due to the way I computed approximate equality between norms). In order to get this done, I realized I was thrashing my Solid State Drive (SSD) due to memory swapping. It died due to that (SSDs have limited writes!), so I had to rebuild the machine with 64 Gb RAM to keep the computations in RAM.
Drop me an email if you find anything that needs correction.
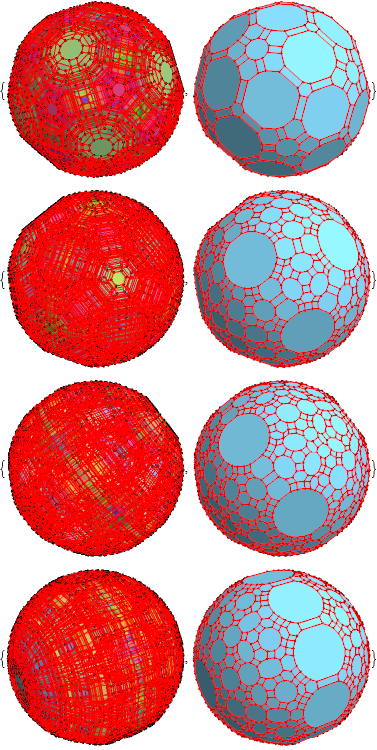
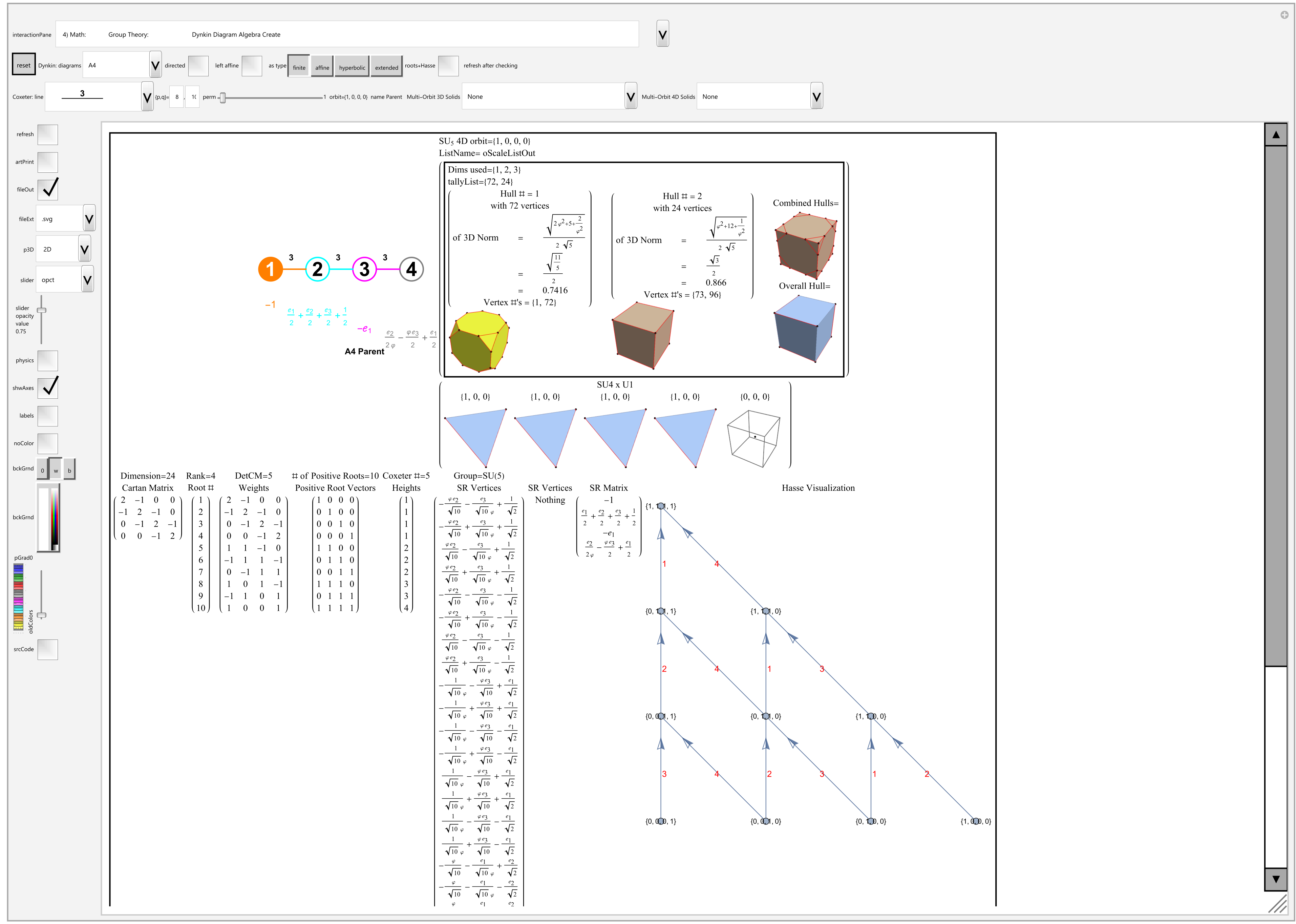
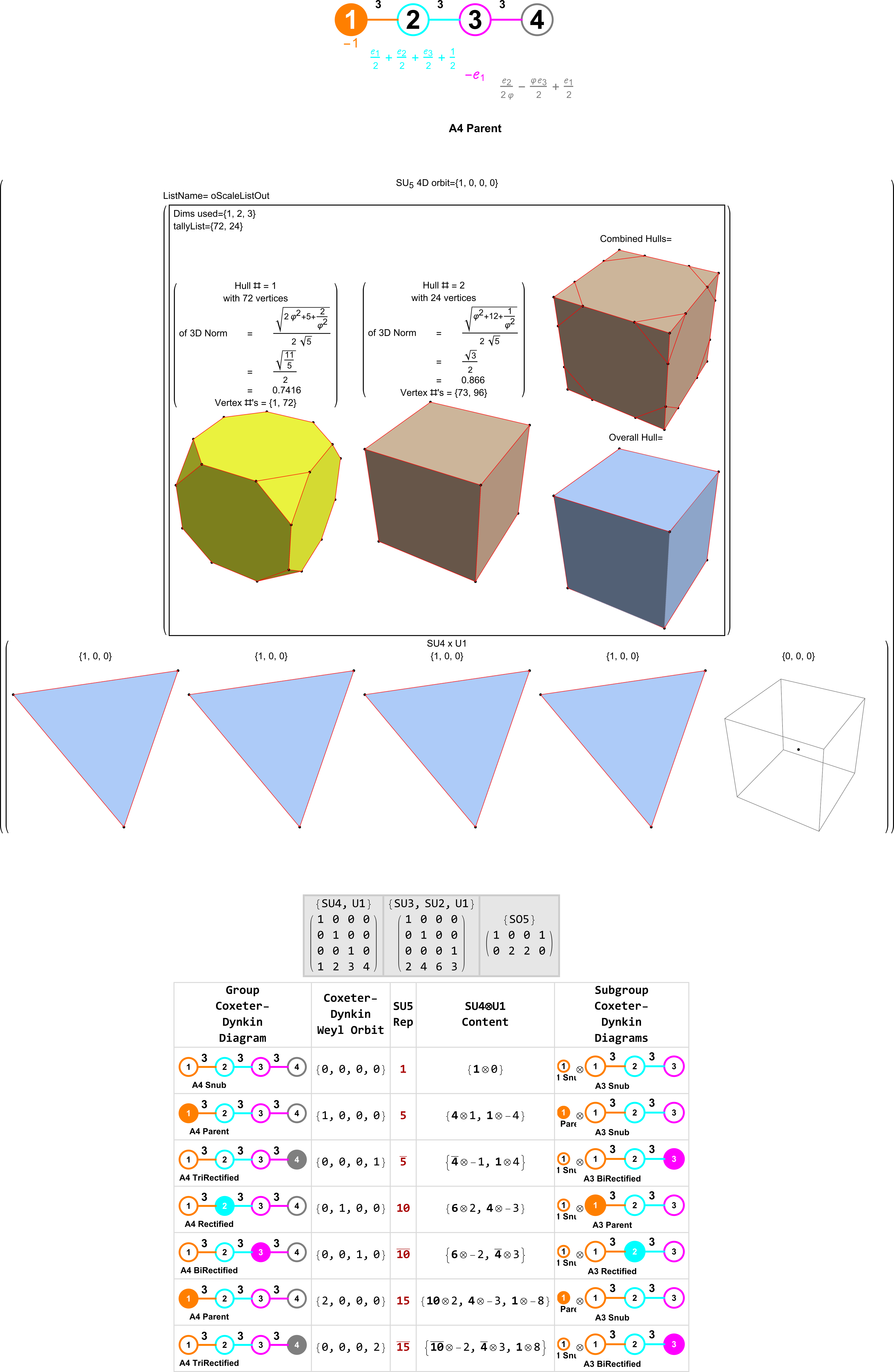
For fully interactive Mathematica NB (and higher quality SVG, PDF, as well as PNG files for all of the combined and overall hull pairs as shown above) in all 15 Weyl orbit permutations, download them here:
H4 600-cell: NB (60 Mb) SVG (50 Mb) PDF (25 Mb) PNG (25 Mb)
F4 288-cell: NB (10 Mb) SVG (25 Mb) PDF (15 Mb) PNG (20 Mb)
D4 24-cell: NB (5 Mb) SVG (15 Mb) PDF (10 Mb) PNG (15 Mb)

Please see several prior posts presenting (with now much improved) sectioning visualizations of Coxeter’s Regular Polytope book Table V here, 120-diminished rectified 120-cell (aka. Swirl-Prism) here, and 90=6×15 matrices of links to the 15 Weyl orbit permutations (with associated Coxeter-Dynkin diagrams) of the 4-polytope 5, 16/8, 24, 600/120 cell sections/animations here.
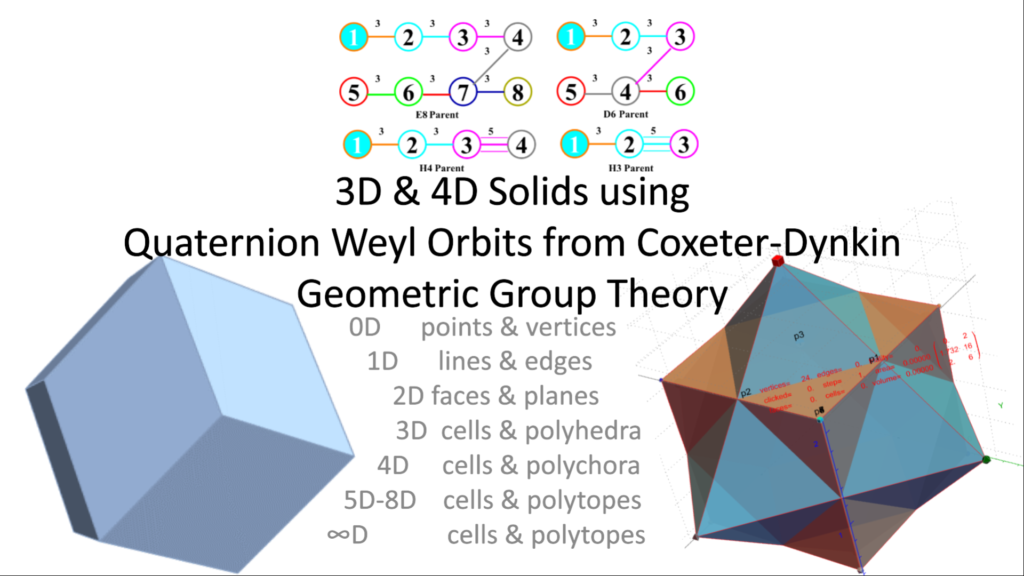
This post now presents the 60=[4 cell-first, vertex-first, face-first, and edge-first orientations of 15 Weyl orbits] visualizations for the self-dual 24-cell (D4), the disphenoidal 288-cell (F4), and H4 600-cell (which has the same content as its dual the 120-cell by the symmetry of the Coxeter-Dynkin diagram).
These are generated using 4 quaternionic rotations. The one off a main orbit orientation (i.e. using the e0=1 identity quaternion rotation) is either the vertex or cell first orientation for each of the 15 Weyl orbit permutations, with the other rotation being e2+e3. Then for edge and face first orientation rotations, depending on the 24, 288, or 600 cell type, they will be one of either e1+e2+e3 & e1+2e2+e3 (for 24 & 288 cells) or e0+φe1 & e0+e1+e2 (for 600/120 cells).
vZome has a very nice (and fun) website curated by Scott Vorthmann with some information on quaternion generation of cell-vertex-face-edge first orientations here.
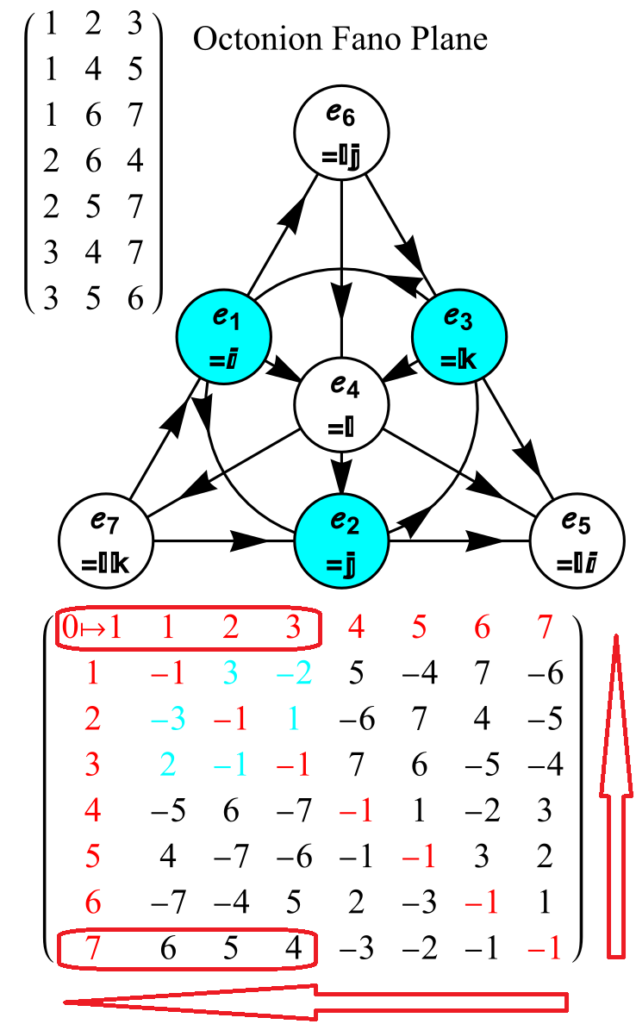
The main orbits are (or can also be) generated by using quaternions and the A, B-C, D-F, E-H group theoretic relationships. I actually use octonionic multiplication operations with multiplication tables from the 480 possible where the first (of 7 triads) are the quaternion of 0123. This means the last four dimensions of the octonion (i.e. 4567 or {l, li, lj, lk}) are {0,0,0,0}.
You can navigate the matrices of links below or simply download the ZIP files for the SVG sectioning for the 600-cell here (800 Mb), 288-cell here (200 Mb), and 24-cell here (125 Mb).
SVG section visualizations:
Orientations for H4 600-cell SVG section file links:
Cell Vertex Edge Face
Orientations for F4 Disphenoidal 288-cell SVG section file links:
Cell Vertex Edge Face
Orientations for D4 24-cell SVG section file links:
Cell Vertex Edge Face
MP3 section animations:
Orientations for H4 600-cell MP3 section animation file links:
Cell Vertex Edge Face
Orientations for F4 Disphenoidal 288-cell MP3 section animation file links:
Cell Vertex Edge Face
Orientations for D4 24-cell MP3 section animation file links:
Cell Vertex Edge Face
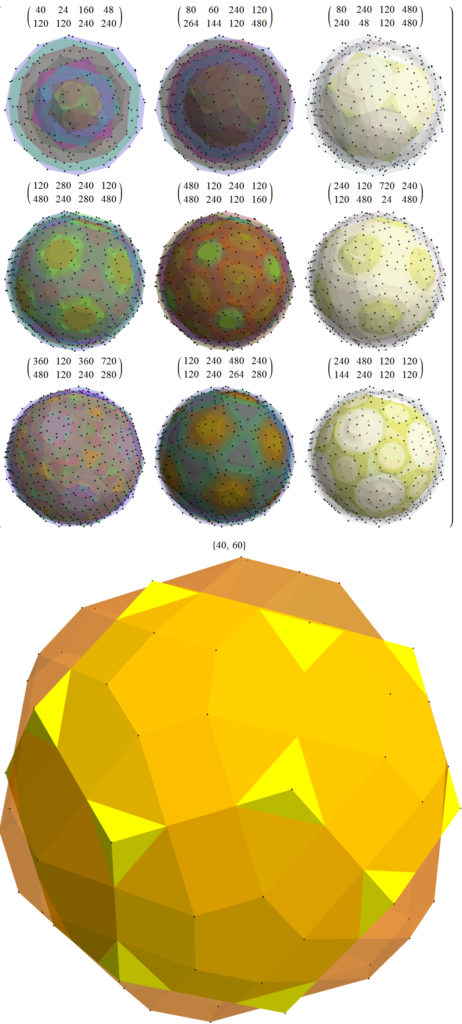
An interesting set of prisms are in the F4 disphenoidal 288-cell’s omni-truncated sections (below):