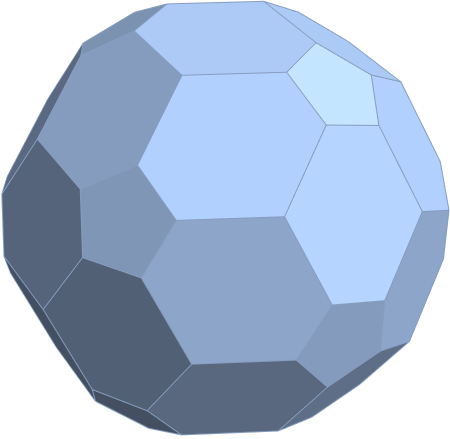
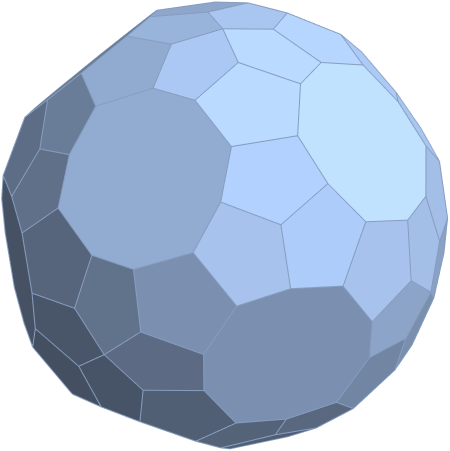
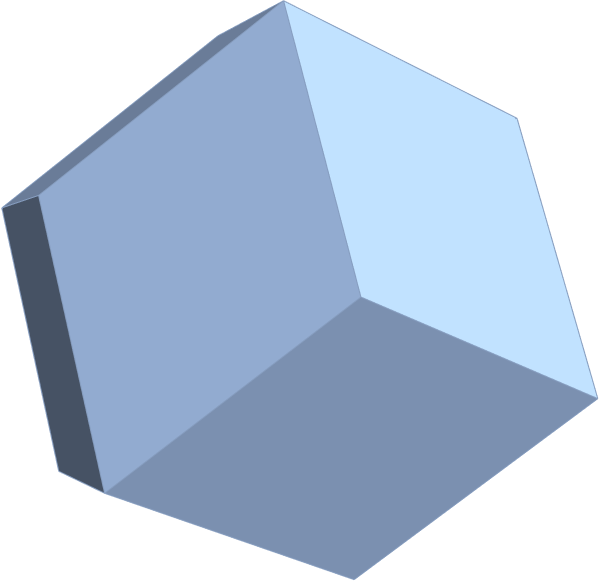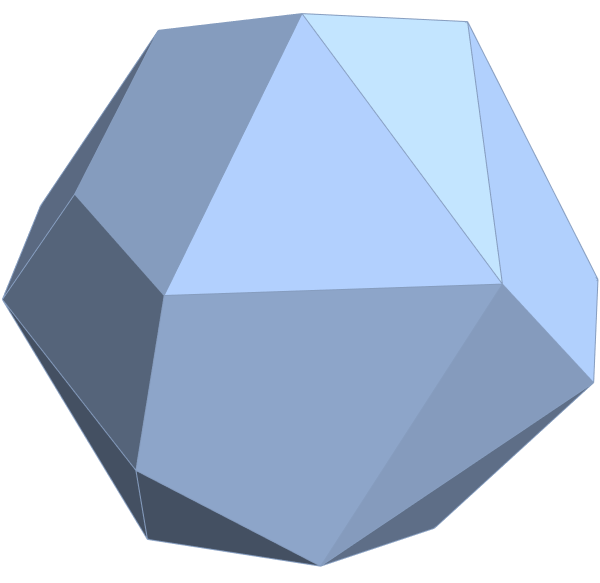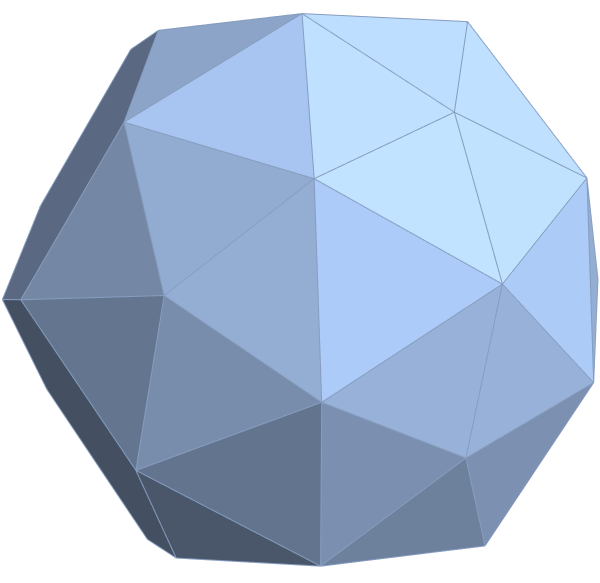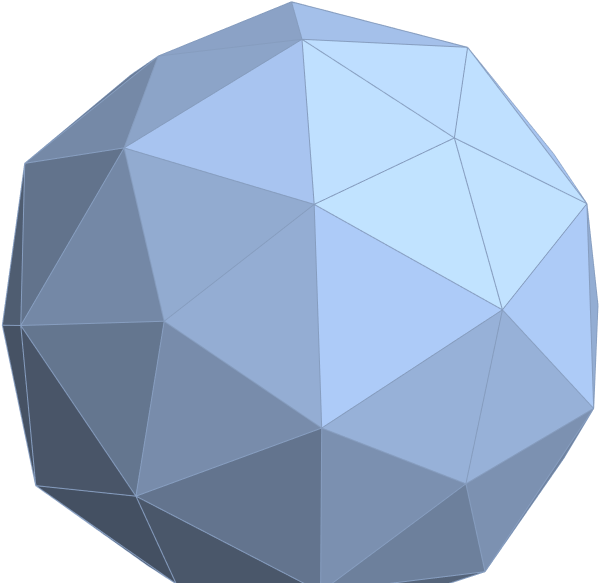
Below are SVG images of output from Pane 1 (Chaos) and Pane 17 (AI) of the VisibLie_E8 visualization tool:
Greg Moxness, Tucson AZ
Collections of 3D Surfaces, 3D Chaotic Attractors, 2D/3D Fractals, and 3D Cellular Automaton
Category Archives: Physics
Added visualization of the embeddings of the maximal subgroups with associated projection matrices of Lie Algebras in the Dynkin Diagram pane (#4) of VisibLie_E8
This is constructed from VisibLie_E8 and uses the Mathematica package Mathgroup. A comprehensive PowerPoint/PDF that gives an overview of the underlying theory and VisibLie_E8 tool capability is in this post.
Disdyakis Triacontahedron Coordinates
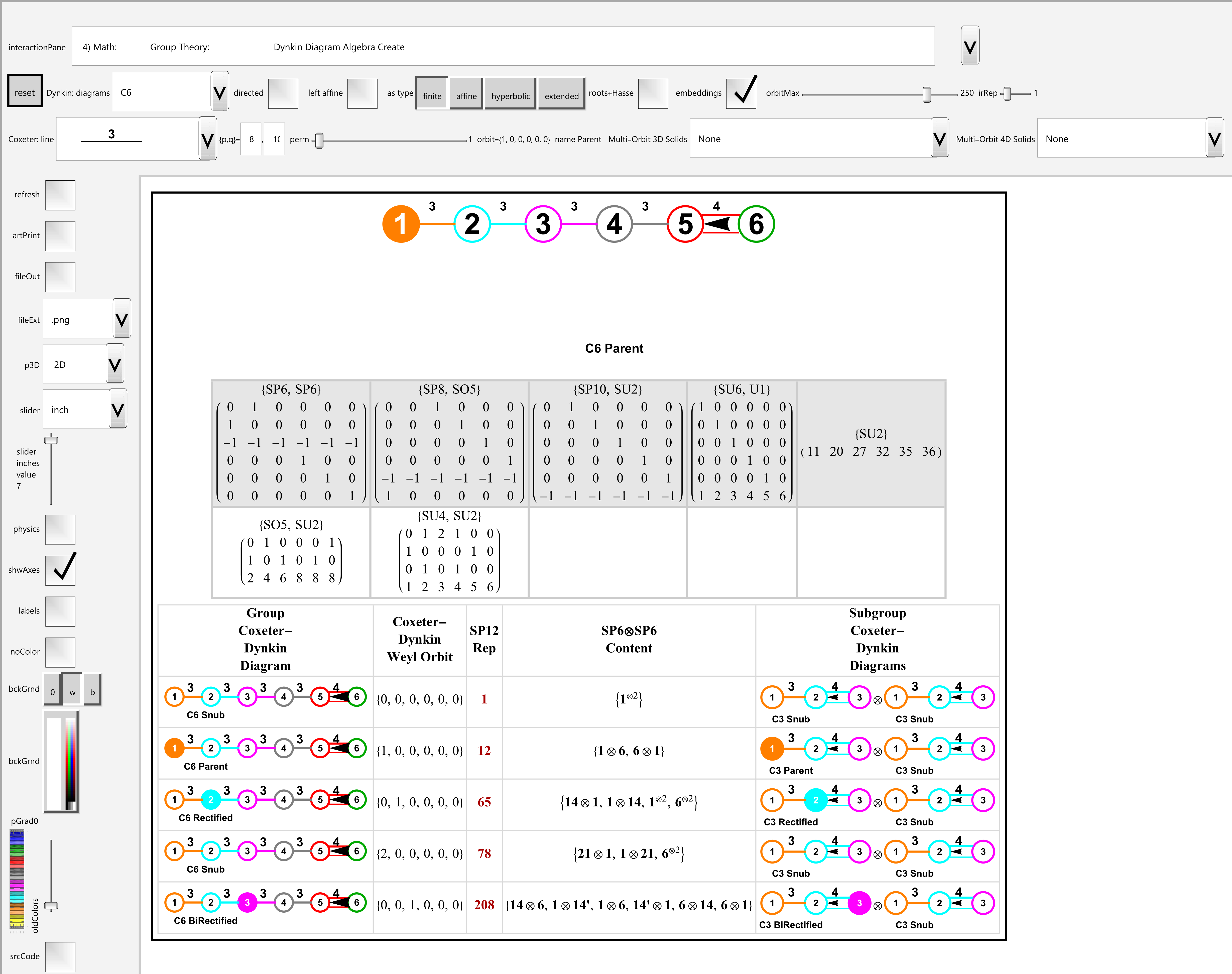
I discovered an error in the WP article on the Disdyakis Triacontahedron. It seemed the scaling factor for determining the coordinates of the Icosidodecahedron hull was added and changed without any citation references. Since the factor seemed off, I analyzed it using the Koca, Mehmet’s paper and Weisstein, Eric W. “Disdyakis Triacontahedron.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/DisdyakisTriacontahedron.html
Please see this Mathematica Notebook for the results here or the PDF here.
Below is the SVG image of the notebook.
Greg Moxness, Tucson AZ
An Update to the Box 1 or Box 4 Question: The Nature of a God/Man Interaction Given Quantum Physics and True Free Will
A4 Group Orbits & Their Polytope Hulls Using Quaternions
Updated: 05/11/2023
This post is a Mathematica evaluation of A4 Group Orbits & Their Polytope Hulls Using Quaternions and nD Weyl Orbits. This is a work-in-process, but the current results are encouraging for evaluating ToE’s.
Please see the this PDF or this Mathematica Notebook (.nb) for the details.
The paper being referenced in this analysis is here.
Of course, as in most cases, this capability has been incorporated into the VisibLie_E8 Demonstration codebase. See below for example screen shots:
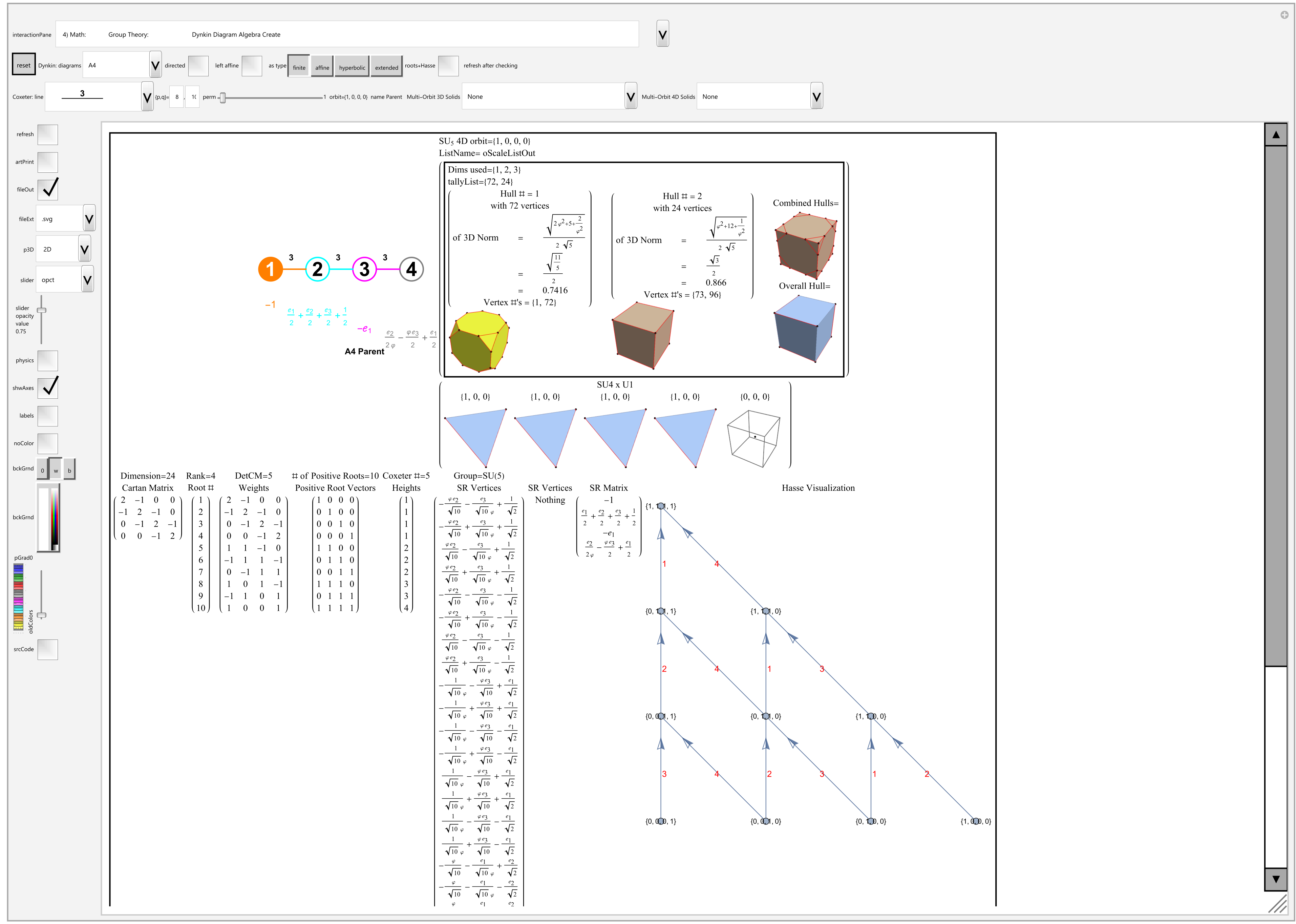
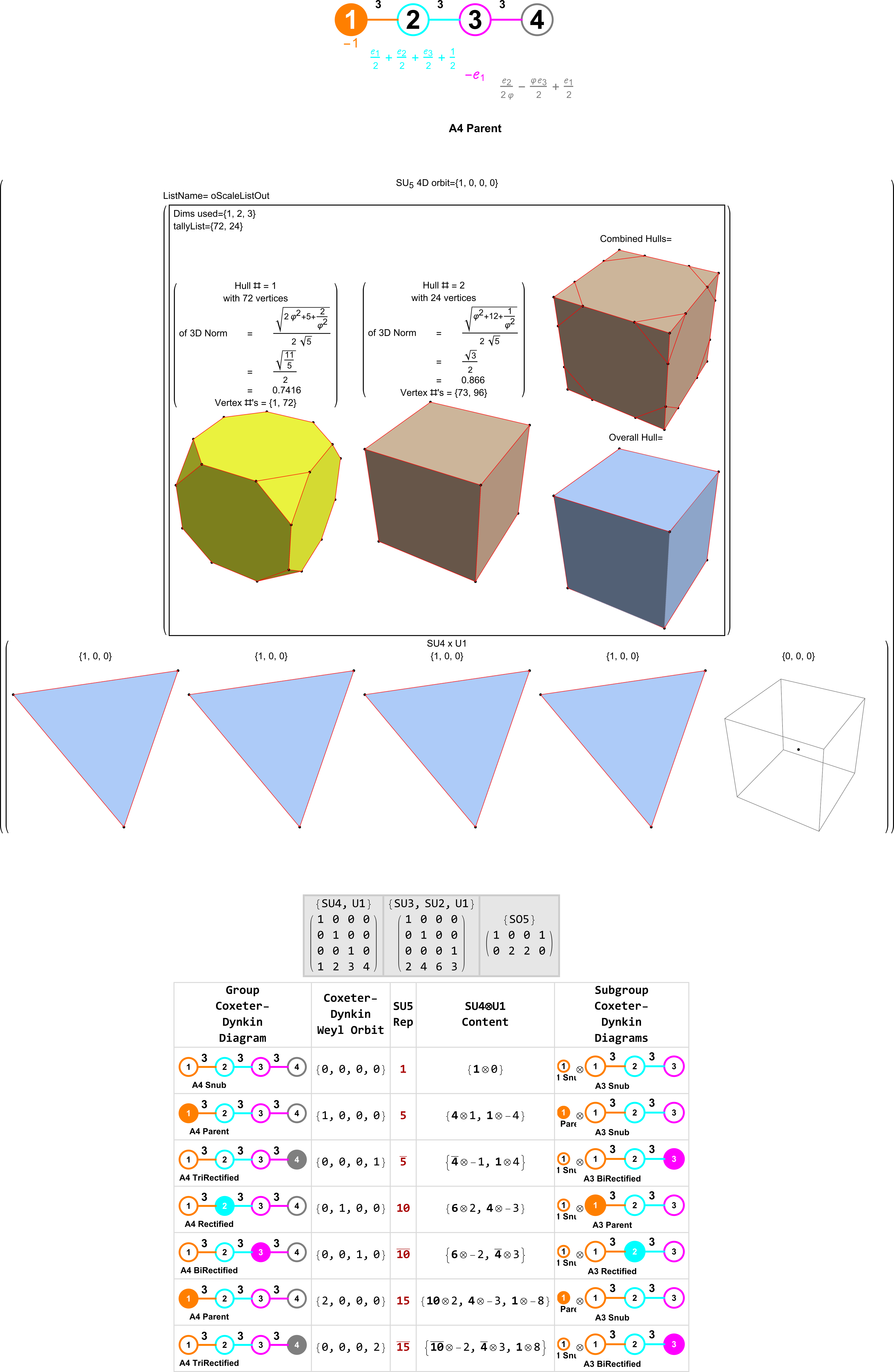
This is an example .svg file output from the same interactive demonstration:
More code and output images below:
Comparing two different 5-Cell Cartesian Coordinate sets
The (diminished) 120-Cell and it’s relationships to the 5-Cell (A4), the 600-Cell (H4), the two 24-Cells (D4), the Dual Snub 24-Cell, and of course E8!
Updated: 05/03/2023
This post is a Mathematica evaluation of important H4 polytopes involved in the Quaternion construction of nD Weyl Orbits.
Please see the this PDF or this Mathematica Notebook (.nb) for the details.
The paper being referenced in this analysis is here.
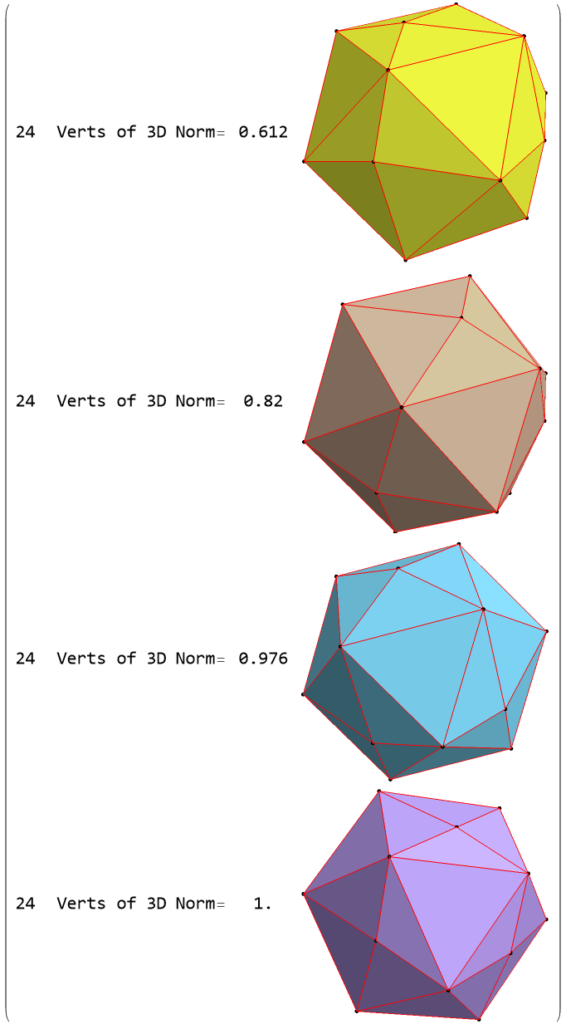
I’ve added this PDF or this Mathematica Notebook (.nb) which is having a bit of fun visualizing various (3D) orbits of diminished 120-cell convex hulls. The #5 subset of 408 vertices (diminishing 192) is completely internal to the normal 3D projection of the 120-cell to the chamfered dodecahedron. The #3 has 12 sets of 2 (out of 3) dual snub 24-cell kite cells (that is 24 out of the 96 total cells).
3D & 4D Solids using Quaternion Weyl Orbits from Coxeter-Dynkin Geometric Group Theory
Click here to view the Powerpoint presentation.
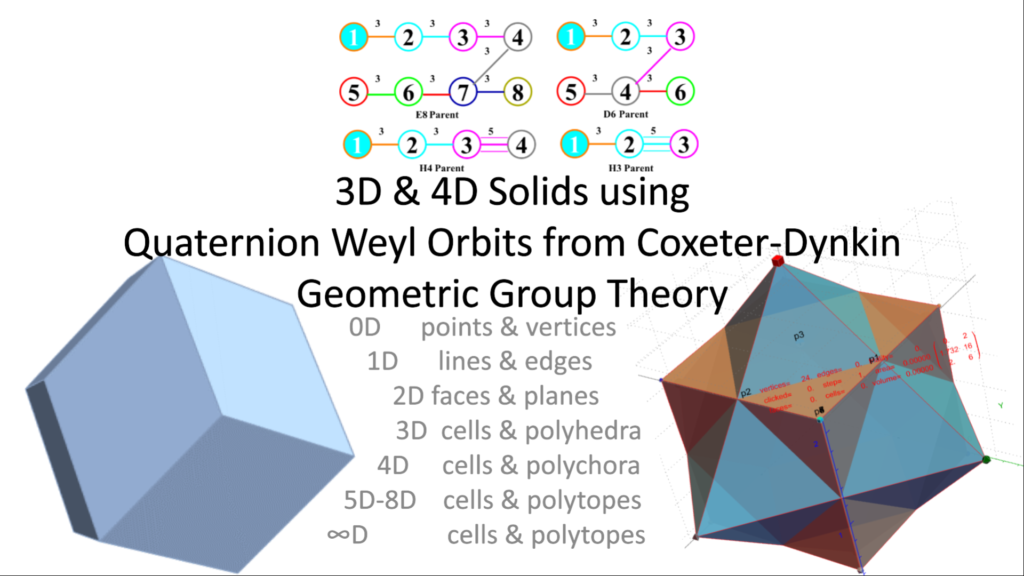
It shows code and output from my VisibLie-E8 tool generating all Platonic, Archimedean and Catalan 3D solids (including known and a few new 4D polychora from my discovery of the E8->H4 folding matrix) from quaternions given their Weyl Orbits.
If you don’t want to use the interactive Powerpoint, here is the PDF version.
See these Mathematica notebooks here and here for a more detailed look at the analysis of the Koca papers used to produce the results :
- Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). “Catalan Solids Derived From 3D-Root Systems and Quaternions”. Journal of Mathematical Physics. 51 (4). arXiv:0908.3272. doi:10.1063/1.3356985.
- Koca, Mehmet; Al-Ajmi, Mudhahir; Ozdes Koca, Nazife (2011). “Quaternionic representation of snub 24-cell and its dual polytope derived from E8 root system”. Linear Algebra and Its Applications. 434 (4): 977–989. doi:10.1016/j.laa.2010.10.005. ISSN 0024-3795. S2CID 18278359.
Or scroll down to see the .svg images here and here.
Greg Moxness, Tucson AZ
A New and Improved E8 Hasse Visualization
This uses the latest Mathematica version 13.2 with code tweaks to better understand what is being presented, including the E8 Algebra roots, weights, and heights. This is used on the E8 group theory page of WikiPedia.
For a more graphic intensive E8 Hasse visualization, see below with both positive and negative roots and more node information and graphics. See here and here for the Mathematica notebook and PDF respectively.
Visualizing the Quaternion Generated Dual to the Snub 24 Cell
I did a Mathematica (MTM) analysis of several important papers here and here from Mehmet Koca, et. al. The resulting MTM output in PDF format is here and the .NB notebook is here.
* The (42) yellow have no overlaps.
* The (51) orange have 2 overlaps.
* The (18) tetrahedral hull surfaces are uniquely colored.
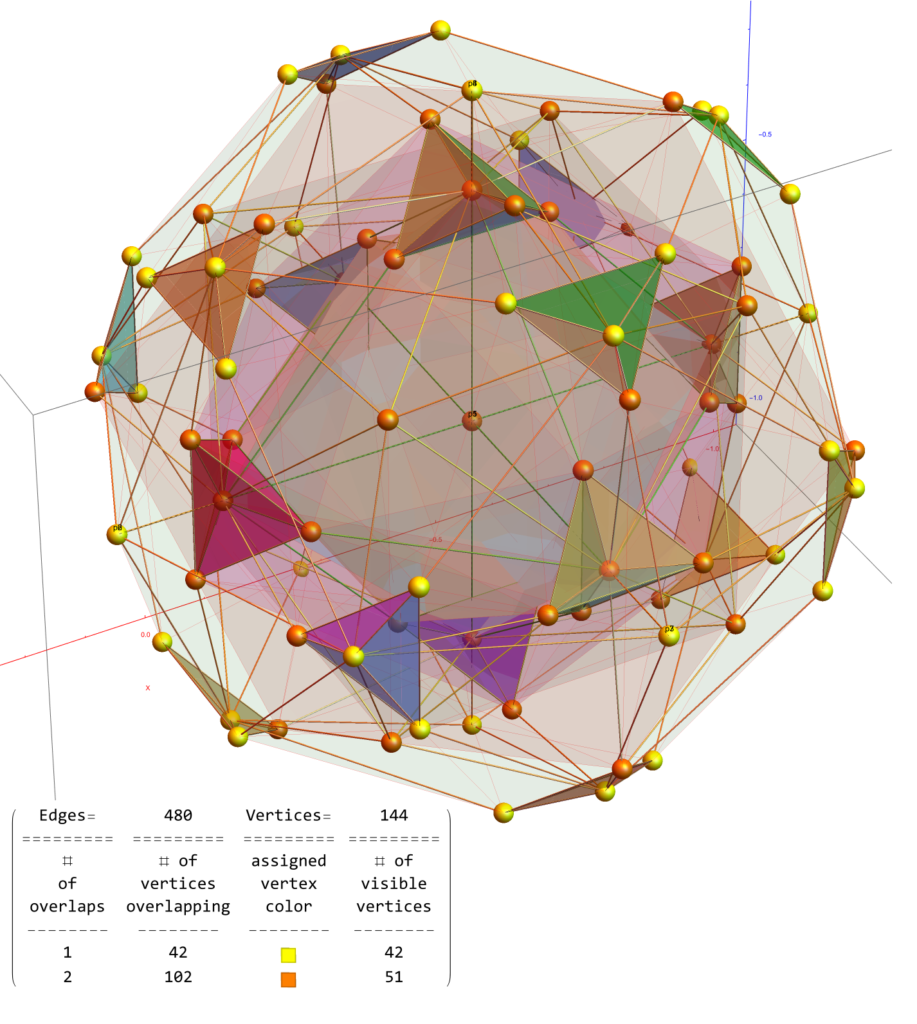
What is really interesting about this is the method to generate these 3D and 4D structures is based on Quaternions (and Octonions with judicious selection of the first triad={123}). This includes both the 600 Cell and the 120 Cell and its group theoretic orbits. The 144 vertex Dual Snub 24 Cell is a combination of those 120 Cell orbits, namely T'(24) & S’ (96), along with the D4 24 Cell T(24).
the W(D4) C3 orbits T'(24)+S'(96)+M (192)
