Based on an excellent 1998 paper by C.S. Rao I’ve modeled the Sri Yantra in Mathematica and incorporated it into the VisibLie_E8 demonstrations (I will upload that soon).

This is a reference figure to verify the model is correct for concurrency (intersecting lines) and concentricity (inner triangles and Bindu point are centered). There are 4 of 18 other constraints used in the diagrams below numerically and/or symbolically solved within the Mathematica code.

Here are 7 of many possible solutions using the 20 constraint rules to produce optimal spherical and plane forms of the Sri Yantra.

Solution 1: Solving constraints (* 1,2,3,4,8 *)

Solution 2: Solving constraints (* 1,2,3,10,15 *)

Solution 3: Solving constraints(* 1,2,4,5,10 *)

Solution 4: Solving constraints (* 1,2,5,6,19 *)

Solution 5: Solving constraints (* 1,2,6,14,19 *)

Solution 6: Solving constraints (* 1,2,8,9,20 *)

Solution 7: Optimum planar

3D using pyramids and new clipping and slicing functions to take off the front (and back) portions of the symmetric 3D object.
I will produce a version option with conical shapes just for fun (soon).

This is a list of the details behind each constraint function Fn

These are 3D hyperbolic tree graphs of some major figures in the Bible. The Hebrew, Greek transliterations for the first verse where they show up are also shown. Mouseover shows the names between the links and the number of times they occur (which changes the thickness of the link).

Another cool new feature I just added is a word translation when you mouse over any word. Clicking on the word or name in the graph changes the statistics to that word.

God

Jehovah

Lord

Adam

Eve

Jeshua

Noah

Abraham

Moses

Jesus

Gabriel

Michael

Satan

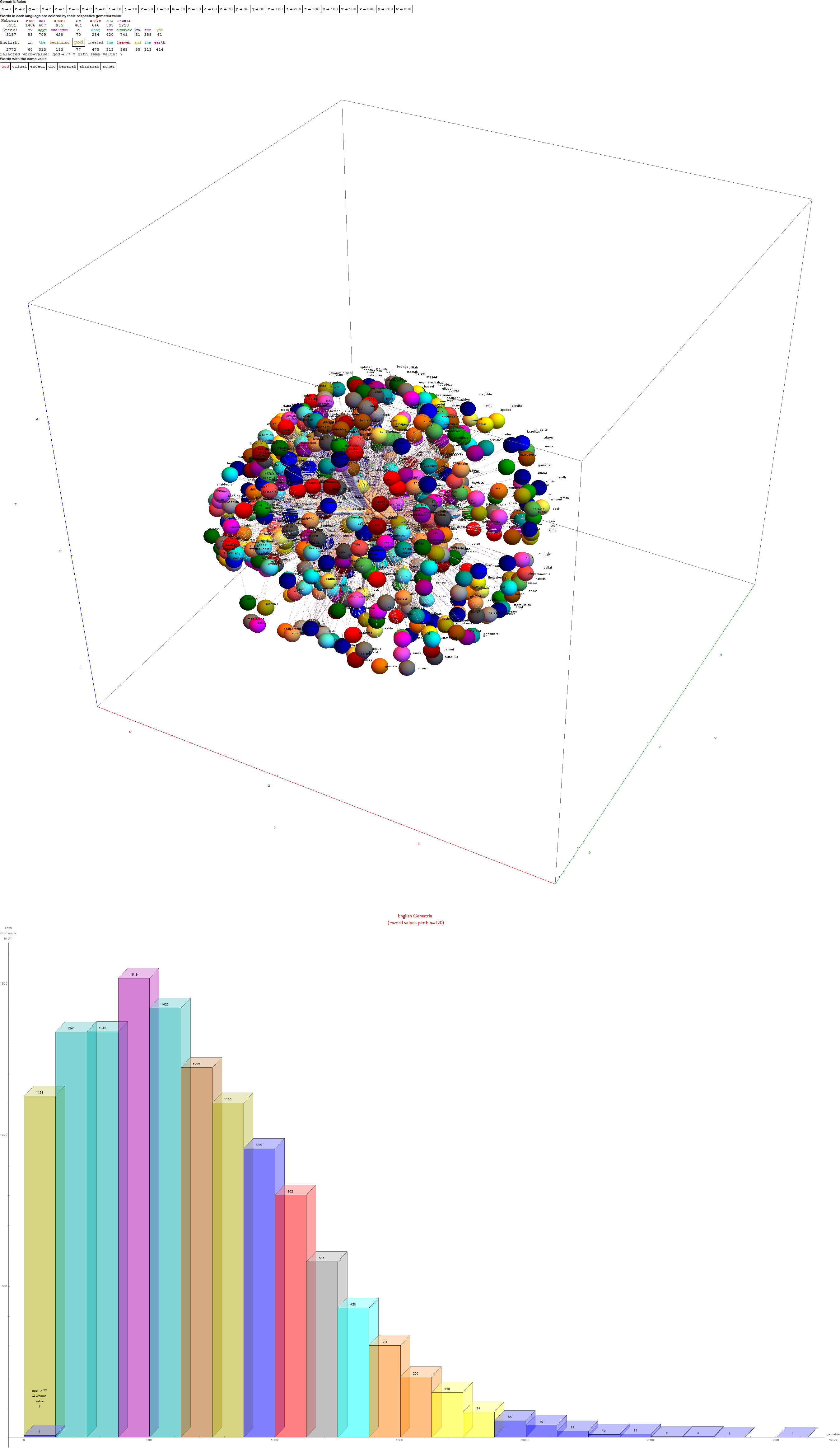
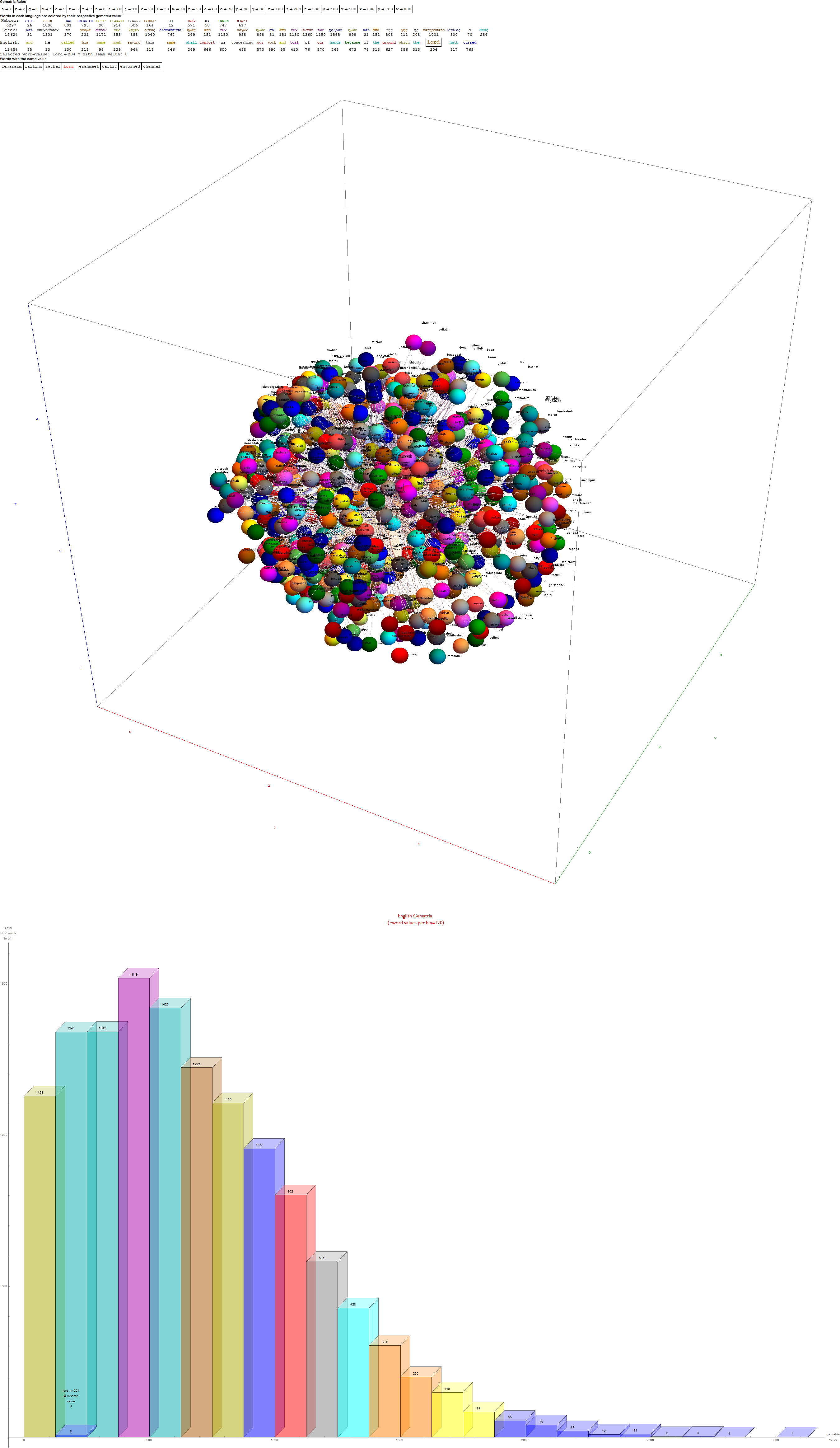
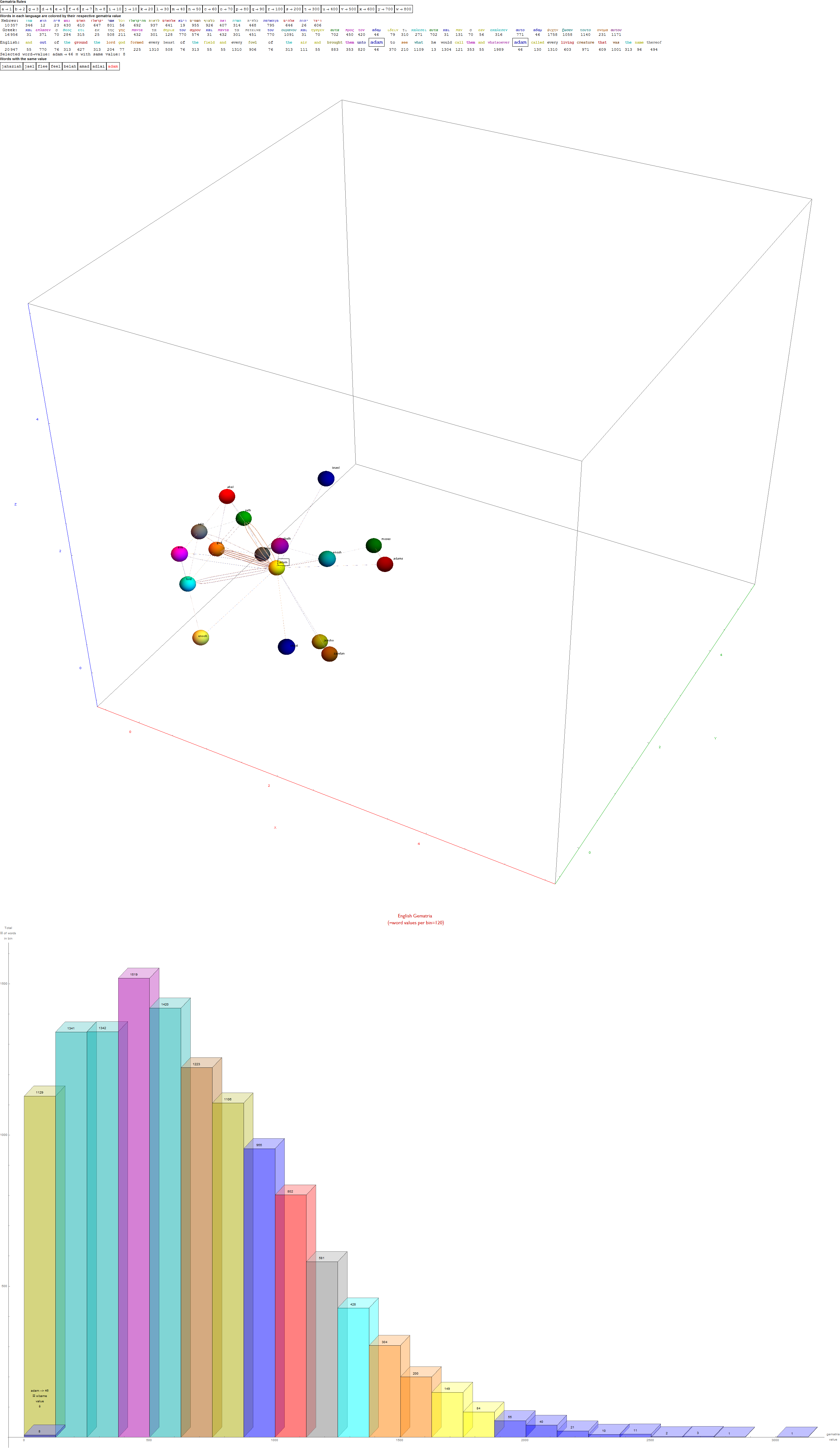
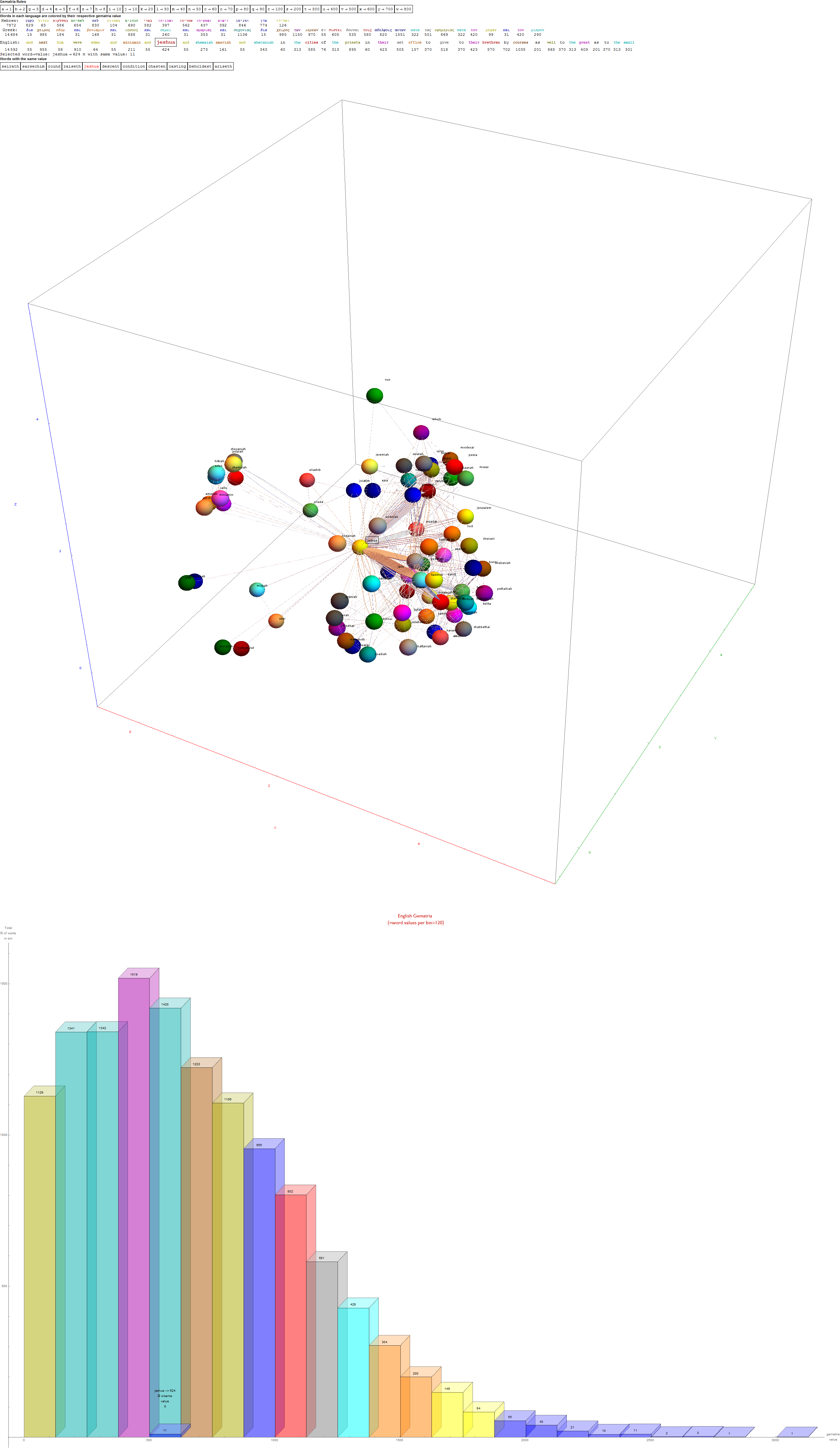
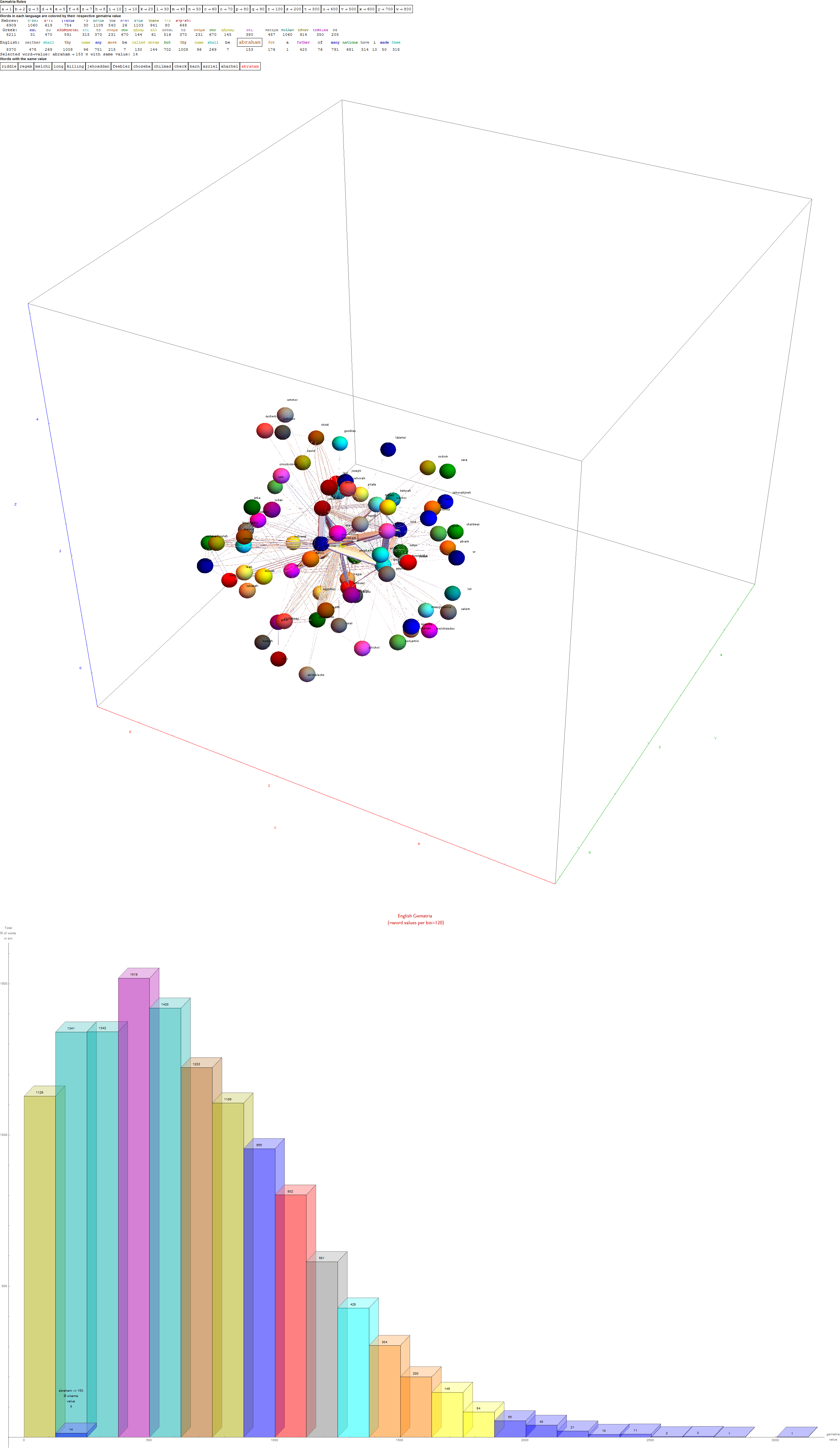
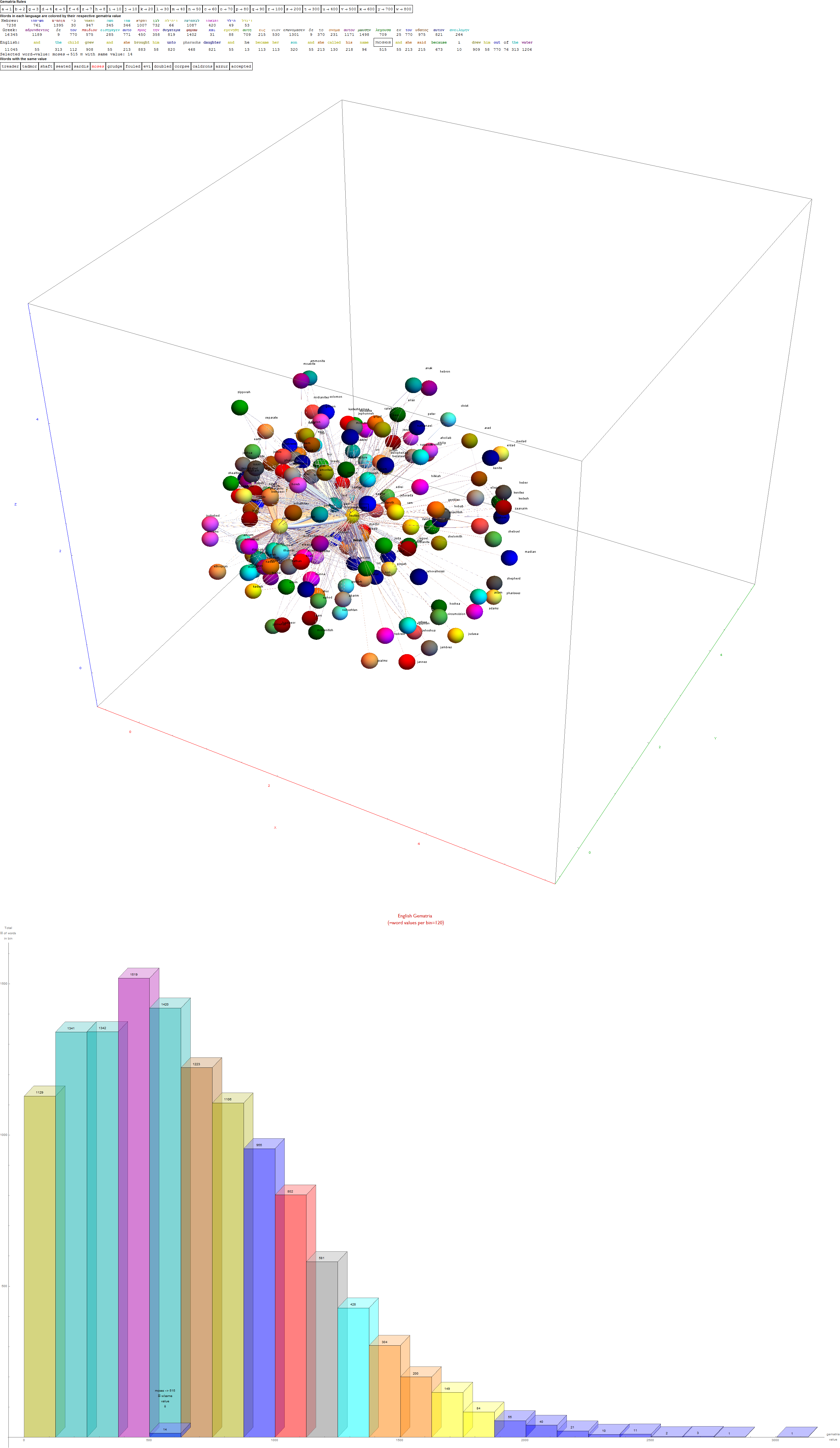
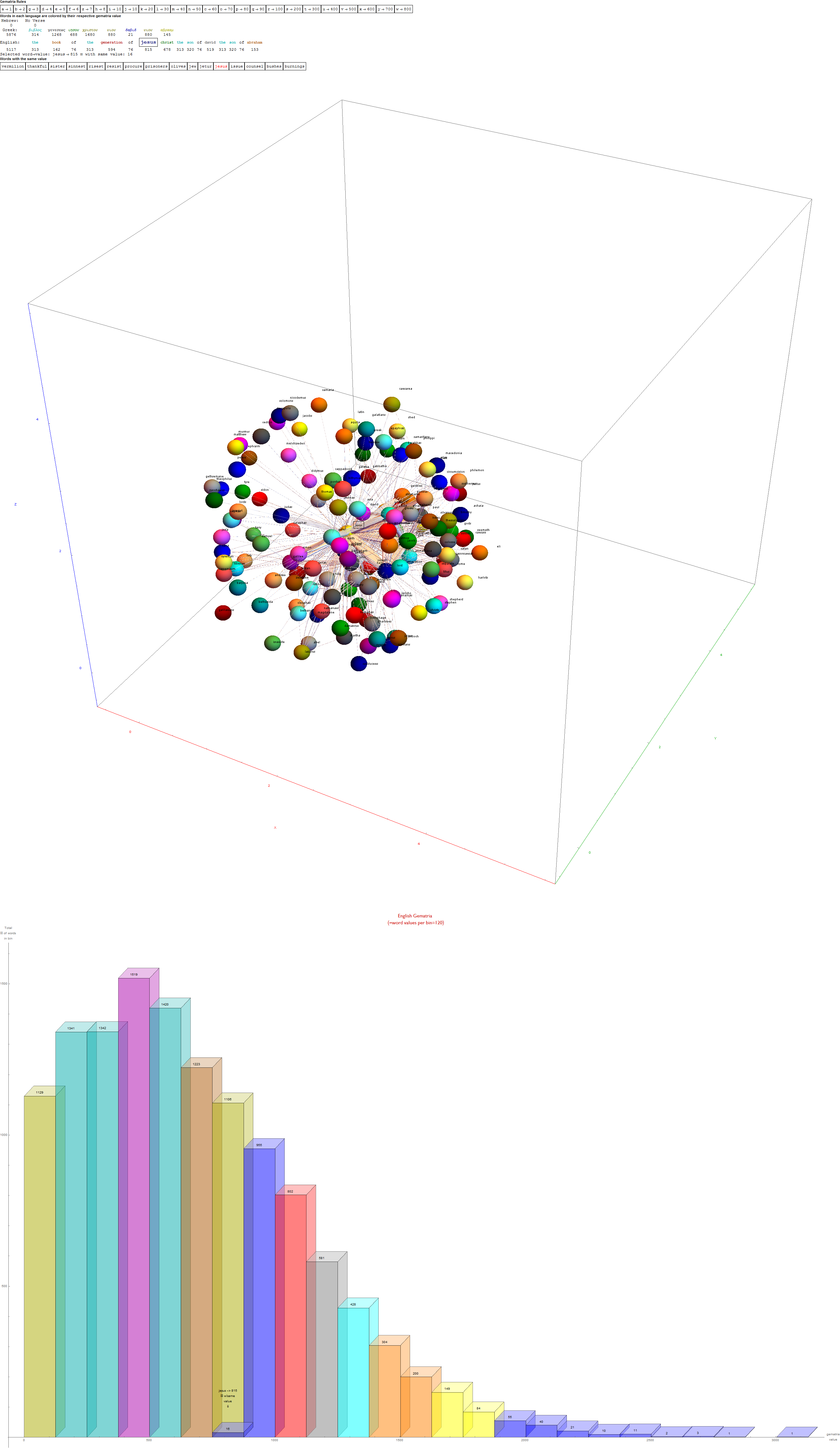
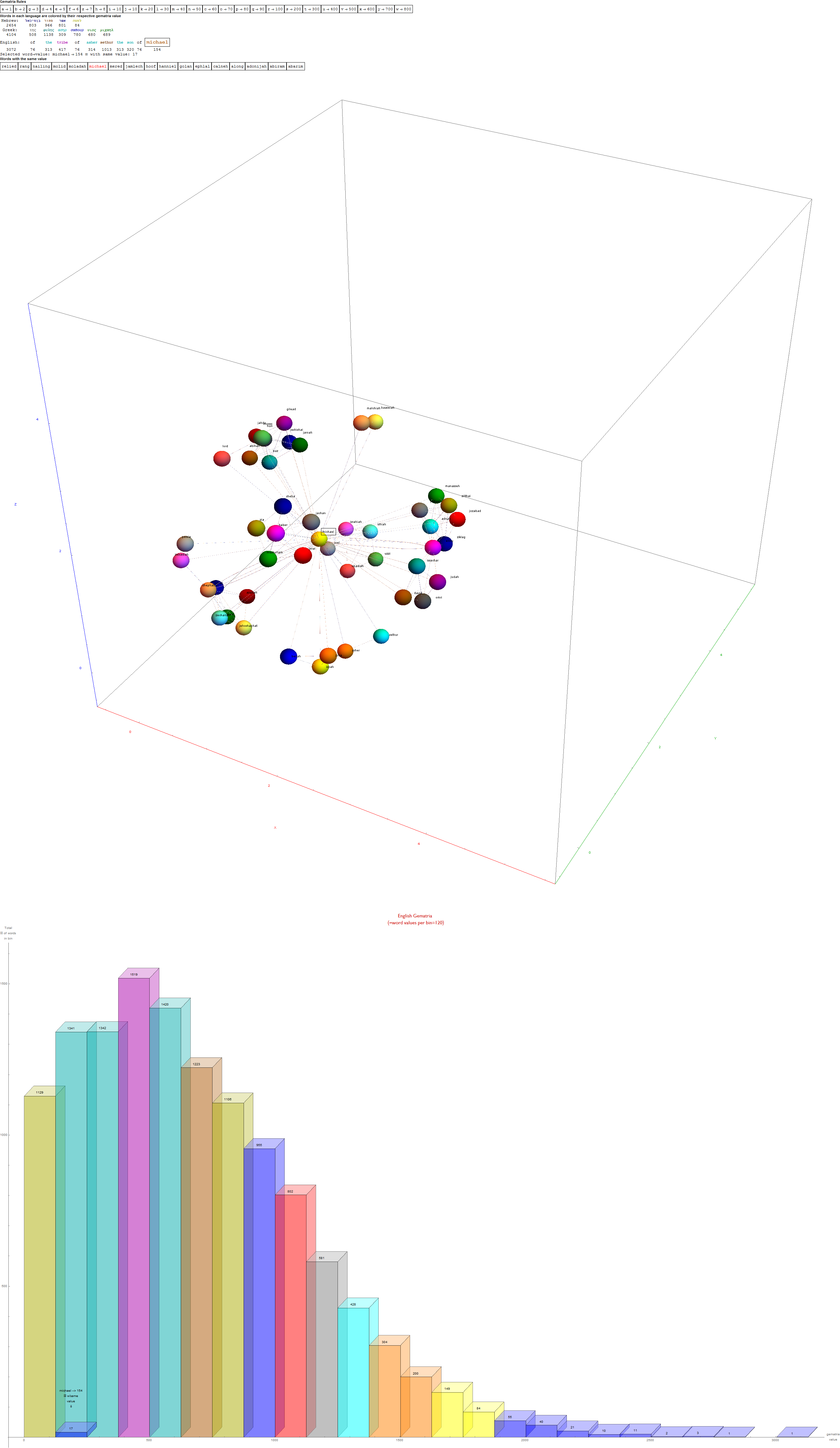
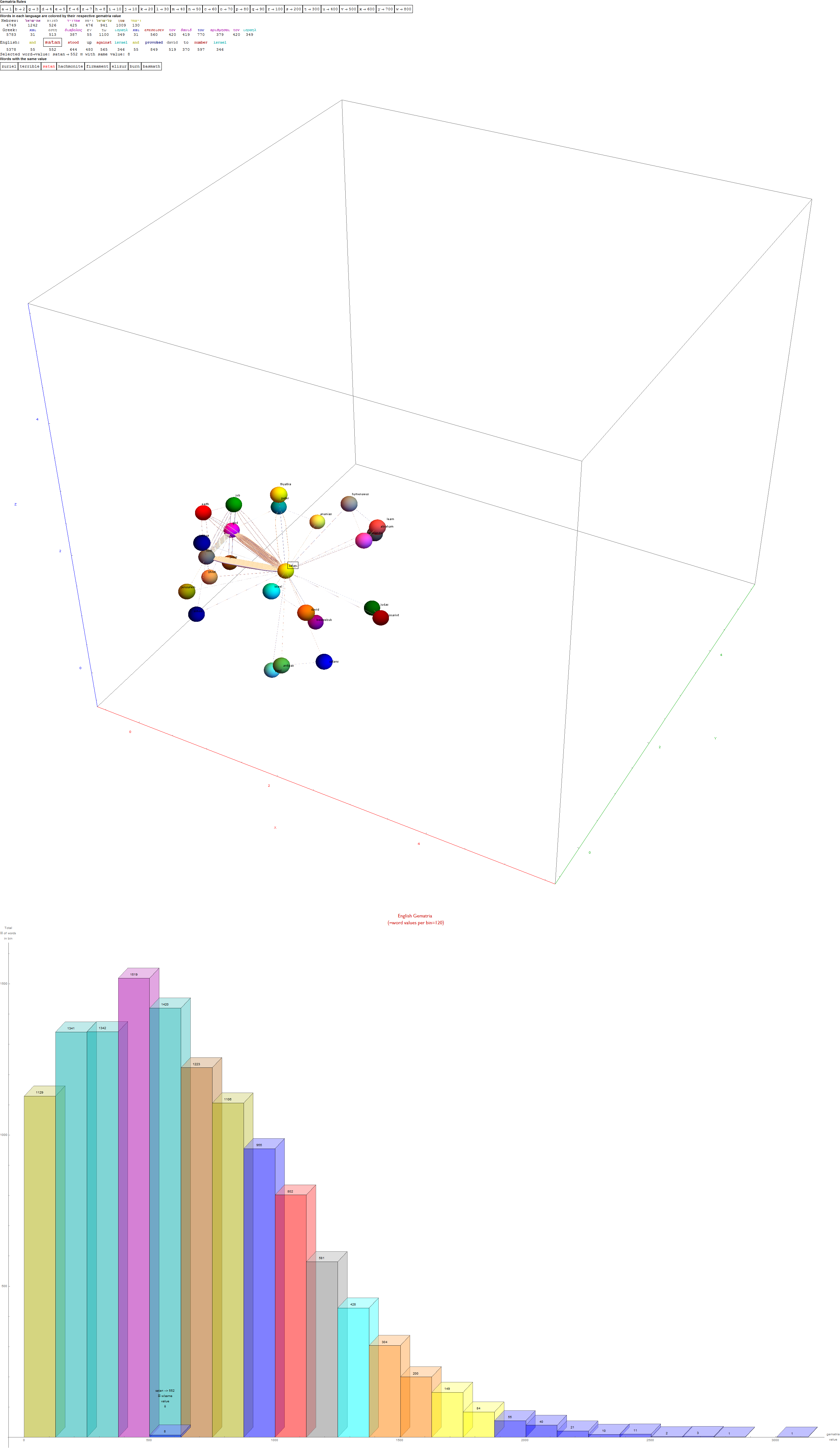
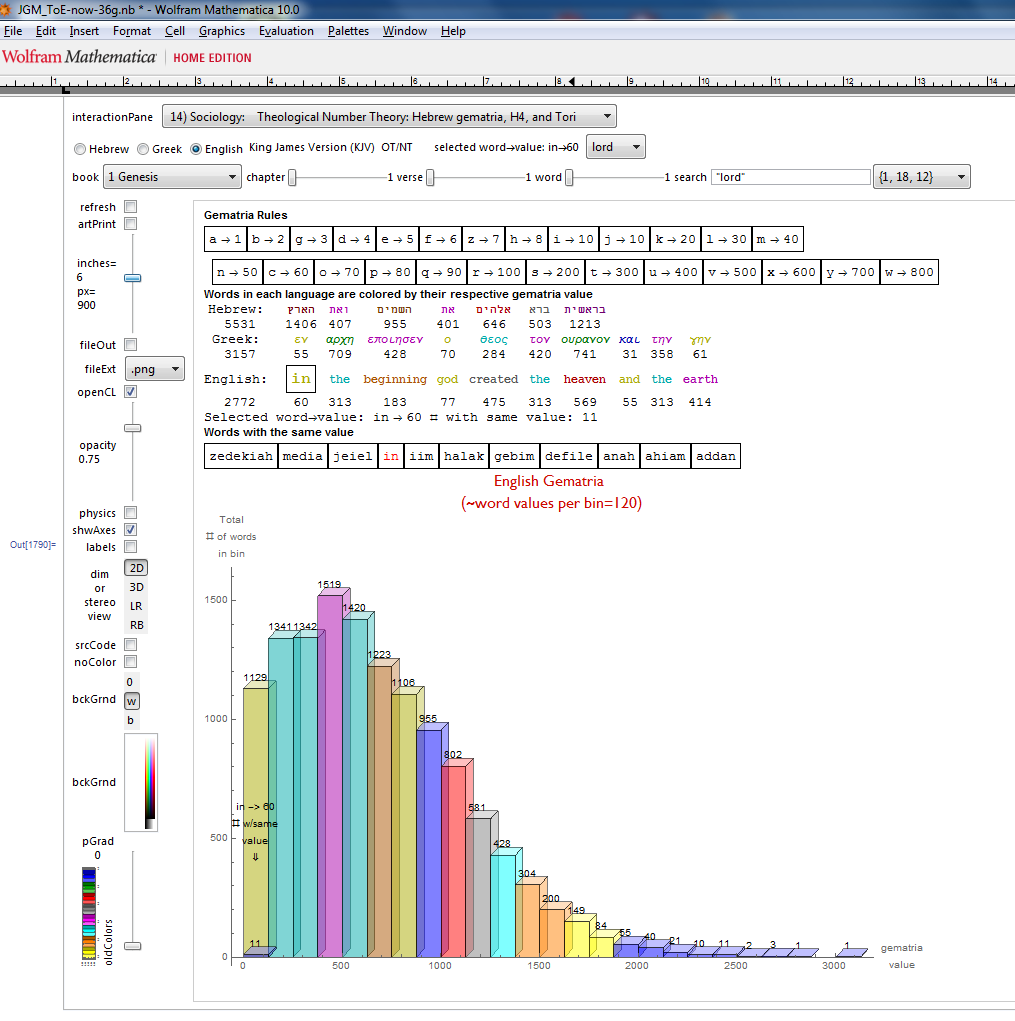
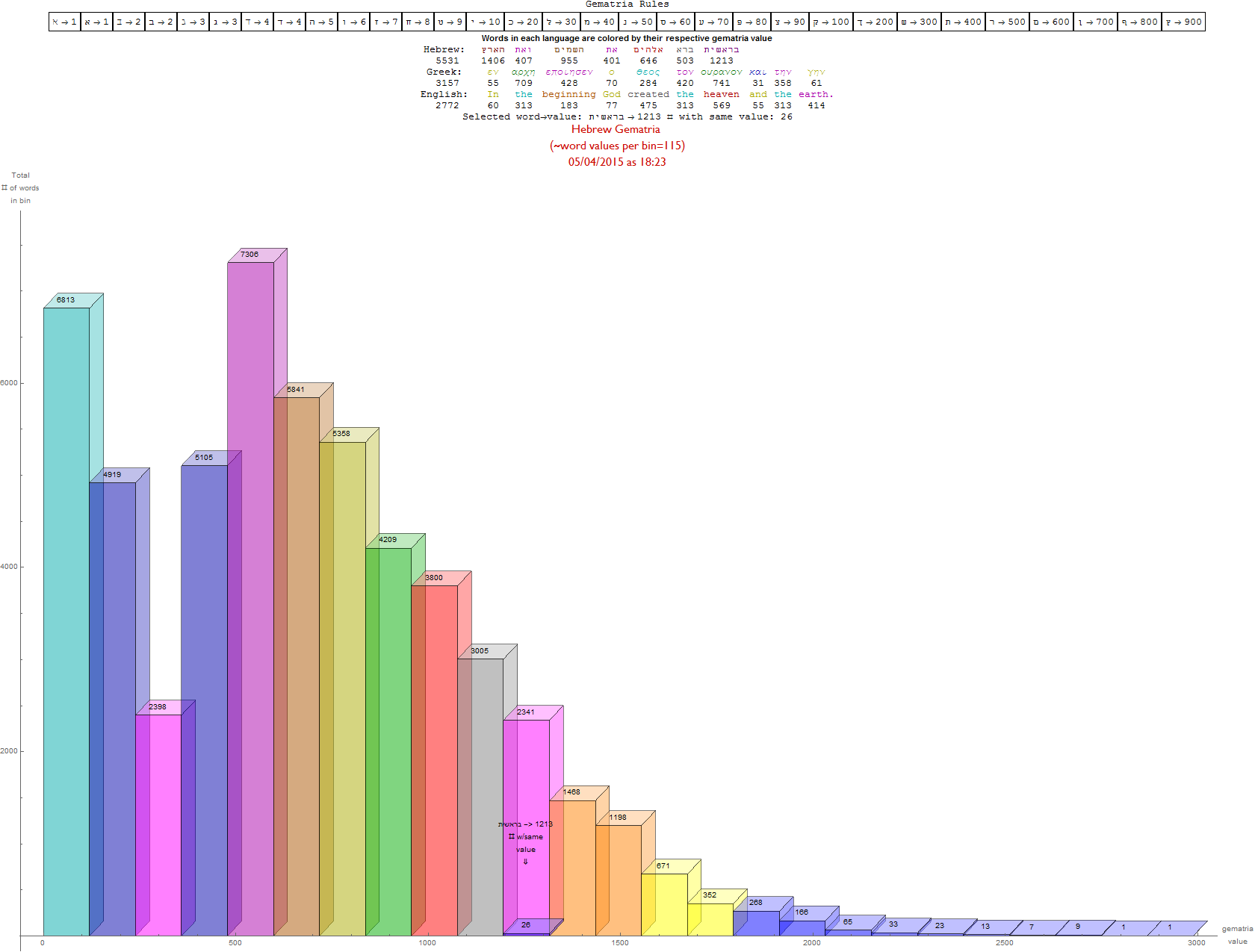
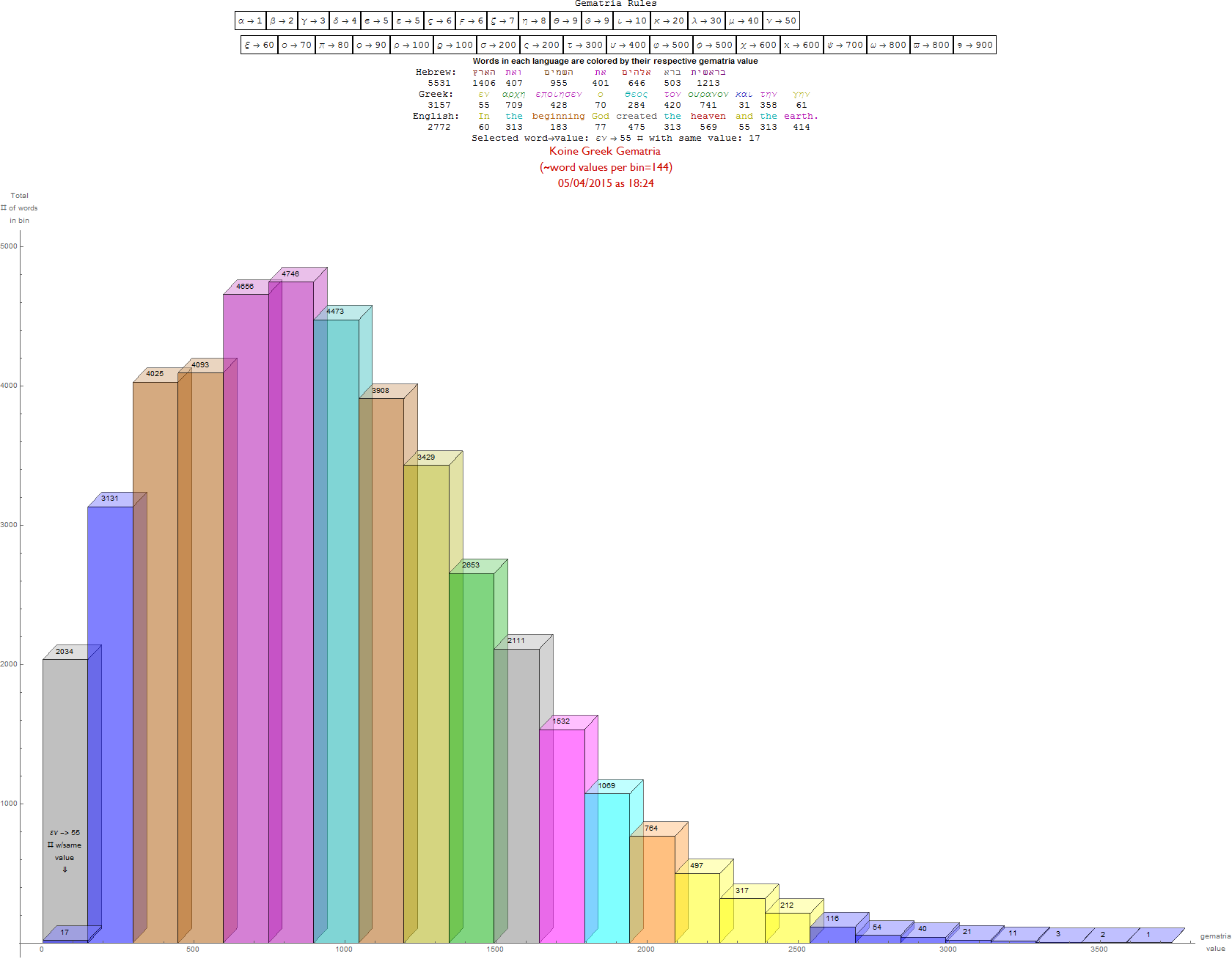
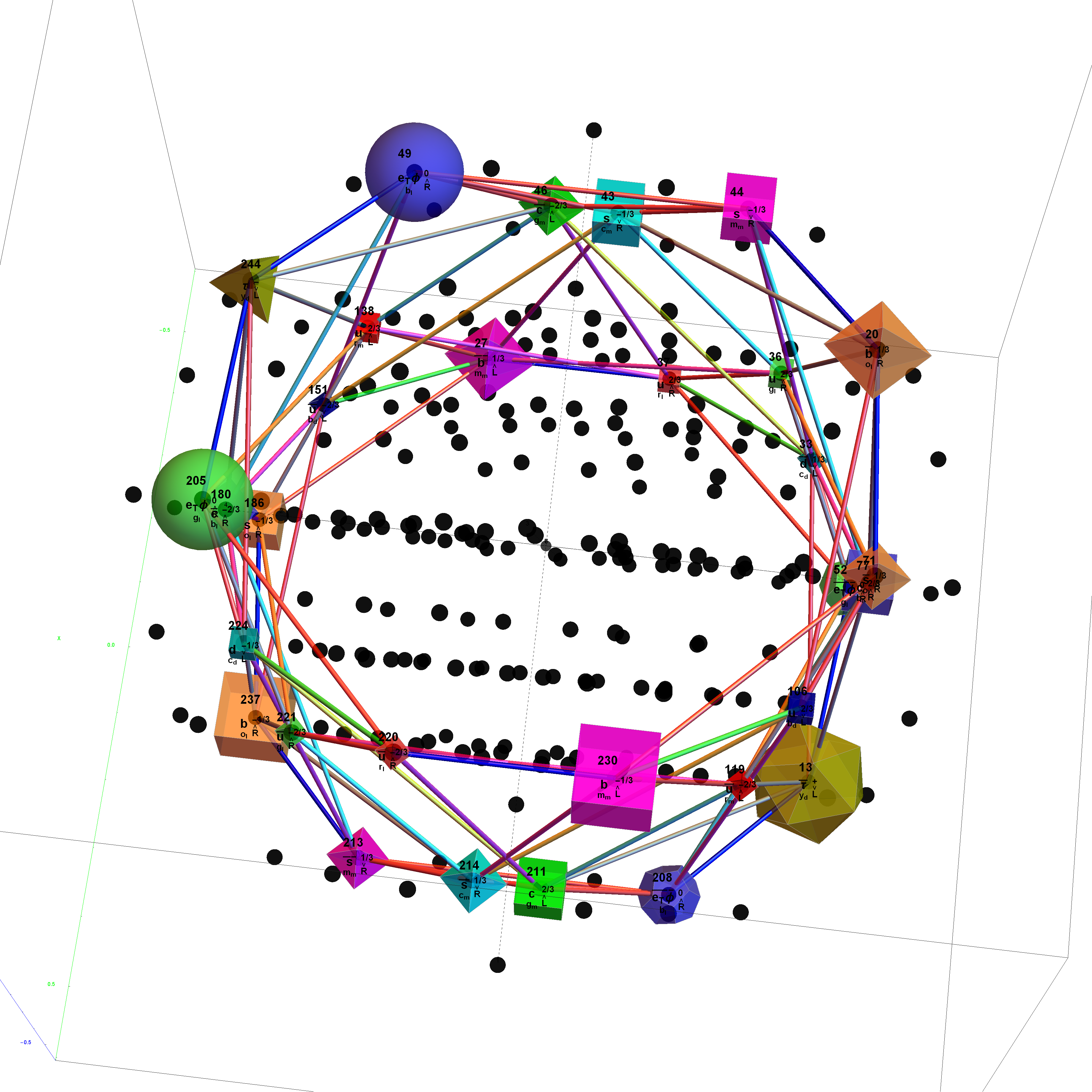
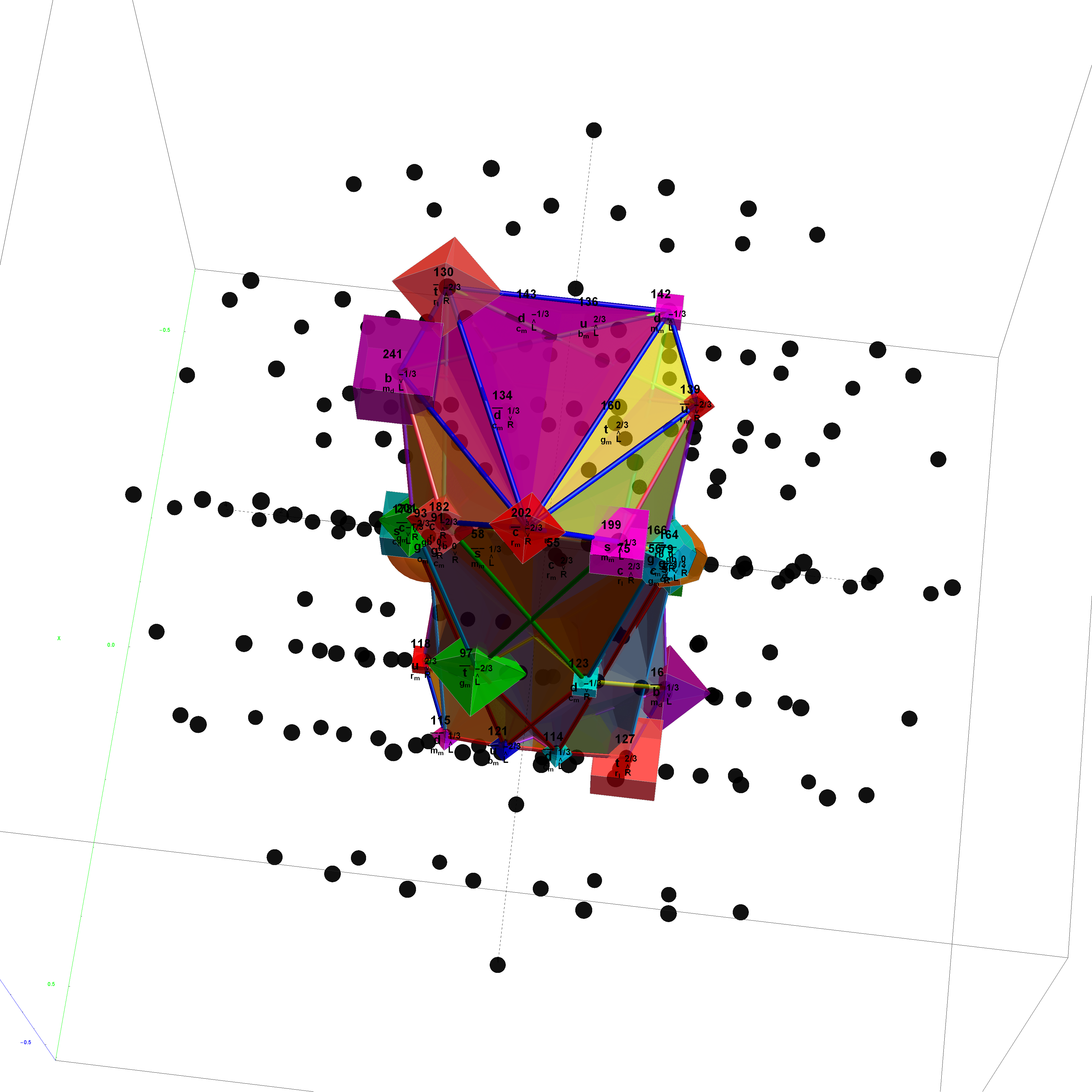
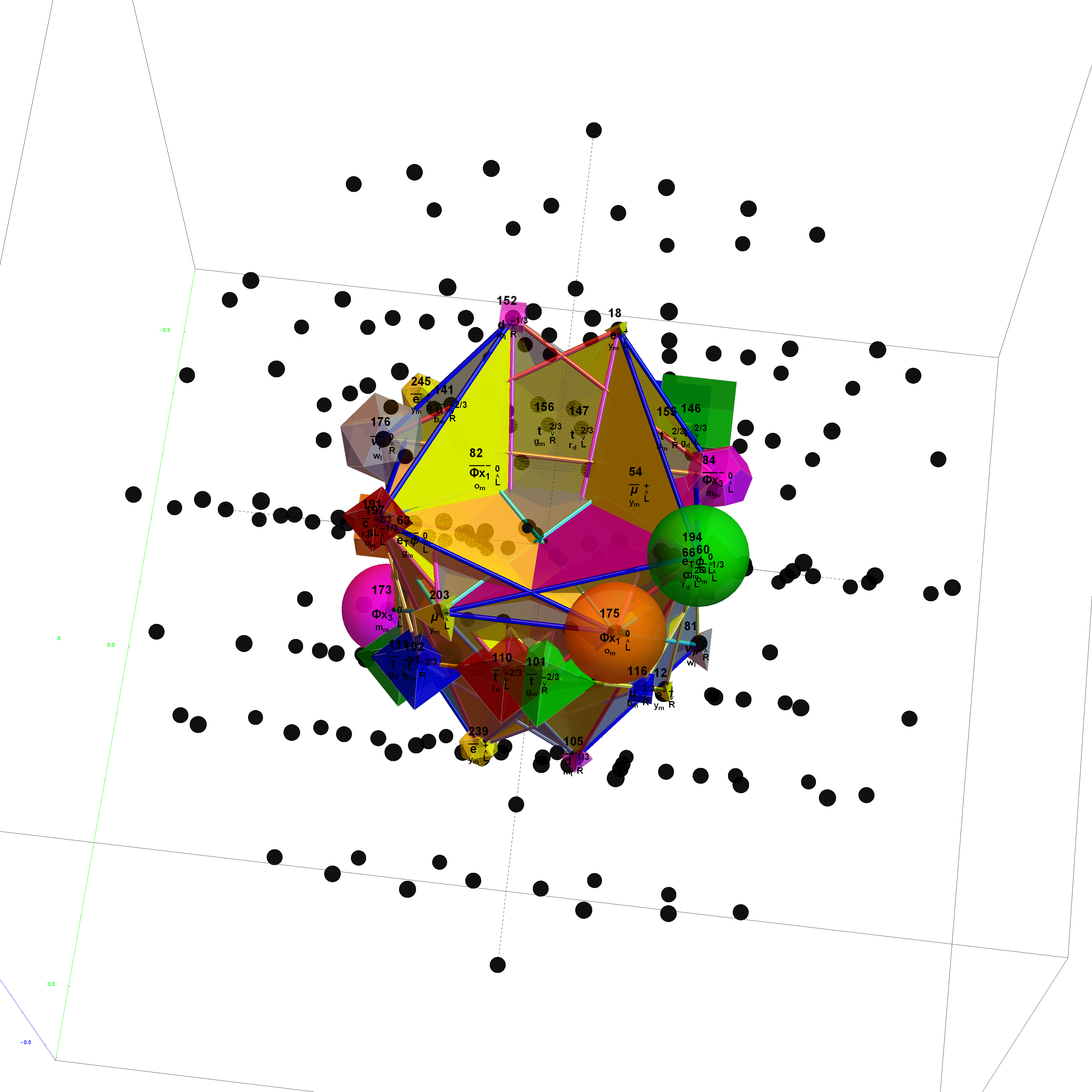
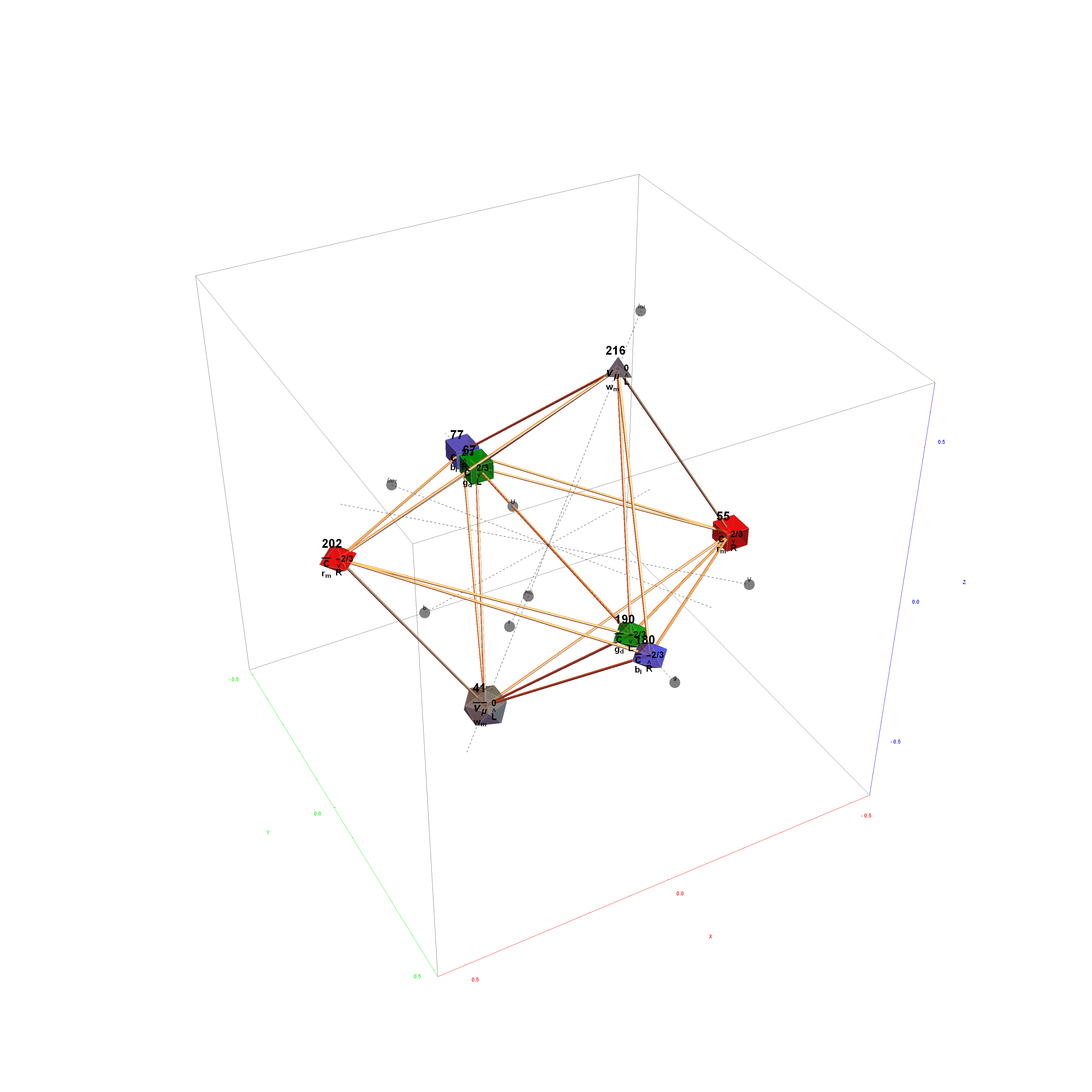
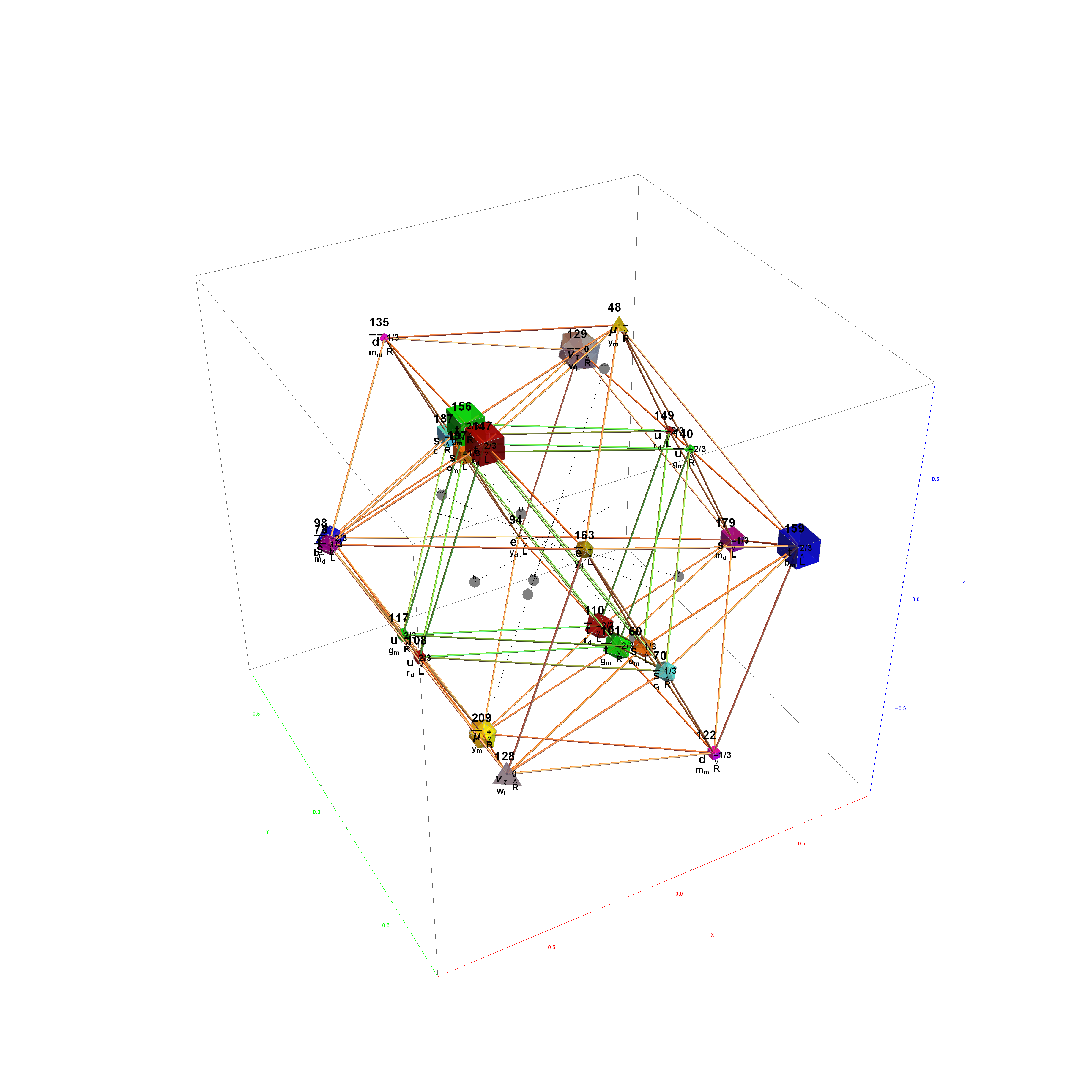
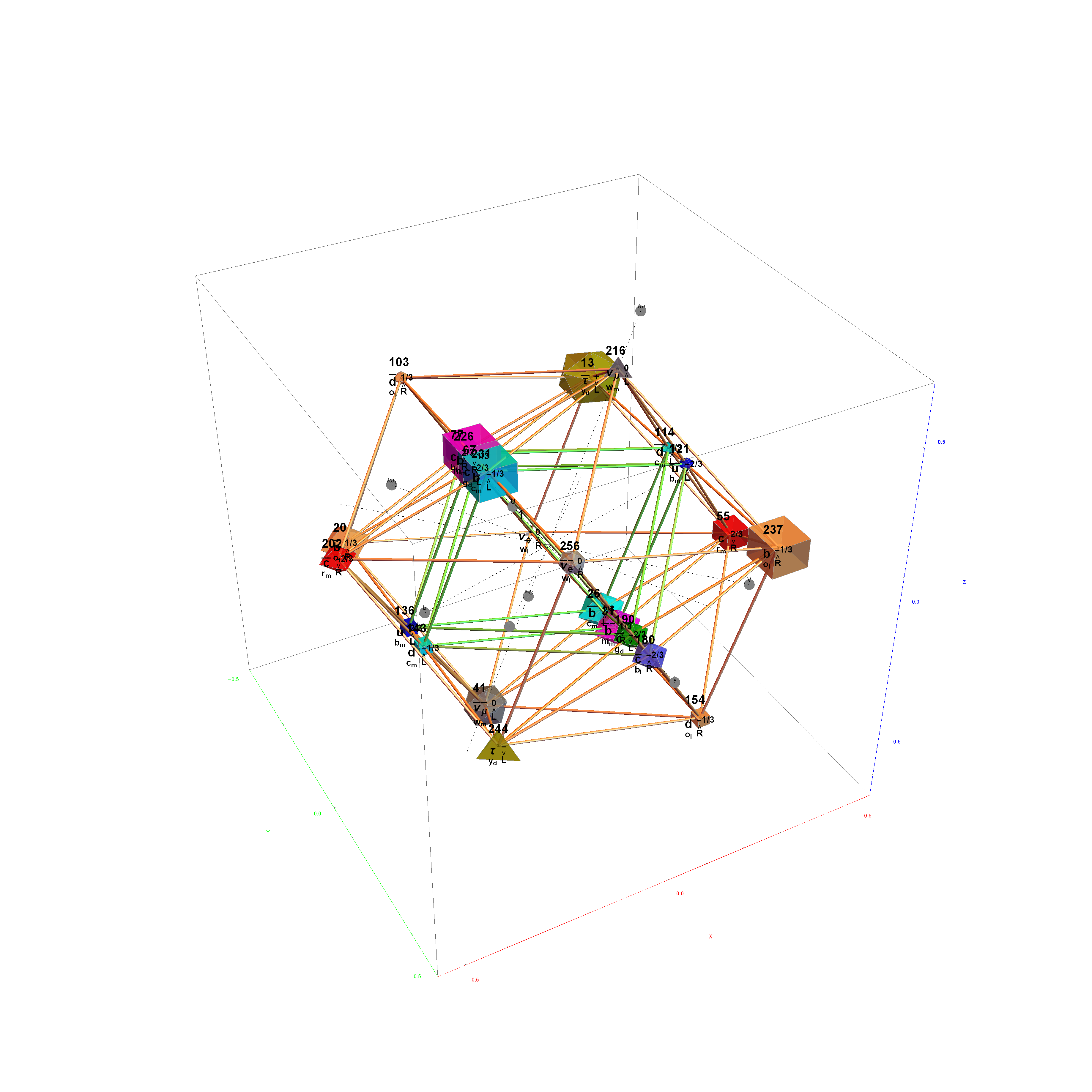
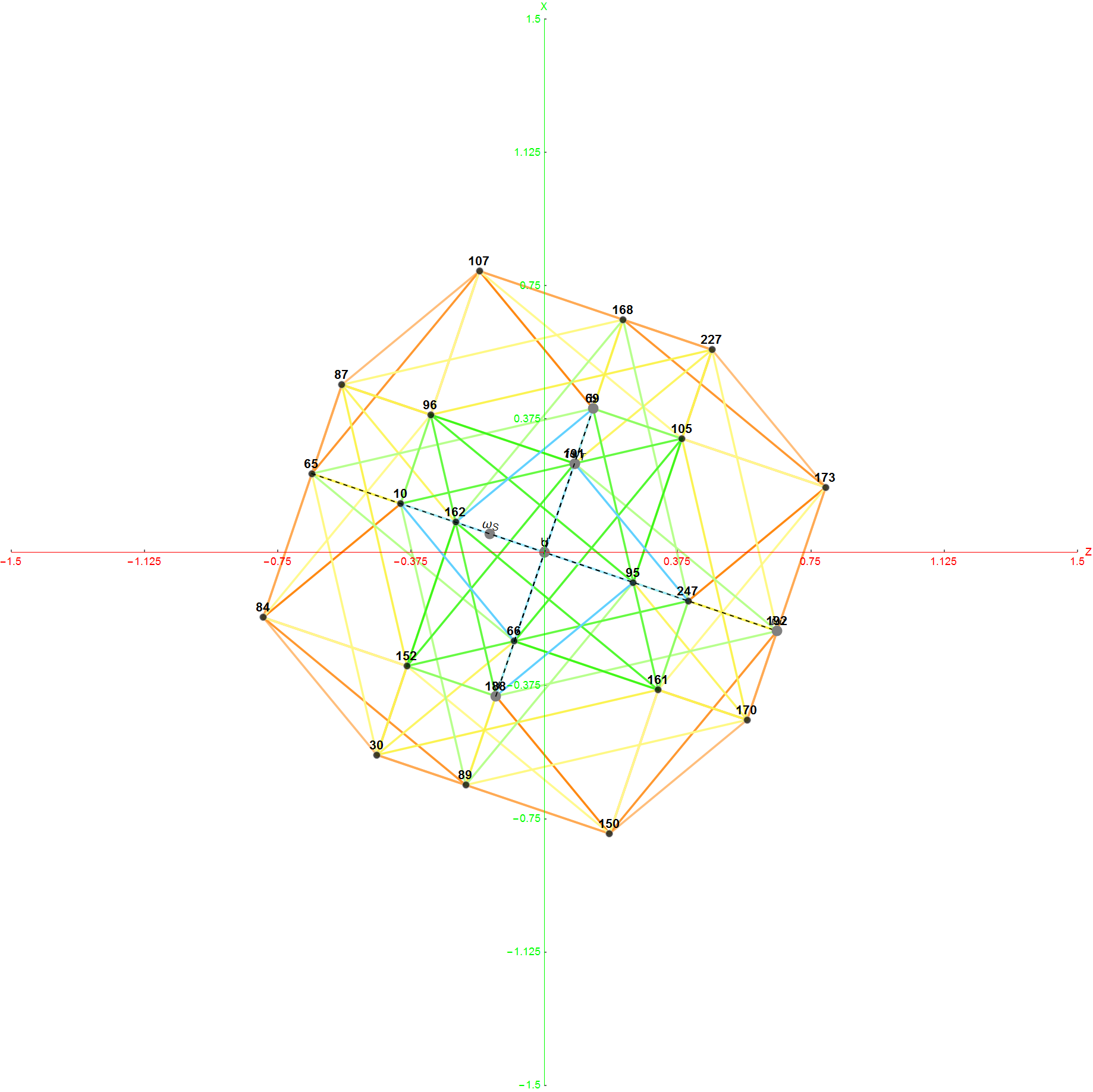
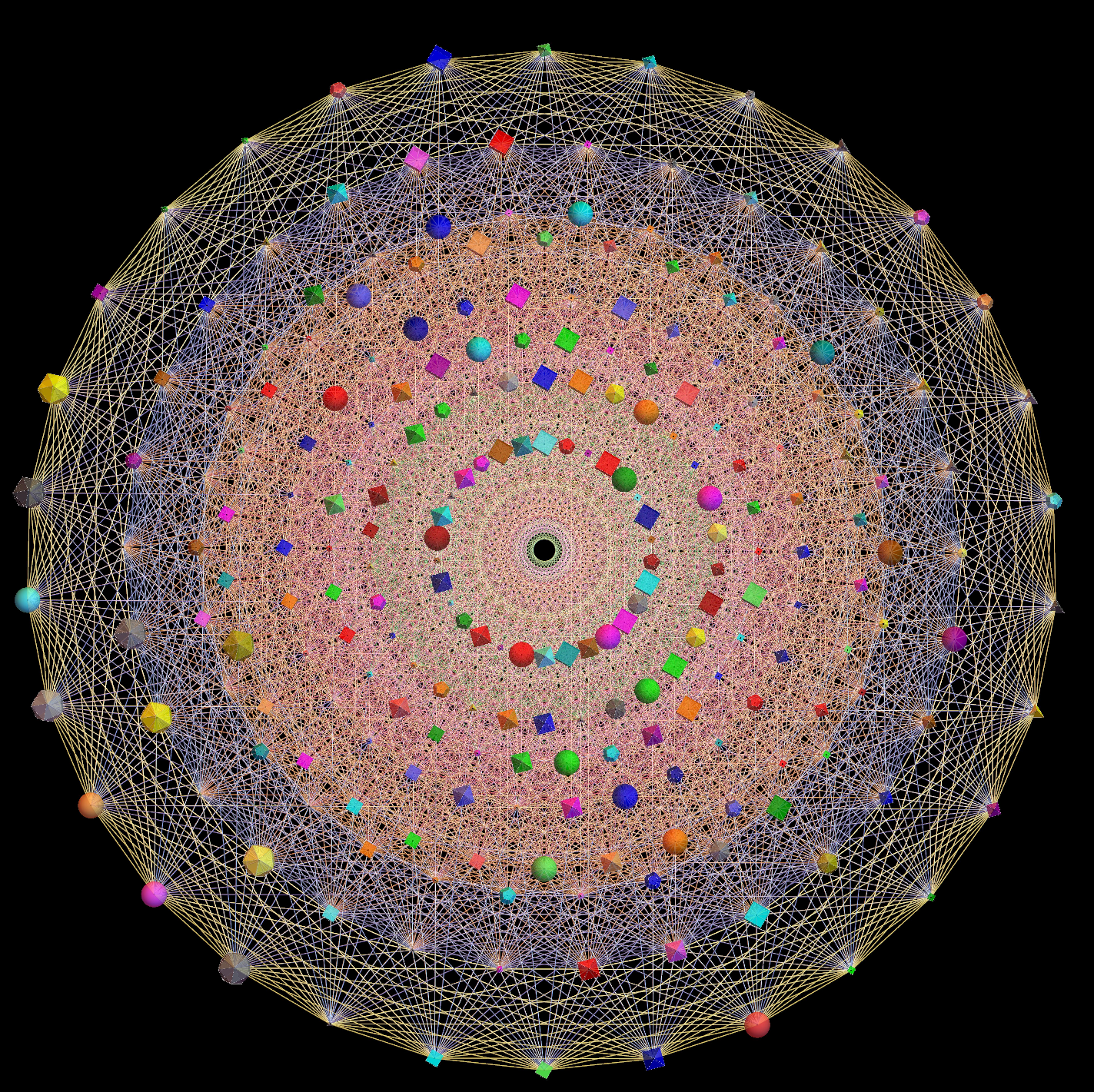
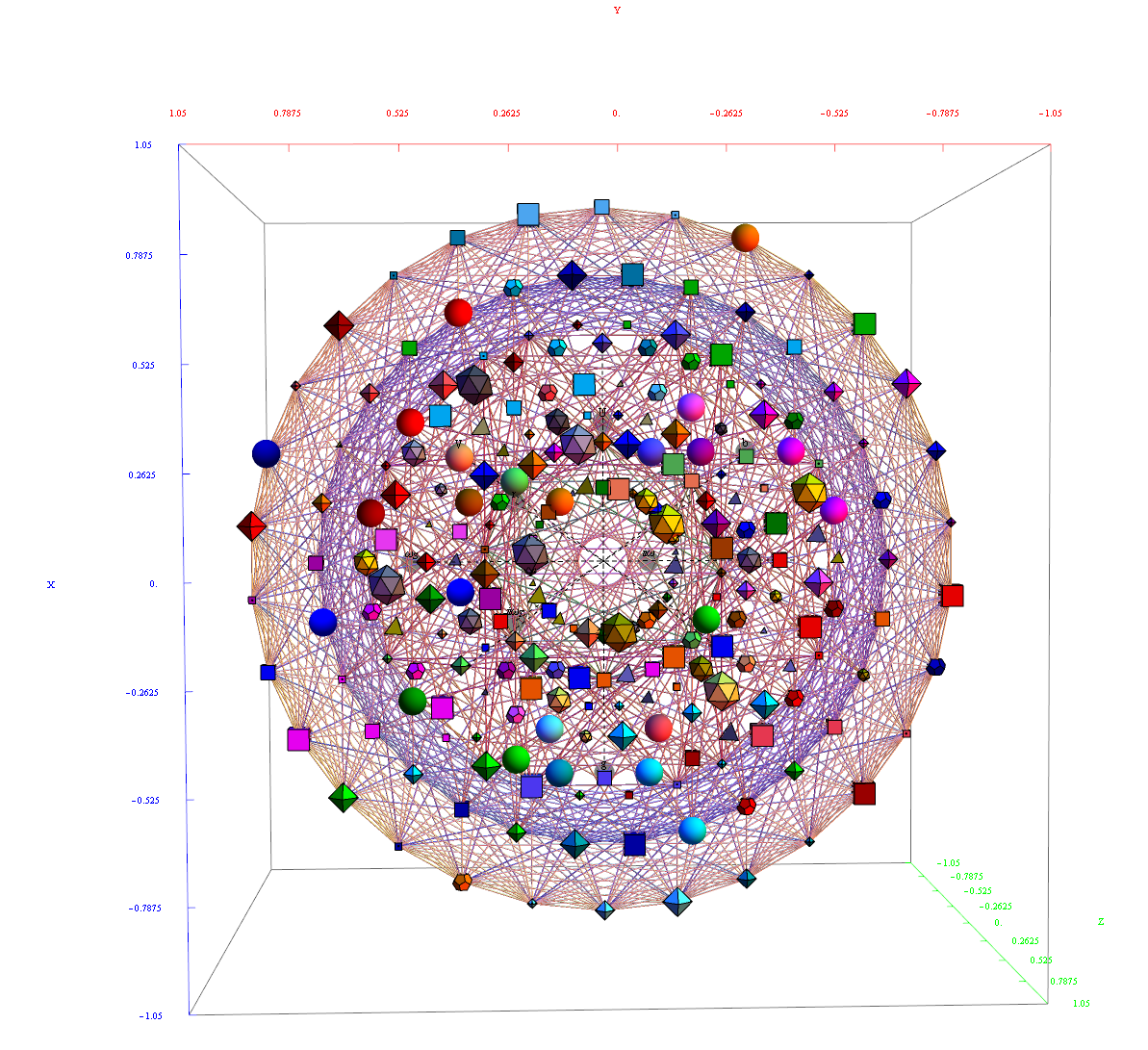
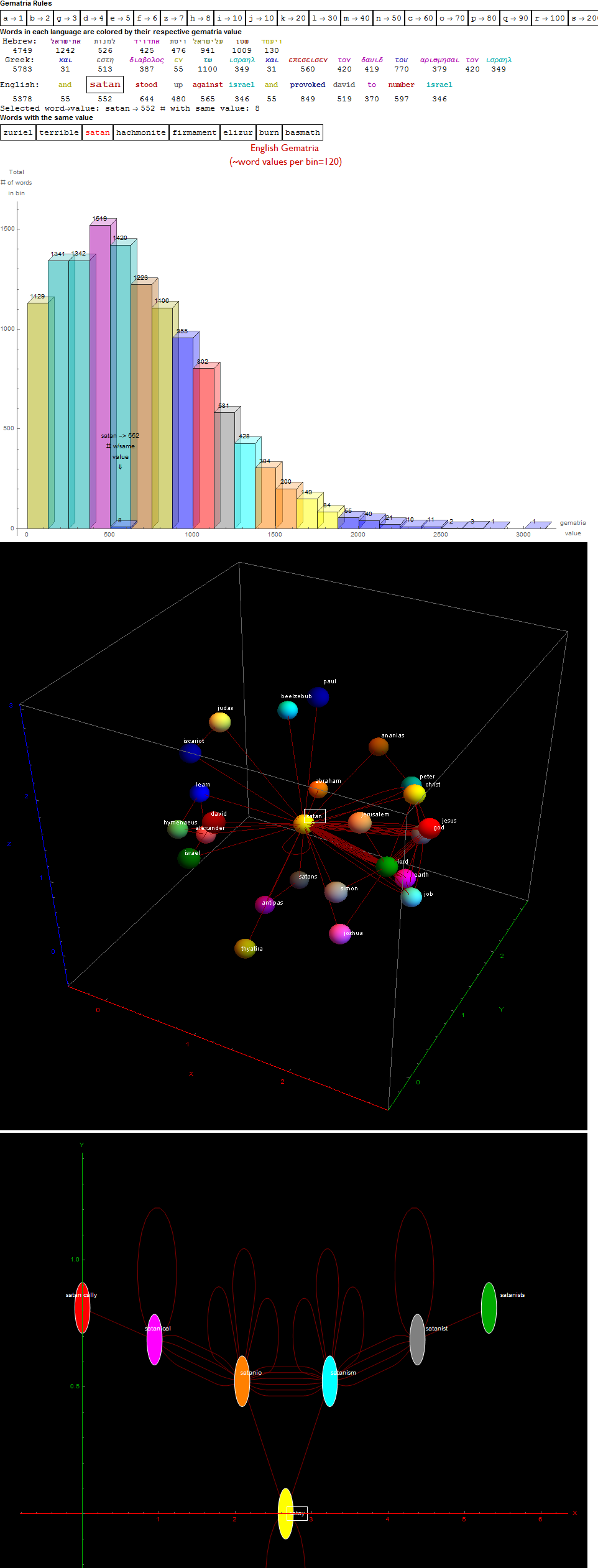
I’ve added some new features in the #15 pane (Gematria). This sociology pane deals with the idea of Old Testament Hebrew and New Testament Koine Greek Gematria. The histogram shows the distribution of words used in the Bible according to their gematria value in Hebrew or Greek. It also presents a clickable 3D hyperbolic tree (graph) of proper names related within verses, as well as a clickable “nearest word” graph. Each word in each book, chapter, verse are select-able by slider or clickable (as are the list of words with the same gematria values).

This combination of UI creates a powerful new way to navigate the bible. Each word in the verse is colored by their value in Hebrew (if Old Testament), Greek and English. It makes use of Wolfram’s curated LanguageData/DictionaryLookup to get a Nearest Word Graph in Hebrew and English. Note: Hebrew is properly presented from right to left.

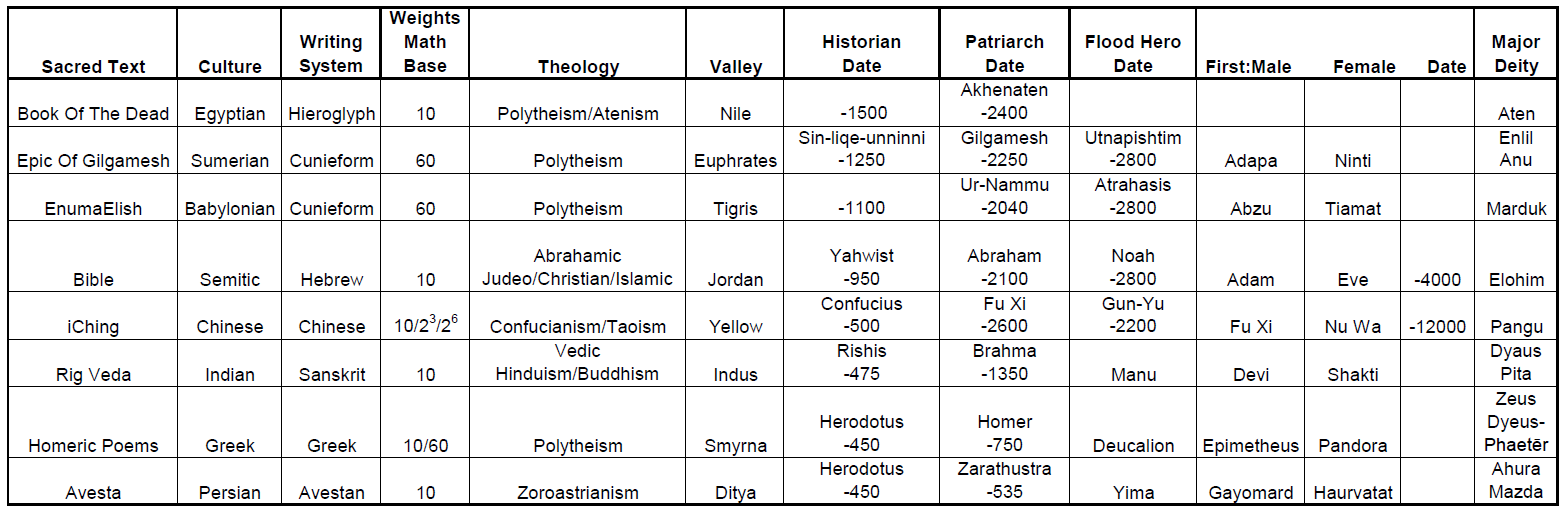
I also decided to attempt to develop visualizations related to the alignment of sociological, theological ancient world history using the recorded sacred texts created at the start of the Bronze age. The time line runs between 4000 BCE and 100 CE and the geopolitical map centers on the cradle of civilization Sumerian (Tigris/Euphrates), and extends from the Egyptian (Nile) to China’s (Yellow), and including Indian (Indus) and Persian cultures.

The list of sacred texts aligned by creation, flood and patriarch figures (e.g. Adam, Eve, Noah, Abraham) and primary deity (e.g. Elohim) were:
1. Egyptian Book Of The Dead
2. Babylonian/Sumerian Kings List/Epic of Gilgamesh/Enuma Elish
3. Hebrew(OT)-Greek(NT) Bible
4. Chinese I Ching
5. Indian Rig Veda
6. Greek Homeric Poems (Illiad/Odyssey)
7. Persian Avesta

Given the amazing advancement of modern science in tracing the genetic lineage of human history along with radioactive dating techniques, it is untenable to interpret these sources literally with any precision. Yet, by understanding their “world view” at the time along with consistently applied “poetic license” across all the texts (e.g. Homer), one can come up with interesting theories for the veracity of their original intentions to document sociologic human history!

For example, it is interesting to note the alignment between the 10 AntiDiluvian (pre-flood) kings in both the Sumerian Kings List and the first 10 patriarchs (starting with Adam) in the Pentateuch. Both have unusually long life-times. When the extremely large (and in most cases rounded) ages of each person are reduced by factors based on the counting system in use (e.g. Sexagesimal (base 60) 10*60^2) for Sumeria and decimal 10^2 or 10^3), the reigns of kings and lifetimes of lineage align as follows:

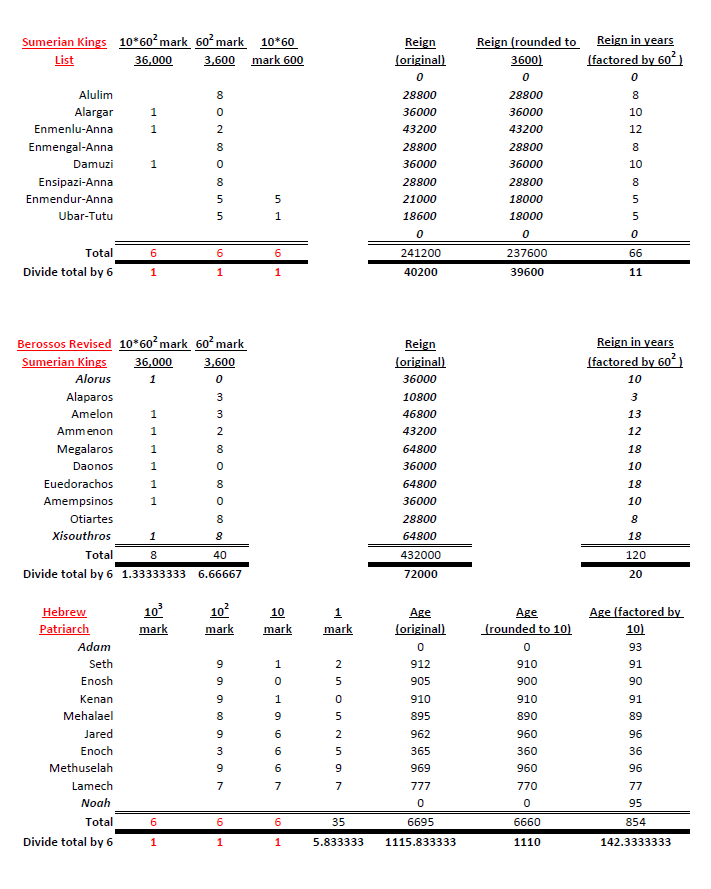
See:
Antediluvian Patriarchs and the Sumerian King List
Reinvestigating the Sumerian Kings List

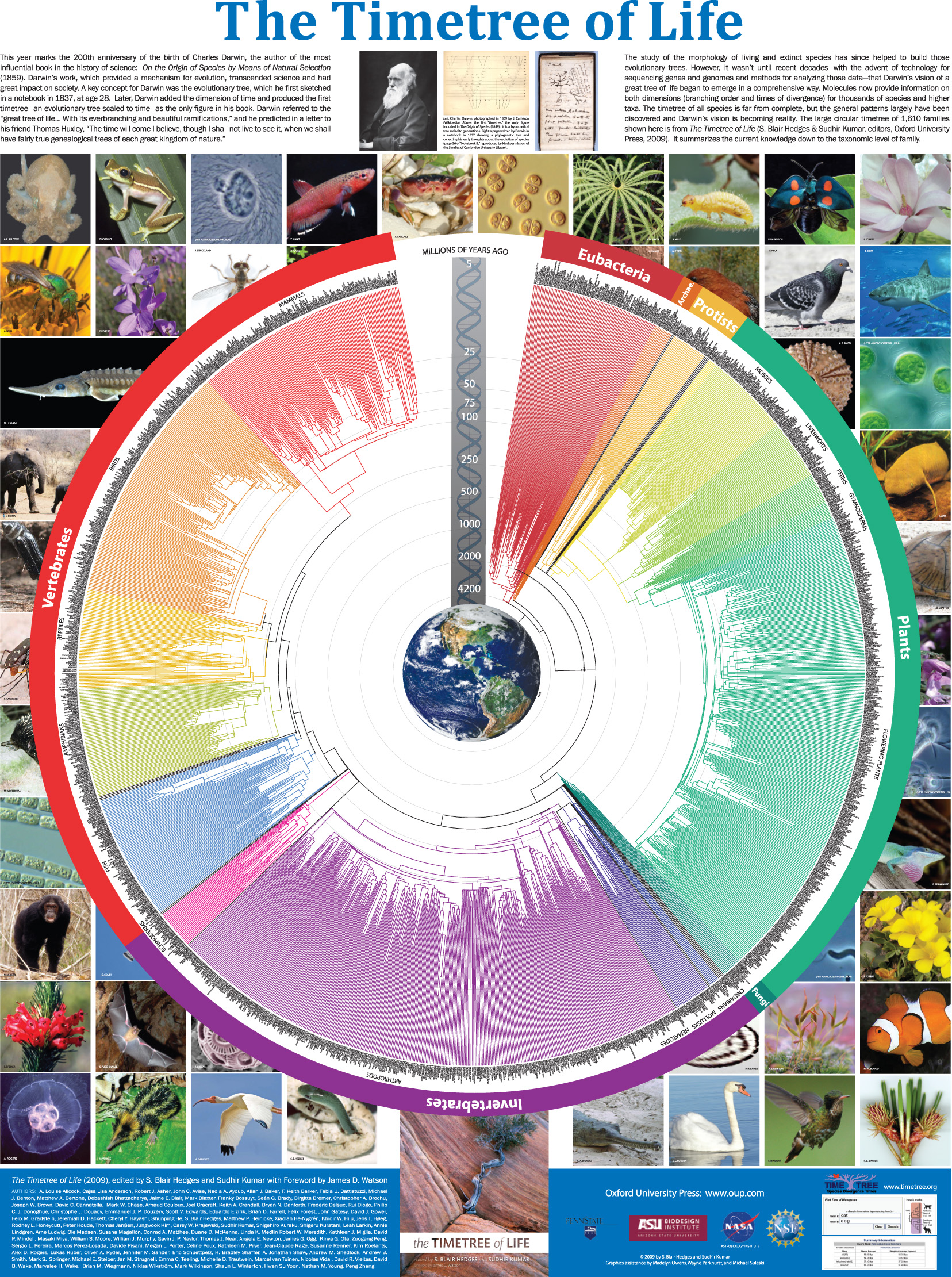
For a modern genetic species analysis visualization, see:
http://www.timetree.org/book.php

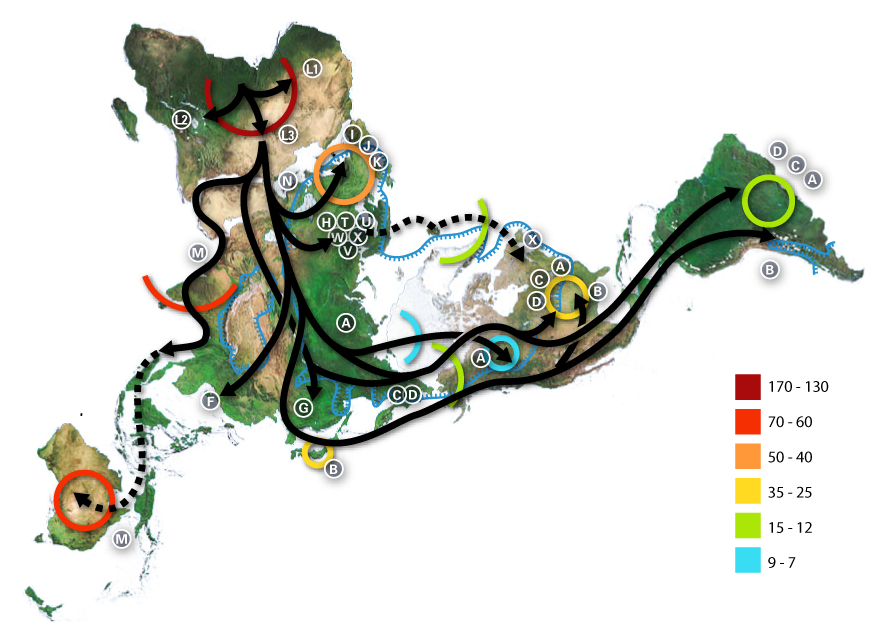
See this Dymaxion Map of genetic analysis of human migration from Wikipedia Commons:

Here is an old artistic map of World History from HistoMap http://www.davidrumsey.com/. It is largely Biblical in its antidiluvian history. While it is not based on modern scientific evidence, it is an interesting mash-up of information from various sources. A more detailed map (horizontal) is here (right-click the image to download and save-as the 20MB PNG file):

Here is another vertical version from the same website:

and another histomap (linear and logarithmic) of the Earth’s Geologic/Evolutionary History (right-click/save-as for a 12MB version):