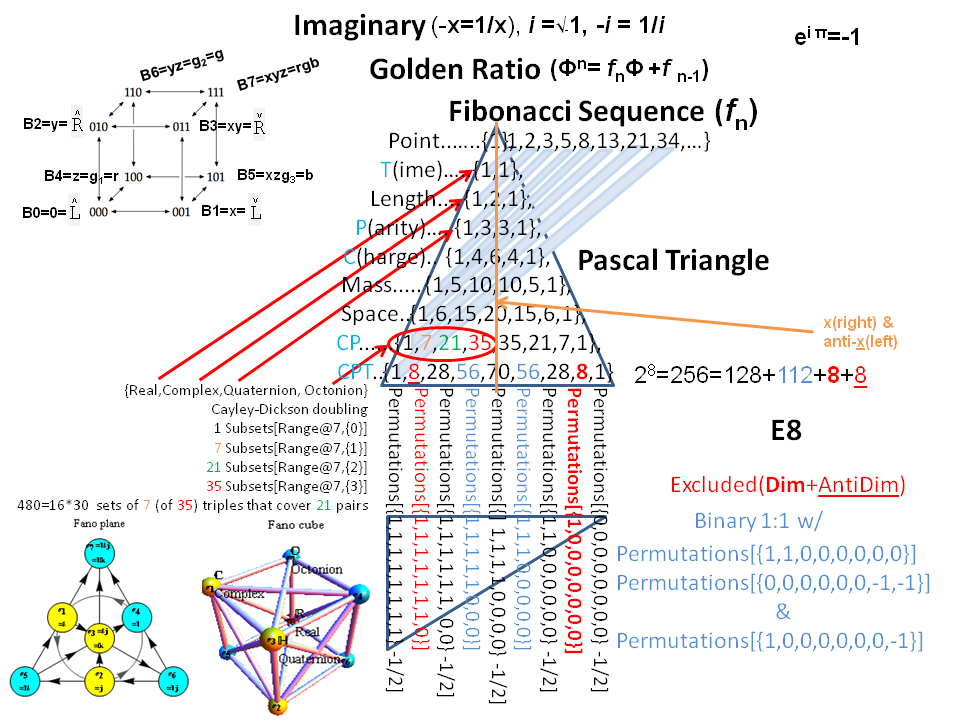
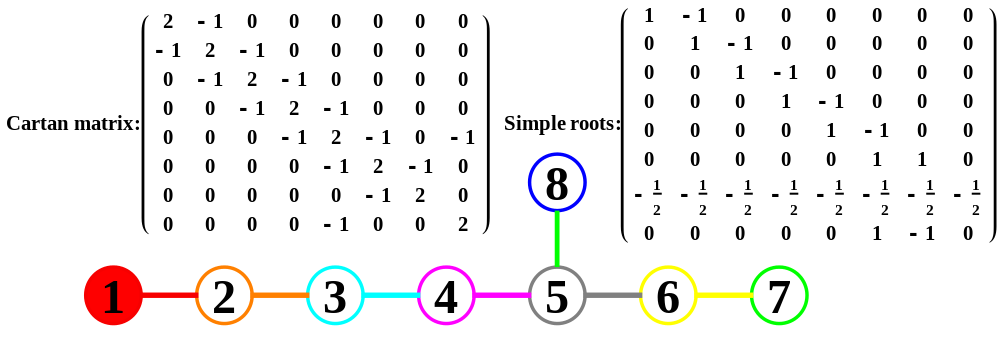
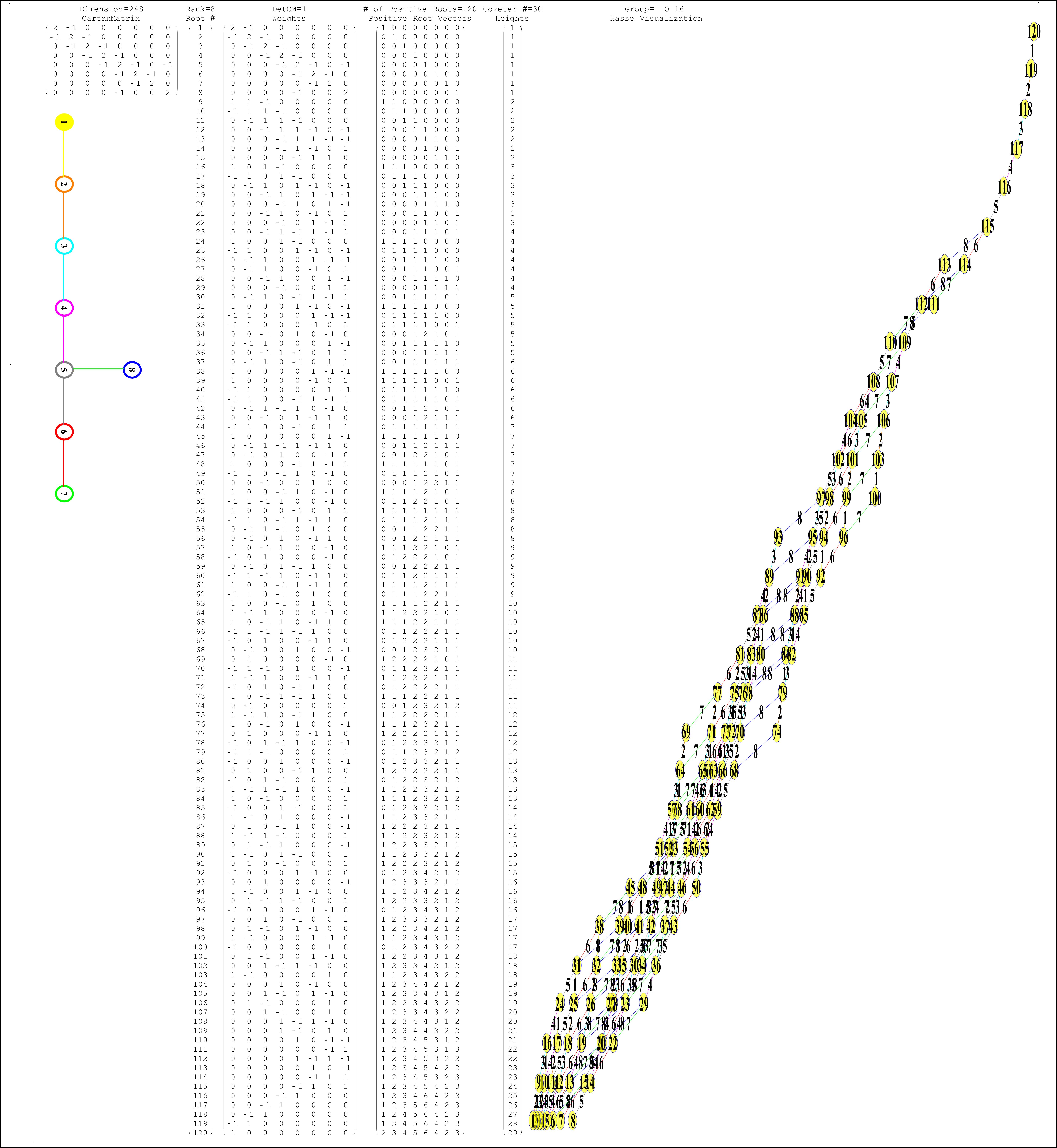
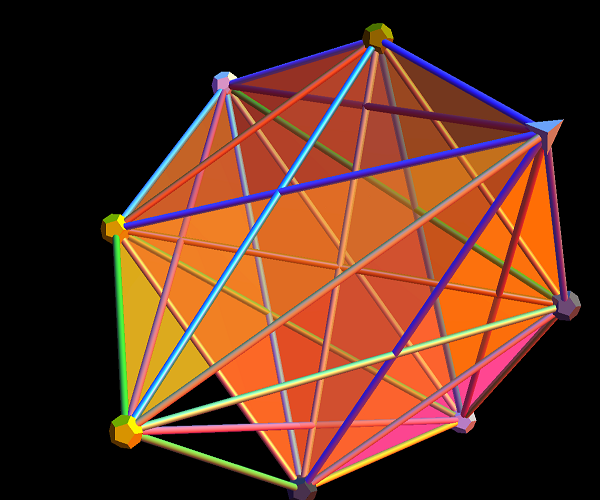
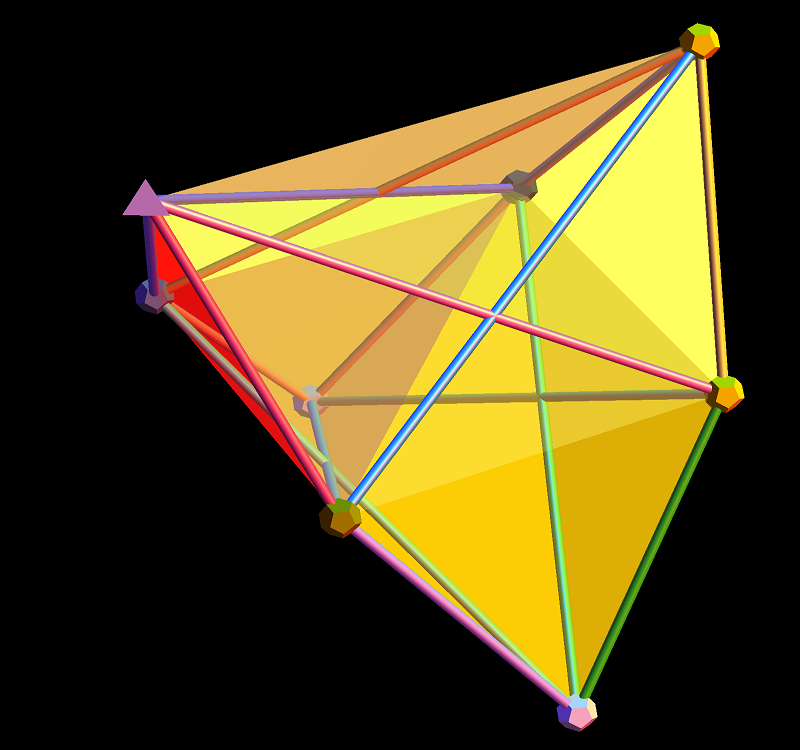
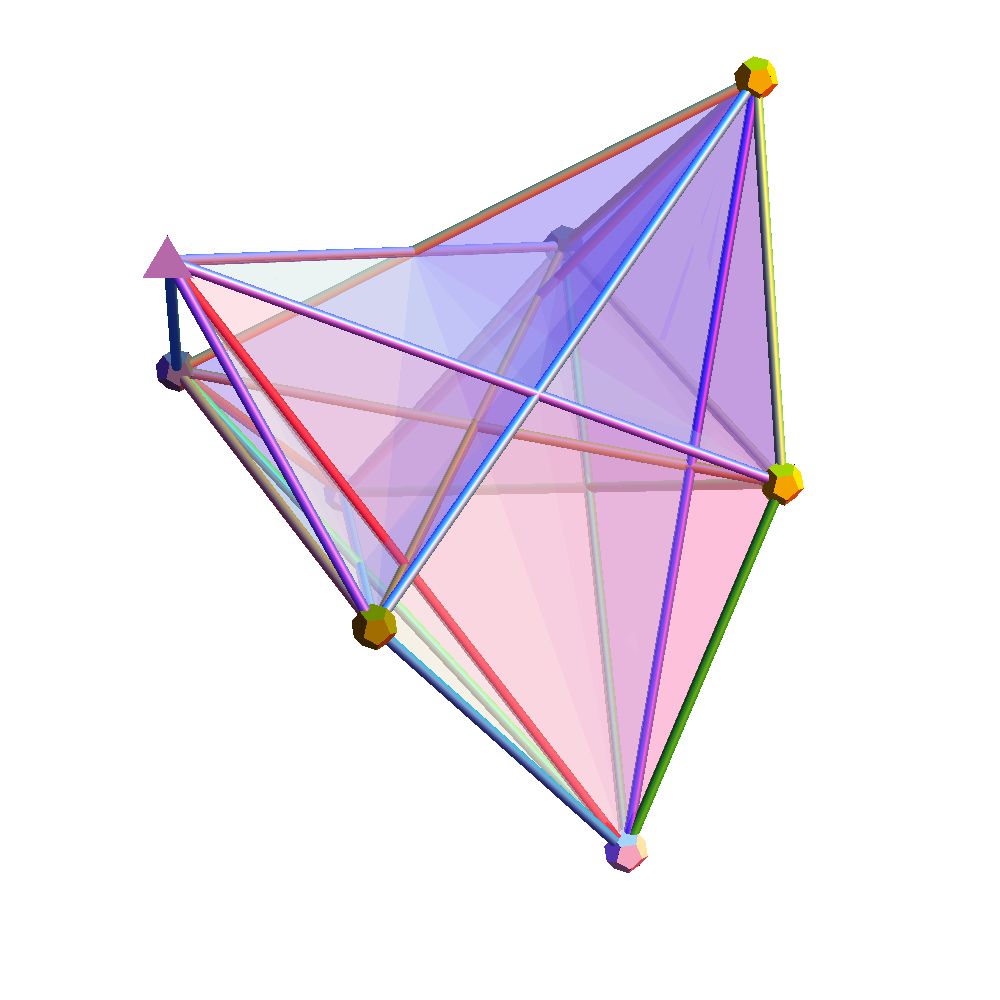
I found the rotation matrix that shows the E8 Dynkin diagram can indeed be folded to H4+H4/φ.
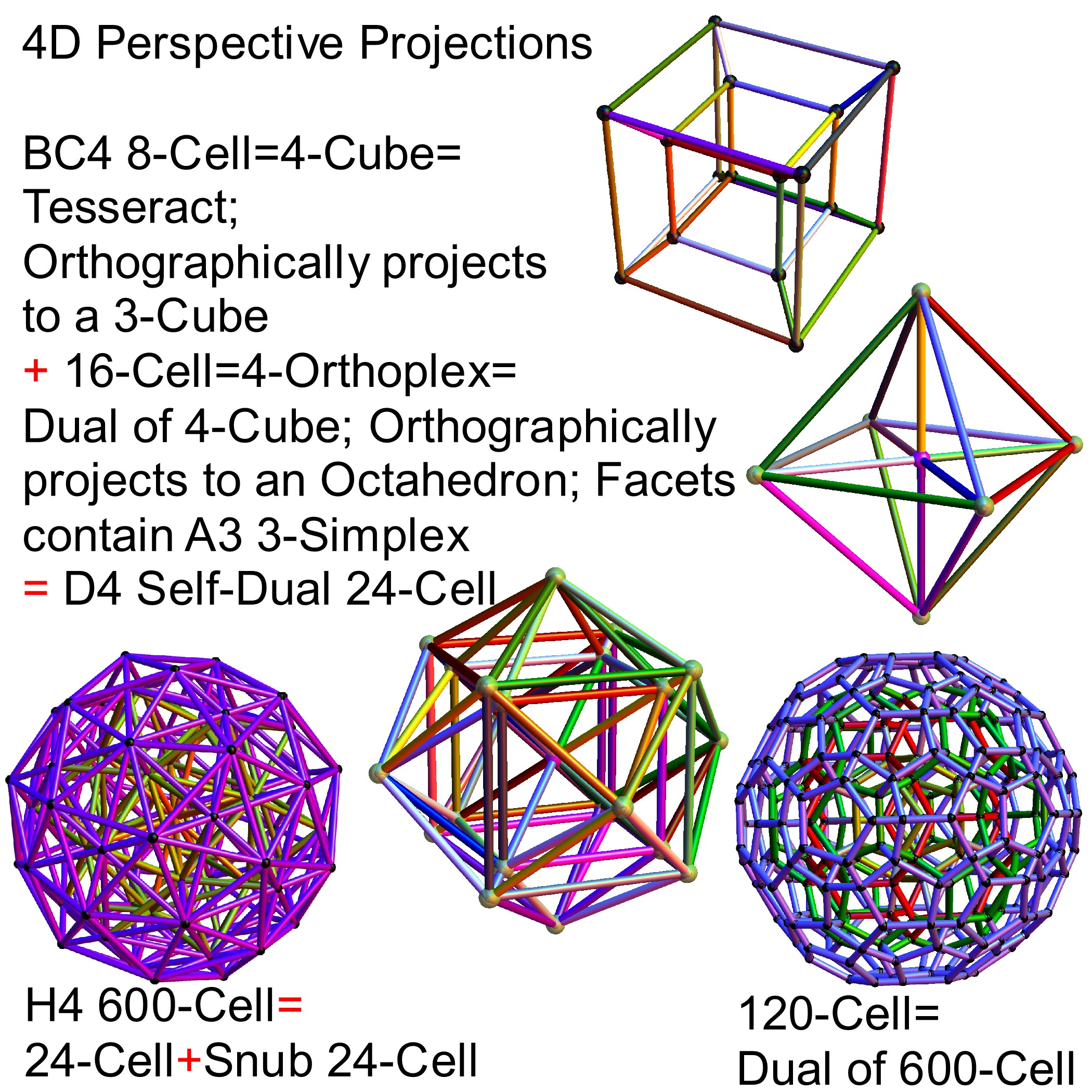
The H4 and its 120 vertices make up the 4D 600 Cell. It is made up of 96 vertices of the Snub 24-Cell and the 24 vertices of the 24-Cell=[16 vertex Tesseract=8-Cell and the 8 vertices of the 4-Orthoplex=16-Cell]).
It can be generated from the 240 split real even E8 vertices using a 4×8 rotation matrix:
x = (1, φ, 0, -1, φ, 0, 0, 0)
y = (φ, 0, 1, φ, 0, -1, 0, 0)
z = (0, 1, φ, 0, -1, φ, 0, 0)
w = (0, 0, 0, 0, 0, 0, φ^2, 1/φ)
where φ=Golden Ratio=(1+Sqrt(5))/2
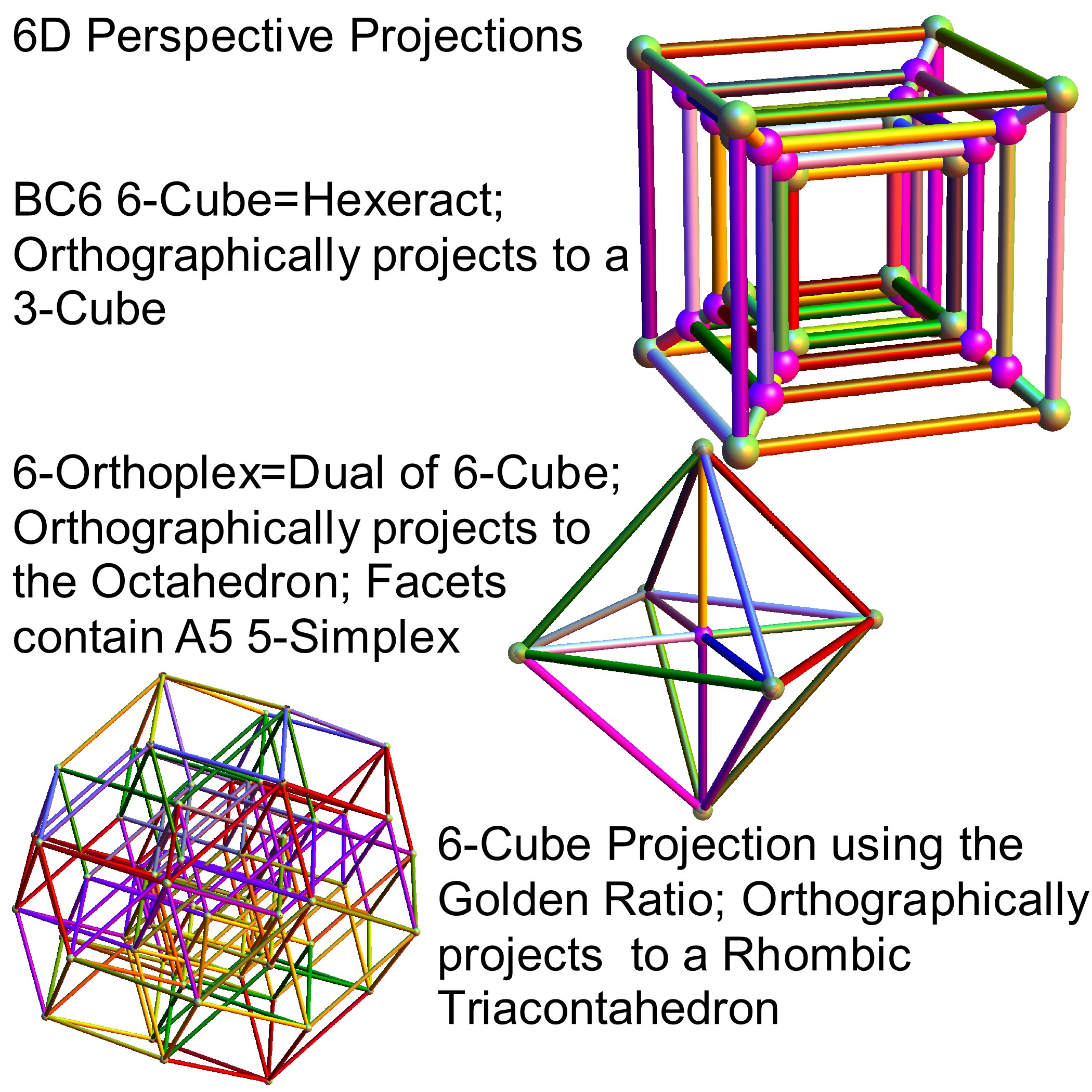
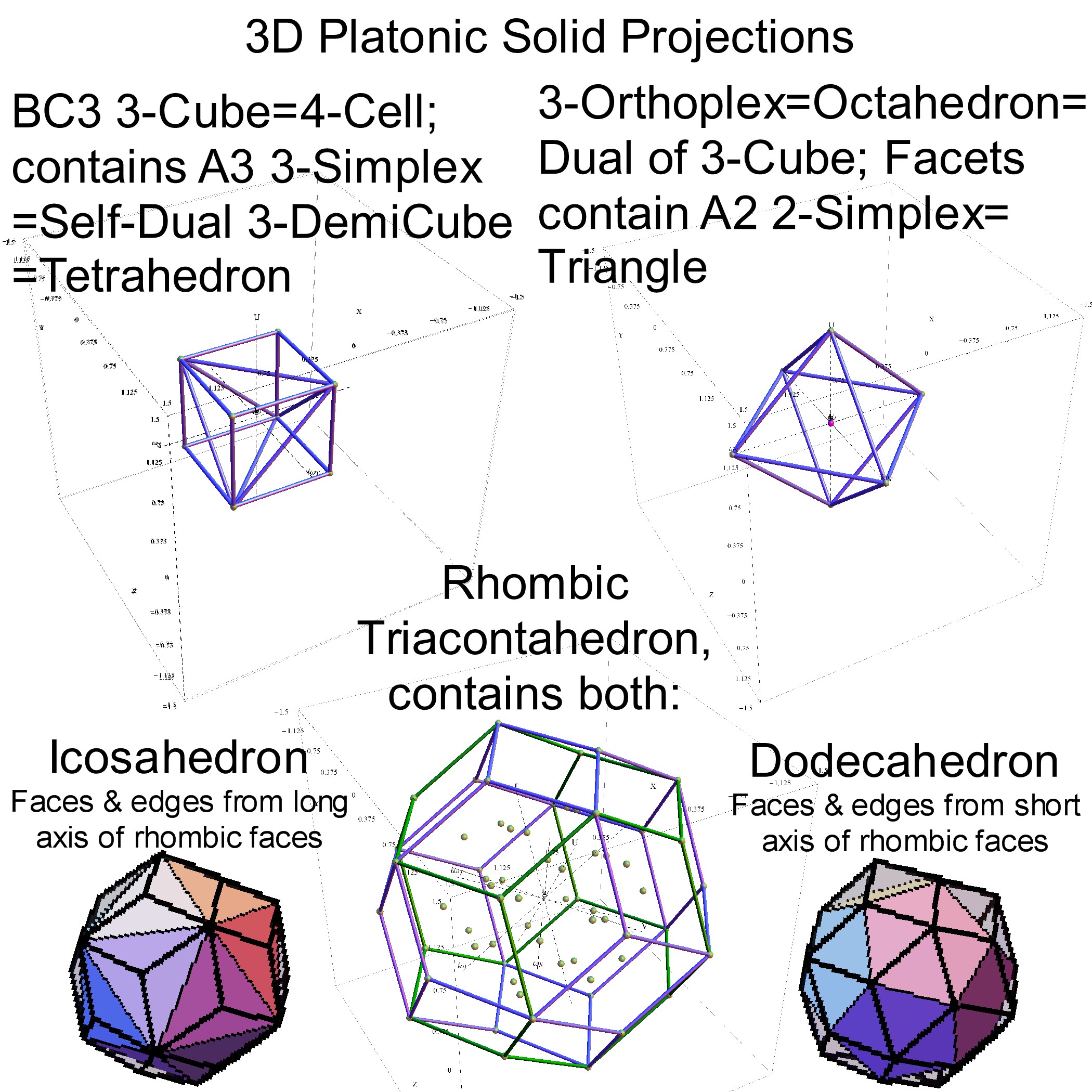
It is also interesting to note that the x, y, and z vectors project to a hull of the 3D Rhombic Triacontrahedron from the 6D 6 cube Hexaract (which then generates the hull of the Dodecahedron and Icosahedron Platonic solids).
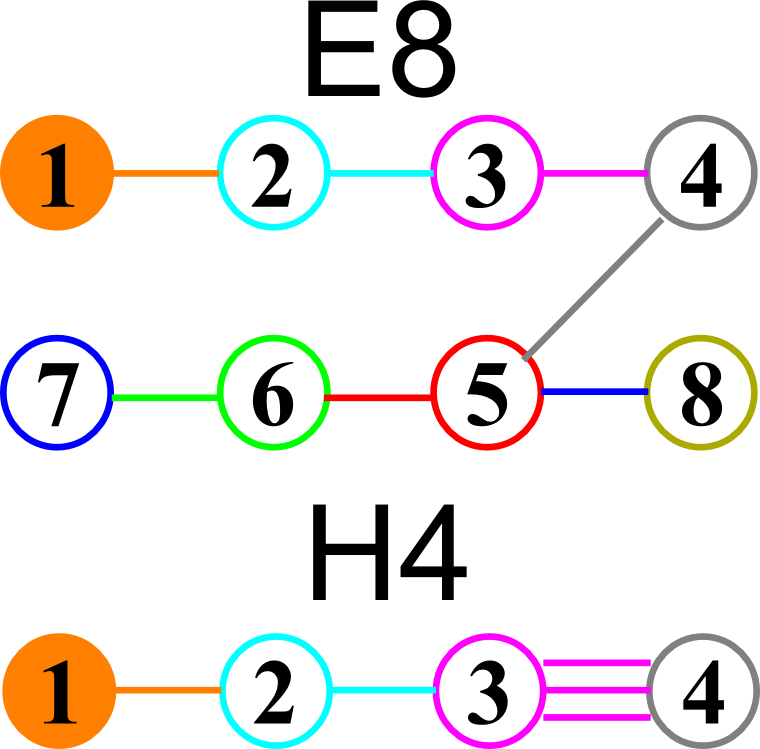
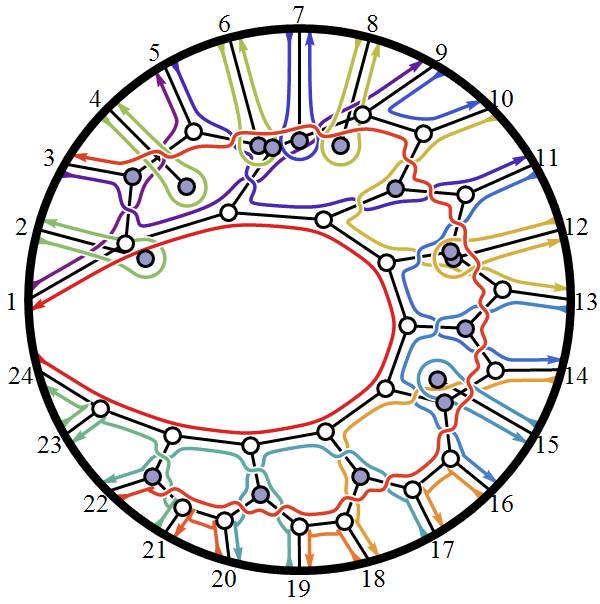
Here’s a look at the Dynkin Diagram folding of E8 to H4+H4/φ:
I find in folding from 8D to 4D, that the 6720 edge counts split into two sets of 3360 from E8’s 6720 length Sqrt(2), but the combined edges and vertices recreate the E8 petrie diagram perfectly.
Some visualizations of this in 8D:
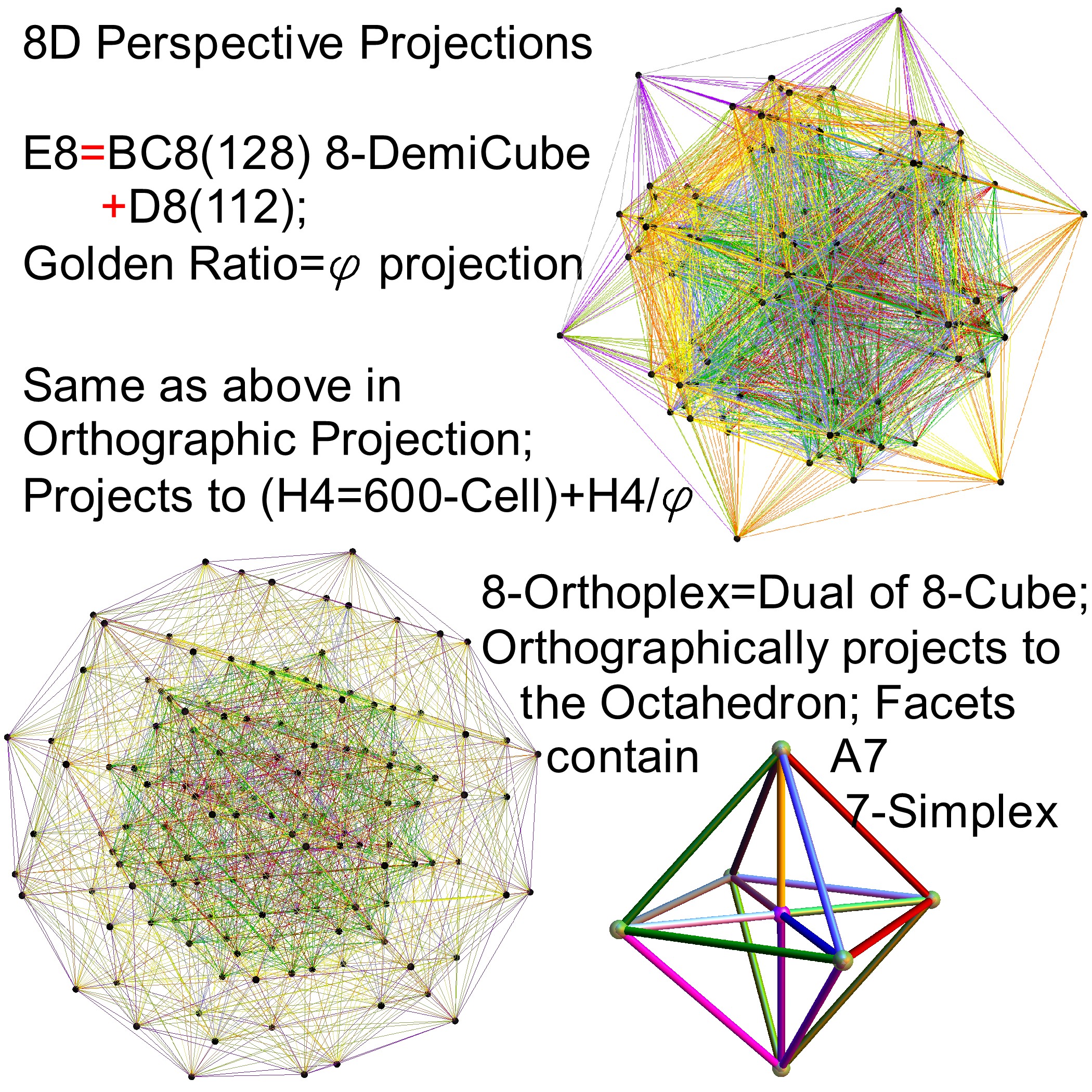
and also showing the Rhombic Triacontrahedron folding from 6D: