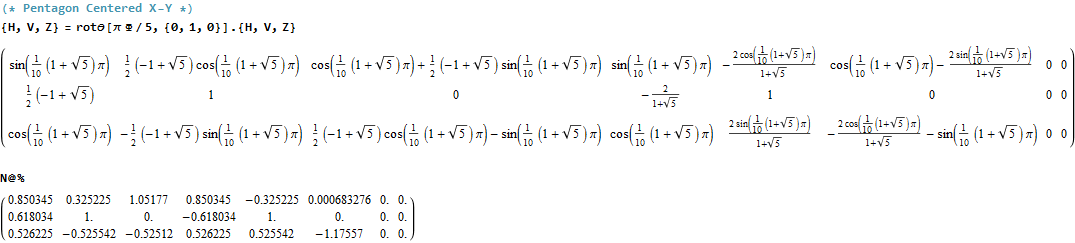For a full discussion of the particle assignment symmetries involved, see http://vixra.org/pdf/1503.0190v1.pdf
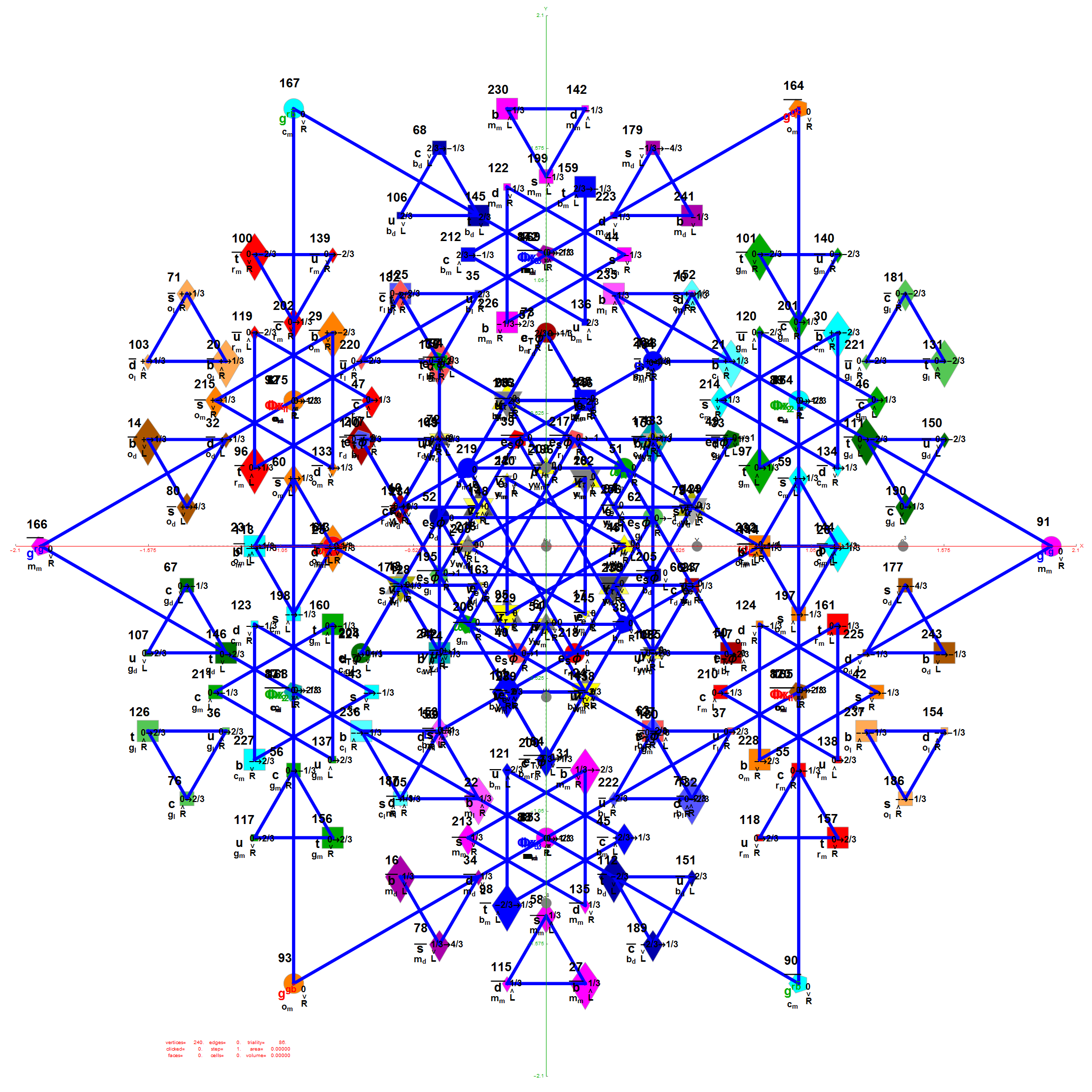
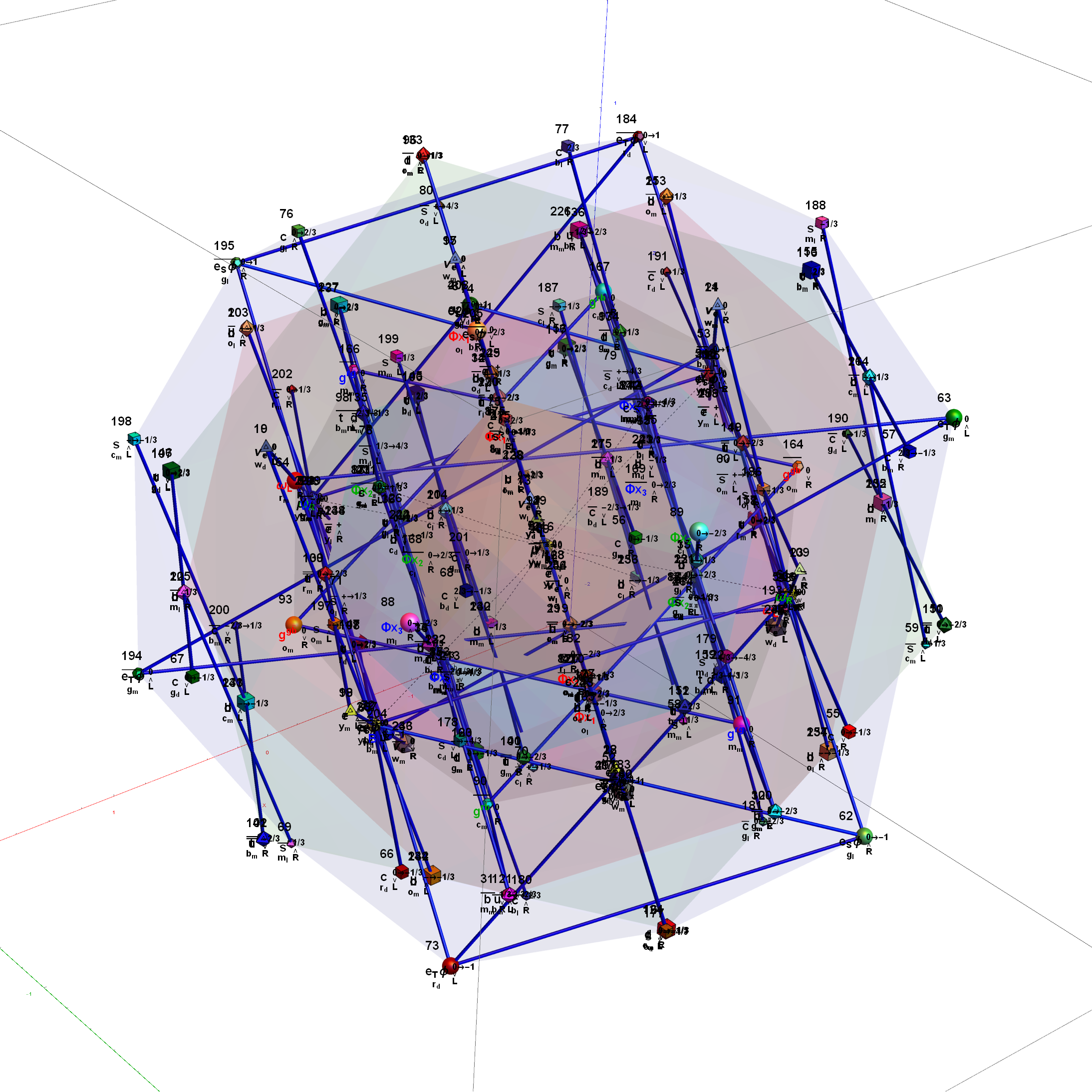
E8 as 240 split real even vertices with vertex color, size, shape, and labels from a modified A.G. Lisi particle assignment algorithm. The vertex number is the position in the Pascal Triangle (Clifford Algebra) representation of E8. The blue lines forming equilateral triangles represent the 10 Bosonic (or Color) Triality (T2) and 76 Fermionic (T4) rotations (using the 8×8 matrices shown below) that transform each member of the triangle into the next member.
E7 as derived from E8 above by taking the vertices of E8 with the last two columns being equal.
E6 as derived from E8 above by taking the vertices of E8 with the last three columns being equal.
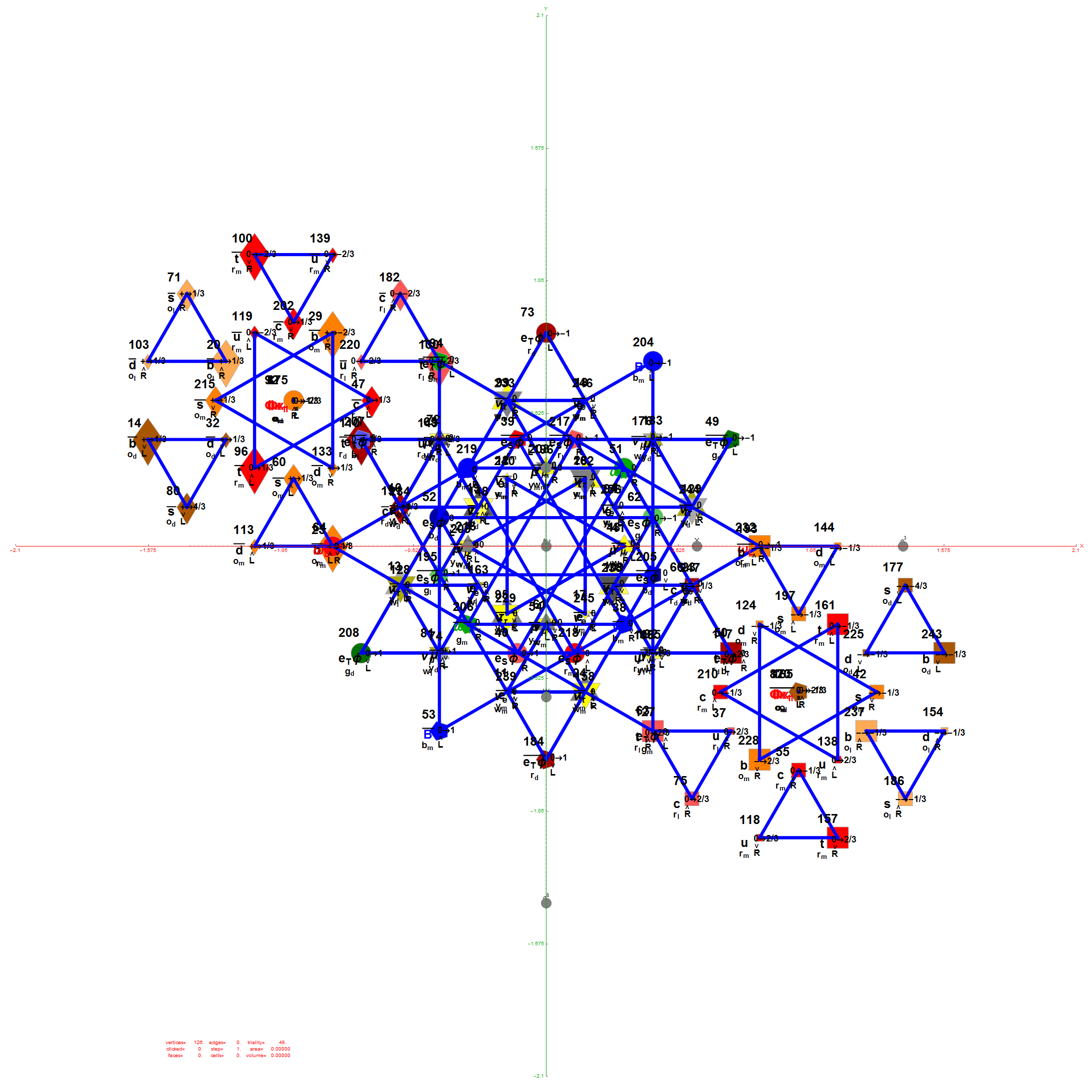
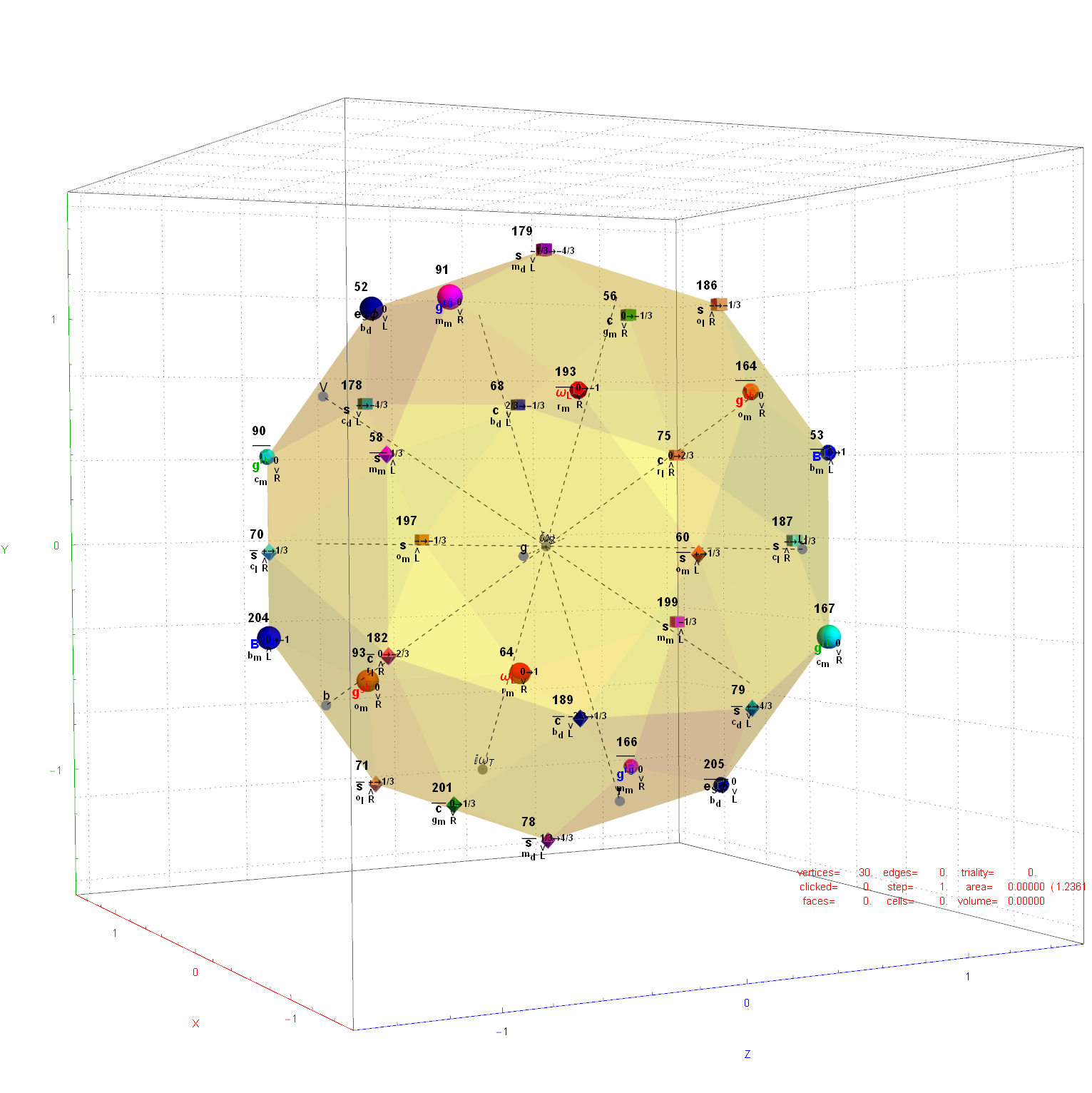
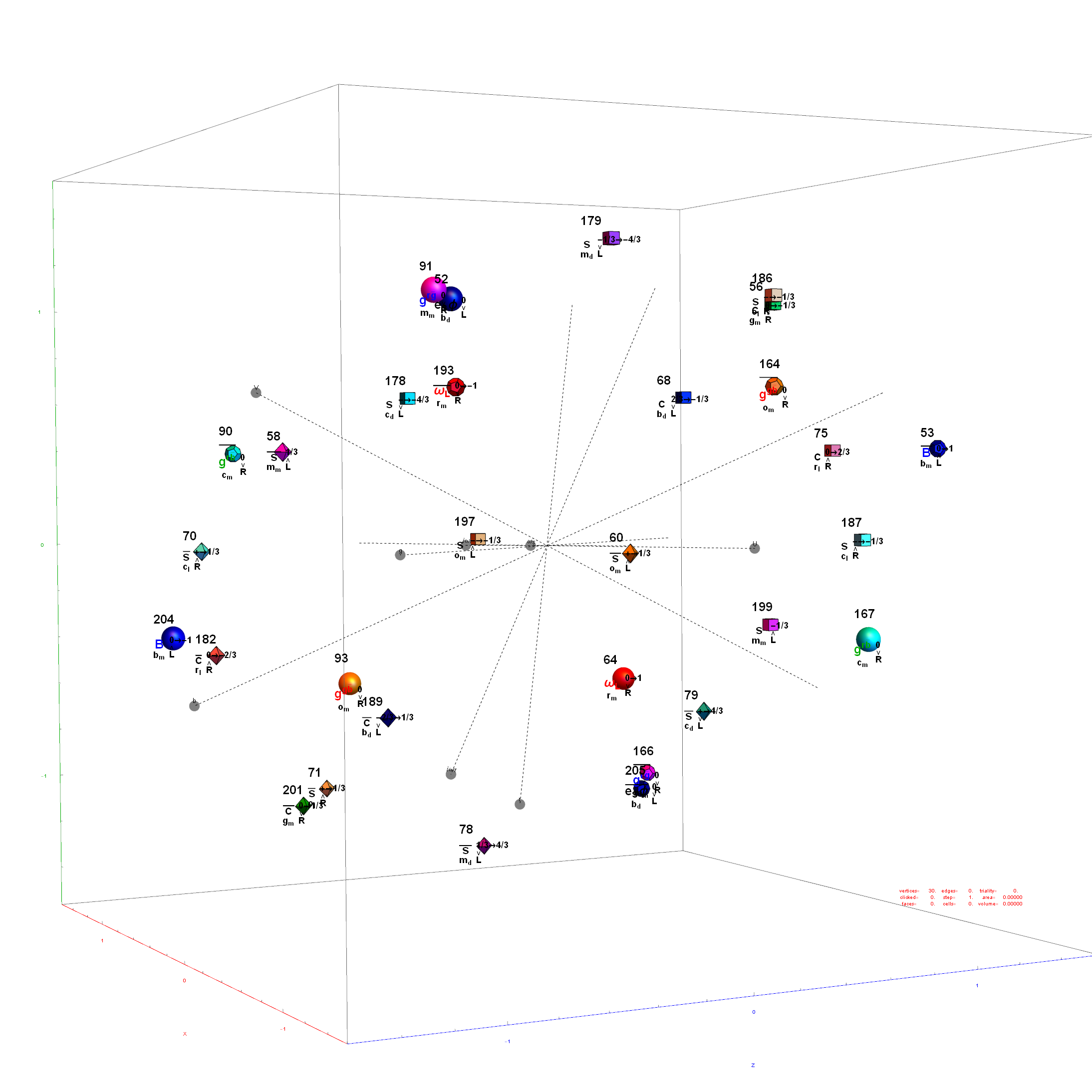
The 48 vertices of F4 are made up of the 112 (D8) +/-1 integer pair vertices that are assigned to bosonic particles, which includes 22 trialities (10 from T2 and 12 from T4). The other 64 of 112 D8 vertices are assigned to the 2nd generation of Fermions. F4 is shown below with its sub-group G2 assigned to the gluons in the larger triality triangles. 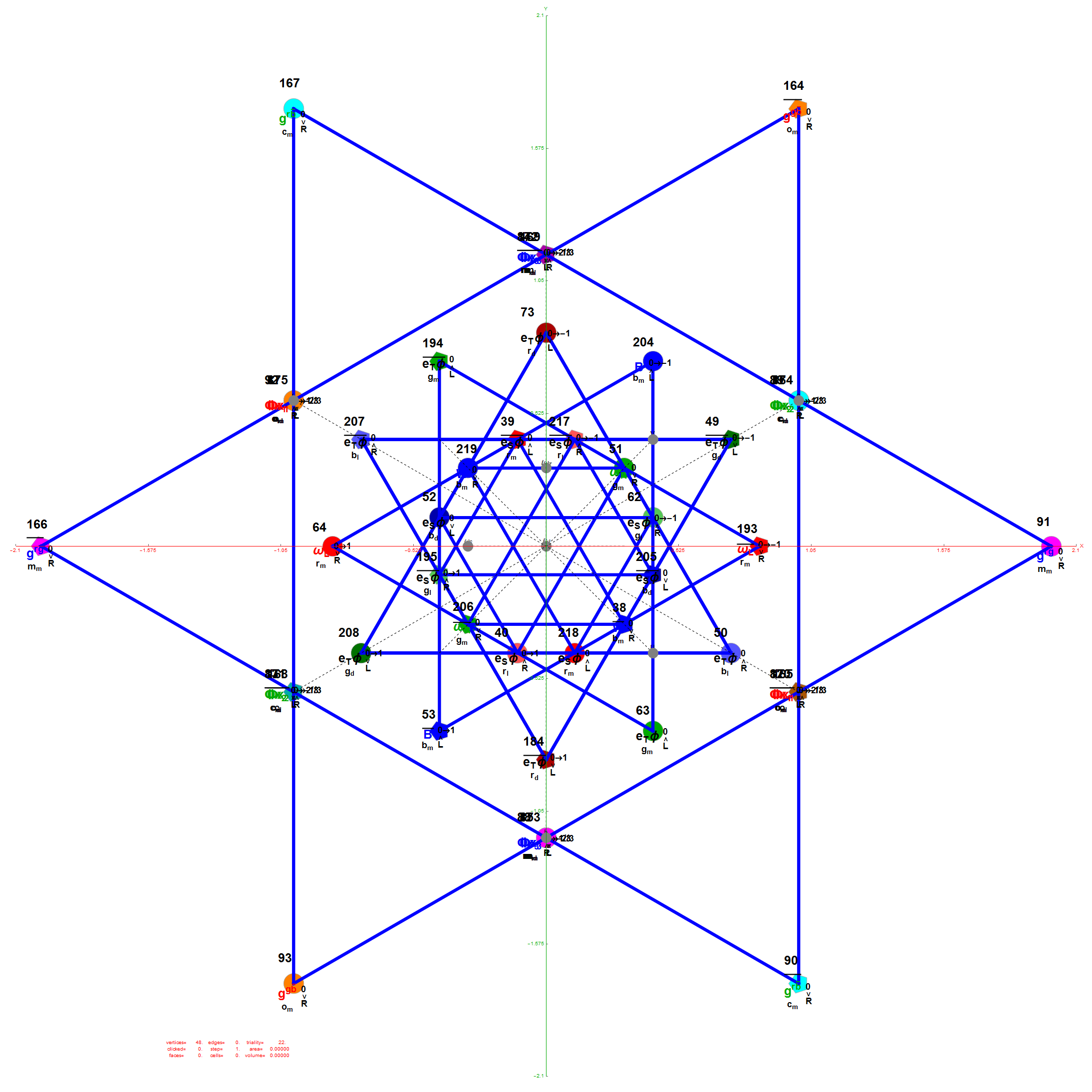 Projection Basis for X and Y are H (first row) and V (second row) in the matrix below respectively
Projection Basis for X and Y are H (first row) and V (second row) in the matrix below respectively
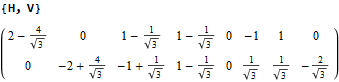 The Triality Matrices are:
The Triality Matrices are:
The 10 Bosonic (Color) Triality Rotation Matrix (T2) equilateral triangles exclusively affect the particles that are derived from F4.
T2 rotates through the bosonic colors indicated by the last 3 columns of the E8 vertices appropriately labeled (r,g,b).
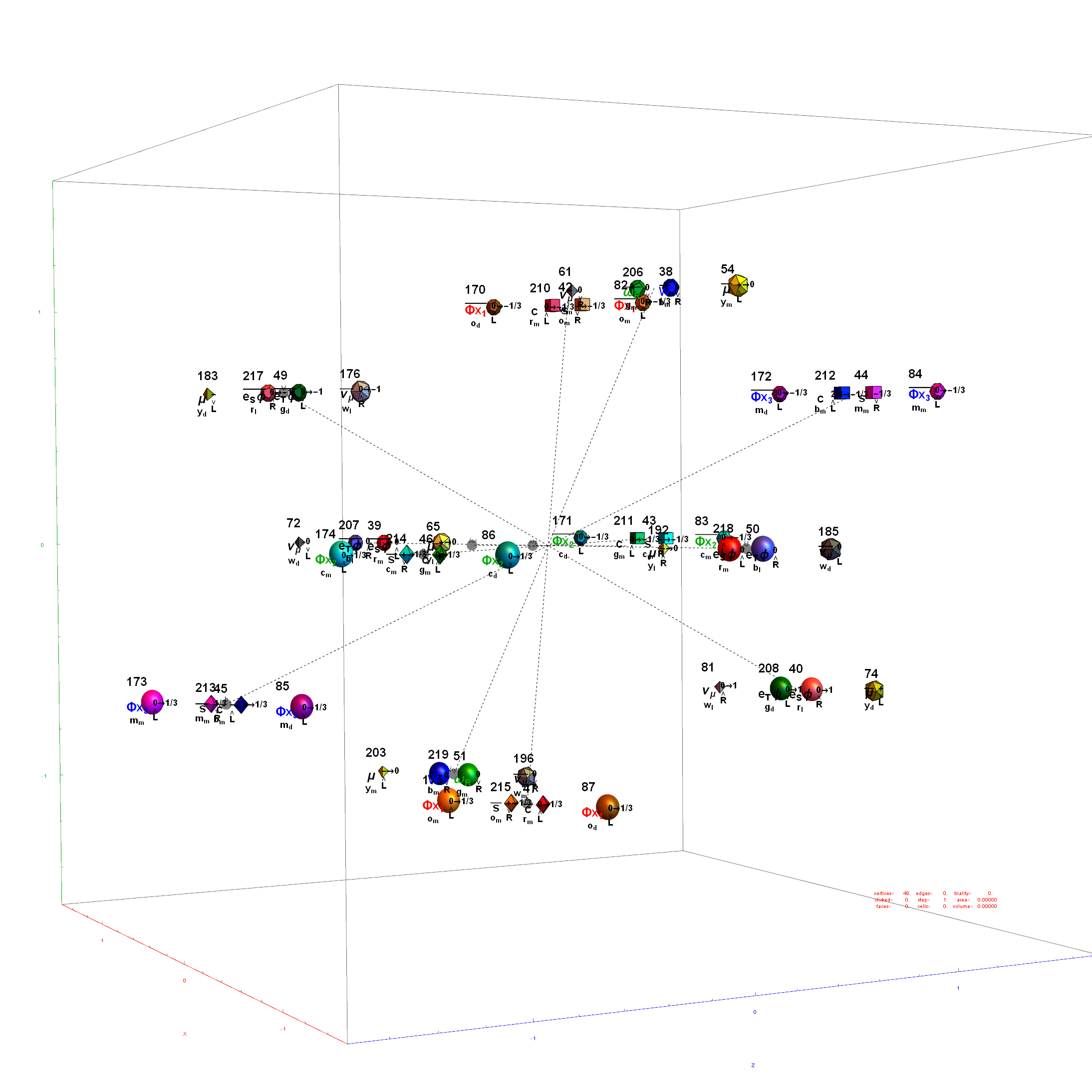
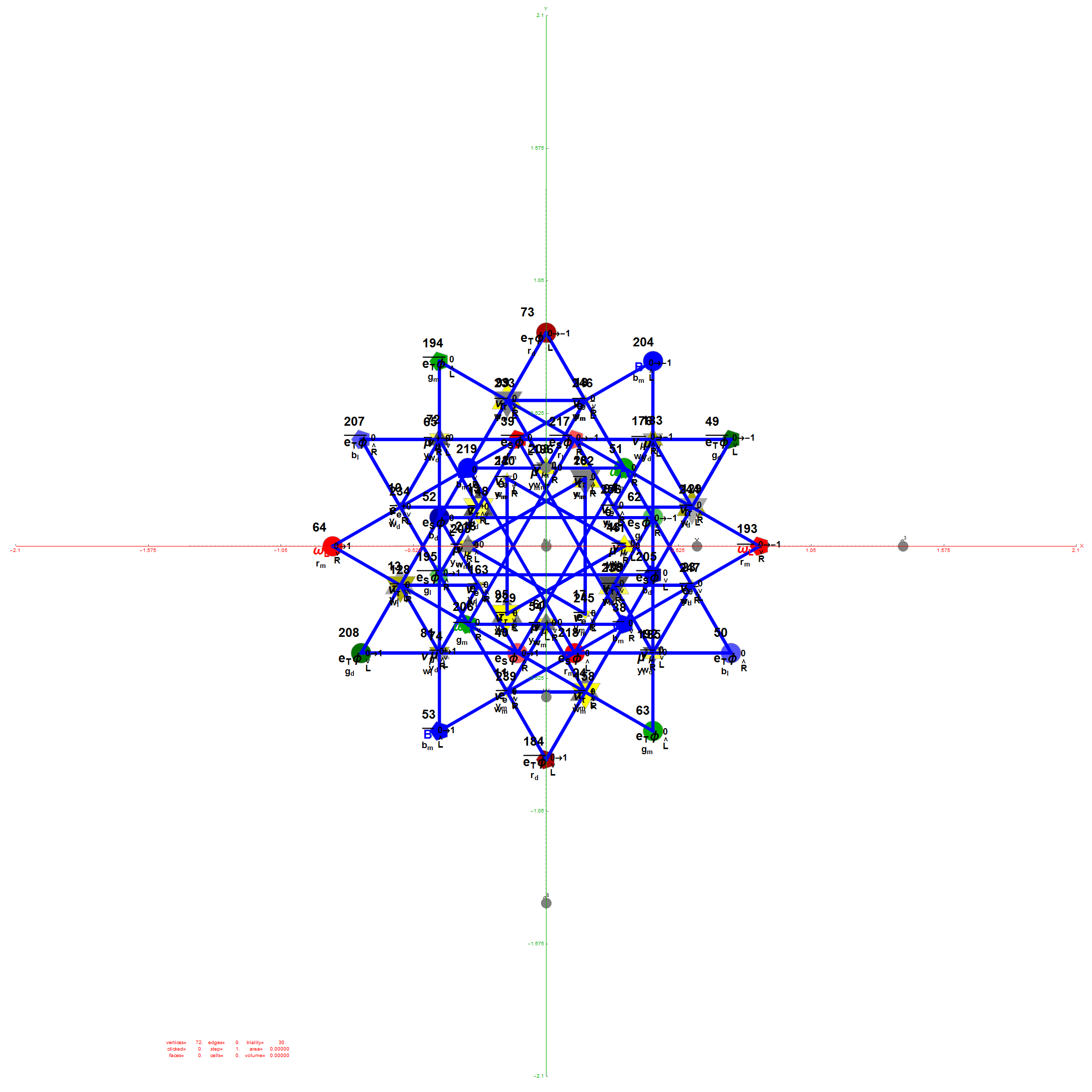
 The 76 Fermionic (Generation) Triality Rotation Matrix (T4) equilateral triangles. There are 64 fermion particle trialities that are derived from the 128 (BC8) half integer vertex assignments plus the 64 fermions assigned from the 112 (D8) +/-1 integer pair vertices. There is always one integer (2nd Generation) and two 1/2 integer vertices (1st and 3rd Generation) in every fermionic triality.
The 76 Fermionic (Generation) Triality Rotation Matrix (T4) equilateral triangles. There are 64 fermion particle trialities that are derived from the 128 (BC8) half integer vertex assignments plus the 64 fermions assigned from the 112 (D8) +/-1 integer pair vertices. There is always one integer (2nd Generation) and two 1/2 integer vertices (1st and 3rd Generation) in every fermionic triality.
That is, T4 rotates through the fermionic generations.
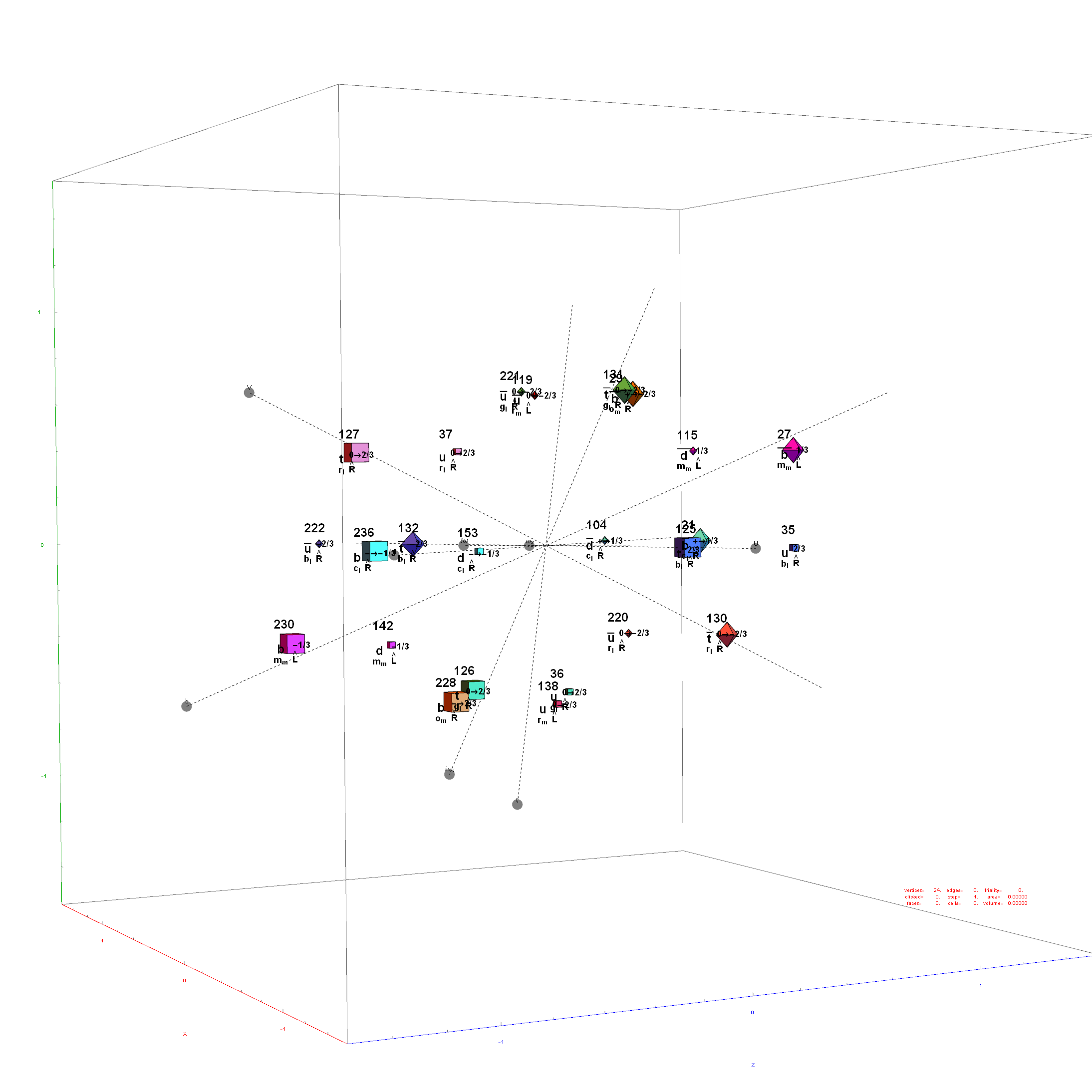
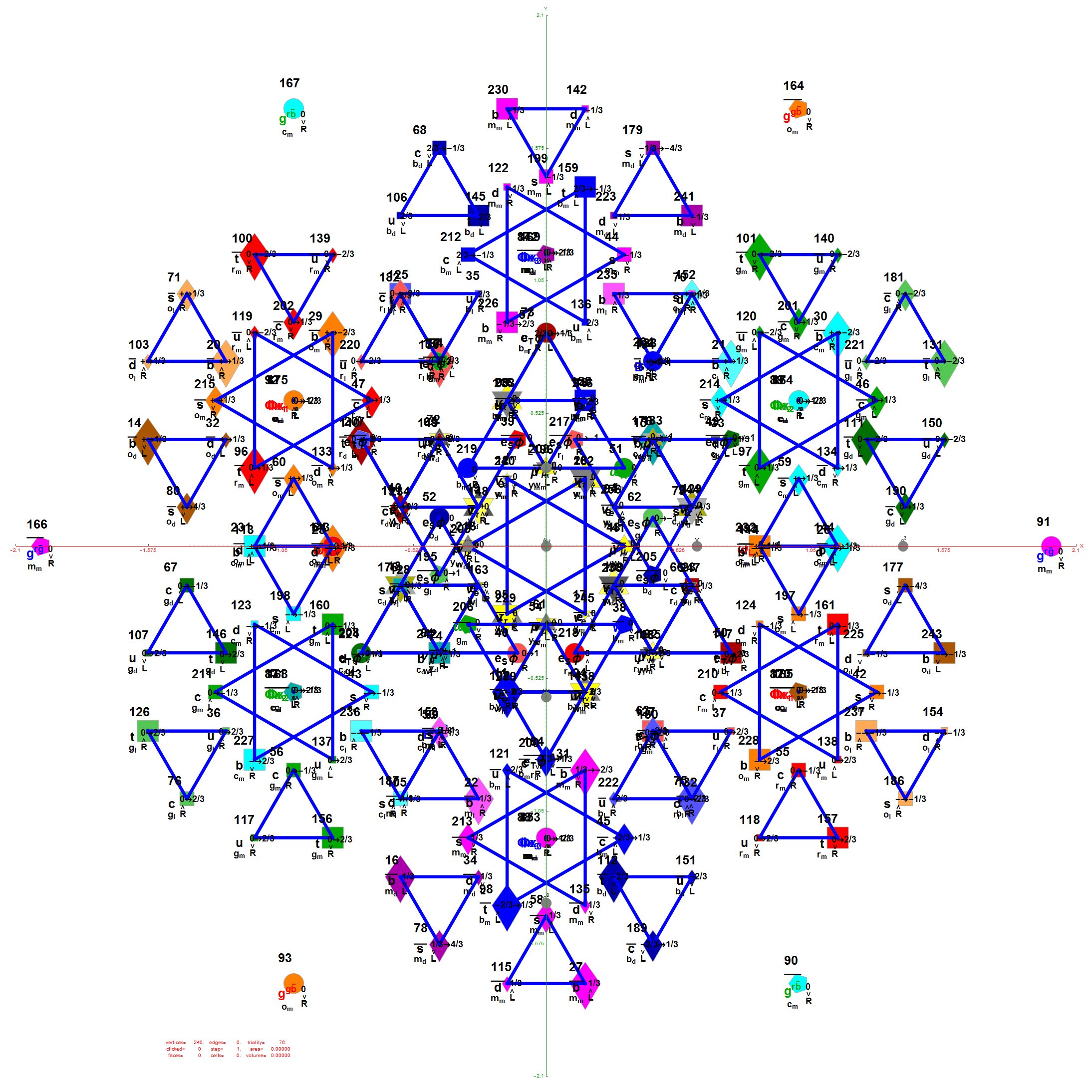 There are 12 trialities from these 76 that are associated with the inner E6 & F4 Lie Group vertices assigned to bosons, shown below with only the 112 (D8) +/-1 integer pair unlabeled vertices:
There are 12 trialities from these 76 that are associated with the inner E6 & F4 Lie Group vertices assigned to bosons, shown below with only the 112 (D8) +/-1 integer pair unlabeled vertices:
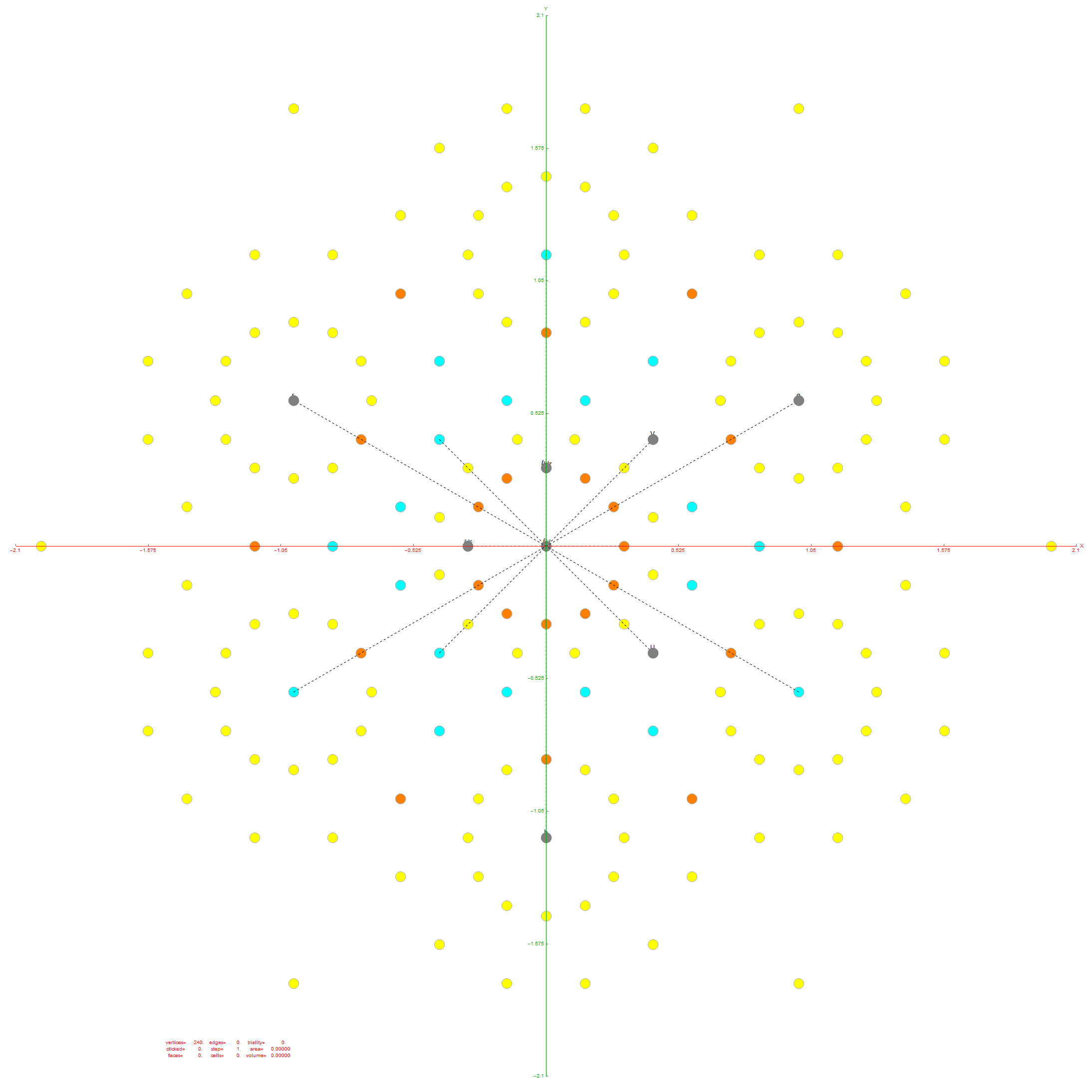
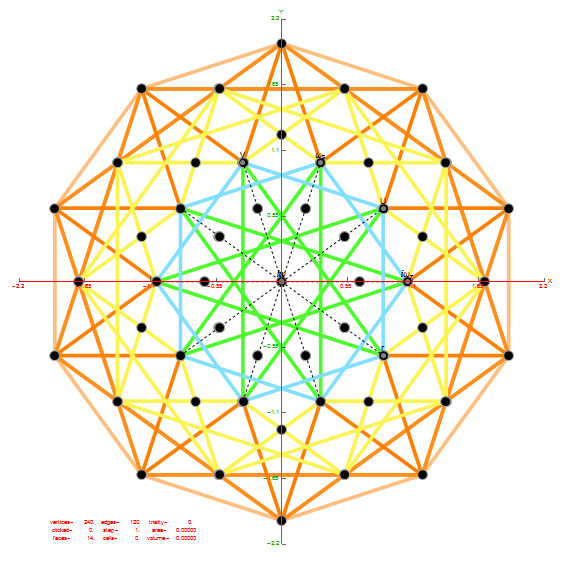
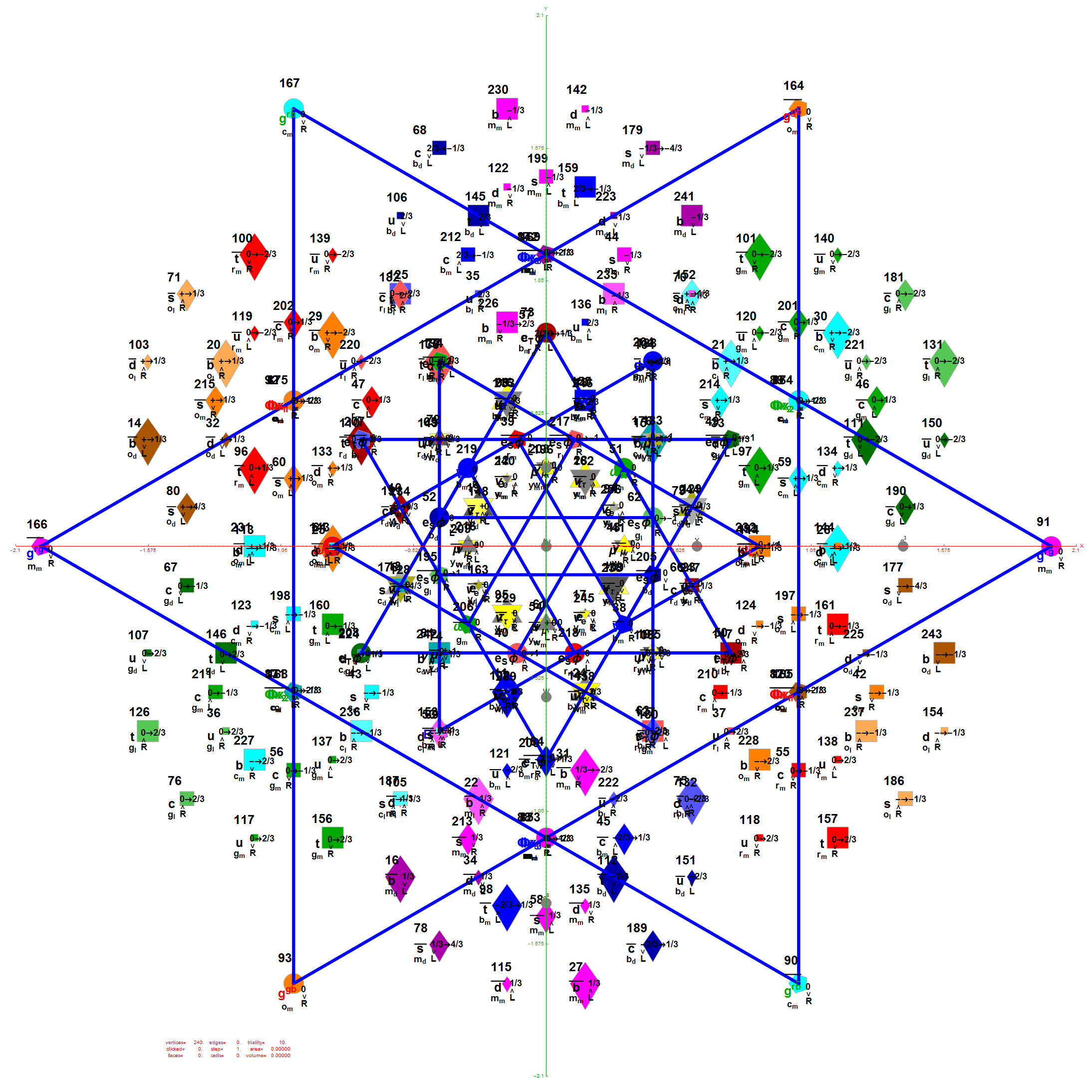
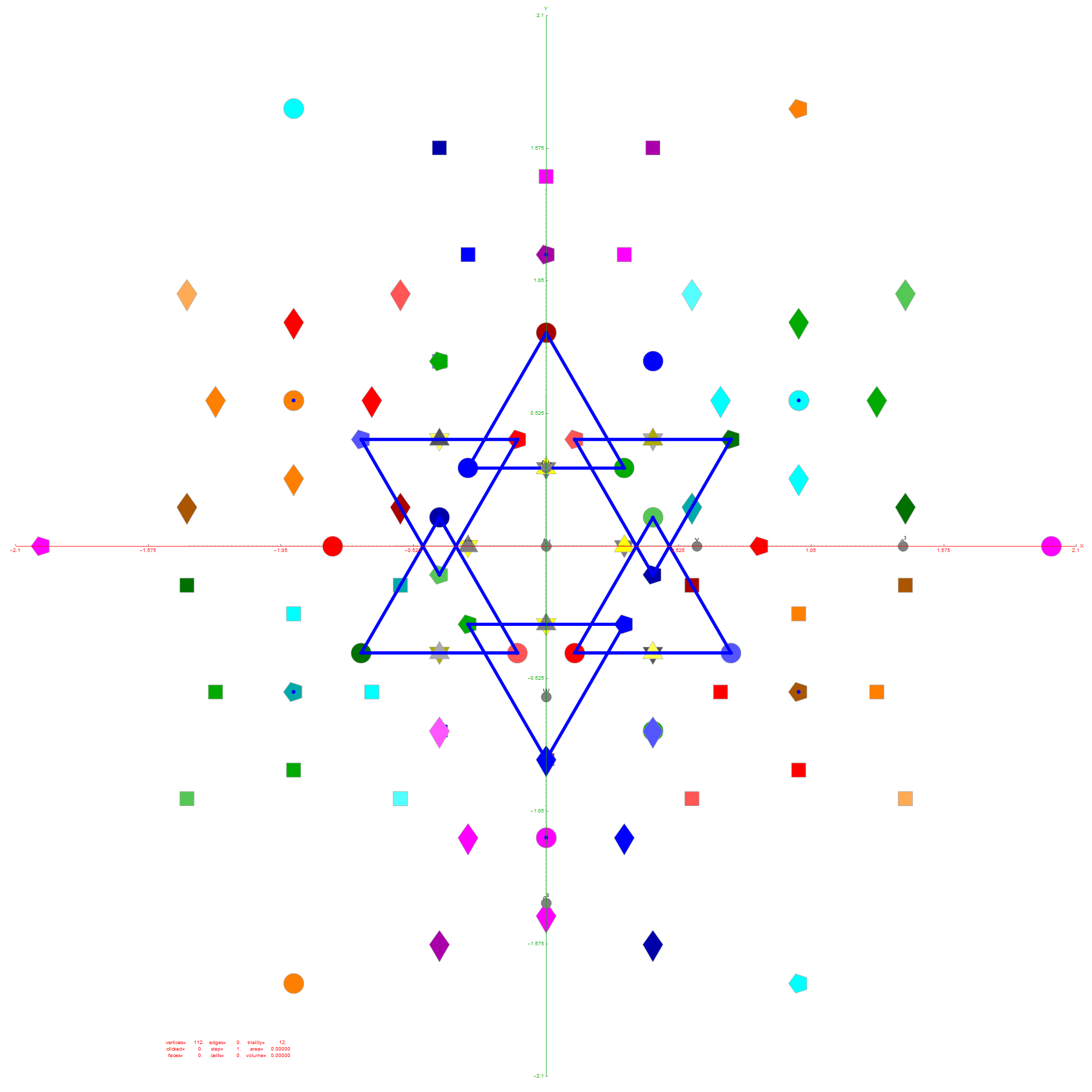 Of course, there are a number of overlapping vertices in this projection stemming from the 112 (D8) +/-1 Bosonic sector. The following image colors the vertices by overlap count, with 120 Yellow with no overlaps, 24 Cyan with 2 overlaps (48), and 24 Cyan with 3 overlaps (72).
Of course, there are a number of overlapping vertices in this projection stemming from the 112 (D8) +/-1 Bosonic sector. The following image colors the vertices by overlap count, with 120 Yellow with no overlaps, 24 Cyan with 2 overlaps (48), and 24 Cyan with 3 overlaps (72).
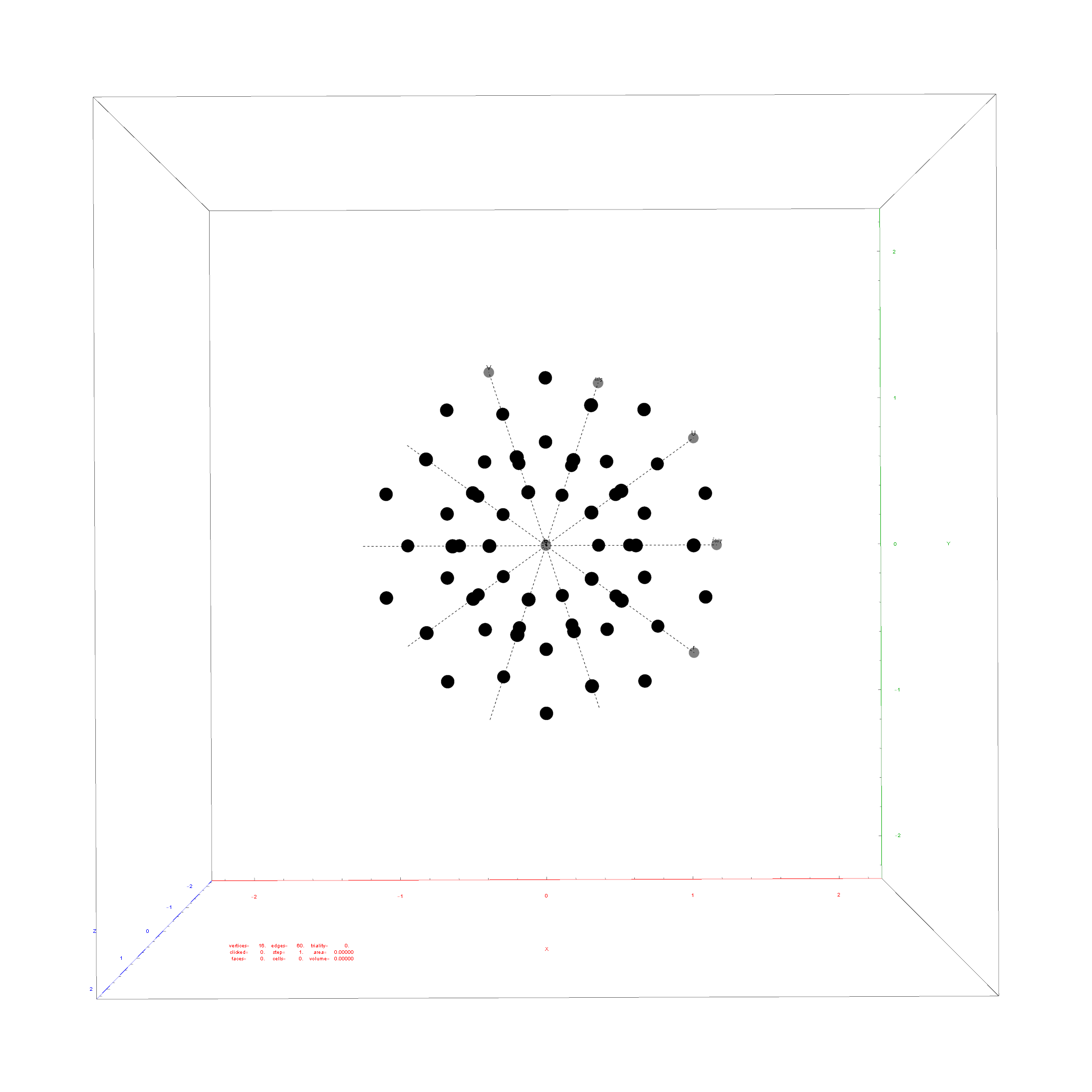
Notice the 8 projection basis vectors with dark gray circles. Of course, these projection basis vectors are the 8 “generator vertices” of E8 vertices with permutations of {+1,0,0,0,0,0,0,0} giving it the full 240+8=248 dimension count. Add to that the -1 “anti-generators” being the opposite end of the projection basis vectors and you get the full 256 vertices representing the full Clifford Algebra on the 9th row of the Pascal Triangle.
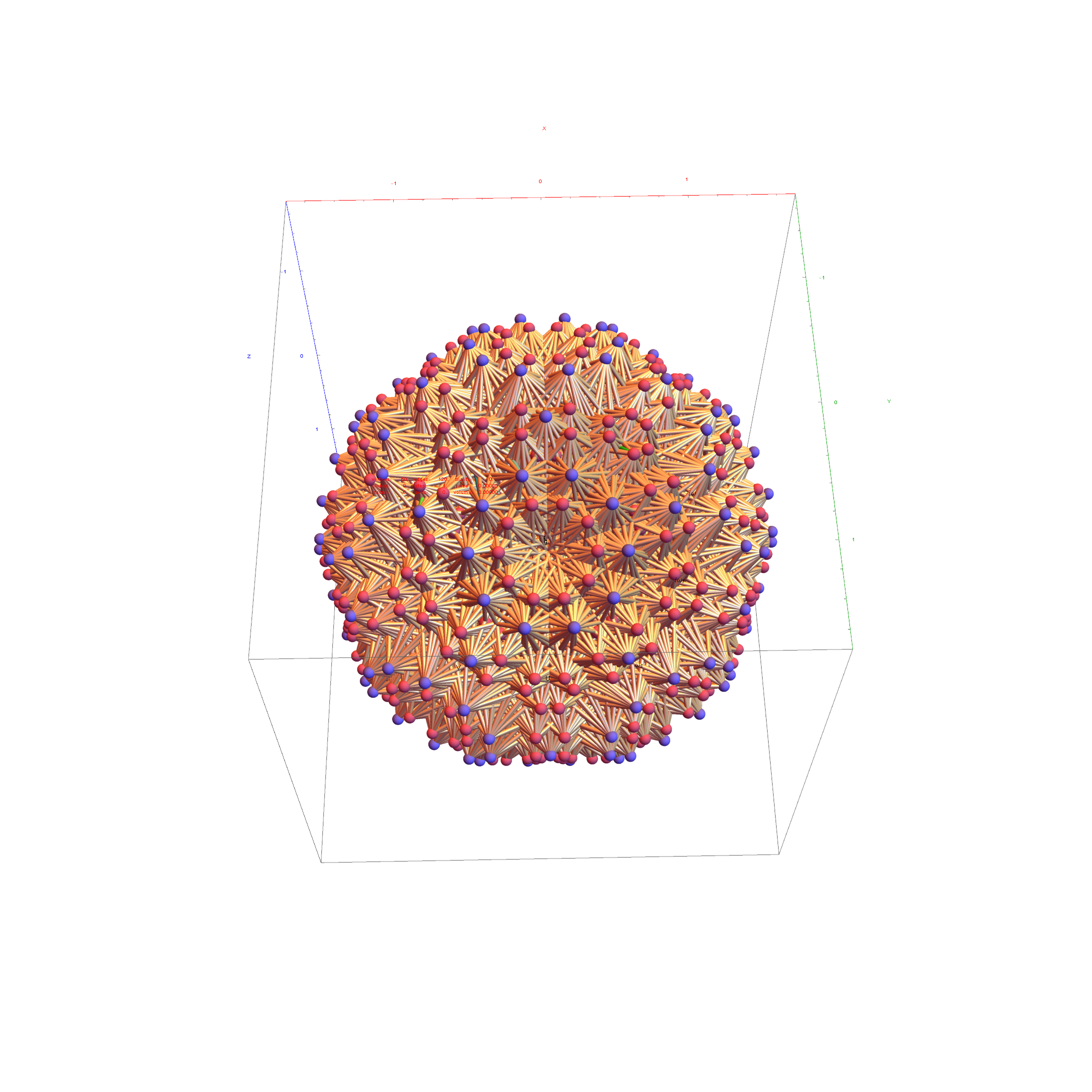
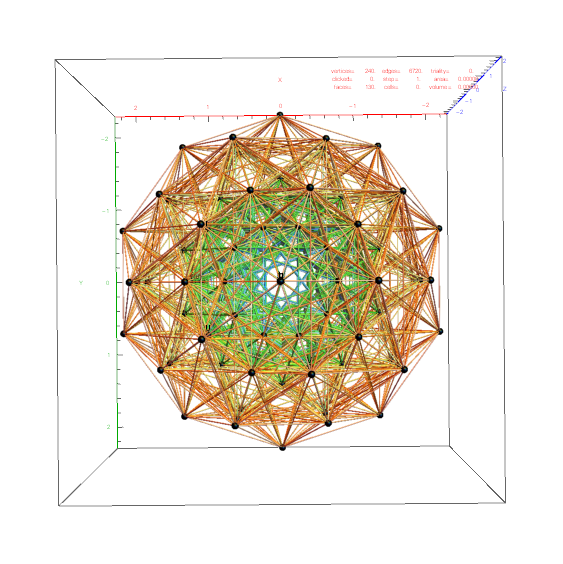
There are 6720 edges in E8 with an 8D length Sqrt[2].
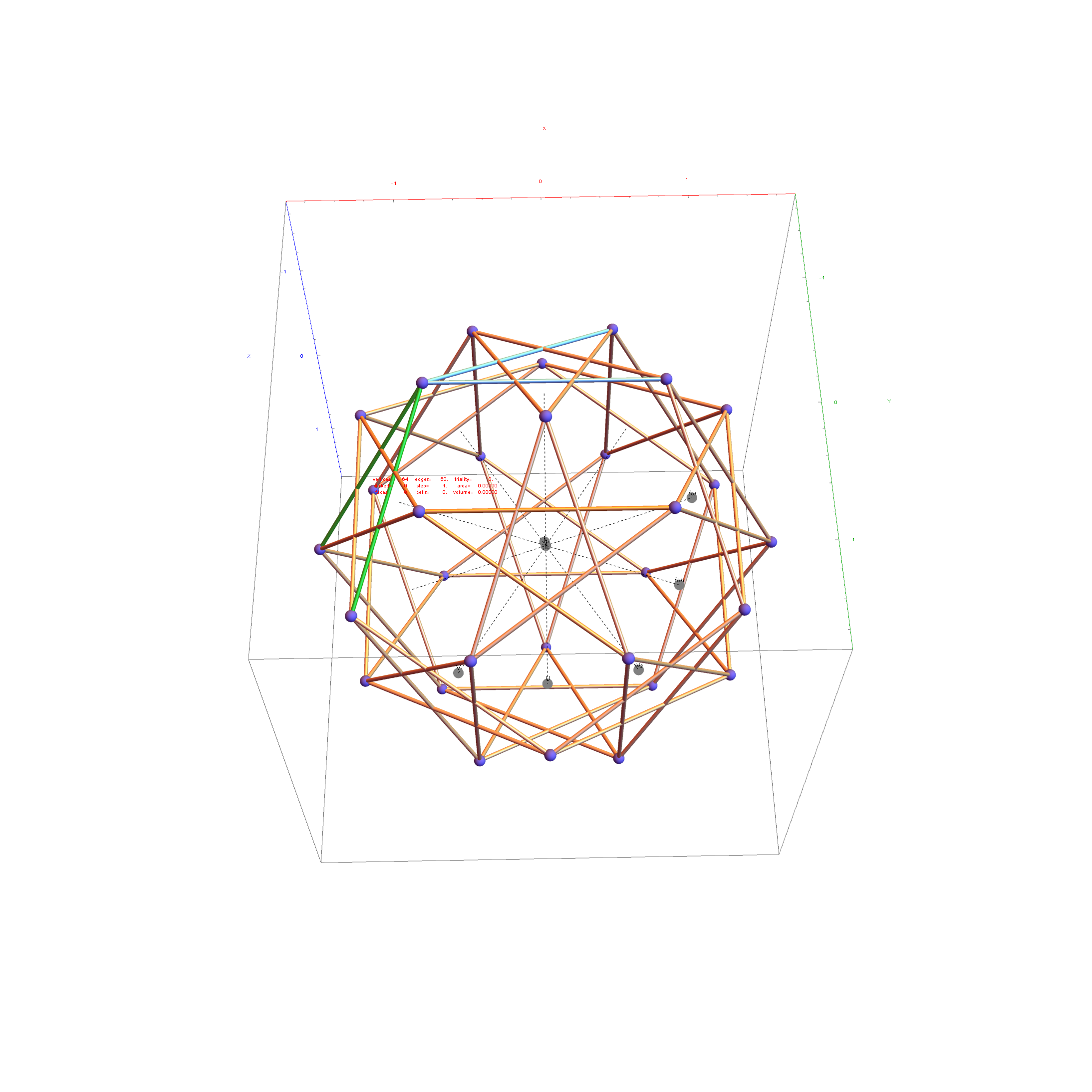
Just for fun, I introduce to you the 6720 rectified E8 vertices taken from the midpoint of each edge and using the same projection with coloring of the spheres based on overlap count. Enjoy!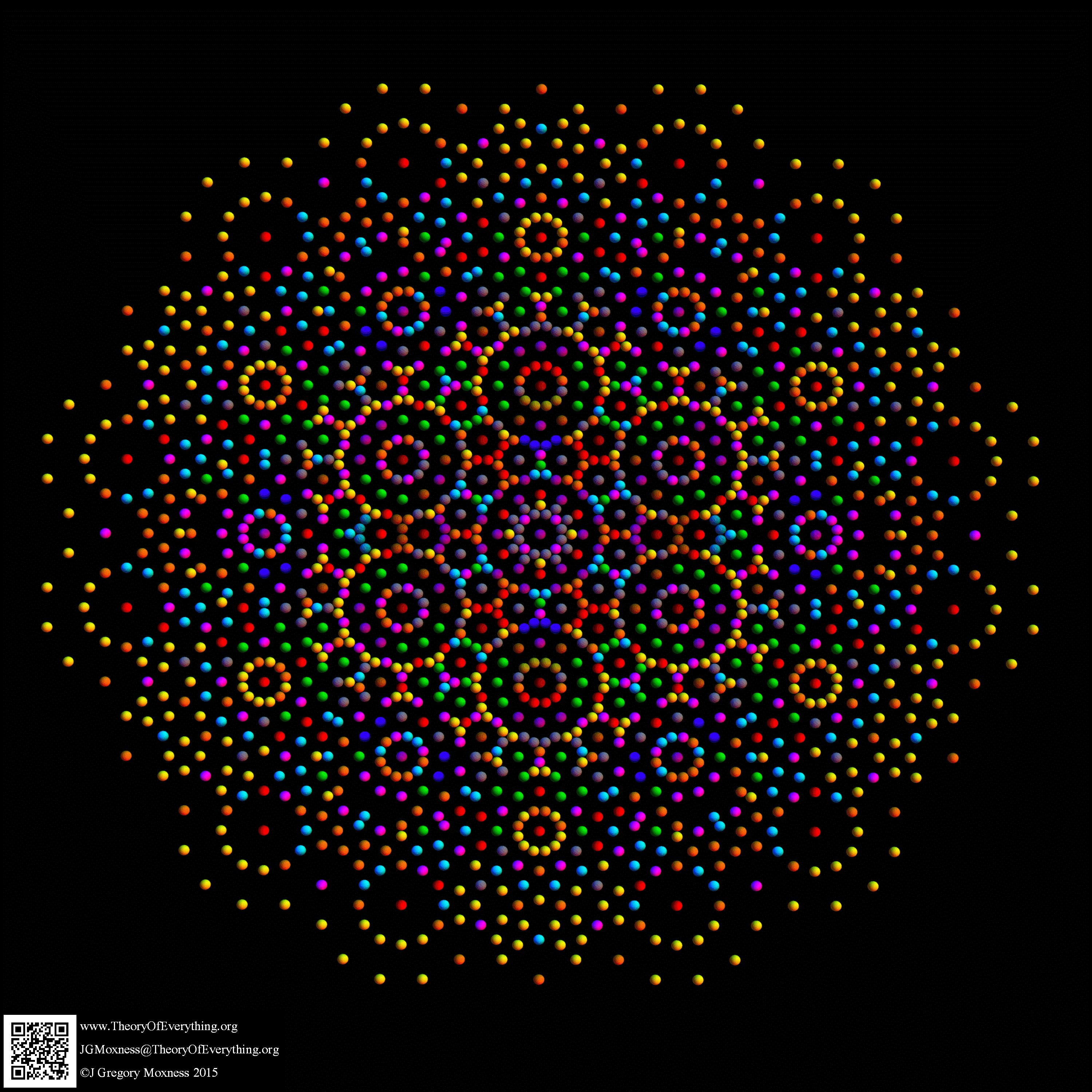
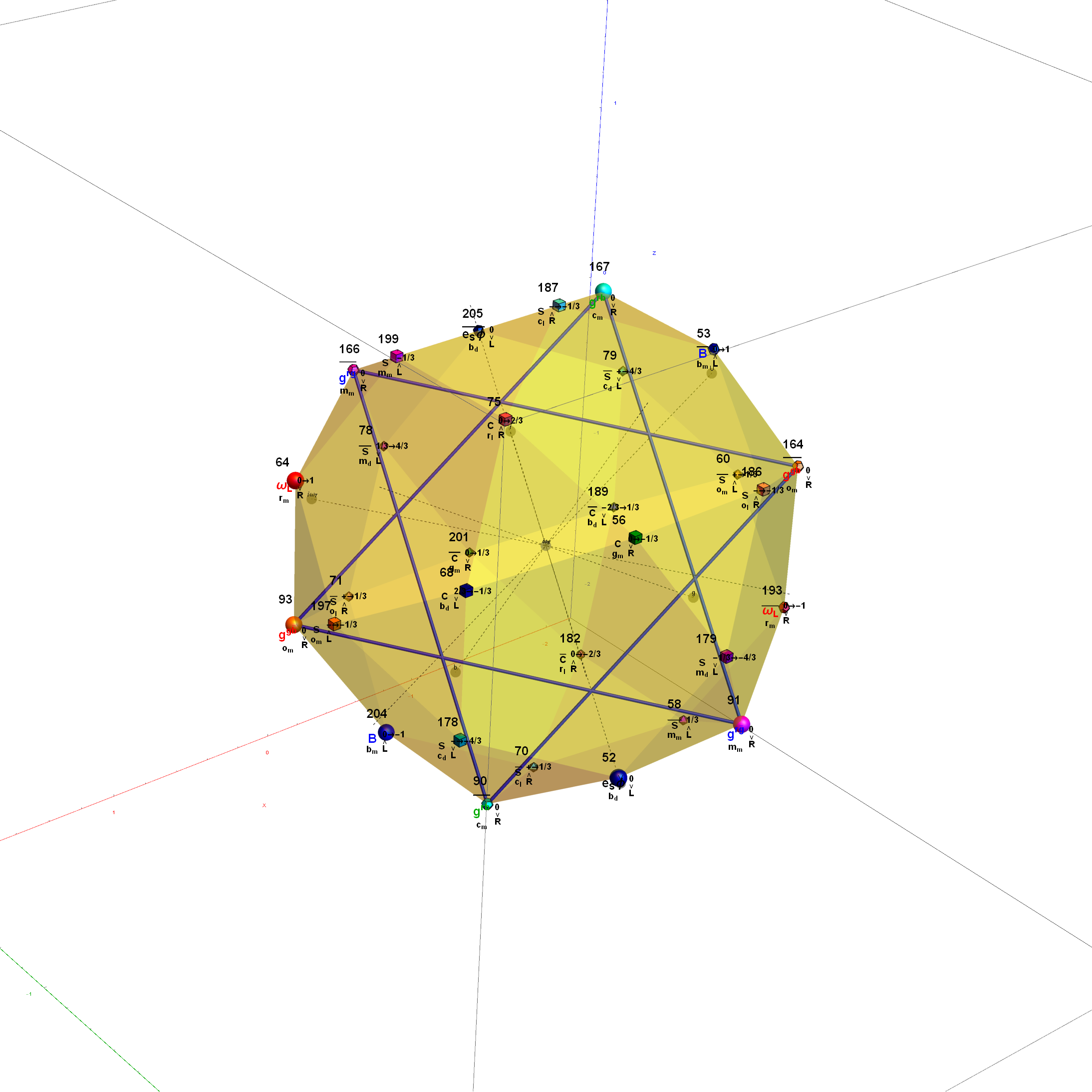
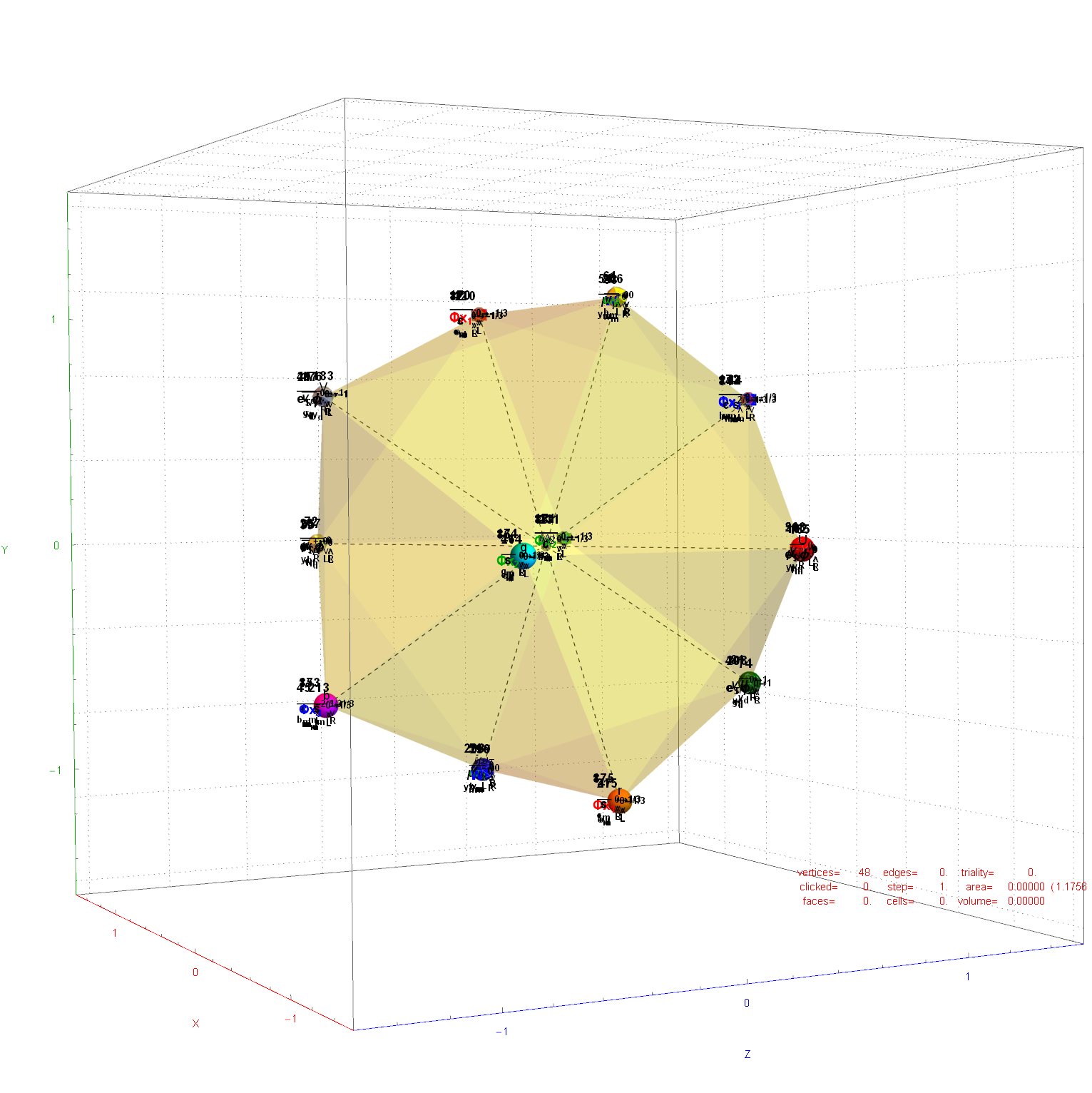
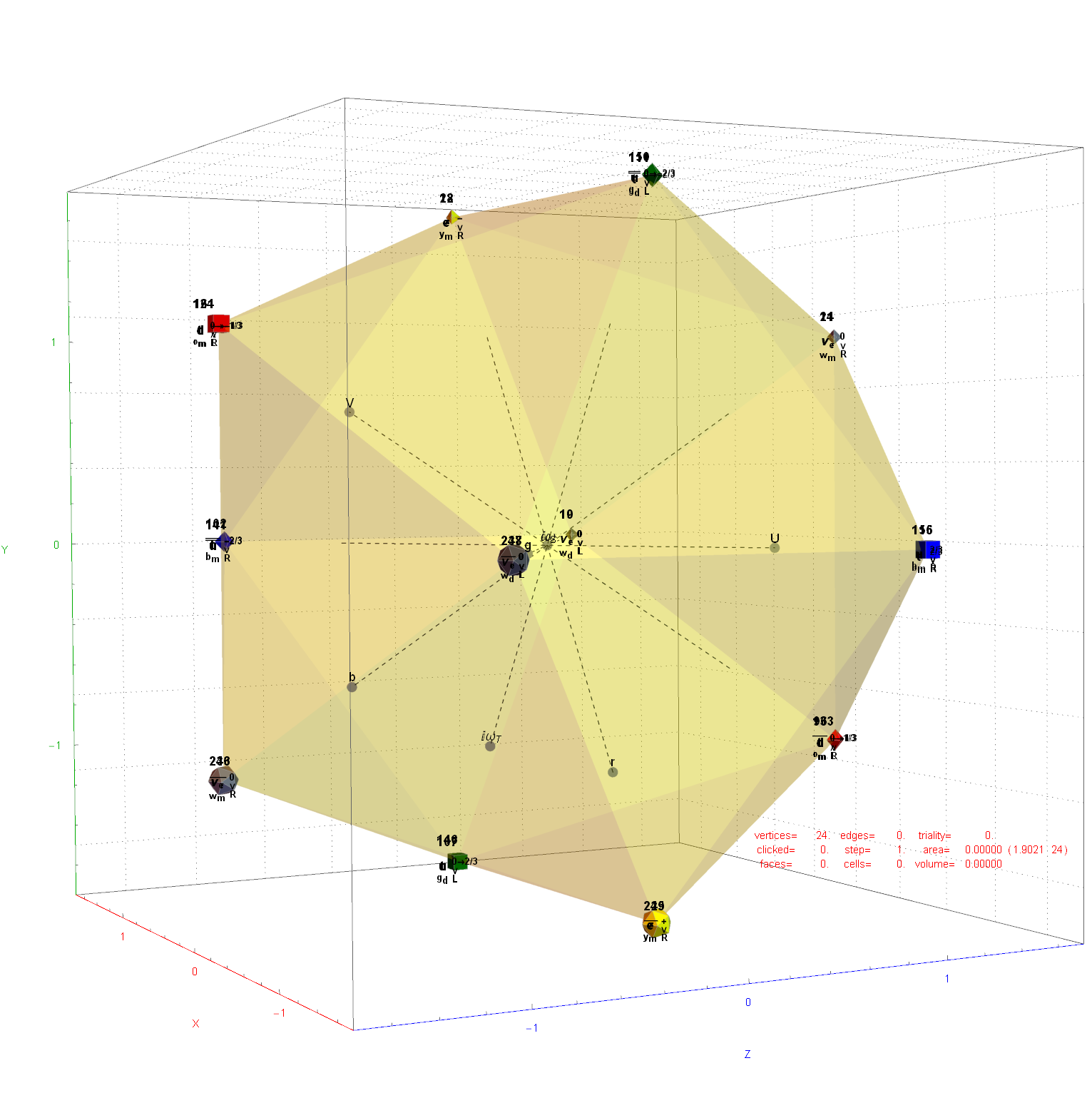
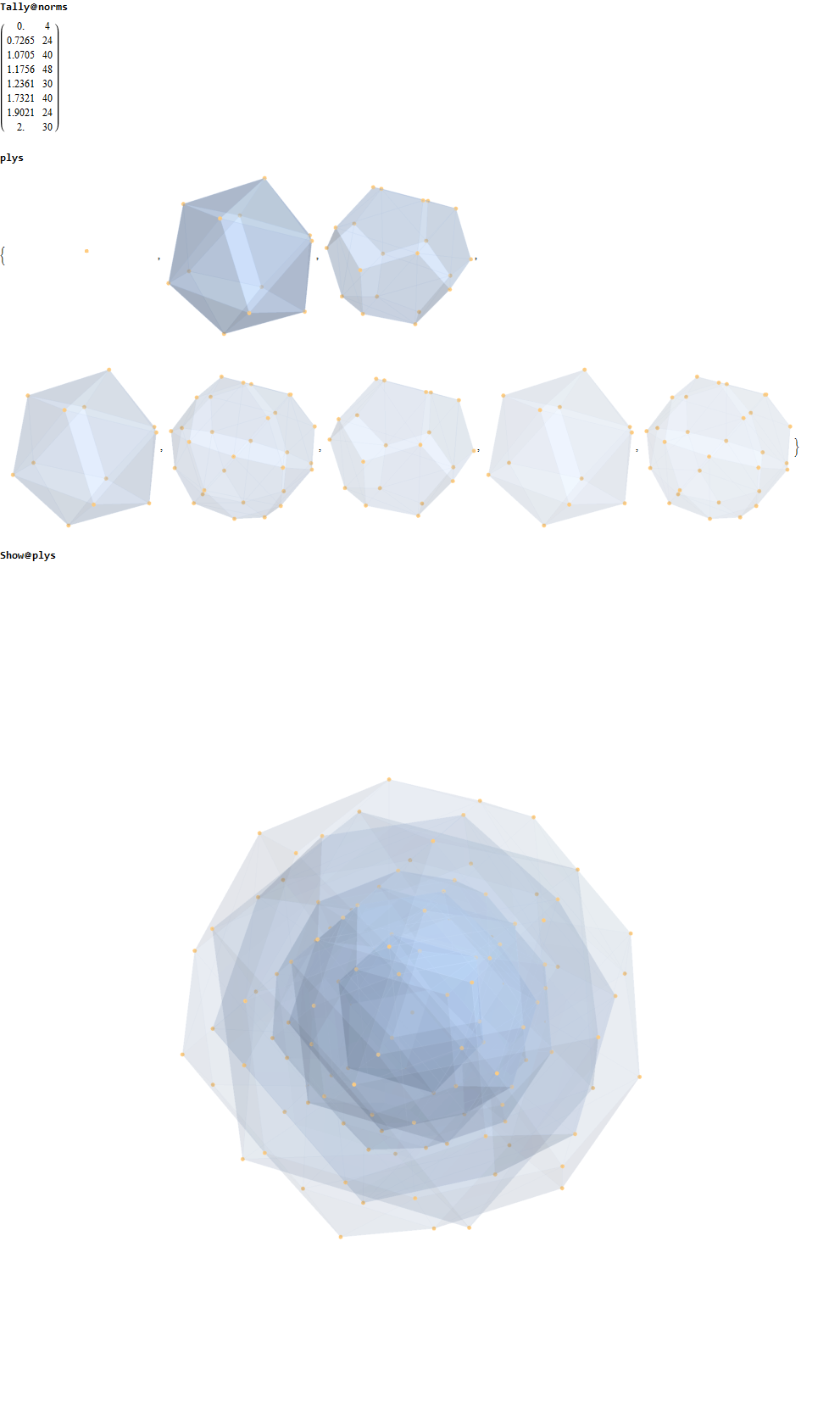
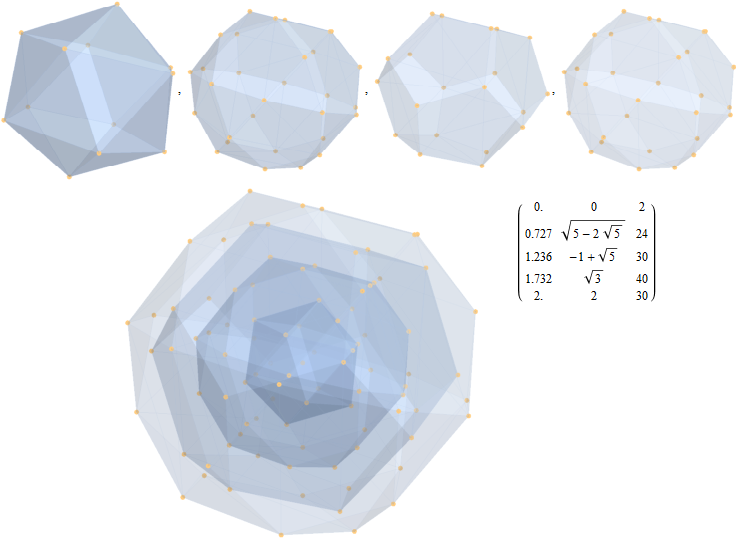
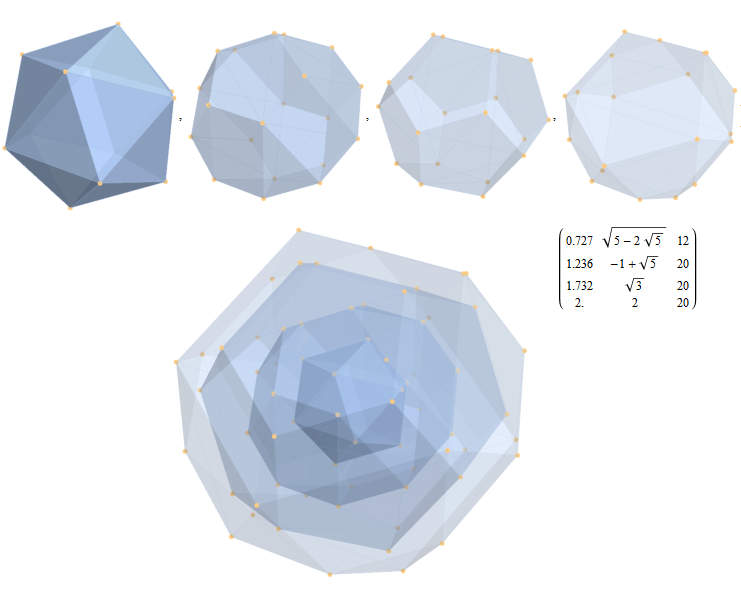
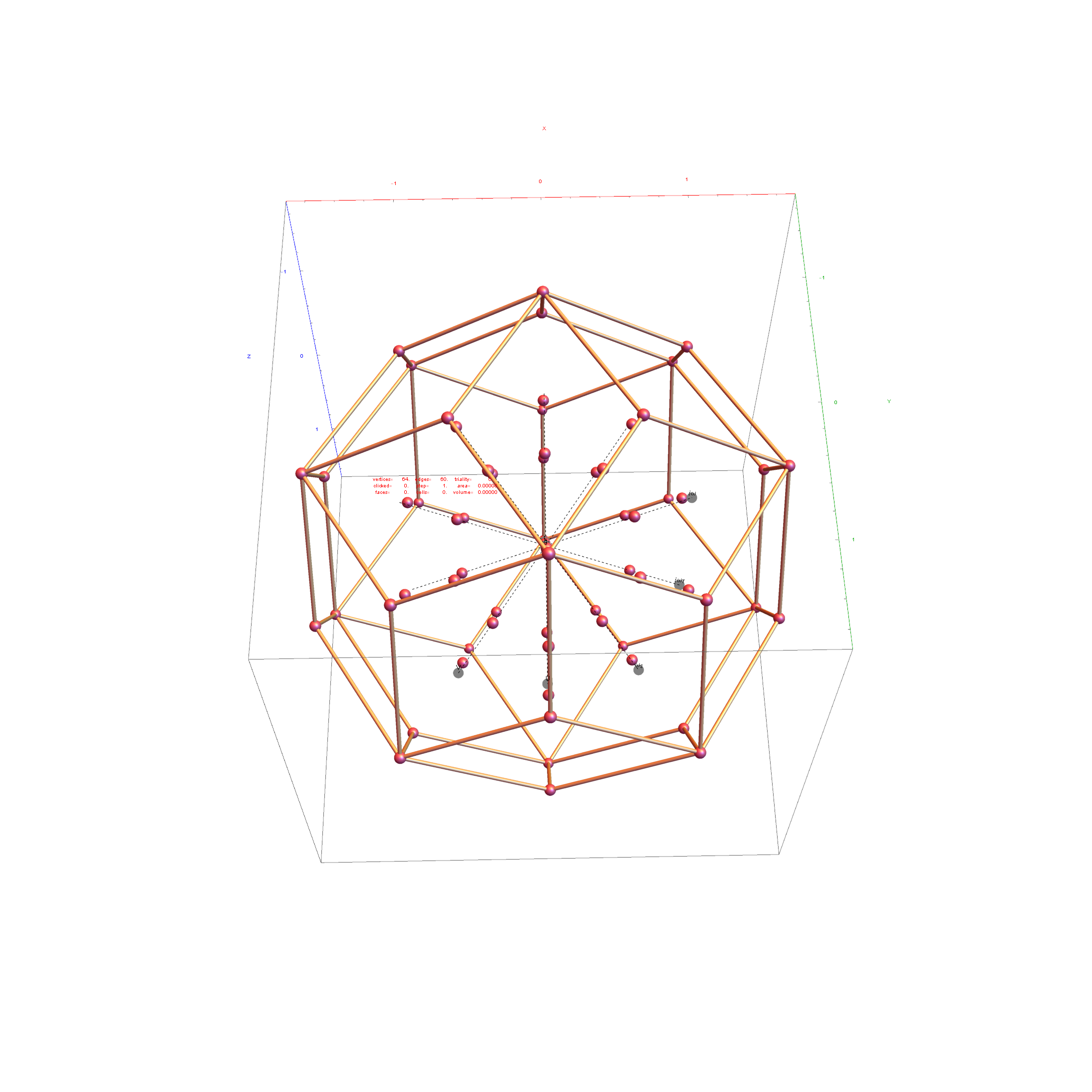
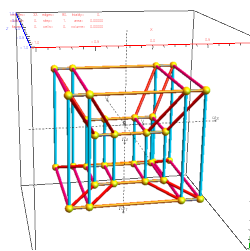
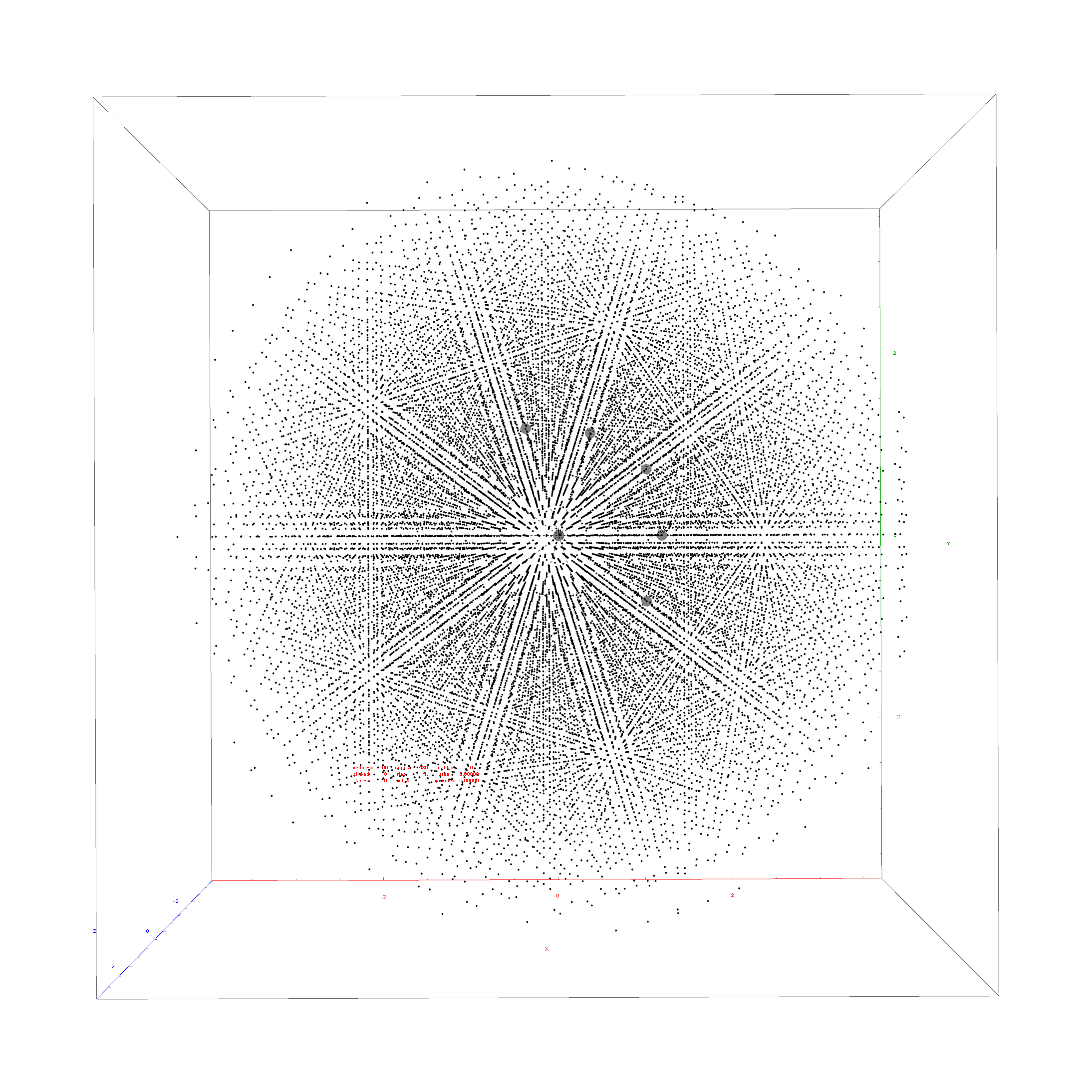
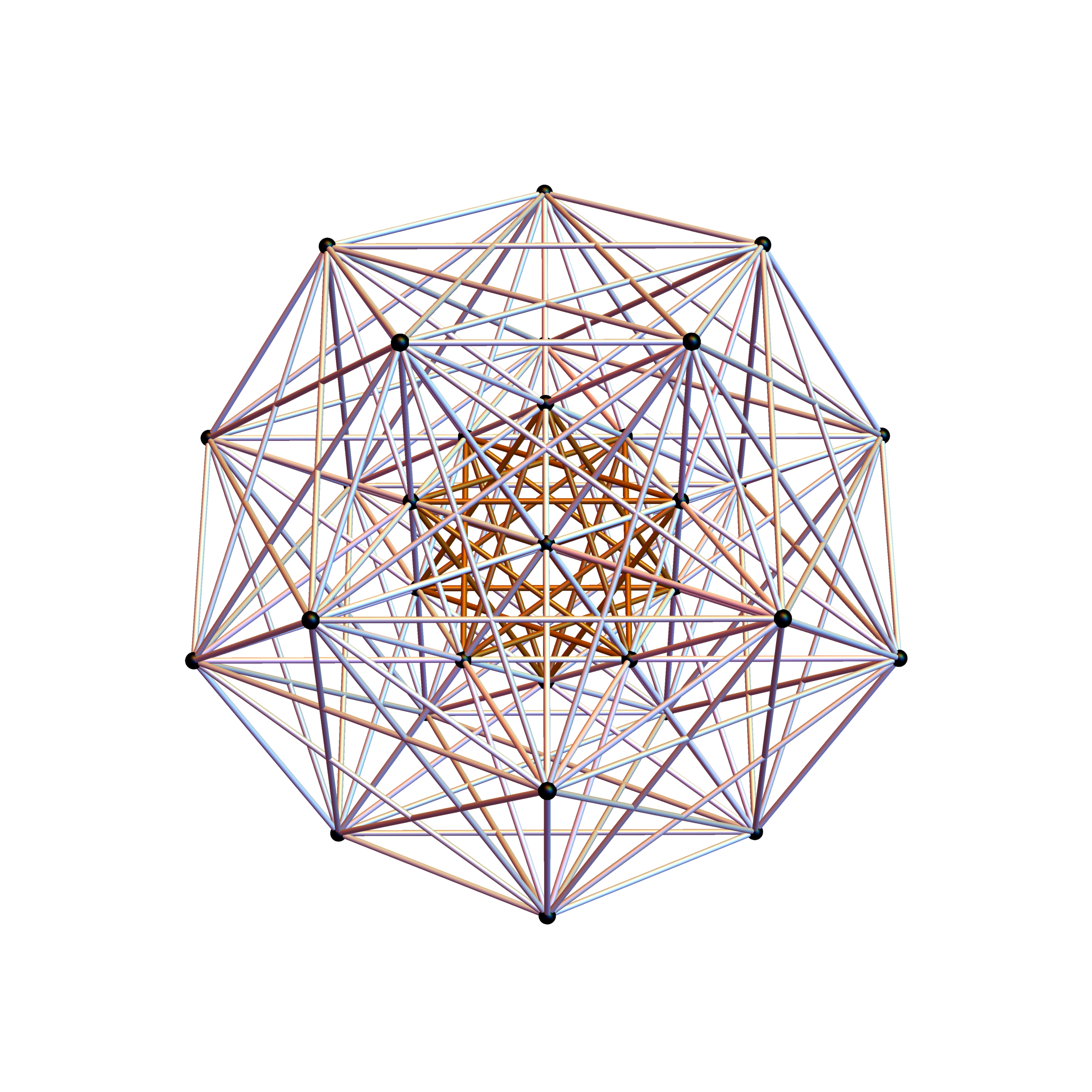
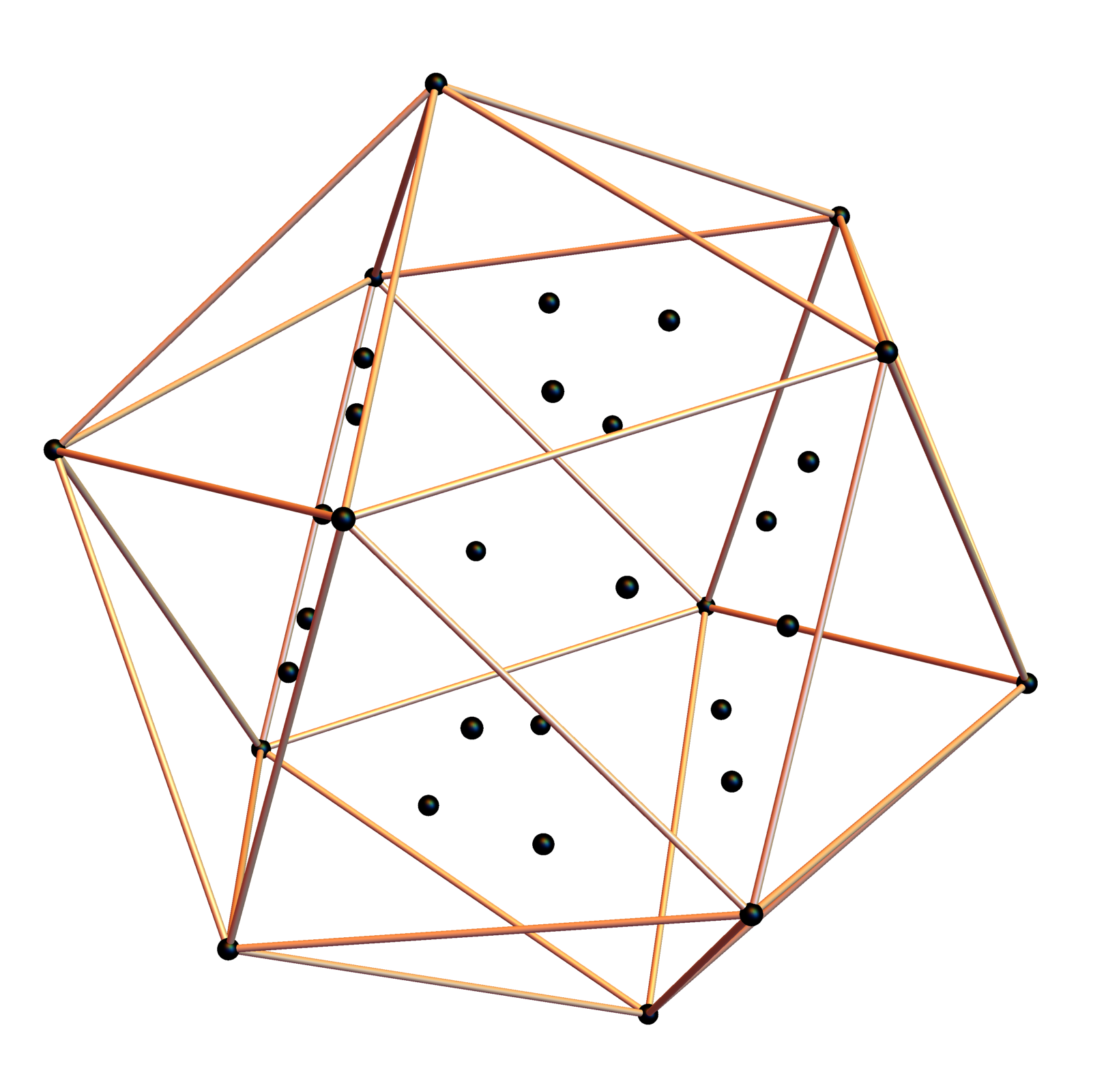
Here are the G2 gluons connected by their trialities shown in a 3D concentric hull projection of E8 using the E8 to H4 folding matrix basis vectors. This is the 4th hull, which is the outer hull of the inner H4 600 cell (an icosadodecahedron). For more on E8 hulls, see this post.
The full F4 group with 10 T2 and 12 T4 trialities affecting the bosons is contained in the outer icosadodecahedron (1st hull) combined with the 3rd (quad icosahedral) and 4th icosadodecahedron hulls.
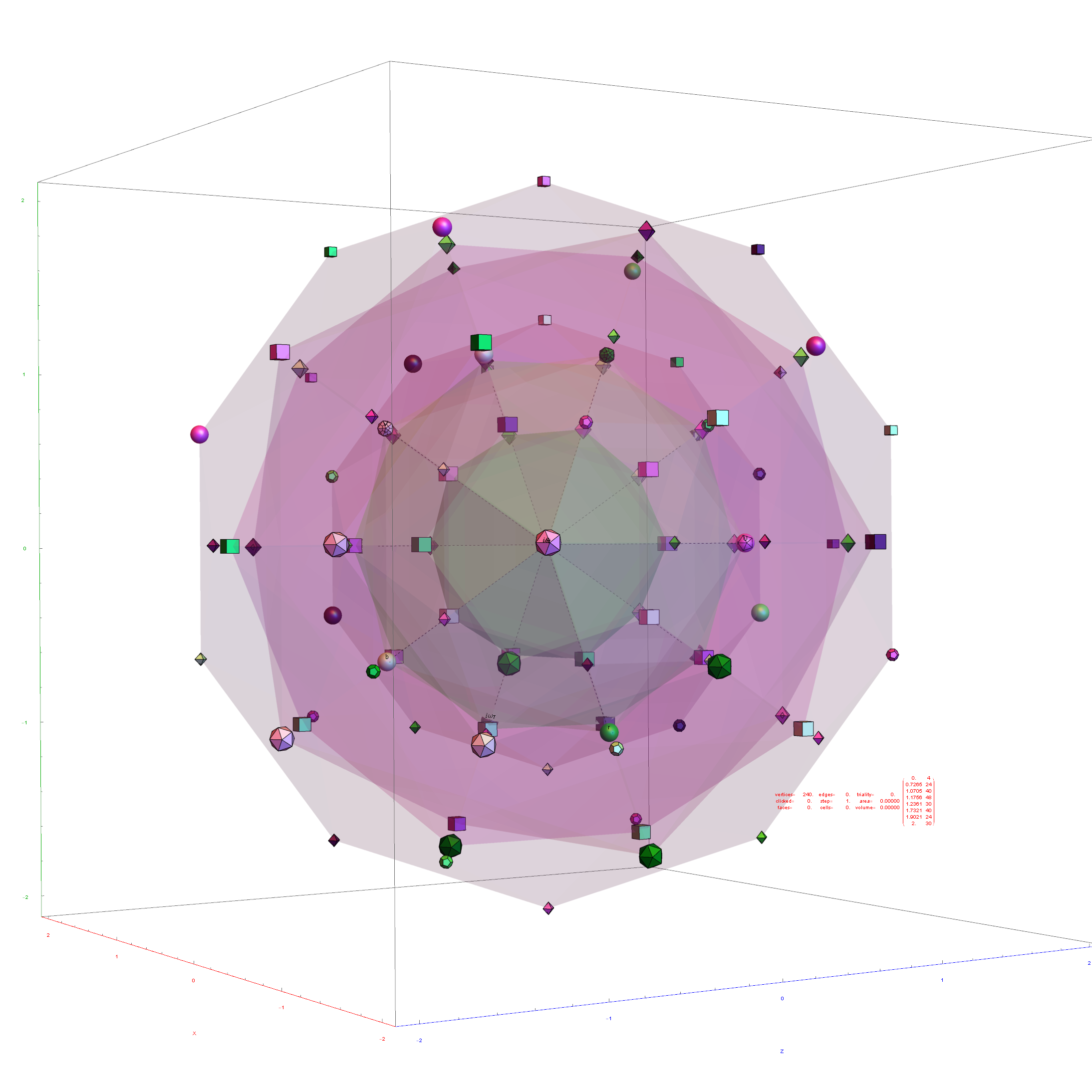
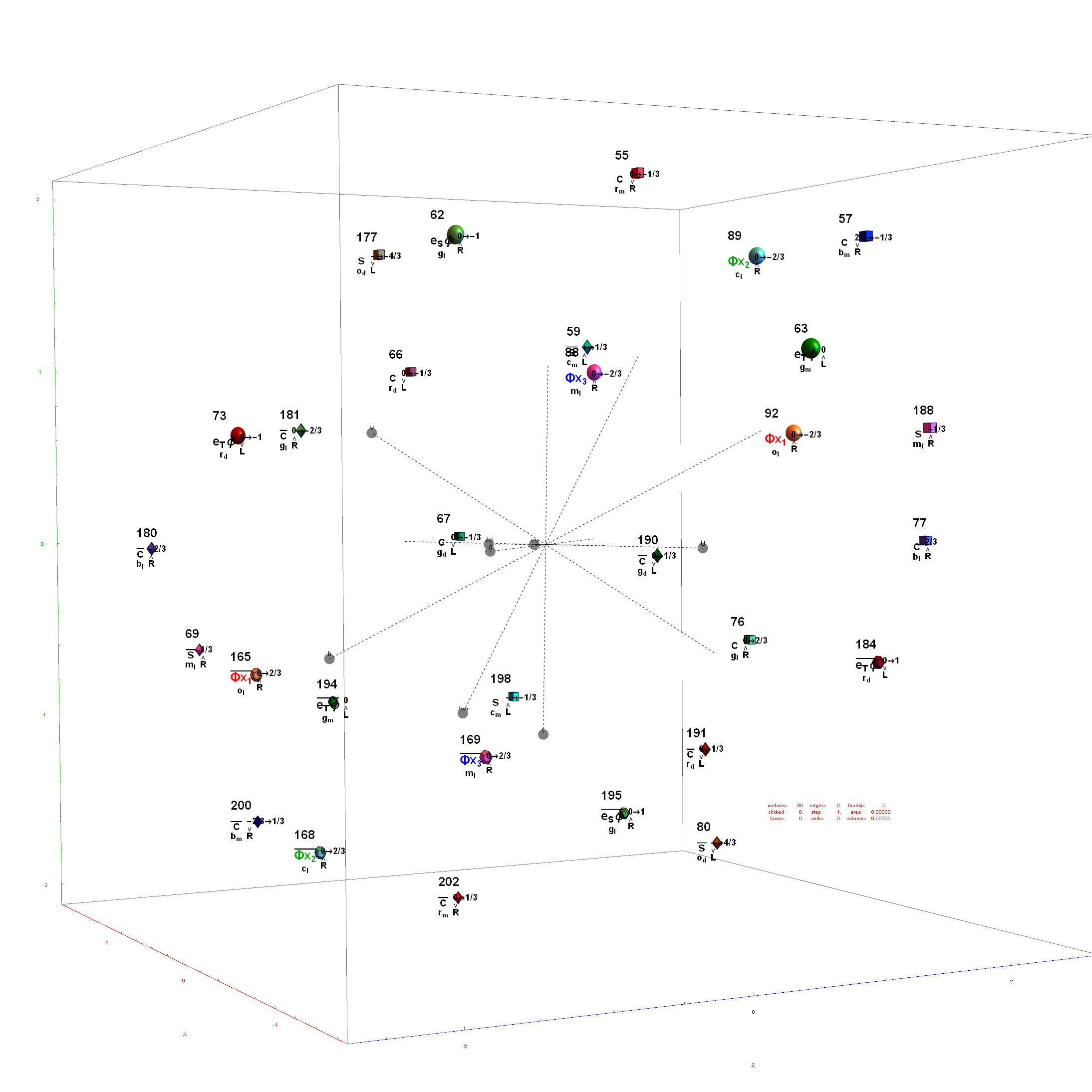
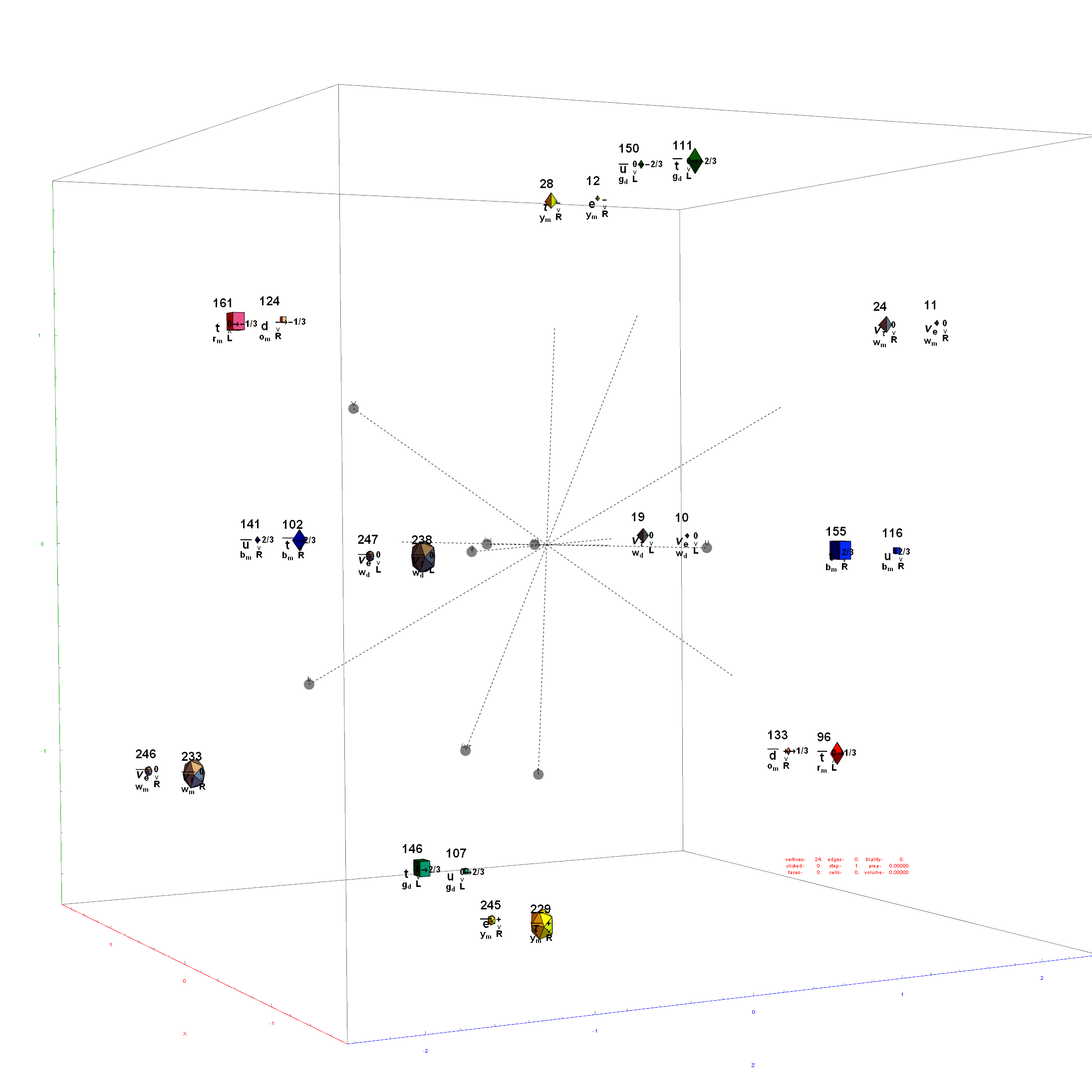
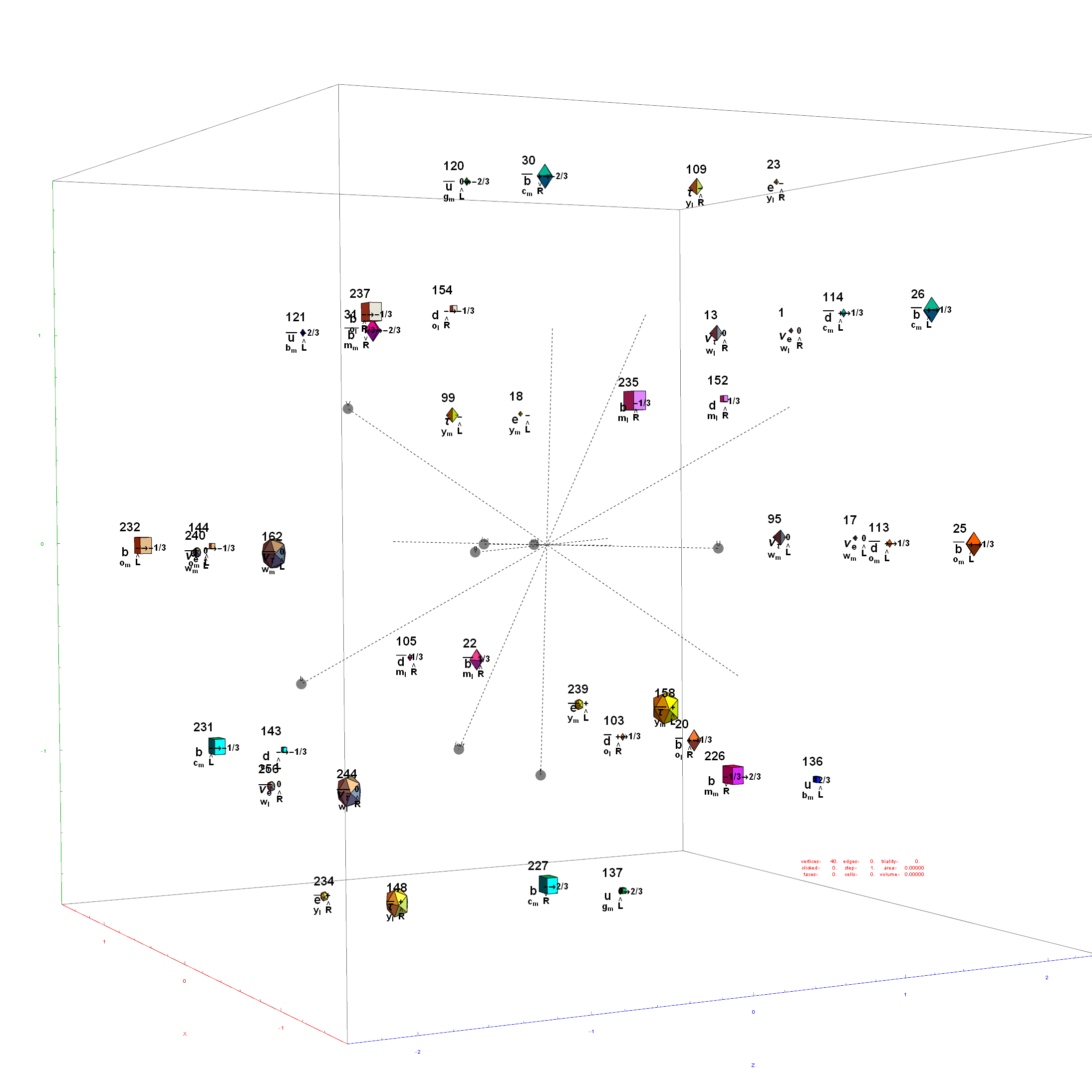
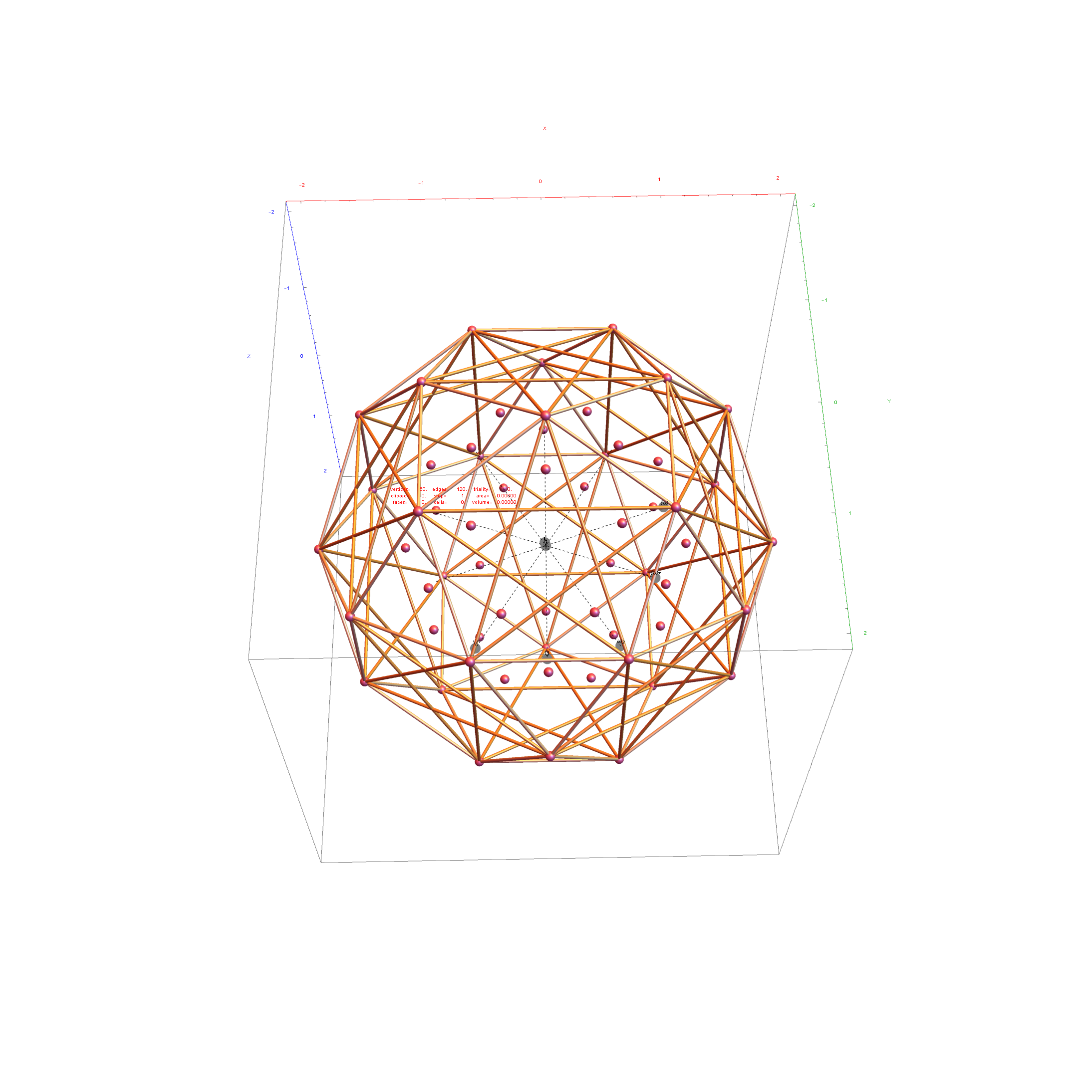
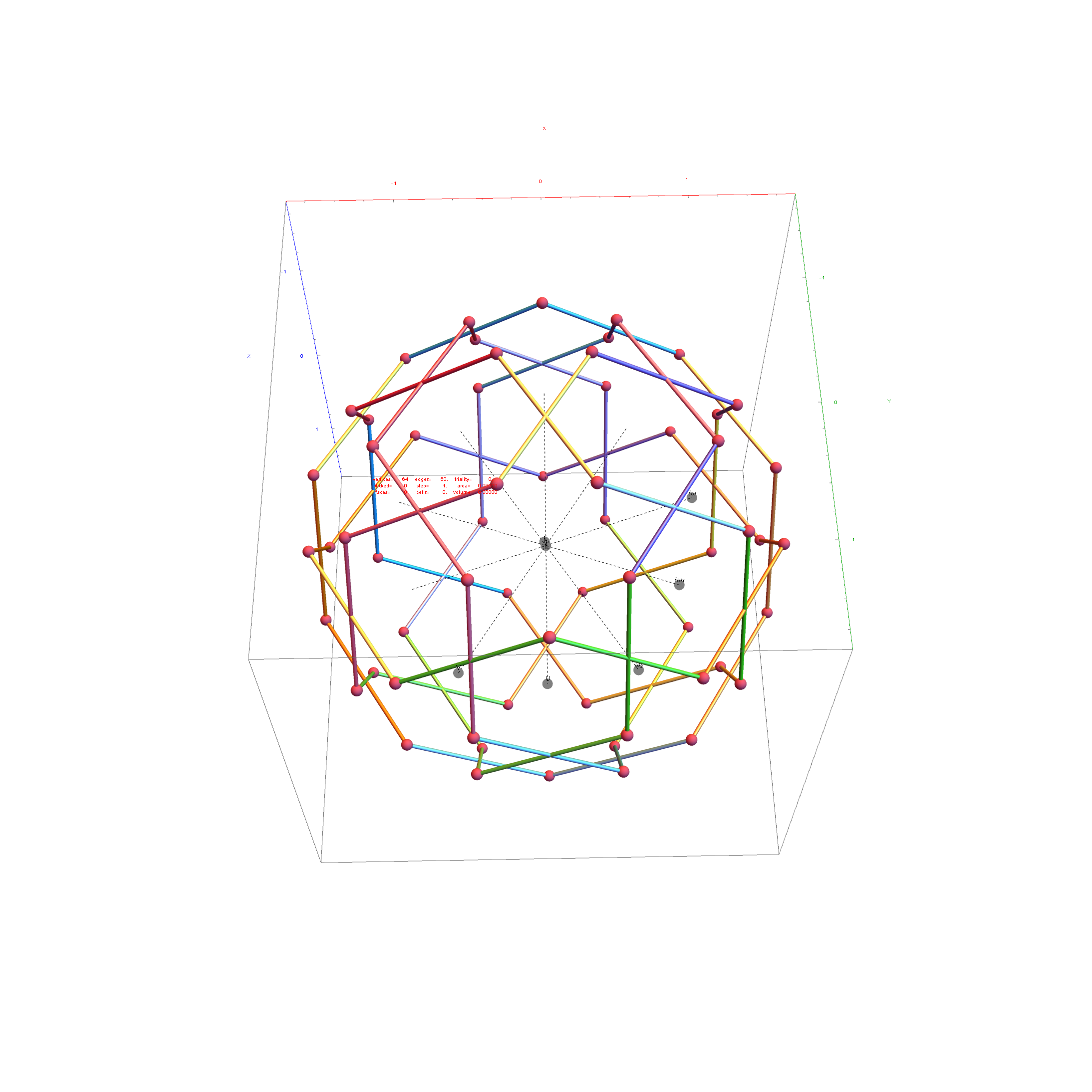
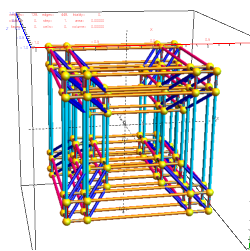
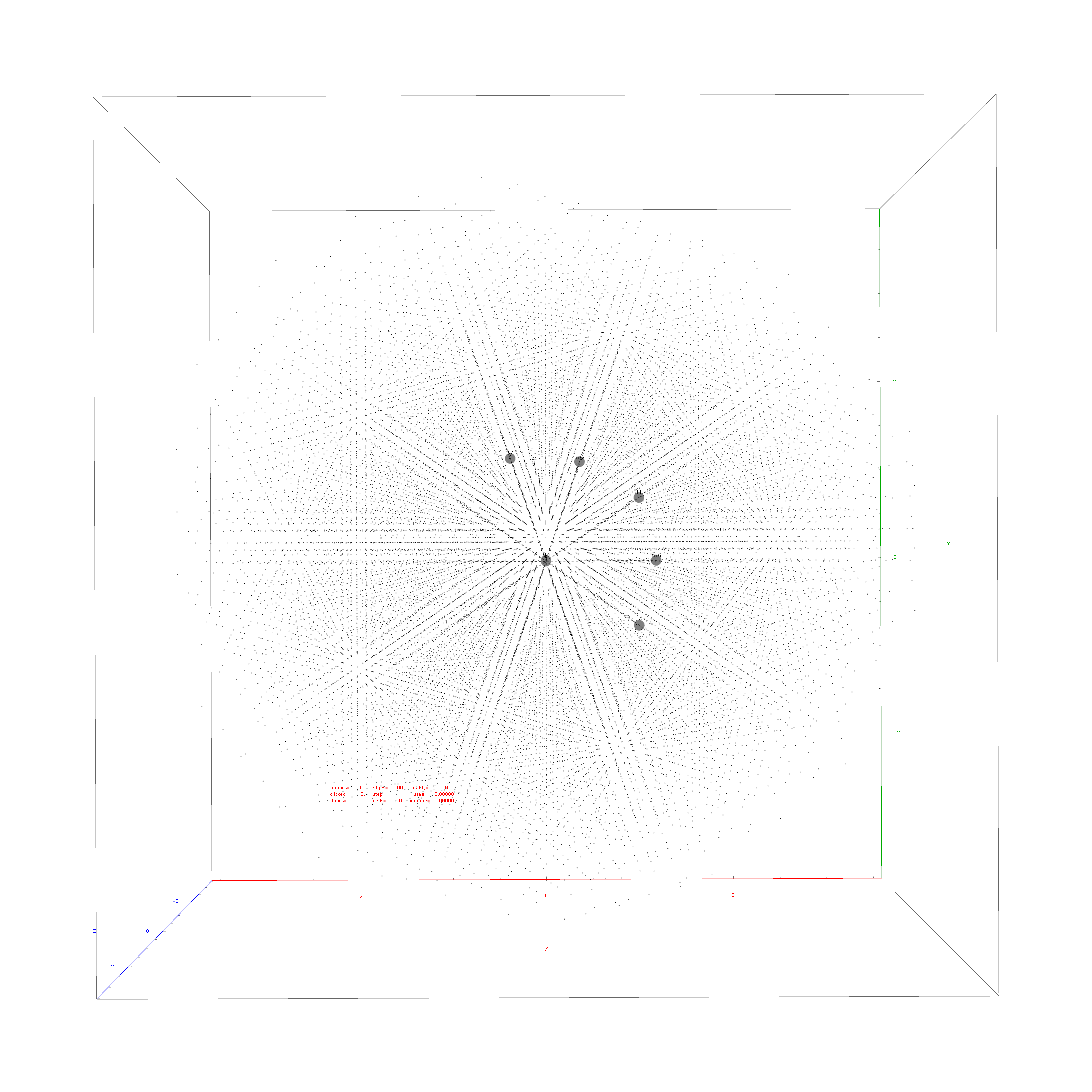
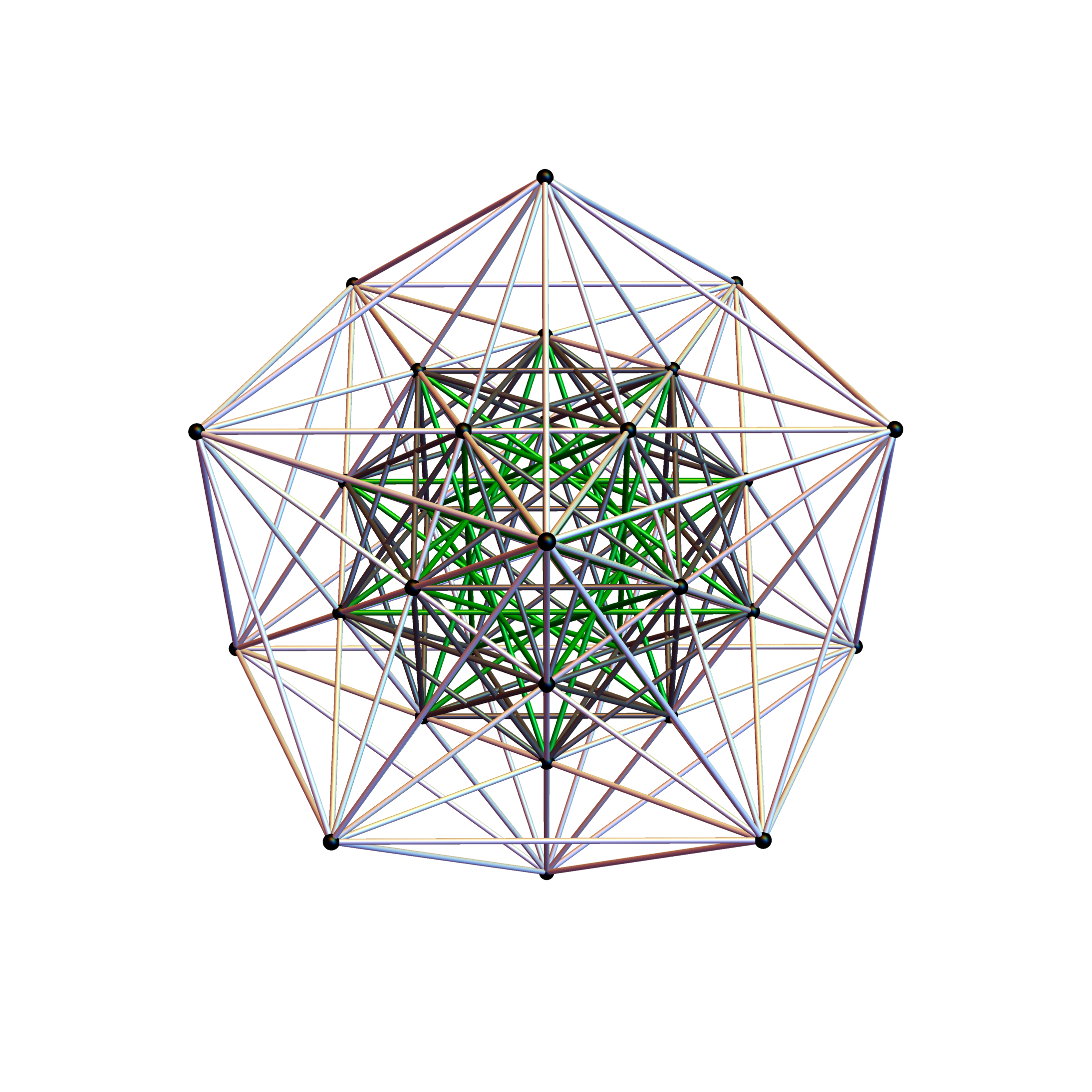
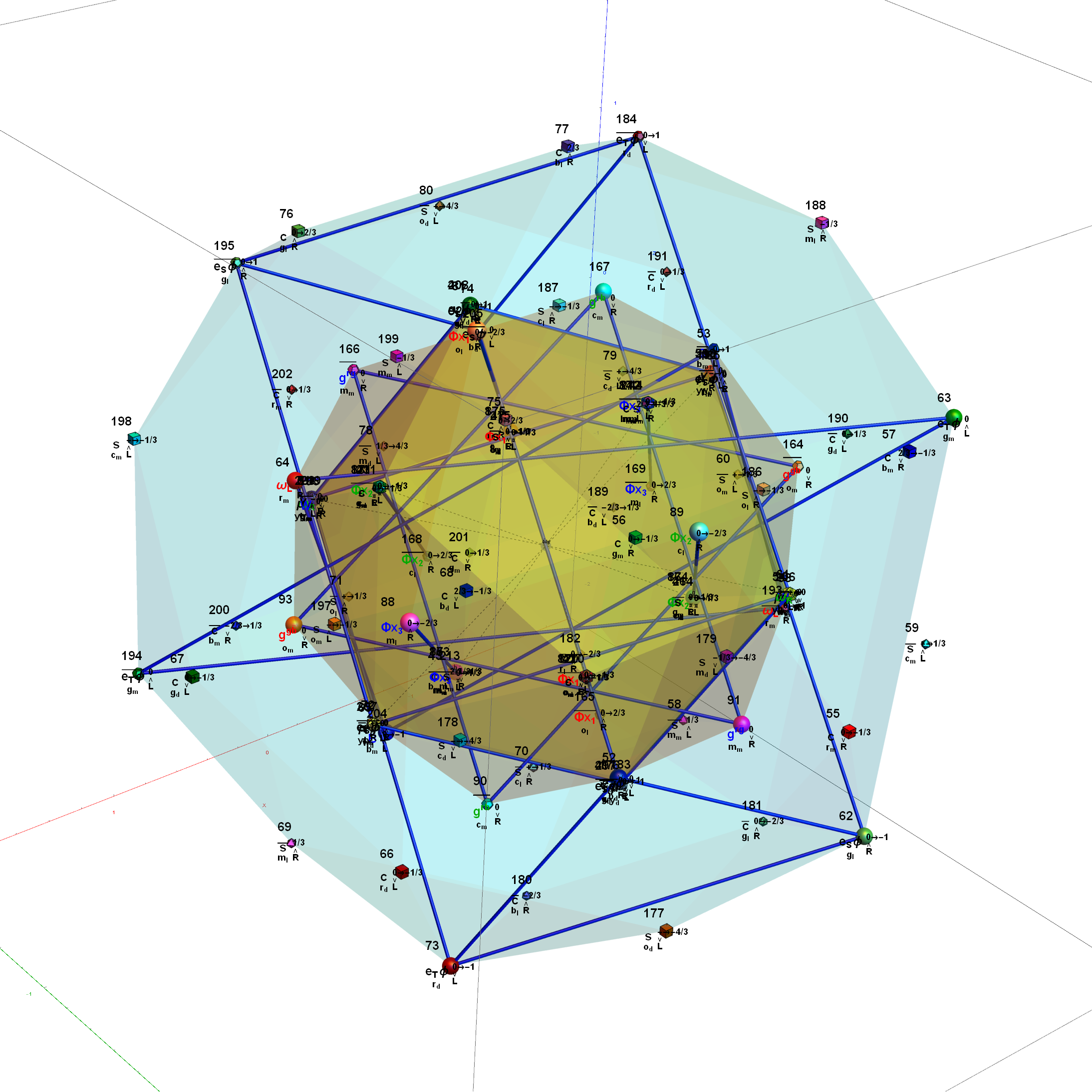 Below is the full E8 with all trialities shown in 3D concentric hull projection.
Below is the full E8 with all trialities shown in 3D concentric hull projection.
Wow – that is nice! Remember, you heard it here first!
BTW – if you find this information useful, or provide any portion of it to others, PLEASE make sure you cite this post. If you feel a blog post citation would not be an acceptable form for academic research papers, I would be glad to clean it up and put it into LaTex format in order to provide it to arXiv (with your academic sponsorship) or Vixra. Just send me a note at: jgmoxness@theoryofeverthing.org.