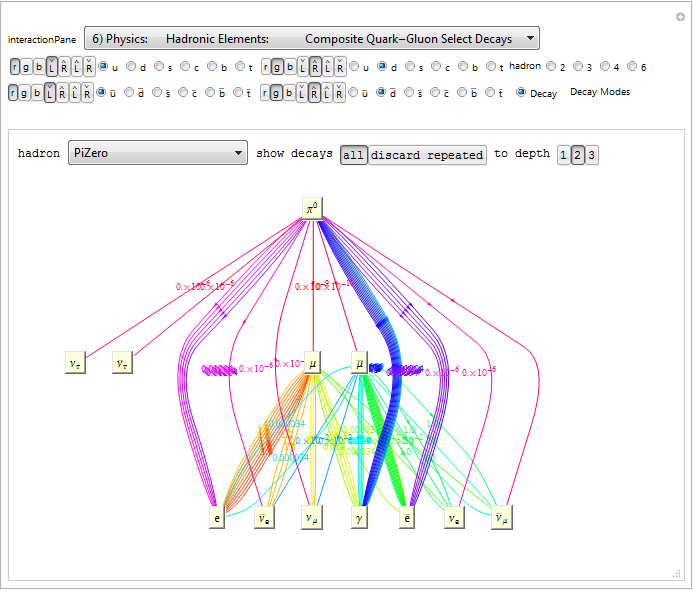
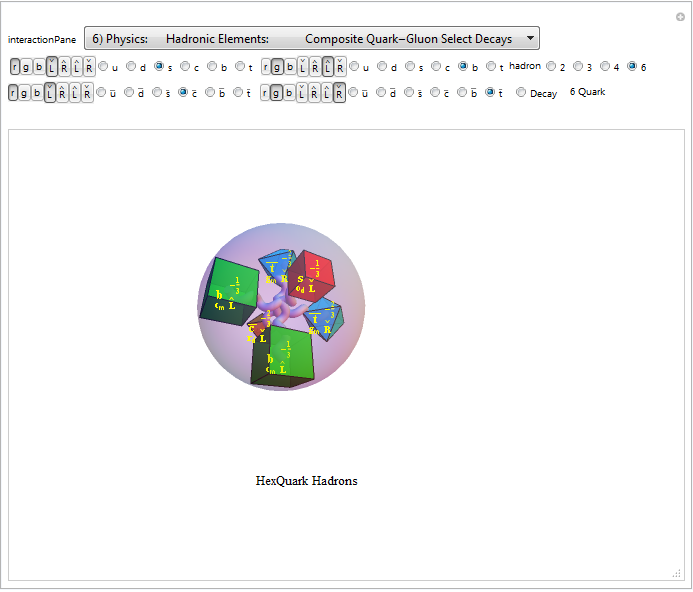
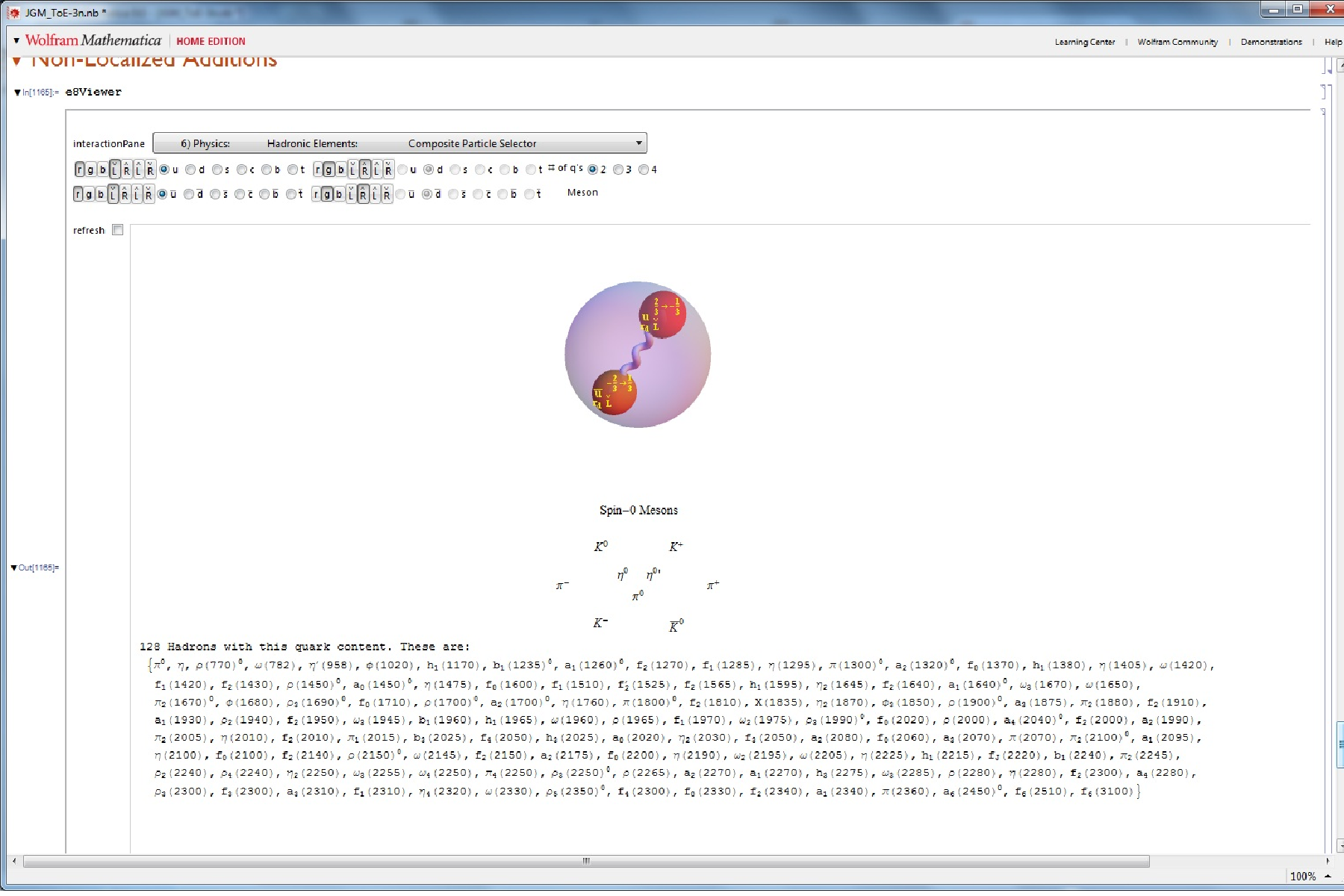
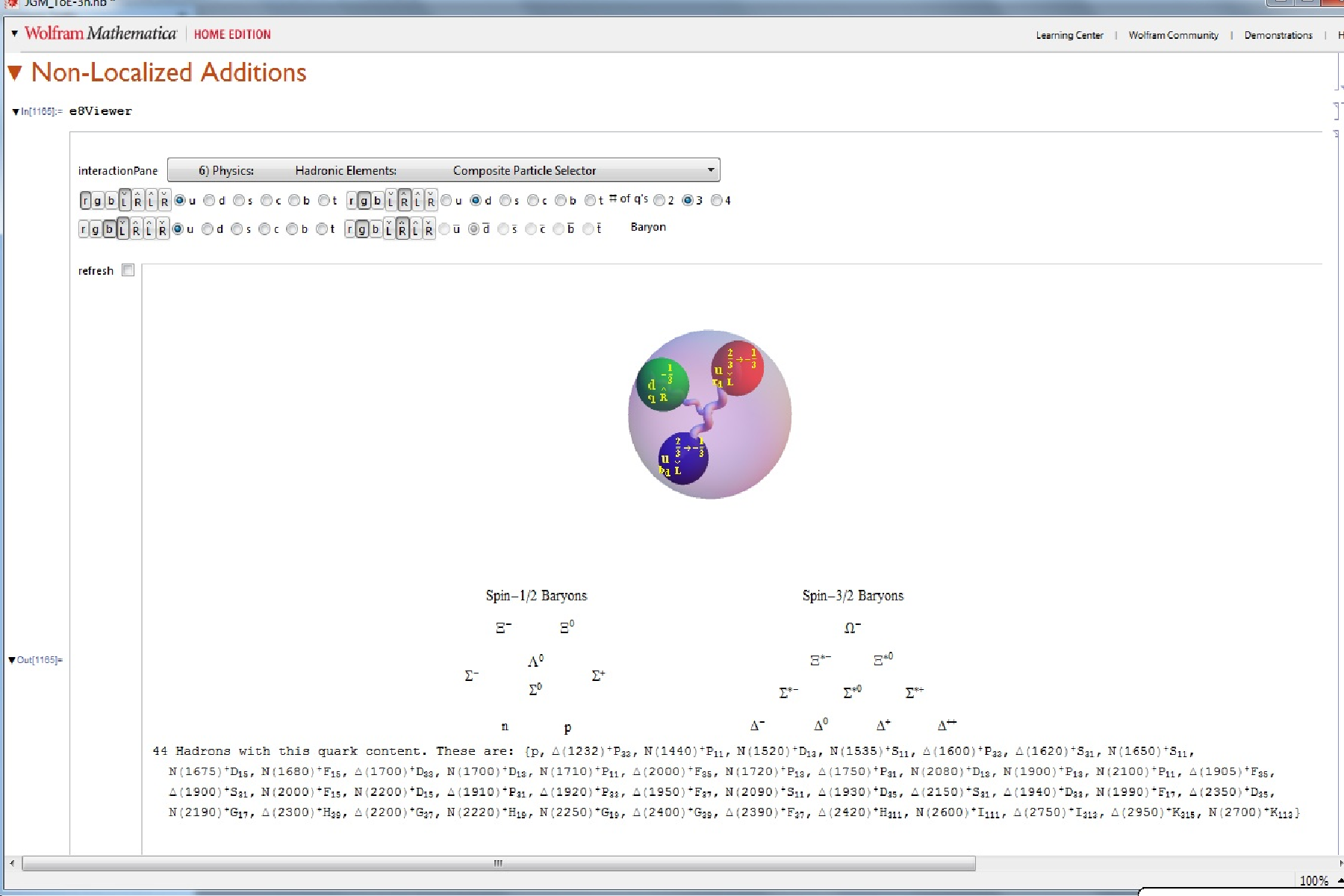
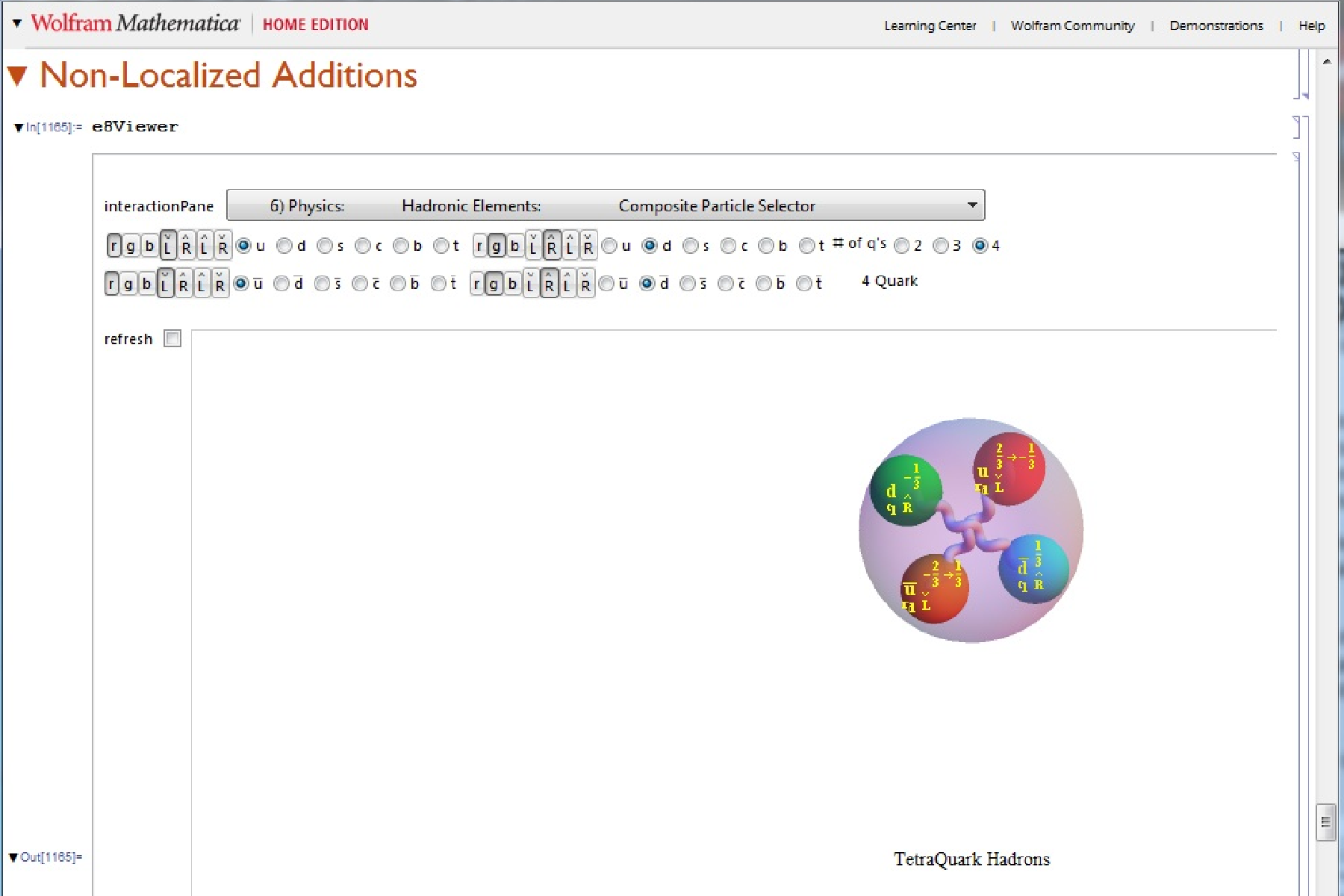
This weekend I integrated a fantastic demonstration by Zeleny which allows the visualization of the composite Quark particle decays. I’ve integrated it into the sixth (Hadron) pane which starts with Blinder’s demonstration to visualize the composite Quark-Gluon particles. These demonstrations are extended by allowing the selection of 2 Quark Mesons, 3 Quark Baryons and recently discovered 4 and 6 Quark Hadrons and also drives content of the E8 sub group projection pane (#3). I also added a query to show all experimentally discovered composite Meson/Baryon particles with the same quark content and added a decay mode button when decays are in Wolfram’s ParticleData Group curated data set.
Tag Archives: Physics
An improved 4D Periodic Table arranged by quantum numbers
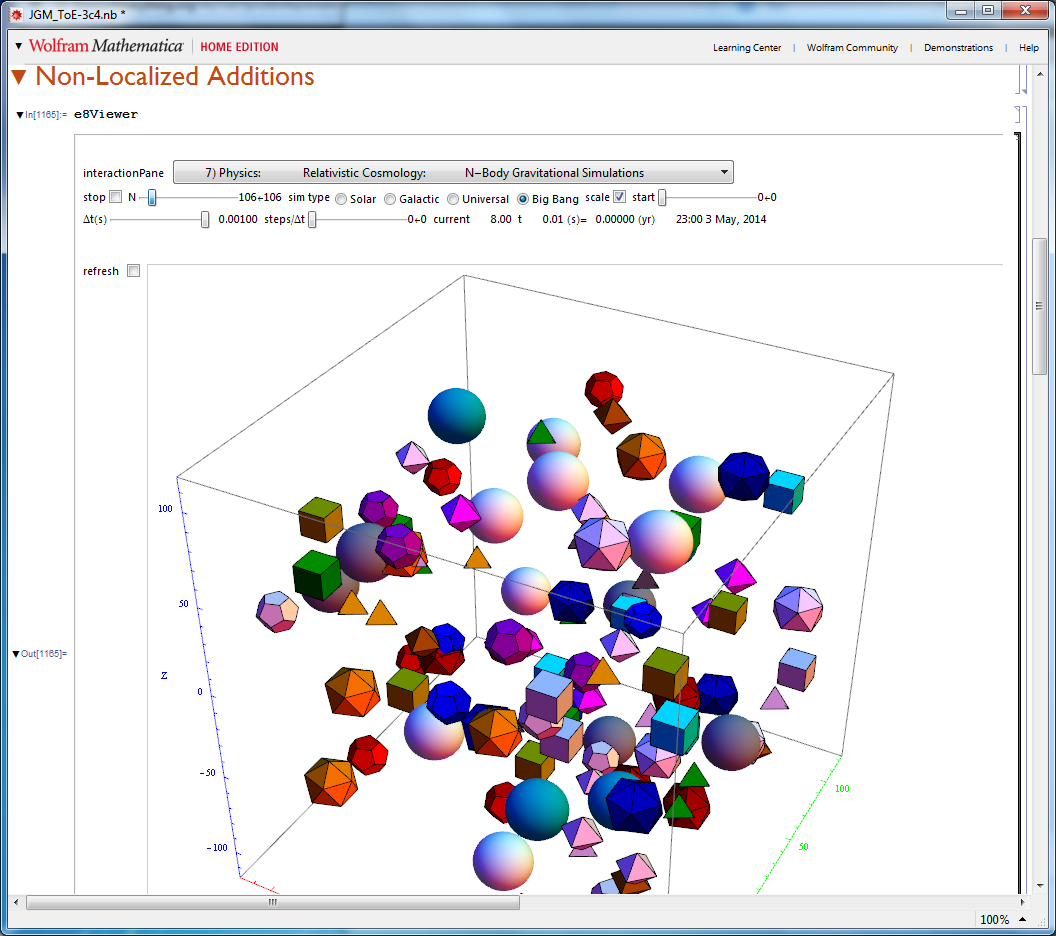
I've added an N-Body Gravitational Simulation Pane and enhanced the Composite Quark Hadron Model Pane
The N-Body Gravitational Simulation (not yet complete) uses Mathematica’s OpenCL GPU computing capability to simulate standard (Solar System), GR (Black Hole Centered Galaxy formation), Large Scale Universal Structure, and Quantum GR (Big Bang Inflationary) physics.
I’ve consolidated the Meson/Baryon panes into a single Hadron pane that now includes the formation of the recently validated TetraQuark Hadrons.
Please see ToE_Demonstration.cdf or as an interactive web page) that takes you on an integrated visual journey from the abstract elements of hyper-dimensional geometry, algebra, particle and nuclear physics, and on to the atomic elements of chemistry. It requires the free Mathematica CDF plugin (25 Mb). ToE_Demonstration.nb is the same as CDF except it includes file I/O capability not available in the free CDF player. This requires a full Mathematica license (25 Mb).
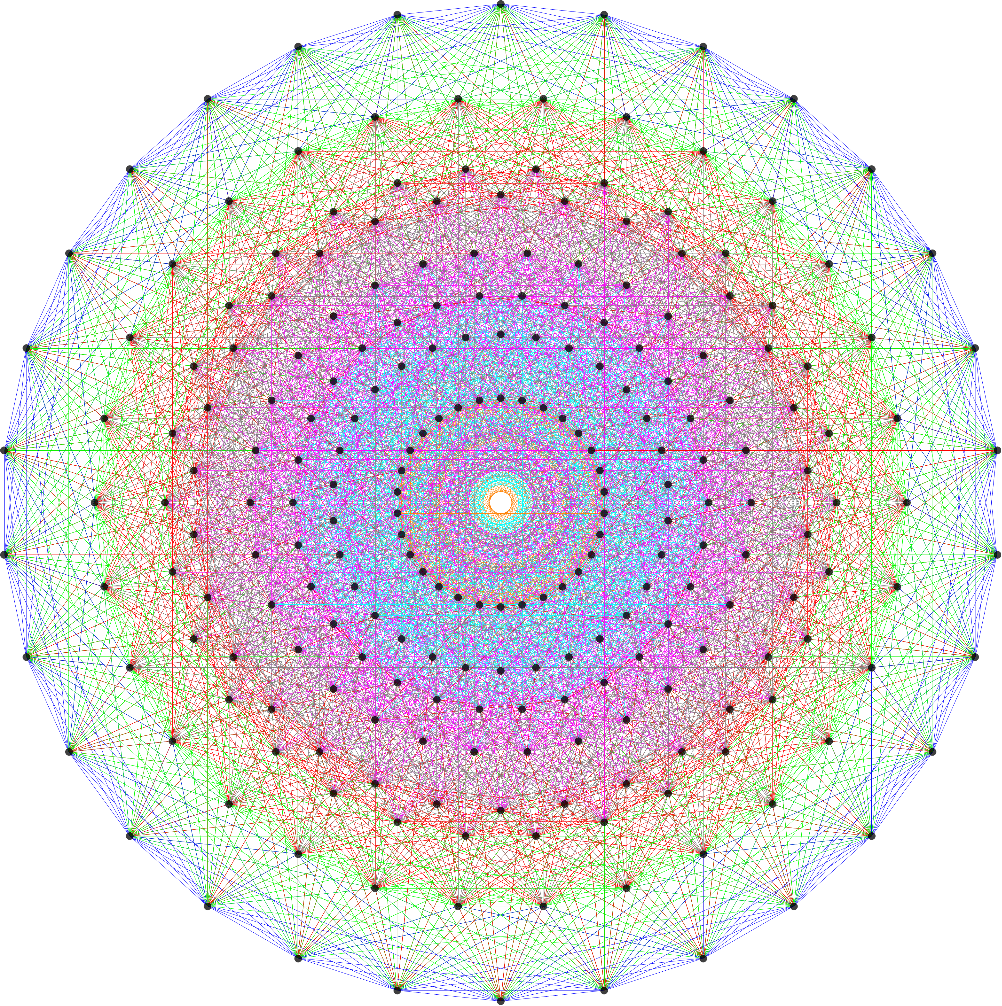
E8 projected
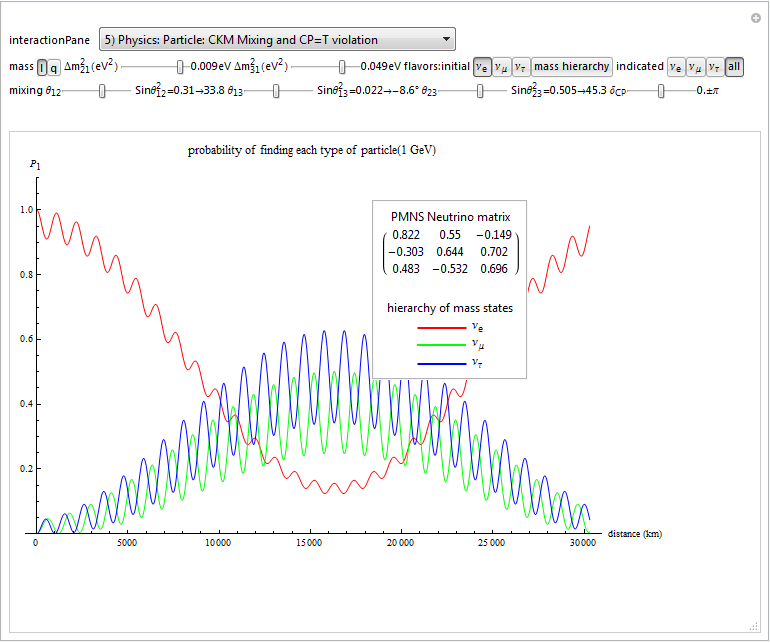
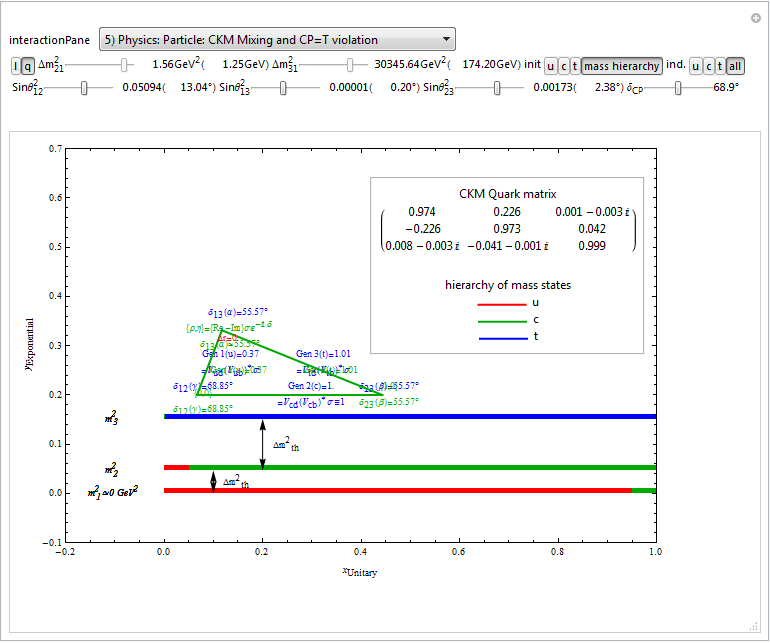
Added PMNS and CKM particle mixing matrix calculations to ToE_Demonstration.CDF
I’ve improved on a great Wolfram demonstration from Balázs Meszéna on Neutrino Oscillations by adding capabilities to view both the PMNS and CKM unitary triangle matrices, print and reference my ToE Neutrino mass predictions, which now accomodate the Koide relationships in particle masses.
Check out the new demonstrations using free interactive web plugin , .CDF, or .NB (for licensed Mathematica users) and social media integrations for comments, pages and posts.
This new pane (#5) presents the Unitarity of CP=T violations by combining the Lepton (Neutrino) Pontecorvo-Maki-Nakagawa-Sakata matrix (PMNS) with the Quark Cabibbo-Kobayashi-Maskawa (CKM) mixing matrix calculations through the Quark-Lepton Complementarity (QLC).
I am also working to incorporate the Koide particle mass relations to MyToE predictions.
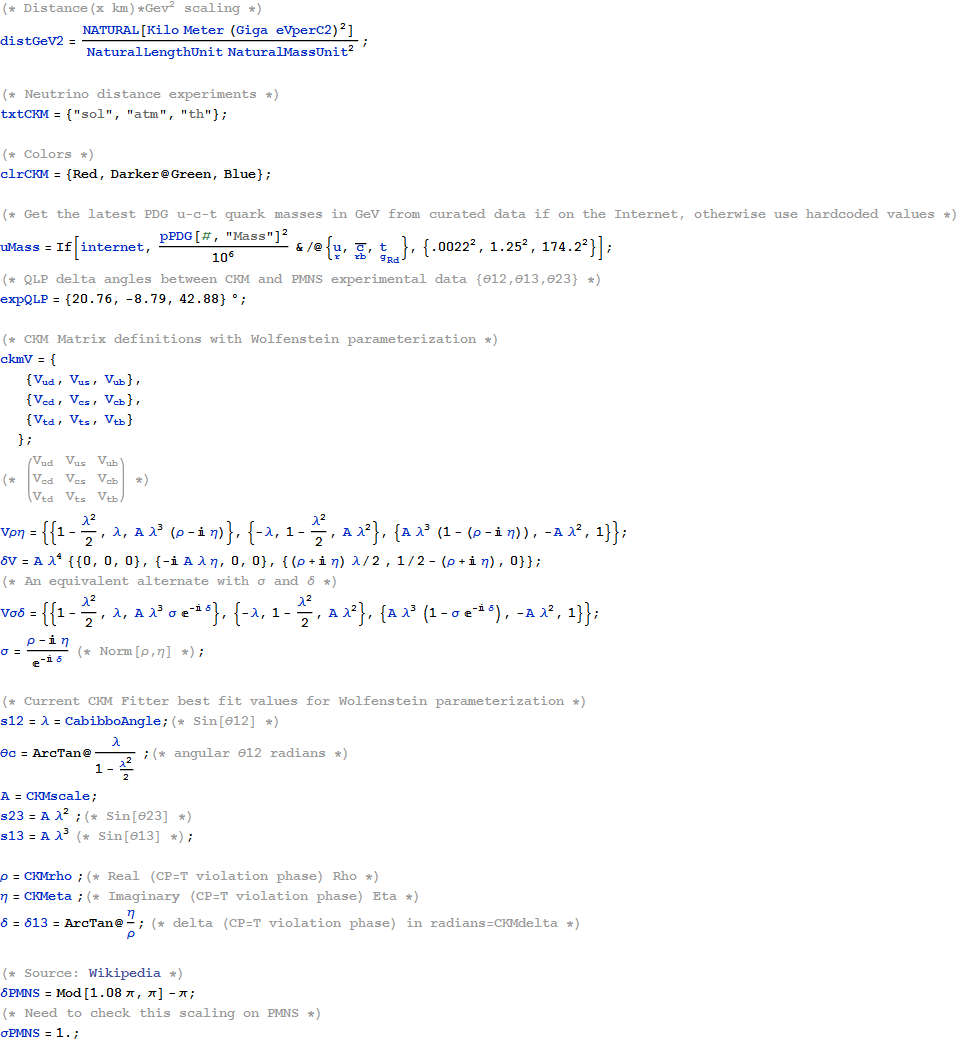
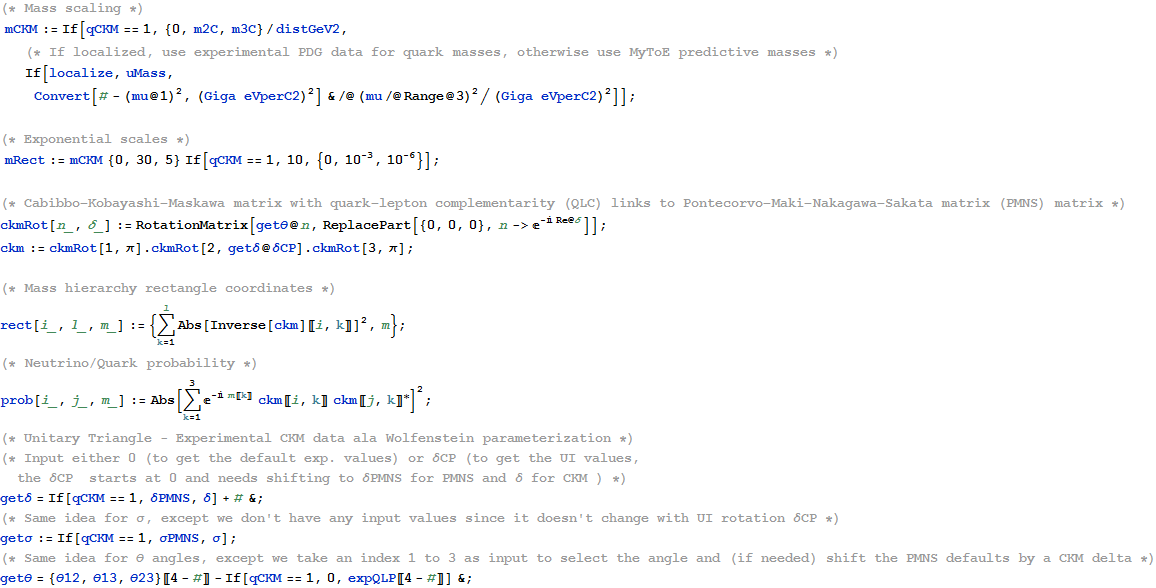
Code snippets showing the CKM and PMNS matrix calculations based on the UI.
New site and demonstration capability added!
Check out the new demonstrations using free interactive web plugin , .CDF, or .NB (for licensed Mathematica users) and social media integrations for comments, pages and posts.
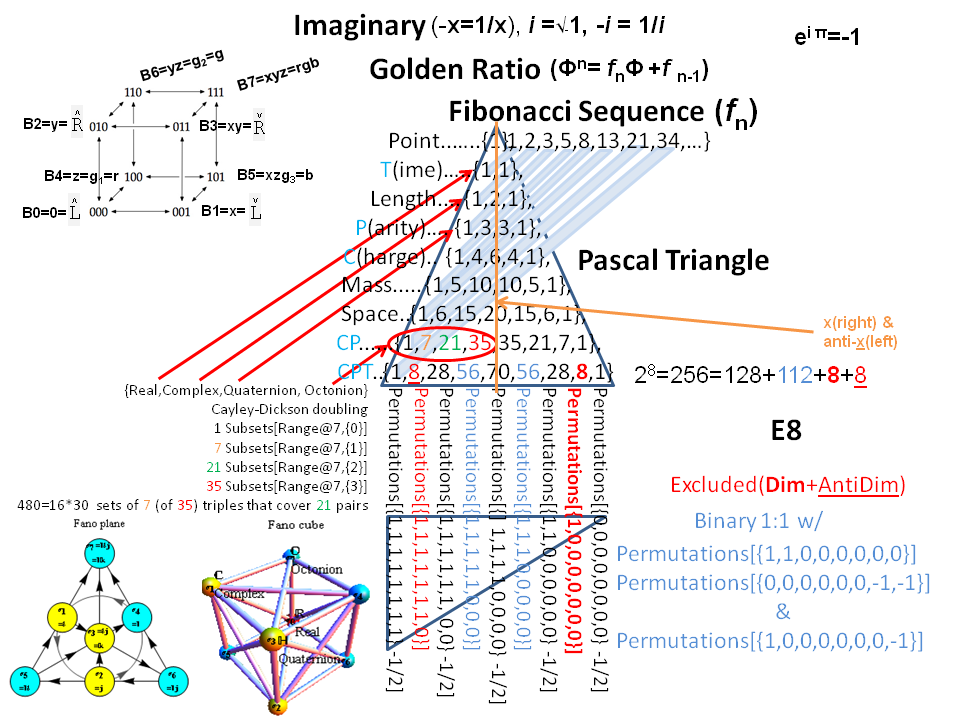
Another look at integrating the Pascal Triangle to Clifford Algebra, E8 Lie Algebra/Groups, Octonions and Particle Physics Standard Model
Modified Lisi split real even E8 particle assignment quantum bit patterns:
Assigning a specific mass, length, time, and charge metrics based on new dimensional relationships and the Planck constant (which defines Higgs mass).
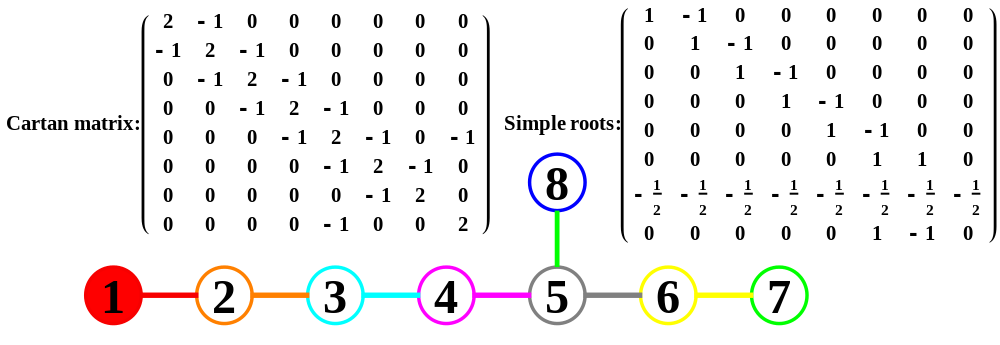
The split real even E8 group used has been determined from this simple root matrix (which gives the Cartan matrix upon dot product with a transpose of itself):
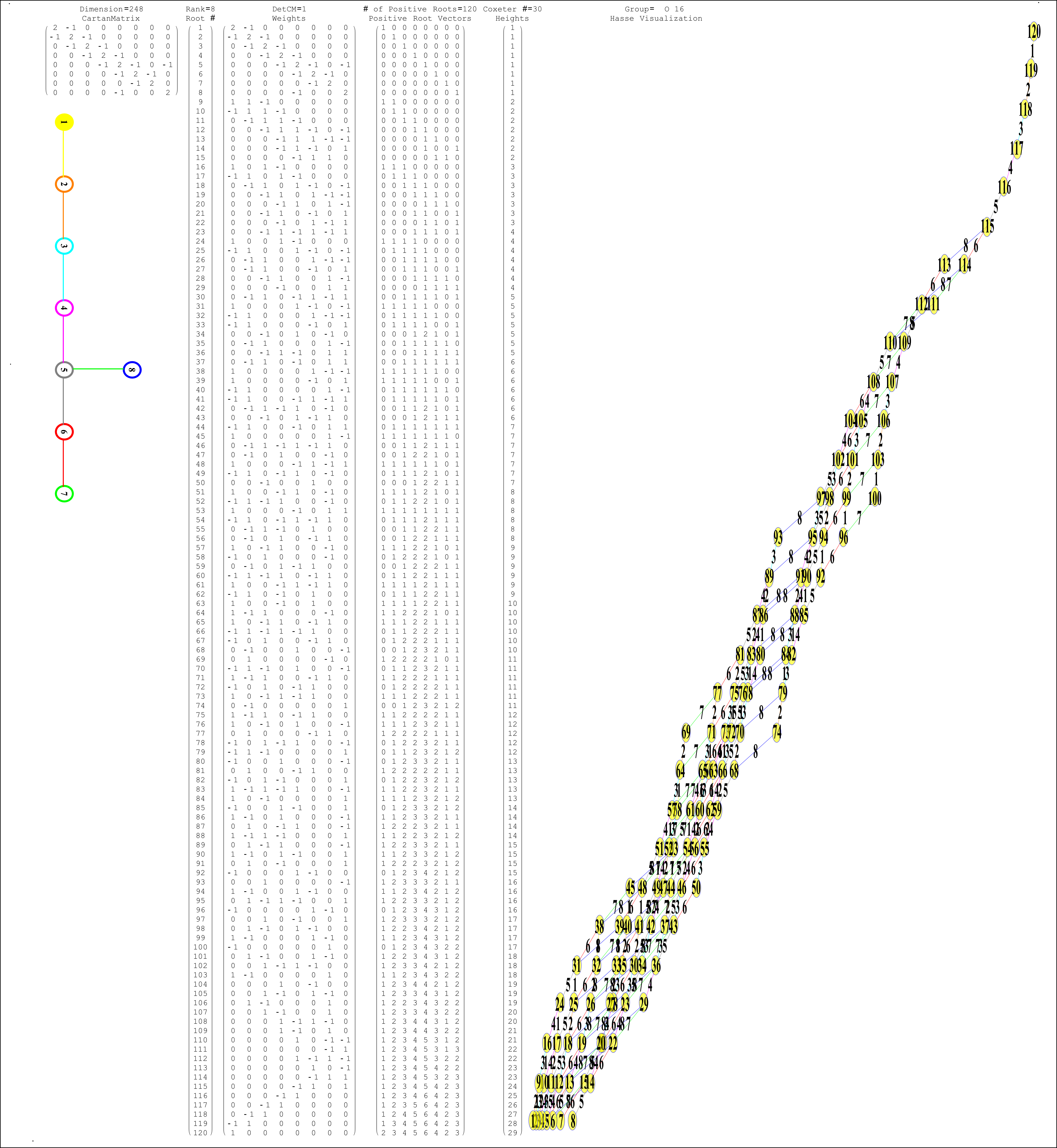
This Dynkin diagram builds the Cartan matrix and determines the root/weight/height with corresponding Hasse diagrams.
More amplituhedron capability (projected hull surface area and volume)
Getting more capability built into ToE_Demonstration.nb where it can now calculate the scattering amplitude by calculating the volume of the projected hull of selected edges in the n-Simplex Amplituhedron (based on a theory by Nima Arkani-Hamed, with some Mathematica code from J. Bourjaily for the positroid diagram). Of course, there is still much work to get this wrapped up…
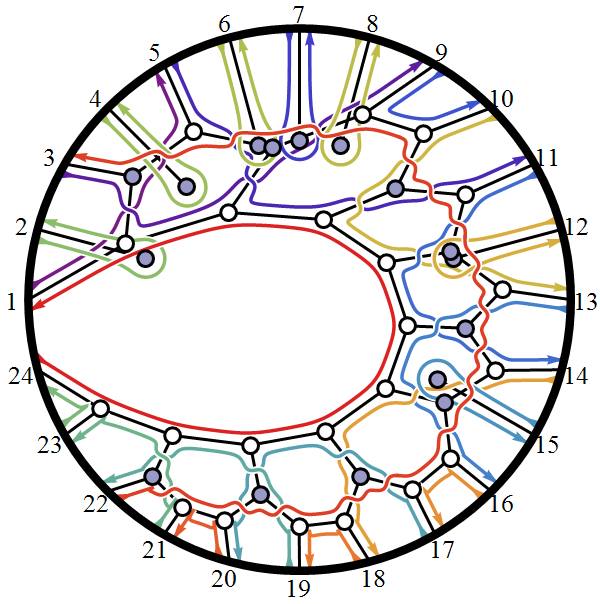
A few more pics of Positive Grassmannian Amplituhedrons…
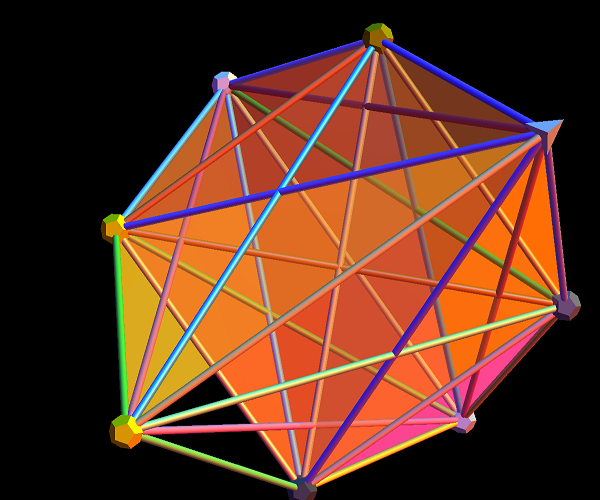
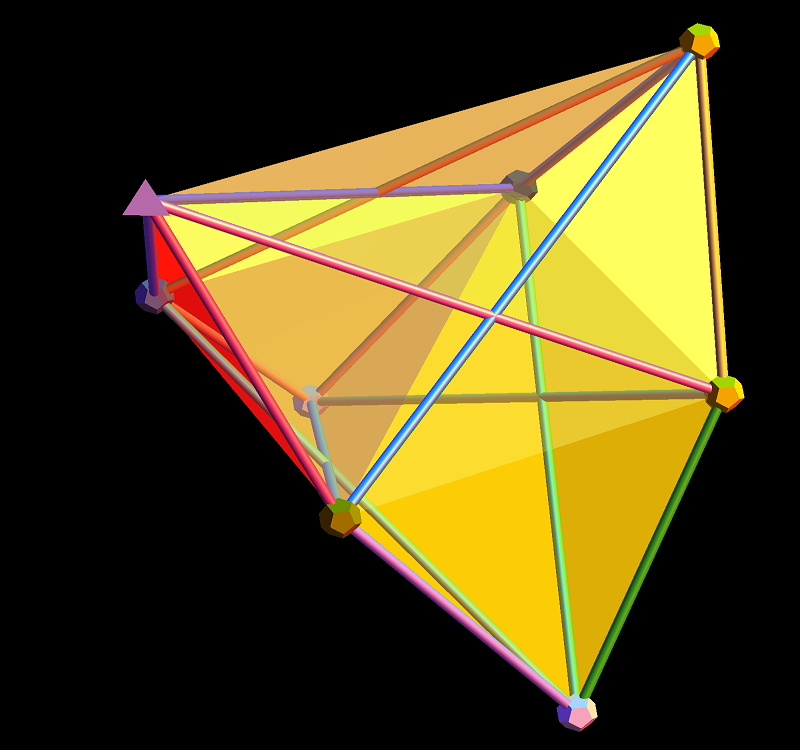
This last diagram is obtained using the following amplituhedron0.m as input to the ToE_Demonstration.nb (when using fully licensed Mathematica) as shown below:
* This is an auto generated list from ToE_Demonstration.nb *)
new := {
artPrint=True;
scale=0.1;
cylR=0.018;
range=2.;
pt={-0.3, 0.0, 0.6};
favorite=1;
showAxes=False;
showEdges=True;
showPolySurfaces=True;
eColorPos=False;
dimTrim=5;
ds=6;
pListName=”First8″;
dsName=”nSimplex”;
p3D=” 3D”;
edgeVals={{Sqrt[11/2], 8}, {Sqrt[9/2 – Sqrt[2]], 4}, {Sqrt[9/2 + Sqrt[2]], 4}};
};new;
Amplituhedron Visualizations!
Playing around trying to visualize the latest in the theoretical high energy particle physics (HEP/TH) determining how particle masses might be predicted from geometric principles (based on a theory by Nima Arkani-Hamed, with some Mathematica code from J. Bourjaily for the positroid diagram).
Positive Grassmannian Amplituhedrons
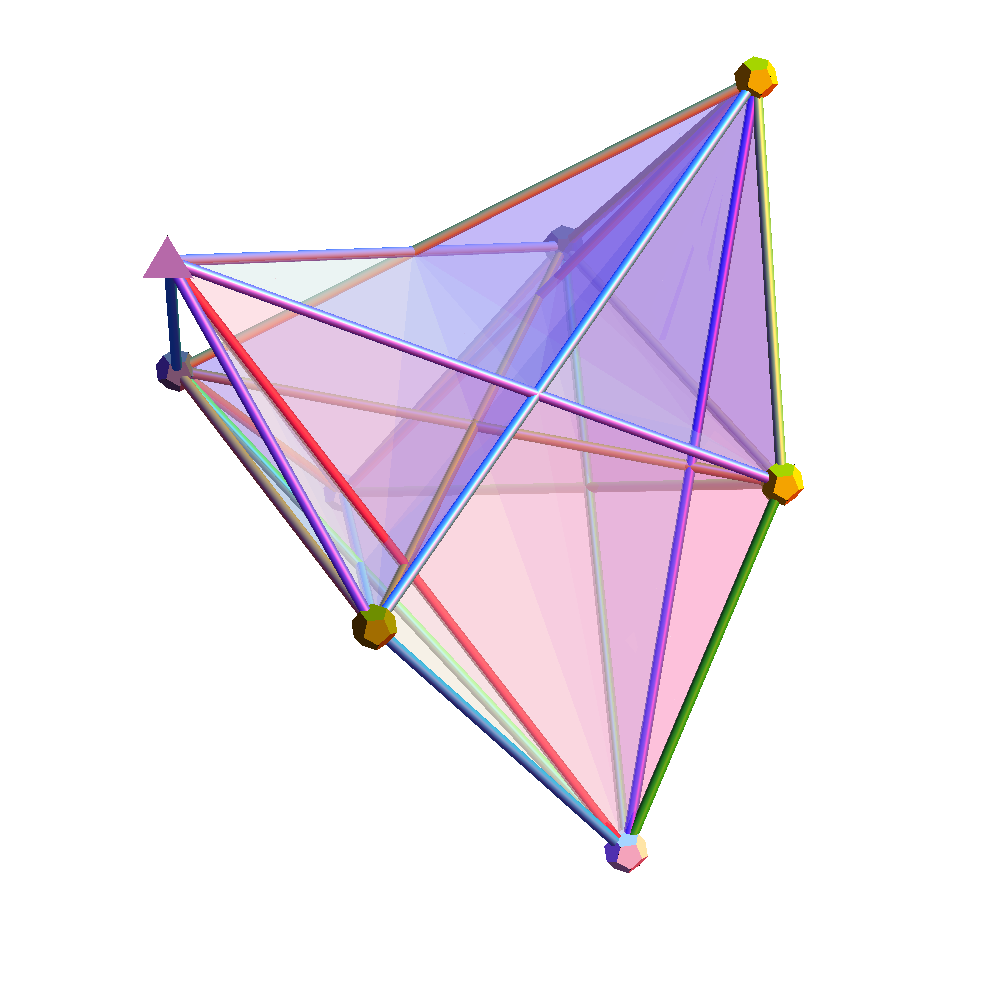
Compare this Mathematica(l) basis to the artistic representation by Andy Gilmore 
Updated demonstrations now include split octonions
I’ve updated the .NB, .CDF and interactive demonstrations to include the ability to visualize the split octonions.