CMS closes major chapter of Higgs measurements
http://cms.web.cern.ch/news/cms-closes-major-chapter-higgs-measurements
Glad to see the more accurate CMS (as well as ATLAS’) Higgs mass homing in on my prediction of 124.443…GeV/c^2 (see http://theoryofeverything.org/TOE/JGM/ToEsummary.pdf).
Can’t wait for more data next year. Of course, validation that the theoretical model works as expected is as important as the experimental verification.
I’ve added an interactive (Chaos) pane (#7). It is taken from Zeleny’s Five Mode Truncation Of The Navier-Stokes Equations. It now includes 2D and 3D visualizations of these equations. This will be a basis for study of a superfluid space-time theory to merge GR with QM.
This weekend I integrated a fantastic demonstration by Zeleny which allows the visualization of the composite Quark particle decays. I’ve integrated it into the sixth (Hadron) pane which starts with Blinder’s demonstration to visualize the composite Quark-Gluon particles. These demonstrations are extended by allowing the selection of 2 Quark Mesons, 3 Quark Baryons and recently discovered 4 and 6 Quark Hadrons and also drives content of the E8 sub group projection pane (#3). I also added a query to show all experimentally discovered composite Meson/Baryon particles with the same quark content and added a decay mode button when decays are in Wolfram’s ParticleData Group curated data set.
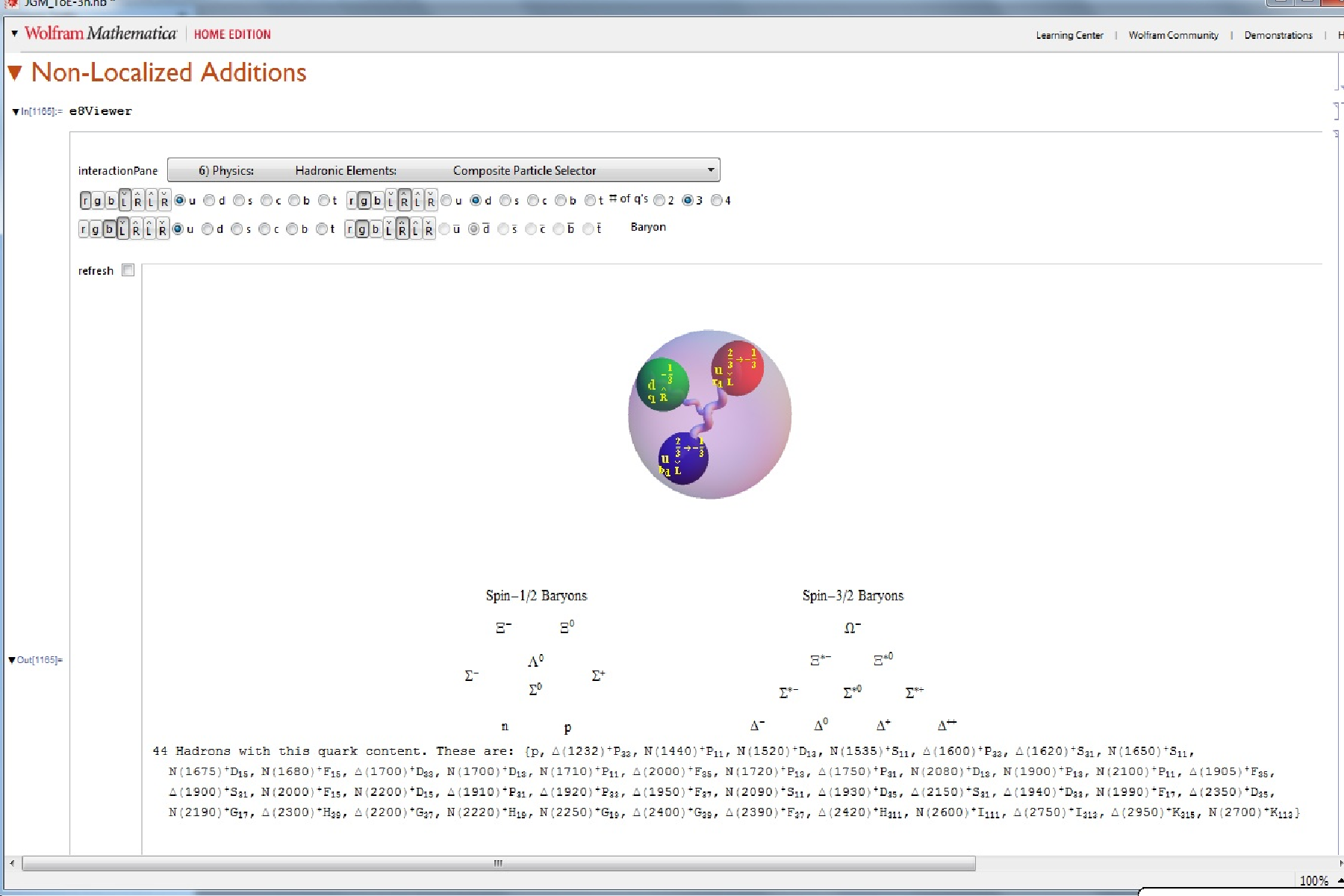
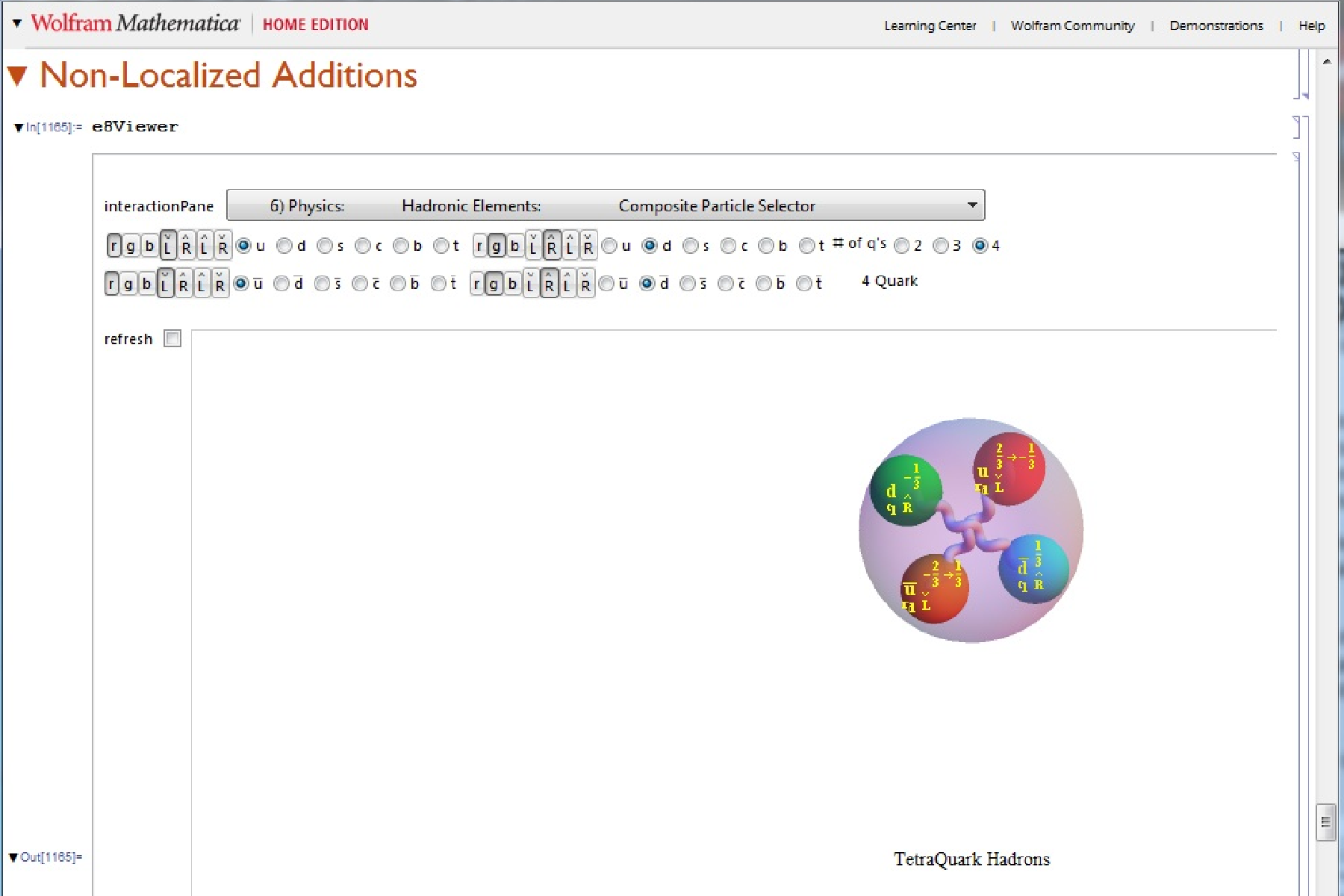
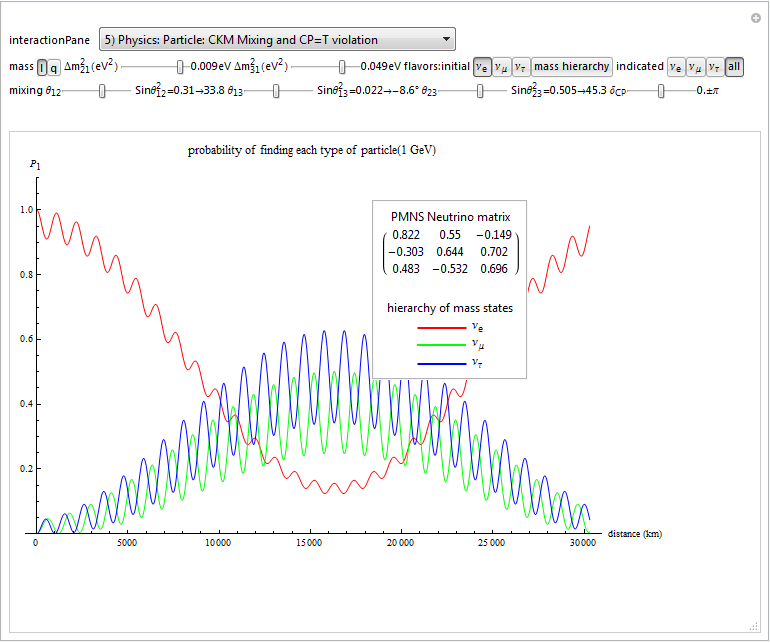
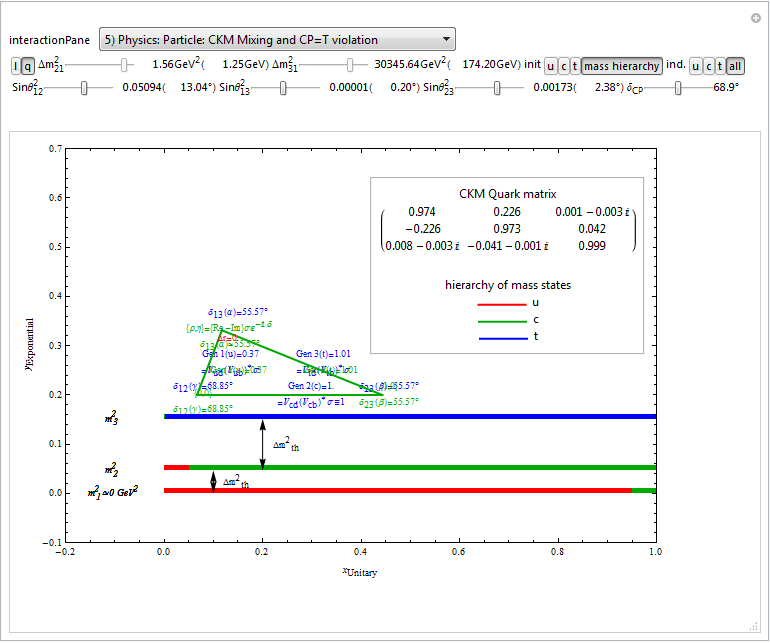
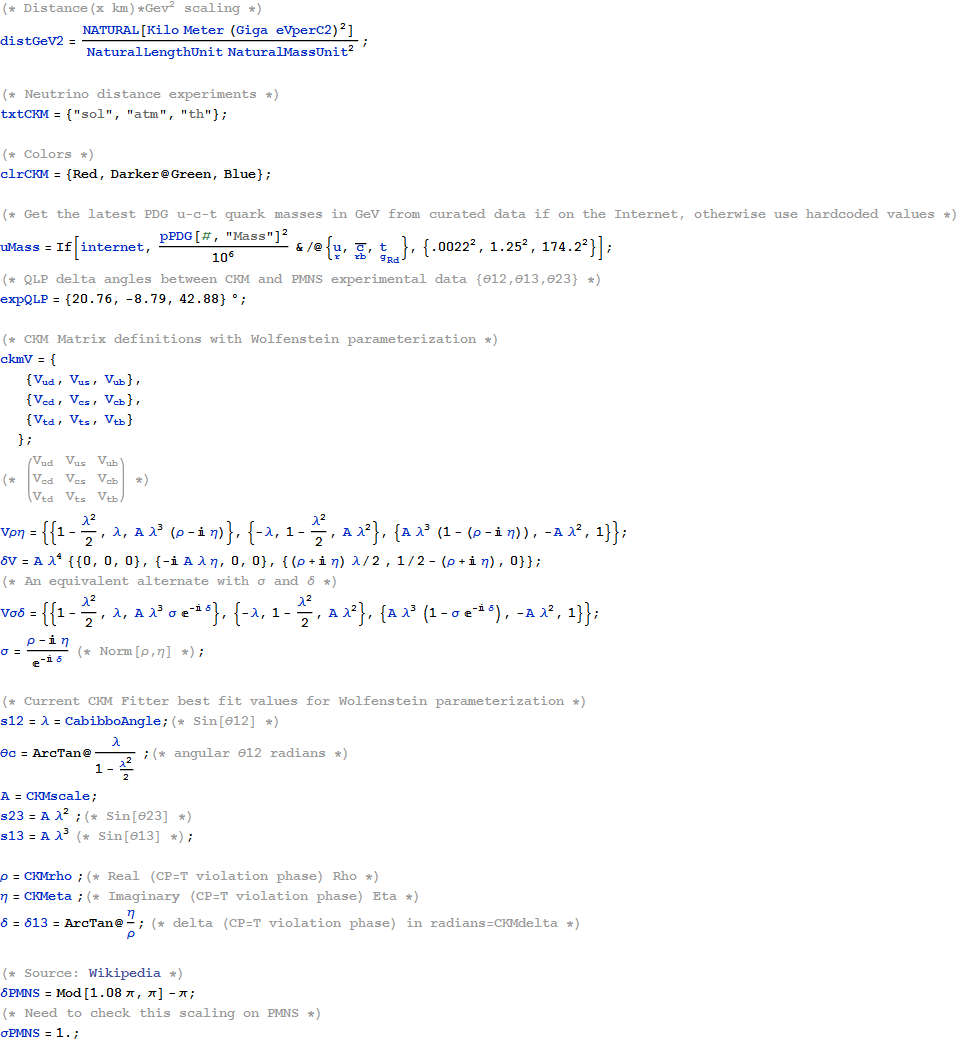
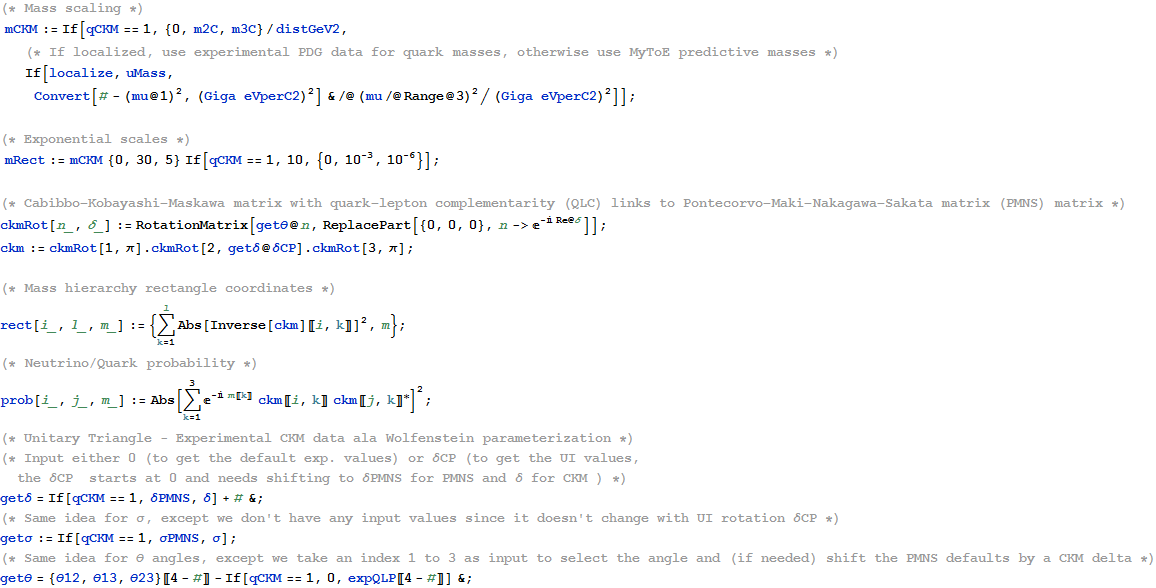
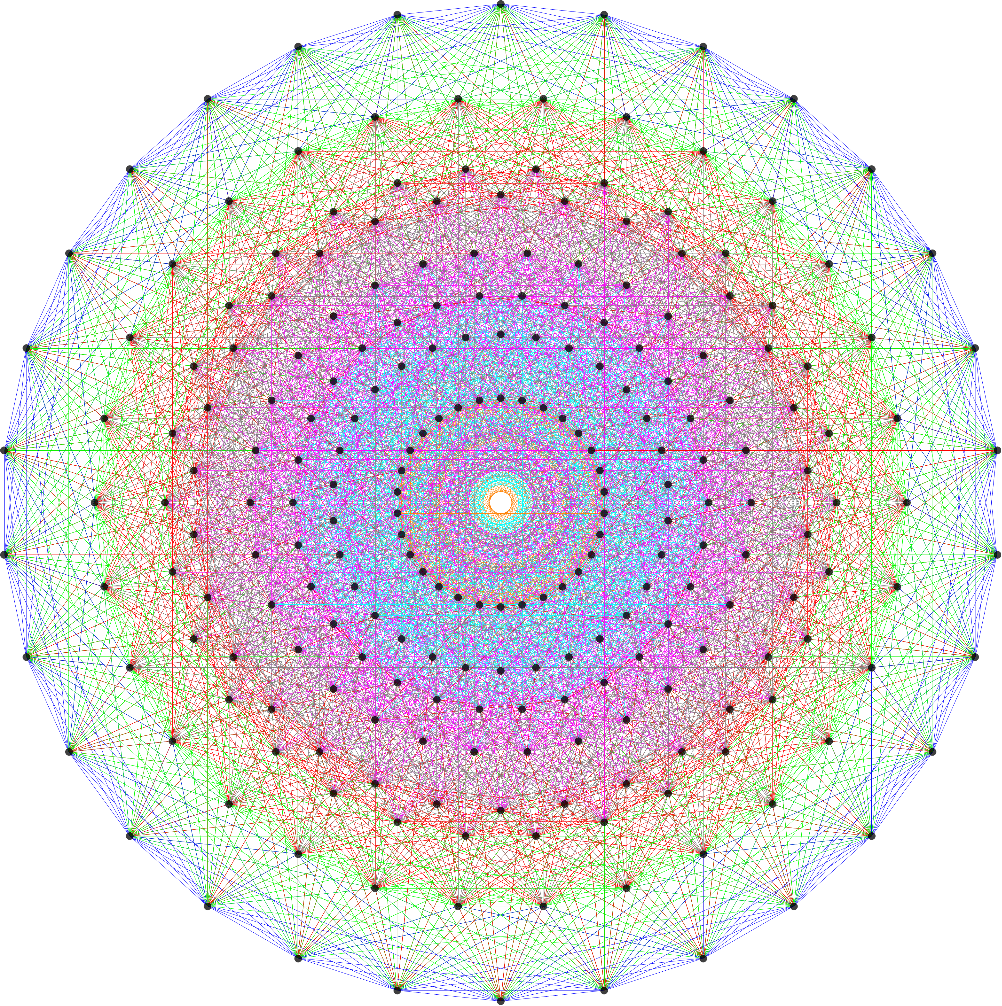
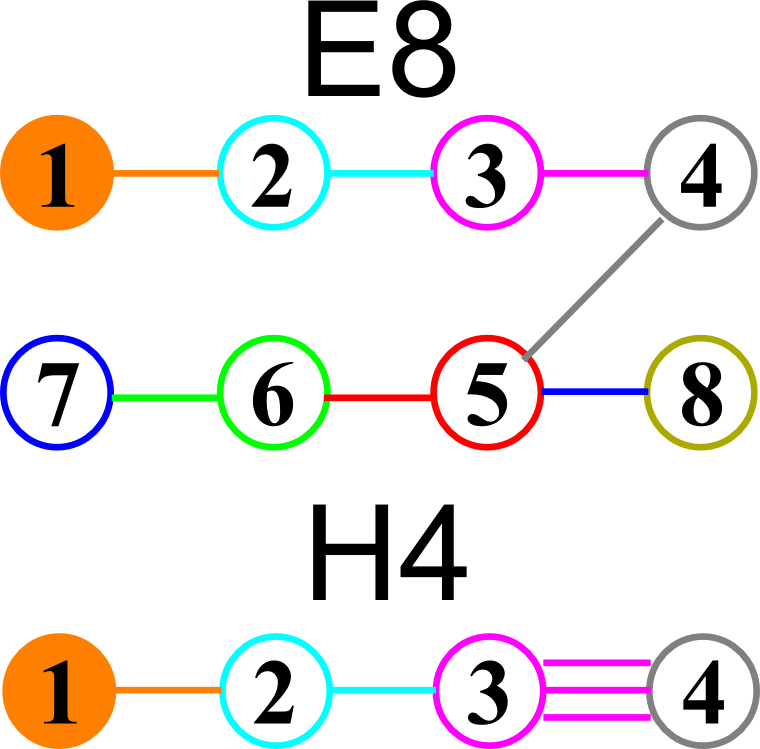
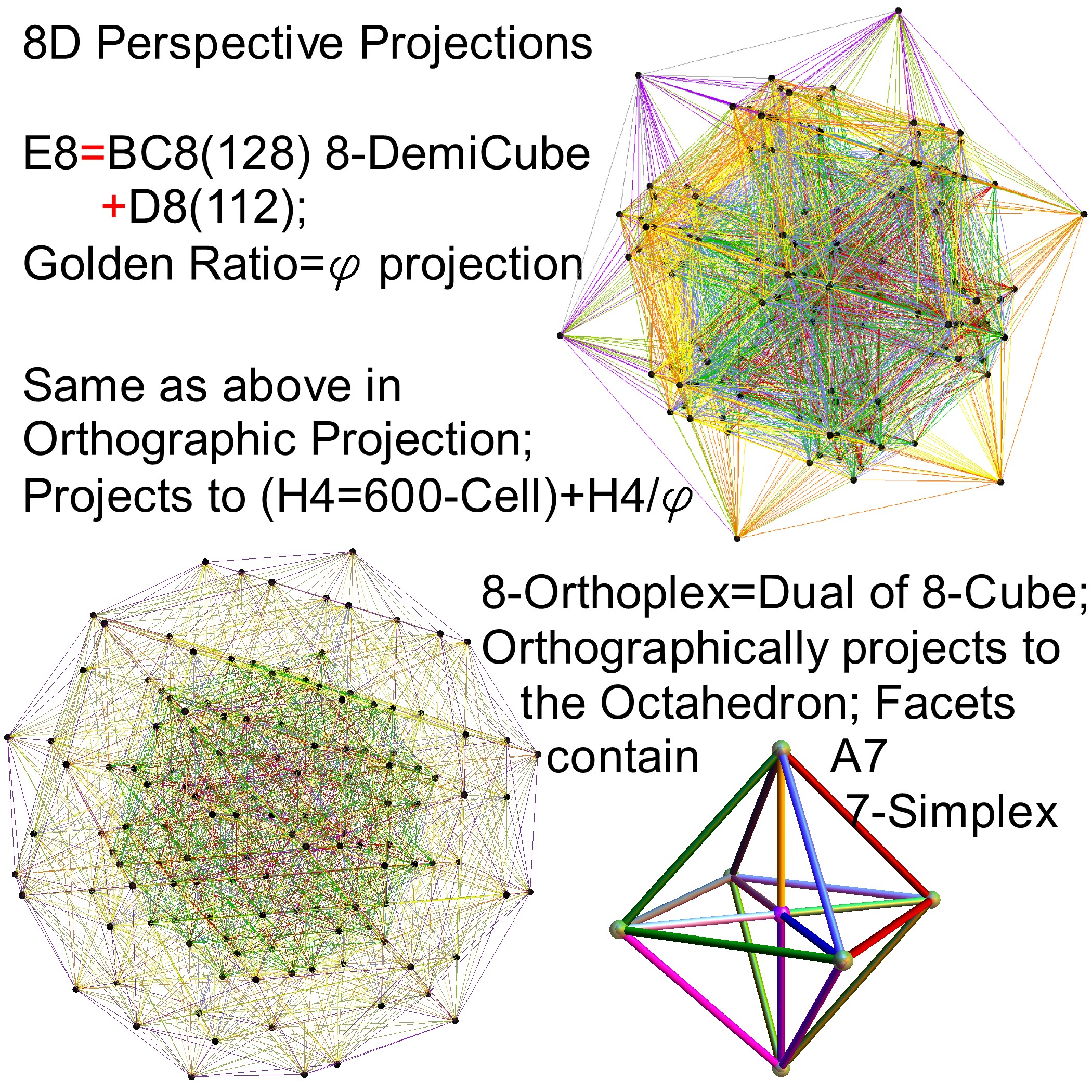
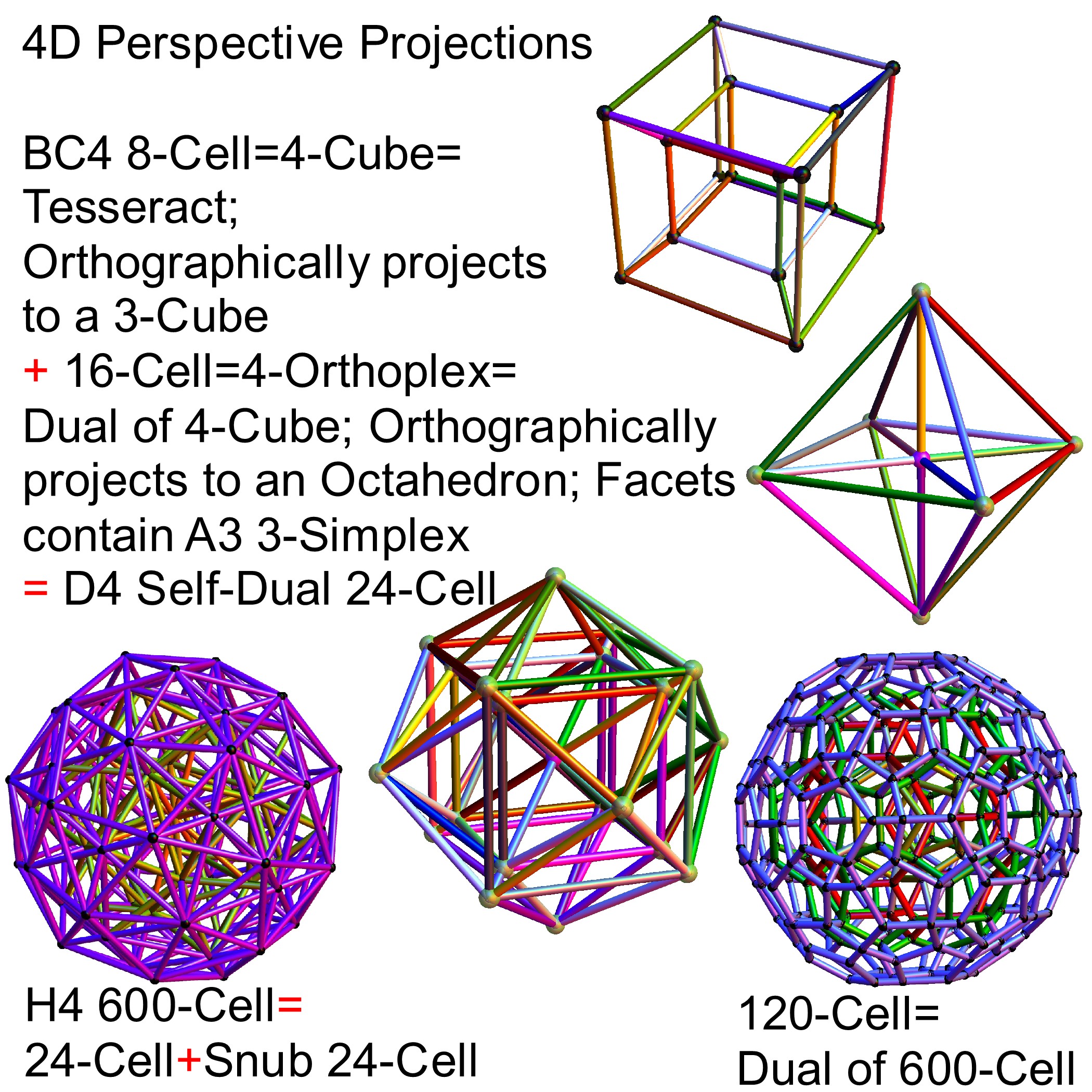
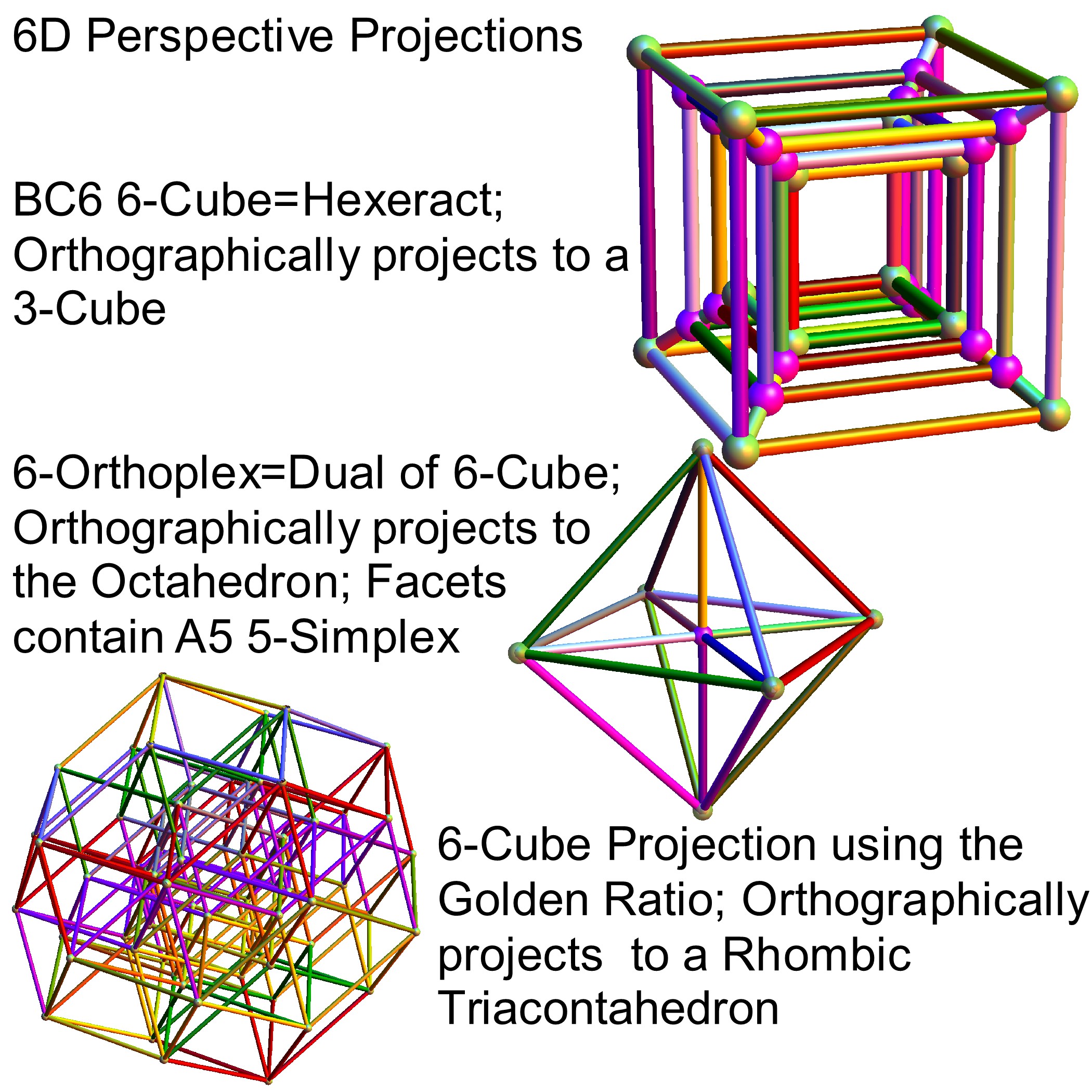
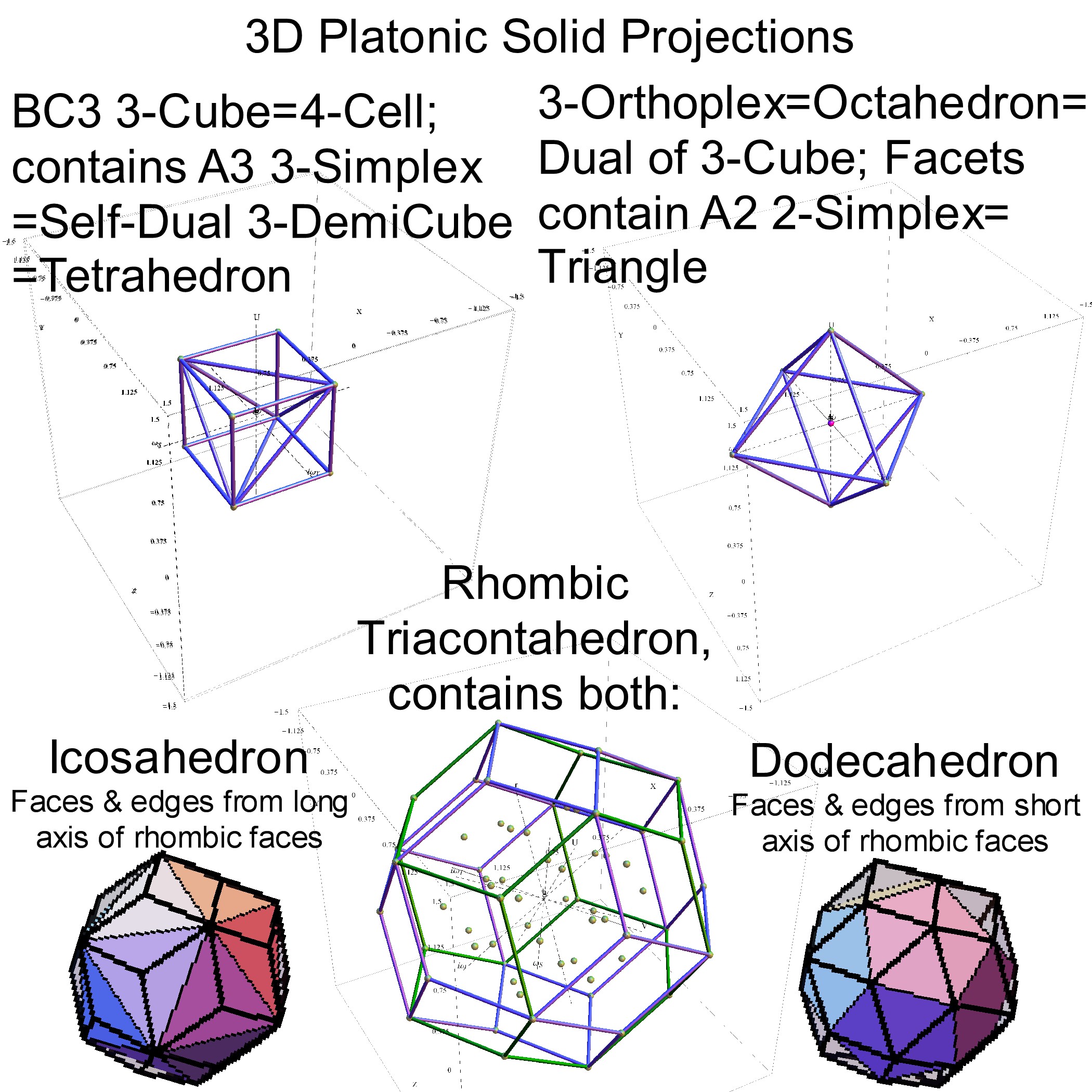
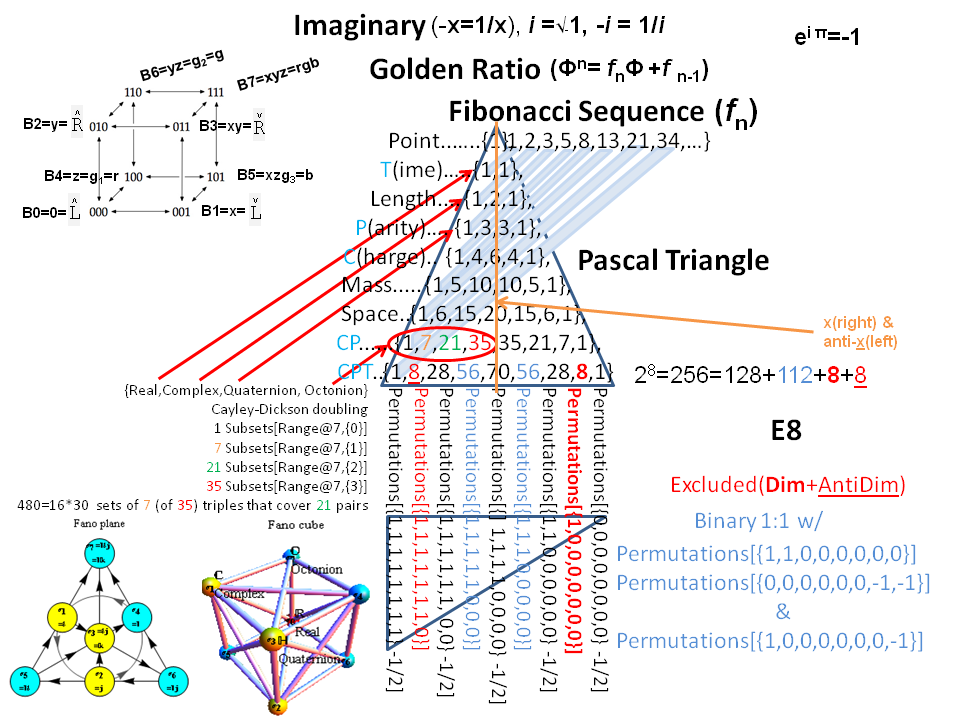
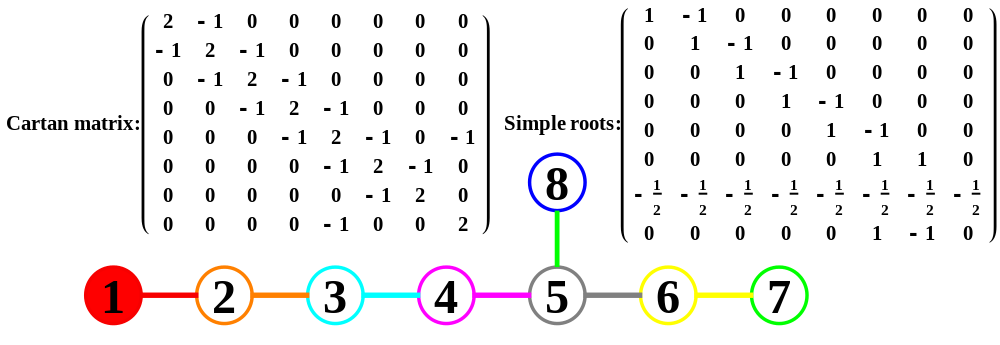
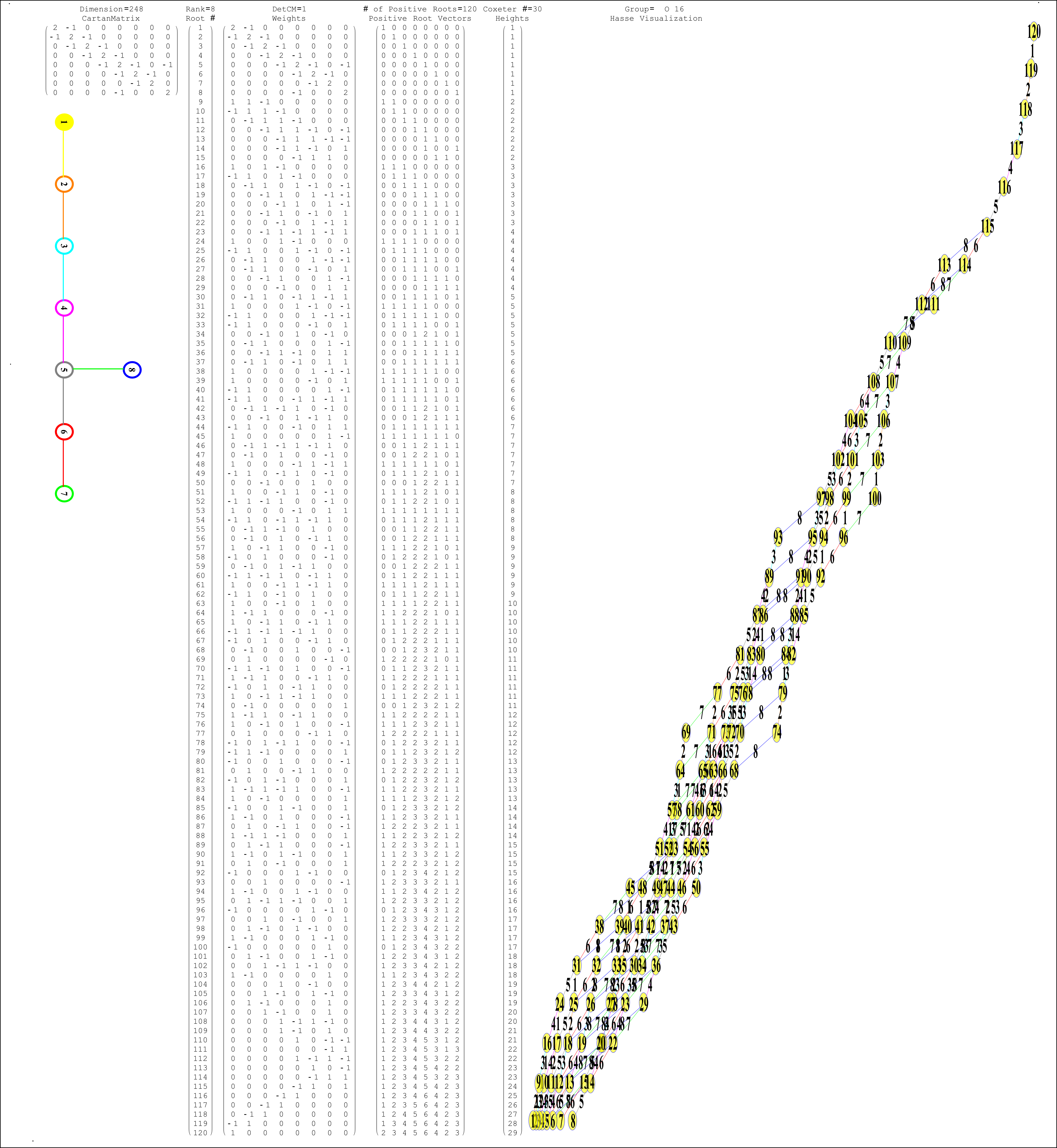
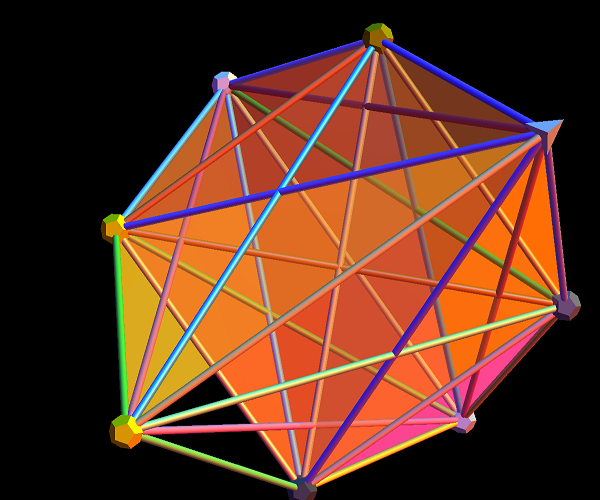
I cleaned up some of the N-Body physics screens, and created a few animation sequences showing the simulation runs available (if you have Mathematica and source code (available upon request and appropriate use-case)).
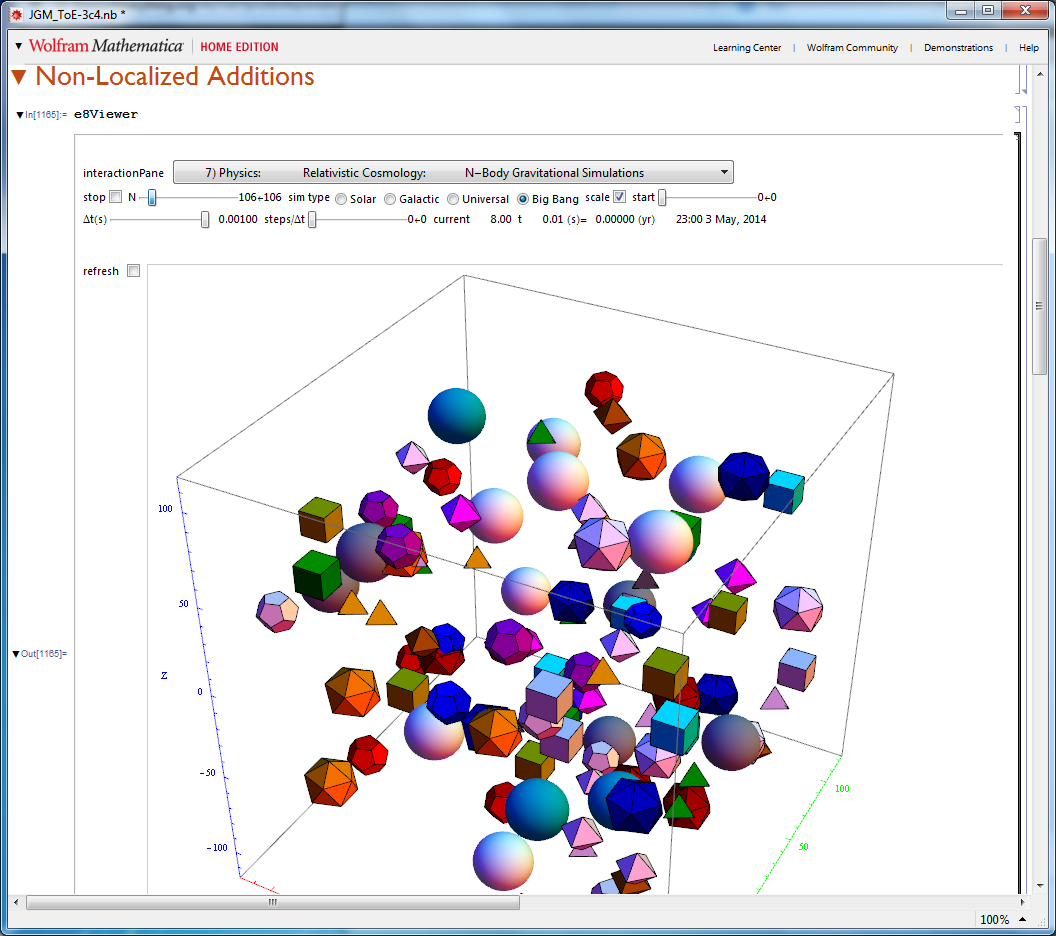
This is a video of a preliminary Galaxy formation in N-Body gravitational physics.
This is a video of the solar system (not yet using the OpenCL N-Body code for GPU parallelism).
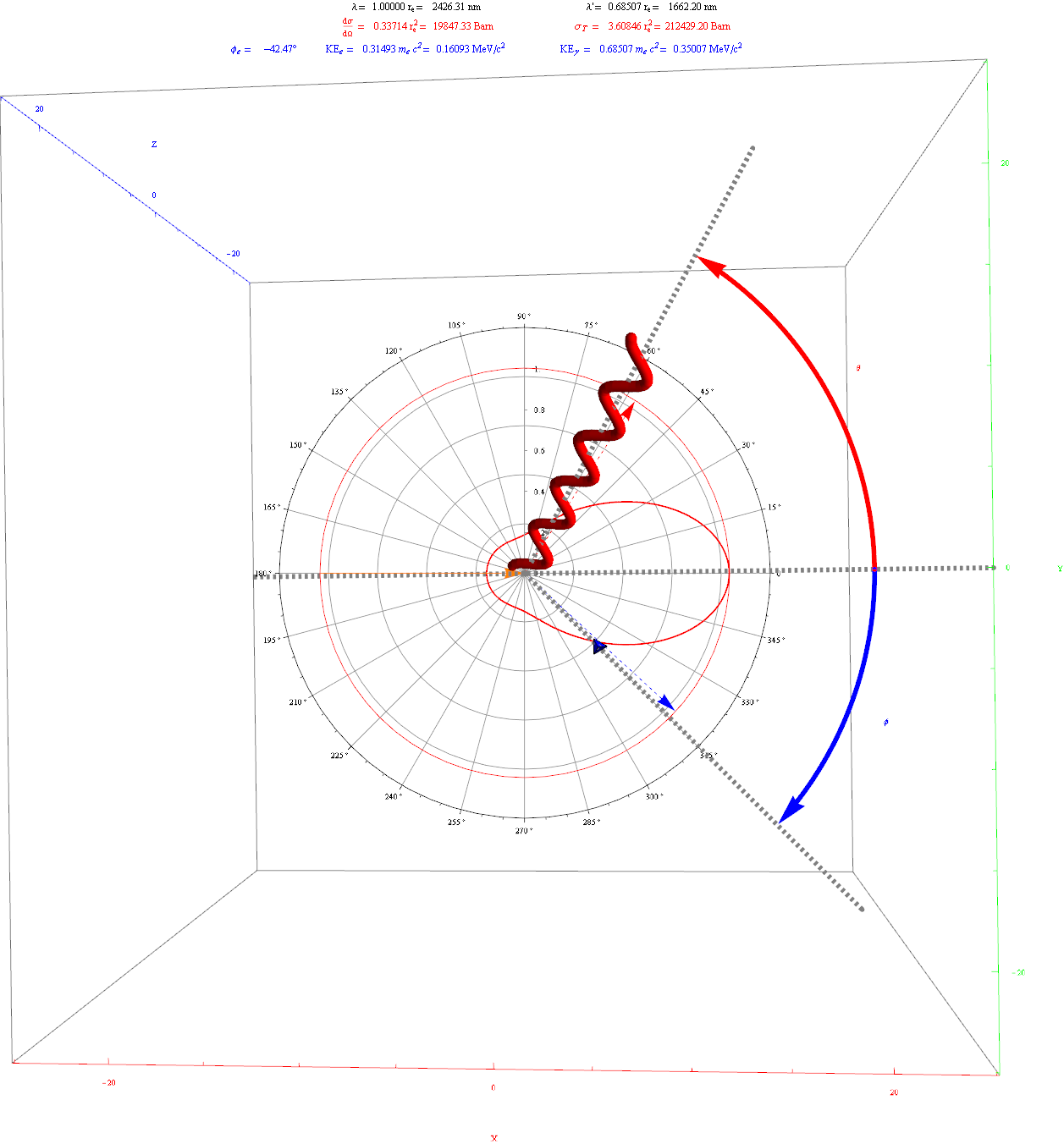
This is a video of the Compton Effect in 3D, which I plan on using to show how Big Bang Inflationary Quantum effects are explained.
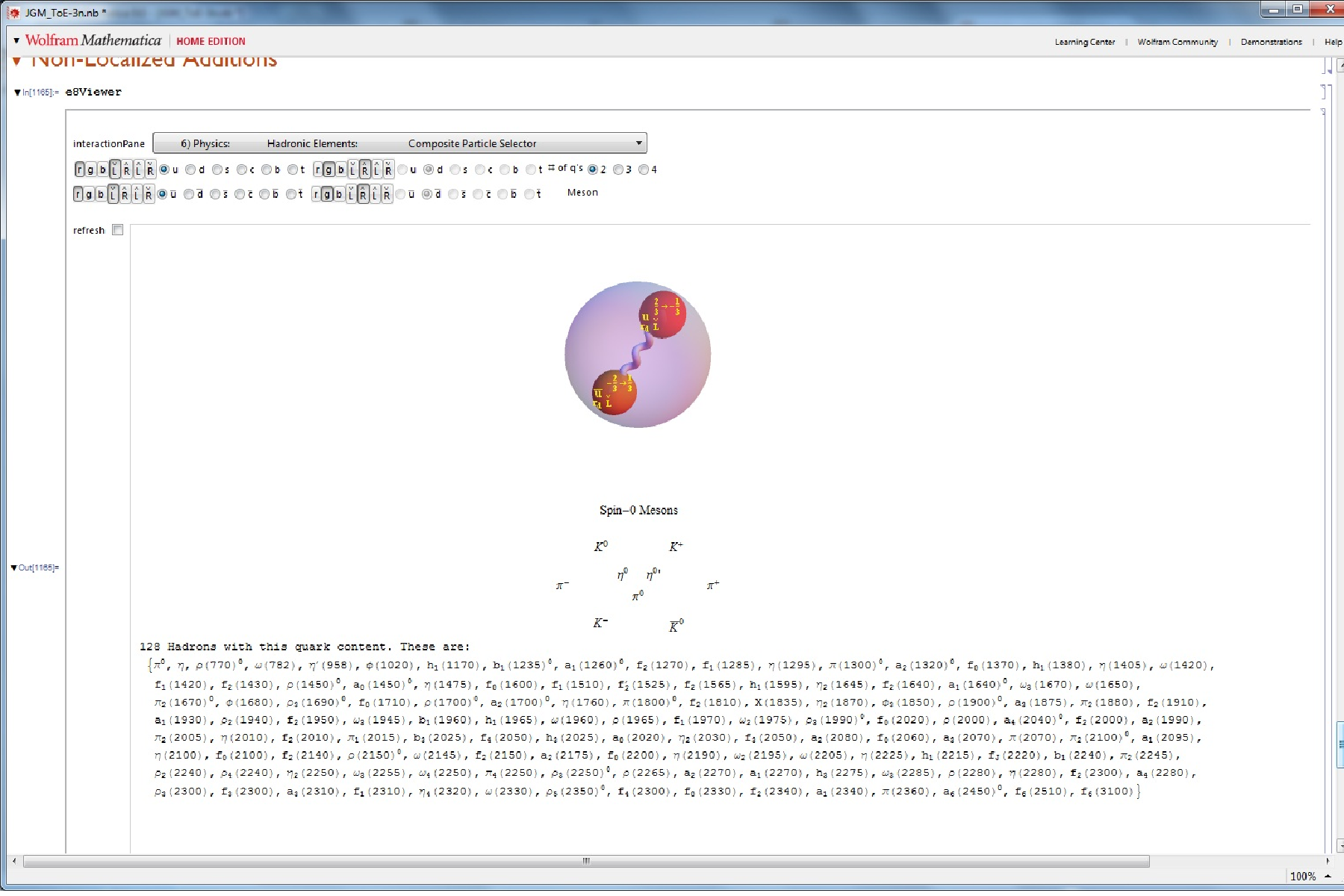
I’ve also improved the capabilities of the other demonstrations.
This has color coded 3D cut-away views of the spherical Schroedinger electron probability densities (making it 4D with 3D objects). The color is based on the l (angular momentum) quantum number. The X-Y-Z position is based n,m,s(pin) quantum numbers.
The N-Body Gravitational Simulation (not yet complete) uses Mathematica’s OpenCL GPU computing capability to simulate standard (Solar System), GR (Black Hole Centered Galaxy formation), Large Scale Universal Structure, and Quantum GR (Big Bang Inflationary) physics.
I’ve consolidated the Meson/Baryon panes into a single Hadron pane that now includes the formation of the recently validated TetraQuark Hadrons.
Please see ToE_Demonstration.cdf or as an interactive web page) that takes you on an integrated visual journey from the abstract elements of hyper-dimensional geometry, algebra, particle and nuclear physics, and on to the atomic elements of chemistry. It requires the free Mathematica CDF plugin (25 Mb). ToE_Demonstration.nb is the same as CDF except it includes file I/O capability not available in the free CDF player. This requires a full Mathematica license (25 Mb).
I’ve improved on a great Wolfram demonstration from Balázs Meszéna on Neutrino Oscillations by adding capabilities to view both the PMNS and CKM unitary triangle matrices, print and reference my ToE Neutrino mass predictions, which now accomodate the Koide relationships in particle masses.
Check out the new demonstrations using free interactive web plugin , .CDF, or .NB (for licensed Mathematica users) and social media integrations for comments, pages and posts.
This new pane (#5) presents the Unitarity of CP=T violations by combining the Lepton (Neutrino) Pontecorvo-Maki-Nakagawa-Sakata matrix (PMNS) with the Quark Cabibbo-Kobayashi-Maskawa (CKM) mixing matrix calculations through the Quark-Lepton Complementarity (QLC).
I am also working to incorporate the Koide particle mass relations to MyToE predictions.
Code snippets showing the CKM and PMNS matrix calculations based on the UI.
I finally got around to watching the Avengers movie and noticed that the Tesseract Cosmic Cube looked much like the hyper-dimensional projections that I make with laser etched optical crystal.
The blue light is projected from a multi-colored LED base.
While I do have tesseract projections, the E8 projection on my home page seems most similar. Here are a few blue crystal photos I’ve taken that are also similar.
