A long and technical post to document a New Years Day (early morning) 2013 discovery!
The 2:1 cover of the 480 octonion permutations over the 240 vertices in E8 provides for a potential approach to resolve the issue of fitting the Standard Model (SM) into the beautifully symmetric structure of E8. This post (to be followed by a paper) describes the basics of that approach. For reference, see this Mathematica visualization demonstration tool for what follows (http://theoryofeverything.org/TOE/JGM/ToE_Demonstration.cdf).
But first, a bit about E8 and particle assignments:
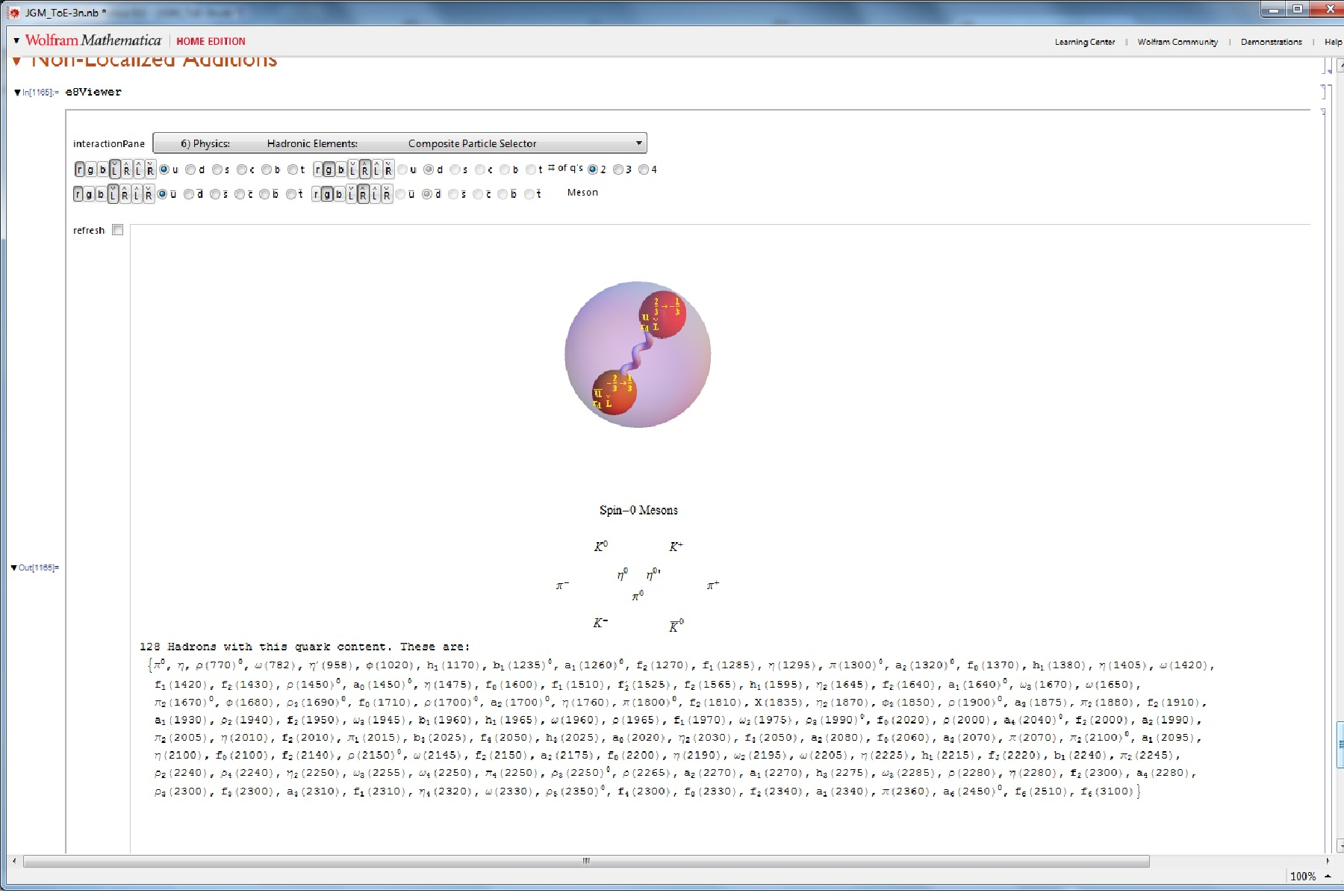
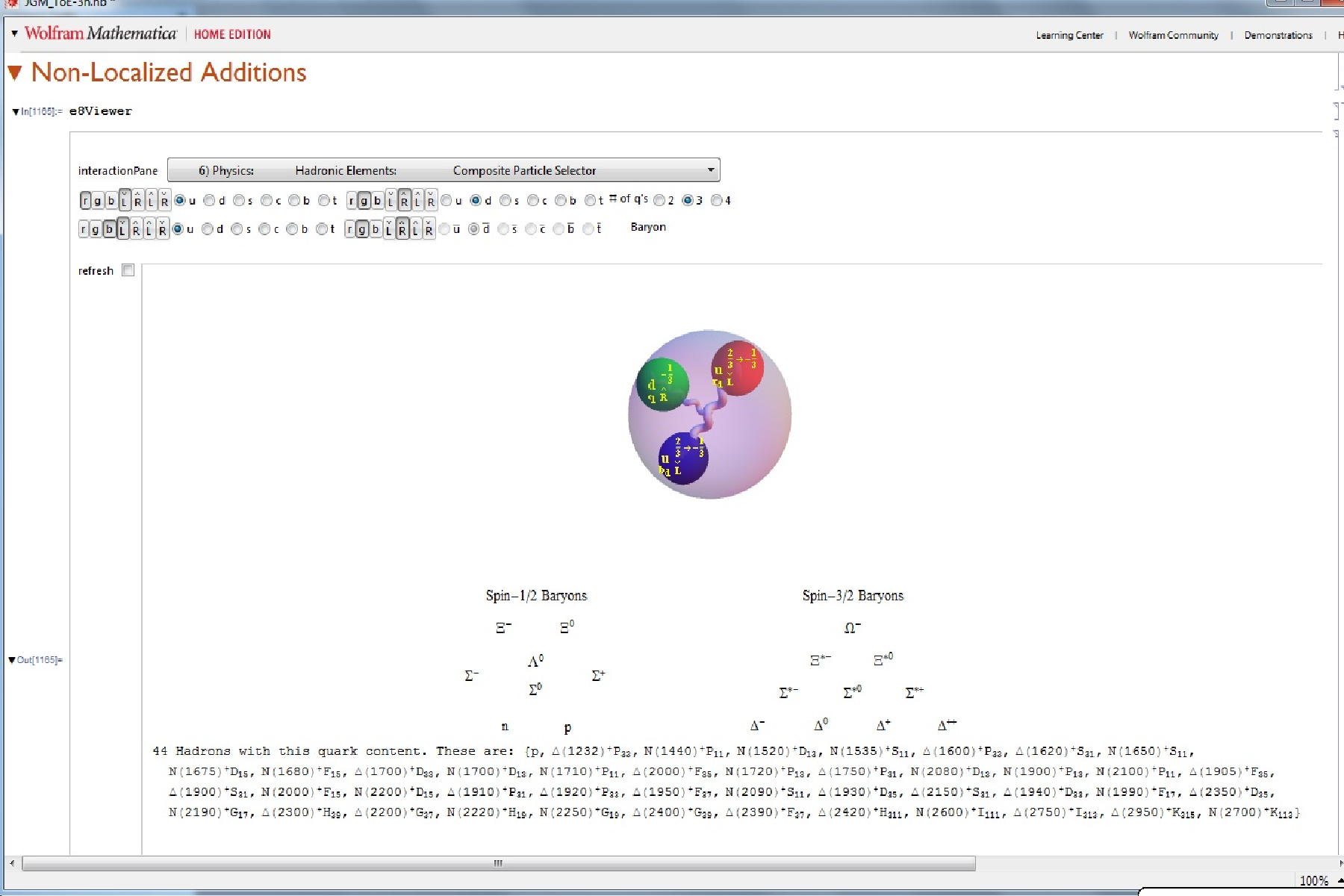
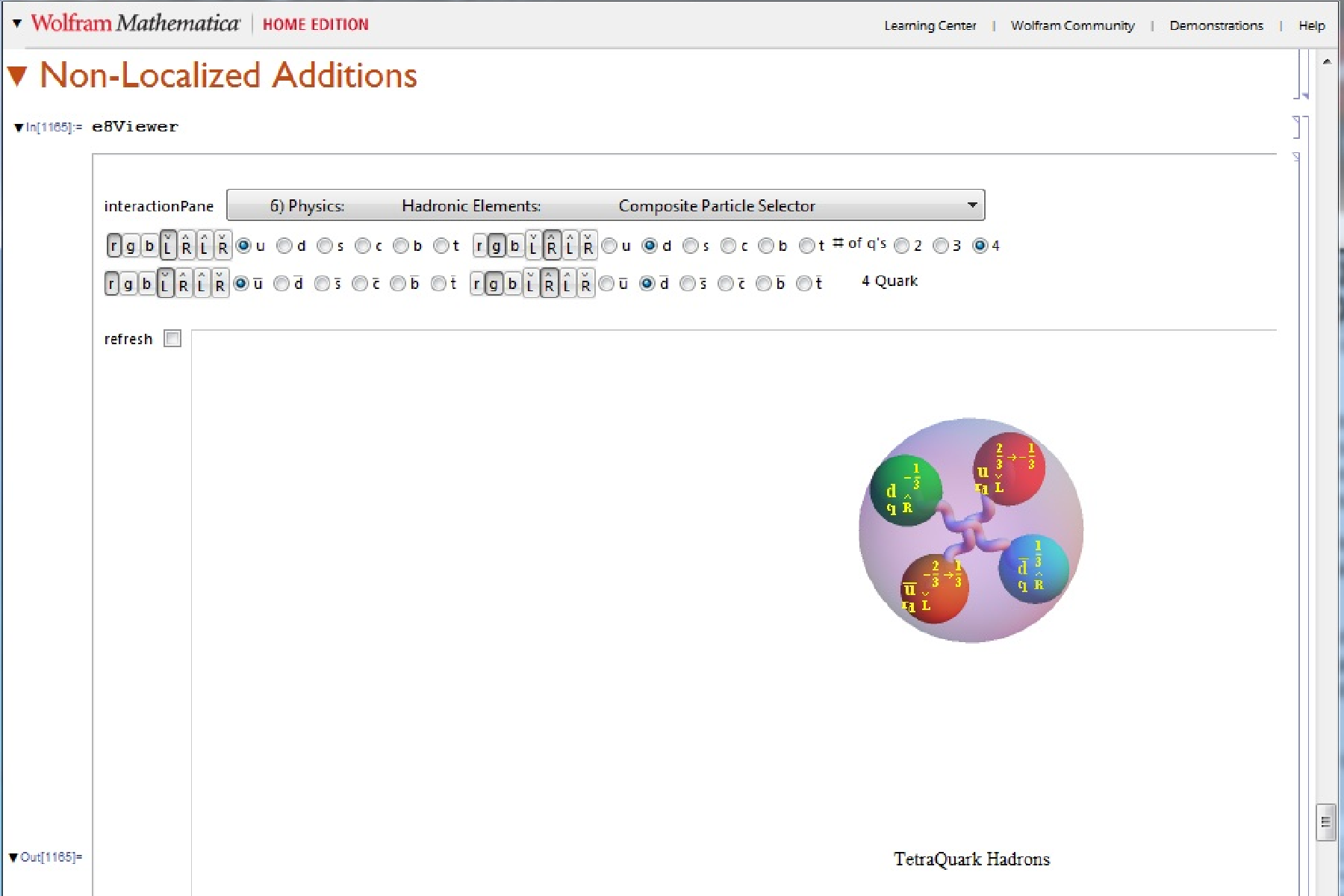
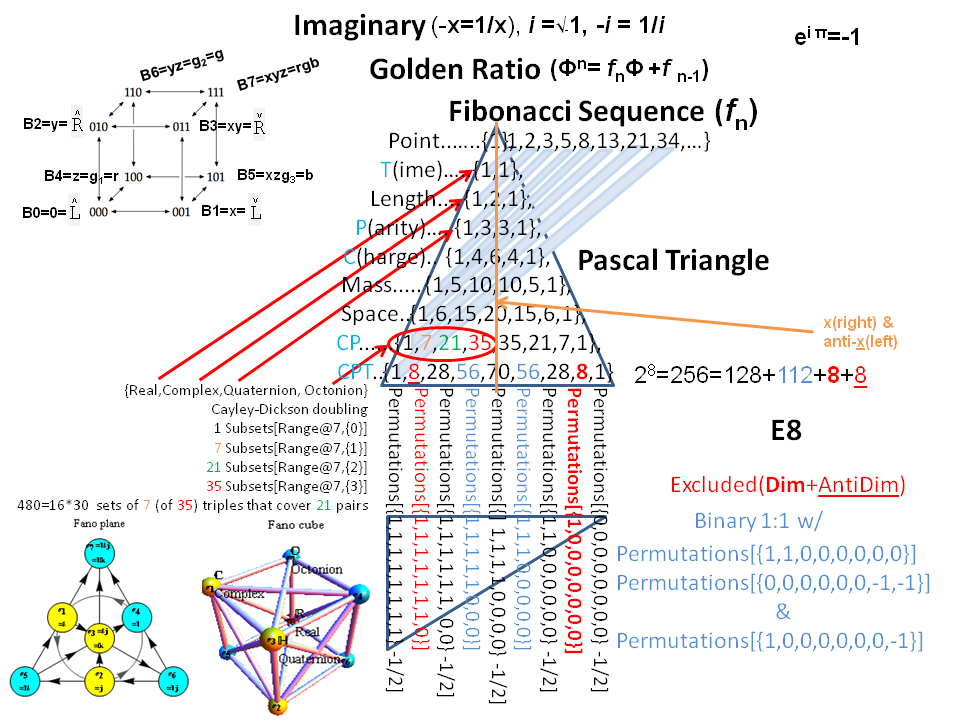
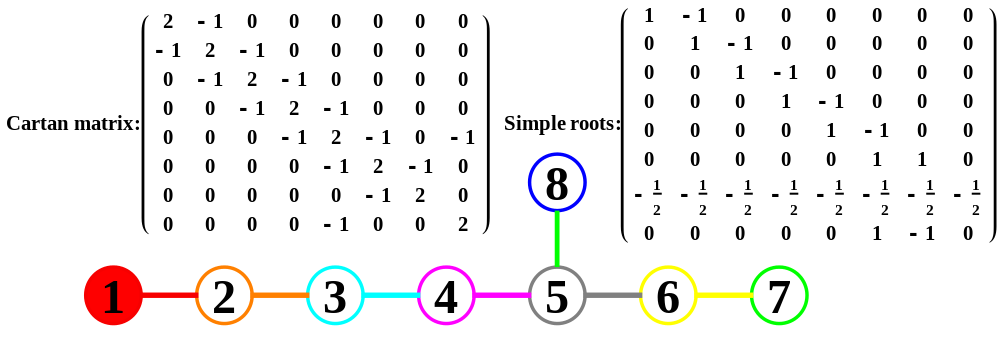
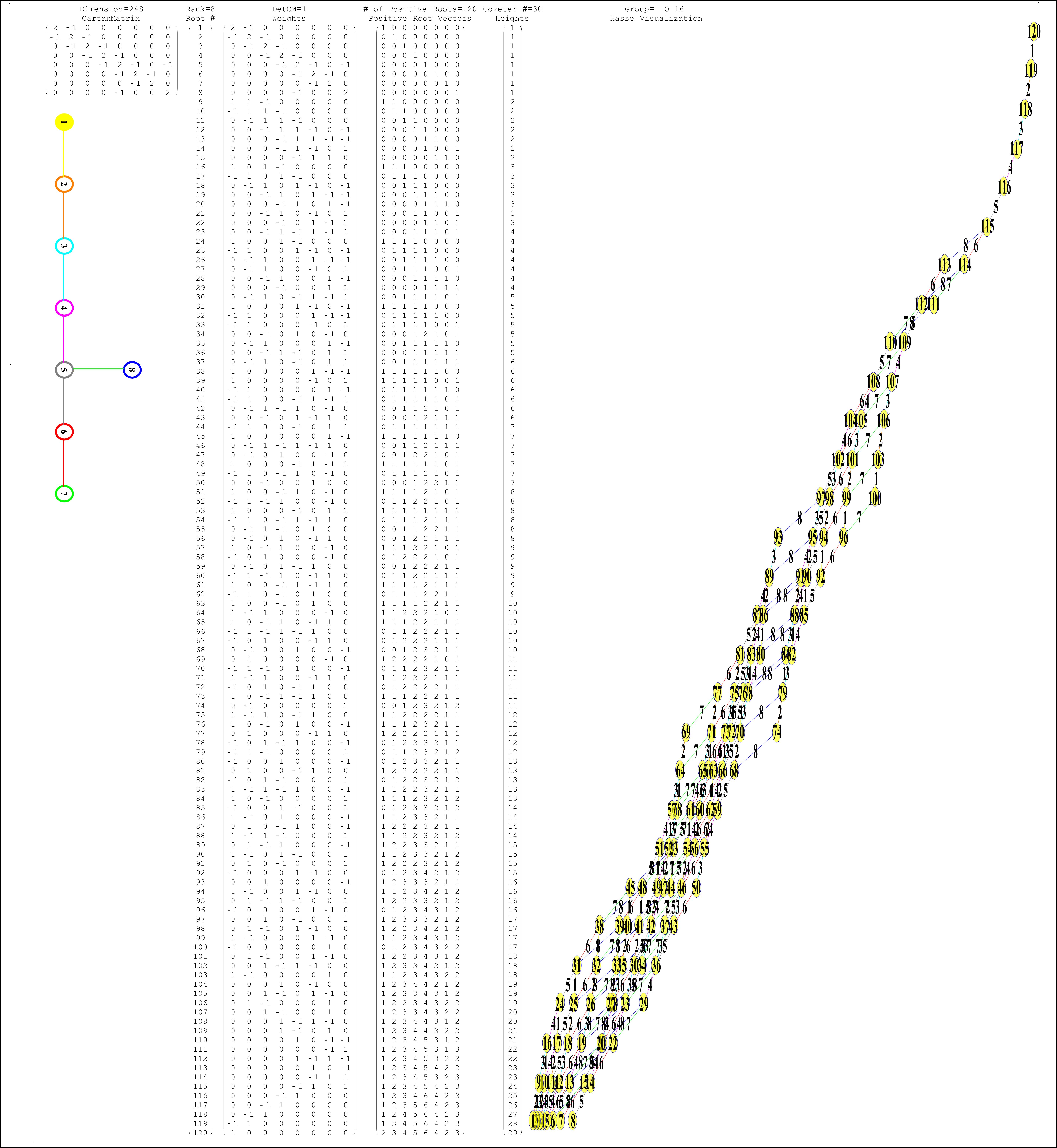
Each vertex in E8 has been mapped (by AG Lisi with minor modifications in assignment) to a fundamental particle in an extended SM. This mapping is controlled in the above referenced demonstration by 8 bitwise quantum parameters which index the 256=240+16 “excluded” particles.
These 8 bits are:
(a)nti – which inverts the binary and negates the E8 vertex and gives the anti-particle of each particle
(p)Type – which differentiates the Neutrinos from electrons (and up quarks from down quarks, etc.)
2 (s)pin – up/down (or x-y or pitch rotation) and left-right (or y-z or roll rotation) spin
2 (c)olor – white (no color) and red-green-blue (e.g. the quark colors)
2 (g)eneration – 0 (no generation for bosons) and 1,2,3 for fermions
A bit about octonions:
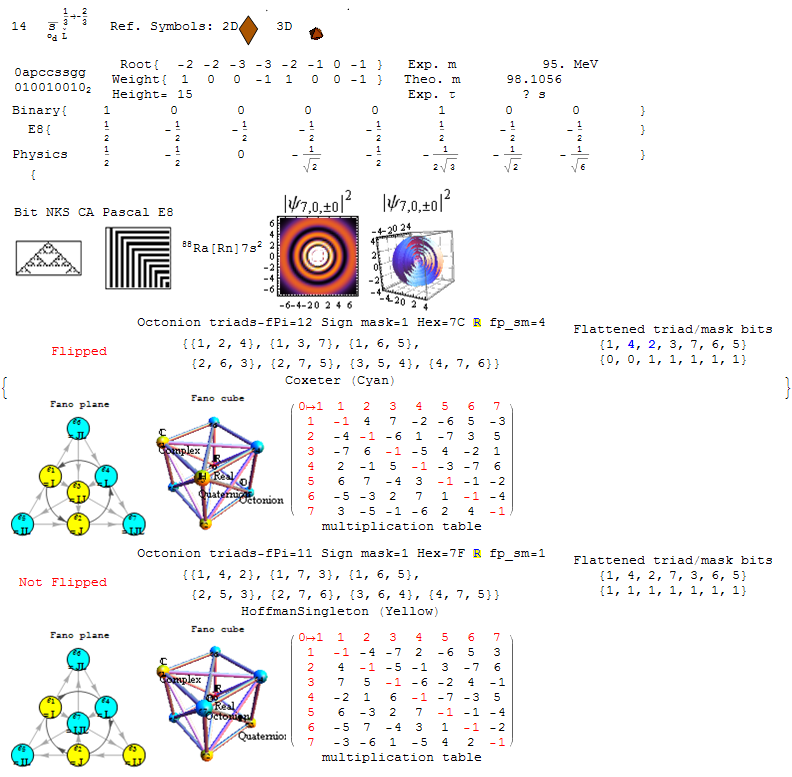
The 480 octonion permutations are generated with a list of 30 sets of triples (3 numbers from 1-7 with no two triples with two numbers in common). These can be visualized as a Fano plane. The Fano plane is easily constructed by taking the first 3 (of 7) triads and deleting the 4th and 7th (of the 9) numbers. This gives a “flattened” list of numbers (1-7) in some permutation order. While there are 7!=5040 possible, only 480 create proper octonions. But how to pair up the 480 to mesh with E8?
There are 16 possible +/- sign reversal (or sign mask (sm) bits also shown as hex number) permutations available in each of the 30 Fano planes (30*16=480). These sm bits also “invert” like the “anti” bits in E8 (which sorts it into a top half/bottom half canonical list built using the 9th row of the Pascal triangle and Clifford algebras). So the 16 sm possibilities split into two sets of 8. This changes the direction of the Fano plane arrows. It turns out with some skillfull pattern matching in constructing the sign masks, the 8 sm bits pair up into two sets of four {1,4,6,7} and {2,3,5,8} giving a kind of “spin” match to E8. These pairs of 4 also operate as a left-right symmetry pattern seen in the structure of E8.
So far so good with 3 bits clearly paired between octonions and E8. The E8 excluded vertices (assigned 0 color and 0 generation bits – bosons) should also be excluded in the octonions. This would indicate the color and generation E8 bits would be indicated by those bits in octonions as well. But how? One hint is the generation 0 boson vs. fermion split of E8. These split E8 into a C8 group of 128 1/2 integer vertices and the 112 D8 integer vertices.
The first discovery several months ago:
In building the visualization for Fano planes, I noticed a pairing was required in order to algorithmically construct the Fano plane for each permutation of octonions. That pairing was aligned with the need to “flip” sequential pairs of numbers in one of the first three triads (the ones that create the flattened list). It also turns out that these pair into 15=7+8 pairs that correlate to the E8(240)=D8(112)+C8(128) groups of vertices.
The 7/8 (or D8/C8) split also provided the indicator on where to assign the “excluded” permutations (they get the 0 color and 0 generation assignment referenced above). It becomes trivial to apply a naive sequential assignment of 30 into two sets of 7/8 into the generation and color bits.
To reach the doubling of the 512=480+32 “excluded” octonion permutations, I added what I call a 9th “flip” bit parameter. This correlates well with A Zee’s approach to grand unification using a 9D SO(18) group theory. It turns out that the pattern required for flipping works in unison with the a and p bits in a binary logic relationship. As the demonstration clearly shows, the p bit flips the two sets of four sm bits. (Hint: this is the key to the eureka moment). Also note: Charge-Parity-Time (CPT) conservation law (symmetry) considerations also strongly link the a, p, and spin bits.
The binary logic relationship with the “flip” bit and the sm bits clearly create two 4 bit quaternion sets (anti+3 spin bit quaternion and a generation+color quaternion). While this double set of quaternions was already obvious to me from the E8 construction (noted in http://theoryofeverything.org/TOE/JGM/DynkinParticleReductions.cdf), it was good to confirm it with octonion integration! It seems that this pair of quaternions could be visualized as Hopf Fibrations on 7-manifolds (see http://www.nilesjohnson.net/seven-manifolds.html for an excellent review of this).
It correlates well with my previous post for the relating of time to octonions, charge to quaternions and 3-space to complex (imaginary) numbers. This idea also validates the dimensional considerations that started me down this path 15 years ago (documented in http://theoryofeverything.org/TOE/JGM/ToE.pdf).
Last night’s eureka moment:
Viewing the p bit as a kind of in/out (or z-x or yaw rotation), it becomes clear that the thing that differentiates electrons from neutrinos (pType) is a third intrinsic spin type. This rotation is well known in 6 degree of freedom (6DoF) models, but is typically ignored due to it not being “required” for 3D rotations.
What this implies is that both the charge and mass differences in these particles can be assigned to the third intrinsic spin (rotation) type. It should be deeply related to the long known Higgs SM mechanism and its recently discovered Higgs particle near my predicted mass of 124.443…GeV. It should also help resolve the Distler and Garibaldi argument with Lisi related to incorporating the 2nd and 3rd generation of fermions into E8.