All posts by jgmoxness

Personal

Nested polytopes with non-crystallographic symmetry

Leave a comment

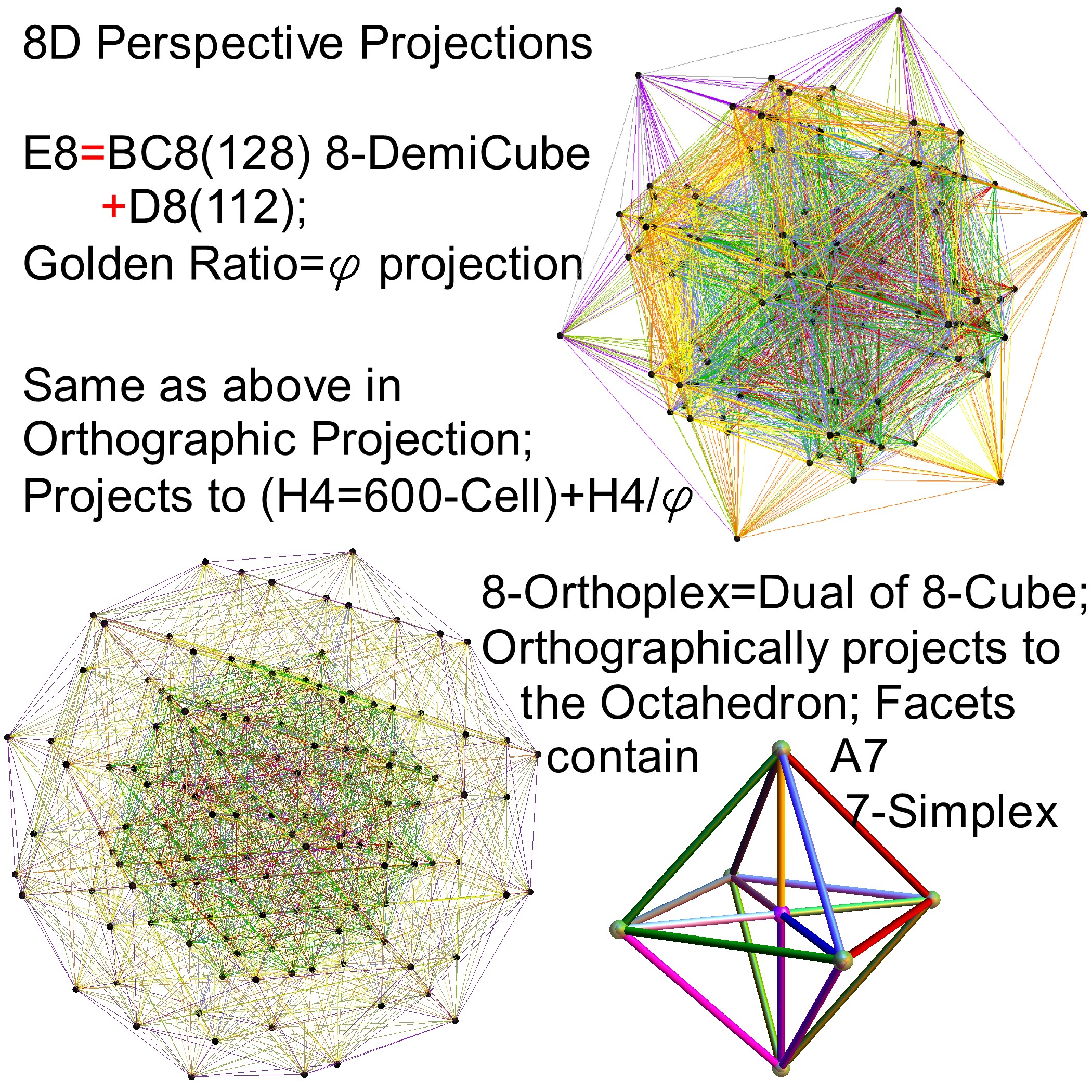
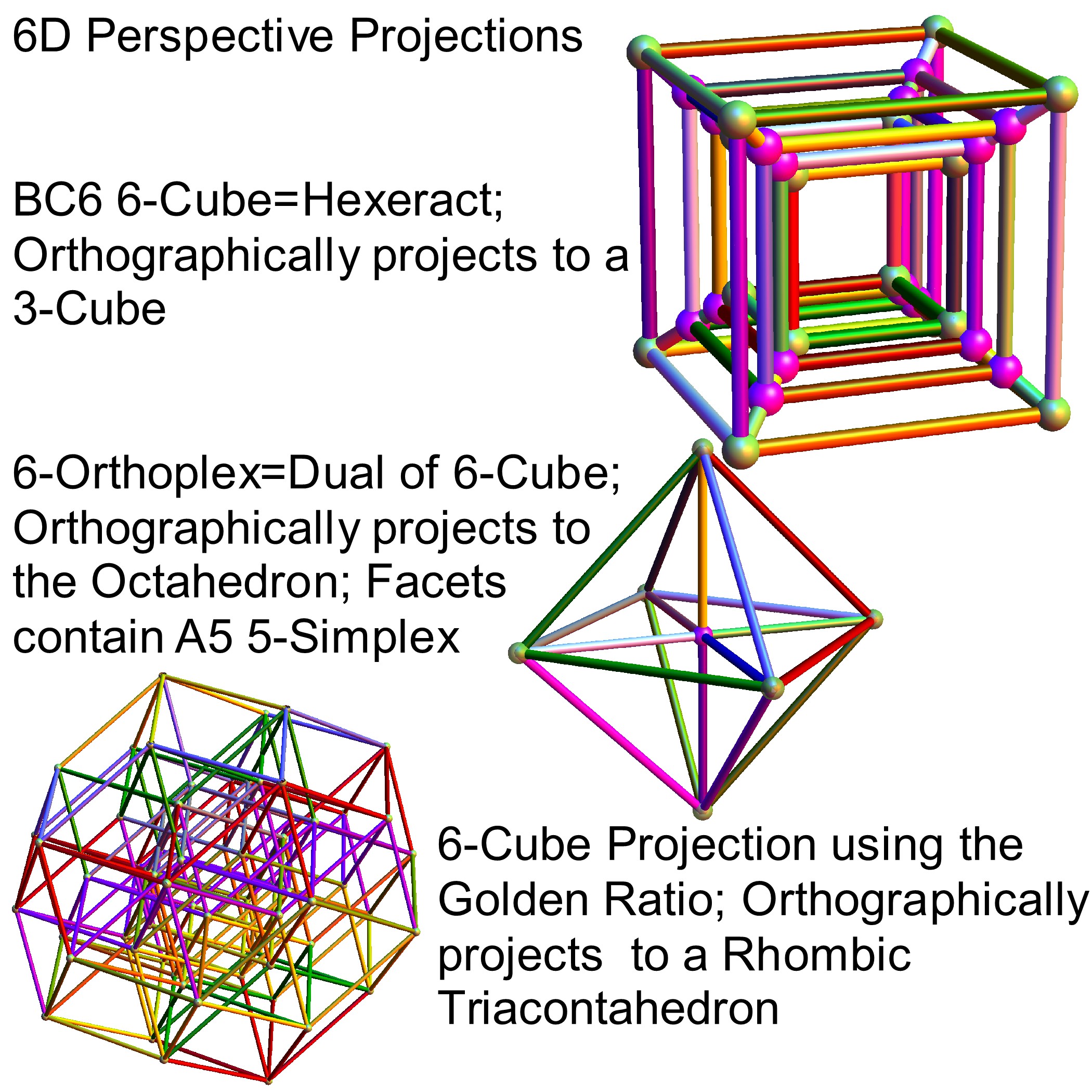
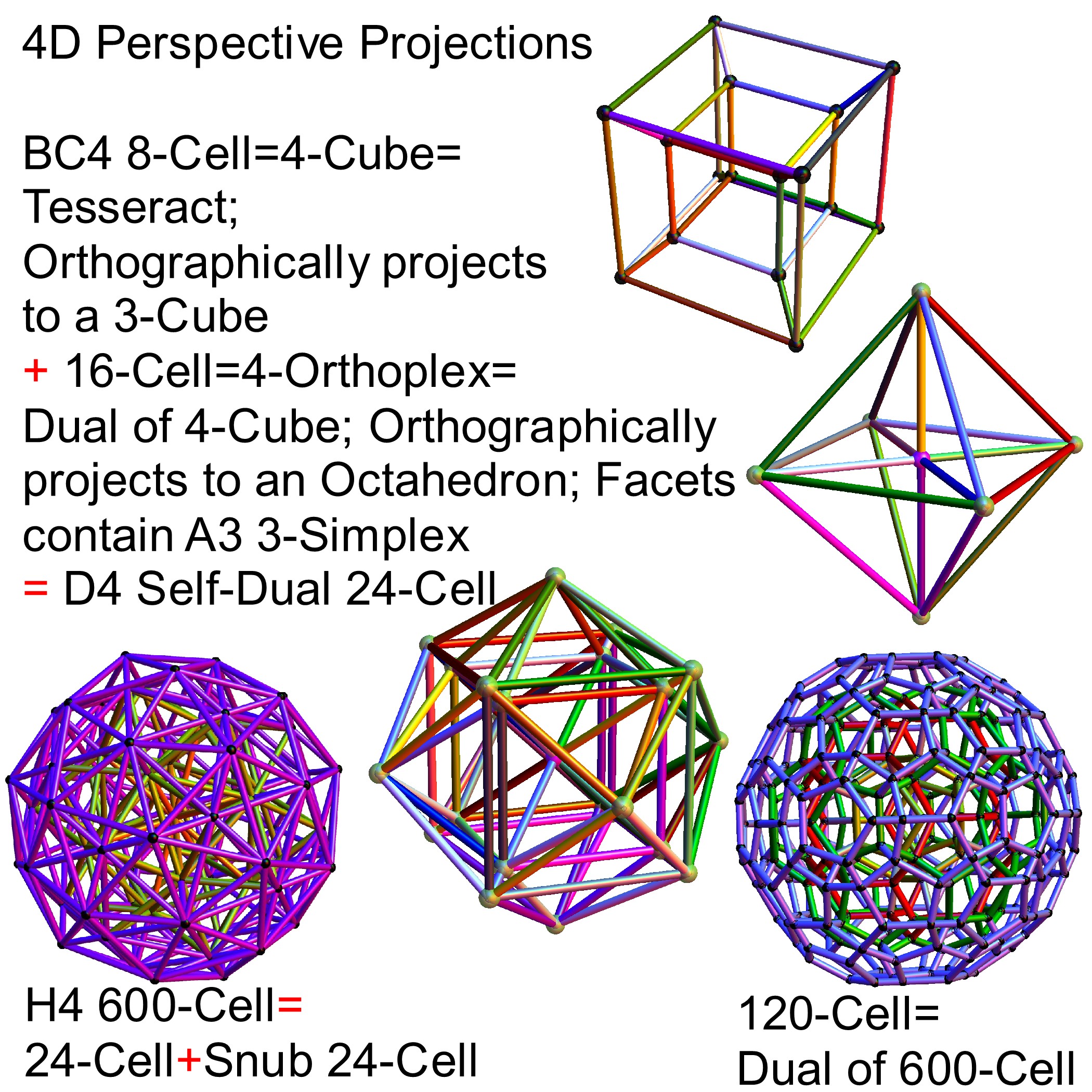
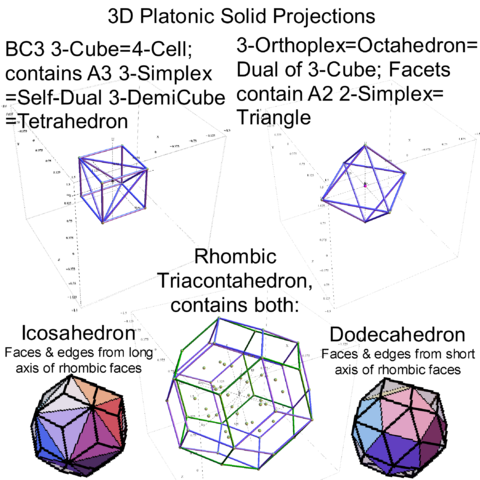
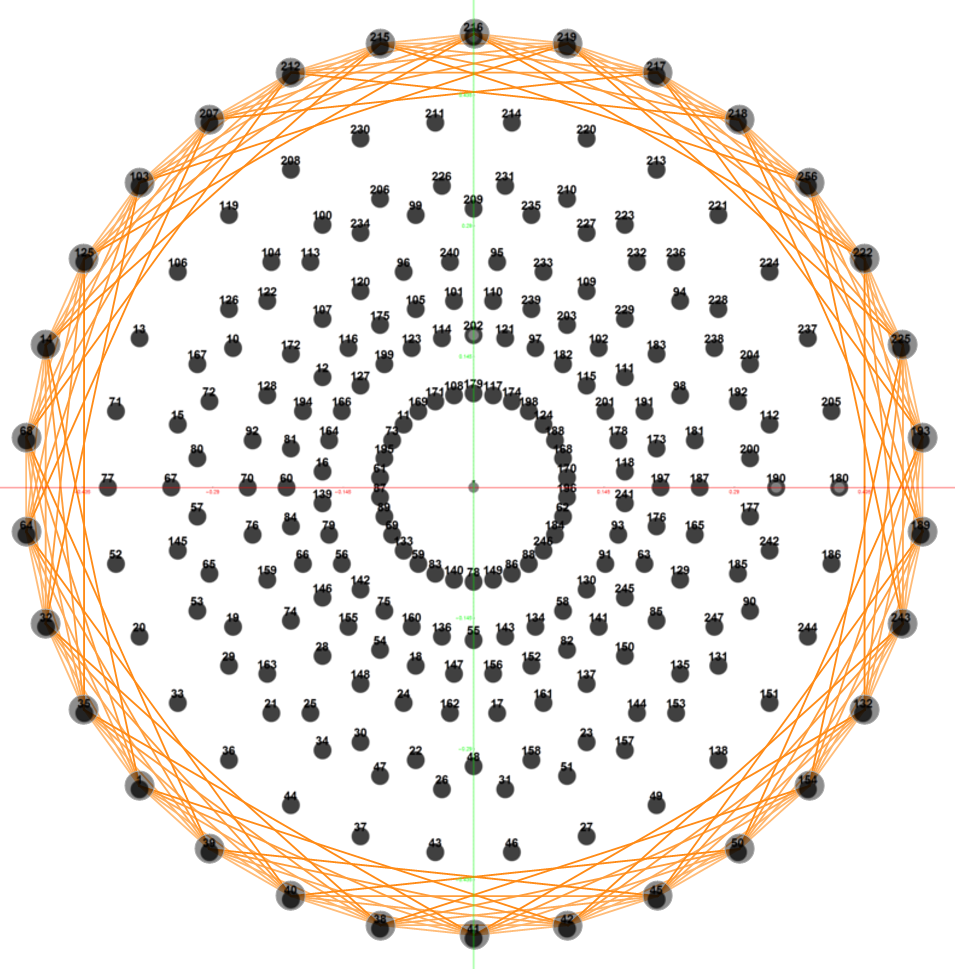
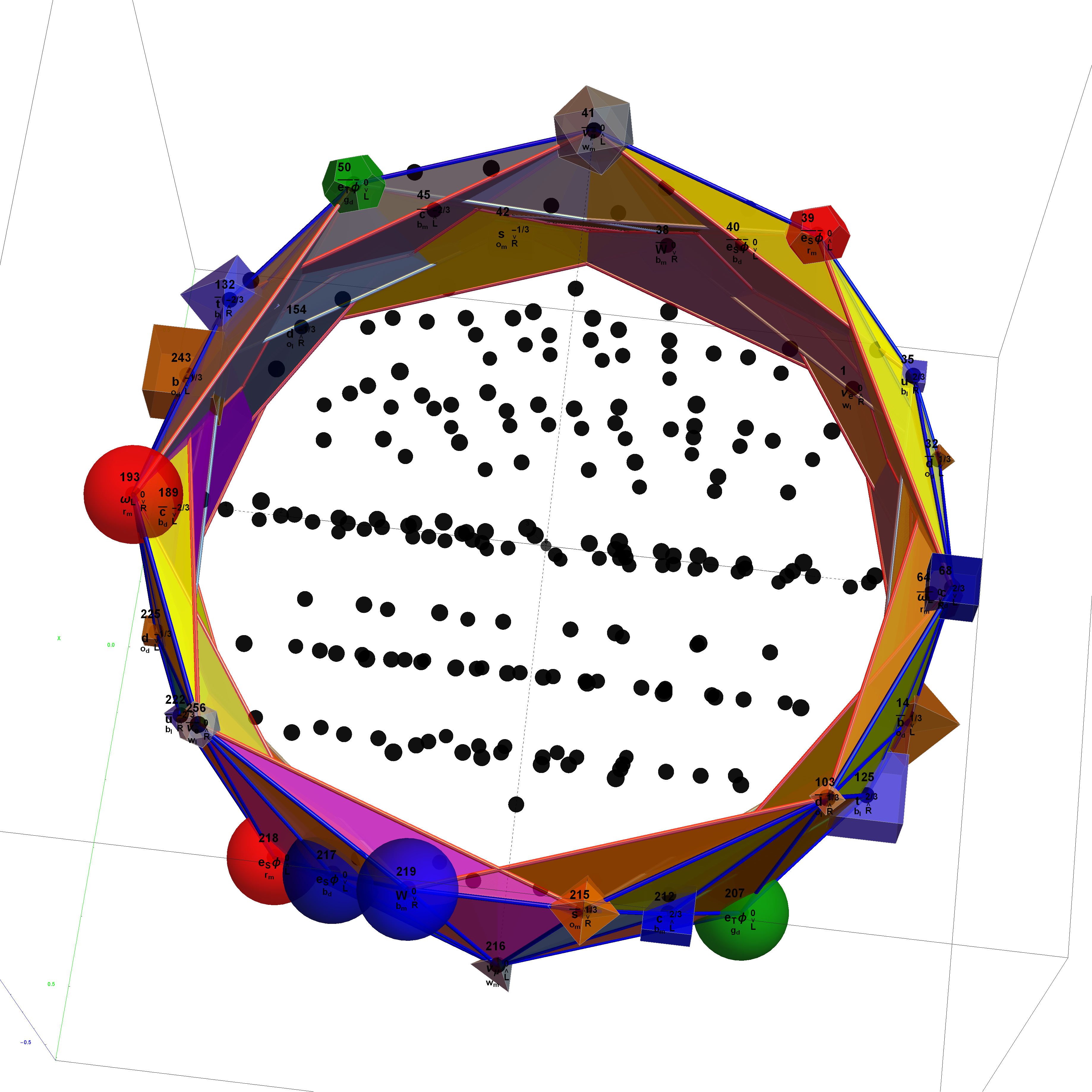
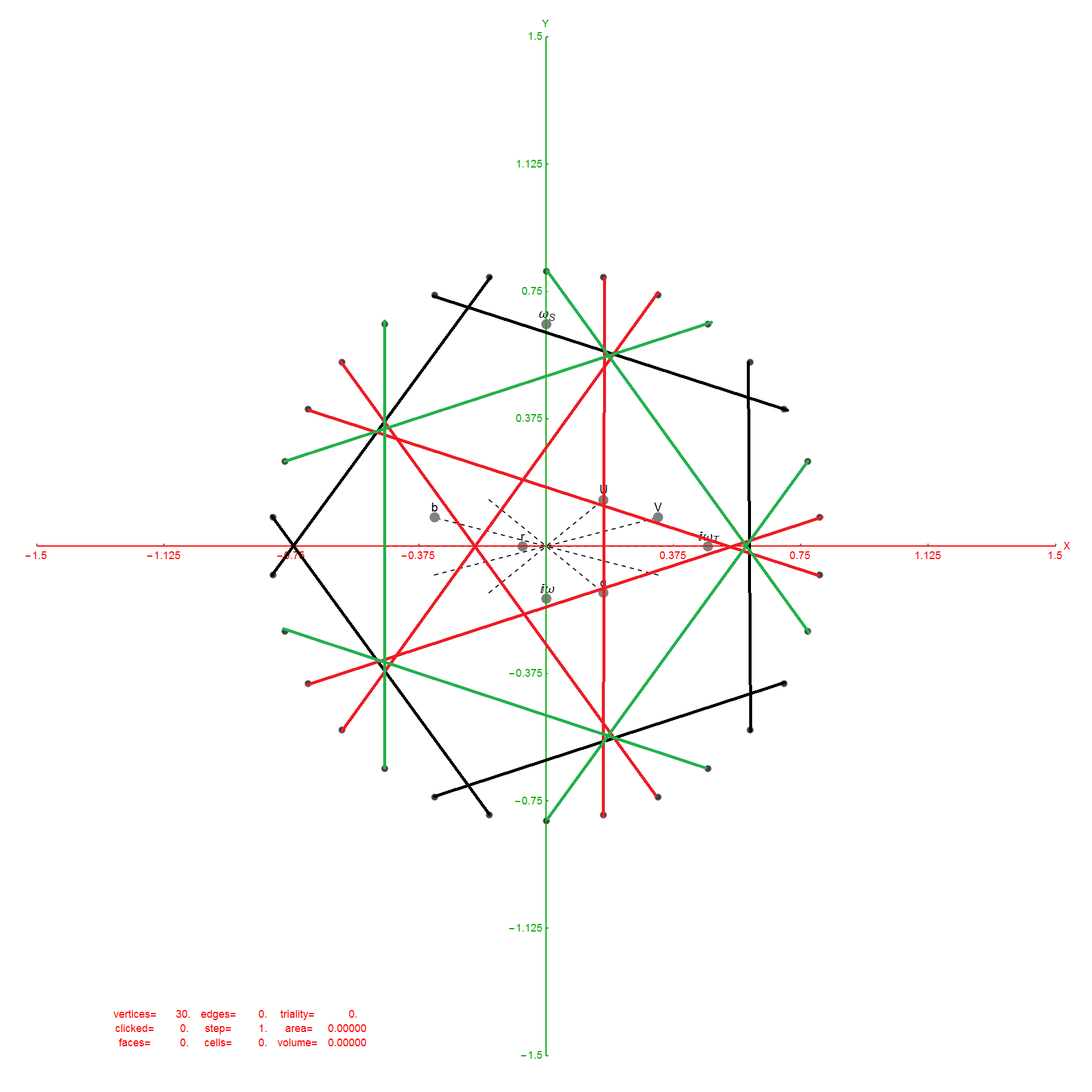
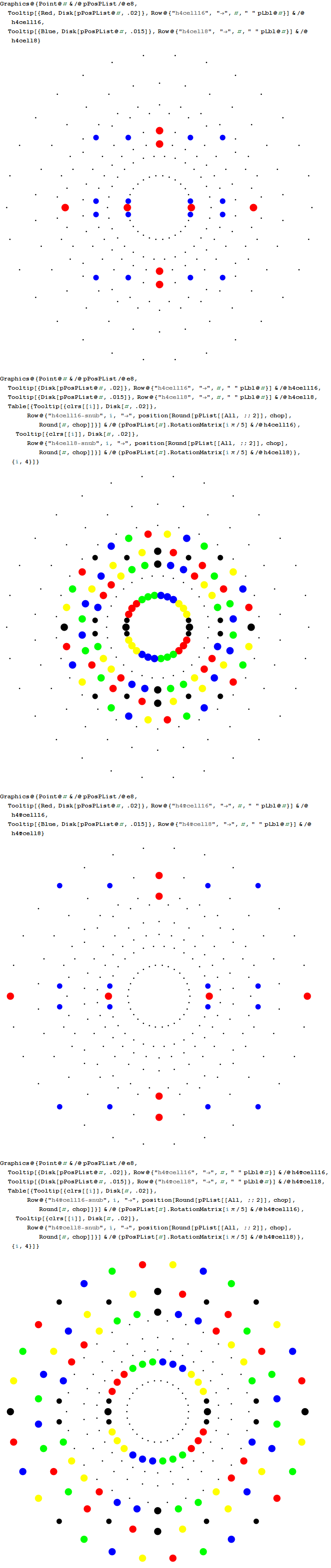
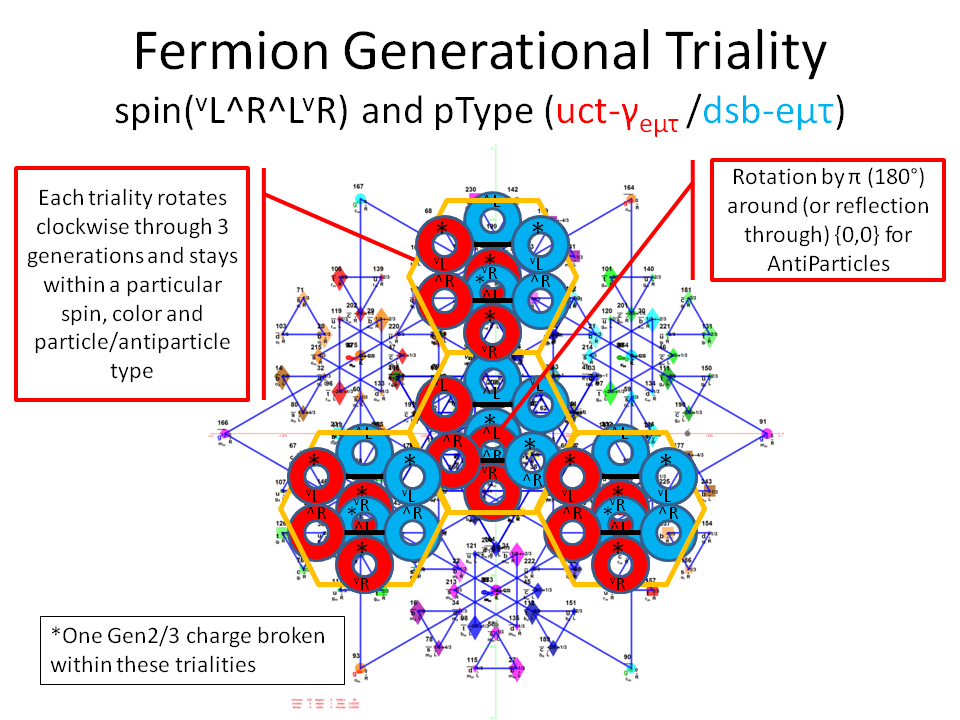
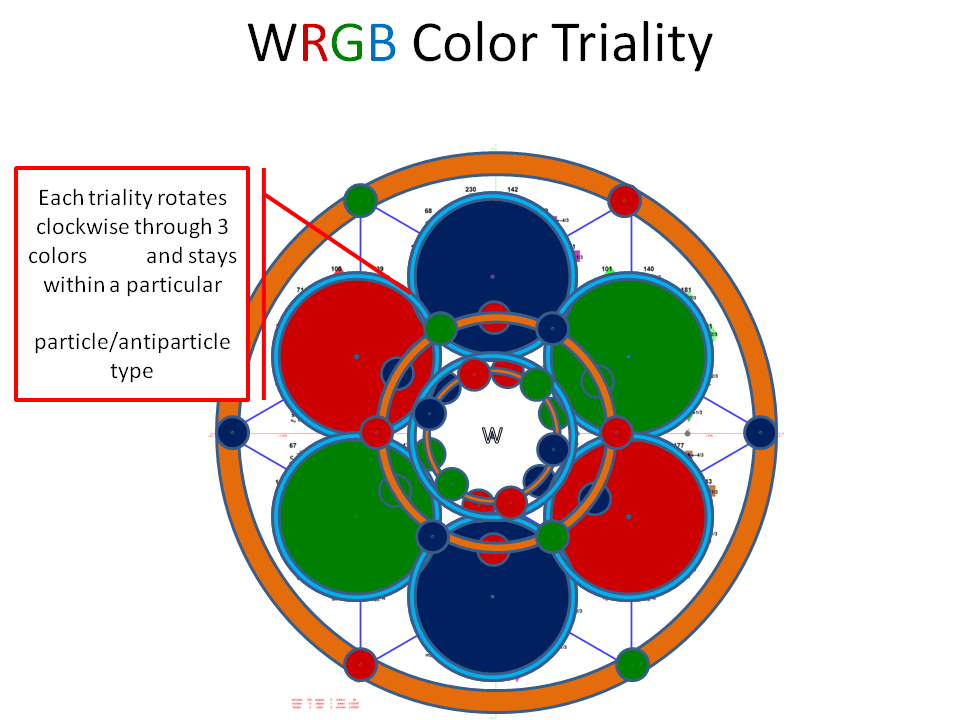
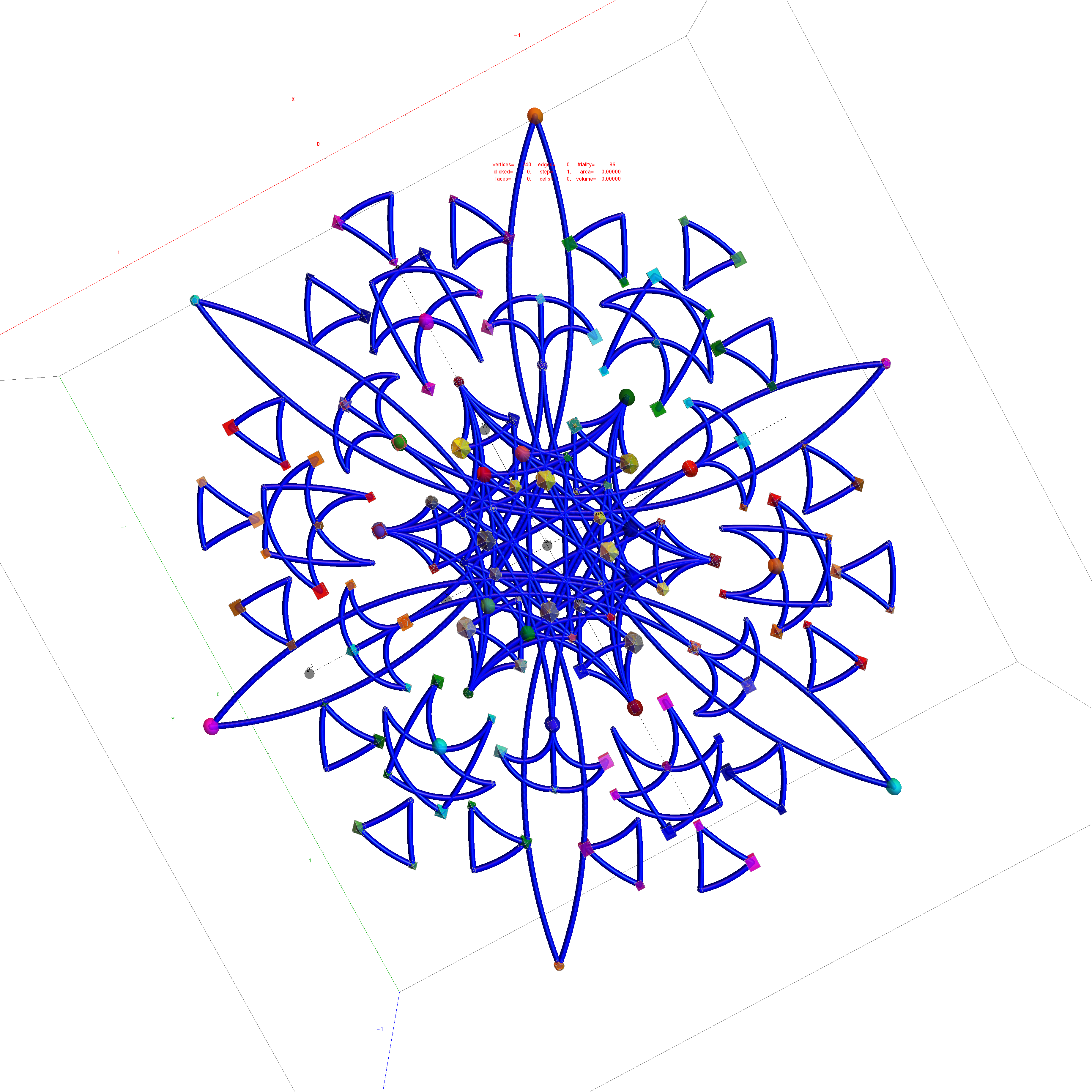
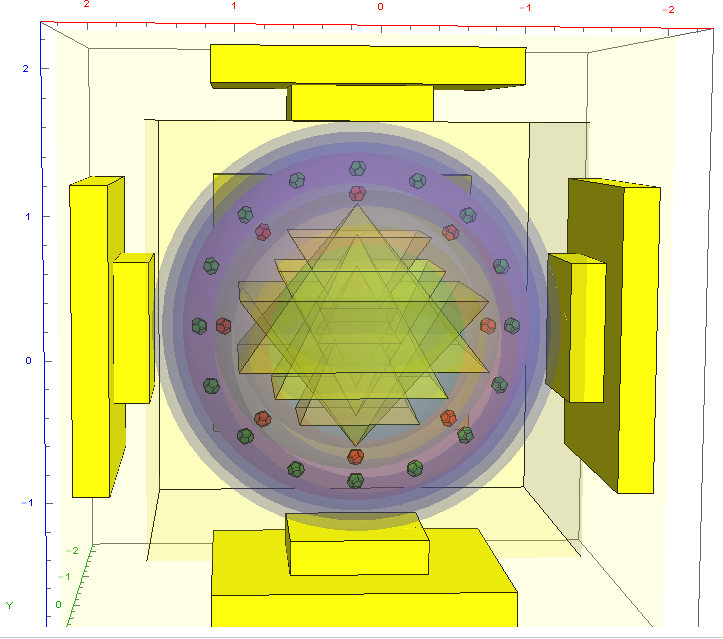
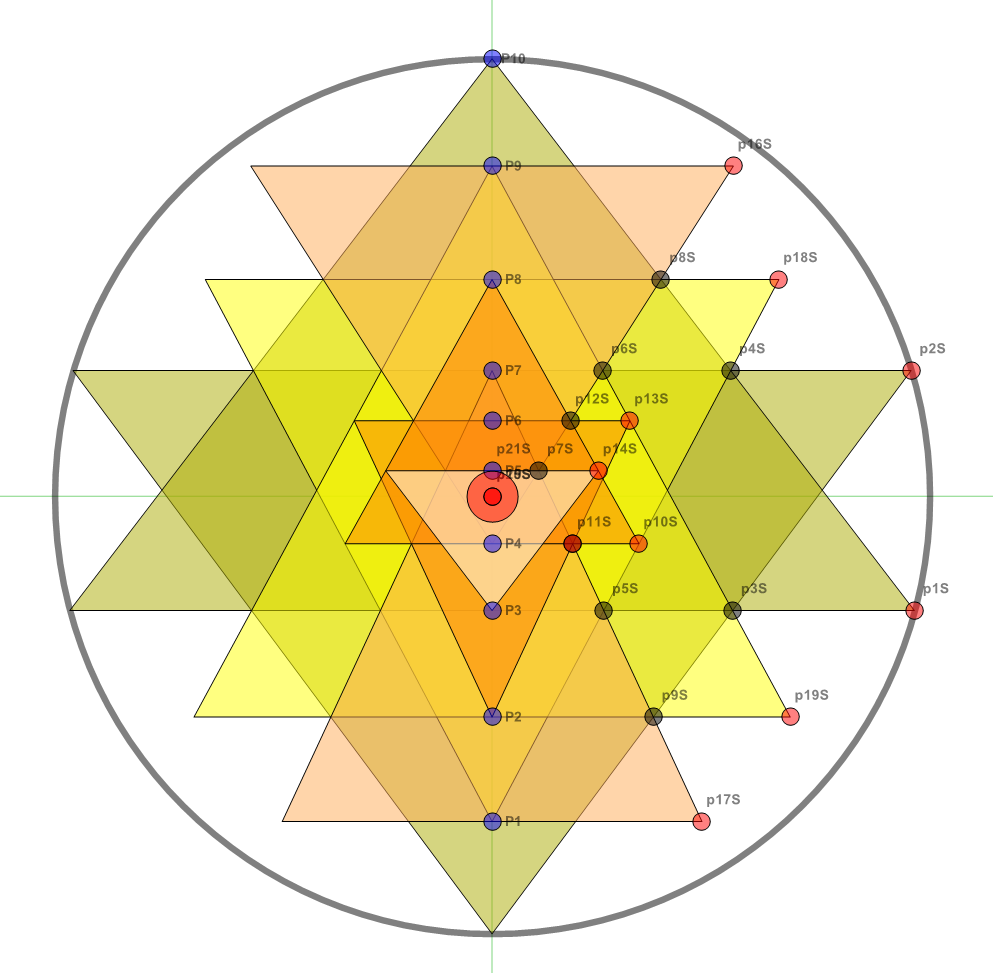
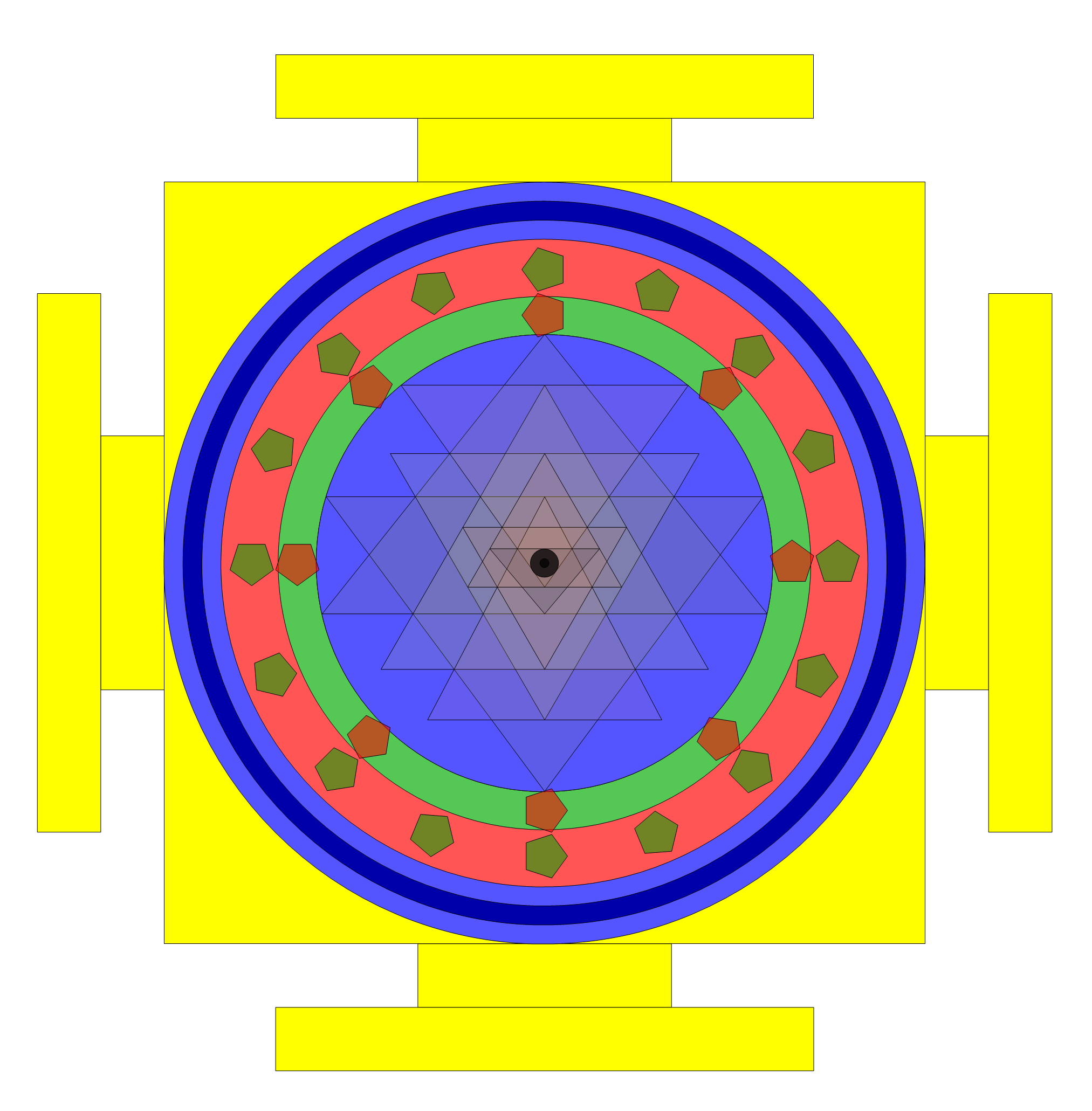
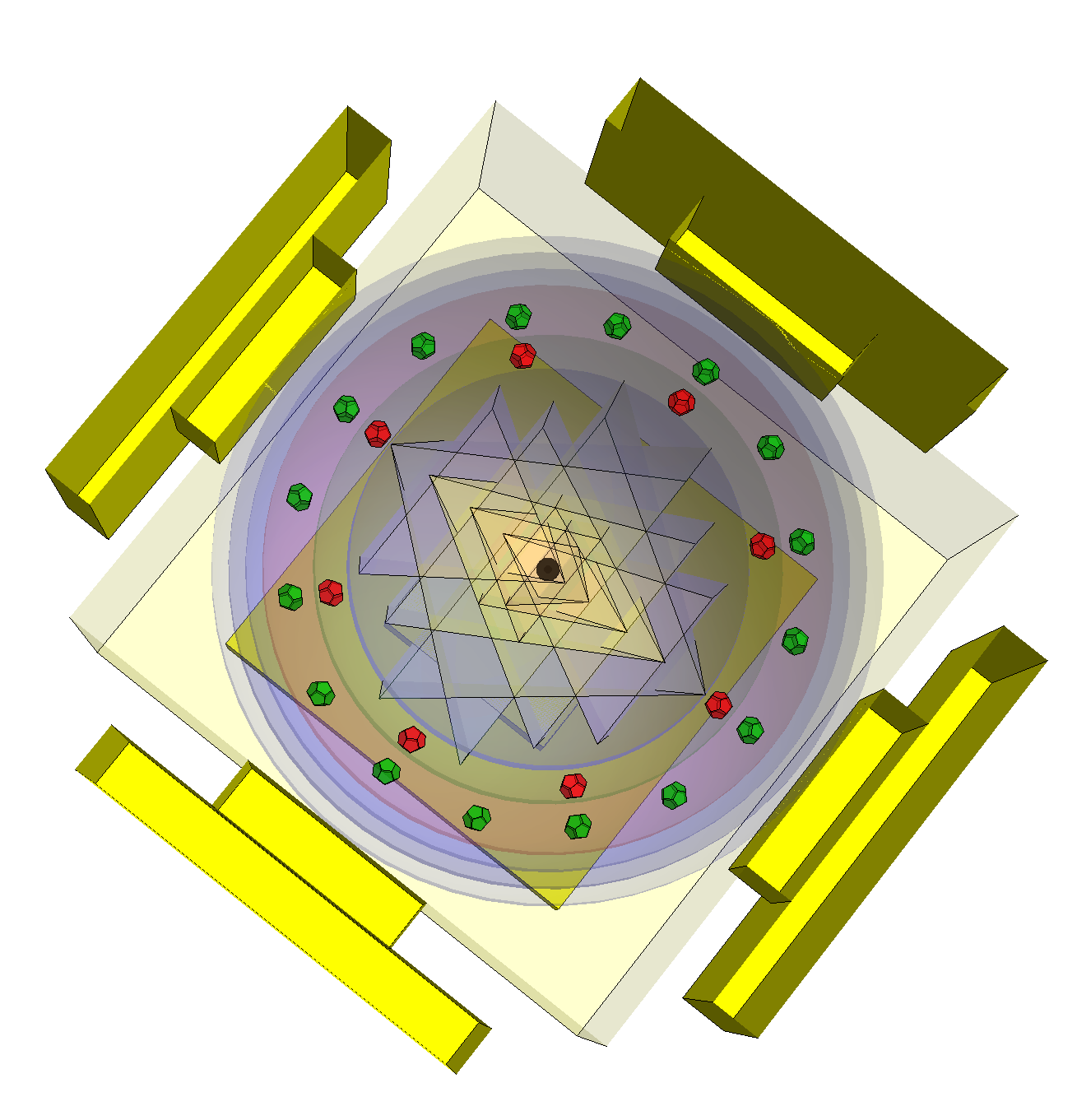
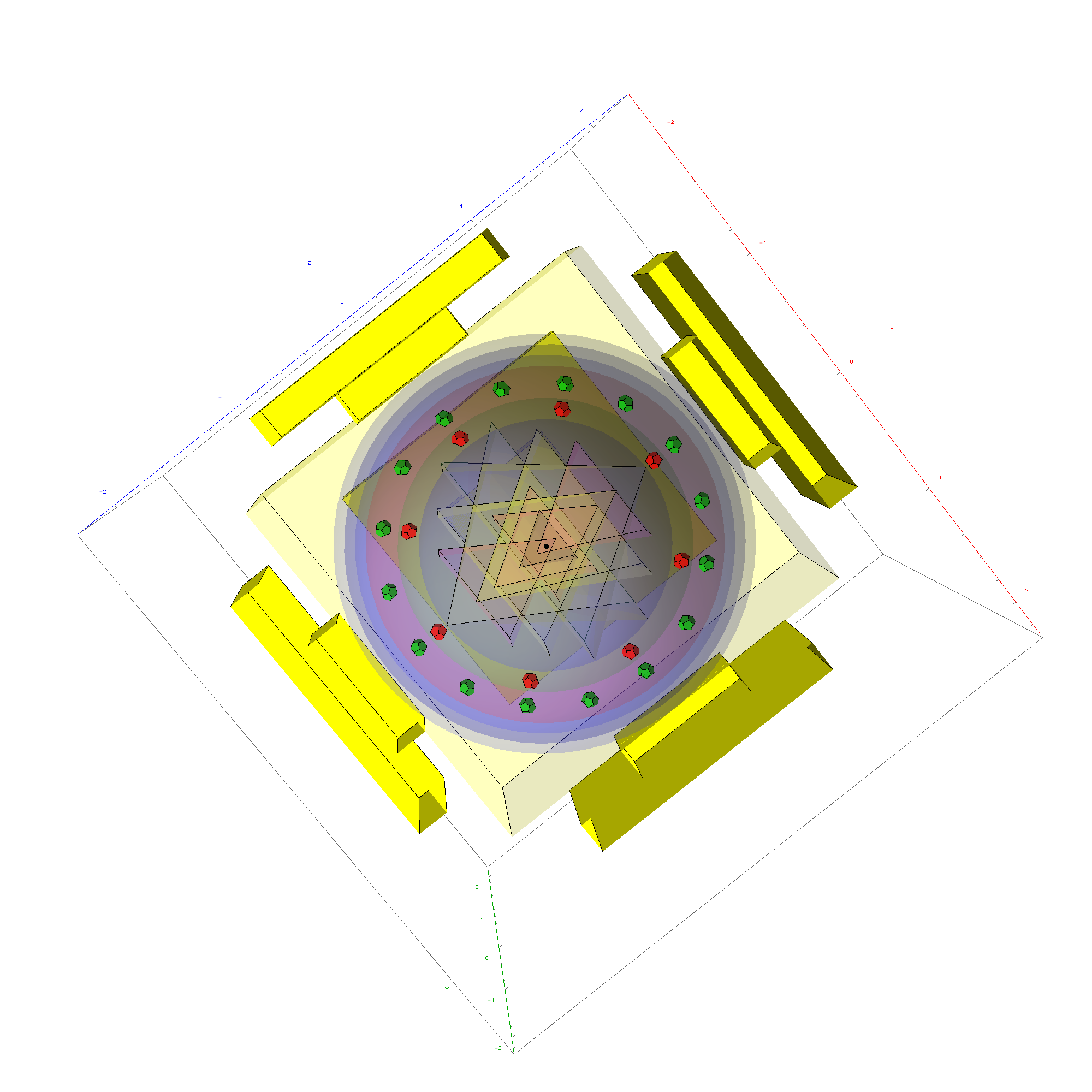
I’ve been following an interesting paper titled “Nested polytopes with non-crystallographic symmetry as projected orbits of extended Coxeter groups” which has used my E8 to H4 folding matrix as a basis for not only understanding Lie Algebras/Groups and hyper-dimensional geometry, but also the genetic protein / viral structures of life (very cool)!

The Nested Polytopes paper was first put into Arxiv in Nov of 2014 at about the same time I submitted my related paper on E8 to H4 folding to Vixra. I created this paper in response to discovering that my Rhombic Triacontahedron / QuasiCrystal (D6 projected to 3D using the E8 to H4 Folding Matrix to E8 to H4 folding) work on Wikipedia and this website was being used by Pierre-Philippe Dechant, John Baez and Greg Egan.

The Nested Polytopes paper has since undergone 4 revisions. The first three seemed to be typical (even minor) tweaks, but with a different author list/order in each. Yet, the latest (V4) seems to have a massive change, different author list and a completely different title “Orbits of crystallographic embedding of non-crystallographic groups and applications to virology”.

While I KNOW they were aware of my work, I wasn’t really surprised they never referenced it – as it isn’t published in academic press. I AM a bit surprised by the extensive changes to a single paper on arxiv. They have removed some of the E8 /H4 references (ref: Koca) and added completely different sources. Makes you wonder what’s up with that?

E8-8D-Polytopes-2

E8-6D-StarPolytopes-2

E8-4D-Polychora-2

E8-3D-Platonic-2

Physics

Fun with Tutte-Coxeter, Beordijk-Coxeter, E8 and H4

Leave a comment

In reference to a G+ post by Baez (w/Greg Egan), it’s interesting to note the link to E8’s outer ring of the Petrie projection of a split real even E8, which creates a Beordijk-Coxeter helix.

Beordijk-Coxeter helix in 2D
helix2Db
Beordijk-Coxeter helix in 3D
cells6004b

The Beordijk-Coxeter helix connects the nearest 6 vertices on the outer ring. The Tutte-Coxeter graph is created in 3 (blk,grn,red) sets of edges by taking the (outer) ring and skipping (6,8,12) or counting (7,9,13) vertices. It shows there are 2 perfect pentagons and 1 pentagram (with different radii due to the difference in distance between the sets of vertices used).

e8ring8-1b

Of course, the crystallographic E8 is manifestly related to the 5 fold symmetry of the pentagon, with its integral relationship to the non-crystallographic H4 group (and its Coxeter-Dynkin diagram) through E8 to H4 folding using the Golden ratio Phi.

It is interesting to note that the skipping of 5+(1,3,7) vertices is similar to the creation of the 120 (240) vertex positions of H4 (E8) Petrie projection by adding to the 24 vertices of the 8-cell and 16-cell (which make up the self-dual 24-cell) the 96 vertices of the Snub 24-cell. This is done through 4 rotations skipping 5 vertices.

Also notice the (1,3,7) are the number of the imaginary parts of Complex, Quaternion, and Octonion numbers, also integrally related to E8.

snub-pics

Personal, Physics

Opinion- Pentaquarks

Leave a comment

The recent announcement for the potential LHC realization of composite particle resonance of the pentaquark (or meson-baryon molecule) is interesting. This, along with a prior confirmation of the dimeson tetraquark Z(4430), and prognostications for hexaquarks (or dibaryons), expand the “zoo” of composite particles now numbering in the thousands.

If by chance we can use these new discoveries to discern the mathematical pattern (symmetry) well enough to predict the particle masses, lifetimes, branching ratios and CKM (quark) PMNS (neutrino) mixing matrix ratios – that would be COOL!

Yet, given the current size of this zoo of particles, it seems that adding a few more bags of quarks to the mix may not do the trick, but I am always hopeful.

IMNSHO (In My Not So Humble Opinion ;-)… it is more a task of “naming the animals”.

or in Ernest Rutherford’s words:
“All science is either physics or stamp collecting.”

“The pentaquark search may be physics’ version of ‘stamp collecting'”. JGM

mesons

outHadron

outHadron

Hexaqark with “Physics” shapes:
hadrons

Decays:
decays

My attempt to organize the stamp collection of chemistry into a 4D periodic table:
4DPeriodicTable-1

Personal, Philosophy, Physics

My E8 F4 projection and so called "Sacred Geometry"

Leave a comment

Please note, this is about the GEOMETRY used in what has come to be called “Sacred Geometry”. Upon further investigation, along with the Kabbalah’s “Tree of Life”, it seems even the Jewish “Star of David” (Solomon) is medieval and may not be sourced in authentic ancient Abrahamic theology.

As it stands, the so-called “sacred” origin of these, including the pentagon that shows up in the icosahedral/dodecahedral Platonic solids due to the Sqrt(5) Golden Ratio (Phi) relationship within my E8 to H4 folding, is likely medieval and mostly pagan. I am merely pointing out that E8 contains the geometry that many find “interesting” for whatever reason, and am not promoting the underlying cults that use them.

Video (Best in HD):

My E8 F4 projection w/blue triality edges and physics particle assignments:
StarOfDavid1

My E8 F4 projection with 6720 edge lines:
E8-F4mox1-black

My E8 F4 projection rectified:
F4Rect-Sacred-1a-StarOfDavid

Star Of David Overlay:
F4Rect-Sacred-1b-StarOfDavid

Metatron’s Cube Overlay:
F4Rect-Sacred-1a-Metatron

Flower of Life Overlay:
F4Rect-Sacred-1a-Flower

Kabbalah Tree of Life Overlay:
F4Rect-Sacred-1a-Tree

Copyright J Gregory Moxness 2015
Rectified E8 and F4 Triality (Original Work)

WikiMedia Commons source images:
Metatron’s Cube (User:Barfly2001)
Flower of Life (User:Life_of_Riley)
Tree of Life (User:AnonMoos)

Physics

A new Lisi Arxiv paper along with a new E8 projection

Leave a comment

For Lisi’s latest ideas on a “Lie Group Cosmology (LGC)” ToE, see http://arxiv.org/abs/1506.08073.
Be warned, it is over 40 heavy pages.

He also posted a new projection on FB.
LatestLisiProjection

He uses the (H)orizontal and (V)ertical projection vectors of:
H = {.12, -.02, .02, .08, .33, -.49, -.49, .63};
V = {-.04, .03, .13, .05, .20, .83, -.45, .19};

Here it is rendered with H and V reordered to match in VisibLie_E8 tool:
H/V order is {2, 3, 4, 7, 1, 6, 5, 8};
Note: the particle assignments in my VisibLie_E8 tool (as in the Interactive visualizations on this website) are not the same and have different triality rotation matrices.
newLisi

The pic below has a slightly altered projection that creates a bit more hexagonal symmetry and integer projections (without deviating more than .05 off his coordinates):
Note: vertex colors indicate the number of overlapping vertices.
This uses H/V projection vectors (reverse ordered back to his coordinate system).
Symbolic:
H={3 Sqrt[3]/40, 0, 0, 3 Sqrt[3]/40, 1/3, 1/2, 1/2, -2/3};
V={-3/40, 0, 3/20, 3/40, 3/20, -4/5, 1/2, -3/20}};
Numeric:
H={.13, 0., 0.,.13,.33,.5, .5,-.66`};
V={-.075, 0., .15, .075, .15,-.8, .5,-.15};
LisiNewNormed

Here is Lisi’s version with my coordinates:
LisiNew2

Here is a version of the full hexagonal (Star of David) triality representation using coordinates I found with the same process used above. Particle color, shape and size are based on the assigned particle quantum numbers (spin, color, generation). There are 86 trialities indicated by blue triangles.
Projection vectors (in my “physics” coordinate system) are:
H={2-4/Sqrt[3],0,0,-Sqrt[(2/3)]+Sqrt[2],0,0,Sqrt[2],0};
V={0,-2+4/Sqrt[3],Sqrt[2/3]-Sqrt[2],0,0,0,0,-Sqrt[2]};

StarOfDavid1

See also a rectified version of this, where the particle overlaps show the inner beauty of E8!!
F4Rect-Sacred-1b-StarOfDavid
The underlying quantum symmetry patterns within this coordinate system are:
Slide4

Slide9

Slide11

Slide10

Philosophy

7 Perfect Sri Yantras in 2D and 3D

4 Comments

Based on an excellent 1998 paper by C.S. Rao I’ve modeled the Sri Yantra in Mathematica and incorporated it into the VisibLie_E8 demonstrations (I will upload that soon).

This is a reference figure to verify the model is correct for concurrency (intersecting lines) and concentricity (inner triangles and Bindu point are centered). There are 4 of 18 other constraints used in the diagrams below numerically and/or symbolically solved within the Mathematica code.

SriYantra-Refernce

Here are 7 of many possible solutions using the 20 constraint rules to produce optimal spherical and plane forms of the Sri Yantra.

Solution 1: Solving constraints (* 1,2,3,4,8 *)
SriYantra1

Solution 2: Solving constraints (* 1,2,3,10,15 *)
SriYantra2

Solution 3: Solving constraints(* 1,2,4,5,10 *)
SriYantra3

Solution 4: Solving constraints (* 1,2,5,6,19 *)
SriYantra4

Solution 5: Solving constraints (* 1,2,6,14,19 *)
SriYantra5

Solution 6: Solving constraints (* 1,2,8,9,20 *)
SriYantra6

Solution 7: Optimum planar
SriYantra7

3D using pyramids and new clipping and slicing functions to take off the front (and back) portions of the symmetric 3D object.
I will produce a version option with conical shapes just for fun (soon).
SriYantra3D1

This is a list of the details behind each constraint function Fn
ConstraintFunctions