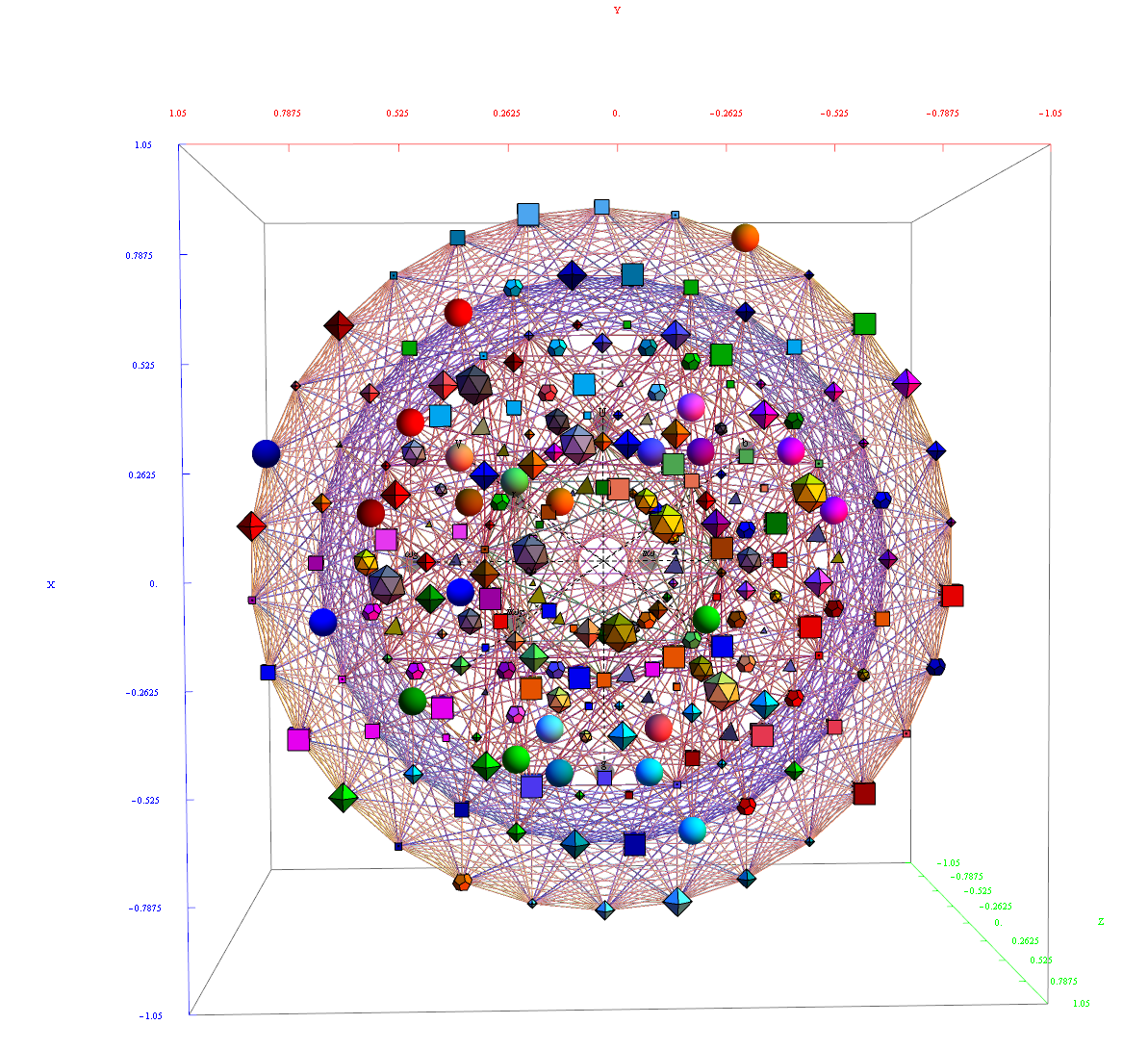
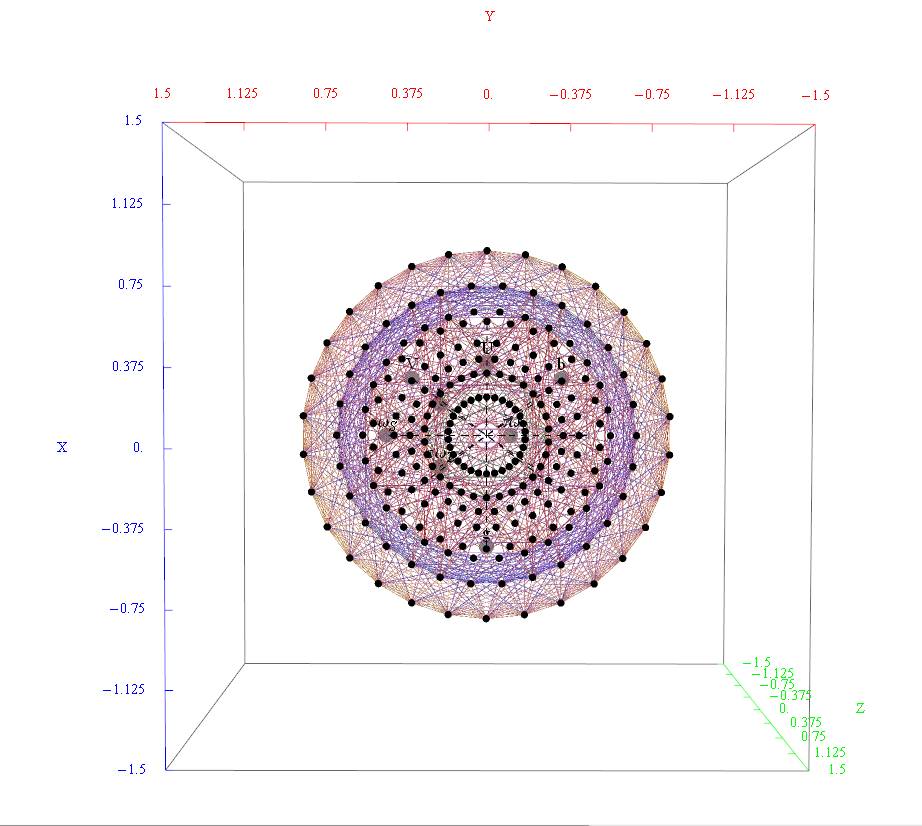
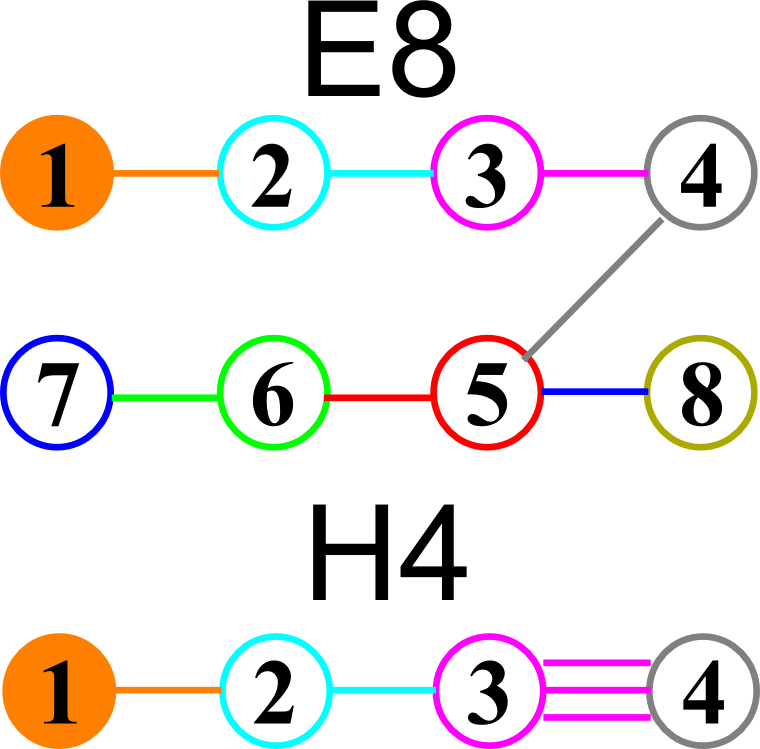
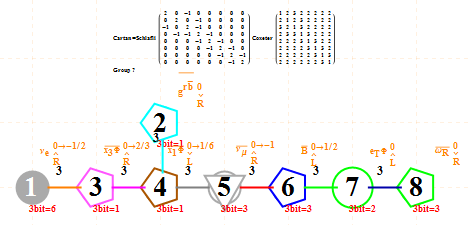
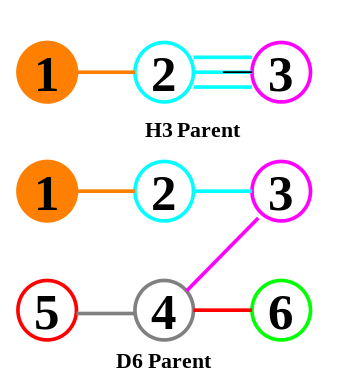
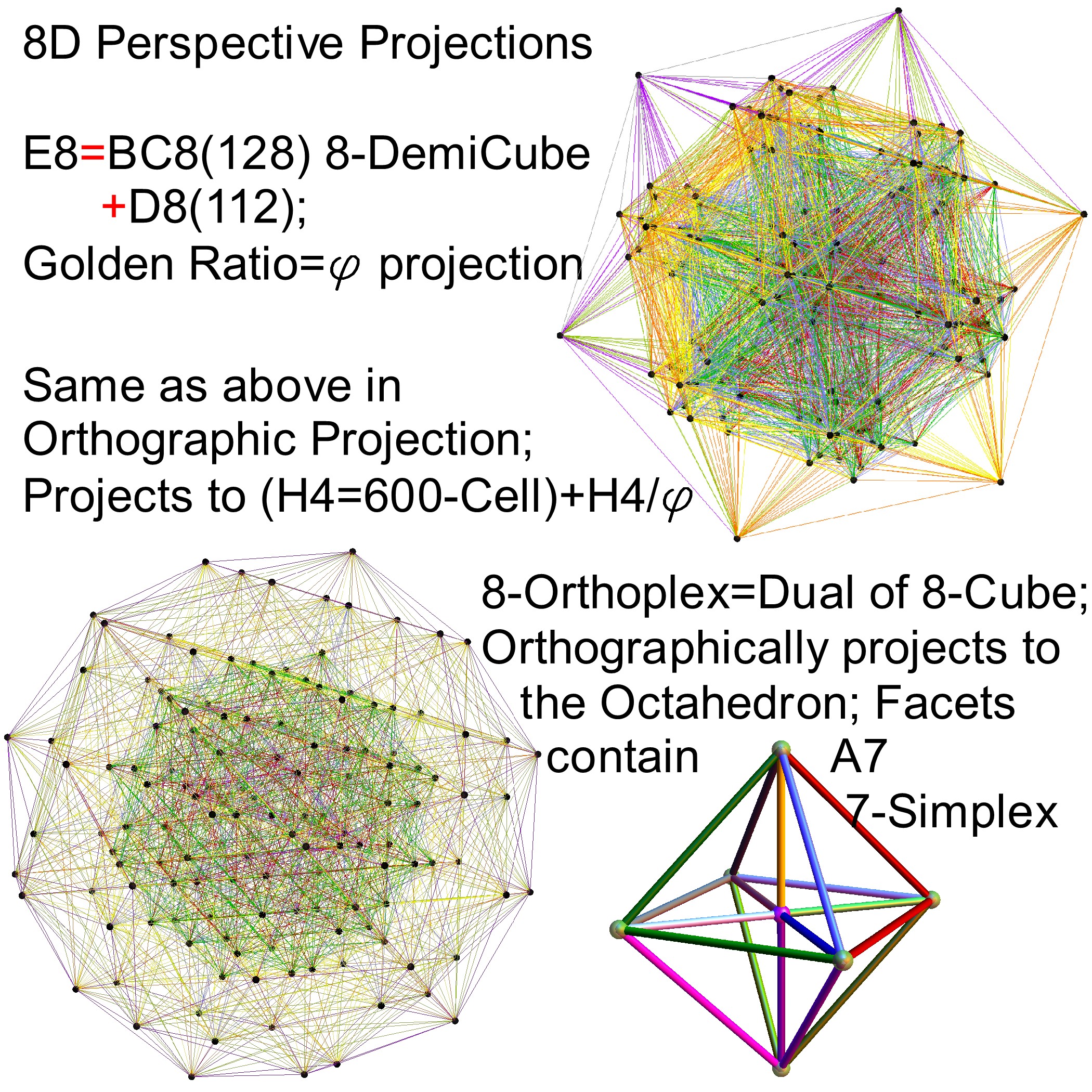
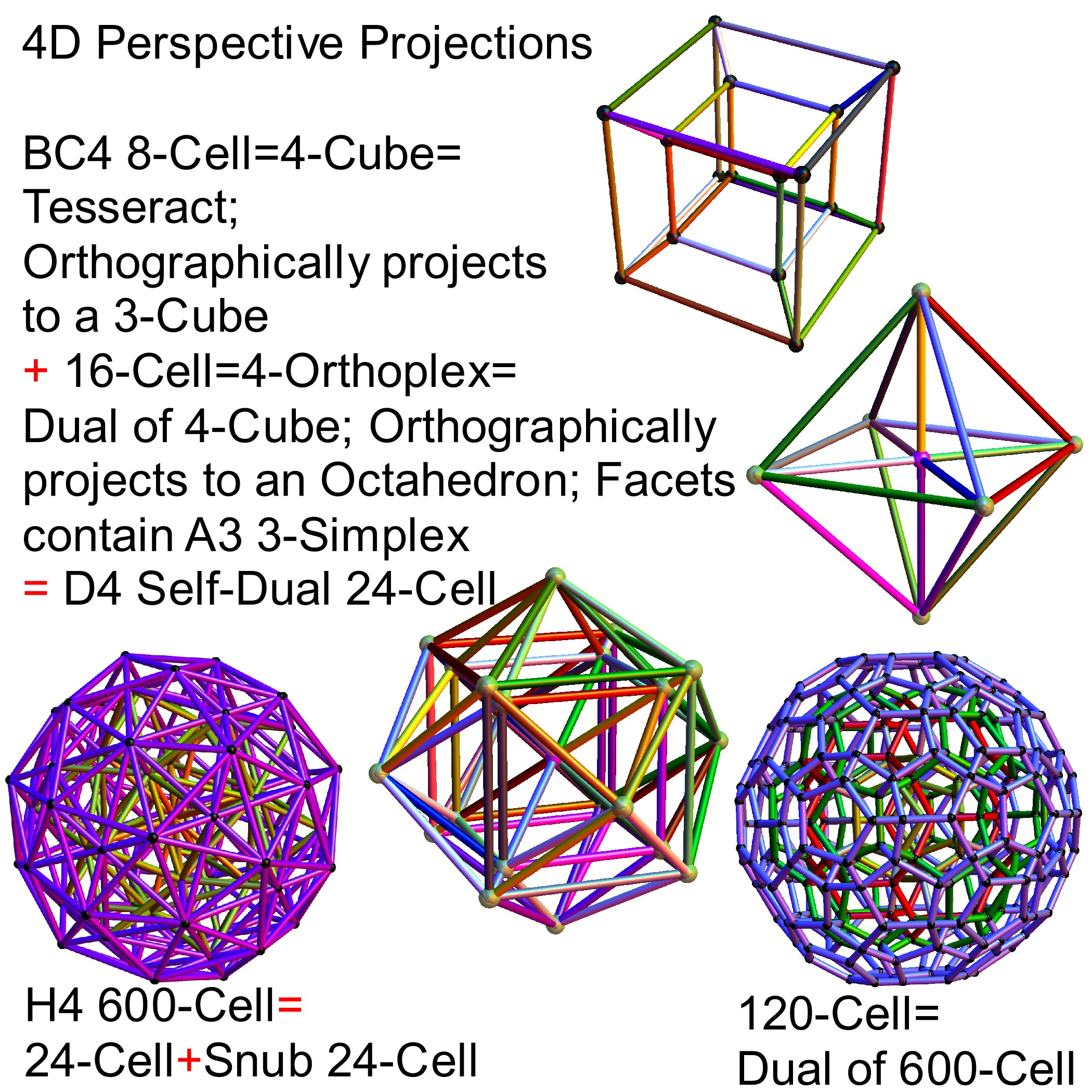
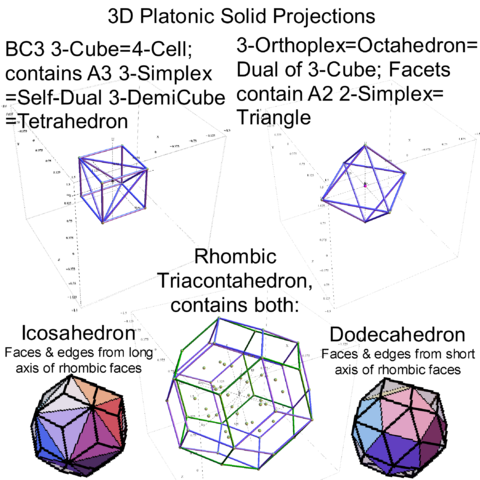
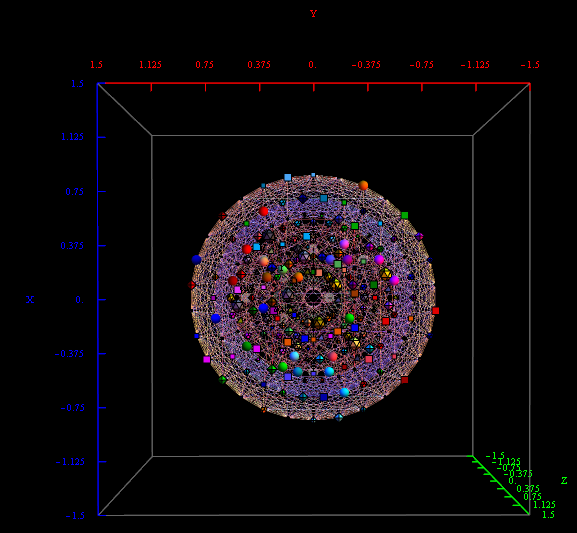
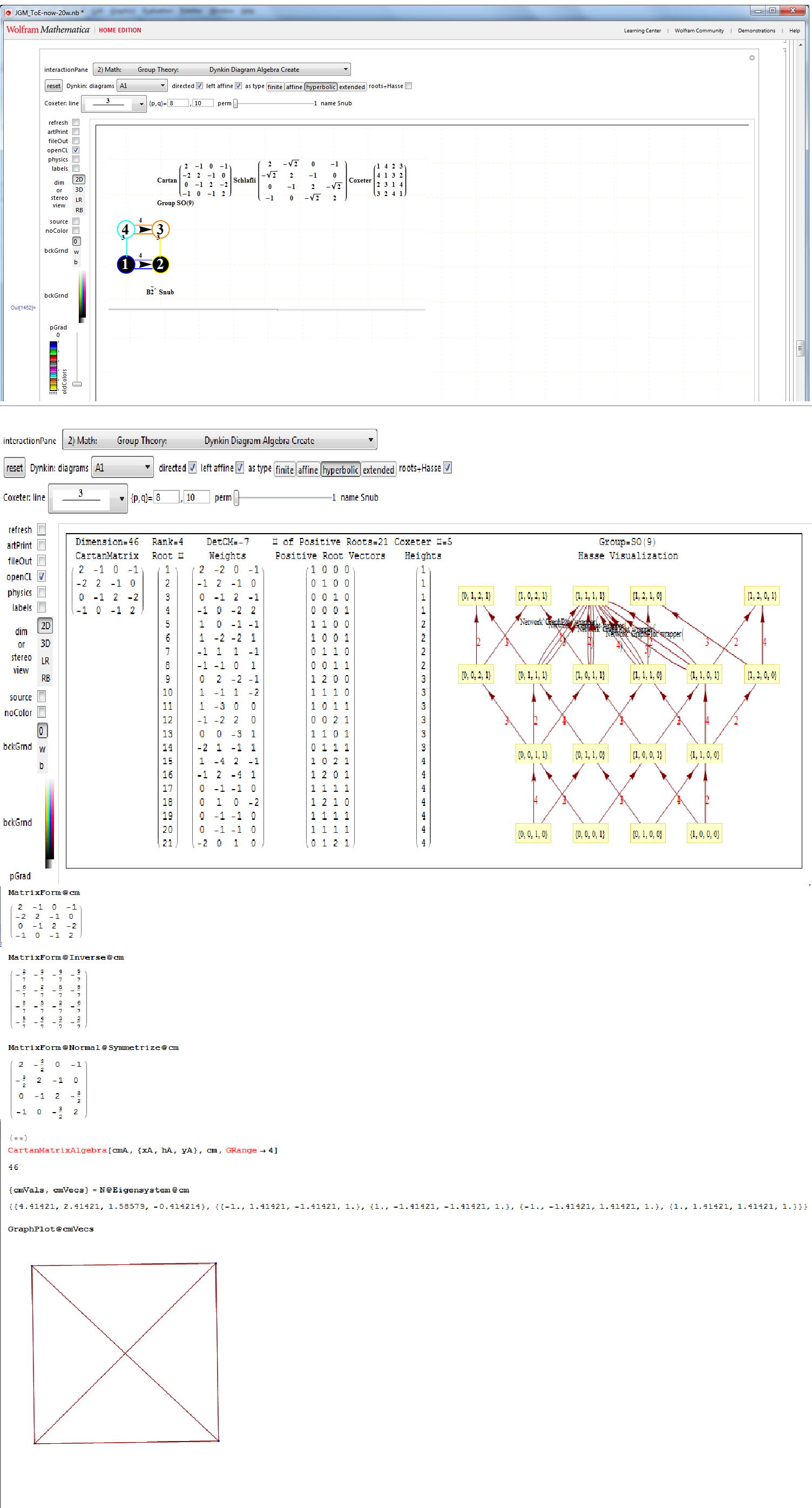
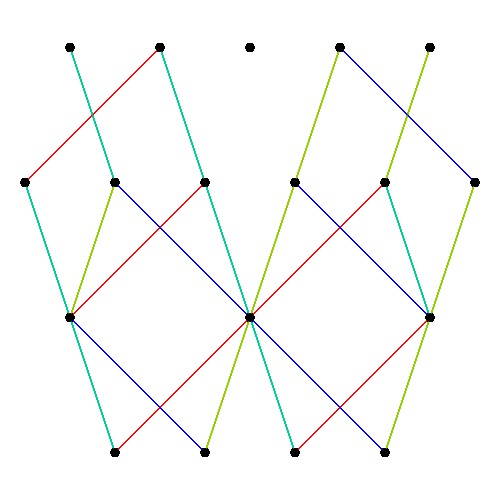
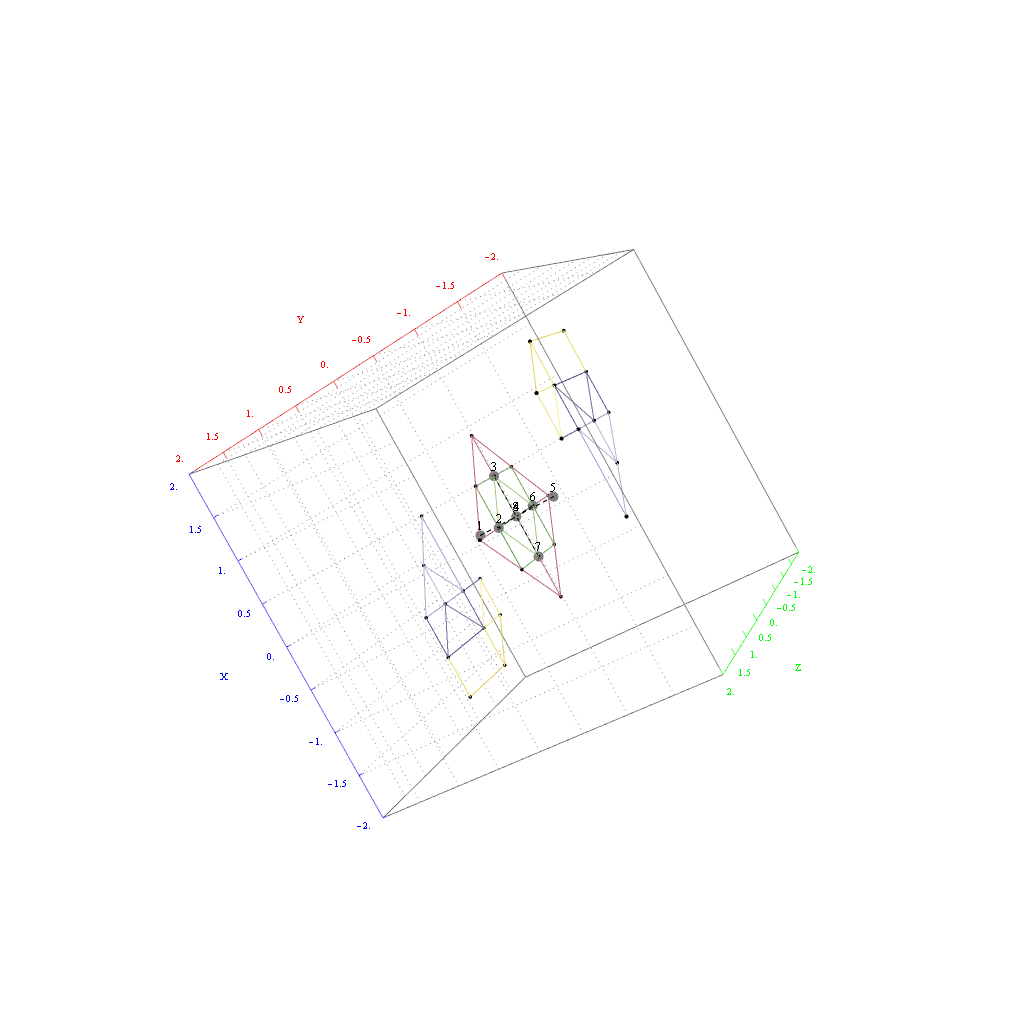
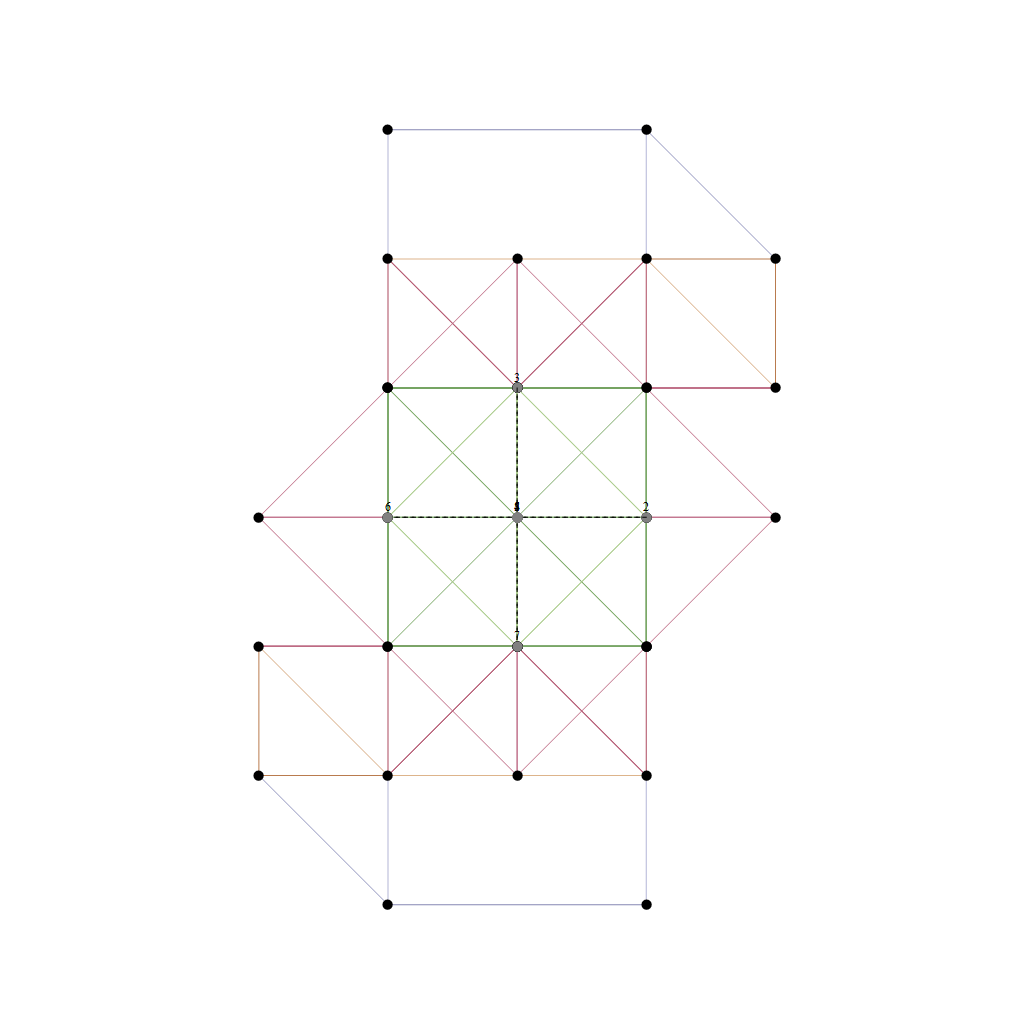
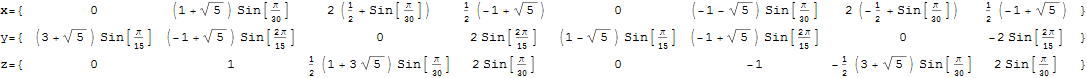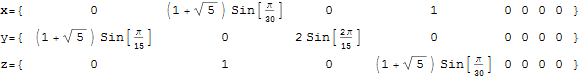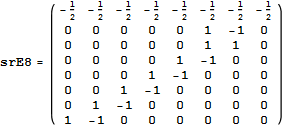The full paper with appendix can be found on this site, or w/o appendix on viXra. (13 pages, 14 figures, 20Mb). The 22 page appendix contains the E8 algebra roots, Hasse diagram, and a complete integrated E8-particle-octonion list.
Abstract:
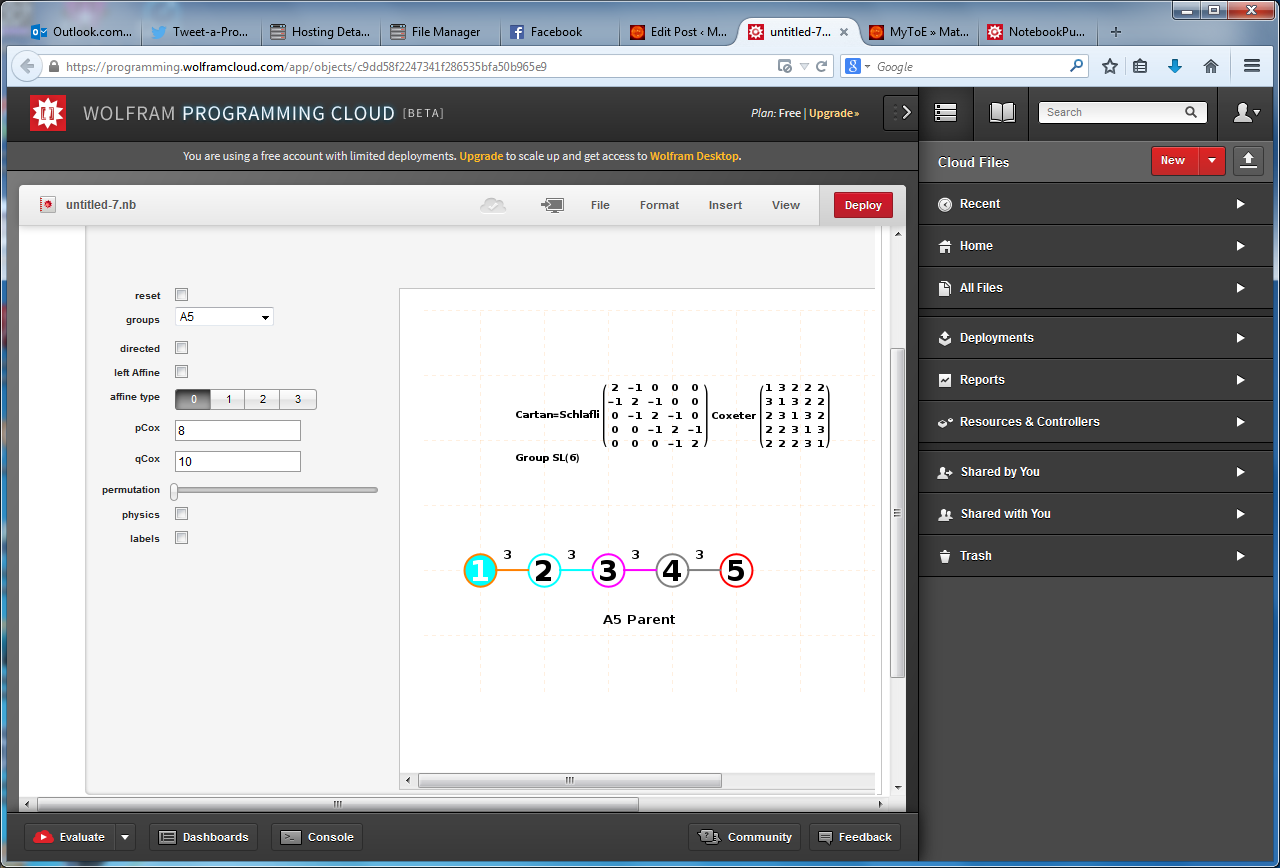
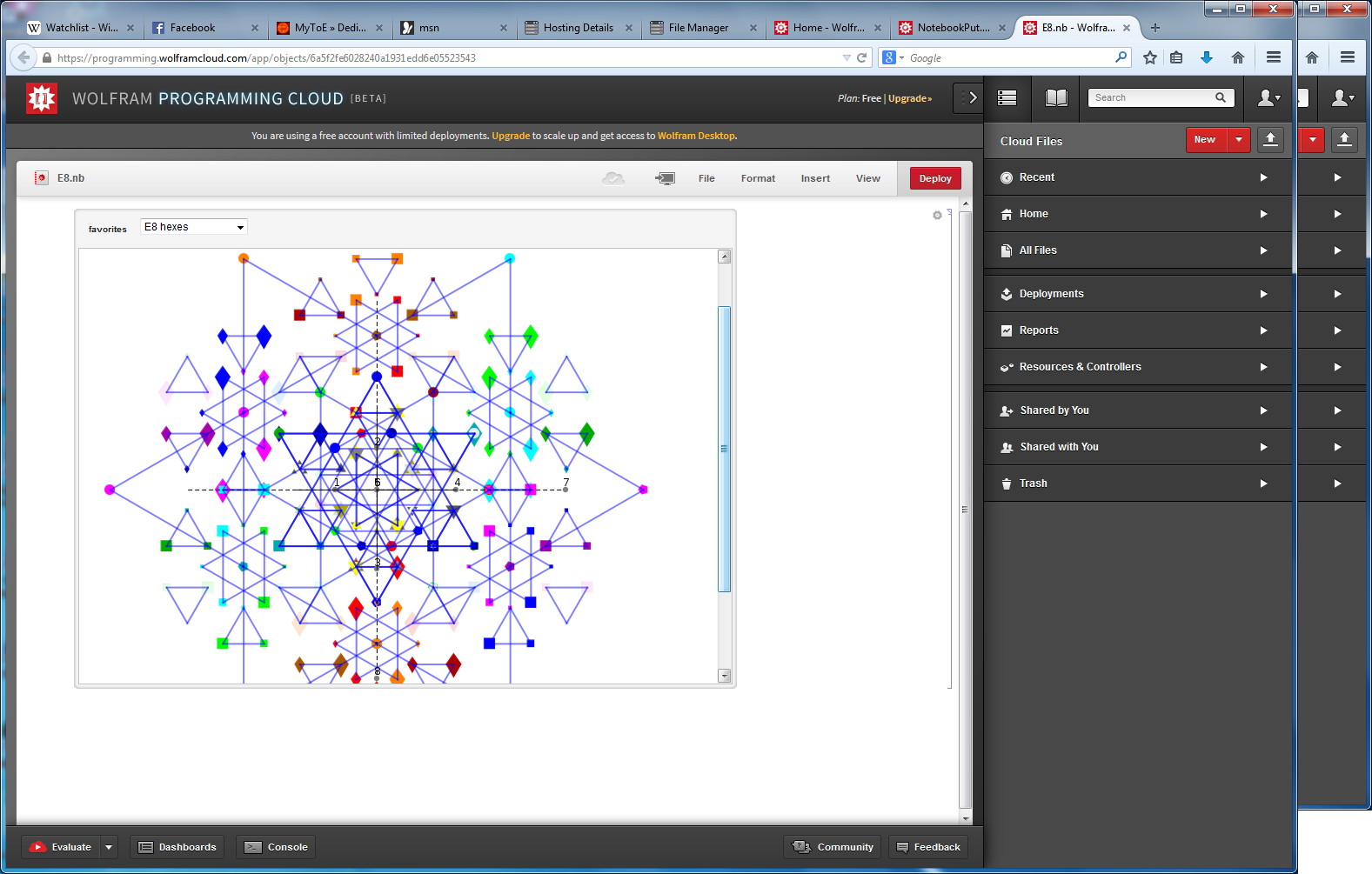
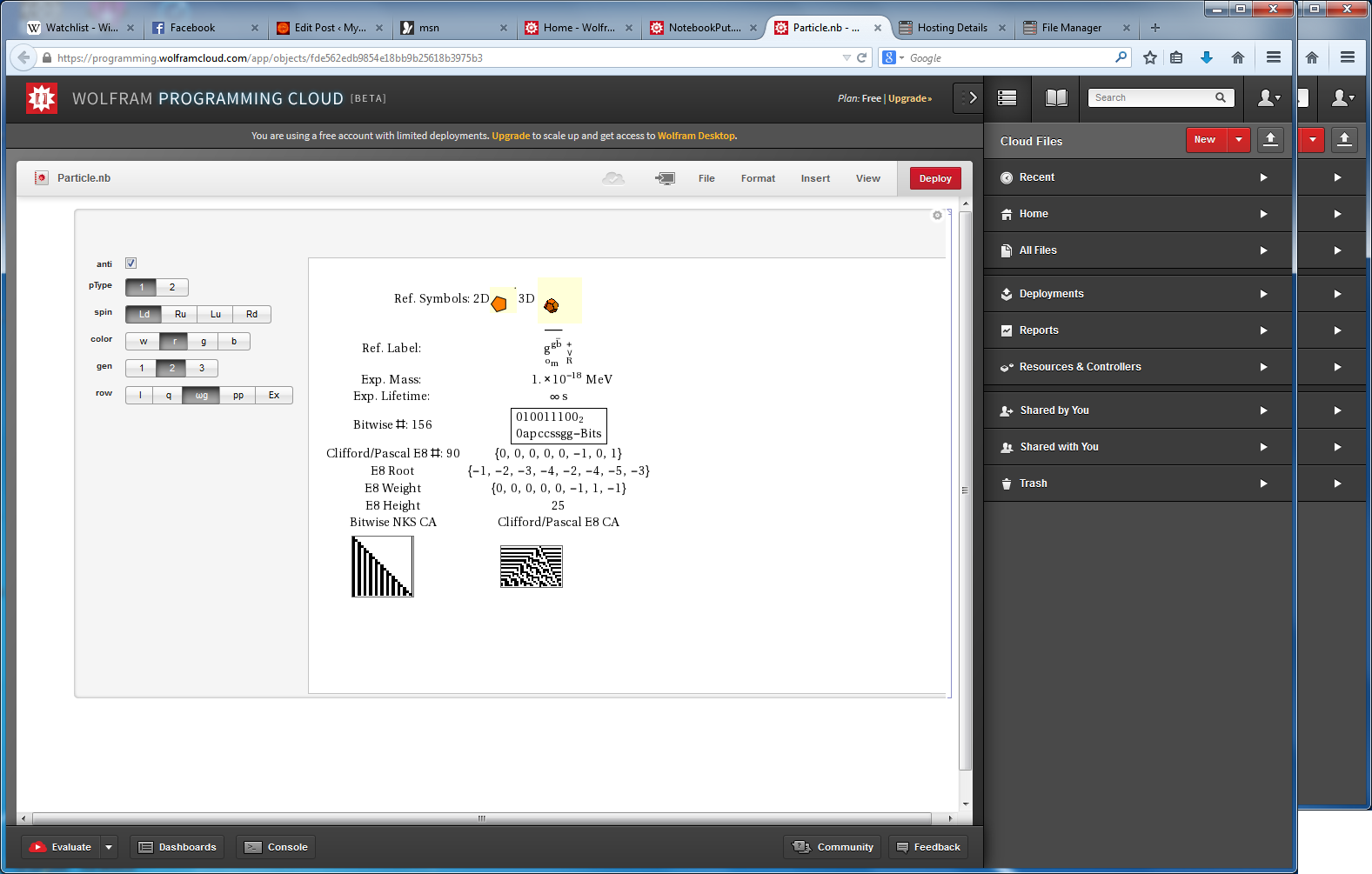
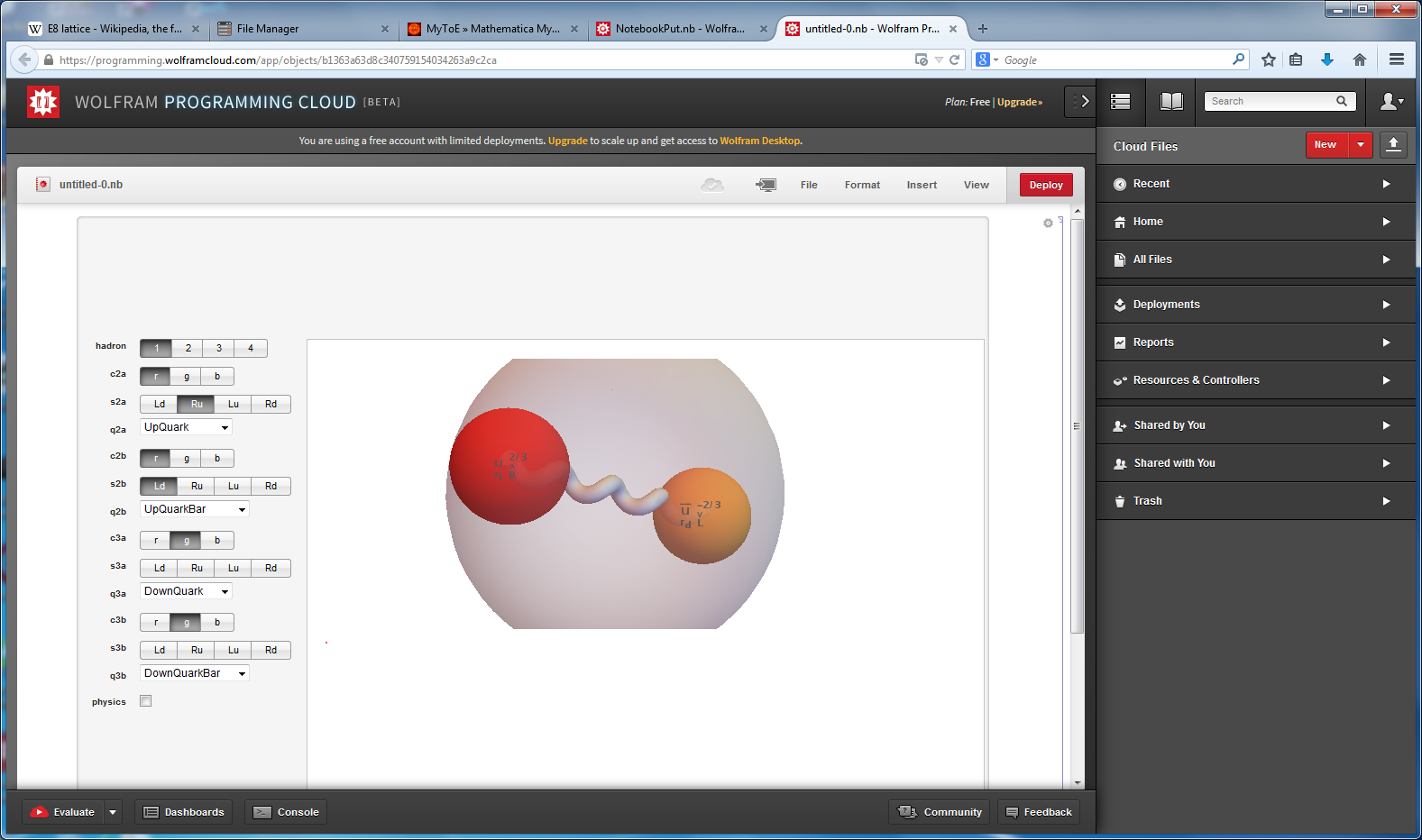
This paper will present various techniques for visualizing a split real even E8 representation in 2 and 3 dimensions using an E8 to H4 folding matrix. This matrix is shown to be useful in providing direct relationships between E8 and the lower dimensional Dynkin and Coxeter-Dynkin geometries contained within it, geometries that are visualized in the form of real and virtual 3 dimensional objects. A direct linkage between E8, the folding matrix, fundamental physics particles in an extended Standard Model GraviGUT, quaternions, and octonions is introduced, and its importance is investigated and described.
If you would like to cite this, you can use this BibTex format if you like (remove the LaTex href tag structure if you don’t use the hyperref package):