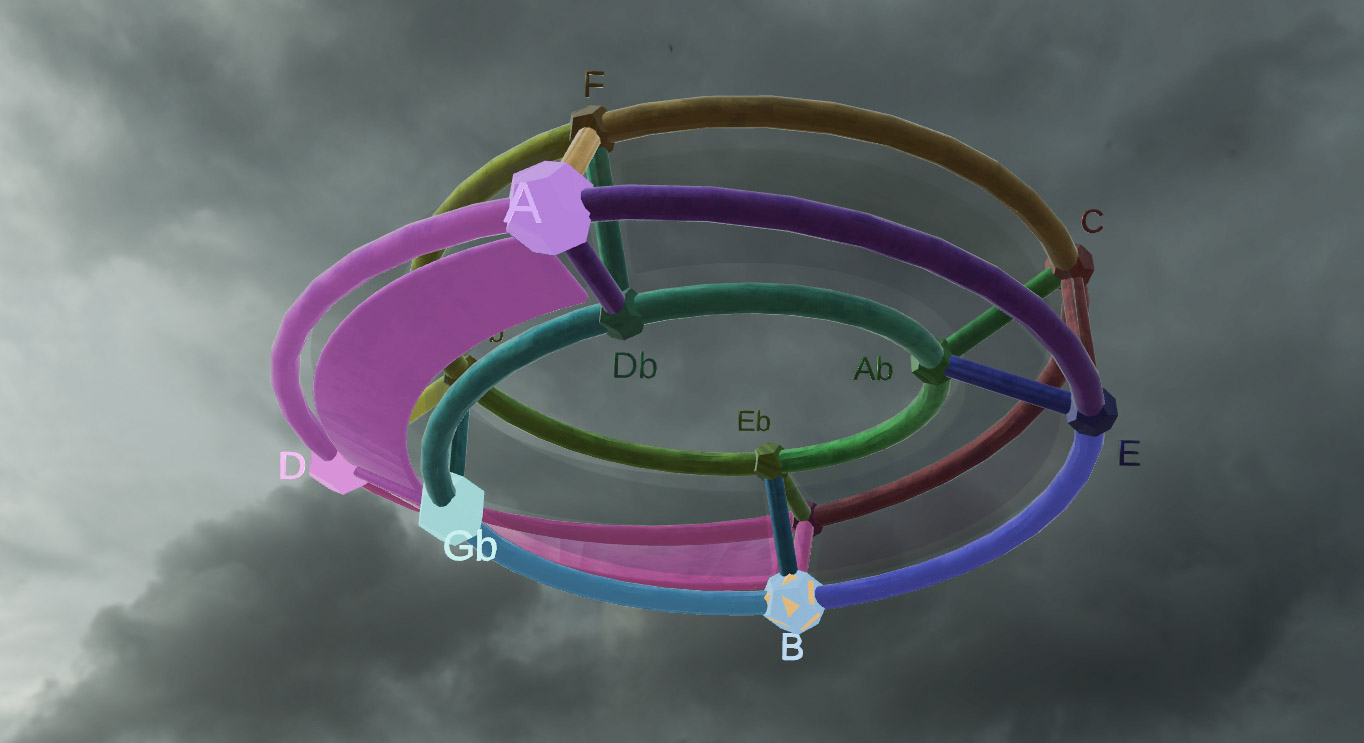
This post is a work in process, so check back for the latest visualizations and data. Today (Dec. 31 2025) I finally finished a major update to the section SVG files. Have a blessed New Year for 2026 and beyond!

So if you downloaded the previous files from the first update of 12/16/2025, you may want to take another look, as some of the output had anomalous data that didn’t render, along with other errors (due to the way I computed approximate equality between norms). In order to get this done, I realized I was thrashing my Solid State Drive (SSD) due to memory swapping. It died due to that (SSDs have limited writes!), so I had to rebuild the machine with 64 Gb RAM to keep the computations in RAM.

Drop me an email if you find anything that needs correction.

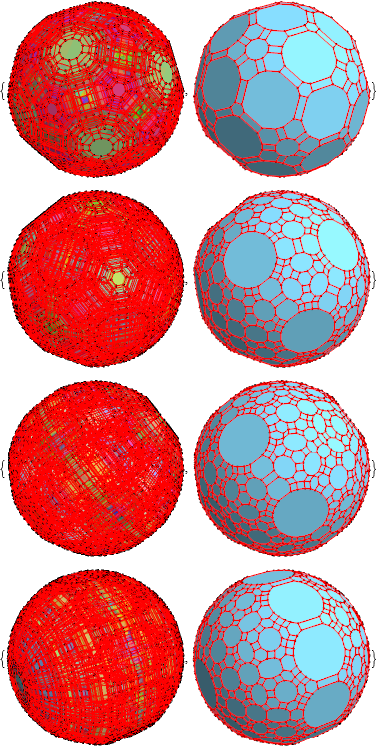
The full Mathematica NB and SVG files for all of the combined and overall hull pairs (like the above PNG), but in all 15 Weyl orbit permutations of the 600-cell are here (NB 65 Mb) and here (SVG 45 Mb). The same for the F4 disphenoidal 288-cells are here (NB 23 Mb) and here (SVG 12 Mb).

Please see several prior posts presenting (with now much improved) sectioning visualizations of Coxeter’s Regular Polytope book Table V here, 120-diminished rectified 120-cell (aka. Swirl-Prism) here, and 90=6×15 matrices of links to the 15 Weyl orbit permutations (with associated Coxeter-Dynkin diagrams) of the 4-polytope 5, 16/8, 24, 600/120 cell sections/animations here.

This post now presents the 60=[4 cell-first, vertex-first, face-first, and edge-first orientations of 15 Weyl orbits] visualizations for both the self-dual 24-cell and 600-cell (which has the same content as its dual the 120-cell by the symmetry of the Coxeter-Dynkin diagram).

These are generated using 4 quaternionic rotations. The one off a main orbit orientation (i.e. using the e₀=1 identity quaternion rotation) is either the vertex or cell first orientation for each of the 15 Weyl orbit permutations, with the other rotation being e₂+e₃. Then for edge and face first orientation rotations, depending on the 24, 288, or 600 cell type, they will be one of either e₁+e₂+e₃ & e₁+2e₂+e₃ (for 24 & 288 cells) or e₀+φe₁ & e₀+e₁+e₂ (for 600/120 cells).

vZome has a very nice (and fun) website curated by Scott Vorthmann with some information on quaternion generation of cell-vertex-face-edge first orientations here.

The main orbits are (or can also be) generated by using quaternions and the A, B-C, D-F, E-H group theoretic relationships. I actually use octonionic multiplication operations with multiplication tables from the 480 possible where the first (of 7 triads) are the quaternion of 0123. This means the last four dimensions of the octonion (i.e. 4567 or {l, li, lj, lk}) are {0,0,0,0}.

You can navigate the matrices of links below or simply download the ZIP files for the 600-cell ZIP here (1 Gb), 288-cell here (225 Mb), and 24-cell here (150 Mb).

SVG section visualizations:

Orientations for H4 600-cell SVG section file links:

              Cell                          Vertex                             Edge                                 Face

Orientations for F4 Disphenoidal 288-cell SVG section file links:

              Cell                          Vertex                             Edge                                 Face

Orientations for D4 24-cell SVG section file links:

              Cell                          Vertex                             Edge                                 Face

MP3 section animations:

Orientations for H4 600-cell MP3 section animation file links:

              Cell                          Vertex                             Edge                                 Face

Orientations for F4 Disphenoidal 288-cell MP3 section animation file links:

              Cell                          Vertex                             Edge                                 Face

Orientations for D4 24-cell MP3 section animation file links:

              Cell                          Vertex                             Edge                                 Face

An interesting set of prisms are in the F4 disphenoidal 288-cell’s omni-truncated sections (below):

If you have access to Wolfram’s Mathematica, see my notebook with code and data that may be helpful here (135Mb). A PDF is here (65Mb). This has detail on the octonion (E8² and E8³) based constructions for both the 24D Leech lattices as well as the 16D Barnes-Wall lattice shown at the bottom of this post.

The Leech lattice is a sub-quotient of the largest of the sporadic finite simple groups, namely the Monster group. It is related to (and can be constructed by) E₈ and the 23rd Niemeier lattice of E₈³. The 24D Leech lattice is interesting to the physics of sphere packing, error-correcting codes, and possibly unifying General Relativity (GR) with Quantum Mechanics (QM). String theory was founded on the ideas related to its relationship to the Monster group and how 24 dimensions relate to the bosonic energy levels of the partition function on a torus. For more on the Monster and Group Theory, see my post here.

But taking things down a 8D (Bott periodic) notch, roughly speaking the 16D Barnes-Wall lattice is related to E₈ in the same way by BW₁₆=E₈².

I found some very nice recent visualizations on the BW₁₆ WP article by Misaki Ohta with related arXiv papers. He provided links to related code and data here. Below are my renderings using that provided information.

It is interesting to note that if one projects the 61440 2nd shortest 16D vectors of BW₁₆  using orthogonal projection mapping ℝ¹⁶ → ℝ² (i.e. to B₈ basis vectors [x=Cos, y=Sin]@(0-15)π/8 used for E₈ below vs. the proper (0-15)π/16 B₁₆ as done above), we get a similar result as projecting the 2nd shortest 8D vectors of E₈ using the same basis shown as grey vertices in Fig 2 of arXiv:2506.11725:

Projecting the 2160 2nd shortest 8D vectors of E₈ using the B₈ basis vectors including 69120 edges of 8D norm=√8 with colors assigned by projected edge length (notice the similarity in the vertex locations of the figure above):

Projecting the 4320 shortest 16D vectors of BW₁₆  using orthogonal projection mapping ℝ¹⁶ → ℝ² using the B₈ basis vectors [x=Cos, y=Sin]@(0-15)π/8 gives the results shown in Fig. 2 as red and blue vertices:

This time with edges colored by projected edge lengths:

Now, getting creative with the 16D projections of the 4230 BW₁₆, if we double the E8 Petrie basis vectors we get a similar result with 480+1 visible vertices with one at the origin w/240 overlapping vertices. There are 240 yellow with no overlaps and 240 blue with 16 overlaps each. There are 604800 norm=4 edges using roughly the same color pallet as my WP E₈ Petrie image. This makes it easier to see the difference between the 4230 BW₁₆ and the normal E₈ Petrie projection, which seem to share the grid-like pattern of the 24-cells within the folded E₈ = H₄ + φ H₄ :

This is the same as above, but using the 61440 vertex BW₁₆ with no edges (given there are millions of them). Please note that the number of visible vertices is the same as E8₂₄₁ at 2160!

Octonion based Barnes-Wall and Leech Lattice visualizations based on my implementation of work from Geoffrey Dixon and Robert Wilson:

This page presents a comprehensive presentation of the 15 permutations of the six 4D polychora (i.e. 5, 16/8, 24, 600/120 cells). It presents them in full SVG format for convenient use in high quality academic papers on the topic (e.g. simply save the SVG and edit in Inkscape or other tool to produce PDF or PNG, etc.). You are free to use these under Creative Commons Attribution-ShareAlike 4.0 International CC BY-SA 4.0 with appropriate attribution.

My cell-first and vertex-first {5,3,3} 120-cell section visualizations with subgroup sections (when the inscribed solid has more than one permutation in its orbit) are available in Wikipedia Commons here and here. Let me know if you need customized hyper-complex and/or hyper-dimensional group-theoretic projection/section visualizations, as my extensive Mathematica code-base may be able to generate it.

The content below uses a 6×15 matrix of 4D to 3D projections of the convex hulls, each with a link to a page with that objects Coxeter section decomposition. I want to give a shout-out (cite) qfbox.info and polytope.miraheze.org for providing vertex coordinates used in the creation of the objects.

There is also another 6×15 table with links to video animations of the sections in the 4D to 3D flatlander from Left/Right (or minus to plus). This is an analog of 3D objects passing through the 2D planar world of flatlanders.

Also available is a Mathematica notebook (360Mb) with code to produce the 4D vertex data as well as the visualized interactive 3D objects. See also an overview of these lists explained in a this Powerpoint presentation, which covers the isomorphisms between them due to the symmetries in the A4, BC4, and H4 Coxeter-Dynkin diagrams that represent them.

Links to the SVG Section Files

Links to Sectioning MP4 Video Animations (i.e. 4D to 3D Flatlander)

For completeness, I am also including a table of 3D polyhedra, namely the Platonic, Archimedean, and Catalan Solids including
their irregular and chiral forms. These were created using
quaternion Weyl orbits directly from the A3, B3, and H3 group
symmetries

.

Another post with more detail on the 5-cell (A4) SU(5)->SU(4) maximal subgroup content generated via quaternions is here.

This is an analysis of the Coxeter Sections for the Swirl Prism 120-Diminished Rectified 600-Cell. The source data, which can be found on either of two polychora sites (qfbox.info and polytope.miraheze.org) seems to have two missing vertices 598 as generated by their permutation lists (vs. the intended 600). The data below, with an added two vertices of {-1,-1,φ³, φ³} and {1,-1,φ³, φ³} in the suspected error sections #3 & #15, is shown in data and 3D convex hull and Coxeter sectioning forms.

This is a post to present a new visualization that algorithmically generates Coxeter’s Regular Polytopes Table V vertex & cell first 600-cell {3,3,5} & 120-cell {5,3,3} polytope sections and compares them with my convex hull projections. I have also visualized the face-first and edge-first versions which Coxeter never addressed. The convex hulls of these match those presented by Robert Webb’s Stella 4D.

The base (H4) objects are generated (from E8 actually) using a interactive group theoretic hypercomplex (octonion/quaternion) hyperdimensional (nD with n<9) Geometric Algebra (GA) / Space-Time Algebra (STA) capable symbolic engine which I created using Mathematica.

These are 4D rotated into vertex/cell/face/edge and then grouped & sorted palindromically using Coxeter’s numbering and scaling. See here, here and here for the PDF, interactive 3D Mathematica Notebook, and Wolfram Cloud (respectively). For best performance, I suggest using the free Wolfram Player if you don’t own a Mathematica license for local manipulation.

The hyper-dimensional (4D) vertices used in these panels were also used to generate Koca’s referenced dual snub-24-cell as visualized on the that Wikipedia page.

This is unique (AFAIK). Several of the Table V section entries are not identified by name. This is sometimes due to the irregular faces such that they lack a formal name (e.g. Coxeter labels section 15 of the vertex first {5,3,3} 120-cell as a 1+8 octahedron aka. an octahedron and an irregular truncated octahedron).

Other times it seems they were simply not recognized due to lack of visualization (e.g. while section 6 (& palindromically paired section 10) of the cell first {5,3,3} 120-cell are labeled as rhombicosidodecahedra, section 8 (and my hull #8) is also an irregular form of the rhombicosidodecahedron. Also on that object, sections 4, 5 (& 12, 11 respectively) are irregular truncated icosahedrons.

On the cell first {5,3,3} 600-cell, unidentified sections 5, 6 (& 11, 10) are seen to be truncated tetrahedra, and 4 (& 12) are irregular cuboctahedra.

As already referenced above, the most irregular is the vertex first {5,3,3} 120-cell with unidentified sections 2, 4 (& 28, 26) now seen as truncated tetrahedra, sections 6, 14 (& 24, 16) as irregular truncated octahedra, and sections 10 (& 20) as irregular cuboctahedra. Section 9 (& 21) is a pair of truncated tetrahedrons (shown below).

Interestingly, Coxeter’s labels for sections 3, 11 (& 27, 19) are “2 icosahedra” (aka. truncated octahedra). Coxeter’s partial label on 12 (& 18) is “Tetrahedron” for the 4 vertices with 24 others unidentified. These 24 are irregular hexagon (8) and rectangular (6) faces forming an irregular truncated octahedron.

Section 7 (& 23) have 24 vertices that are two irregular cuboctahedra each with triangular (8) and rectangle (6) faces.

Another notable section is found with 9-gon or nonagon faces in sections 13 (& 17), which are generated by the chiral left/right “chamfered tetrahedrons” (3 per corner).

This likely derives from the 8-simplex A8 SU(9) as a subgroup of E8 as shown in the E8 subgroup tree (with more detail in this post). This folds to the H4 family of polytopes via my E8 <-> H4 folding matrix.

Since Coxeter never presented any {3,3,5} / {5,3,3} edge-first or face-first sectioning, here is my attempt at visualizing them. Please note the top section of the SVG output below now includes the XYZW vertex +/- & cyclic position permutation base values and other data collected in the process. There is also a 4D perspective projection below that uses a distance factor to change perspective. Note the differences between the edge-first (distance=1) vs. the face-first (distance=10) showing how the 4D perspective changes on both the {3,3,5} 600-cell / {5,3,3} 120-cell :

And just for more fun… here are combinations of the above displayed together producing 720 and 1200 vertex overall hulls that are nice and/or interesting!

Please see this Powerpoint for an interactive presentation (160 Mb).

Below (and here and here in PDF and Mathematica Notebook form or here on the Cloud) are the I & I’ 600-cells based on quaternion construction from the T & T’ 24-cells. These are also documented in Coxeter’s book “Regular Polytopes” as {3,3,5} vertex first & cell first “sections” in Table V (respectively) vs. the projections shown here with one of the four dimensions projected to 0 such that the hulls are palindromic pairs of sections (e.g. for 9 sections, section 1-4 pairs with 9-6 in vertex counts equal to hull vertex counts 1-4 and the center section 5 = hull 5).

For completeness, here are the J’ (alternate) & J form of the 120-cells based on quaternion construction from the T & T’ 24-cells. These are also documented in Coxeter’s book “Regular Polytopes” as {5,3,3} vertex first & cell first “sections” in Table V (respectively) vs. the projections shown here with one of the four dimensions projected to 0 such that the hulls are palindromic pairs of sections (e.g. for 31 sections, section 0-14 pairs with 30-16 in vertex counts equal to hull vertex counts 1-15 and the center section 15 = hull 16).

Below is an interactive Mathematica 4D visualization of the 8,16, 24, 120, and 600 cells (including alternate forms 24p, 120p, 600p). Click here or on the image below to open in a new tab.

For a paper with much of the content below, please see: theoryofeverything.org/TOE/JGM/E8_and_H4_in_QM_and_QC.pdf, and associated Mathematica notebook here.

The wreath product of the Monster group with Z2 (M ≀ Z2) is the BiMonster, a quotient of the Y₅₅₅ Dynkin diagram which contains six E8(Y₁₂₄) Dynkin diagrams and the 23rd Niemeier lattice E8³ root system. This can be reduced to Y₄₄₄ by applying the spider relation to E8³ .

Happy Family generations:
Red=Mathieu groups (1st)
Green=Leech lattice groups (2nd)
Blue=other Monster subquotients (3rd)
Black=Pariahs

Each color coded node represents one of the 24 Niemeier lattices, and the lines joining them represent the 24-dimensional odd unimodular lattices with no norm 1 vectors. The Coxeter number of the Niemeier lattice is to the left. The red node index number indicates the row in the table above.

”The Freudenthal magic square includes all of the exceptional Lie groups apart from G2, and it provides one possible approach to justify the assertion that ”the exceptional Lie groups all exist because of the octonions: G2 itself is the automorphism group of the octonions (also, it is in many ways like a classical Lie group because it is the stabilizer of a generic 3-form on a 7-dimensional vector space, see prehomogeneous vector space.”

This E8SubgroupTree.nb Mathematica Notebook (140Mb), viewable using the free viewable Player, which has interactive Tooltips on group nodes (with group data and Hasse diagram) and Tooltips on the subgroup edges (with its individual maximal embedding chart). Also in the notebook is one cell with a table of all of the above data plus the Dynkin diagram based maximal embedding charts and an example 2D or 3D polytope projection.