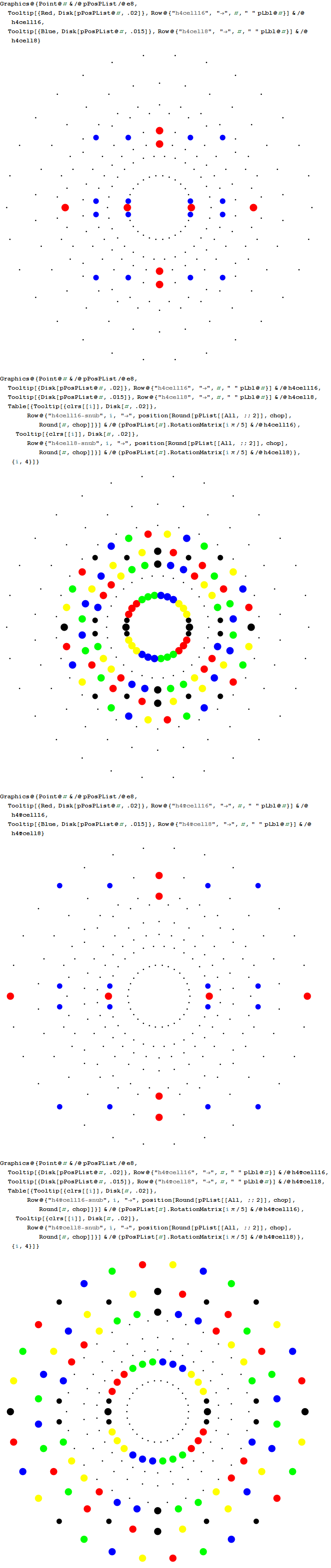
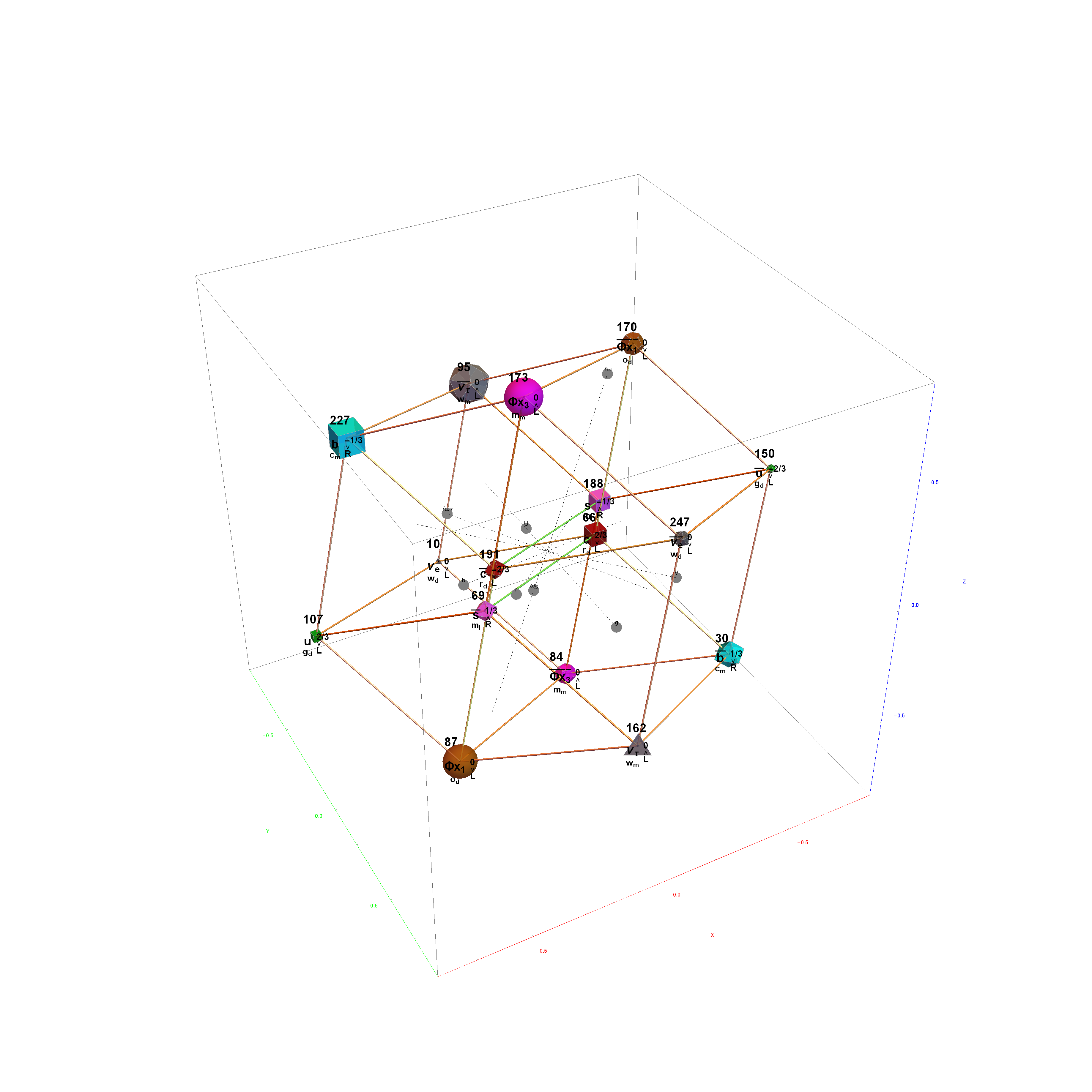
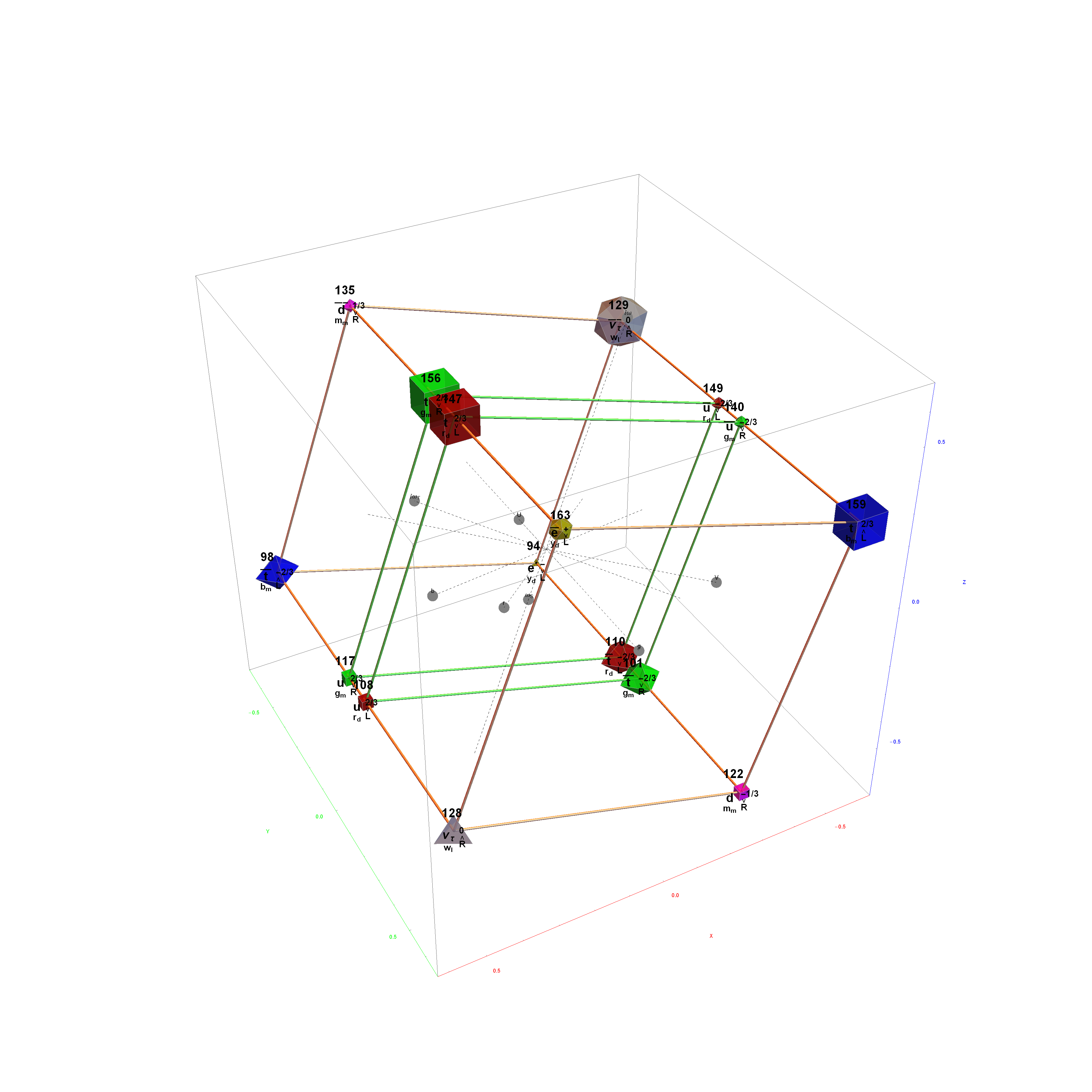
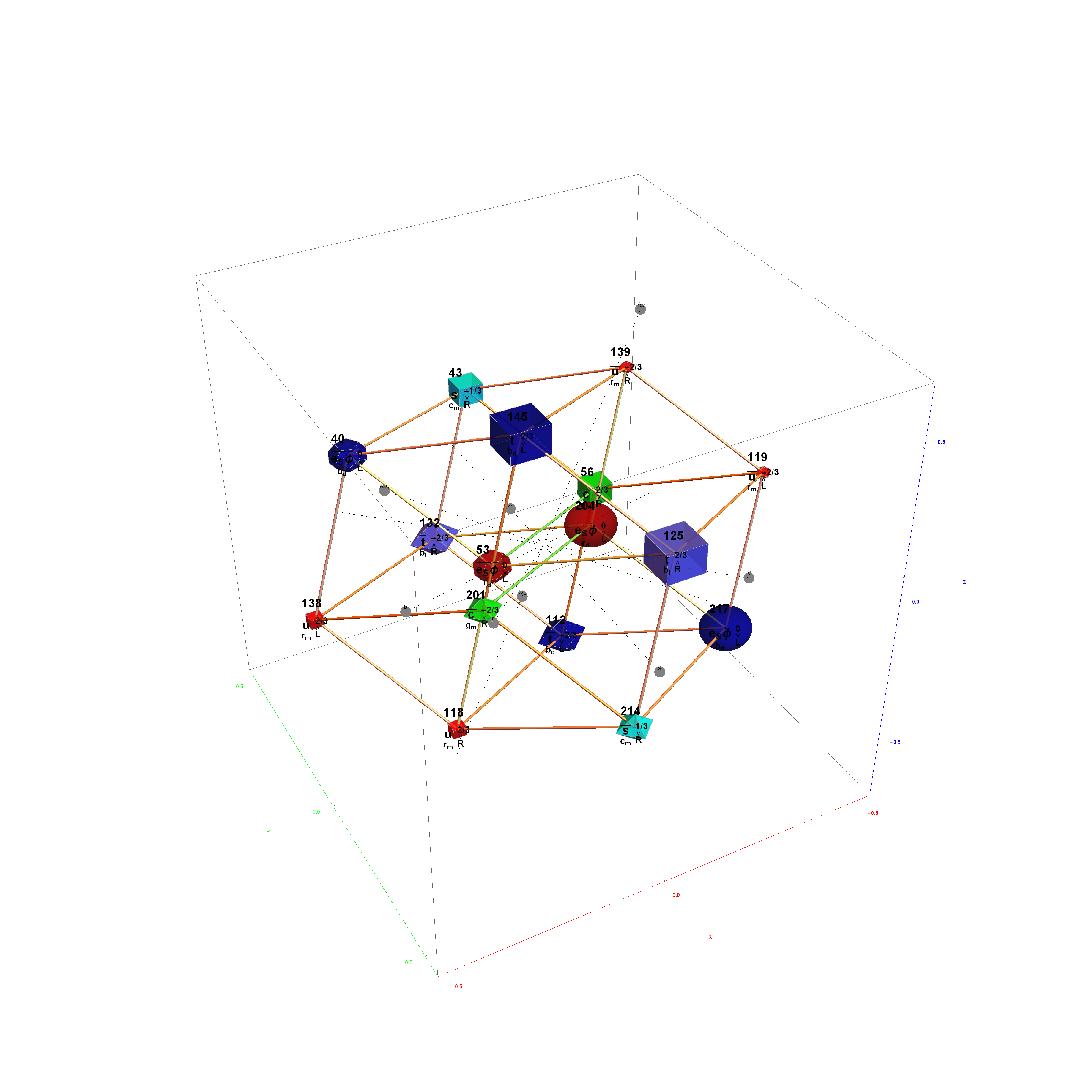
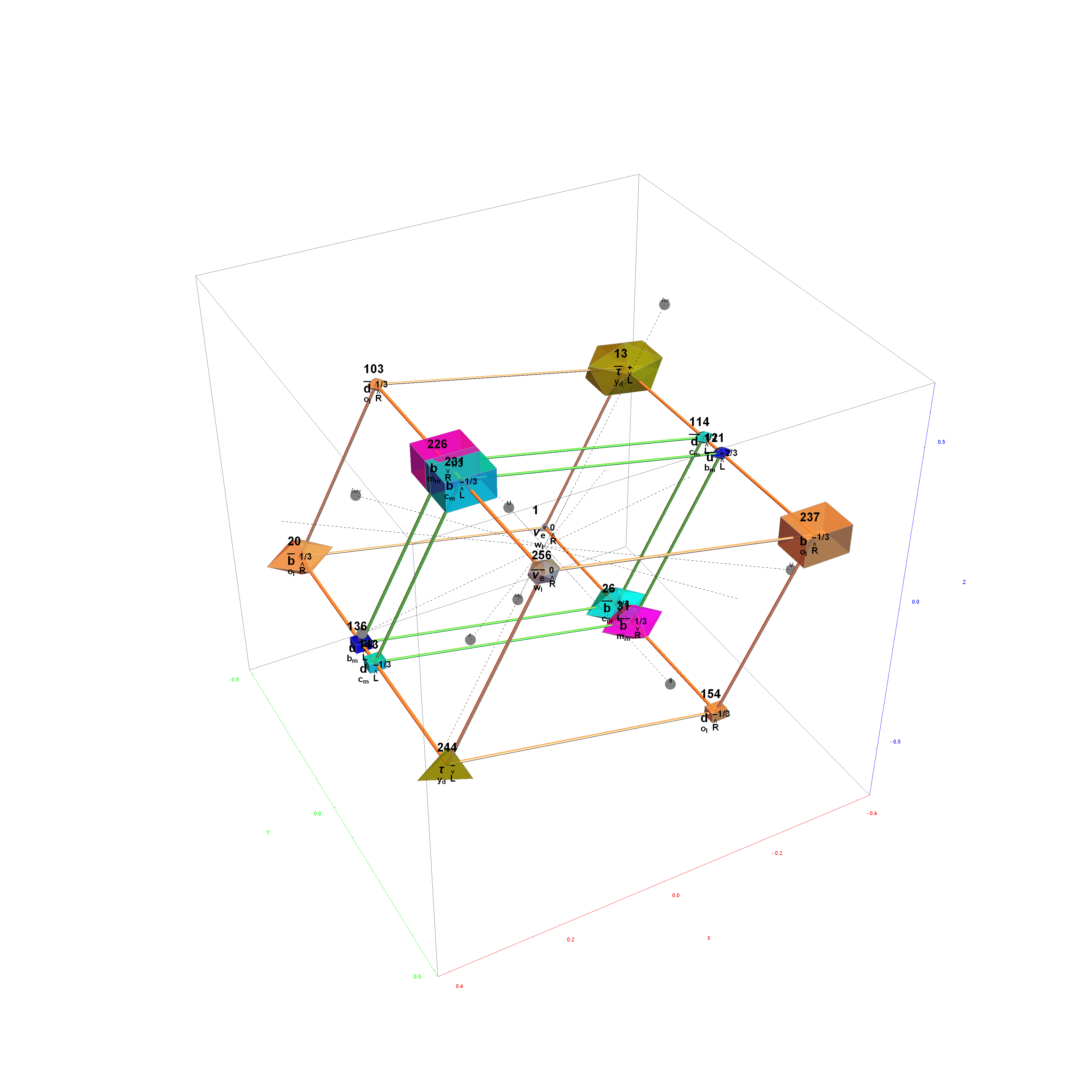
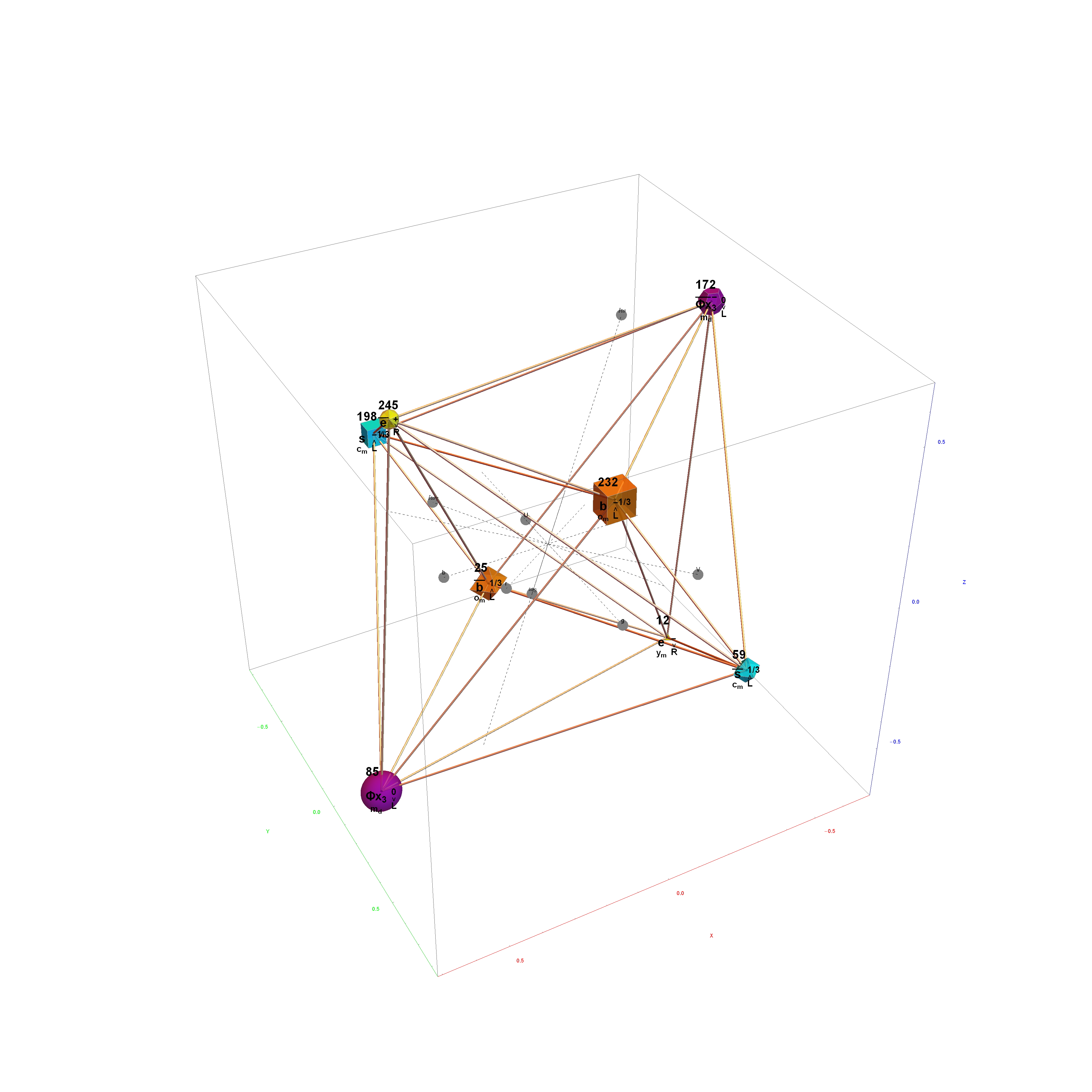
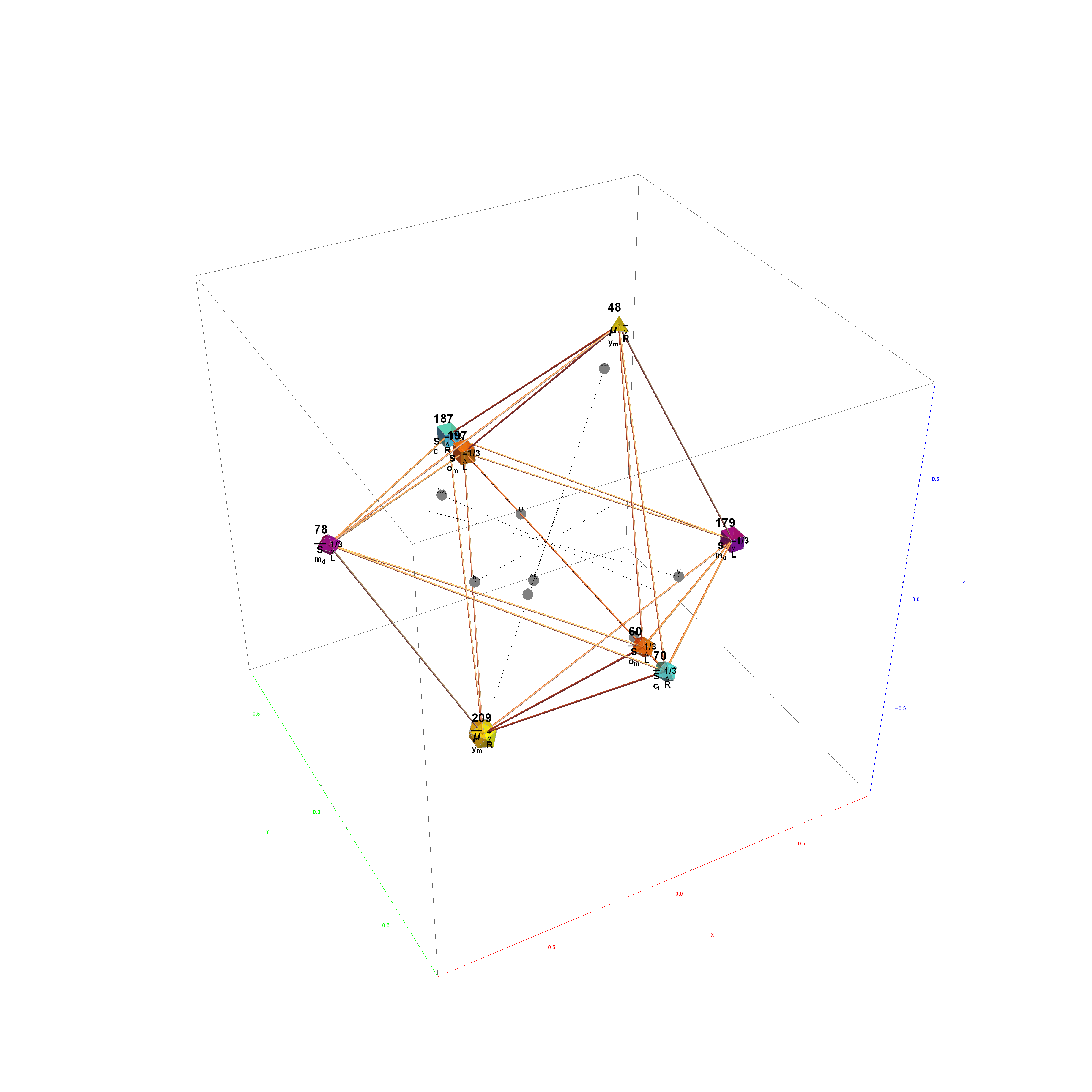
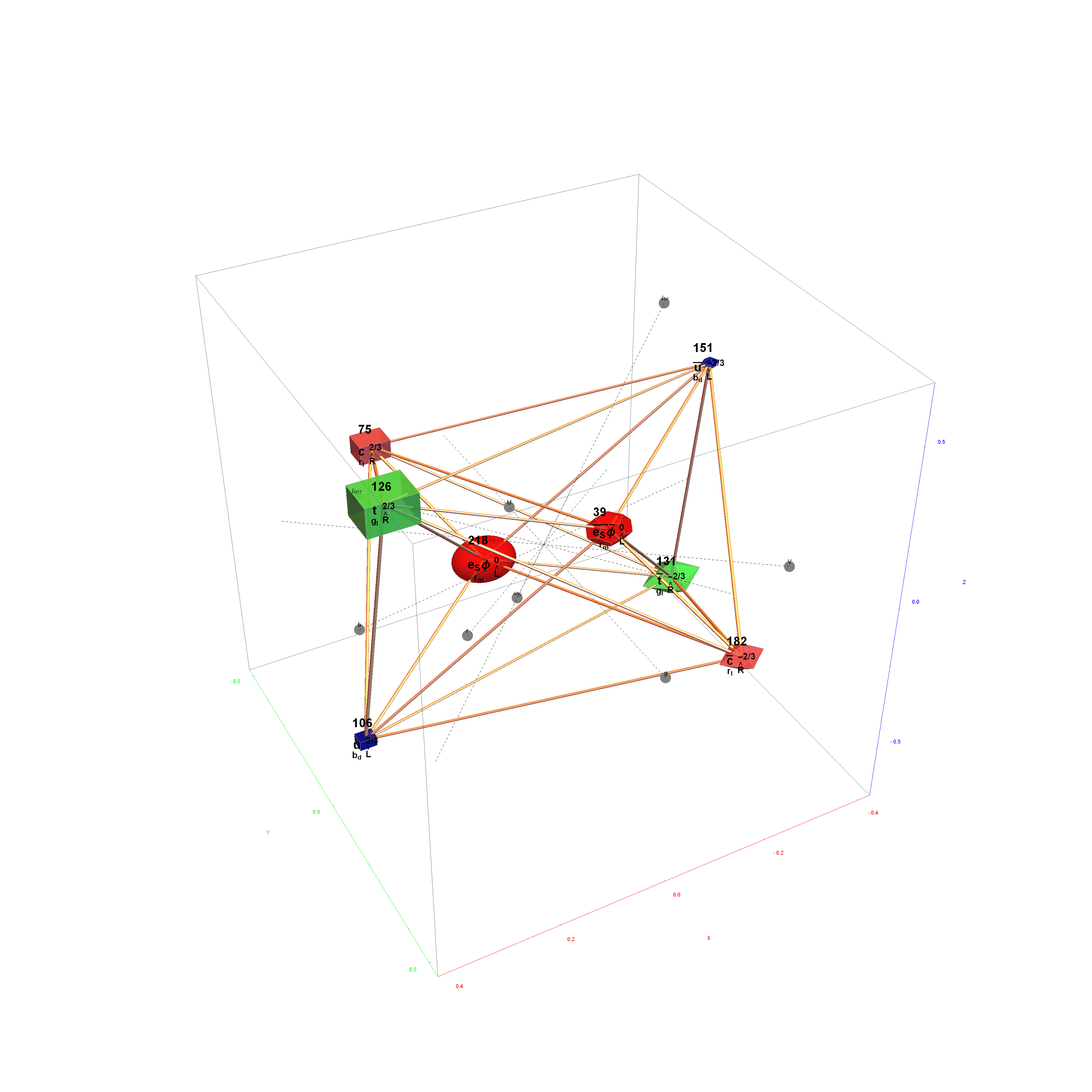
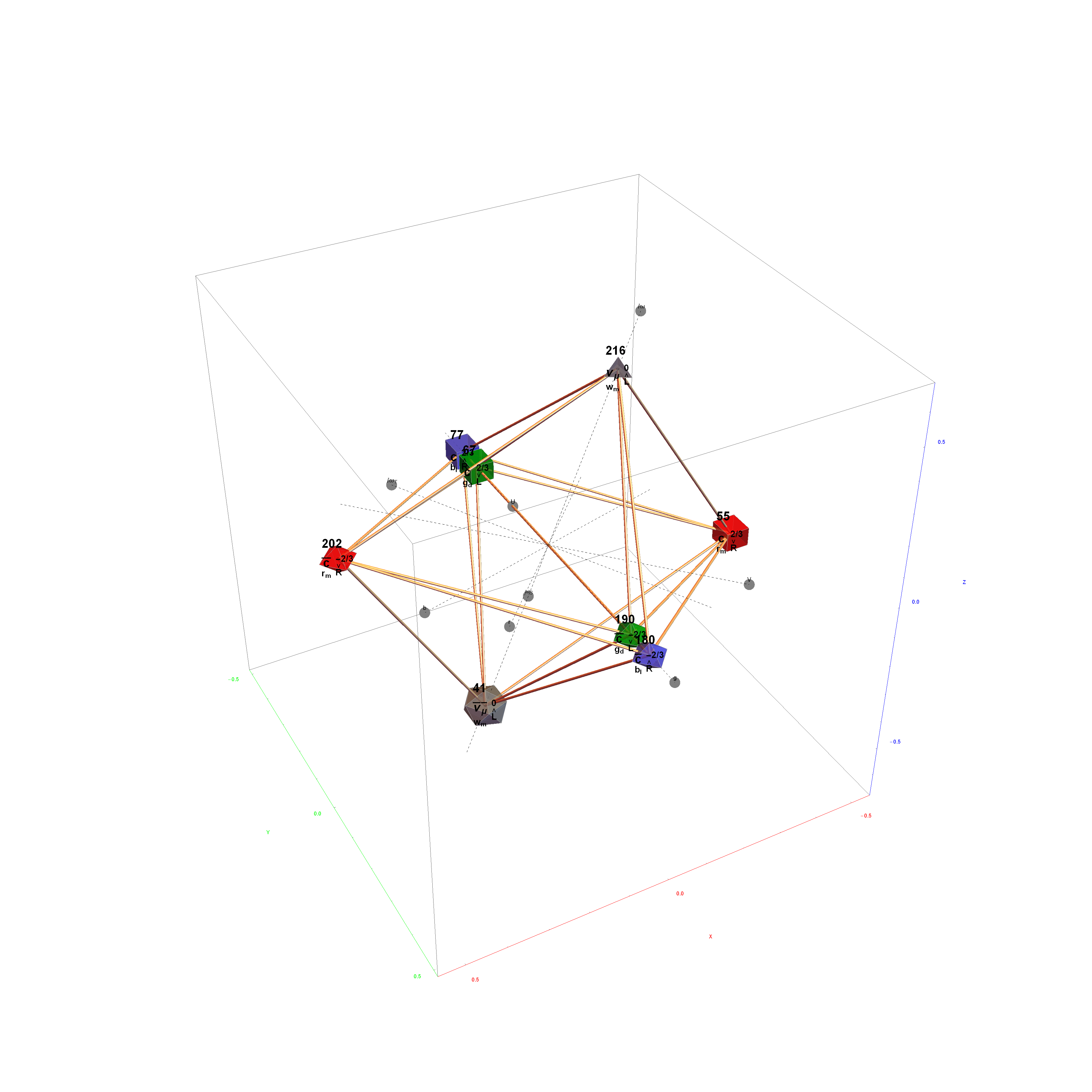
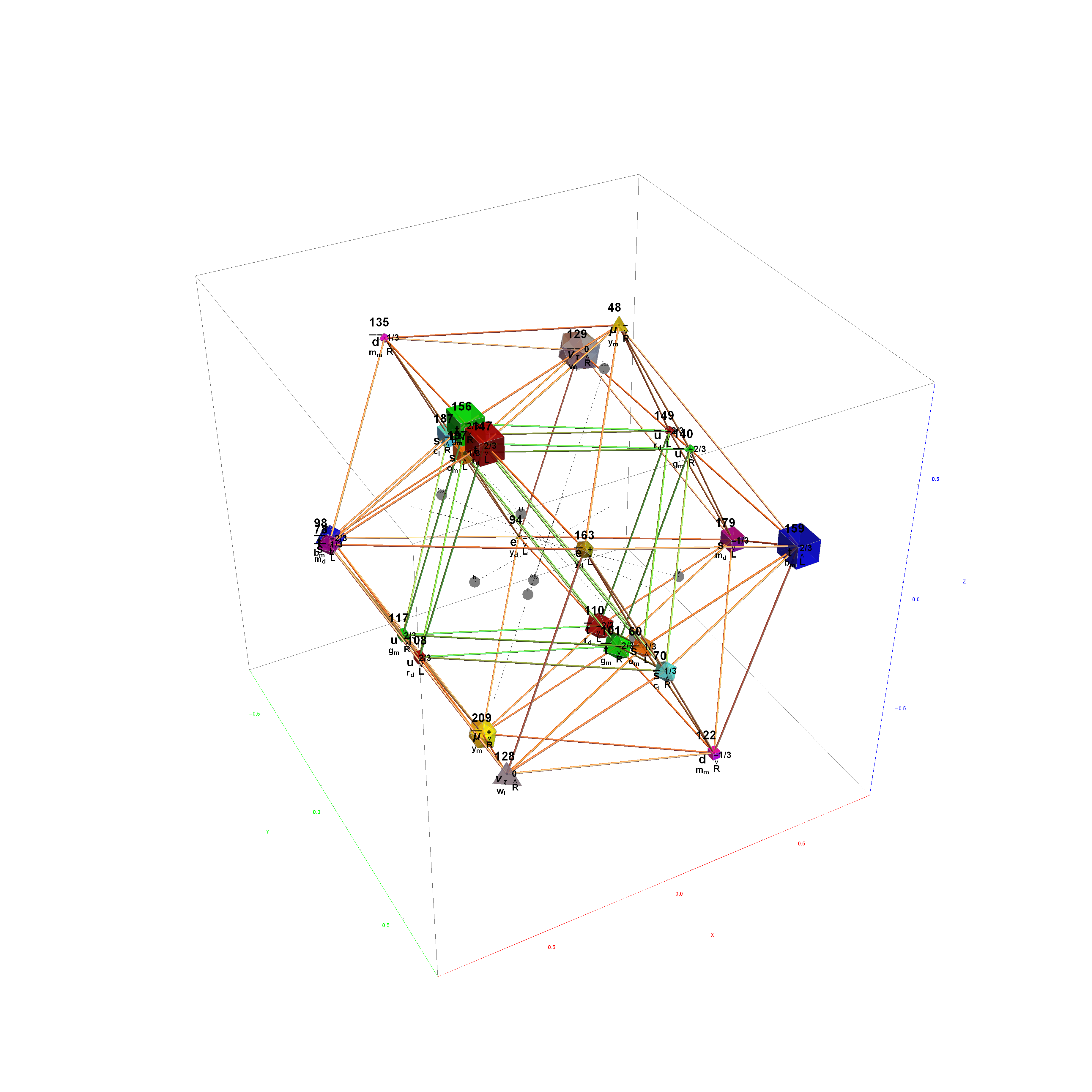
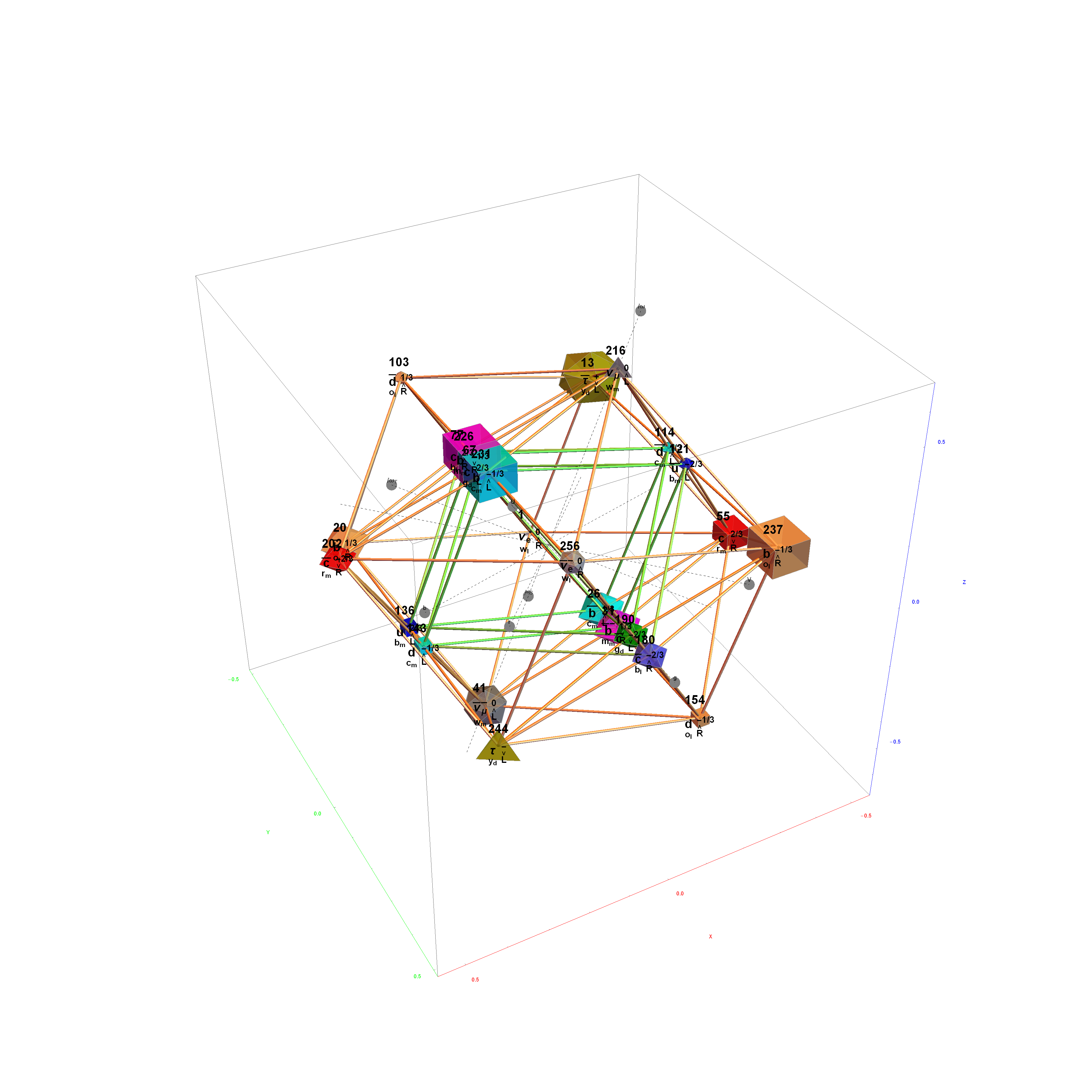
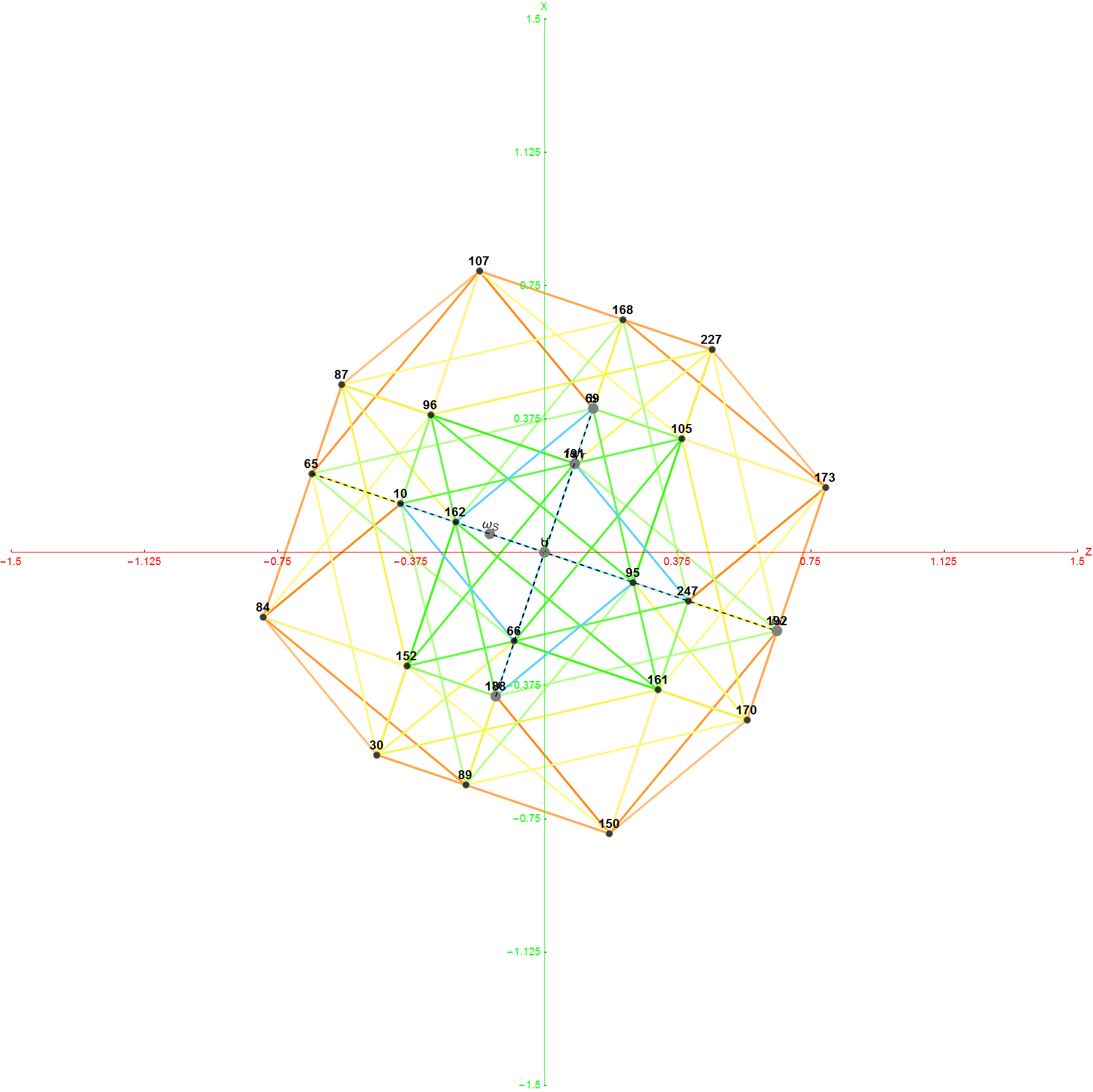
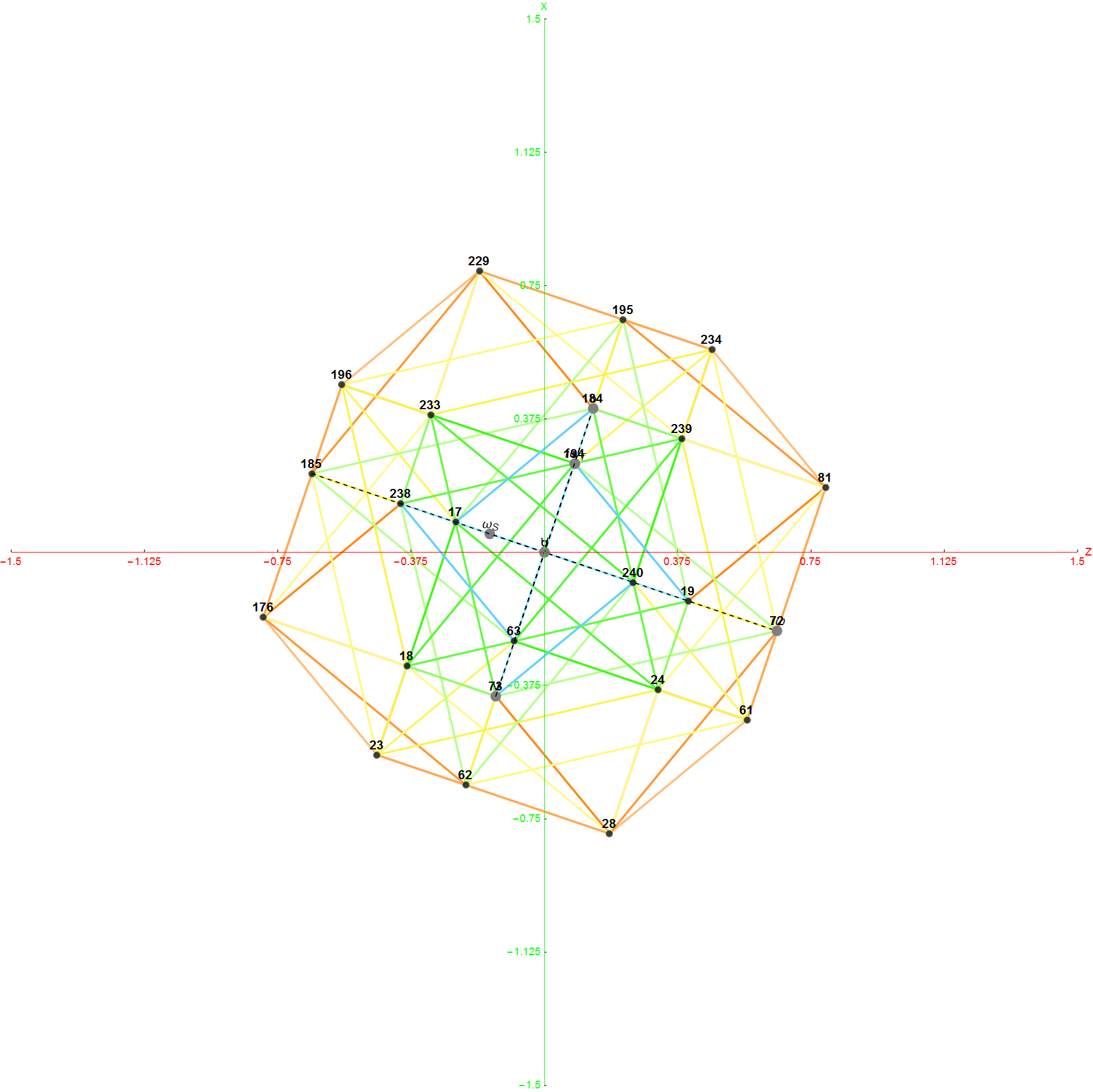
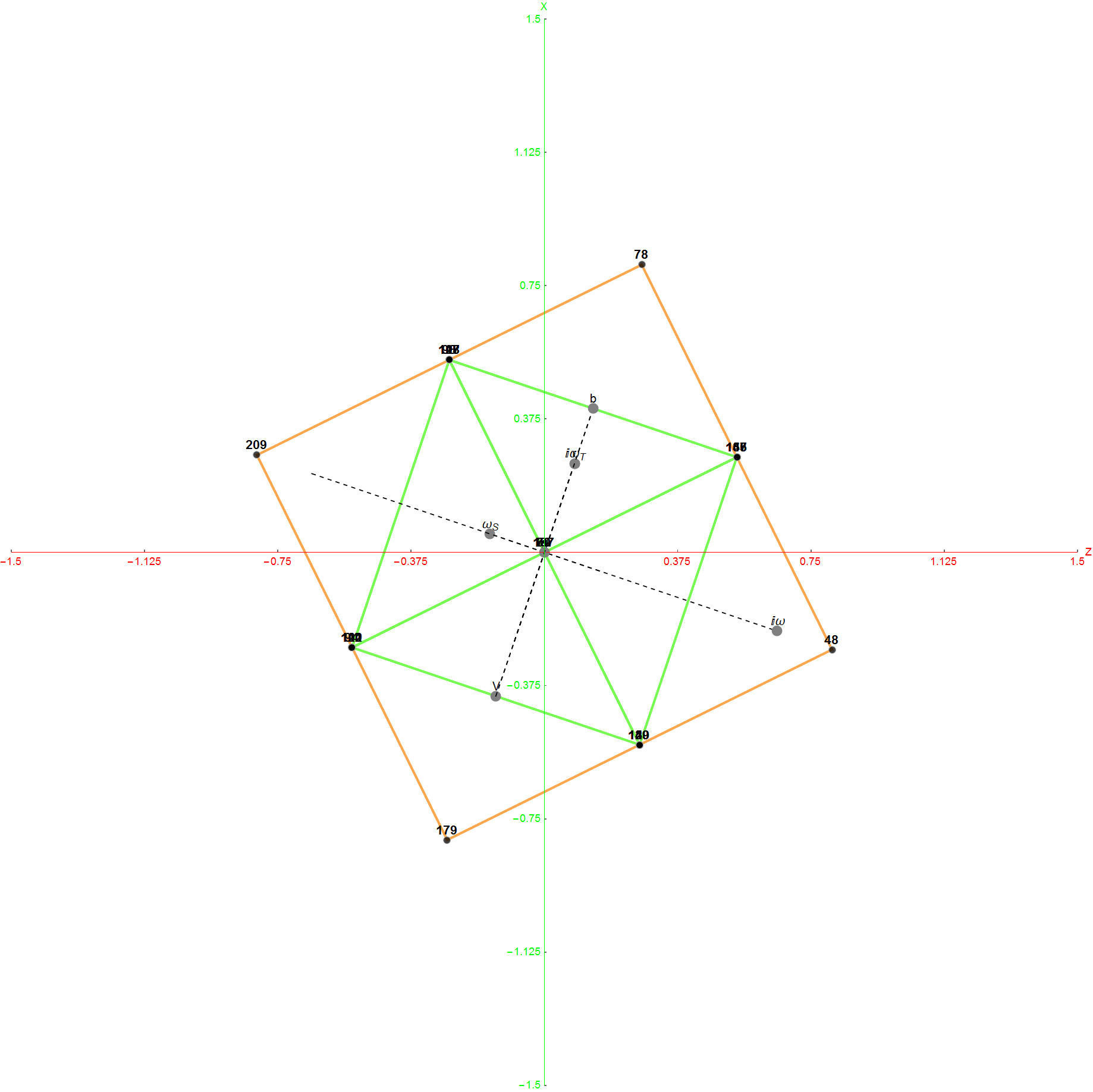
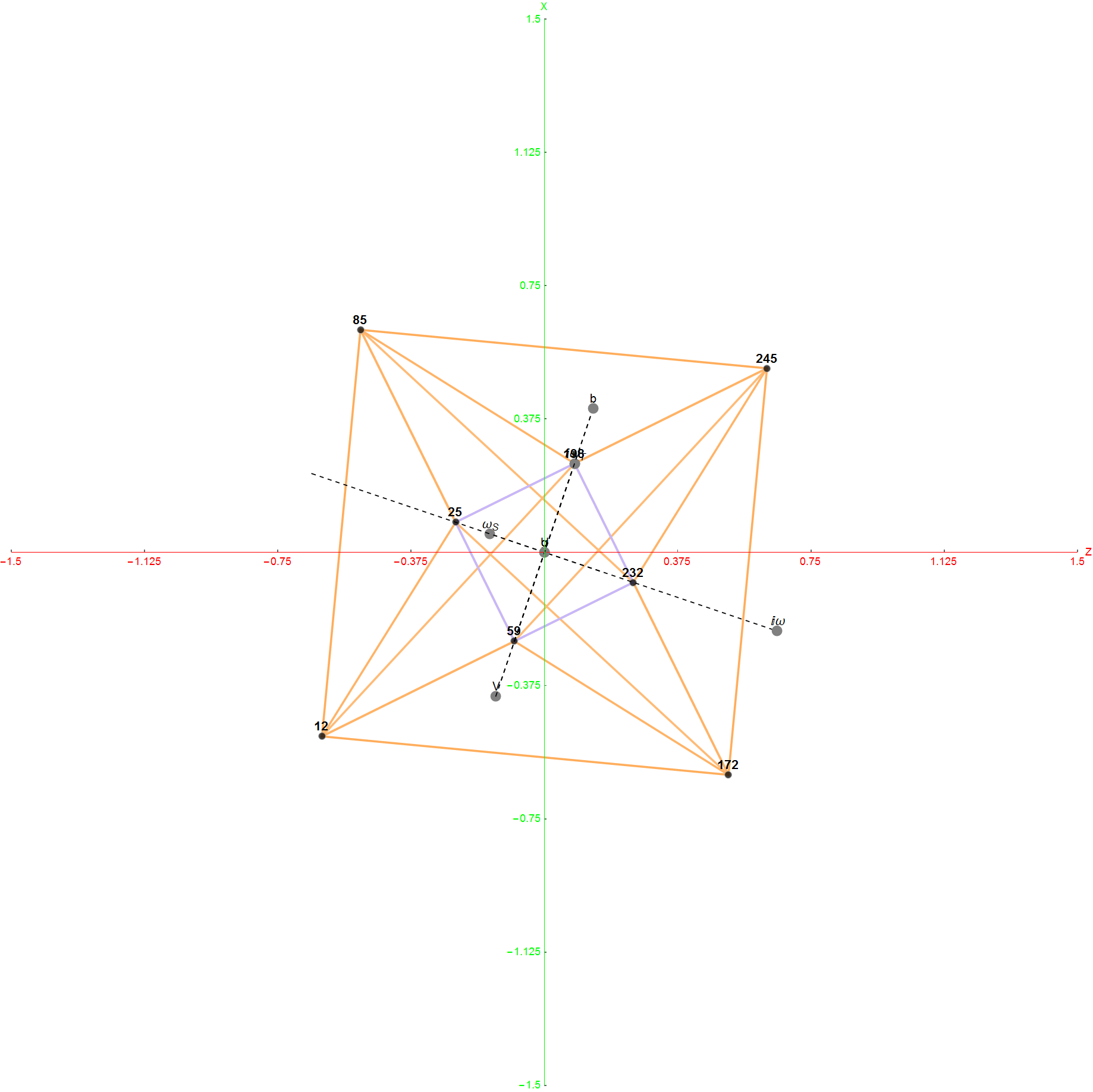
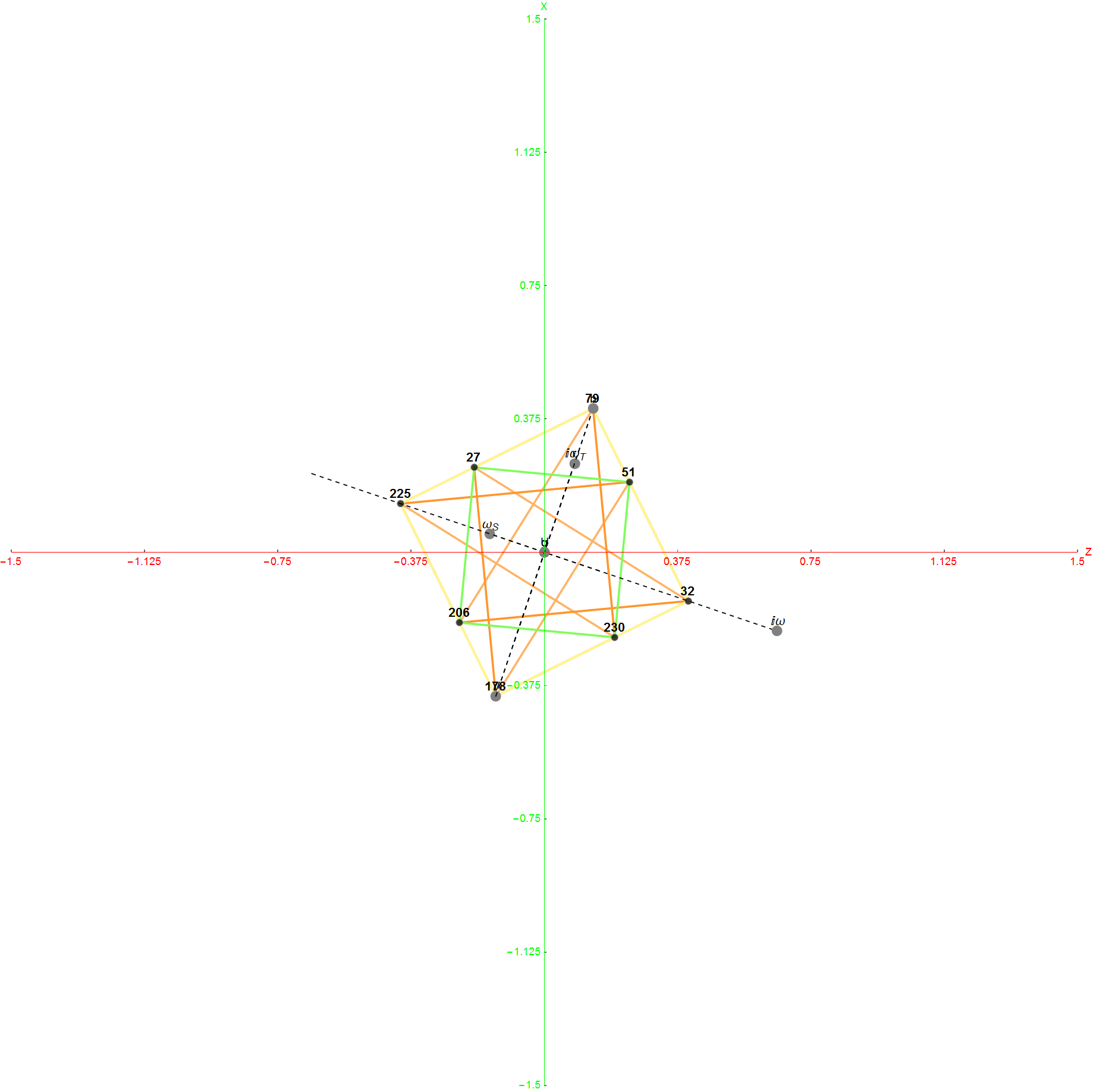
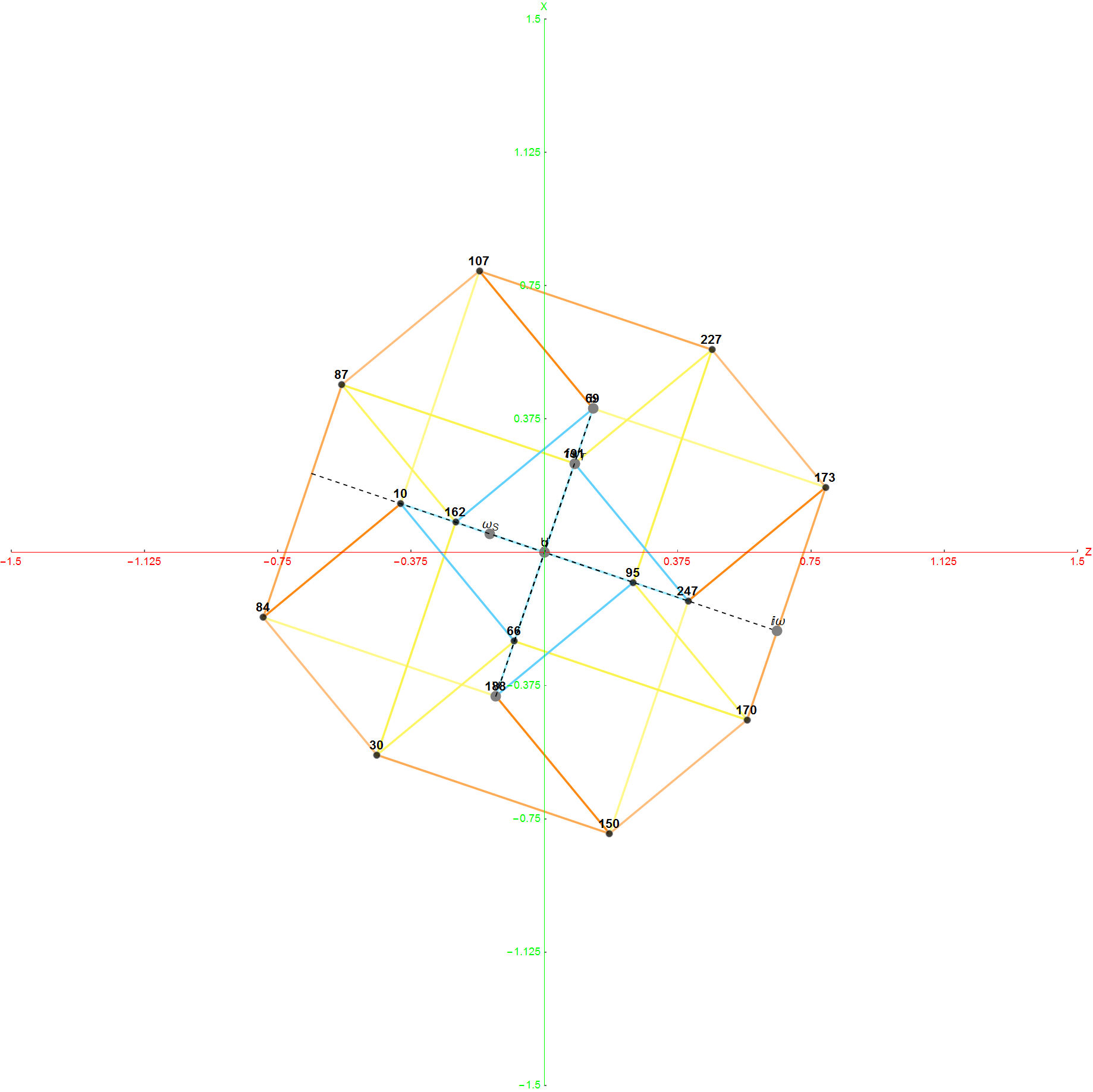
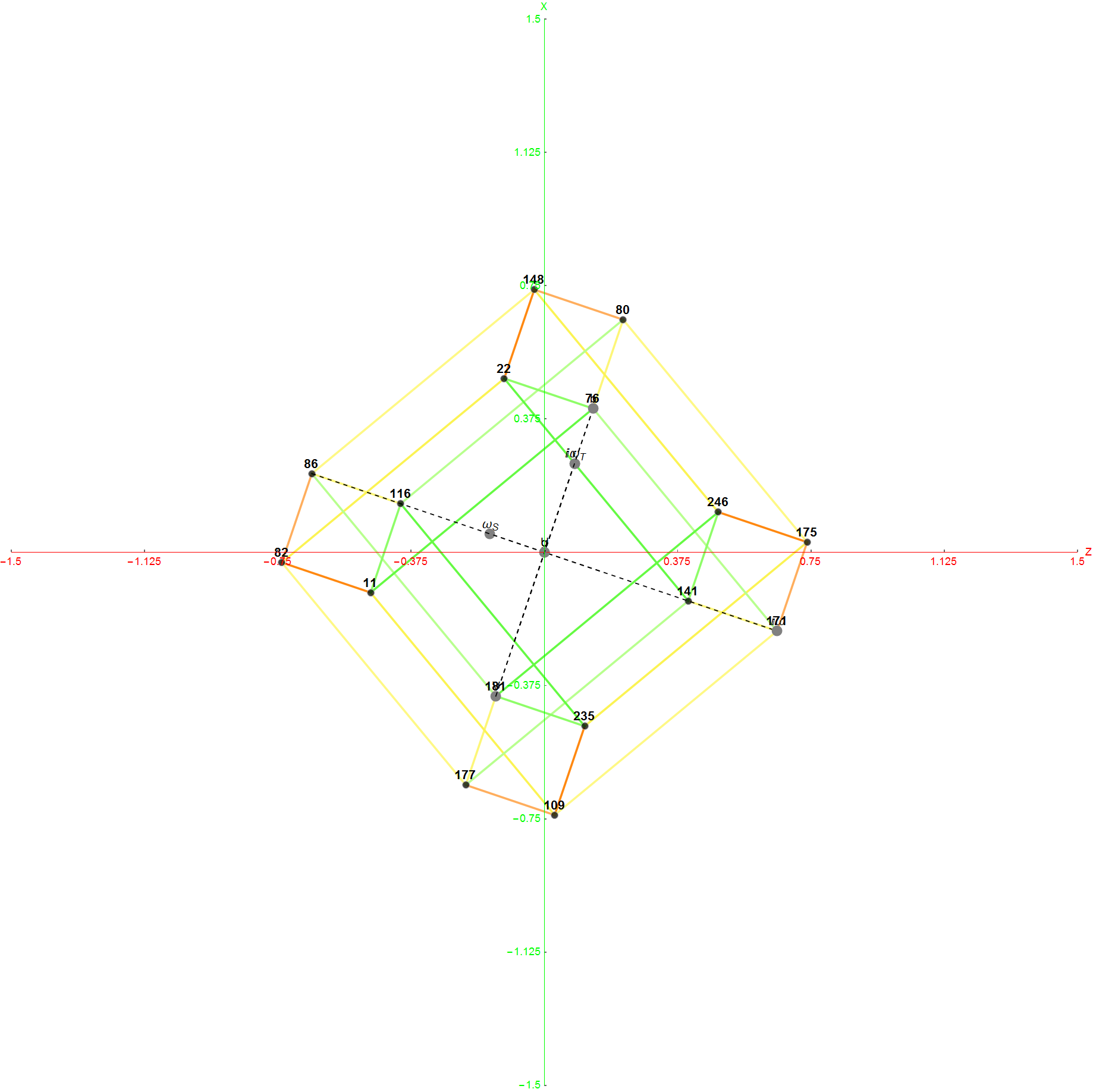
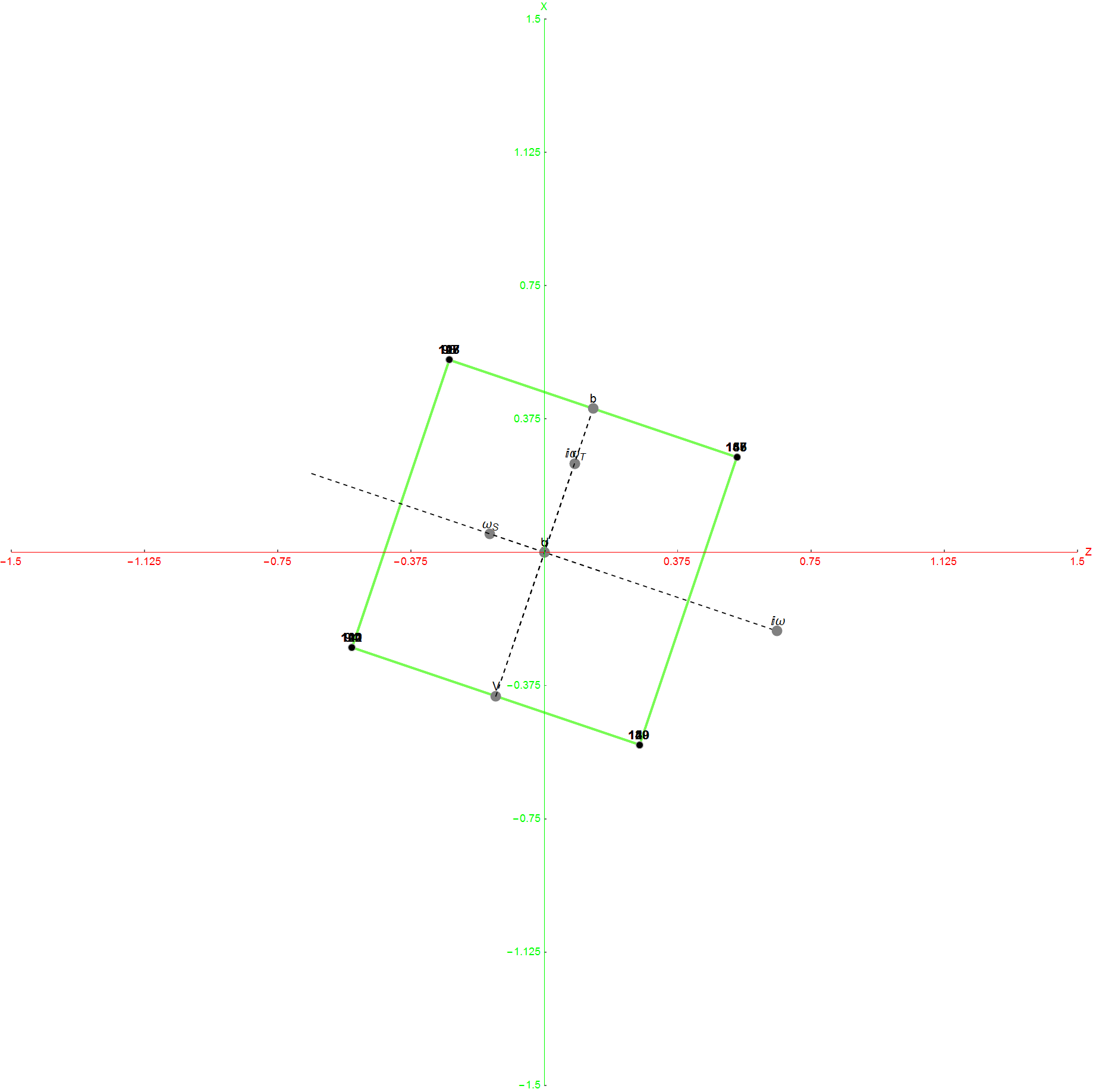
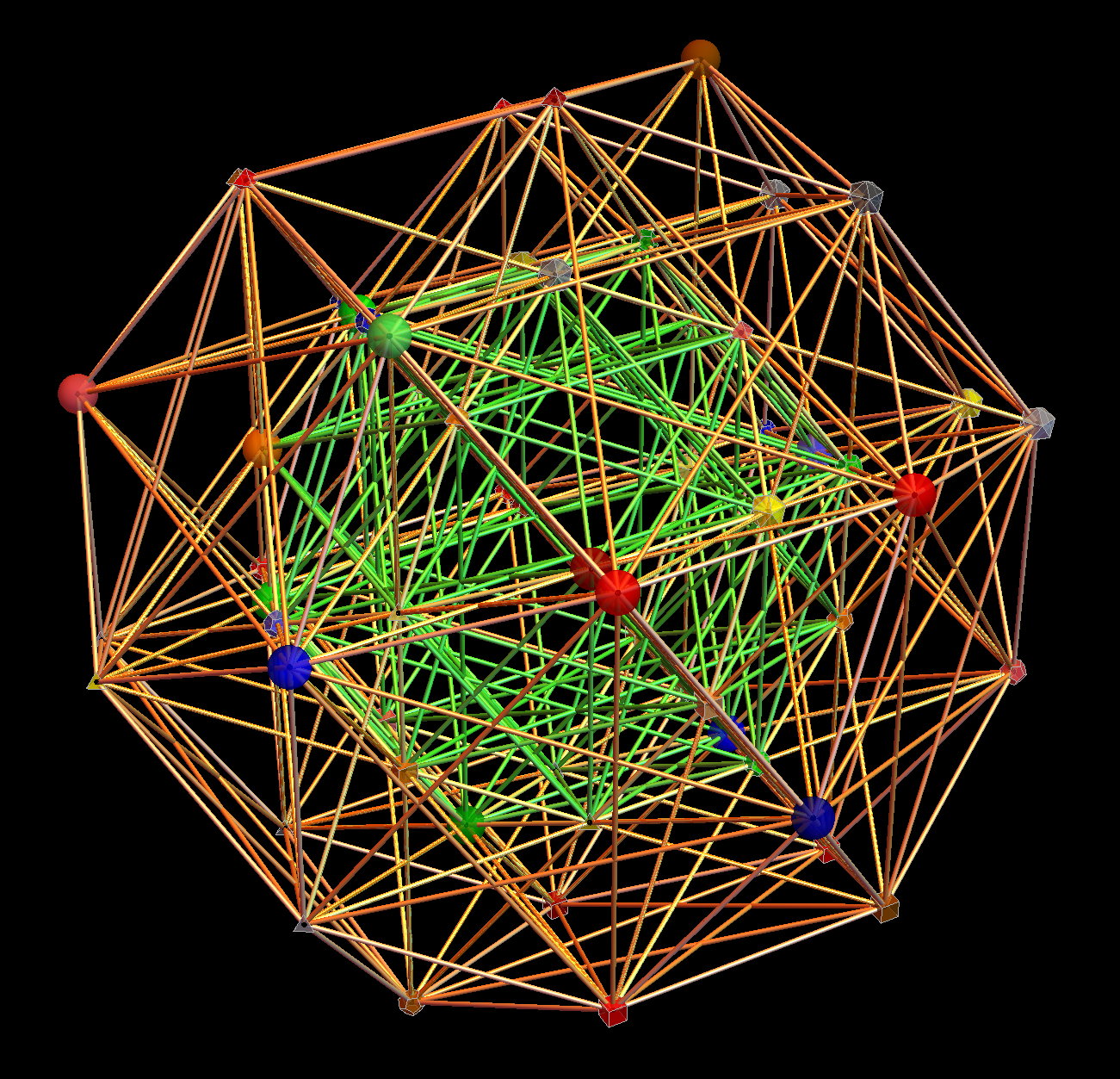
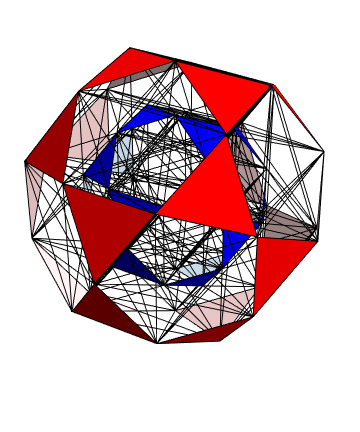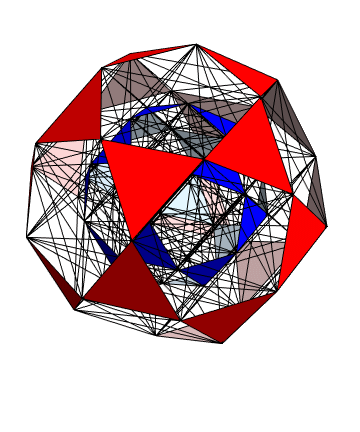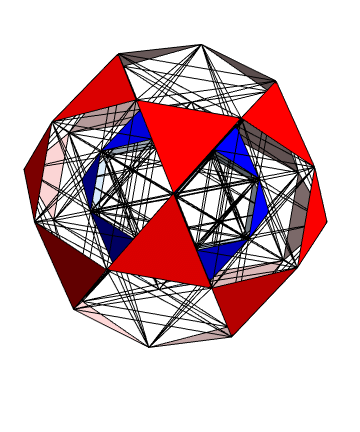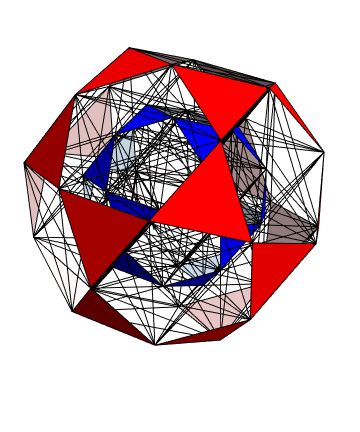
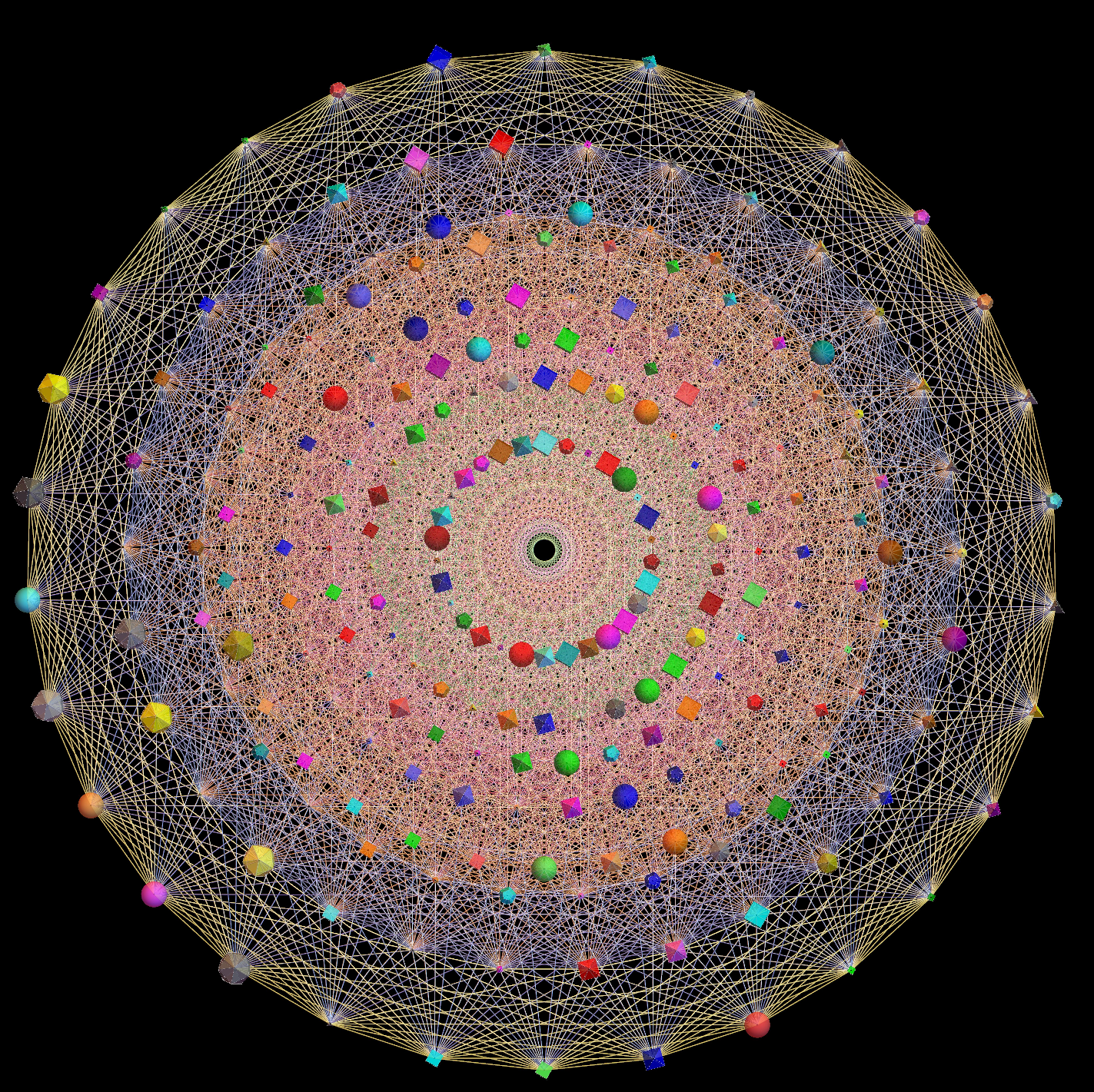
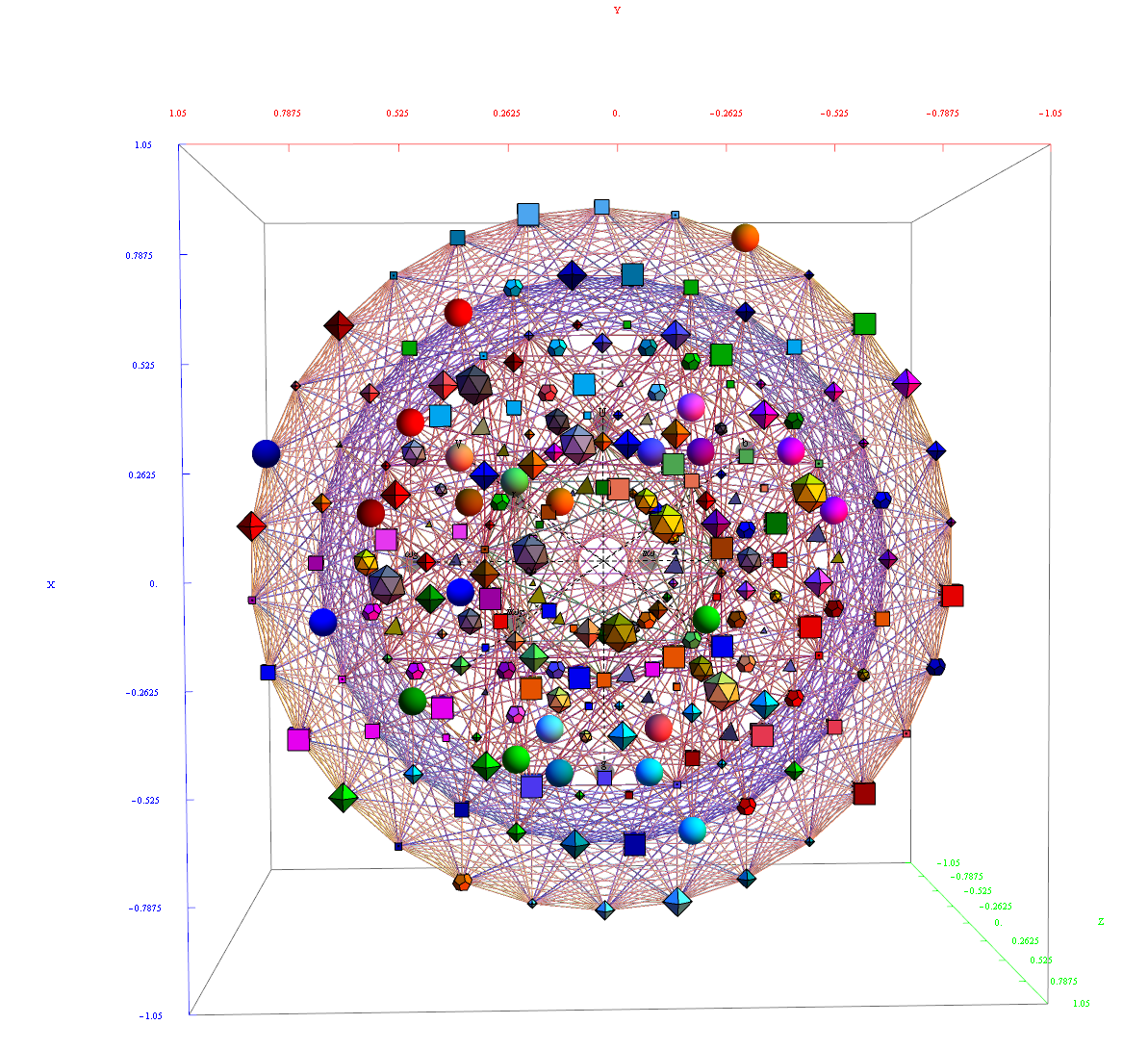
The Boerdijk–Coxeter helix is a 4D helix (of 3D tetrahedral cells) that makes up the vertices on 4 of the concentric rings of E8 Petrie projection (or the H4 and H4φ rings of the 2 600 cells in E8).
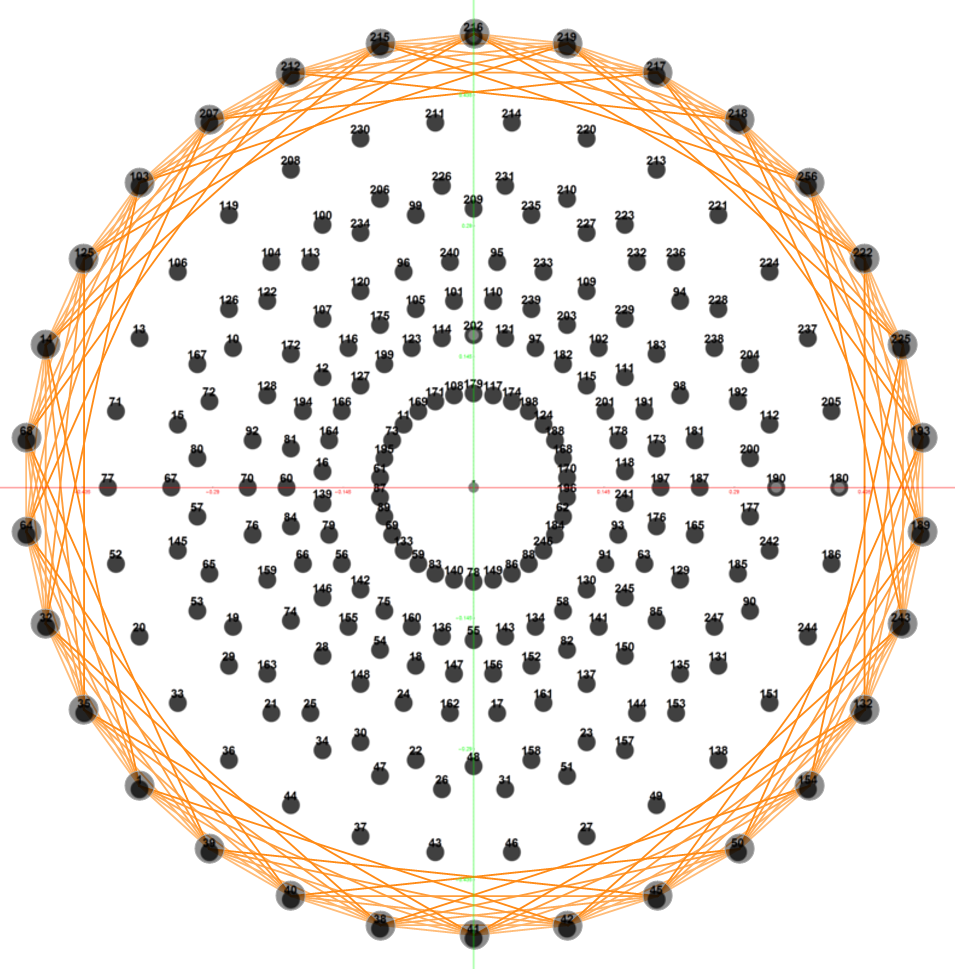
Outer (Ring 4) of H4 in 2D with non-physics vertices of all 8 rings of E8 in the background
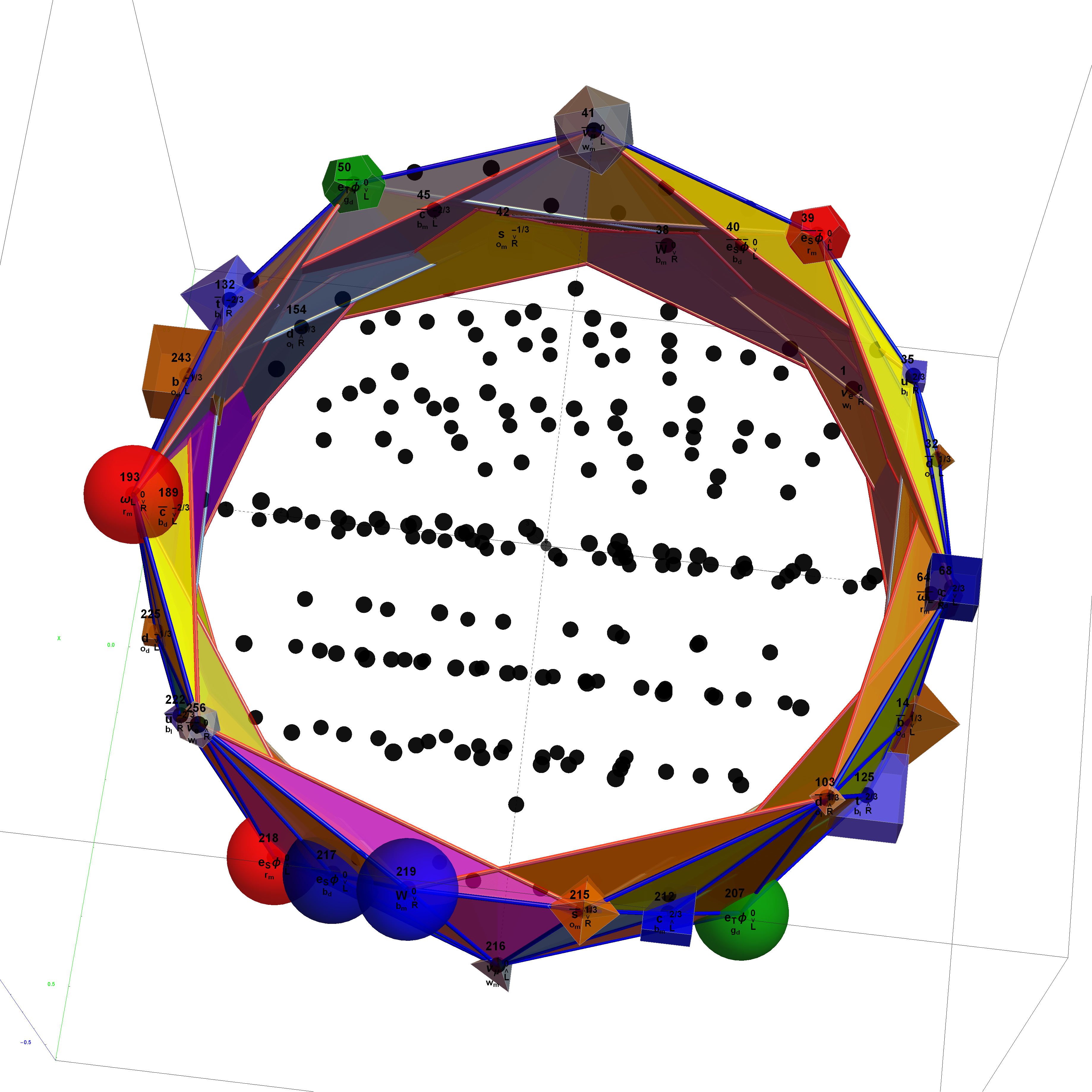
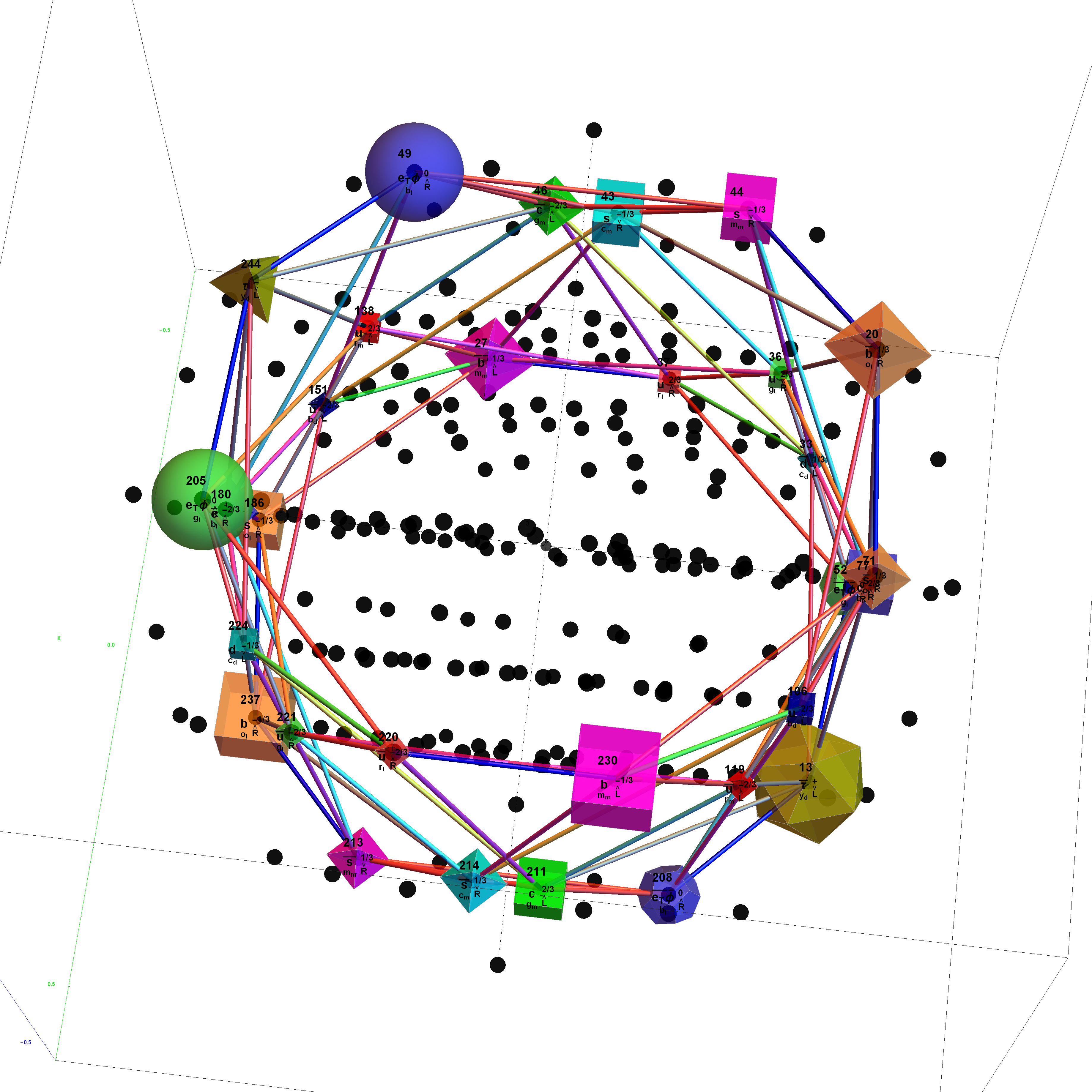
Outer (Ring 4) of H4 in 3D with physics vertices
Ring 3 of H4 in 3D with physics vertices
Ring 2 of H4 in 3D with physics vertices
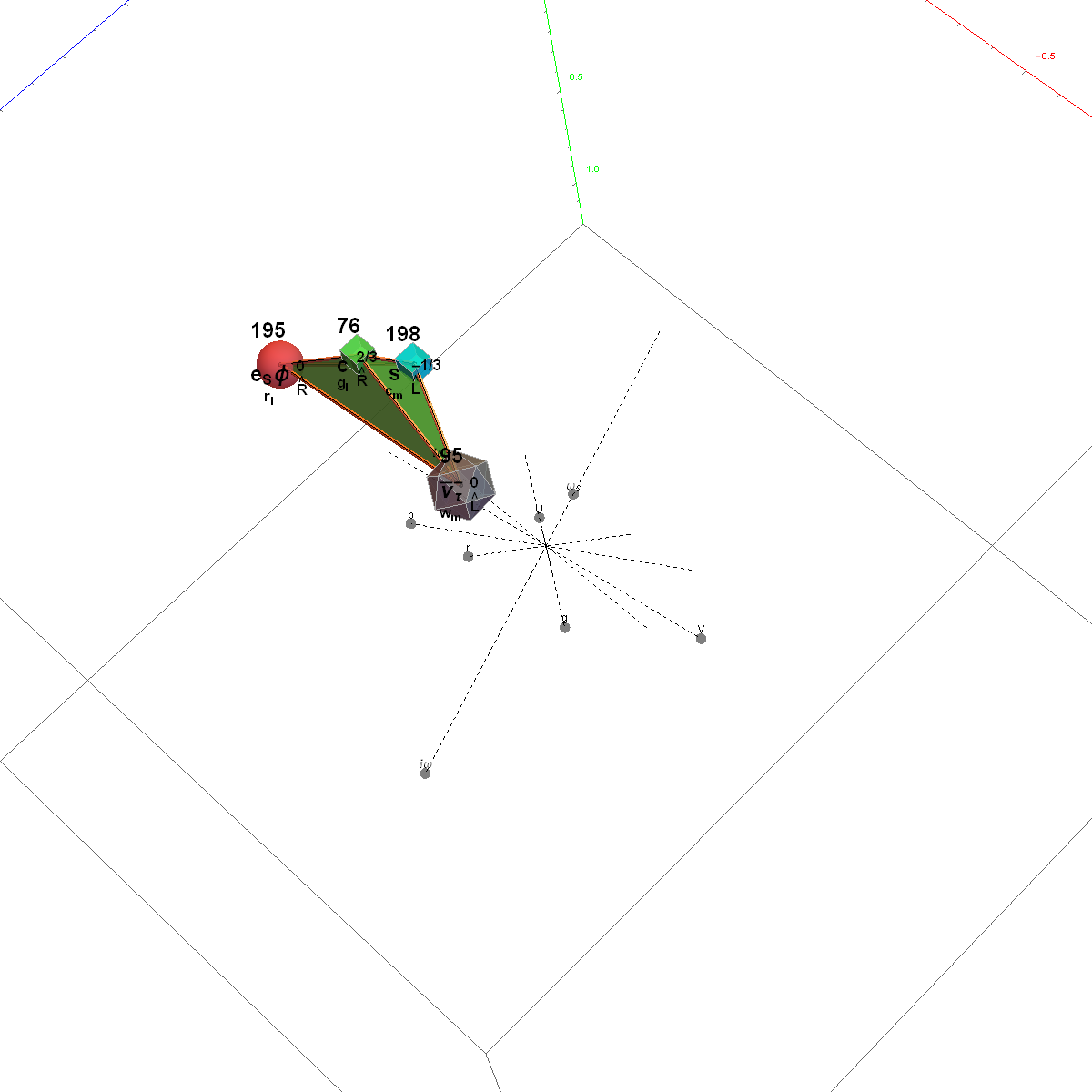
Inner (Ring 1) of H4φ in 3D with physics vertices
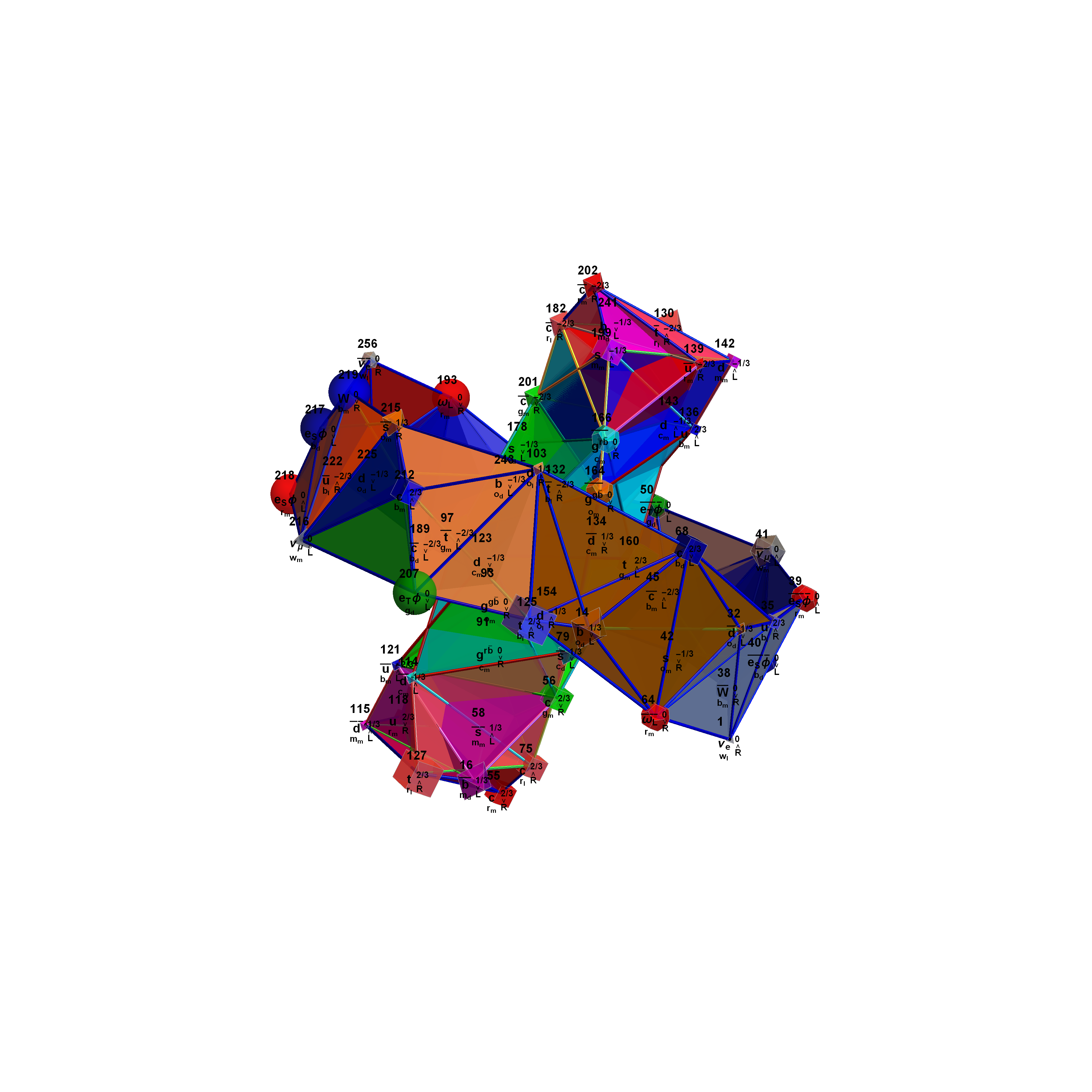
Combined 4 rings of H4 in 3D with physics vertices
Outer (Ring 4) of H4φ in 3D with physics vertices

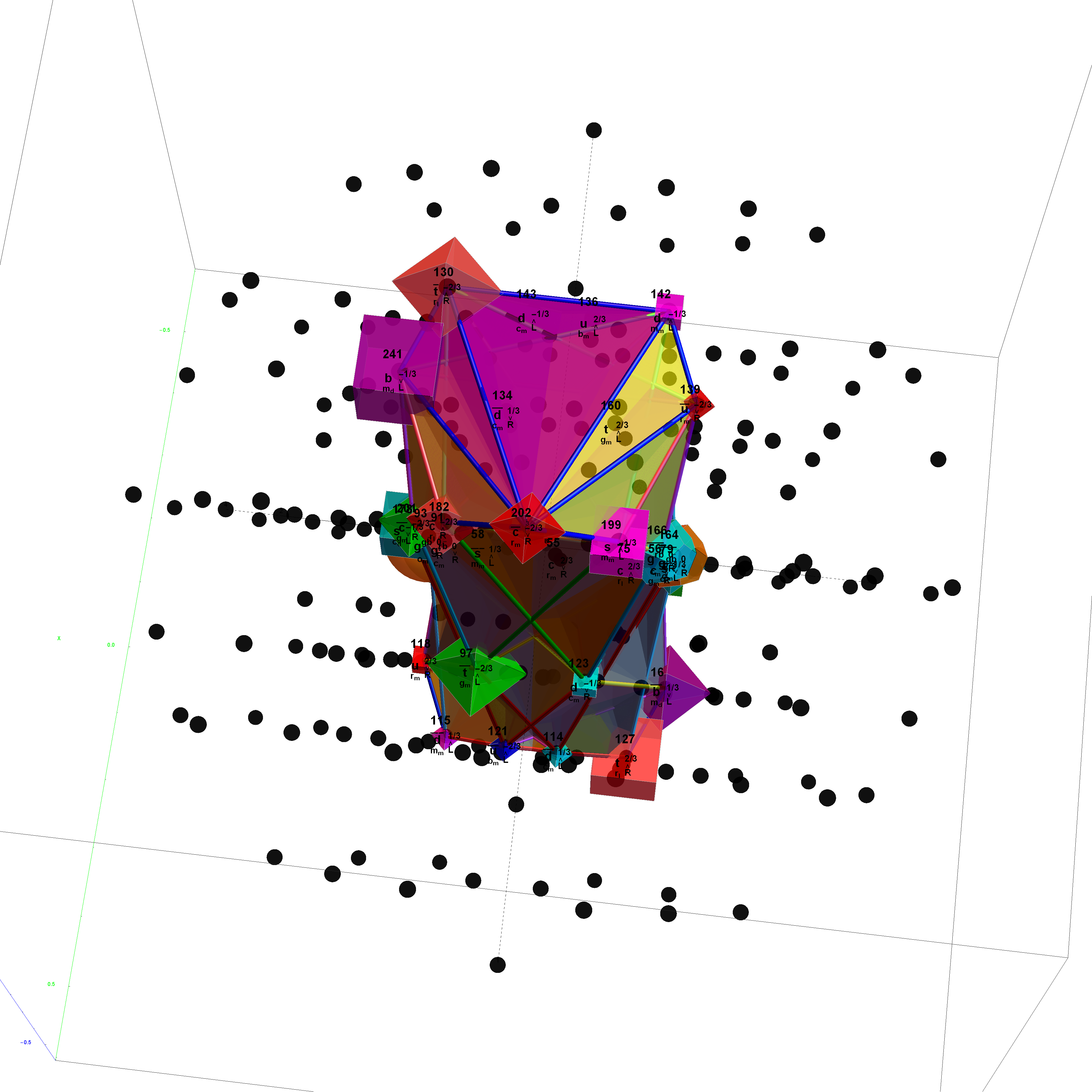
Ring 3 of H4φ in 3D with physics vertices
Ring 2 of H4φ in 3D with physics vertices
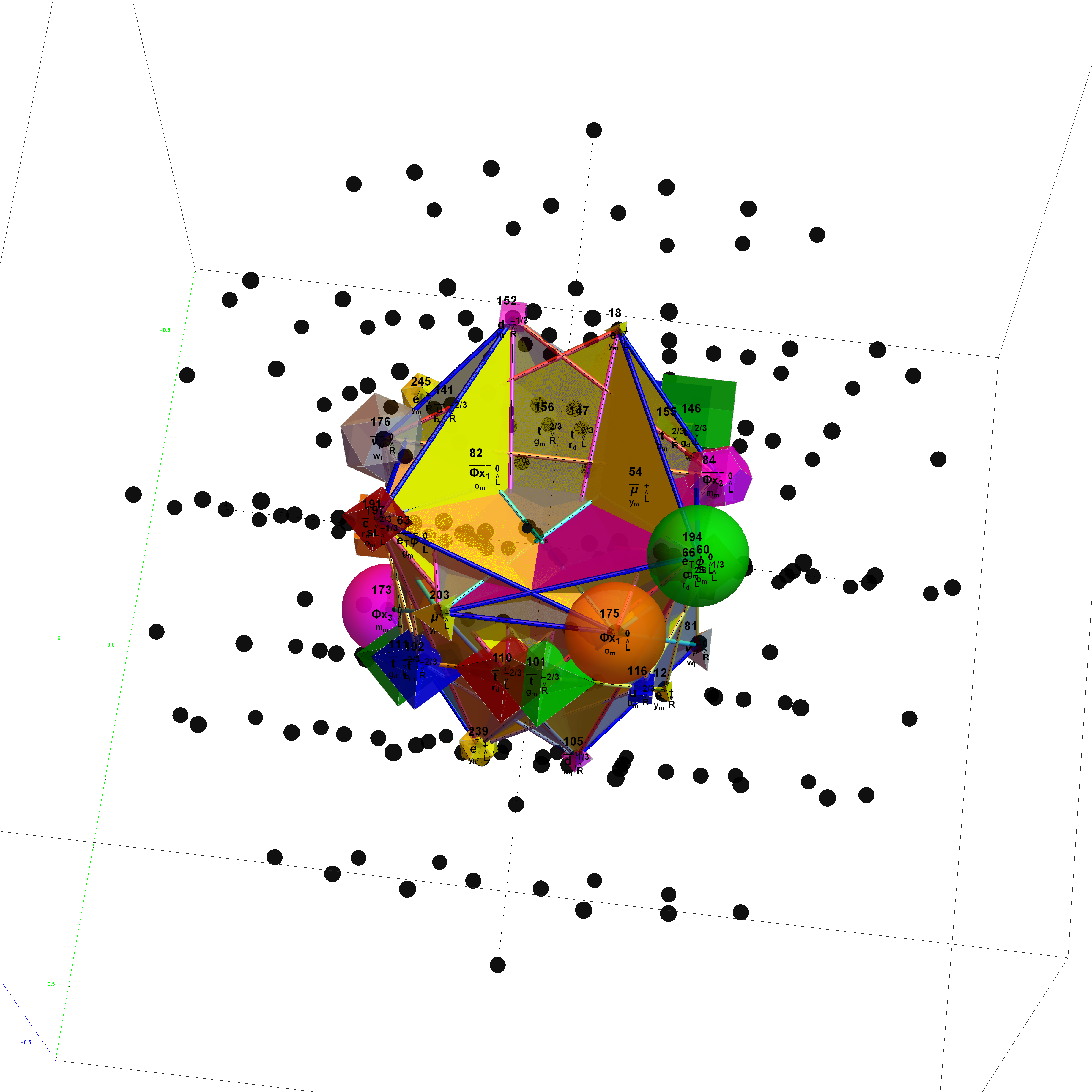
Inner (Ring 1) of H4φ in 3D with physics vertices
Combined 4 rings of H4φ in 3D with physics vertices
Combined 8 rings in 3D with physics vertices